Near-Critical Fluctuations and Cytoskeleton-Assisted Phase Separation Lead to Subdiffusion in Cell Membranes

Abstract

We address the relationship between membrane microheterogeneity and anomalous subdiffusion in cell membranes by carrying out Monte Carlo simulations of two-component lipid membranes. We find that near-critical fluctuations in the membrane lead to transient subdiffusion, while membrane-cytoskeleton interaction strongly affects phase separation, enhances subdiffusion, and eventually leads to hop diffusion of lipids. Thus, we present a minimum realistic model for membrane rafts showing the features of both microscopic phase separation and subdiffusion.

Introduction

Anomalous subdiffusion in cell membranes is an intriguing phenomenon whose molecular origins are still a subject of debate (1–3). From the general viewpoint, the phenomenon is related to (dynamic) microheterogeneities in the properties of the cell membrane by creating a rugged energy landscape for the diffusing protein or lipid molecule. The current understanding of membrane microdomains embraces the concepts of lipid rafts (4) and cytoskeleton-based picket fence (5). The general concept of membrane rafts (6) implies a dynamic interplay between the membrane local composition and phase, and local membrane-protein interactions, which can result in local lipid demixing and phase separation. This view is supported by the recent experimental evidence demonstrating that local lipid demixing and phase separation can be induced by crosslinking (7), change in the local membrane curvature (8), and interaction with a cytoskeleton (9). Additionally, the presence of the membrane-associated actin network leads to a shift in the membrane phase transition temperature and, potentially, to broadening of the phase transition (9).

The efficiency of external perturbations in changing the local properties of the membrane should be strongly enhanced in the vicinity of the membrane critical point. This is indeed supported by recent experimental observations (10). Moreover, it was suggested that dynamic microdomains in the cell membrane are nothing but near-critical fluctuations in the local composition and phase of the membrane (11). All this is in agreement with the observation that the composition of the cell membrane is adjusted to keep it above the phase transition temperature, and is regulated in response to environmental changes to maintain this condition (12). In cases where this mechanism fails, cold shock damage takes place (13).

In this article, we address the relationship between membrane microheterogeneity and anomalous subdiffusion in cell membranes by carrying out Monte Carlo simulations of two-component lipid membranes on experimentally relevant spatial scales (∼1 μm) and time intervals (∼1 s), with a special emphasis on interactions with the model membrane skeleton.

We demonstrate that:

• 1.Near-critical fluctuations in a free lipid membrane can lead to transient anomalous subdiffusion.
• 2.Phase separation in two-component (and, hence, multicomponent) lipid membranes can be strongly affected by interaction with the membrane skeleton, which, depending on the temperature and membrane composition, can either lead to precipitation of highly dynamic membrane domains (rafts), or prevent large-scale phase separation.
• 3.Interaction with the membrane skeleton enhances anomalous subdiffusion and eventually leads to hop-diffusion of lipids. Thus, we construct a minimum realistic model for membrane rafts showing the features of both microscopic phase separation and anomalous subdiffusion.

The binary lipid system consisting of DMPC (1,2-dimyristoyl-sn-glycero-3-phosphocholine) and DSPC (1,2-distearoyl-sn-glycero-3-phosphocholine) is chosen as a generic model of a two-component membrane. The particular choice of this system is motivated by the fact that it is well studied both in vitro (14–21) and in silico (see (20–22) and references therein). Even though the exact temperature range of phase separation in this membrane is too high for most living organisms, the main qualitative conclusions of the study related to behavior of cell membranes are not affected by the particular thermodynamic parameters of the lipid mixture.

From the physical perspective, it is assumed that living organisms try to maintain the composition of cell membranes to keep them above the phase transition temperature (12). Therefore, to be biologically relevant, in this article we mostly focus on the upper part of the phase diagram.

Materials and Methods

Experimental

The saturated phospholipids DMPC and DSPC with the melting temperatures 297 and 328 K were purchased from Avanti Polar Lipids (Alabaster, AL). Multilamellar vesicle suspensions were obtained by rehydration of a dry lipid film. Excess heat capacity curves of DMPC/DSPC multilamellar vesicle suspensions in a 10 mM HEPES buffer, pH 7.4, were obtained using a VP-DSC calorimeter (MicroCal, Northampton, MA) at a scan rate of 2–3 K/h.

The empirical phase diagram based on the temperatures of the onset and completion of the phase transition determined from the scanning calorimetry data as described in Sugár et al. (20) and Hac et al. (21) are in agreement with previously reported results (see the Supporting Material).

Monte Carlo simulations

Our approach to lattice-based Monte Carlo (MC) simulations of a two-component membrane is generally similar to the one described previously (20,21). To facilitate efficient simulations on experimentally relevant spatial scales (∼1 μm) and time intervals (∼1 s), where a particular type of lipid packing and fine molecular details should be of little importance, we further simplified the model and represented the membrane as a square lattice, each node of which represents a molecule of one of the two lipid types, which can be in either gel or fluid conformational state.

An elementary MC step consists of two substeps:

• 1.An attempt to change the state of a randomly chosen lipid and
• 2.An attempt of position exchange of a randomly chosen next-neighbor pair of lipids.

As in Hac et al. (21), a rate function was introduced for the next-neighbor exchange step to ensure ∼40 times slower lipid diffusion in the gel phase. For an L × L lattice, an MC cycle consists of a chain of L² elementary MC steps. For every lipid composition and temperature studied, the membrane was first equilibrated, if required, and simulations were run for (6 – 20) × 10⁶ MC cycles to collect the necessary data. More details on the simulation procedure are given in the Supporting Material.

Simulations were carried out on an L × L = 600 × 600 (400 × 400 when modeling the effects of the membrane skeleton) square lattice with periodic boundary conditions. By assuming the average lipid headgroup size of 0.8 nm, this corresponds to a membrane with an experimentally relevant size of 0.48 × 0.48 μm² (0.32 × 0.32 μm²). By comparing the DMPC diffusion coefficient obtained in our simulations of pure DMPC in the fluid phase at 304 K with its experimental values at the same temperature (3–6 μm²/s (23–25)), we found that one MC cycle corresponds to ∼50 ns, and thus, our simulations cover processes on timescales up to ∼0.3–1 s.

Model for the membrane skeleton

The membrane skeleton was modeled by a random Voronoi tessellation satisfying the periodic boundary conditions. For simulations with L = 400, random tessellations with N = 36 compartments were used, which gives the average linear size of the compartment $\ell =L{N}^{-1/2}=66.6\text{lattice}\text{units}\approx 53\text{nm}.$ The generated filament meshwork was projected onto the square lattice, thereby creating a set of pixels representing the locations of the filaments. Each of these locations can be assigned to be a cytoskeleton pinning site. To mimic the membrane-cortical skeleton interaction, a simple rule inspired by experimental data on lipid interactions with transmembrane proteins (26) was followed: a lipid located at a filament pinning site is forced to assume the gel conformation with no explicit restrictions on its mobility. Thus, the pinning site does not present an obstacle for lipid diffusion: its effect on diffusion is indirect and takes place solely due to a lower lipid mobility in the gel-state local environment. The effect of the varying strength of the membrane-skeleton interaction was modeled by randomly assigning a fraction of filament position pixels to be filament pinning sites. Simulations were carried out with the filament pinning density set to 25%, 50%, and 100%; in these cases the total number of pinning sites amounted to ∼1%, 2%, and 4% of the total membrane area.

Our choice of immobile pinning sites is justified by experimental observations demonstrating that band 3 and ankyrin strongly bound to the membrane skeleton show a very low diffusion coefficient of ∼10⁻⁴–10⁻³ μm²/s over time intervals up to tens of seconds (27,28).

It should be pointed out that the approach used in this work to account for interactions of lipid molecules with membrane proteins is conceptually similar, though not identical, to the one used in several previous MC simulation-based studies (29–32). In these works, it was assumed that proteins, preferentially wetted by one of the membrane phases, could freely diffuse in the membrane, which results in their accumulation in this phase and, in the case of two-component membranes, in fact enhances large-scale phase separation. (The situation is more complicated in the case of active proteins; for details, see (32) and references therein.) It was found out that, under certain conditions, interaction of a single-component membrane with small transmembrane proteins or peptides can even lead to emergence of a closed loop of gel-fluid coexistence with a lower critical point (33). It should be pointed out, however, that these works focused only on structural properties of protein-loaded membranes, and did not address the issues of diffusion in the membrane.

What sets this work apart from the above-mentioned studies, is that here we consider interaction of the membrane with the immobile cytoskeleton and study its effects on phase separation and diffusion of lipids in the membrane.

Analysis of lipid diffusion data

Positions of a small fraction of lipid molecules (150 for simulations with L = 600 and 50 for simulations with L = 400, which amounted to 0.04% and 0.03%, respectively) were recorded, and the time- and ensemble-averaged mean-square displacement (MSD) was determined as

$$MSD\left(\tau \right)=\frac{1}{t_{\max }-\tau }\sum _{t=1}^{t_{\max }-\tau }\left\{{\left[x\left(t\right)-x\left(t+\tau \right)\right]}^2+{\left[y\left(t\right)-y\left(t+\tau \right)\right]}^2\right\},$$ (1)

where τ, t, and t_max are times measured in units of MC cycles; here, τ denotes the time lag, and t_max is the total length of the lipid molecule trajectory. No difference between time- and ensemble-averaged MSD (Eq. 1) and time-only- and ensemble-only-averaged MSDs beyond the statistical error level was observed.

In the case of normal diffusion, the MSD grows in a linear fashion with time: $MSD\left(\tau \right)=4D\tau$ in two dimensions, where D is the translational diffusion coefficient. In the case of anomalous subdiffusion, the MSD shows a slower sublinear power-law growth $MSD\left(\tau \right)\sim {\tau }^{\beta }\text{with}0<\beta <1$ (see, e.g., (34)). An alternative description of diffusion showing deviations from the normal behavior (also in cases where it cannot be described in terms of subdiffusion) can be provided using an effective time-dependent diffusion coefficient D(τ).

Therefore, to characterize the behavior of the MSD curves, the local exponent of the mean-square displacement

$${\beta }_{\text{M}\text{S}\text{D}}\left(\tau \right)=d\log MSD\left(\tau \right)/d\log \tau$$ (2)

and the effective time-dependent diffusion coefficient

$$D\left(\tau \right)=\frac{1}{4}dMSD\left(\tau \right)/d\tau$$ (3)

were calculated.

Simulation of FCS experiments

To simulate fluorescence correlation spectroscopy (FCS) (35) measurements, the tracked particles (as above, in the amount of 150 for simulations with L = 600 and 50 for simulations with L = 400) were assumed to be fluorescent. Fluorescence intensity fluctuations $\delta F\left(t\right)=F\left(t\right)-\langle F\rangle$ about the mean intensity 〈F〉 in a two-dimensional Gaussian detection spot $\exp \left(-2r^2/r_0^2\right)$ were recorded, and their autocorrelation function $G\left(\tau \right)=\langle \delta F\left(t\right)\delta F\left(t+\tau \right)\rangle /{\langle F\rangle }^2$ was calculated. The detection spot size was set to r₀ = 31 lattice units ≈ 25 nm, the size experimentally achievable using the stimulated emission depletion (STED) FCS technique (36). We additionally note that this detection spot is much smaller than the lattice size (r₀/L ≈ 0.05 for L = 600 and r₀/L ≈ 0.08 for L = 400), which allowed us to avoid artifacts in the fluorescence autocorrelation function and additionally ensured that our simulations are experimentally relevant.

FCS curves were averaged over nine different positions on the lattice; when studying the effects of the membrane skeleton, the results were additionally averaged over five random realizations of the filament network.

Simulated FCS curves were analyzed using the model

$$G\left(\tau \right)=G\left(0\right)/\left[1+{\left(\tau /{\tau }_{\text{D}}\right)}^{{\beta }_{\text{F}\text{C}\text{S}}}\right].$$ (4)

For β_FCS = 1, this expression corresponds to normal diffusion, while for 0 < β_FCS < 1 it provides a simple way to describe anomalous subdiffusion in FCS (35). In the case of normal diffusion, τ_D is related to the diffusion coefficient of fluorescent particles D and detection spot size r₀: ${\tau }_{\text{D}}=r_0^2/\left(4D\right).$

Note that since FCS is sensitive not only to the MSD(τ), but also to the higher moments of the distribution of displacements of a diffusing particle, the connection between G(τ) and MSD(τ) is straightforward only in the case of a Gaussian distribution of displacements (35). As a result, in the case of anomalous diffusion of particles, generally β_FCS ≠ β_MSD.

Results and Discussion

Phase and component separation in the membrane

With appropriate tuning of lipid interaction parameters, the empirical heat capacity-based phase diagram obtained from our MC simulation is in agreement with our experimental data (Fig. 1), as well as with previously published experimental and simulation data on the same lipid system (see Supporting Material). At the same time, the empirical phase diagram constructed on the basis of heat capacity data may differ from the real phase diagram of the system and thus not provide an insight into the microscopic structure and the dynamics of the membrane.

Figure 1.

(Left-hand panel) Component and lipid state separation phase diagram of DMPC/DSPC lipid mixtures. Phase transition temperatures as determined from experimental (Δ) and simulated (○) excess heat capacity curves. Lipid state spinodal (- - -), lipid state binodal (– – –), and lipid demixing curves (—). (Right-hand panel) Representative snapshots of equilibrium membrane configurations at temperatures and membrane compositions corresponding to solid squares in the left-hand panel. Lattice size: 600 × 600; scale bar: 200 lattice units ≈ 160 nm.

More details on the phase diagram can be obtained based on binodal and spinodal curves of the system. The binodal curves, also known as coexistence curves, are the boundaries of the region in the phase diagram in which the equilibrated system shows a complete separation of the two phases. The spinodal encloses the region where the mixture is unstable with respect to small local fluctuations of the composition and always lies inside the area enclosed by the binodal, with the exception of a critical point, where the binodal and spinodal touch.

To reconstruct the binodals and spinodals of the DMPC/DSPC lipid mixture, we analyzed the static structure factors (37) for lipids S_L(k) and lipid states S_S(k) (see the Supporting Material), reflecting the character of spatial fluctuations of the membrane composition and state.

We found that outside the phase coexistence region, the Ornstein-Zernike (OZ) approximation (37) $S^{\text{OZ}}\left(k\right)=S\left(0\right)/\left[1+{\left(k\xi \right)}^2\right],$ where k is a wavenumber, and ξ is a correlation length, provided an excellent description of the lipid-state structure factors S_S(k). The temperature dependences of S_S(0) and ξ_S were used to estimate spinodal and binodal curves. In particular, the spinodals were determined by extrapolating 1/S_S(0) dependence to zero crossing (37,38), and binodals were determined from the condition d(1/ξ_S)/dT = 0 (38). Interestingly, in some regions of the phase diagram, the binodal deviates quite strongly from the phase coexistence boundary estimated from the excess heat capacity data (Fig. 1). This discrepancy indeed shows that the analysis of heat capacity data does not necessarily recover the real phase diagram of the system. Here, this behavior reflects the continuous character of the phase transition in the membrane, whose proper description requires a combined component and state phase diagram (39).

What process is reflected by the excess heat capacity curves where they fail to describe the fluid-gel phase separation?

An analysis of the structure factors S_L(k) for the lipid species helps to answer this question. It appears that, generally, two OZ components are required to describe these data: $S_{\text{L}}\left(k\right)=S_{\text{L}1}^{\text{OZ}}\left(k\right)+S_{\text{L}2}^{\text{OZ}}\left(k\right).$ Parameters of component 1 only weakly depend on the temperature and reflect demixing of lipids in the same state. Parameters of the second component S_L2(0) and ξ_L2 show strong temperature dependences similar to those of S_S(0) and ξ_S, and thus describe appearance of dynamic microscopic domains, which cannot be treated as distinct thermodynamically stable phases (22). We therefore define the lipid demixing curves as a set of points on the phase diagram satisfying the condition S_L1(0) = S_L2(0).

The fact that the lipid demixing curves are in excellent agreement with the calorimetry-based empirical phase diagrams supports the above reasoning, as do the snapshots presented in Fig. 1. Note that in this region the membrane undergoes near-critical fluctuations. On the other hand, in the coexistence region, equilibrated membranes show complete phase separation and form large-scale lipid domains (Fig. 1).

The above analysis of the structure factors S_L(k) and S_S(k) and equilibrated membrane snapshots shows that in the part of the phase diagram where the lipid-demixing curve closely approximates the binodal, the phase transition from the fluid state to the fluid-gel coexistence has a quasiabrupt character. On the other hand, in the region where the lipid demixing curve strongly deviates from the binodal, the membrane shows characteristic near-critical fluctuations (Fig. 1), and the transition becomes continuous as the system approaches the critical point ($\text{DMPC}/\text{DSPC}\approx 20:80,$ $T_{\text{c}}=320.5\pm 0.2\text{K}$—see (40) for details).

Remarkably, this behavior is qualitatively similar to recent experimental observations on three-component lipid membranes (11): depending on the membrane composition, the transition to the two-phase coexistence takes place either in an abrupt manner—when the membrane does not pass through a critical point, or via critical fluctuations—when the membrane does pass through a critical point. A more detailed consideration of the phase diagram of the DMPC/DSPC system based on MC simulations will be published elsewhere (40).

In the fluid-gel phase coexistence region, large-scale phase separation takes place. Since no explicit or implicit penalties are imposed (41–43) on the domain size in our model, and domain growth is driven by minimization of the line tension energy, phase separation results in formation of a single circular-shaped domain of the minority phase (Fig. 1).

Effect of the cytoskeleton on phase separation in the membrane

In the region of near-critical fluctuations, the membrane is expected to be very sensitive to external perturbations, including the interaction with the membrane skeleton. It appears that in the vicinity of the critical point, the interaction with the membrane skeleton leads to immediate condensation of the gel phase on the skeleton filaments, and formation of membrane domains, in a good agreement with results of experiments on lipid bilayers with a reconstituted actin skeleton (9). These domains dynamically change their shape, but nevertheless stay pinned to the filaments (Fig. 2). Note that the effect of the filaments is remarkably robust with respect to the filament pinning density. We strongly believe that these domains represent the minimal model of membrane rafts (6). The minimum character of this model stems from the fact that, in the present scenario, domain formation is thermodynamically driven and does not require any active processes like chemical cross-linking of membrane components or lipid recycling.

Figure 2.

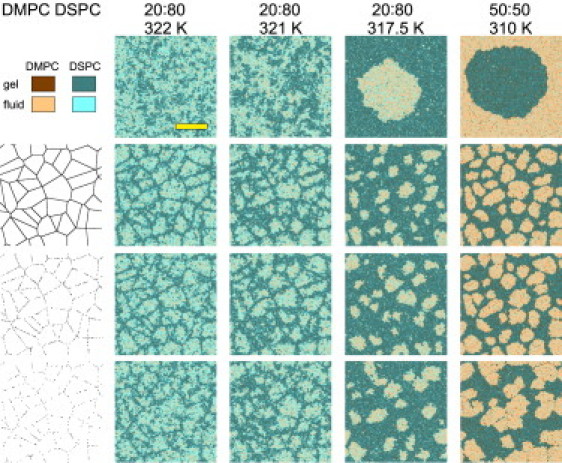
Effect of the membrane skeleton on the phase separation in a DMPC/DSPC membrane. Representative snapshots of membrane configurations are shown for the free membrane (first row), and membrane interacting with a network of filaments at 100% (second row), 50% (third row), and 25% pinning density (fourth row). Snapshots for the free membrane, as well as for the membrane interacting with filaments at T = 321 and 322 K, represent fully equilibrated configurations; snapshots for the membrane interacting with filaments at T = 310 and 317.5 K correspond to equilibration time of 6 × 10⁶ MC cycles (see text for discussion). For presentation purposes, the filaments are drawn thicker than they are in reality. Lattice size: 400 × 400; scale bar: 125 lattice units ≈ 100 nm.

If the membrane is abruptly cooled down from the all-fluid state to a temperature in the fluid-gel coexistence region of the phase diagram, phase separation takes place, and domains of the fluid and gel phase start to nucleate and coarsen with time. In a free membrane, domains grow according to the power law $R\left(t\right)\sim t^n$ with the growth exponent n depending on the particular domain growth mechanism (44). In our simulations for a free membrane, depending on the lipid composition and temperature, n takes values from 1/4 to 1/3 (Fig. 3), consistent with general expectations for the domain growth in two dimensions (44) and in agreement with experimental results (see, e.g., (45); for a more detailed discussion, see (40)).

Figure 3.

Effect of the membrane skeleton on the domain growth in DMPC/DSPC 50:50 membrane abruptly cooled from the all-fluid state down to T = 310 K in the fluid-gel phase coexistence region. Kinetics of domain growth when the membrane is free (upper curve) and in the presence of membrane skeleton with the filaments pinning density of 50% (lower curve). (Solid line) Power law dependence R(t) ∼ tⁿ, with n = 0.32; (dashed line) stage of the slow logarithmic growth R(t) ∼ ln t in the presence of membrane skeleton. Representative membrane configurations obtained in our MC simulations at time instants 10⁴, 10⁵, and 10⁶ MC cycles are shown at the corresponding curves. Lattice size: 400 × 400.

In a finite-size system with a linear dimension L, domain coarsening eventually stops, and a single circular-shaped domain is produced (Fig. 1) with the radius $R_{\infty }\simeq {\left(X/\pi \right)}^{1/2}L,$ where 0 < X < 1/2 is the fraction of the minority phase.

Remarkably, we found that the presence of the membrane skeleton strongly inhibits or even eventually prevents large-scale phase separation in the phase coexistence region (Fig. 2). As a result, the radius of the membrane domains in this case is largely determined by the characteristic compartment radius $R_{\text{comp}}\simeq \ell /2$ of the filament network. The way we account for interaction of lipid molecules with filaments at their pinning sites is similar to a theoretical model (the random-field Ising model (46)) implying the presence of static random position-dependent perturbations in a two-dimensional system of spins. This model predicts that the initial power-law domain growth R(t) ∼ tⁿ is strongly slowed down at intermediate stages, and crosses over to an extremely slow logarithmic growth R(t) ∼ log t; eventually the domains are expected to reach the perturbation strength-dependent maximum size R′ < R_∞ in an exponential time to create an equilibrium disordered state (47,48). In our system, the perturbation strength is determined by the filament pinning density and the average compartment radius R_comp. Therefore, if the interaction of the membrane with the cytoskeleton is strong enough, and $R_{\infty }^2\gg R_{\text{comp}}^2,$ one can expect that the domain growth stops when domains reach the characteristic size $R_{\text{comp}}\lesssim R^{\prime }<R_{\infty }.$

We indeed observed an extreme slowing down of the domain growth in the presence of the membrane skeleton and crossover to the slow logarithmic growth (Fig. 3). As is evident from the figure, at the end of a simulation run of 6 × 10⁶ MC cycles, the domain sizes are indeed R(t) ∼ R_comp. Although some growth is still observed at this stage, it is so slow, that at present it is unclear whether the system will evolve toward a equilibrium disordered state featuring a number of small domains, as suggested elsewhere (47, 48), or the slow logarithmic growth will continue further to produce eventually (after an extremely long time) a single domain with the size R_∞. What is clear, though, is that the time required for complete equilibration is so long, that from the practical viewpoint one can state that indeed the presence of the membrane skeleton prevents large-scale phase separation in the membrane. This becomes especially clear if one takes into account that a membrane in a live cell is not in the equilibrium state, and a number of other processes affecting the membrane state and composition, e.g., lipid recycling, take place in parallel on different spatial- and timescales.

Thus, the cytoskeleton-induced inhibition of large-scale phase separation can serve as one of the possible explanations why micrometer-scale membrane domains are observed in giant plasma membrane vesicles (49), but not in cell membranes.

In addition, our observations suggest that the established cryoprotective role played by the cytoskeleton (50) may consist in delaying phase-separation-induced cold shock damage of living cells.

Diffusion of lipids in the free membrane

At higher temperatures, away from the phase transition and the near-critical fluctuations region, the membrane is in the homogeneous all-fluid state, and, not unexpectedly, lipid diffusion is normal (Fig. 4).

Figure 4.

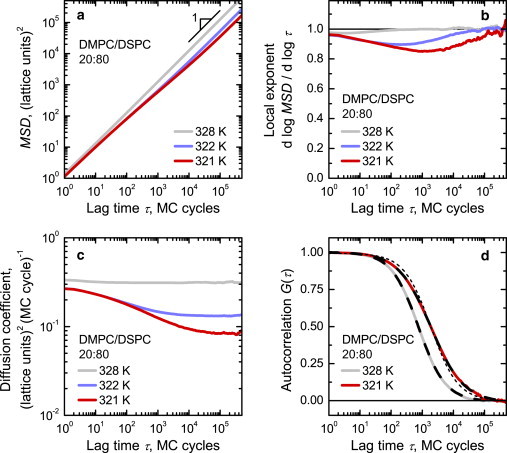
Effect of the proximity to the phase transition on diffusion of DMPC lipids in a DMPC/DSPC 20:80 membrane. Mean-square displacement MSD(τ) (a), local exponent β_MSD(τ) (b), time-dependent diffusion coefficient D(τ) (c), and FCS autocorrelation G(τ)/G(0) (d). (a–c) top to bottom: T = 328, 322, and 321 K. (d): T = 328 (left) and 321 K (right). For clarity, data for 322 K are omitted in (d). (d) additionally shows fits to the FCS diffusion model Eq. 4 giving β_FCS = 1.01 at 328 K and ${\beta }_{\text{FCS}}=0.86$ at 321 K (– – –). For comparison, a fit of 321 K data with fixed β_FCS = 1.0 is shown (- - -).

This picture changes upon approaching the critical point in the region of near-critical fluctuations where interpenetrating fluctuating domains form in the membrane. The analysis of the immediate environment of the DMPC and DSPC lipids shows that, while the DSPC lipid does not have a pronounced preference for the state of its local environment and therefore is evenly distributed between fluid and gel domains, the DMPC lipid shows a strong preference for the fluid local environment and is thus predominantly partitioned into fluid domains. Under these conditions, the DSPC lipid shows no significant deviation from the normal diffusion behavior (data not shown). By contrast, quite unexpectedly, the DMPC lipid was found to demonstrate very pronounced anomalous subdiffusion (Fig. 4).

At a first glance, this subdiffusive behavior is rather surprising, especially in the light of the seminal work by Kawasaki (51) demonstrating that the diffusion coefficient of a two-component mixture does not vanish upon approaching the critical point, which implies normal diffusion, at least in the long-time asymptotic regime. A closer look at the data shows, however, that the subdiffusive behavior is in fact transient, though it covers several orders of magnitude in time, and at longer times the crossover to the normal diffusion takes place. One can also notice that at very short time lags, diffusion is normal as well. This behavior is also evident from the plots of the local exponent β_MSD(τ) and effective time-dependent diffusion coefficient D(τ) extracted from the MSD(τ) dependences (Fig. 4, b and c).

How can this crossover from normal diffusion to a subdiffusive behavior, and back to normal diffusion at long times, be explained?

By recalling that the DMPC lipid is preferentially partitioned into fluid domains and having a look at the corresponding membrane snapshots (Fig. 1), we realize that DMPC molecules diffuse on a dynamically rearranging fractal-like fluid phase pattern. Therefore, at early times, when the DMPC molecule explores its immediate environment, normal diffusion should take place. Later, although at times shorter than a characteristic time of rearrangement of this dynamic fractal structure, the motion of DMPC lipid molecules is subdiffusive, similar to what is expected in the case of diffusion on fractal-like percolation clusters (52). At much longer times, evolution of these clusters leads to dynamic percolation behavior (see, e.g., (53)), which results in a crossover from the subdiffusive motion to normal diffusion. In contrast to diffusion on static percolation clusters, where crossover to normal diffusion occurs only above the percolation transition (52), in the case of lipid diffusion in a near-critical membrane, crossover to normal diffusion will always take place irrespectively of whether the fluid phase is above or below the percolation threshold.

This subdiffusive behavior is also clearly observed in our simulations of FCS experiments (Fig. 4 d). Upon a closer approach to the critical point of the system, the autocorrelation functions of fluorescence intensity fluctuations G(τ) progressively stronger deviate from the dependence expected for normal diffusion (i.e., Eq. 4 with β_FCS = 1). A good description of G(τ) data in this case can only be obtained with β_FCS < 1. For example, we find that for DMPC/DSPC 20:80 mixture at T = 321.0 K the best fit is obtained with β_FCS = 0.86 (Fig. 4 d), and a smaller β_FCS = 0.79 is required to fit G(τ) at T = 320.7 K, which is closer to the critical point (data not shown).

A new important result of this work is that transient anomalous subdiffusion spanning several orders of magnitude in time can be observed in a system close to its critical point. We emphasize that the appearance of the transient subdiffusive behavior in the region of near-critical fluctuations is not related to any specific properties of the system and should be observed close to criticality in various systems independent of their origin, including, of course, multicomponent lipid membranes.

It is well known that phase separation in lipid bilayers produces domains with typical sizes ranging from a few to several tens of micrometers (provided that there are no restrictions on the domain growth). In agreement with that, we observe in our simulations that, within the coexistence region, an equilibrated membrane always shows complete phase separation resulting in a single circular-shaped domain of the minority phase. Therefore, in this case, the only reasonable way to carry out FCS measurements requires parking the detection spot into the bulk of the majority phase away from the interphase boundary, or into the center of the minority phase domain. Exactly this approach is used in experimental FCS studies on membranes showing large-scale phase separation (see, e.g., (54–56)). Not unexpectedly, this approach results in normal diffusion in both phases with phase-dependent diffusion coefficients. This behavior is also observed in our simulations (data not shown).

In contrast to that and quite surprisingly, an MC simulation study of Hac et al. (21) reported FCS curves strongly deviating from the normal diffusion model exactly in the phase coexistence region, i.e., where large-scale phase separation takes place. These results were attributed (21) as resulting from subdiffusive motion of lipids, which is in contradiction with the macroscopic phase separation in the system. This seeming contradiction is resolved upon careful examination of the approach to simulations in (21). There, the diameter of the FCS detection spot was approximately equal to the simulation box size. In this case, the FCS detection spot covers effectively the whole simulated membrane, and, even in the presence of large-scale phase separation, motion of lipids in both fluid and gel phases contributes to the FCS results, which explains deviations of FCS curves from the normal diffusion model observed in (21) in the fluid-gel phase coexistence region and rule out the interpretation of these results in terms of subdiffusion. Moreover, the situation simulated there is very unlikely for experiments on single lipid bilayers within the phase coexistence region, where membrane domains typically have radii of a few to several tens of micrometers, whereas the typical FCS detection spot size is ∼200 nm for the standard FCS (35), and down to 25 nm for STED FCS (36).

Here we should also mention a previous lattice-based simulation study by Sugár and Biltonen (57) addressing the character of lateral diffusion of lipid molecules in DMPC/DSPC 50:50 membranes. There, in agreement with our results, diffusion is normal at T > 320 K, i.e., in the all-fluid membrane state (compare to Fig. 1). Deviations from the normal diffusion for the DMPC/DSPC 50:50 mixture found in (57) within the temperature range T = 300–320 K (i.e., exactly where the large-scale phase separation for this lipid composition takes place; see Fig. 1) were interpreted in terms of subdiffusive motion of lipids. As in (21), the spatial scales on which deviations from normal diffusion were observed in (57) approach the system size. Hopping of lipid molecules between the macroscopic gel and fluid domains definitely leads to deviations from normal diffusion at these large observation scales, although these deviations can hardly be interpreted in terms of anomalous subdiffusion.

We emphasize that our results presented in this article unambiguously show that local component and phase fluctuations in a near-critical membrane lead to the transient anomalous subdiffusion spanning several orders of magnitude in time. Under suitable experimental conditions, we believe, this subdiffusive behavior can be observed experimentally using, e.g., the (STED) FCS technique.

Effects of membrane-cytoskeleton interaction on lipid diffusion

Interaction with the membrane skeleton strongly affects the character of diffusion in the region of near-critical fluctuations (Fig. 5). With increasing the filament pinning density, the interaction of the membrane with filaments becomes more pronounced: it first enhances the anomalous diffusion and eventually leads to hop-diffusion of lipid molecules. In the presence of filaments, the faster diffusion process clearly corresponds to Brownian motion within compartments defined by the membrane skeleton, whereas the slower diffusion is due to hopping between the compartments, and therefore it strongly depends on the filament pinning density. Note that gel phase condensation at the membrane skeleton substantially increases the effective thickness of filaments and thus enhances their influence on lipid diffusion.

Figure 5.

Effect of the membrane skeleton on diffusion of DMPC lipids in a DMPC/DSPC 20:80 membrane at 322 K. Mean-square displacement MSD(τ) (a), local exponent β_MSD(τ) (b), time-dependent diffusion coefficient D(τ) (c), and FCS autocorrelation G(τ)/G(0) (d). (a–c) top to bottom, and (d) left to right: filament pinning density equals 0% (free membrane), 25%, 50%, and 100%.

Remarkably, in this case our results for the mean-square displacement MSD(τ) (Fig. 5 a) and effective time-dependent diffusion coefficient D(τ) (Fig. 5 c) are in good qualitative agreement with results of single-molecule tracking experiments in cell membranes (58), where results were interpreted in terms of a picket-fence model. Our MSD(τ) data also qualitatively agree with a theoretical model for diffusion on an infinite periodic square meshwork of penetrable barriers (59), except for, in our case, the short-time motion of a molecule within a compartment is subdiffusive due to near-critical fluctuations. We again emphasize that even a relatively low pinning density of the cytoskeleton filaments leads to appearance of rather strong barriers for diffusing lipids due to filament-induced local condensation of the gel phase.

Our simulations of STED FCS experiments with the experimentally achievable detection spot size (36,60) show (Fig. 5 d) that, while at early times all FCS curves exhibit behavior characteristic of subdiffusion, interaction with the membrane skeleton leads to appearance of a second slow diffusion component. The contribution of this slow component increases with the filament pinning density. Clearly, this component is related to the large-scale diffusion that involves crossing the filament-induced barriers on the membrane. This two-component character of G(τ) is in qualitative agreement with the recent STED FCS measurements of lipid diffusion in cell membranes (60). It would be very interesting to follow the dependence of the FCS autocorrelation functions and the respective apparent diffusion coefficients on the spatial scale using the variable detection spot FCS technique (61,62), as has been done in Eggeling et al. (60). This work is currently in progress.

Here, we point out once again that in our model the pinning sites do not represent obstacles for diffusing lipids, and affect lipid diffusion only indirectly, via the lower lipid mobility in the local gel-state environment (see Materials and Methods). We anticipate that in the case where pinning sites would be presented by immobile particles preferentially wetted by gel-phase lipids, the effects of the membrane-filament interaction on diffusion of lipids should become even more pronounced. This issue will be addressed in our future work.

Conclusions

In conclusion, in this article, we carried out Monte Carlo simulations of model two-component lipid membranes on experimentally relevant spatial scales and time intervals. This allowed us to better understand the details of the dynamics of phase and component separation, and by this means to address the relationship between membrane microheterogeneity and anomalous subdiffusion in cell membranes.

We observed that interaction of the near-critical membrane with the cytoskeleton strongly affects phase separation: for the membrane in the state of near-critical fluctuations, it leads to local phase separation and formation of dynamic domains with a size of a few tens of nanometers, which conform to the current understanding of membrane rafts (6).

We find that in a membrane showing near-critical fluctuations, lipids show subdiffusive behavior covering several orders of magnitude in time. The interaction of the membrane with the cytoskeleton enhances subdiffusion and eventually leads to hop-diffusion of lipids.

In the fluid-gel phase coexistence region of the phase diagram, interaction of the membrane with the cytoskeleton is found to tremendously slow down large-scale phase separation in the membrane, which may explain the established connection between the cytoskeleton and cold-shock resistance of organisms (50).

The concepts of lipid rafts (4) and cytoskeleton-related picket fence (5) are frequently discussed as the alternative viewpoints on the origin of anomalous diffusion in cell membranes. In our article, we bring these two concepts together to show that not only they do not contradict one another, but instead work in synergy, resulting in formation of cytoskeleton-induced dynamic lipid domains in the near-critical membrane. By this means we construct what, we believe, is a minimum raft model, since the domain formation is driven solely by thermodynamics and does not require either chemical cross-linking of membrane components, or lipid recycling.