Abstract
The ability of macrocycles, enzymes, ion channels, transporters, and DNA to differentiate among ion types is often crucial to their function. Using molecular dynamics simulations on both detailed systems and simple models, we quantify the importance of several factors which affect the ion selectivity of such molecules, including the number of coordinating ligands, their dipole moment, and their vibrational motion. The information resulting from our model systems is distilled into a series of selectivity maps that can be used to read off the relative free energy associated with binding of different ions, and to provide an estimate of the importance of the various factors. Although our maps cannot capture all elements of real systems, it is remarkable that they produce differential site-binding energies that are in line with experiment and more-detailed simulations for a variety of systems—making them useful for understanding the origins of selective binding and transport. The chemical nature of the coordinating ligands is essential for creating thermodynamic ion selectivity in flexible molecules (such as 18c6), but as the binding site becomes more rigid, the number of ligands (as in ion channels) and the reduction of thermal fluctuations (as in amino-acid transporters) can become important. In the future, our maps could aid in the determination of the local structure from binding energies and assist in the design of novel ion selective molecules.
Introduction
Many biological molecules, including ion channels, transporters, enzymes, macrocycles, and DNA, selectively bind or transport ions. In most cases, the differentiation between ion types is critical to the function of the molecule. For example, potassium channels must be able to rapidly move K+ out of a cell while preventing the passage of Na+, otherwise the electrochemical gradient across the cell membrane would be lost, and the cell would die (1). Ions also play important and specific roles in the structure and function of many enzymes; binding of the wrong ion can inactivate such molecules, thus perturbing important regulatory systems (2). Natural macrocyclic ionophores such as valinomycin and nonactin, as well as synthetic counterparts such as crown ethers and cryptands, can also selectively complex ions and have found uses in electrophysiology, in catalysis, and in building ion-selective electrodes.
The discrimination between K+ and Na+ is particularly interesting given their prevalence in biology and their identical charge, spherical nature, and similar size. There has been a long history of describing selectivity in small macrocyclic ligands which particularly highlighted the role of rigidity in creating a cavity that preferentially bound ions of a certain size (3). Biological macrocycles such as valinomycin, however, are conformationally flexible, and pioneering free energy simulations highlighted the importance of the solvation energies of the ions and the strength of the electrostatic interaction with the closest ligands as playing an important role in creating selectivity in addition to structural (steric) considerations (4,5). Recently, there has been much discussion of the origins of selectivity in potassium channels that are able to discern between K+ and Na+ ions with up to 1000-fold preference for K+ (6–9). Selectivity is achieved in a narrow region of the channel known as the selectivity filter, which is lined with carbonyl oxygens that coordinate permeating ions (10,11), creating a thermodynamic preference for binding K+ relative to Na+ in the range of 5–6 kcal/mol (6–9,12,13). The preference has been suggested to at least partly arise due to the channel better-compensating the energy cost of dehydrating K+ than of Na+.
Many of the explanations for ion selectivity in K+ channels are thermodynamic in nature, and this article works from this basic premise. For a long time the most widely held view attributed selectivity to the better structural fit of K+ into the selectivity filter binding sites than could occur for the smaller Na+ (14,15), seemingly consistent with the crystal structures (10,16). However, in its simplest form, such an explanation requires that the protein maintains a large degree of rigidity because the two ions differ in ionic radius by only 0.38 Å. Noskov et al. (12) and Noskov and Roux (17) challenged this structural explanation of selectivity, arguing that not only is the channel likely to be too flexible for this mechanism to work, but also that such flexible sites can still achieve K+ selectivity.
They showed that the balance of local ion-ligand and ligand-ligand interactions can create preferences for different ions in flexible/dynamic ion binding sites, in line with ideas presented by Eisenman (18) and previously suggested to operate in valinomycin (4). Thus, the precise selectivity is determined by the chemical nature and the number of ligands coordinating the ion, which determine the magnitude of the ion-ligand and ligand-ligand interactions. Considerable subsequent analysis has attempted to assess the relative importance of the ligand type and ligand number in potassium channels. Although all investigators acknowledge that both can be important, some emphasize the role of restriction of coordination numbers (13,19–21), others reemphasize the chemical nature of the ligands (22,23), and others maintain a more agnostic view (24–26). Kinetic factors have also been suggested to be important in preventing intracellular Na+ from permeating the pore (27).
All the factors discussed for K+ ion channels are likely to be important to a greater or lesser extent for ion selectivity in a large range of biological ion binding sites. It is our aim to investigate the conditions in which each factor becomes important in creating ion selectivity in a number of specific biological molecules. Although there is an infinite range of factors over which to explore selectivity, here we systematically explore only four factors:
-
1.
The magnitude of the dipole moment of the coordinating ligands.
-
2.
Restrictions on the number of coordinating ligands, and the somewhat related concepts of:
-
3.
Cavity size of the coordination site and
-
4.
The thermal fluctuations in the positions of the ligands.
Factors 2–4 are imposed by the protein scaffold and share some characteristics with a weak interpretation of the early structural fit hypothesis, whereas factor 1 is an intrinsic property of the coordinating ligands.
Admittedly, the factors chosen for investigation in this article are arbitrary. For example, one could choose instead to examine the ion-ligand and ligand-ligand energy contributions. We chose the above set of factors because we believe they afford the most explanatory power, since they can used to directly analyze binding-site structures found in the Protein DataBank. Furthermore, as defined below, the energetic contributions arising from these factors can be defined in such a way that they additively combine to the total selectivity of the site.
Model systems have been used to isolate each of the factors above to investigate the conditions under which each dominates the contribution to ion selectivity. The models range from an ion in a liquid of ligands of variable dipole moment, to an ion surrounded by a fixed number of ligands constrained within a sphere and, finally, to an ion surrounded by ligands tethered with variable force constants to the vertices of classic coordination polyhedra at a fixed distance from the central ion. The resulting information yields insight into the interplay of the various factors in achieving selectivity in a range of biological molecules. The understanding gleaned from these models is tested against additional detailed atomistic molecular dynamics simulations on the full biological molecules in question and with experimental data.
The use of model systems to study selectivity in ion channels was pioneered by Noskov et al. (12). In this article, we hope to extend this work and show how the binding energy explicitly depends simultaneously on all the factors described. Bostick et al. (21) have also used simplified models and molecular dynamics simulations to investigate ion selectivity. Binning techniques with an ion solvated in a liquid were used to derive how the free energy of binding depends on the average ion-ligand separation and the average coordination number. In this article, we explore more parameters, in particular the dipole moment of the ligand and the dynamic flexibility of the coordinating atoms. Like Noskov et al. (12) and Bostick et al. (21), we produce selectivity maps, but in our case, these are obtained by using constrained (biased) sampling of the configuration space. We have previously used simplified molecular dynamics (MD) models and quantum mechanical (QM) models to examine selectivity in KcsA (13). Varma and Rempe (19) and Dudev and Lim (25) examine a larger range of parameters within a QM framework highlighting similar trends to those seen in MD, but such QM approaches cannot easily cover the same range of parameters as the MD simulations carried out here.
The question arises: Are the simplified models used in this article capable of producing quantitative or even semiquantitative ion binding energies? First, this depends on whether the free energy of binding is dominated by local contributions. Second, it depends on whether we can calculate accurate energies for the locally interacting atoms; in general, this is a question of the accuracy of the force field or other methods used. The veracity of the first assumption can be tested by comparison with large-scale atomistic calculations. The second can be tested against more accurate calculations and/or experimental data.
Nonlocal effects such as strain energy with atoms not directly coordinated to the ion and cases where different ion types have a different number of coordinating ligands when in the same site could be important and therefore would cause simplified models like ours to break down. A number of these effects have been examined in detail and are briefly presented here and at length in the Supporting Material. Provided one keeps in mind these limitations, the selectivity maps that we produce from our models could be of great value for interpreting and understanding ion selective binding.
Methods
Model systems
Four local factors affecting ion selectivity (dipole moment of the ligand, number of ligands, cavity size, and thermal fluctuations) were investigated using free energy perturbation molecular dynamics (FEP MD) simulations. Ion exchange reactions were used to compare selectivity between ions. Fig. 1 is an overview of the three families of model systems, successively more elaborate and nuanced, used to model a generalized ion binding site. The most complex model considers an FEP between two ions, where each of the dipole moments (characterized by q), the number of ligands (n), the distance of the ligands from each ion ( and ), and the thermal fluctuation of the ligands (characterized by k) are systematically varied. By building up from a simple system, each of these factors can be investigated in turn. Once we have chosen to examine particular factors, the only obvious way in which to explore them is to build them up in the sequence shown in the Fig. 1 and described below.
Figure 1.
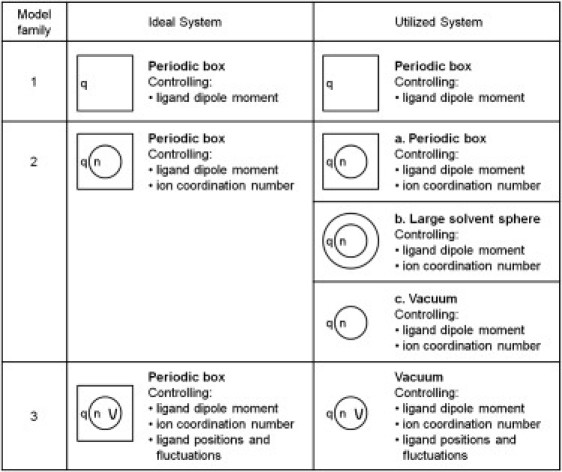
Families of model systems used in this study. The first family is used to examine the influence of the ligand dipole moment (characterized by the charge on the ligands q) on ion selectivity whereas families 2 and 3 introduce the effect of the ion coordination number (n) and harmonic restrictions on the ligand position and thermal motion (characterized by , and k), respectively. Ideally, a consistent nonoverlapping set of systems would be employed (left). However, due to limitations in computational power, the simplified systems on the right were used. (Squares represent periodic boxes of model ligands, large circles represent spherical finite droplets of model ligands, and small circles represent constraints on the number of ligands that can coordinate the ion.)
In the first family of model systems, Fig. 1, family 1, we looked at the influence of ligand dipole moment in isolation by considering the exchange of an ion M+ (where M = Li, Na, Rb, and Cs) with K+ between water and a second solvent, Sol(q), with controllable dipole moment (controlled by the partial charge q):
| (1) |
The change in free energy ΔG indicates the partitioning of the two ions (M+ and K+) between the solvents. The ΔG value for the exchange reaction is calculated as the combination of two individual FEP simulations (28) (one for each solvent) in which an ion of one type is slowly morphed into another over a number of steps. Bulk water was represented by a 30 × 30 × 30 Å TIP3P periodic water box with a counterion while the second solvent was a 30 × 30 × 30 Å box of abstract ligands based on the structure of formaldehyde molecules. The model ligands are not intended to represent formaldehyde itself, but rather an abstract, simple dipole that we can manipulate as a crude representation of a range of ligands of different chemical composition. The dipole moment of the abstract ligands was set by altering the partial charge on the carbon and oxygen atoms (C = q, O = −q, H1 = 0, H2 = 0). The model ligand box simulation was equilibrated with partial charge 0.51 under an NPT ensemble before subsequent FEP simulations were conducted under an NVT ensemble, such that the ligand density was the same for all values of the partial charge.
In the second family of binding-site models, Fig. 1, family 2, restrictions on the coordination number of the ion were imposed to add to the effect of the ligand dipole moment. This was done by forcing n ligand oxygen atoms into the first solvation shell of the ions, yielding another ion exchange reaction:
| (2) |
For this purpose, the oxygen atoms were held with a flat-bottom, steep harmonic potential within a 3.5 Å sphere (4.0 Å for Cs+) representing position of the first minimum in the radial distribution function of K+ in water. Three varieties of this second family of model sites were considered as shown in Fig. 1; all comprised of the n ligands forming the binding site which were surrounded by (a) periodic box of model ligand molecules, (b) finite spherical droplets of model ligand molecules, and (c) a vacuum. The significance of these different models is discussed below.
Whether a K+ ion is thermodynamically likely to leave the bulk water to enter a binding site was determined from the FEP-MD of another ion exchange reaction:
| (3) |
The free energy was calculated by conducting two FEP calculations: the first where K+ disappears in a 30 × 30 × 30 Å TIP3P periodic water box, and the second where K+ appears in a model ligand system. The electrostatics in these simulations was conducted using a cutoff of 12 Å, so that problems associated with using a lattice sum method could be avoided (29). Two additional sources of error could potentially arise due to the use of the double-annihilation method (30) and the sensitivity of the system to the boundary conditions and the treatment of electrostatics (29). Correction terms were calculated for each of these factors (see the Supporting Material). ΔGentry for the other ion types is determined by combining Eqs. 2 and 3.
In a final family of binding sites, Fig. 1, family 3, the influence of cavity size and thermal fluctuations was investigated on top of the ligand dipole and coordination number. In these the n ligands coordinating the ion were placed at the vertices of optimal coordination polyhedra (trigonal bipyramidal for n = 5, octahedral for n = 6, and cubic for n = 8). The size of the binding cavity was controlled by placing a harmonic restraint with force constant k on the oxygen atoms at a distance and from K+ and Na+, respectively, and the thermal fluctuations of the coordinating ligands (measured by the root-mean-square deviation (RMSD) of the oxygen atoms relative to a fixed ion) controlled by the magnitude of k. The oxygen atoms were additionally constrained to the same 3.5 Å sphere about the ion to maintain the desired coordination number, avoiding entropic divergences that could arise in an unconstrained system. To determine the effects of restricting ligand thermal fluctuations on selectivity, two separate sets of FEP were required. This is to account for the changing ion-ligand distance when different ions occupy the binding site:
| (4) |
| (5) |
There is now a complete description of the ion exchange reaction between K+ and Na+ in a hypothetical binding site incorporating each of the local factors:
| (6) |
The change in free energy from the exchange reaction of K+ and Na+ between water and the binding site that includes all our factors of interest is then (as dictated by equations (2) + (4) − (5)):
| (7) |
Unless otherwise stated, simulations are run using NAMD2 (31) with the CHARMM27 force field (32) at 310 K with 1 fs timesteps. More detailed simulation setups are provided in the Supporting Material.
Energy contributions
To determine the contribution to selectivity from the various factors, we combined the results of the ion exchange reactions described above. The free energy contribution from ligand dipole alone is derived from the first family of model systems as ΔGq (Eq. 1). In the idealized case, depicted on the left side of Fig. 1, the only difference between the first and second families of model system is the constraint on the ligand number, and thus, the free energy contribution from coordination number restriction, ΔGn, can be determined from Eqs. 1 and 2:
| (8) |
The only difference between the second and third families of model system is the inclusion of a harmonic restraint placed on the oxygen atoms of the coordinating ligands and by placing these atoms at r to control cavity size and thermal fluctuations. Thus, the free energy contribution is calculated from Eqs. 4 and 5 as
| (9) |
Defined in this way, the components are strictly additive, i.e., the total free energy difference in model system 3 is the sum of these three free energy contributions.
Unfortunately, using the idealized model systems described above is computationally expensive. As each contribution is added, the number of parameters used to describe the model system increases, and thus the number of simulations needed to survey the parameter space increases significantly. To this end, some approximations were used in our systems to decrease the time needed to conduct the FEP, as depicted on the right side of Fig. 1. The ideal model system 2 (using a periodic box of model ligands) was used for one set of parameters only, namely (n, q) = (8, 0.5). To reduce the size of the medium surrounding the binding site, subsequent simulations were conducted by keeping only the model ligand molecules within in a 10.5 Å radius sphere around the ion and simulating the system in a spherical constraint rather than with periodic boundaries (model 2b).
To reduce the size of the system even further, a final family of models were used in which all model ligand molecules not directly coordinating the ion were removed. One could argue which model system best represents the environment of a protein binding site, and for this reason we include results of all model systems in Table 2 (seen later), or in the Supporting Material. For our energy components to remain strictly additive, a consistent family of model systems must be used. Because we have introduced approximations, our energy components should be seen as indicative rather than as strictly additive; however, as shown in the Supporting Material, the difference in the relative contributions of each of the factors found using the ideal and approximate model systems is small.
Table 2.
Predicted, simulated, and experimental K+ /Na+ ion selectivities for various structures
| Structure | ΔG Predicted | ΔG Simulated/ (Ref.) | ΔG Experimental/ (Ref.) | ΔG Predicted ɛ > 1 | % χn | % χq | % χr |
|---|---|---|---|---|---|---|---|
| 1. K+ channel model | 6.6 | 5.6 (13) | 5–6 (6–9) | 5.5 | 60 | 40 | 0 |
| 2. Na+ channel model | −2.6 | −5.3 | ∼−3 (40) | −3.5 | −30 | −70 | 0 |
| 3. LeuT Na1 | −1.8 | −6.1 (36) | <−5 (41) | −3.2 | −20 | −10 | −70 |
| 4. LeuT Na2 | −0.7 | −3.2 (36) | −2.7 | −10 | −30 | −60 | |
| 5. GltPh Na1 | −2.2 | −1.3 | <−3 (42) | −3.6 | −20 | −5 | −75 |
| 6. GltPh Na2 | 1.0 | −0.6 | −0.3 | −10 | 45 | −45 | |
| 7. DNA quadruplex | 6.7 | 4.0 | 1.7 (43) | 5.5 | 60 | 40 | 0 |
| 8. ARK | 0.8 | 1.3 | >0 (44) | −0.4 | −45 | −25 | 30 |
| 9. Valinomycin | 3.0 | 7.2 | 5–7 (45,46) | 1.1 | −35 | 65 | 0∗ |
| 10. 18-crown-6 | 3.1 | 2.6 | 0–2 (47) | 3.1 | 0 | 100 | 0 |
| 11. NaK channel | ∼0 | −1.0–1.0 (35) | ∼0 (48) | — | — | — | — |
| 12. Nonactin | 0.2 | 0.7 | 0.7–1.0 (47) | — | — | — | — |
Predicted selectivities determined with the binding site surrounded by vacuum and by bulk solvent (ɛ > 1) are shown. A percentage breakdown of contributions toward selectivity from coordination number restriction, χn; ligand dipole moment, χq; and cavity size/ligand thermal motion, χr, is included. A positive value indicates a contribution toward K+ preference whereas a negative value indicates a contribution toward Na+ preference. Dashes indicate that the coordination number is different for Na+ and K+, making an estimate of contribution to selectivity difficult.
In contrast to other studies (as discussed in the text), nonlocal effects that are important in valinomycin are not included in this number.
The fractional contribution to ion selectivity is defined as
| (10) |
| (11) |
| (12) |
where χq, χn, and χr are portions from dipole moment, coordination number restriction, and cavity size/thermal fluctuations, respectively. To obtain these values, ΔGq and ΔGn were calculated using the 2B family of model systems from Fig. 1. This was done so that the fractional contributions corresponding to these could be broken down in an additive fashion. The term was calculated using model 3.
Biological simulations
For comparison with the model systems, FEP simulations are also conducted on full biological systems (e.g., full protein, solvation box and lipid, and periodic boundaries under an NPT ensemble) for each molecule studied. Details of each simulation system are given in the Supporting Material . The RMSD information was calculated by Celik et al. (33) during simulations investigating substrate binding in the leucine transporter.
Results and Discussion
Influence of ligand dipole moment
The role played by the dipole moment of the coordinating ligands is elucidated by investigating the free energy changes involved in an ion-exchange reaction for the group I ions between water and a second solvent with a dipole moment controlled by adjusting the partial charge on each end of the dipole. For simplicity in our results, we refer to only the positive value of the partial charge on the ligands q. Because the parameters for Li+, Rb+, and Cs+ are less well developed, results for these ions are included only to show qualitative trends.
As can be seen in Fig. 2, the smaller ions (Li+ and Na+) selectively partition into the solvents of greater dipole moment and the larger ions (Rb+ and Cs+) into that with smaller dipole moment. A binding site with highly charged ligands is therefore likely to be selective to smaller ions and vice versa, confirming that selectivity can, in principle, be generated by considering only the dipole moment of the ligands. This supports previous studies that suggest the presence of highly charged ligands could be responsible for the Na+ selectivity of sodium channels (12,13) and the binding sites within the GluR5 kainate receptor (34). The ligands used in our model systems represent an abstract generalized dipole, and this must be taken into account when equating them to real chemical groups. For example, the dipole moment of the protein backbone carbonyl group will be somewhere between a bare carbonyl group (∼3.0 Debye, partial charge 0.51) and that with an amide plane, as with n-methyl acetamide (∼4.0 Debye, charge ∼0.65). In the case of the potassium channel KcsA selectivity filter, the dipole moment of the carbonyl group could contribute, at most, 2 kcal/mol (out of a total of 5–6 kcal/mol) toward K+ selectivity.
Figure 2.
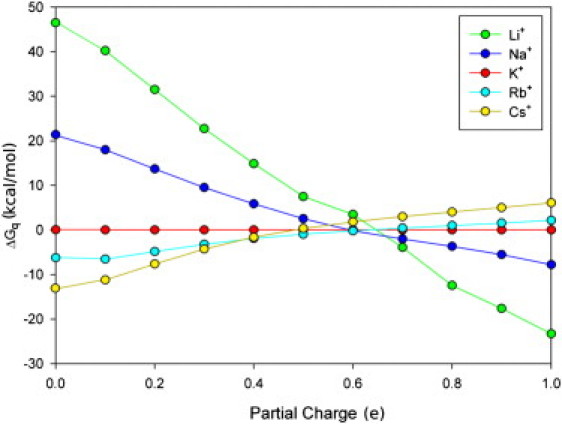
Influence of ligand dipole moment on ion selectivity. Negative values indicate that an ion M+ is more likely to leave water and enter the alternate solvent than K+.
Influence of coordination number and dipole moment
The influence that restricting the number of ligands around the ion has on ion selectivity can be examined through ion exchange reactions in the second family of model systems in which we control the ions coordination number n as well as the partial charge on the ligands q as above. This allows us to map the expected ion selectivity of a binding site both qualitatively and quantitatively, as shown in Fig. 3. In addition, we show the conditions in which an ion is thermodynamically unlikely to leave the bulk water environment and enter the site by the black exclusion zone (ΔGentry > 0) because such a binding site is not likely to be useful in a biological context.
Figure 3.

Influence of coordination number and ligand charge on ion selectivity. (A) Selectivity between K+ and Na+ is shown with 2 kcal/mol contour differences. Regions that yield K+ selectivity are indicated in red, Na+ selectivity in blue, and regions where ions will not leave water to enter the site in black. The numbers in circles correspond to the molecules in Table 2: 1. K+ channel model; 2. Na+ channel model; 7. DNA quadruplex; and 8. valinomycin. (B) Selectivity map for multiple group I ions with regions shown that are selective for Li+ (green), Na+ (blue), K+ (red), Rb+ (cyan), and Cs+ (yellow). The percentage contribution to selectivity between K+ and Na+ by (C) the restriction of coordination number, χn and (D) the partial charge on the coordinating ligands, χq. Color indicates whether this contribution is toward K+ (reds) or Na+ (blues) selectivity. (E) The effect on Na+/K+ selectivity when two of the n ligands are water molecules. (F) The effect on Na+/K+ selectivity when the coordination number of Na+ can be different to that of K+ with q = 0.5.
The selectivity maps shown in Fig. 3, A and B, enable us to predict the thermodynamic selectivity of a (flexible/liquid like) binding site based only upon the number and charge of the coordinating ligands. It can be seen in Fig. 3 B that smaller ions can be selected either by increasing the charge on the ligands or reducing the number of coordinating ligands. Selecting a large ion is most easily done by having a large number of ligands with small dipole moment (the thin, yellow Cs+ selective region at low coordination number and large dipole moment is effectively nonselective because of the small free energy difference—see contour lines in Fig. 3 A). The applicability of this map can be determined by examining how well it predicts the selectivity of known ion selective structures. Our previous work on the potassium channel, for example (13), indicates that an ion in the selectivity filter has a coordination number of 8. Assuming a carbonyl ligand partial charge of 0.5–0.6, the related point on the selectivity map (1. in Fig. 3 A) shows a free energy difference between K+ and Na+ of ∼5.5–6.5 kcal/mol, similar to both experimental estimates (6–9) and those from detailed MD studies of the system (12).
Similar predictive success can also be achieved for a number of other ion selective molecules such as a model Na+ channel, DNA quadruplex, and aminoimidazole riboside kinase (ARK), as indicated on Fig. 3 A. Some discrepancies arise if the partial charge on all the ligands is not equal. For instance, the presence of some fully charged ligands favors smaller ions (12,35), while the presence of water dissipates selectivity (24,35) (as seen in Fig. S7 in the Supporting Material). However, using the average charge of the ligands gives a good indication of the likely selectivity using Fig. 3 A. By extending our model, it is also possible to quantify selectivity when the coordination number of Na+ can be different from that of K+, as is shown in Fig. 3 F and in greater detail in the Supporting Material. Remarkably, our simple system replicates the trends in ion selectivity seen in a variety of complex molecules.
The origins of selectivity discussed so far consists of the chemical nature of the ligands and the restriction of coordination number. How much each of these contributes toward the total ion selectivity for each value of n and q is shown in Fig. 3, C and D. It can be seen from the white band in Fig. 3 D that when q ∼0.6, the dipole moment does not differentiate between the ions at any coordination number. Any selectivity at this partial charge is thus dominated by coordination number restriction. The vertical blue band at n = 4 – 6 in Fig. 3 C representing selectivity for Na+ is expected as these coordination numbers are known to be most favorable for Na+ (13,20). Similarly, coordination numbers n > 6 favor K+. Looking at the parameters for a potassium ion channel, the restriction of coordination number contributes ∼60% (3.9 kcal/mol) of total ion selectivity while the dipole moment contributes the remaining 40% (2.6 kcal/mol) (assuming a carbonyl partial charge of 0.51).
Influence of cavity size and ligand thermal fluctuations
There are some structures such as the leucine transporter (LeuT) and aspartate transporter (GltPh) for which the map shown in Fig. 3 A does not accurately predict selectivity. This is because we have yet to consider the third possible origin of ion selectivity—the effects of restricted cavity size or ligand fluctuations which have previously been shown to be important in LeuT (36). To examine, in a general context, how structural restraints that influence cavity size and ligand fluctuations can affect ion selectivity, we constructed the third family of model binding sites. This gave us additional control of the equilibrium ion-oxygen distance for each ion type and as well as the size of the thermal fluctuations of the ligands, controlled by the harmonic force constant k.
Because we are adding three new parameters to our investigation of selectivity (, , and k), only particular combinations can be easily visualized. In the first instance, we show selectivity for various values of and for three specific force constants, as shown in Fig. 4 A and Fig. S10, A and B. When the force constant is small, cavity size and ligand fluctuations are relatively unconstrained and so there is little contribution from these toward selectivity (Fig. S10, A and B). With a larger force constant, Fig. 4 A, the situation is a bit more complicated. If = and the force constant is large, the cavity size is being rigidly constrained, and this can create selectivity using a classic snug fit mechanism (a complete map of this case is shown in Fig. S9). If the cavity is large (>∼2.5 Å), K+ will be more favored in the site. If it is small (<∼2.5 Å), Na+ will be more favored. In our detailed simulations of complete biological molecules, we find that this rigid cavity situation never arises. That is, the size of the binding cavity is always different with Na+ bound than with K+, even in the transporters in which cavity size was expected to be restricted. For example, in the second ion-binding site, S2, in the LeuT, the average ion-ligand distance is 2.69 Å for K+ and 2.31 Å for Na+, very close to the average ion-ligand distances found for those ions in a solvent. Thus, we believe that the most useful case to examine in our model systems is where and are taken to be the first peak in the radial distribution function of the equivalent unconstrained system (∼2.4 and 2.7 Å, respectively).
Figure 4.
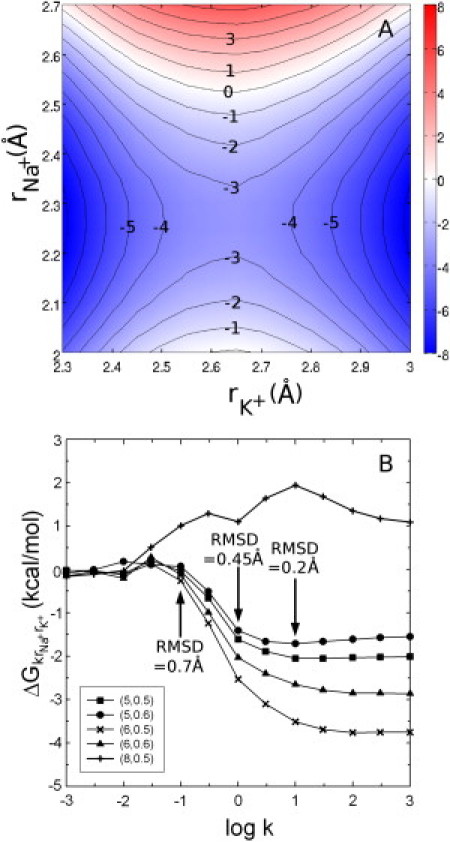
Influence of cavity size and ligand thermal fluctuations on ion selectivity. (A) Selectivity between K+ and Na+ is shown with 1 kcal/mol contour levels with k = 3.0 kcal/mol/Å2. (B) The effect of decreasing the ligand RMSD on selectivity for five different systems with different values of partial charge and ligand number. Cases with five or six ligands correspond to binding sites in the transporters, while that with eight ligands corresponds to KcsA. (Arrows) RMSD at specific k values for the (n, q) = (6, 0.5) system.
In this case, the cavity size is not being rigidly constrained, that is, the ion-ligand distance can be optimized for the ion type. However, the thermal fluctuations of the ligands are still being influenced by the harmonic restraint. At large RMSD (small k), the contribution of limited ligand fluctuations toward ΔG is 0. Decreasing fluctuations (increasing k) contributes to Na+ selectivity in the cases with five or six ligands and toward K+ selectivity in the eight-ligand case, as shown in Fig. 4 B. This shows that even when the radius of the cavity is not constrained, reducing the magnitude of the thermal fluctuations of the coordinating ligands can create ion selectivity. The possibility of ligand fluctuations influencing selectivity has been suggested previously (12), but here we show that it can be important even when the equilibrium cavity size is allowed to optimize for each ion type, as well as separating these effects from those of ligand type, number, and cavity size.
In the two transporters considered in this study, an ion-ligand distance close to that seen in solution is maintained for each ion; however, the ligands display smaller-than-usual RMSD fluctuations of ∼0.3–0.5 Å. In comparison, the ligand RMSD in the enzyme ARK is between 0.55–0.6 Å, while in KcsA it is >0.7 Å (12). Examining Fig. 4 B, it is evident that decreased fluctuations of the ligands will have a substantial effect on ion selectivity in the transporters, a small effect in ARK, and little effect with KcsA. Thus, it is the last situation considered with respect to cavity size and ligand flexibility, reduced ligand fluctuations but not constrained cavity size, that we believe is the most informative for the molecules studied here. The influence of reduced ligand thermal vibrations adds to possible influences of the other effects.
From models to reality
Having considered four mechanisms of ion selectivity, we now have the necessary tools to determine in which biological molecules each of these mechanisms is likely to be important. To demonstrate the practicality of this model, we compare predictions from the maps with experimental data for a number of different ion selective biological molecules with ion binding sites of differing chemical composition, as shown in Table 1. The results of this study are shown in Table 2. In addition, we ascertain how well the model systems capture reality by conducting additional detailed MD simulations of each molecule in its natural environment, as detailed fully in the Supporting Material. For each molecule, n, q, , , and RMSD of the coordinating ligands (calculated from the detailed simulations) was used to predict selectivity of the ion binding site (ΔG) via the selectivity maps. MD FEP simulations of each molecule were conducted within the detailed molecular dynamics simulations for comparison, and experimental data was gathered from the literature.
Table 1.
The chemical nature of the ligands surrounding the ion within each binding site
| Structure | Carbonyl | Hydroxyl | Carboxyl | Water | Ether |
|---|---|---|---|---|---|
| K+ channel model | 8 | 0 | 0 | 0 | 0 |
| Na+ channel model | 1 | 0 | 4 | 0 | 0 |
| LeuT Na1 | 4 | 1 | 1 | 0 | 0 |
| LeuT Na2 | 3 | 2 | 0 | 0 | 0 |
| GltPh Na1 | 4 | 0 | 2 | 0 | 0 |
| GltPh Na2 | 5 | 0 | 0 | 0 | 0 |
| DNA quadruplex | 8 | 0 | 0 | 0 | 0 |
| ARK | 4 | 0 | 1 | 0 | 0 |
| Valinomycin | 6 (4) | 0 (1) | 0 | 0 | 0 |
| 18-crown-6 | 0 | 0 | 0 | 2 (2) | 6 (4) |
| NaK | 6 (4) | 0 | 0 | 2 | 0 |
| Nonactin | 3 | 3 (2) | 0 | 0 | 1 |
Entries with two numbers indicate number of ligands with K+ (no parentheses) and Na+ (with parentheses).
As can be seen in Table 2, the trends seen in our selectivity maps are comparable with the values derived through detailed simulation and experiment (except for valinomycin, which is discussed below). As well as yielding selectivity for the correct ion, the simple maps give an indication of the magnitude of this selectivity. A strength of this map approach is that an estimate of the relative importance of each mechanism investigated can be determined, as shown in Table 2. It should be noted that such relative contributions should be taken as indicative values only, rather than being strictly quantitative. They are nevertheless very useful for gaining an understanding and intuition of the systems.
From these results, it is possible to see that different molecules make use of different means to differentiate between ions, but that all the factors described tend to have some influence in each case. As we and others have suggested previously, the ability of potassium channels to enforce a large coordination number around the permeating ions appears to be important in determining the thermodynamic favorability of the binding sites for K+. The specific chemical nature of the carbonyl ligands is also important, accounting for up to 40% of the total, if we assume a carbonyl partial charge of 0.51; but less if the effective dipole moment on the backbone carbonyls is larger. The large size of the thermal fluctuations of the carbonyl oxygens seen in the crystallographic and simulation data (12), as well as the ability of the site to shrink around small ions in our simulations, suggest that the cavity size and restrictions of the fluctuations of the ligands have little influence on the selectivity of the site.
The enzyme ARK, on the other hand, has a smaller average dipole moment on the ligands, something that favors the binding of K+ over Na+. Combined with a moderate reduction in the RMSD of the ligands that also favors K+, this overcomes the effect of the small number of ligands surrounding the ion would otherwise favor Na+. As noted above, the ligands in the LeuT and GltPh binding sites have smaller-than-usual fluctuations, which appear to be important in determining the Na+ selectivity of both binding sites, even though previous work has suggested only one of these is rigid in LeuT (36). The presence of the zwitterionic leucine in site Na1 of LeuT also creates a significant preference for Na+ over K+ in accord with previous results (36) and our simple models with some fully charged ligands (Fig. S7). In GltPh, site Na2 contains no fully charged ligands, and thus, has a relatively lower average dipole moment than the other transporter binding sites. For these reasons, it seems that reduced ligand fluctuation plays a large role in determining the selectivity in each of the transporter sites, which is further enhanced in the Na1 sites by the presence of acidic residues.
The selectivity filters of sodium channels contain a conserved DEKA motif. The presence of highly charged ligands around the permeating ion would create a preference for Na+ in accord with our maps and previous suggestions (12,13). In addition, there is likely to be a smaller number of ligands surrounding the ions in this case than in K+ channels, which also leads to some degree of Na+ selectivity in our model. Our maps also suggest that the flexible crown ether, 18-crown-6, relies on the dipole moment of coordinating oxygens to achieve K+ selectivity over Na+.
Our results also support the understanding of the differing selectivity of K+ and NaK channels. Crystallographic and computational studies of the NaK channel indicate that the slight differences in the structure of NaK channel enable water molecules to more easily contact the permeating ion (24,35,37). As shown in Fig. 3 E, and in greater detail in the Supporting Material, the substitution of two carbonyl groups with two water molecules reduces selectivity by >2 kcal/mol. Previous studies also show that coordination numbers are less constrained in NaK than in KcsA (24,35,37). As shown in Fig. 3 F, this can reduce selectivity by a further 4 kcal/mol. Together these effects lead to little differentiation between Na+ and K+. The number of coordinating ligands also changes with ion type in nonactin, resulting in a small predicted selectivity similar to the case of NaK.
Although our model systems enable us to visualize trends in factors that create ion selectivity, there are some elements of real biological systems that they cannot capture. In our model, the ligands are not bound to one another, and the strain in the molecular scaffold that may arise when the ligands adopt particular configurations, a nonlocal effect, is only approximated through a harmonic potential. Understanding when molecular strain is likely to influence selectivity requires knowledge of the particular molecule in question. It can be expected to be smaller in cases where the individual ligands have a large degree of flexibility, such as when they are not directly bound to one another as in large proteins and many of the cases studied here. One exception is valinomycin: although Na+ can optimize its coordination number, this comes at the energy cost of breaking a hydrogen bond in the backbone of the molecule, a nonlocal effect that is poorly captured by our harmonic strain model.
We note that in some situations there are differences between the simple model systems and real molecules. In LeuT, one of the ion binding sites abuts the fully charged zwitterionic leucine being transported by the protein. As noted above, our maps become less accurate (in this case the role of dipole moment is underestimated) when the charge on any of the ligands deviates far from the average. The accuracy of the simple model can be improved by including inhomogeneous charges as done in the Supporting Material. We also do not include differential polarizations of the ligands in the presence of different ions.
To further analyze the validity of our approach, we consider how altering the force-field model or simulation protocol influences our results. As shown in the Supporting Material, use of the OPLS force field (38,39) in place of CHARMM27 (32) within our model systems changes the predicted selectivity by <1 kcal/mol for all the conditions corresponding to the molecules studied. Changing the setup of the model system has a small effect on the exact degree of selectivity seen in our model systems, but does not change the overall trends. For example, the environment of a real ion binding site could influence its selectivity, and it has previously been suggested that this can change the coordination numbers of ions in the site (19). To examine this, selectivity maps were created with the model binding sites surrounded by a bulk medium (shown in the Supporting Material) in addition to those in which the site is surrounded by vacuum (as in Fig. 3). The effect of this is to increase the dielectric constant around the site, and as can be seen by the corresponding column in Table 2 (ΔGɛ > 1), this leads to a slight shift in the predicted selectivity toward Na+ over K+ compared to the predictions made in vacuum. This result is in accord with the suggestions of Varma and Rempe (19): increasing the dielectric constant around the site makes it possible for ligands to reduce their interaction with the ion and replace them with interactions with surrounding molecules. This situation is more favorable to Na+ than K+ as it allows for an effective reduction in coordination number. The differences in the predictions made with and without a surrounding dielectric medium (shown in Table 2) give an indication of the uncertainty inherent to our scheme, due to the fact it does not attempt to mimic the specific environment of each of the biological binding sites studied.
We have presented a scheme for understanding the mechanisms behind ion selectivity that involves four factors that can influence the thermodynamic stability of a binding site. By conducting detailed simulations in parallel with our simplified models, we hope to have achieved a useful compromise that allows general principles to be laid out while checking that this is still a plausible representation of reality. Although our scheme cannot capture all the effects that can contribute to ion selectivity, we have shown that it is applicable to a large range of biological and synthetic molecules, each of which employs these factors in different degrees. We believe that our results provide valuable insight into fundamental biological processes, and can be used to estimate the nature of uncharacterized sites or assist in the development of novel ion selective molecules.
Acknowledgments
We thank Prof. H. B. Bürgi for his careful reading of the manuscript, Leyla Celik for the LeuT RMSD data, and Rasha Ruhayel for help preparing Fig. 1.
The authors gratefully acknowledge support of this work from the National Health and Medical Research Council, an award under the Merit Allocation Scheme of the National Computational Infrastructure (NCI) National Facility, and additional computer time from iVEC, all in Australia.
Supporting Material
References
- 1.Hille B. 3rd Ed. Sinauer; Sunderland, MA: 2001. Ionic Channels of Excitable Membranes. [Google Scholar]
- 2.Page M.J., Di Cera E. Role of Na+ and K+ in enzyme function. Physiol. Rev. 2006;86:1049–1092. doi: 10.1152/physrev.00008.2006. [DOI] [PubMed] [Google Scholar]
- 3.Dietrich B. Coordination chemistry of alkali and alkaline-earth cations with macrocyclic ligands. J. Chem. Educ. 1985;62:954–964. [Google Scholar]
- 4.Åqvist J., Alvarez O., Eisenman G. Ion-selective properties of a small ionophore in methanol studied by free energy perturbation simulations. J. Phys. Chem. 1992;96:10019–10025. [Google Scholar]
- 5.Marrone T.J., M. Merz K., Jr. Molecular recognition of K+ and Na+ by valinomycin in methanol. J. Am. Chem. Soc. 1995;117:779–791. [Google Scholar]
- 6.Yellen G. Ionic permeation and blockade in Ca2+-activated K+ channels of bovine chromaffin cells. J. Gen. Physiol. 1984;84:157–186. doi: 10.1085/jgp.84.2.157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Heginbotham L., MacKinnon R. Conduction properties of the cloned Shaker K+ channel. Biophys. J. 1993;65:2089–2096. doi: 10.1016/S0006-3495(93)81244-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.LeMasurier M., Heginbotham L., Miller C. KcsA: it's a potassium channel. J. Gen. Physiol. 2001;118:303–314. doi: 10.1085/jgp.118.3.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Nimigean C.M., Miller C. Na+ block and permeation in a K+ channel of known structure. J. Gen. Physiol. 2002;120:323–335. doi: 10.1085/jgp.20028614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Doyle D.A., Morais-Cabral J., MacKinnon R. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 1998;280:69–77. doi: 10.1126/science.280.5360.69. [DOI] [PubMed] [Google Scholar]
- 11.Zhou Y., Morais-Cabral J.H., MacKinnon R. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 Å resolution. Nature. 2001;414:43–48. doi: 10.1038/35102009. [DOI] [PubMed] [Google Scholar]
- 12.Noskov S.Y., Bernèche S., Roux B. Control of ion selectivity in potassium channels by electrostatic and dynamic properties of carbonyl ligands. Nature. 2004;431:830–834. doi: 10.1038/nature02943. [DOI] [PubMed] [Google Scholar]
- 13.Thomas M., Jayatilaka D., Corry B. The predominant role of coordination number in potassium channel selectivity. Biophys. J. 2007;93:2635–2643. doi: 10.1529/biophysj.107.108167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Mullins L. The penetration of some cations into muscle. J. Gen. Physiol. 1959;42:817–829. doi: 10.1085/jgp.42.4.817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bezanilla F., Armstrong C.M. Negative conductance caused by entry of sodium and cesium ions into the potassium channels of squid axons. J. Gen. Physiol. 1972;60:588–608. doi: 10.1085/jgp.60.5.588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lockless S.W., Zhou M., MacKinnon R. Structural and thermodynamic properties of selective ion binding in a K+ channel. PLoS Biol. 2007;5:e121. doi: 10.1371/journal.pbio.0050121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Noskov S.Y., Roux B. Ion selectivity in potassium channels. Biophys. Chem. 2006;124:279–291. doi: 10.1016/j.bpc.2006.05.033. [DOI] [PubMed] [Google Scholar]
- 18.Eisenman G. Cation selective glass electrodes and their mode of operation. Biophys. J. 1962;2:259–323. doi: 10.1016/s0006-3495(62)86959-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Varma S., Rempe S.B. Tuning ion coordination architectures to enable selective partitioning. Biophys. J. 2007;93:1093–1099. doi: 10.1529/biophysj.107.107482. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Bostick D.L., Brooks C.L., 3rd Selectivity in K+ channels is due to topological control of the permeant ion's coordinated state. Proc. Natl. Acad. Sci. USA. 2007;104:9260–9265. doi: 10.1073/pnas.0700554104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Bostick D.L., Arora K., Brooks C.L., 3rd K+/Na+ selectivity in toy cation binding site models is determined by the ‘host’. Biophys. J. 2009;96:3887–3896. doi: 10.1016/j.bpj.2008.12.3963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Dixit P.D., Merchant S., Asthagiri D. Ion selectivity in the KcsA potassium channel from the perspective of the ion binding site. Biophys. J. 2009;96:2138–2145. doi: 10.1016/j.bpj.2008.12.3917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yu H., Noskov S.Y., Roux B. Hydration number, topological control, and ion selectivity. J. Phys. Chem. B. 2009;113:8725–8730. doi: 10.1021/jp901233v. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Fowler P.W., Tai K., Sansom M.S. The selectivity of K+ ion channels: testing the hypotheses. Biophys. J. 2008;95:5062–5072. doi: 10.1529/biophysj.108.132035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Dudev T., Lim C. Determinants of K+ vs Na+ selectivity in potassium channels. J. Am. Chem. Soc. 2009;131:8092–8101. doi: 10.1021/ja900168k. [DOI] [PubMed] [Google Scholar]
- 26.Roux B. Exploring the ion selectivity properties of a large number of simplified binding site models. Biophys. J. 2010;98:2877–2885. doi: 10.1016/j.bpj.2010.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Thompson A.N., Kim I., Nimigean C.M. Mechanism of potassium-channel selectivity revealed by Na+ and Li+ binding sites within the KcsA pore. Nat. Struct. Mol. Biol. 2009;16:1317–1324. doi: 10.1038/nsmb.1703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Zwanzig R.W. High temperature equation of state by a perturbation method. I. Nonpolar gases. J. Chem. Phys. 1954;22:1420–1426. [Google Scholar]
- 29.Kastenholz M.A., Hünenberger P.H. Computation of methodology-independent ionic solvation free energies from molecular simulations. II. The hydration free energy of the sodium cation. J. Chem. Phys. 2006;124:224501. doi: 10.1063/1.2201698. [DOI] [PubMed] [Google Scholar]
- 30.Gilson M.K., Given J.A., McCammon J.A. The statistical-thermodynamic basis for computation of binding affinities: a critical review. Biophys. J. 1997;72:1047–1069. doi: 10.1016/S0006-3495(97)78756-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.MacKerell A.D., Jr., Bashford D., Karplus M. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 33.Celik L., Schiøtt B., Tajkhorshid E. Substrate binding and formation of an occluded state in the leucine transporter. Biophys. J. 2008;94:1600–1612. doi: 10.1529/biophysj.107.117580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Vijayan R., Plested A.J.R., Biggin P.C. Selectivity and cooperativity of modulatory ions in a neurotransmitter receptor. Biophys. J. 2009;96:1751–1760. doi: 10.1016/j.bpj.2008.11.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Noskov S.Y., Roux B. Importance of hydration and dynamics on the selectivity of the KcsA and NaK channels. J. Gen. Physiol. 2007;129:135–143. doi: 10.1085/jgp.200609633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Noskov S.Y., Roux B. Control of ion selectivity in LeuT: two Na+ binding sites with two different mechanisms. J. Mol. Biol. 2008;377:804–818. doi: 10.1016/j.jmb.2008.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Alam A., Jiang Y. Structural analysis of ion selectivity in the NaK channel. Nat. Struct. Mol. Biol. 2009;16:35–41. doi: 10.1038/nsmb.1537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Jorgensen W.L., Tirado-Rives J. The OPLS potential function for protein, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988;110:1657–1666. doi: 10.1021/ja00214a001. [DOI] [PubMed] [Google Scholar]
- 39.Jensen K., L. Jorgensen W. Halide, ammonium, and alkali metal ion parameters for modeling aqueous solutions. J. Chem. Theory Comput. 2006;2:1499–1509. doi: 10.1021/ct600252r. [DOI] [PubMed] [Google Scholar]
- 40.Cahalan M., Begenisich T. Sodium channel selectivity. Dependence on internal permeant ion concentration. J. Gen. Physiol. 1976;68:111–125. doi: 10.1085/jgp.68.2.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Yamashita A., Singh S.K., Gouaux E. Crystal structure of a bacterial homologue of Na+/Cl−-dependent neurotransmitter transporters. Nature. 2005;437:215–223. doi: 10.1038/nature03978. [DOI] [PubMed] [Google Scholar]
- 42.Boudker O., Ryan R.M., Gouaux E. Coupling substrate and ion binding to extracellular gate of a sodium-dependent aspartate transporter. Nature. 2007;445:387–393. doi: 10.1038/nature05455. [DOI] [PubMed] [Google Scholar]
- 43.Hud N.V., Smith F.W., Feigon J. The selectivity for K+ versus Na+ in DNA quadruplexes is dominated by relative free energies of hydration: a thermodynamic analysis by 1H NMR. Biochemistry. 1996;35:15383–15390. doi: 10.1021/bi9620565. [DOI] [PubMed] [Google Scholar]
- 44.Andersson C.E., Mowbray S.L. Activation of ribokinase by monovalent cations. J. Mol. Biol. 2002;315:409–419. doi: 10.1006/jmbi.2001.5248. [DOI] [PubMed] [Google Scholar]
- 45.Grell E., Funck T., Eggers F. Structure and dynamic properties of ion-specific antibiotics. Membranes. 1975;3:1–126. [PubMed] [Google Scholar]
- 46.Rose M., Henkens R. Stability of sodium and potassium complexes of valinomycin. Biochim. Biophys. Acta. 1974;372:426–435. [Google Scholar]
- 47.Izatt R.M., Bradshaw J.S., Christensen J.J. Thermodynamic and kinetic data for cation-macrocycle interaction. Chem. Rev. 1985;85:271–339. [Google Scholar]
- 48.Shi N., Ye S., Jiang Y. Atomic structure of a Na+- and K+-conducting channel. Nature. 2006;440:570–574. doi: 10.1038/nature04508. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


