Lung volume does not alter the distribution of pulmonary perfusion in dependent lung in supine humans

Abstract

There is a gravitational influence on pulmonary perfusion, including in the most dependent lung, where perfusion is reduced, termed Zone 4. Studies using xenon-133 show Zone 4 behaviour, present in the dependent 4 cm at total lung capacity (TLC), affects the dependent 11 cm at functional residual capacity (FRC) and almost all the lung at residual volume (RV). These differences were ascribed to increased resistance in extra-alveolar vessels at low lung volumes although other mechanisms have been proposed. To further evaluate the behaviour of perfusion in dependent lung using a technique that directly measures pulmonary perfusion and corrects for tissue distribution by measuring regional proton density, seven healthy subjects (age = 38 ± 6 years, FEV₁= 104 ± 7% predicted) underwent magnetic resonance imaging in supine posture. Data were acquired in the right lung during breath-holds at RV, FRC and TLC. Arterial spin labelling quantified regional pulmonary perfusion, which was normalized for regional proton density measured using a fast low-angle shot technique. The height of the onset of Zone 4 behaviour was not different between lung volumes (P= 0.23). There were no significant differences in perfusion (expressed as ml min⁻¹ g⁻¹) between lung volumes in the gravitationally intermediate (RV = 8.9 ± 3.1, FRC = 8.1 ± 2.9, TLC = 7.4 ± 3.6; P= 0.26) and dependent lung (RV = 6.6 ± 2.4, FRC = 6.1 ± 2.1, TLC = 6.4 ± 2.6; P= 0.51). However, at TLC perfusion was significantly lower in non-dependent lung than at FRC or RV (3.6 ± 3.3, 7.7 ± 1.5, 7.9 ± 2.0, respectively; P < 0.001). These data suggest that the mechanism of the reduction in perfusion in dependent lung is unlikely to be a result of lung volume related increases in resistance in extra-alveolar vessels. In supine posture, the gravitational influence on perfusion is remarkably similar over most of the lung, irrespective of lung volume.

Introduction

In the human lung the distribution of pulmonary blood flow is not uniform. For example, in the upright lung during a breath-hold at 1 litre above functional residual capacity (FRC) blood flow is higher in gravitationally dependent lung than in non-dependent regions, reflecting a gravitational influence on pulmonary blood flow (West & Dollery, 1960; Anthonisen & Milic-Emili, 1966). This observation, amongst others, led to the zone model of pulmonary perfusion (West et al. 1964), whereby blood flow is dictated by the relationship between alveolar, pulmonary arterial, and pulmonary venous pressures. Thus, in the most gravitationally non-dependent lung, the alveolar pressure exceeds pulmonary arterial pressure preventing flow (Zone 1, normally not present in the lung). As pulmonary arterial pressure increases hydrostatically down the lung, flow is a function of the difference between pulmonary arterial and alveolar pressures since pulmonary venous pressures are still very low (Zone 2). Finally in Zone 3 pulmonary blood flow is a function of the differences between pulmonary arterial and pulmonary venous pressures. This gravitational effect on pulmonary blood flow was later shown to be most pronounced at total lung capacity (TLC), and disappeared almost entirely at residual volume (RV) (Hughes et al. 1968).

In addition, to the above findings, a Zone 4 was also described, where pulmonary perfusion was a decreasing function of height in the most dependent lung (Hughes et al. 1968). The zone of reduced perfusion in dependent lung encompassed almost the entire lung at RV and affected only the dependent 4 cm of the lung at TLC. Zone 4 behaviour was ascribed to greater resistance in extra-alveolar vessels (Hughes et al. 1968) at low lung volumes, acting to reduce perfusion in these regions. Extra-alveolar vessels are composed of pulmonary arterial and venous vessels down to the level of those entering or leaving the alveolar septa, whereas alveolar vessels are those in the alveolar walls (Riley, 1959). Negative pressures associated with lung inflation are thought to increase the volume of the extra-alveolar vessels by radial traction, thus decreasing resistance and increasing flow. However, measurements of resistance particularly in the larger extra-alveolar vessels are not affected by lung inflation (Sun et al. 1987), and thus this idea is not fully supported. Other potential mechanisms including hypoxic pulmonary vasoconstriction in regions of low alveolar 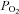(Petersson et al. 2006), or local vascular branching structure patterns (Burrowes et al. 2005a; Burrowes & Tawhai, 2005) which have also been invoked as the mechanism of decreased perfusion in dependent lung.

Quantitative functional magnetic resonance imaging (MRI) techniques in humans (Mai & Berr, 1999; Bolar et al. 2006; Henderson et al. 2009) allow absolute quantification of perfusion and when combined with measures of regional lung density correct for regional lung expansion (Hopkins et al. 2007; Prisk et al. 2007) as the lung is inflated, allowing perfusion to be expressed as ml min⁻¹ g⁻¹. We tested the hypothesis that the reduction in perfusion in dependent lung was due to increased resistance in extra-alveolar vessels. If this were true, then the reduction in perfusion in dependent lung would be greater at low lung volumes than at high lung volumes. To test this, we acquired perfusion and lung density images using MRI in supine healthy subjects at three different lung volumes: RV, FRC and TLC.

Methods

Subjects

This study was approved by the Human Subjects Research Protection Program of the University of California, San Diego. Seven healthy subjects (2 female, 5 male) participated after giving informed consent. This study conformed to the standards set by the Declaration of Helsinki. Subjects underwent screening using respiratory and MRI safety questionnaires. In addition all subjects had normal pulmonary function as measured by spirometry (Table 1).

Table 1.

Subject characteristics and spirometry (n= 7, means ±s.d.)

Age (years)	38 ± 6
Height (cm)	174 ± 9
Weight (kg)	75 ± 20
FVC (l)	5.20 ± 1.11
FVC (% of predicted)	109 ± 8
FEV1 (l)	4.06 ± 0.73
FEV1 (% of predicted)	104 ± 7
FEV1/FVC ratio (%)	79 ± 8
FEV1/FVC ratio (% of predicted)	96 ± 10

FVC, forced vital capacity; FEV₁, forced expiratory volume in 1 s. Predicted values from (Crapo et al. 1982).

Protocol overview

Subjects underwent a brief period of training to familiarize them with the study protocol, and the desired lung volumes. The subjects were instructed to maintain an open glottis to prevent any alteration in alveolar pressure during the measurements. Measures of perfusion and lung density were then acquired in the supine posture during breath-holds at RV, FRC and TLC. The order of the lung volume measurements was balanced between subjects, controlling for any potential ordering effect.

Data collection

Subjects were scanned using a Vision 1.5T whole body magnetic resonance scanner (Siemens Medical Systems, Erlangen, Germany) and positioned supine in the scanner, with a custom-designed rigid plastic cage over the torso. The phased-array torso coil was positioned on the plastic cage to ensure a constant distance between the anterior and posterior elements of torso coil. A water phantom doped with gadolinium (Berlex Imaging, Magnevist, 469 mg ml⁻¹ gadopentetate dimeglumine, 1:5500 dilution) was placed next to the subject within the field of view for absolute quantification of perfusion and lung density (see below). Data were acquired by imaging the right lung in the sagittal plane to eliminate motion artifacts from the aorta and heart present within the left hemithorax. Data from adjacent 15 mm images were obtained in triplicate during breath holding at each lung volume. For each image acquired during the 8–10 s breath hold, a constant lung volume was ensured by overlaying sequential images and visually inspected using the diaphragm position. Any images showing diaphragm movement were discarded, and additional images obtained to ensure a complete data set for each individual. Images were obtained starting in the medial lung adjacent to the heart and large vessels and progressing laterally until the imaging plane included the lateral chest wall. This was accomplished in three to five slices for each subject at FRC, depending on lung size. The middle three slices at each lung volume were selected for each subject, or in the case where four slices were obtained, data from the most lateral slice were not used.

Using ASL to image pulmonary blood flow

Regional pulmonary blood flow was assessed using a 2D arterial spin labelling (ASL) flow-sensitive alternating inversion recovery with an extra radiofrequency pulse (FAIRER) sequence with a half-Fourier acquisition single-shot turbo spin-echo (HASTE) imaging scheme (Bolar et al. 2006; Henderson et al. 2009). The technique for quantifying regional pulmonary perfusion was modified from one previously reported (Mai & Berr, 1999; Mai et al. 1999) to allow for acquisition of quantitative data within a single breath hold (Bolar et al. 2006). It has been described in detail (Bolar et al. 2006; Henderson et al. 2009) and is therefore only briefly described here.

Arterial spin labelling is an MRI technique which inverts the magnetization of protons (primarily in water molecules) in a spatially selective way using a combination of radiofrequency pulses and spatial magnetic field gradient pulses. These ‘tagged’ protons in blood act as an endogenous tracer, allowing the measurement of regional pulmonary blood flow. This is done by acquiring two images of each lung slice during each measurement within a single breath-hold. The signal of blood is prepared differently in the two images: In the first ‘control’ image, an inversion pulse is applied to the section being imaged (a spatially selective inversion), leaving the arterial blood outside the imaged section undisturbed, producing a strong MRI signal. To ensure an accurate inversion over the imaged slice, the spatial thickness of this pulse is three times the slice thickness (Bolar et al. 2006). In the second image, termed the ‘tag’ image, the magnetization of the arterial blood both inside and outside the imaged section is inverted at the beginning of the experiment with an inversion pulse applied to the whole lung (i.e. spatially non-selective inversion). Both images are acquired after a delay, T_I, which is set to 80% of one R–R interval, and therefore represents one systolic period. During this delay, blood flows into each voxel of the imaged slice and there is relaxation of the magnetization. The difference in ASL signal (control – tag) measured for each voxel then reflects the amount of blood delivered during the time between inversion and imaging (inversion time, T_I), weighted with a decay factor due to the relaxation of the blood magnetization during that interval (Henderson et al. 2009). In essence, the ASL signal measured is analogous to a microsphere experiment, in the sense that labelled blood is delivered and then measured before it has a chance to leave the tissue by venous flow.

Imaging parameters were as follows: inversion time (T_I) = 600–800 ms, echo time (T_E) = 36 ms, field of view = 400 mm, slice thickness = 15 mm, image matrix size = 128 × 256. The total scan time was approximately 8–10 s. The 15 mm-thick sagittal slices have a field of view of 40 × 40 cm and a resolution of 256 × 128 pixels and thus the voxels are ∼1.5 × 3 × 15 mm (∼0.07 cm³) in size.

Image processing

Correction for coil inhomogeneity

A torso coil was used to maximize the signal-to-noise ratio in the images, since it has substantially higher gain than the body coil built into the scanner. Unlike the body coil, which is quite homogeneous, the torso coil exhibits a degree of inhomogeneity in signal strength that varies in all three directions. To correct for this inhomogeneity, the image obtained from the torso coil was corrected to the homogeneous (but noisy) body coil image for each subject as previously described (Hopkins et al. 2007; Henderson et al. 2009). This was done for the quantification of the regional lung density data and regional perfusion in ml min⁻¹ cm⁻³ (see below).

Quantification of regional perfusion in ml min⁻¹ cm⁻³

A water phantom doped with gadolinium (Berlex Imaging, Magnevist with 469 mg ml⁻¹ gadopentetate dimeglumine) with a T₁ of 1650 ms and T₂ of 976 ms was included in the field of view for each image for absolute quantification (Henderson et al. 2009). For quantification in the lung, we assumed a T₁ of 1430 ms and T₂ of 117 ms for human pulmonary arterial (mixed venous) blood under normal in vivo conditions (haematocrit ∼0.4 and oxygen saturation ∼75%) (Spees et al. 2001), and a calibration factor to account for difference in T₁ and T₂ between arterial blood and the phantom was applied. Perfusion in units of ml min⁻¹ cm⁻³ (averaged over a cardiac cycle) was then calculated (Henderson et al. 2009).

Quantification of regional lung density in g cm⁻³

A proton density image was acquired in each of the sagittal slices previously imaged for perfusion measurements using a fast low-angle shot (FLASH) sequence during a separate breath hold. Sequence parameters were repetition time (T_R) = 6 ms, echo time (T_E) = 0.9 ms, flip angle = 4 deg, slice thickness = 15 mm, and image size 128 × 128. The resulting signal in each voxel, after correcting for coil inhomogeneity, is related to the signal derived from the water phantom (which is by definition 100% water) to obtain regional lung proton (water) density in units of g H₂O per cm³ lung. The resulting proton density was then calculated by correcting the signal for the rapid T₂* decay of signal from the lungs based on published values of T₂* of 2.0, 1.8 and 1.2 ms for RV, FRC, and TLC, respectively (Theilmann et al. 2009). This proton density, which reflects protons in both tissue and blood, is subsequently referred to as density.

Quantification of regional density-normalized perfusion in ml min⁻¹ g⁻¹

In order to account for differences in regional lung expansion, the perfusion measurements were normalized by the regional lung density measurements. This was done by resizing the ASL images to match the resolution of the FLASH proton density images (voxels of 3 × 3 × 15 mm, giving an effective resolution of ∼0.14 cm³) using bilinear interpolation in MATLAB (The MathWorks, Natick, MA, USA). Then a mutual information-based technique that included translation and rotation was used to register the two images (Pluim et al. 2003) using a custom-designed program in MATLAB. This allowed the calculation of perfusion expressed in units of ml min⁻¹ g⁻¹ by dividing the quantified perfusion image obtained using ASL (ml min⁻¹ cm⁻³) by the quantified density image obtained using FLASH (g H₂O/cm³ lung) to give perfusion in millilitres per minute per gram lung. This approach considers the lung as two compartments: one that is air, and one comprising everything else. The non-air compartment, which is composed of lung tissue and blood elements, constitutes the weight of the lung and thus the weight affecting the gravitational deformation. To the extent that regional lung water content reflects overall density (and thus the regional air/non-air content distribution), this then reflects perfusion in millilitres per minute per gram of lung. In addition to normalizing by the proton density distribution, this approach also accounts for any heterogeneity in the coil sensitivity profile since coil heterogeneity cancels out with the division of the ASL images by the FLASH images. In this paper, density-normalized perfusion will subsequently be referred to as perfusion (in units of ml min⁻¹ g⁻¹).

Data analysis

Voxel by voxel data for density (g cm⁻³) and perfusion (ml min⁻¹ g⁻¹) for the three lung slices for each subject were compiled into a composite dataset for each subject at each lung volume and analysed as follows. To evaluate overall changes in lung density and perfusion with lung volume the mean values at each lung volume for each subject were calculated. The vertical (gravitational) distribution of density and perfusion for each subject was assessed by averaging in 1 cm increments, using the most dependent portion of the lung as the zero reference point, for each lung volume. For lung density, a linear regression was performed to calculate the slope of the relationship between lung density and height. To compare with the work of Anthonisen & Milic-Emili (1966) and Hughes et al. (1968) the point of maximum perfusion was identified for each subject at each lung volume, and the slope of the linear relationship between height and perfusion above this point was calculated for comparison. In addition, since distributions of perfusion across vertical distances may not necessarily be best expressed as linear relationships, the volume of the three slices was divided into three gravitationally based regions of interest, dependent, intermediate, and non-dependent regions, to allow for comparison between regions. This was done by identifying the image with the greatest anterior to posterior width from the three contiguous sagittal images obtained at each lung volume and dividing it horizontally into three regions of interest with equal vertical distance. The remaining two contiguous lung slices were divided into three regions of interest using the same horizontal coordinates. Mean density and perfusion were then obtained for each of these regions.

Statistical analysis

Repeated measures ANOVA (Statview 5.0.1, SAS Institute, Cary, NC, USA) was used to statistically evaluate changes in the major dependent variables (density, perfusion, slope of density and perfusion relationships, point of maximum perfusion) over the three lung volumes. Additional repeated measures ANOVA with two repeated measures, gravitational region (3 levels: dependent, intermediate, non-dependent region), and lung volume (3 levels: RV, FRC and TLC) were performed to evaluate regional information. Dependent variables for this analysis were perfusion in units of ml min⁻¹ g⁻¹ and lung density in units of g cm⁻³ of lung. Where overall significance occurred, post hoc testing was conducted using Fisher's protected least significant difference. All data are presented as means ±s.d., and the null-hypothesis (no effect) was rejected for P < 0.05, two tailed.

Results

Subject descriptive and spirometry data are given in Table 1. Our subjects had normal pulmonary function as indicated by spirometry. The total duration of each study was about 1 h. Heart rate averaged 65 ± 6 beats min⁻¹ and mean arterial oxygen saturation measured by pulse oximetry was 98 ± 1% during data collection. Representative images of density and perfusion for a mid-sagittal slice in one subject during breath holds at the three lung volumes are shown in Fig. 1. Overall, there was excellent reproducibility of breath holds between measures of density and perfusion and the correlation between the number of voxels imaged in the two measures was R= 0.999. The absolute value of the difference in lung volume between measures, calculated from the total number of voxels in the images, was less than 3%.

Figure 1. Density and perfusion images (first and second row, respectively) for a mid-sagittal slice obtained during breath holds at RV, FRC and TLC (first, second and third column, respectively) in supine posture in one normal subject.

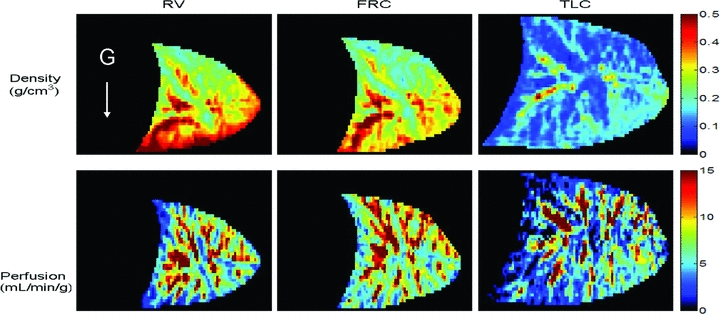
The diaphragmatic surface of the lung is oriented towards the left of the image, the white arrow indicates the direction of the gravitational vector. The volume of the lung at FRC is slightly greater than RV, but this difference is small when compared to the changes from FRC to TLC. This is consistent with the decrease in FRC in the supine posture that occurs as a result of a shift of the abdominal contents and diaphragm cephalad, such that it is closer to RV than in the upright posture.

Lung density

Mean data

Mean lung density data averaged from the composite dataset for each lung volume are given in Table 2. As expected from increased inflation, density decreased progressively from RV to TLC. At TLC mean lung density was significantly less than at FRC or RV (P < 0.0001), which did not differ from one another (P= 0.61).

Table 2.

Density and perfusion data for the right lung at RV, FRC and TLC (means ±s.d., n= 7)

Lung volume	RV	FRC	TLC	Pvolume
Volume of right lung imaged (ml)	523 ± 91	580 ± 133	1203 ± 207*	<0.0001
Mean density (g cm−3)	0.37 ± 0.11	0.36 ± 0.12	0.18 ± 0.04*	<0.0001
Density slope (g cm−4)	−0.059 ± 0.025	−0.062 ± 0.022	−0.010 ± 0.017*	<0.0001
Density slope R2	0.28 ± 0.10	0.30 ± 0.12	0.03 ± 0.02*	<0.0001
Mean perfusion (ml min−1 g−1)	7.8 ± 2.5	7.2 ± 2.2	6.1 ± 2.9	0.052
Height of maximum perfusion (cm)	8.2 ± 2.6	10.3 ± 5.3	7.5 ± 3.1	0.23
Height of maximum perfusion (%)	65 ± 14	66 ± 11	45 ± 9*	0.0006
Slope of perfusion above maximum (% cm−1)	−7.9 ± 3.3	−7.8 ± 3.4	−6.7 ± 3.4	0.52
Relative dispersion of perfusion (mean/s.d.)	0.69 ± 0.12	0.68 ± 0.10	1.45 ± 0.34*	<0.0001

RV, residual volume; FRC, functional residual capacity; TLC, total lung capacity; P_volume, omnibus P for the effect of lung volume.

^*Significantly different from RV and FRC P < 0.05.

Regional data

The average lung density plotted as a function of distance from the most dependent portion of the lung for the three lung volumes is shown in Fig. 2 top panel. There was a linear relationship between lung density and vertical height, but the strength of the association was less well defined at TLC (P < 0.0001) than FRC or RV. The slope of this relationship was also significantly less at TLC (P < 0.0001) than the other two lung volumes. At TLC, the slope of the relationship between density and vertical height was not significantly different from zero (P= 0.19) indicating largely uniform inflation in the vertical direction. However the slope of the relationship between density and vertical height for both FRC and RV were significantly different from zero (P < 0.001) and were not significantly different from one another (Table 2). When the lung was divided into three gravitational regions (Table 3), lung density at RV and FRC increased from non-dependent to dependent regions (P < 0.0001), consistent with the linear regression data and was similar between the two lung volumes. However, at TLC, lung density was greater in the gravitationally intermediate region when compared to the non-dependent and dependent lung regions (P < 0.0001, Table 3), which is likely to be because of the presence of large vessels in the region of the lung hilum.

Figure 2. Mean ±s.d. density (top) and perfusion (bottom) vs. distance from the most dependent portion of the lung.

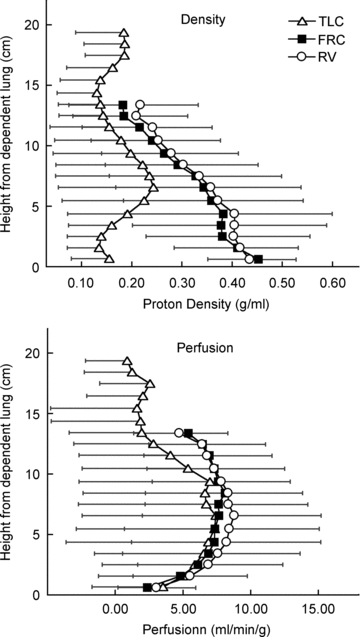
Note that the x and y axes have been reversed in these figures so that vertical height increases up the figure. Data are for all 3 lung slices in 7 subjects and were averaged for all voxels lying within the same vertical (isogravitational) plane at 1 cm increments. There is only a small difference between RV and FRC, consistent with the lung volume changes described above. The density is markedly less at TLC compared to FRC or RV, consistent with the greater air volume of the lung at TLC. The perfusion distributions are largely similar between lung volumes. At TLC, the perfusion distribution although similar to RV and FRC over most of the vertical height, is less in the most non-dependent lung, but this difference is only significant (P < 0.05) at heights above 11.5 cm. The height of maximum perfusion was not different between lung volumes, nor was the slope of the relationship between perfusion and vertical height above this point. Statistical details are given in Table 2.

Table 3.

Regional density data at RV, FRC and TLC (means ±s.d., n= 7)

Lung volume	RV	FRC	TLC	Pvolume
Non-dependent density (g cm−3)	0.27 ± 0.10†	0.25 ± 0.10†	0.15 ± 0.03*†	0.0002
Intermediate density (g cm−3)	0.37 ± 0.11†	0.35 ± 0.13†	0.22 ± 0.05*†	0.0004
Dependent density (g cm−3)	0.43 ± 0.11†	0.41 ± 0.12†	0.17 ± 0.04*†	0.0001
Pregion	<0.0001	<0.0001	0.0001

P_volume, omnibus P for the effect of lung volume; P_region, omnibus P for the effect of lung region.

^*Significantly different from RV and FRC, P < 0.05

^†significantly different from the other 2 regions, P < 0.005.

Lung perfusion

Mean perfusion

Mean perfusion for the entire right lung at the three lung volumes is given in Table 2. Although perfusion at TLC was lower (6.1 ± 2.9 ml min⁻¹ g⁻¹) when compared to RV (7.8 ± 2.5 ml min⁻¹ g⁻¹) or FRC (7.2 ± 2.2 ml min⁻¹ g⁻¹), these differences were of borderline statistical significance. Overall perfusion heterogeneity as measured by the relative dispersion (coefficient of variation =s.d./mean) averaged 0.68 ± 0.10 at FRC and was similar at RV (0.69 ± 0.12), similar to previous studies at FRC (Hopkins et al. 2007; Arai et al. 2009), but was markedly increased at TLC to 1.45 ± 0.34 (P < 0.0001). This resulted from reduction in the mean perfusion/voxel (reflecting increased lung inflation) in the face of an unchanged s.d.

Regional data

The average perfusion (ml min⁻¹ g⁻¹) plotted as a function of distance from the most dependent portion of the lung for the three lung volumes is shown in Fig. 2, bottom panel. The height of maximum perfusion averaged 10.3 ± 5.3 cm at FRC and was somewhat less at both TLC and RV although these differences were not statistically significant (P= 0.23, Table 2). There was no significant (P= 0.52) effect of lung volume on the slope of the linear relationship between height and perfusion above the point of maximum perfusion, which averaged −7.5 ± 3.3% cm⁻¹ over all lung volumes (Table 2).

Over all lung volumes (Table 4) perfusion showed the general pattern of being greater in the mid lung than either the dependent or non-dependent lung as previously reported (Hopkins et al. 2007). Perfusion was not significantly different between lung volumes in the dependent lung (Table 4, P= 0.51). Similarly there were no significant differences in perfusion between lung volumes in the intermediate lung regions (P= 0.26). However in the non-dependent region at TLC perfusion was significantly lower than either FRC or RV (3.6 ± 3.3 versus 7.7 ± 1.5 and 7.9 ± 2.0 ml min⁻¹ g⁻¹, P < 0.001, Table 4 and Fig. 2).

Table 4.

Regional perfusion data at RV, FRC and TLC (means ±s.d., n= 7)

Lung volume	RV	FRC	TLC	Pvolume
Non-dependent perfusion (ml min−1 g−1)	7.9 ± 2.0	7.7 ± 1.5	3.6 ± 3.3*†	<0.001
Intermediate perfusion (ml min−1 g−1)	8.9 ± 3.1	8.1 ± 2.9	7.4 ± 3.6	0.26
Dependent perfusion (ml min−1 g−1)	6.6 ± 2.4†	6.1 ± 2.1†	6.4 ± 2.6	0.51
Pregion	0.007	0.009	0.002

P_volume, omnibus P for the effect of lung volume; P_region, omnibus P for the effect of lung region.

^*Significantly different from RV and FRC, P < 0.005

^†significantly different from other 2 regions, P < 0.05.

Discussion

The results of this study show that in healthy supine subjects, the influence of gravity on the distribution of perfusion is remarkably similar, irrespective of lung volume, except in the most non-dependent portion of the lung, where it is reduced at TLC compared to other lung volumes. In particular the distribution of perfusion in the gravitational middle and dependent lung is not different between lung volumes. These data suggest that the mechanism of the reduction in perfusion dependent lung (Zone 4 effect) is not a result of low regional lung volume acting to increase resistance in extra-alveolar vessels as previously suggested.

Effect of lung volume on the overall distribution of perfusion

Throughout much of the vertical height the distribution of perfusion is largely similar between lung volumes, and both the height of the point of maximal perfusion (in cm) and the slope of the relationship between perfusion and height above the point of maximal perfusion were not significantly different between lung volumes. As such, the data from the present study suggest that the influence of lung volume on the distribution of pulmonary perfusion in the vertical (gravitational plane) is less than previously reported (Hughes et al. 1968). In the most non-dependent lung, perfusion is reduced at TLC compared to FRC or RV. One possible explanation for this is that the greater vertical height of the lung at TLC may allow the influence of gravity on pulmonary blood flow to become more apparent. Alternatively, at high lung volumes, alveolar wall stretching may affect perfusion. Since the capillaries are the walls of the alveolus and are interdependent between alveoli, lung expansion acts on the capillaries potentially either increasing or decreasing the calibre of these vessels, depending on the degree of expansion. In the non-dependent lung where alveolar size is already large at TLC, the vascular resistance may increase further and redistribute blood away from the non-dependent into the dependent lung regions.

Potential mechanisms for the reduction of perfusion in dependent regions of the supine human lung

In the original work describing Zone 4, the zone where pulmonary perfusion was a decreasing function of height in the most dependent lung, Zone 4 was attributed to increased resistance in the extra-alveolar vessels (Hughes et al. 1968). The calibre of the vessels is considered to represent a balance between expansion of the lung parenchyma, with radial traction acting to increase (Permutt, 1965) and interstitial pressure and inherent vascular tone acting to decrease (Hughes et al. 1967) the calibre of the extra-alveolar vessels. In the dependent lung at volumes less than TLC, the lung is less well expanded, and thus resistance in the extra-alveolar vessels is expected to increase. Indeed, data from several studies suggest that this is the case (e.g. Hughes et al. 1967, 1968). However increased lung inflation also elongates pulmonary blood vessels axially, increasing resistance to flow (Sun et al. 1987), and it has been shown in isolated lung preparations that the effects on extra-alveolar vessels of radial traction and axial elongation induced by lung inflation are largely counterbalanced (Sun et al. 1987). Consistent with this idea, data from the present study suggest that perfusion to the most dependent lung changes little with lung inflation, and thus this mechanism is unlikely to be the explanation for reduced perfusion in the dependent lung.

Modelling studies suggest that vascular structure and longer vascular pathways (increasing resistance) are the primary determinant of the reduced flow in dependent lung irrespective of posture (Burrowes et al. 2005a,b;). Our data are also consistent with this, since the vascular branching structure of the lung does not change with lung volume. Some authors have suggested that hypoxic pulmonary vasoconstriction in regions of dependent airway closure (Prefaut & Engel, 1981; Petersson et al. 2006) or inherent vascular tone in extra-alveolar vessels (Nemery, 1983) could also account for reduced perfusion in dependent lung under some conditions and this cannot be ruled out in our data. However, using the same techniques as the present study in a similar subject population, breathing hyperoxic gas mixtures had essentially no effect on the distribution of pulmonary blood flow measured at FRC (Arai et al. 2009), making this explanation for reduced perfusion in dependent lung unlikely.

Correction for regional tissue distribution in the measurement of pulmonary perfusion

In healthy humans imaging studies consistently show a gravitational gradient in pulmonary perfusion (Anthonisen & Milic-Emili, 1966; Maeda et al. 1983; Brudin et al. 1994a; Kosuda et al. 2000; Keilholz et al. 2001). In part these gradients are a result of gravitationally induced tissue distortion and alterations in regional density (Hopkins et al. 2007; Petersson et al. 2007). This is because dependent lung will contain more lung tissue (capillaries) and less air per unit volume, and thus have a greater density. When imaged externally there will be a correspondingly larger apparent regional perfusion in dependent than non-dependent regions (Hopkins et al. 2007). Thus, in imaging studies, it is important to correct for lung distribution inside the thorax, as many authors have done.

In xenon studies of pulmonary blood flow, (Ball et al. 1962; Anthonisen & Milic-Emili, 1966; Hughes et al. 1968) this was accomplished by injecting the tracer dissolved in saline at the lung volume of interest, and then after a few seconds having the subject inhale to TLC where images were acquired. At TLC the assumption is made that the alveolar size is uniform and thus non-uniform tissue distribution is eliminated. As seen in Fig. 2, our lung proton density data largely support this idea. In the present study, we accounted for distribution of the lung inside the thorax by measuring the regional water content (proton density) and expressing our measurements of perfusion in ml min⁻¹ g⁻¹. Although, the blood volume component of the our density measurements is not part of the lung tissue, the weight of the blood represents a significant portion of the weight of the lung and has an important contribution to the effect that gravity has on the lung. However it should be noted that this approach does not fully correct for the distribution of alveolar tissue, as discussed below. It is important to note that the distribution of blood volume is unlikely to change during the short 8 s breathhold over which the imaging took place and is not likely to account for the differences in perfusion in dependent lung observed at different lung volumes observed in our study.

Study limitations

Our techniques have technical limitations that largely affect absolute quantification (see Henderson et al. 2009 for details). We have corrected for absolute calibration by incorporating reference phantoms in our imaging protocols, and the absolute quantification derived thus reflects the accuracy of the reference phantoms. However, since this factor is constant over the course of the study it cannot affect the conclusions. Correction for heterogeneity of the coil elements potentially affects the measurements of regional lung density, but not the measurements of density normalized perfusion. This is because both the proton density measurements and the un-normalized perfusion measurements are subjected to the same coil sensitivity profile and thus cancel out.

Our measurements are limited by our ability to acquire data during a short (∼8 s) breathhold, and also by the need to acquire the perfusion and density images during separate breathholds, which may introduce some error into these measurements, particularly in inexperienced subjects. However, our subjects were well trained, the level of the breathhold volume was highly reproducible (R= 0.999), and our measures of perfusion highly reliable (Levin et al. 2007), and thus the error associated with this is minimal. A significant advantage of our techniques is that the number of images that can be acquired is not limited by issues such as dye or radiation dosage, and thus we are able to make multiple measurements in each subject under each condition and average the results, increasing confidence in the results. Our density quantification measures only free protons (essentially water) and the measured density distribution may be incorrect if lung tissue without protons is distributed differently than water in the lung. In our work is not possible to correct our distribution of blood flow by tissue distribution per se, because our density measures include all protons – those that are both in the tissue and in blood. Thus the pattern of the density normalized perfusion distribution we obtain will differ from those in which tissue distribution is uniform (such as the early data collected at TLC; Hughes et al. 1968) to the extent that the distribution of blood volume differs from the distribution of lung tissue. There are two pieces of evidence that suggest that this is a relatively small effect. Firstly, if the distribution of blood volume differed greatly from the distribution of lung tissue, with dependent vessels having a significantly greater blood volume than the non-dependent lung, it would be expected that in our measures at TLC a persistent density slope would be observed, and the most dependent lung would have greater density than the non-dependent lung. However, this is not the case, and our measures of proton density do not show a gravitational gradient at TLC, in keeping with previous assumptions (Hughes et al. 1968). Secondly, in studies where the measurements of blood volume and extravascular density were obtained using positron emission tomography (Brudin et al. 1987) the ratio of extravascular lung density to blood volume varied remarkably little over most of the vertical height of the supine lung, and overall lung density (air, tissue, blood) largely tracks with the regional air content (i.e. alveolar size) (Brudin et al. 1994b) and not the distribution of blood volume.

Our study examined only the right lung to avoid imaging artifacts from the heart on the left side of the chest. However, in the upright posture the distribution of perfusion has been shown to be similar between the left and right lung (West & Dollery, 1960) and this effect is likely to be small. Differences in posture (supine compared to upright) are one possible reason why the results of our study could differ from previous work (Hughes et al. 1968). This is because the gradient in intra-pleural pressures is less in supine than upright posture. However, other studies have supported the idea that the gravitational influence on pulmonary perfusion is still present in the supine lung (Brudin et al. 1987, 1994a; Prisk et al. 1994; Hopkins et al. 2007; Petersson et al. 2007) even though the vertical height is reduced. Since the posture does not vary between lung volumes in our study and the ‘Zone 4’ effect is clearly evident, this should not affect the interpretation of our results.

Using high resolution quantitative techniques, the present study shows that the distribution of pulmonary blood flow as a function of vertical height is largely similar irrespective of lung volume. In particular, the region of reduced perfusion seen in dependent lung (Zone 4) does not change with lung inflation, although perfusion is reduced in the most non-dependent lung at TLC. Taken together these data suggest that the effect of low lung volumes acting to increase resistance in extra-alveolar vessels may be less than previously thought, and does not account for reduced perfusion in dependent lung. Modelling studies suggest that vascular branching structure affects regional blood flow because neighbouring regions of lung are supplied by similar parent vessels and thus share similar perfusion characteristics. In addition in the lung periphery, longer vascular pathways are associated with increased vascular resistance and thus flow is decreased in these regions (Burrowes et al. 2005a,b;). In light of our previous work showing no change in the distribution of perfusion with hyperoxia, and the current findings that perfusion in the dependent lung does not change with lung volume, the effect of local branching structure on regional blood flow appears to be the most likely explanation.

Glossary

Abbreviations

ASL

arterial spin labelling

FAIRER

flow sensitive alternating inversion recovery with an extra radiofrequency pulse

FEV₁

forced expiratory volume in 1 s

FLASH

fast low-angle shot

FRC

functional residual capacity

FVC

forced vital capacity

MRI

magnetic resonance imaging

RV

residual volume

T₁

longitudinal relaxation time

T₂

transverse relaxation time

T₂*

apparent transverse relaxation time

T_E

echo time

T_I

inversion time

TLC

total lung capacity

Author contributions

This study was performed in the Pulmonary Imaging Laboratory at the University of California, San Diego. S.R.H., G.K.P. and D.L.L. participated in the conception and design of the experiments. S.R.H., T.J.A., A.C.H., D.L.L. and G.K.P. participated in the data collection, and ACH and TJA performed analysis and compilation of the quantified MRI data. R.B.B. and A.C.H. participated in developing analysis tools and techniques. All the authors were involved in further data analysis and interpretation of the data. S.R.H. wrote the manuscript with the assistance of G.K.P., and with additional intellectual input from R.B.B. All authors approved the manuscript as submitted.

Author's present address

D. L. Levin: Department of Radiology, Mayo Clinic, Rochester, MN, USA.