Effect of Cell-Free Layer Variation on Arteriolar Wall Shear Stress

Abstract

Relationship between a cell-free layer and wall shear stress (WSS) in small arterioles has been of interest in microcirculatory research. However, influence of temporal variation in the cell-free layer width on the WSS in vivo has not been fully elucidated. In this study, we tested the hypothesis that the layer variation would increase the WSS, and this effect would be enhanced by red blood cell aggregation. The cell-free layer width in arterioles (29.5–67.1 μm ID) in rat cremaster muscles were obtained with a high-speed video camera, and the layer width data were introduced into WSS estimation. Dextran 500 was administrated to elevate the aggregation level of red blood cells to those seen in normal human blood. The variation of the layer was quantified by the variability (coefficient of variation), and its effect on WSS was studied under normal and reduced flow conditions. We found that the dextran-induced red blood cell aggregation significantly elevated the variability (p < 0.01) at low pseudoshear rates of 9.2 ± 0.6 s⁻¹. The WSS estimated without taking account of the variability showed underestimation of its value than that of with consideration of the variability under all flow conditions, and this effect became more pronounced with increasing the variability. The variation of the cell-free layer should, therefore, be considered in the determination of the WSS particularly in the presence of red blood cell aggregation under reduced flow condition.

Introduction

The arteriolar wall shear stress (WSS) has been of interest as a dominant mechanical force in regulating endothelial cell (EC) functions and vessel homeostasis.8,33 A significant role of the WSS is to stimulate release of endothelium-derived nitric oxide (NO) which is a mediator of smooth muscle relaxation.10,33 The production rate of NO in general relies on the exposed level of the WSS to ECs, and the relationship between them was reported to be proportional.13,26 In addition, the oxygen release from arterioles appears to be related to WSS since the latter was significantly increased by a reduction in oxygen concentration in the vessels.6 Due to its physiological importance, there have been a large number of studies to estimate WSS in small vessels both in vivo 2,22,29 and in vitro. 12,32 However, due to the technical difficulties associated with WSS measurement and complexity of the microvascular structure, in vivo information of the WSS under various rheological conditions has been very limited.31

One of the prominent hemodynamic features in microvascular blood flow is the phase separation of red blood cells and plasma, which leads to formation of a cell-free layer adjacent to the endothelium in arterioles and venules.18,19 This phenomenon is being attributed to the tendency of red blood cells and their aggregates to migrate toward the vessel center.9,19,24 Thus, the cell-free layer formation can be influenced by a number of rheological factors such as hematocrit, red blood cell deformability, aggregability, vessel diameter, and flow rate.24 In our previous study, we confirmed that the layer formation in arterioles can be enhanced by a combination of red blood cell aggregation induction and flow reduction.25

There are several physiological implications of the cell-free layer. It could attenuate the flow resistance in microvessels by reducing friction between red blood cells and ECs.35,36 Alternatively, the layer may become a diffusion barrier for oxygen transport to tissues or reduce the scavenging of NO by red blood cells.5,7,21 The cell-free layer exhibits dynamic changes in its width, and previous studies have shown that it is important to consider such variation in the layer as it may alter the effective magnitude of WSS response.18,34 Temporal changes in the cell-free layer width were evident from previous studies that were performed to simulate physiological and pathophysiological states of red blood cell aggregation.18,25 An increase in red blood cell aggregation coupled with a reduction in flow under pathophysiological conditions was found to result in a more irregular interface between the red blood cell core and cell-free layer, providing evidence of greater layer variation under rheological abnormalities.25 While the cell-free layer itself is capable of attenuating WSS by lowering effective blood viscosity, the variation in the layer could potentially offset this effect by a certain extent through augmenting the WSS and this effect may be more pronounced under pathophysiological conditions.34 Such modulation of WSS in microvessels could also be a critical determinant of EC response to blood flow since these cells are highly sensitive to microscale subcellular shear stress distribution.3 Despite the considerable physiological implications that the cell-free layer can impose through WSS changes in microvascular flow, in vivo quantitative information on how the layer variation can affect the WSS has not been available.

As the cell-free layer characteristics are dependent on red blood cell aggregation, the first part of this study was carried out to provide information on how this blood rheological property could affect the layer variation. We then examined how such changes in layer variation could influence the WSS in vivo. We hypothesized that the layer variation would induce an increase in WSS and this effect would be enhanced by red blood cell aggregation. A new method of approximating the WSS in vivo was proposed and validated by an in vitro microtube system. The rat cremaster muscle was exteriorized for visualization of the cell-free layer formation in arteriolar blood flow, and Dextran 500 was used to induce red blood cell aggregation in the rat. In addition, our recently developed image analysis method16 was employed to provide detailed temporal information of the cell-free layer under different rheological conditions in the arterioles.

Materials and Methods

Animal Preparation

Animal handling procedures were provided according to the Guide for the Care and Use of Laboratory Animals (Institute for Laboratory Animal Research, National Research Council, Washington, DC: National Academy Press, 1996) and approved by the local Animal Subjects Committee. A total of 12 arterioles in the cremaster muscles from Wistar-Furth rats (202.8 ± 18.5 g) were used in this study. The animal was placed on a heating pad to maintain body temperature at 37 °C during surgery, and a tracheal tube was inserted to assist ventilation. The femoral artery was catheterized for blood withdrawals and pressure measurements, whereas the jugular vein was catheterized for administration of anesthetic, Dextran 500 (average molecular mass of 460 kDa; Sigma) dissolved in saline (6%), and other solutions. The rat cremaster muscle was exteriorized and prepared for intravital microscopy. An in vivo metrics 1.5 mm ID pneumatic cuff was placed on the abdominal aorta to adjust arterial pressure to the muscle. A heating element maintained the muscle temperature at 35 °C during the entire experiment. The detailed descriptions on the animal preparation have been reported in our earlier studies.15,18

Hematocrit, Aggregation, and Arterial Pressure Measurements

The hematocrit was measured with a microhematocrit centrifuge (Readacrit, Clay Adams) and aggregation level of red blood cell was determined with an aggregometer (Myrenne aggregometer; Myrenne, Roetagen, Germany) periodically during the experiments. A physiological data-acquisition system (MP 100 System; BIOPAC Systems, Goleta, CA) was used to monitor arterial pressure in the femoral artery.

Experimental Protocol

An unbranched region was selected for the study based on stable flow, clear focus, and contrast of the image. An intravital microscope (Ortholux II, Leitz) was used with a water-immersion objective (40×, Olympus) and a long working distance condenser (Instec, Boulder, CO), which has numerical apertures of 0.7 and 0.35, respectively. A blue filter (Spectra Physics, no. 59820) with peak transmission at 400 nm and spectral bandpass of 300–500 nm was used to enhance the contrast between red blood cells and the background field. The blood flow was recorded at 1125–4500 frames/s with a high-speed video camera (FASTCOM ultima SE, Photron USA) for 1–4 s, depending on the flow rate in the vessel.

In this study, we obtained data from 4500 frames for all conditions, at normal and reduced arterial pressures before and after dextran infusion. The pneumatic cuff pressure was increased with an air-filled syringe to lower the femoral artery pressure to ~50 mmHg and maintained by manual adjustment. Dextran 500 was used to induce red blood cell aggregation. A total of 200 mg/kg body wt was infused over the time course of 1–2 min to achieve an estimated plasma dextran concentration of ~0.6%. Our previous studies17,18 reported that this concentration of Dextran 500 raised the aggregation level up to those seen in normal human blood. After dextran treatment, an additional blood sample was taken to determine hematocrit and aggregation level.

Pseudoshear Rate Determination

The edge velocity of the red blood cell core was determined by tracking movements of outermost cells manually across 10 digital frames using image analysis software (SigmaScan Pro 5). The pseudoshear rate 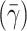used in this study was defined as follows:

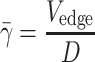1

where V _edge is the mean edge velocity of red blood cell core and D is the vessel diameter.

Cell-Free Layer Width and Its Variability

The cell-free layer width at a specific location was determined from the positions of the inner vessel wall and the outer edge of the red blood cell core. A typical example of the variation in the layer width is shown in the lower part of Fig. 1. The detailed image analysis method to determine the width of the layer is available in our earlier reports.16,18 To quantify the layer variation, the statistical concept of coefficient of variation (variability) was employed, which represents the ratio of the standard deviation of the layer width to its mean.

Figure 1.

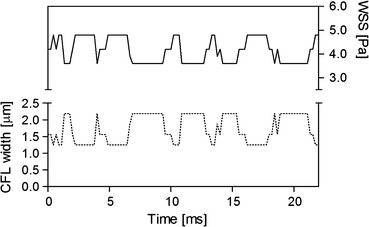
Relationship between the cell-free layer (CFL) width and wall shear stress (WSS). The solid and dotted lines represent the WSS and CFL width obtained in an arteriole (50 μm ID), respectively. Only 100 data selected from 4500 frames are shown here

Wall Shear Stress Estimation

In estimation of the WSS, we assumed that the plasma flow in the cell-free layer is steady and the velocity gradient in the layer is linear. Thus, the WSS (τ) could be estimated with the plasma viscosity and slope of the linear velocity profile as follows:

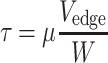2

where μ is the plasma viscosity and W is the cell-free layer width. The dextran treatment increases plasma viscosity as well as level of red blood cell aggregation.20,28,39 However, in our in vivo study, the plasma viscosity effect on the WSS was isolated by using the same plasma viscosity value (1.3 cP)37 in determination of the WSS for all conditions. As shown in the upper part of Fig. 1, using Eq. (2), the WSS is inversely related to the cell-free layer width. The WSS (τ*) under the influence of the temporal variation in the layer width was obtained by averaging the individual WSS (τ _i) derived from each value of the layer width (Eq. (3)) at respective times. The result was then compared to that obtained without consideration of the variation in the layer width. For the latter, the cell-free layer widths over 4500 frames were averaged and the resultant mean width was used to estimate the WSS (Eq. (4)). In Eqs. (3) and (4), i denotes a frame number.

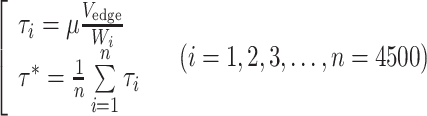3

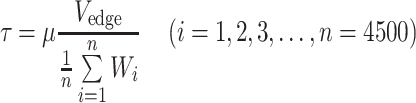4

In Vitro Setup

We constructed an in vitro microtube system to test our hypothesis that WSS may be estimated from the cell-free layer width and plasma viscosity (Eq. (3)). The inner diameter of each glass microtube (Polymicro Technologies, Phoenix, USA) was determined from pressure-flow measurements with distilled water while the length of the tube was measured with the vernier caliper. The inner diameter and length were 50–52 μm and 55–60 mm, respectively. The ratio of length to inner diameter was over 1000:1 so that pressure drops in other parts of the system could be neglected. Reflective index (RI) of the glass tubes (fused silica) was 1.45 for the halogen light spectrum from 650 to 1050 nm and the tubes were immersed in kerosene (RI = 1.45) during blood flow visualization to minimize measurement error for the cell-free layer width, which could be caused by the common RI problem in circular tubes. Heparinized rat blood samples were obtained from donor rats, and all the measurements were completed within 1 h after blood withdrawals. The estimated WSS values using Eq. (3) were compared with those calculated using Eq. (5) shown below with pressure drop information obtained with the differential pressure transducer (MP 100 System, CA, USA) and a syringe pump (Harvard Apparatus, MA, USA). The plasma viscosity was determined with a cone-and-plate viscometer (Brookfield Engineering Laboratories, Inc., MA, USA)

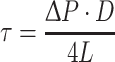5

where ∆P is the pressure difference between inlet and outlet of the microtube and L and D are the length and inner diameter of the microtube, respectively.

Statistical Analysis

A statistical software package (Prism 4.0, GraphPad) was used for all statistical analyses. An unpaired t-test was utilized to compare two groups before and after dextran treatment while linear and nonlinear regressions were performed to find a significant relation between the two parameters. All physiological and rheological values are represented as means ± SD. For all tests, p < 0.05 was considered to be statistically significant.

Results

In Vitro Validation

As shown in Fig. 2, the WSS estimated from the cell-free layer width and plasma viscosity agreed within ±20% with that determined with the pressure drop measurements, and R ² value for the linear regression was 0.76. The error range was similar to that reported with the μ-PIV method by Long et al.23 using fluorescent nano-particles. The pseudoshear rate range used for this comparative study was 130–290 s⁻¹. The good agreement of the WSS estimated from the cell-free layer method with that determined by the conventional pressure drop measurement indicates that the cell-free layer method has promise for in vivo use and thus may provide valuable new information where it is currently lacking.

Figure 2.

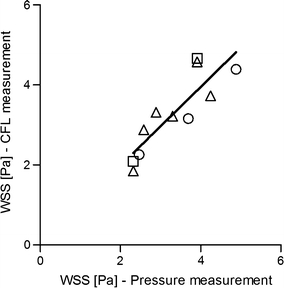
In vitro validation of the WSS estimation with the cell-free layer width and plasma viscosity. The solid line represents the linear regression fit (y = 0.984x + 0.014; R ² = 0.76) for the combined group of three different conditions (○: without dextran treatment at 30% hematocrit, ∆: with dextran treatment at 30%, and □: without dextran treatment at 35%)

Systemic Values in In Vivo Experiments

Control arterial pressure was 112 ± 13.7 and 108 ± 4.7 mmHg before and after dextran treatment, respectively. After arterial pressure reduction, the pressure fell to 47 ± 7.9 and 47 ± 5.5 mmHg in normal and dextran-treated rats, respectively. For both control and reduced pressure cases, there was no significant difference between the two pressure values before and after dextran treatment. The index of red blood cell aggregation (M) determined by the Myrenne aggregometer was 0.0 (no aggregation) before dextran treatment, whereas it increased to 9.9 ± 1.4 after dextran treatment, which is similar to levels found in normal human blood.17,18 Systemic hematocrit was 39 ± 1.8% and 38 ± 1.0% before and after dextran treatment, respectively, with no significant changes. The diameter range of arterioles used in this study was 29.5–67.1 μm.

Cell-Free Layer Characteristics

Pseudoshear rate in arterioles at normal arterial pressure was 187.9 ± 52.5 and 177.4 ± 32.8 s⁻¹ before and after dextran treatment. After reduction of arterial pressure, the pseudoshear rate dropped to 34.0 ± 19.9 and 31.5 ± 18.4 s⁻¹ before and after dextran treatment, respectively. Our recent study25 with similar pressure reduction to that in this study reported that flow velocity in arterioles might be nonuniformly reduced by the arterial pressure drop. Thus, to examine red blood cell aggregation effect on the cell-free layer variability, we divided all the data into three different pseudoshear rate groups based on their mean values (<10 s⁻¹, >40 s⁻¹, and <60 s⁻¹, >100 s⁻¹). Thus cell-free layer data were grouped into three flow conditions, at 182.8 ± 43.8, 47.9 ± 3.0, and 9.2 ± 0.6 s⁻¹. There was no significant effect of dextran treatment on the cell-free layer variability (Fig. 3) at relatively high pseudoshear rates (182.8 ± 43.8 and 47.9 ± 3.0 s⁻¹), whereas red blood cell aggregation significantly increased the layer variability (p < 0.01) at 9.2 ± 0.6 s⁻¹.

Figure 3.

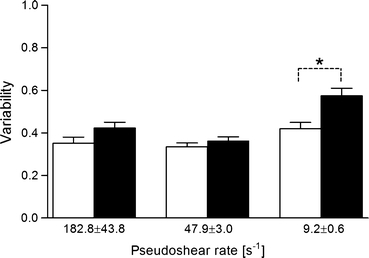
Effect of red blood cell aggregation on variability of the cell-free layer. □: Before dextran infusion. ■: After dextran infusion. * p < 0.01

Wall Shear Stress

Figure 4 shows the ratio of the WSS with consideration of the variation in the cell-free layer (τ*) to that when there is no variation in the layer width (τ). The ratio was higher than 1.0 regardless of pseudoshear rates and increased with an elevation of the variability at all pseudoshear rates. Furthermore, this effect became more pronounced at low shear rates based on the larger coefficient (B₂) that describes the steepness of the fitted curve. There was a slight shift in range of the layer variability from 0.26–0.67 to 0.34–0.81 after dextran treatment, which is not surprising according to the findings shown in Fig. 3.

Figure 4.

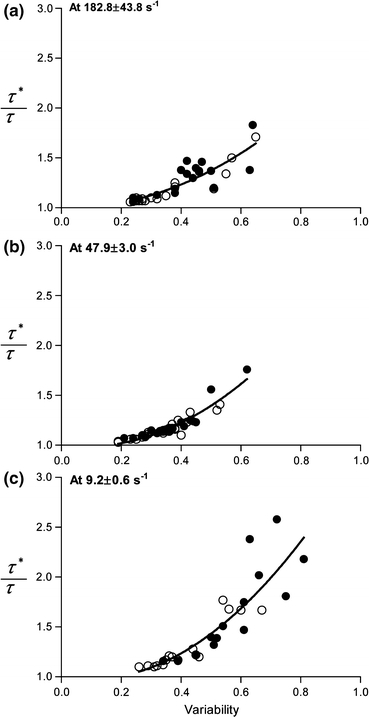
Ratio between estimated WSS values with (τ*) and without (τ) consideration of variations in the cell-free layer width as a function of the layer variability. The nonlinear regression was performed with a quadratic function (y = B ₀ + B ₁ x + B ₂ x ², where B ₀ is 1) for the combined group (before (○) and after (●) dextran treatment). y = 1 − 0.07x + 1.64x ²; R ² = 0.76 at 182.8 ± 43.8 s⁻¹. y = 1 − 0.36x + 2.31x ²; R ² = 0.88 at 47.9 ± 3.0 s⁻¹. y = 1 − 0.52x + 2.77x ²; R ² = 0.77 at 9.2 ± 0.6 s⁻¹

Discussion

The salient finding of this study is that cell-free layer variability in the arterioles was significantly augmented by aggregation induction at reduced flow rates, which in turn could potentially lead to an enhancement of WSS in the arterioles.

Limitations in WSS Approximation

In this study, the averaged edge velocity of red blood cell core was used in estimation of the WSS although blood flow might still be unsteady in arterioles.27,38 We have previously pointed out that during the cardiac cycle, the edge velocity of the red blood cell core at normal arterial pressure might vary by ±6–7% from the mean value.18 Therefore, by considering the pulsatile nature of the arteriolar flow, the actual variation of the WSS may differ from our estimation by a maximum of 6–7%. However, under reduced flow conditions, the flow pulsatility would be much lower than that in normal flow conditions. Thus, effects of the unsteady flow on the WSS estimation in low shear conditions may not be as significant. The spatial resolution of the cell-free layer width measurement with the current microscope system was reported to be ~0.4 μm,18,25 which limits the accuracy of our WSS estimation since one of the key parameters in Eq. (2) determining the WSS is the width of the cell-free layer. Thus, variability in the layer width smaller than the systemic spatial resolution cannot be detected with the current system.

Estimated Arteriolar WSS

A number of studies have provided information on arteriolar WSS in a variety of species and tissues. The WSS in resting cat sartorius muscle arterioles (~60 μm ID) was estimated to be ~6 Pa with bulk viscosity of blood at 45% hematocrit.27 A previous study carried out with the rat cremaster muscle estimated the WSS to be approximately 1.0–4.5 Pa in larger arterioles (160–220 μm ID) using 3.8 cP of blood viscosity.2 In a recent review by Reneman and Hoeks,31 the WSS in mesenteric arterioles was found to be 0.51–5.0 Pa in rabbits and 4.71 ± 2.34 Pa in cats. Pries and coworkers30 reported that the WSS of ~5 Pa with a substantial variation observed in rat mesenteric arterioles (>15 μm ID). In this study, the mean arteriolar WSS varied from ~0.3 to 7.5 Pa under normal and reduced flow conditions, which is in agreement with the range of values reported in previous studies. However, since the WSS is a function of several rheological conditions such as vessel size, viscosity, and flow velocity, it may not be feasible to directly compare the WSS values under different physiological and rheological situations.

Effect of Aggregation on Cell-Free Layer Variability and WSS

As shown in Fig. 3, the variability of the cell-free layer significantly (p < 0.01) increased after dextran treatment only at 9.2 ± 0.6 s⁻¹, which was reflected in a shift of the variability range toward higher magnitudes after dextran infusion in Fig. 4c. Although there were no statistical differences in the variability before and after dextran treatment at the other two shear rates (182.8 ± 43.8 and 47.9 ± 3.0 s⁻¹), it appeared to be consistent that the variability increased after dextran treatment. These findings were in consensus with those reported in previous in vitro 1 and in vivo studies18,25 performed in narrow vertical tubes (28–101 μm ID) perfused with human blood and in arterioles in rat cremaster muscle (10–60 μm ID), respectively. The results in this study imply that red blood cell aggregation may play a major role in altering the cell-free layer variability, in particular at regions of blood flow characterized by low pseudoshear rates (<10 s⁻¹). Similarly, our earlier in vivo studies18,25 have substantiated that apparent changes in cell-free layer characteristics under similar aggregating conditions are only observed at low pseudoshear rates (<50 s⁻¹). It should be noted that pseudoshear rates used in this study were based on the flow velocity near the vessel wall, whose magnitude would be less than that of mean cellular velocity. Therefore, for the same flow conditions, the pseudoshear rates reported here should be smaller than those in previous studies, which were based on the mean cellular velocity.

As shown in Fig. 4, the layer variability ranged approximately from 0.2 to 0.6 even without dextran induction under similar flow conditions. It should be noted that the variability data were obtained from 12 arterioles which can have different local hematocrits. Furthermore, it is well known that local hematocrits can take on a wide range of values even for vessels of the same order in the same arteriolar network.11 Since cell-free layer characteristics are dependent on hematocrit, it is expected that the cell-free layer can exhibit a wide range of variability between similar diameter vessels even in the absence of red blood cell aggregation and/or under similar flow conditions.

The results shown in Fig. 4 suggest that the variability of the cell-free layer can be an important parameter which causes an elevation of the WSS, particularly at low pseudoshear rates where red blood cell aggregation could enhance the layer variability. In a computational study by Sharan and Popel,34 they showed that the effective blood viscosity near the vessel wall increased with greater interface roughness between red blood cell core and the cell-free layer in vessel ranges of 25–70 μm at 45% hematocrit. Their finding is qualitatively in agreement to that in this study, as an increased effective viscosity would lead to an augmentation in WSS. Therefore, we emphasize here the importance of considering the cell-free layer variation in WSS determination which otherwise could result in an underestimation of the WSS, by as much as two folds, with high variability (~0.7) observed under aggregating condition at 9.2 ± 0.6 s⁻¹ (see Fig. 4).

Figures 5a and 5b represent respective conceptual sketches of flowing red blood cells in a vessel illustrating the effect of temporal variation in the cell-free layer on WSS. We compared the two cases (Figs. 5a and 5b) with the same mean width of the cell-free layer. When the WSS was obtained from blood flow with no variation in the cell-free layer width (Fig. 5b), the mean WSS could be lower than that in the situation with variation in the layer width (Fig. 5a). Our previous studies18,25 have shown that a wider cell-free layer would allow a higher degree of variability of the layer and vice versa. In the event where the magnitude of WSS is small due to a thick cell-free layer, the corresponding large variability in the layer may partially compensate the effect of the thick layer on the WSS. It should be further noted that for there to be no change in the WSS on the average, individual cell-free layer width data should be symmetrically distributed about their mean value. As shown by our previous study,25 the layer width data follow a non-Gaussian distribution and, therefore, are not symmetrical about their mean value; hence, a change in the WSS on the average is expected.

Figure 5.

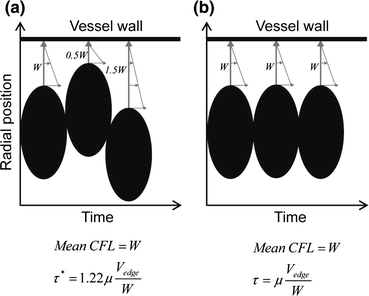
Two-dimensional sketch of red blood cells flowing in a vessel illustrating the effect of temporal variation in the cell-free layer on wall shear stress. (a) and (b) represent two different situations for τ* (with consideration of the layer variation) and τ (without consideration of the layer variation). The same cellular velocity was assumed in the two situations. Black ellipsoids represent individual red blood cells

Physiological Implication

The inverse relationship between the cell-free layer width and the WSS suggests that NO production could be inevitably affected by the layer formation since WSS is a mechanical stimulus for endothelium-derived NO synthesis. However, overall NO bioavailability that ultimately influences vascular tone would also be dependent on other physiological aspects associated with the layer. The cell-free layer could act as a diffusion barrier that could potentially minimize NO scavenging by the red blood cells.5,14,21 In addition, we presented here the possibility of cell-free layer variability to improve NO preservation by enhancing the WSS. All of these factors may contribute to the local regulatory mechanism of vasodilation. In normal flow conditions, it is likely that the WSS can sufficiently stimulate the production of NO in the endothelium, in a way that could cancel out any potential scavenging effect of NO by the red blood cells. On the contrary, in low flow conditions, the diminishing magnitude of the WSS acting on the endothelium due to the effects of lower hydrodynamic forces and more prominent cell-free layer formation in the presence of aggregation can attenuate NO production. It has been demonstrated that enhanced red blood cell aggregation in suspensions used for perfusion of glass capillaries led to the down-regulation of NO synthesizing mechanisms in human umbilical vein ECs coating the capillaries.40 In vivo studies have also supported this finding.4 In contrast, our findings would suggest that an enhanced layer variability due to aggregation induction could oppose the above response on endothelial NO production by augmenting the WSS. It should be noted that this variability effect might be offset by reduction of WSS due to the thicker cell-free layer.