Pharmacokinetic analysis of pralidoxime after its intramuscular injection alone or in combination with atropine-avizafone in healthy volunteers

Abstract

BACKGROUND AND PURPOSE

Treatment of organophosphate poisoning with pralidoxime needs to be improved. Here we have studied the pharmacokinetics of pralidoxime after its intramuscular injection alone or in combination with avizafone and atropine using an auto-injector device.

EXPERIMENTAL APPROACH

The study was conducted in an open, randomized, single-dose, two-way, cross-over design. At each period, each subject received either intramuscular injections of pralidoxime (700 mg), or two injections of the combination: pralidoxime (350 mg), atropine (2 mg), avizafone (20 mg). Pralidoxime concentrations were quantified using a validated LC/MS-MS method. Two approaches were used to analyse these data: (i) a non-compartmental approach; and (ii) a compartmental modelling approach.

KEY RESULTS

The injection of pralidoxime combination with atropine and avizafone provided a higher pralidoxime maximal concentration than that obtained after the injection of pralidoxime alone (out of bioequivalence range), while pralidoxime AUC values were equivalent. Pralidoxime concentrations reached their maximal value earlier after the injection of the combination. According to Akaike and to goodness of fit criteria, the best model describing the pharmacokinetics of pralidoxime was a two-compartment with a zero-order absorption model. When avizafone and atropine were injected with pralidoxime, the best model describing pralidoxime pharmacokinetics becomes a two-compartment with a first-order absorption model.

CONCLUSIONS AND IMPLICATIONS

The two approaches, non-compartmental and compartmental, showed that the administration of avizafone and atropine with pralidoxime results in a faster absorption into the general circulation and higher maximal concentrations, compared with the administration of pralidoxime alone.

Introduction

Organophosphates are extensively used around the world as agricultural insecticides and have an important toxicity, which is a serious global public health problem. These agents were developed chiefly by Schrader shortly before and during World War II, first as agricultural insecticides and later as potential chemical warfare agents (Schrader, 1952). The extreme toxicity of these compounds was found to be due to their irreversible inactivation of acetylcholinesterase (drug target/receptor nomenclature in this paper follows Alexander et al., 2009), which resulted in long-term inhibitory activity.

The toxic signs include hypersecretion, respiratory distress, tremor, seizures/convulsions, coma and death (Hardman and Limbird, 2001; Wetherell et al., 2007). The increased cholinergic activity in the brain most likely induces the initial phase of seizures, whereas sustained seizures are probably linked to increased glutamatergic activity leading to excitotoxic lesions predominantly in piriform cortex, entorhinal cortex, amygdala and hippocampus (Carpentier et al., 1992; Lallement et al., 1992; McDonough et al., 1995; McDonough and Shih, 1997).

Administration of the muscarinic antagonist, atropine, early in the cycle (<5 min) can prevent or stop convulsions, but cannot stop them once they are established (McDonough and Shih, 1997; Taysse et al., 2006). Use of glutamatergic antagonists has been partly successful. Non-competitive N-methyl-d-aspartate antagonists are able to terminate seizures even if treatment is delayed for 40 min. However, such agents have severe side effects on respiration (Shih, 1990; Shih et al., 1991; McDonough and Shih, 1993; Carpentier et al., 1994). Glutamatergic activity may also be reduced by enhancing the inhibitory GABAergic function. It has been shown that the GABAergic agonist, diazepam, can stop seizures if injected 5–10 min after their occurrence. Later administration of diazepam has unreliable effects, inasmuch as seizures can recur and only an incomplete neuroprotection is achieved (McDonough and Shih, 1997).

Reactivation of inhibited acetylcholinesterase is considered to be an important element in post-exposure treatment. Bis-pyridinium oximes can reactivate the phosphorylated enzyme if they are given prior to the change from the reactivatable to the unreactivatable state, a process referred to as ‘aging’. If treatment with oximes is delayed, the phosphate bound to the inhibited cholinesterase loses an alkyl group and becomes resistant to oxime therapy (Pawar et al., 2006). The oximes pralidoxime and obidoxime have been widely used to treat this type of intoxication (Wetherell et al., 2007). Pralidoxime is one oxime commonly used as acetylcholinesterase reactivating agent. Its effect results from a molecular nucleophilic reaction with the organophosphate, removing it from the acetylcholinesterase site, thereby restoring the capacity of acetylcholinesterase to hydrolyse acetylcholine.

At present, the balance of published evidence favours early treatment of organophosphate toxicity (Eddleston et al., 2008; Eddleston, 2008) and the three drug treatment is currently packaged in a single auto-injector device containing a combination of avizafone hydrochloride (a diazepam prodrug), atropine sulphate and pralidoxime methyl sulphate. The formulation is a lyophilized powder to be diluted with water for injection before i.m. administration. A few clinical trials have been published evaluating the pharmacodynamic effects and doses needed in the treatment of organophosphorous pesticide poisoning (Pawar et al., 2006; Hmouda et al., 2008). However, no study has evaluated pralidoxime pharmacokinetics after its i.m. administration alone, or in combination with atropine-avizafone in humans.

The Pharmacie Centrale des Armées has developed an auto-injector device containing the three compounds. Two clinical studies have been conducted so far to evaluate the pharmacokinetics of the compounds and the safety of use of the device in healthy volunteers. The aim of the first study (Abbara et al., 2009) was to assess the relative bioavailability of diazepam after the i.m. injection of avizafone in healthy volunteers, and to determine the effect of atropine and pralidoxime on avizafone biotransformation after injection of the combination in healthy volunteers. The aim of the second study, the subject of the present paper, was to assess the pharmacokinetic parameters of pralidoxime in healthy human volunteers after i.m. administration of pralidoxime methylsulphate, alone or in combination with avizafone and atropine using the bi-compartmental auto-injector device.

Methods

Study design

The study was conducted in an open, randomized, single-dose, two-way, cross-over design, with two weeks washout period between the treatments, and was carried out at a single centre: Aster S.A.S Paris, France. All subjects had given written informed consent and the Ethics Committee had approved the clinical protocol.

Twenty healthy adult male volunteers aged between 18 and 45 years (29.7 ± 6.3 years, mean ± SD) were included in the clinical study. The mean weight of all subjects was 78.6 ± 9.40 kg (mean ± SD). All volunteers were assessed as healthy, based on medical history, clinical examination, blood pressure, electrocardiogram and laboratory investigation. There was no individual with either a history or evidence of hepatic, renal, gastrointestinal and haematological abnormalities, or any acute/chronic disease or drug allergy.

Each subject received the following treatments by i.m. injection: either 700 mg of pralidoxime methyl sulfate (Pharmacie Centrale des Armées, Orléans, France), or two injections of 350 mg of pralidoxime methyl sulfate combined with 20 mg of avizafone hydrochloride and 4 mg of atropine sulfate (Pharmacie Centrale des Armées, Orléans, France) using the bi-compartmental auto-injector (AIBC). This device, AIBC, contained in the first compartment the three components as lyophilized powders and, in the second compartment, 2.5 mL of water for injection.

Safety assessments included vital signs (supine and standing systolic and diastolic blood pressure and pulse), a physical examination, a 12-lead electrocardiogram and monitoring of adverse events.

To evaluate pralidoxime pharmacokinetics, blood samples were collected before i.m. administration, and 0.0833, 0.25, 0.5, 0.75, 1, 1.5, 2, 3, 4, 6, 8, 12 and 24 h after treatment administration. Blood samples were centrifuged and plasma was separated and stored at −80°C until drug assay.

In order to determine pralidoxime concentrations, protein precipitation was carried out with 150 µL of acetonitrile containing diazepam-D₅ as internal standard. Samples were then vortex-mixed, then centrifuged. The supernatant was transferred to micro-vials and 10 µL was injected into the chromatographic system. Samples were analysed by reverse phase high performance liquid chromatography using a C-8 X-Terra column maintained at 40°C. The mobile phase was nebulized using an electrospray source and the ionized compounds were detected using a triple quadrupole mass spectrometer (Abbara et al., 2008).

Calibration curves were linear over the range 5–2500 ng·mL⁻¹, with regression coefficient r²≥ 0.99. Based on quality control samples, the overall relative standard deviation was less than 12%. The overall relative error was less than 10%. The lower limit of quantification was 5 ng·mL⁻¹.

Data analysis

Data were analysed using two approaches. The non-compartmental approach was used to determine the main pharmacokinetic parameters related to pralidoxime bioavailability. The compartmental approach was used to obtain the best mathematical model fitting the data.

Non-compartmental approach

The non-compartmental model independent analysis was performed using WinNonLin® Pro v.4.1 (Pharsight Corporation, USA). For each subject, data corresponding to both treatments were analysed separately. Data were used to estimate individual maximal concentration (C_max) and time necessary to reach maximal concentration (t_max). In addition, for each treatment the terminal slope (λz), and the area under the concentration-time curve (AUC) were estimated. λz was estimated as the slope of the log-linear terminal portion of the plasma concentration versus time curve, determined using unweighted linear least squares regression analysis. The best number of concentrations was chosen as that giving the highest coefficient of determination, as recommended. Area under concentration-time curve was computed from 0 to 24 h using the combination of linear/log-linear trapezoidal method (implemented in WinNonLin) and extrapolated to infinity using the equation AUC_0–∞= AUC_0−t+ C_last/λz, where C_last is the last quantified concentration above the lower limit of quantification.

Additionally, from these estimated parameters, terminal half life after each treatment was derived as t_1/2= Ln2/λz.

Two parameters: AUC and C_max were then compared using the two one-sided test approach, which is also referred to as the confidence interval approach or Schuirmann test.

The 90% confidence limits are estimated for the sample means. The interval estimate is based on a Student's distribution of data. In this test, a 90% confidence interval about the ratio of pharmacokinetic parameter means of the two drug products must be within ±20% for measurement of the rate (C_max) and extent of drug bioavailability.

This approach was performed on the log-transformed AUC and C_max values. The t_max were then compared using a non-parametric test (Wilcoxon test, R 5.2.0 software, R development core team 2007).

Compartmental modelling approach

Pharmacokinetic models studied

The models compared in this study are standard WinNonMix® models. In order to describe the absorption after the i.m. injection, two absorption kinetic models were compared. First, the two-compartment model with first-order absorption and elimination rates described by the equation:

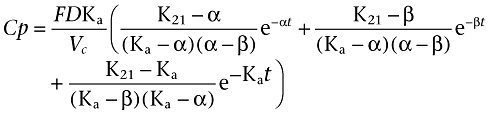Where K_a is the absorption rate constant, D is the dose administered by i.m. injection, F is the fraction of drug absorbed, α and β are constants that depend solely on K₁₂, K₂₁ (transfer constants between compartments 1 and 2) and K_e (elimination constant), and V_c is the volume of distribution in the central compartment.

The second model was a two-compartment model with zero-order absorption rate and first-order elimination rate and was described by the equation:

For t ≤ T

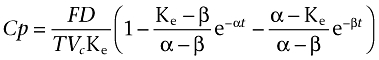and for t > T

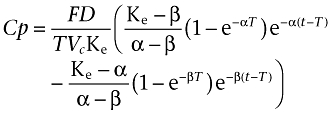Where T represents the duration of absorption, D the dose administered by i.m. injection, F is the fraction of drug absorbed, α and β are constants that depend solely on K₁₂, K₂₁ (transfer constants between compartments 1 and 2) and K_e (elimination constant), and V_c is the volume of distribution in the central compartment.

Estimation method

Population pharmacokinetic analysis was performed using WinNonMix software implementing the first-order conditional estimation method. WinNonMix computed the minimum value of the objective function, a statistic that is proportional to minus twice log-likelihood of the data.

Inter-individual variability in the parameters assigned a log-normal distribution across the population. Therefore, the distribution of the pharmacokinetic parameters was defined by: P_i= P_tot* exp (ηi), where Pi is the individual model parameter and P_tot is the population value with ηi being the normally distributed inter-individual variability with mean zero and variance ω².

A number of statistical models were tested for the residual error (additive, proportional, and combined additive and proportional), which was modelled using a combined error model. C_obs,ij= C_pred,ij*(1 +ε₁) +ε₂ where C_obs,ij and C_pred,ij are the observed and predicted concentrations, respectively for ith individual and denote the residual random error with mean zero and variance σ². The residual error describes the intra-individual variability and contains inexplicable error that arises from, for example, measuring experimental errors and model mis-specification.

The pharmacokinetic parameters were V_c, K_e, K₁₂, K₂₁, and an absorption parameter: K_a in the case of first-order absorption. In the case of zero-order absorption, T was fixed and determined as time necessary to reach the maximal concentration and that for each subject and each treatment individually.

From these parameters, several derived pharmacokinetic parameters were computed: AUC, t_max and C_max.

Comparison of models

The Akaike Information Criterion (AIC) was used to identify the best combination of models, as the first-order and the zero-order absorption models are not nested. This criterion can be viewed as the sum of a measure of the goodness of fit, and of a penalty function proportional to the number of estimated parameters in the model.

The goodness of fit was assessed graphically by evaluation of the agreement between the observed and the predicted pralidoxime concentrations, reductions in the range of weighted residuals, and uniformity of the distribution of weighted residuals about zero across the range of both the predicted concentrations and the time since last dose. In addition, increases in the precision of the parameter estimates and reduction in both inter-individual variability and residual variability were also used to discriminate between competing models.

Results

Non-compartmental approach

The mean plasma concentrations of pralidoxime (Table 1), obtained after both treatments, are plotted in Figure 1 on semi-logarithmic scale. Table 2 shows the main and derived pharmacokinetic parameters of pralidoxime obtained after a non-compartmental analysis of the data for both treatments. The results regarding pralidoxime relative bioavailability after both treatments are summarized in Table 3.

Table 1.

Mean (with SD) pralidoxime plasma concentrations in healthy volunteers after the two treatments: pralidoxime alone and pralidoxime, atropine, avizafone in AIBC

	Pralidoxime		AIBC
Time (h)	Concentration (ng·mL−1)	SD	Concentration (ng·mL−1)	SD
0.0833	1925.27	1780.91	2795.46	1596.98
0.25	3479.37	1711.76	4515.50	1482.86
0.5	3277.83	1039.29	3706.75	1125.36
0.75	2951.95	757.52	3260.98	816.37
1	2522.73	473.07	2679.63	808.15
1.5	2003.37	598.04	2073.77	586.08
2	1682.65	512.09	1652.55	547.03
3	1168.34	384.01	1108.46	516.58
4	897.18	374.13	755.09	241.64
6	383.92	137.21	357.25	124.67
8	230.46	112.49	209.43	101.39
12	85.67	60.15	72.13	38.19
24	6.79	4.28	7.38	4.35

Figure 1.

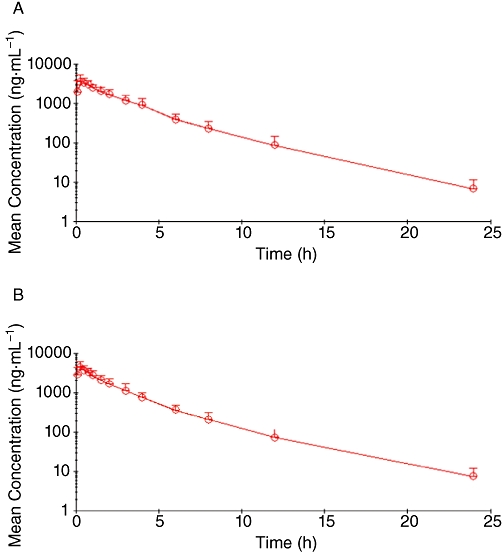
Semi-logarithmic plot of time course of pralidoxime mean concentrations after the intramuscular administration of pralidoxime alone (A), and pralidoxime with atropine and avizafone using the bi-compartmental auto-injector AIBC (B).

Table 2.

Estimated pharmacokinetic parameters of pralidoxime obtained with the non-compartmental approach

	Pralidoxime		AIBC
	Mean	SD	Mean	SD
AUC 0-t (h. ng·mL−1)	10 044	2488	10 187	2704
AUC 0-∞ (h. ng·mL−1)	10 070	2438	10 220	2650
tmax (h)#	0.63	0.52	0.33	0.21
Cmax (ng·mL−1)	3 988	1572	4 635	1408
λz (h−1)	0.235	0.033	0.215	0.028
t1/2 (h)	2.94	0.41	3.22	0.42

^#Medians for t_max: pralidoxime 0.50 h; AIBC 0.25 h.

Table 3.

Relative pralidoxime bioavailability after the two treatments: pralidoxime and AIBC

	Geometric means
Parameters	Pralidoxime	AIBC	Ratioa	P	90% CI
Cmax (ng·mL−1)	3725	4386	0.849	–	0.685–1.053b
AUC 0-t (h. ng·mL−1)	9764	9819	0.994	–	0.924–1.07
tmaxc (h)	0.50	0.25	–	<0.01	–

^aPralidoxime/AIBC.

^bBioequivalence criteria not met.

^cMedian.

The co-administration of atropine and avizafone with pralidoxime seemed to increase pralidoxime C_max. Application of the Schuirmann test showed that although the AUC 90% confidence interval was still in the range of 0.80–1.25, the C_max 90% confidence interval was out of this range. Pralidoxime concentrations reached their maximal value earlier when pralidoxime was administered in combination with avizafone and atropine (P = 0.0045).

Compartmental modelling approach

On a log scale, data appeared to exhibit a bi-exponential decline. Hence, two-compartment open models were studied in order to describe the pharmacokinetics of pralidoxime after the two treatments. A two-compartment model with zero-order absorption and first-order elimination was chosen to predict pralidoxime concentrations when it was given alone.

Meanwhile, two-compartment model with first-order absorption and elimination described, with a good fit, pralidoxime concentrations after its i.m. administration with atropine and avizafone. Figure 2 shows the population predicted concentrations for all individuals compared with the observed data. Inter-individual variability was described by an exponential error model, whereas residual variability was described by a combined exponential and additive error model.

Figure 2.

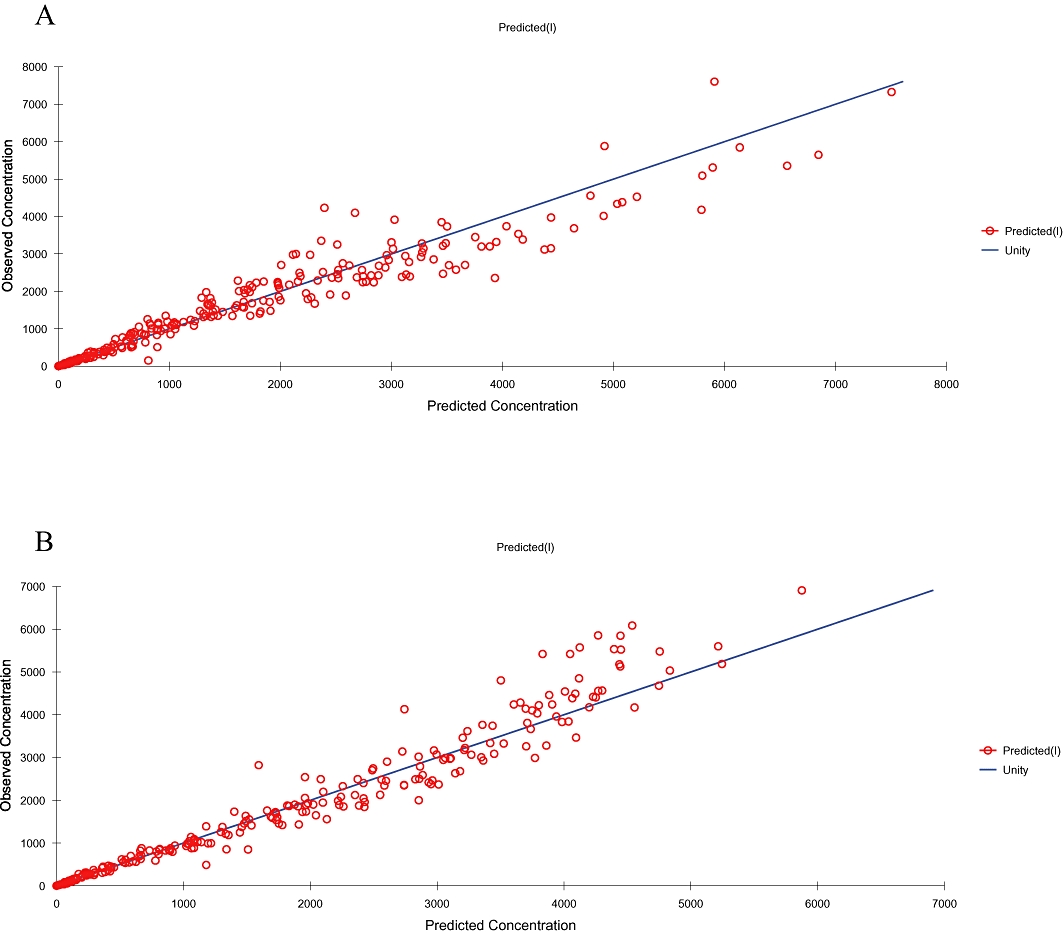
Scatterplot of observed versus individual predicted plasma pralidoxime concentrations indicated a closer distibution around the line of unity for pralidoxime alone (A) and AIBC (B).

For the chosen models, no trend was noted in the plots of standardized residuals versus predicted concentrations or versus time, as shown in Figure 3. The pharmacokinetic parameters estimated with the iterative reweighted least squares method are summarized in Table 4. The standard errors of individual estimates were also obtained, except for the time of absorption T in the model with zero-order absorption, which was fixed and determined as the t_max estimated using the non-compartmental approach. From the estimated pharmacokinetic parameters, AUC and C_max were derived for both treatments, while t_max was derived only for the treatment with pralidoxime in combination with atropine and avizafone (Table 5).

Figure 3.

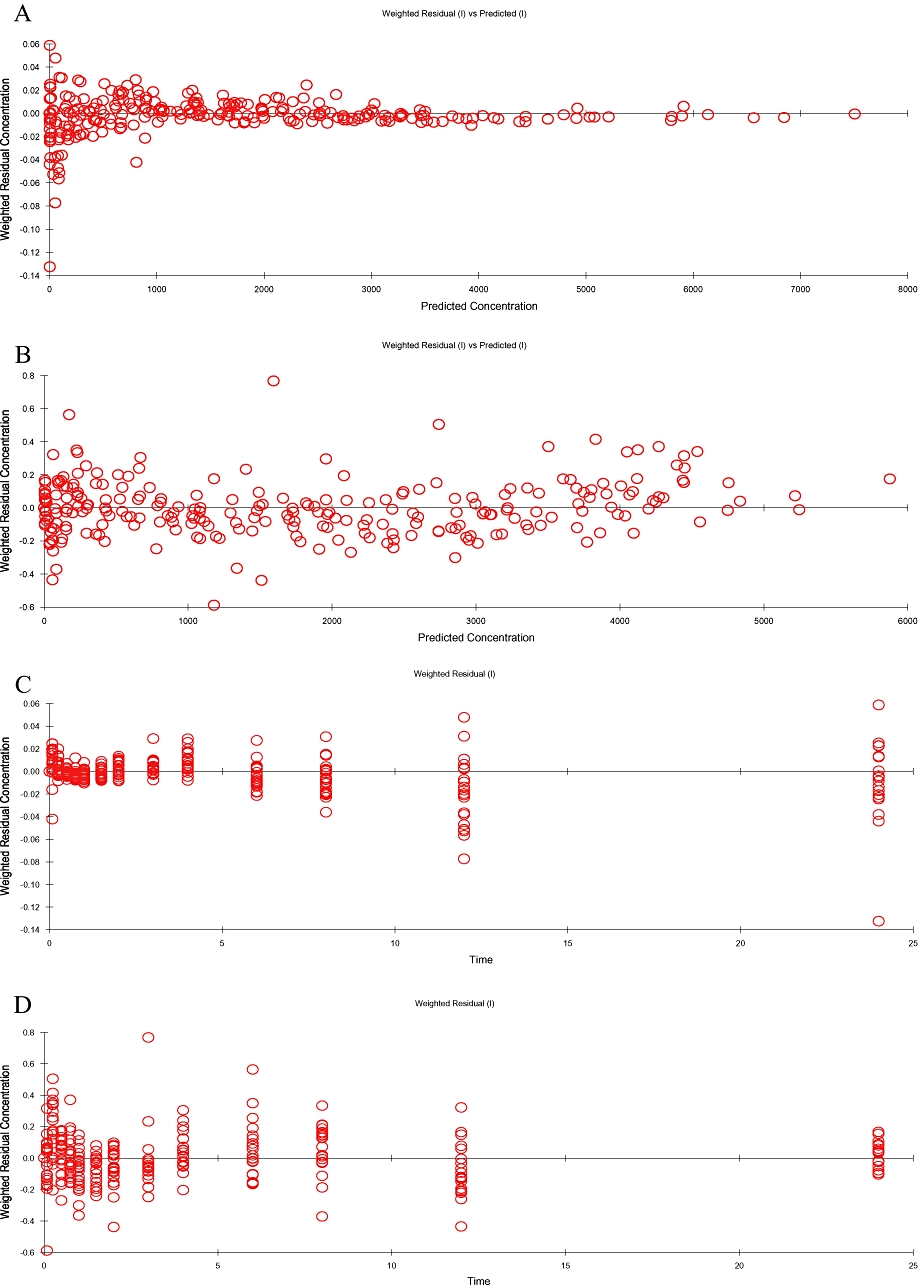
Assessement of predictive performance of final population models for both treatments: pralidoxime and AIBC. Plots of residual versus predicted concentrations for pralidoxime (A) and AIBC (B), and residual versus time for pralidoxime (C) and AIBC (D).

Table 4.

Population pharmacokinetic parameter details of pralidoxime obtained with the best fitting model for the two treatments; pralidoxime and AIBC

	Pralidoxime		AIBC
	Estimate	s.e. of estimation	Estimate	s.e. of estimation
Vc (L)	197.2	10.84	311.7	30.25
Ka (h−1)	–	–	10.07	2.20
Ke (h−1)	0.685	0.036	0.45	0.023
K12 (h−1)	0.527	0.071	0.079	0.017
K21 (h−1)	0.357	0.024	0.25	0.02
Population variability*
Vc	39.70%		31.10%
Ka	–		70.70%
Ke	22.90%		16.6%
K12	144%		2.28%
K21	89.70%		7.48%
Residual error	1.30%		18.70%

^*Expressed as coefficient of variation.

Table 5.

Mean (with SD) of main individual derived pharmacokinetic parameters and estimation CV% of pralidoxime obtained with the compartmental modelling approach

	Pralidoxime		AIBC
	Mean	SD	Mean	SD
AUC0-∞ (h. ng·mL−1)	10 164	2159	10 291	2629
AUC estimation CV%	4.78%	0.146%	9.84%	2.06%
tmax (h)	–	–	0.31	0.15
tmax estimation CV%	–	–	14.4%	0.94%
Cmax (ng·mL−1)	3 987	1031	4 333	723
Cmax estimation CV%	5.96%	0.93%	9.86%	2.43%

Discussion

This study was the first in human subjects designed to determine the pharmacokinetic parameters of pralidoxime after its i.m. administration either alone or in combination with atropine and avizafone.

Therefore, a non-compartmental approach and a compartmental modelling analysis were used. Because treatments were administered within a 2 week interval, inter-individual variability in the pharmacokinetic parameters has been taken into account, with the assumption that plasma clearance remained constant. As mentioned above, the non-compartmental analysis followed by the confidence interval approach (FDA, 2001), showed that pralidoxime appeared in plasma earlier and exhibited higher concentrations, when it was administered in combination with avizafone and atropine, than when it was given alone. Meanwhile, the total exposure of pralidoxime, assessed by AUC, appeared to be the same when pralidoxime was injected either alone or combined with avizafone and atropine. The co-administration of avizafone and atropine with pralidoxime appeared to have no effect on pralidoxime elimination half-life, a finding comparable with that already published after i.v. infusion in both organophosphate-poisoned patients and healthy volunteers (Willems et al., 1992).

The compartmental modelling analysis was achieved using a non-linear least squares method. The basic problem in this method is finding the values of θ, the model parameter, which minimizes the residual sum of squares and is essentially a problem in optimization. A constant coefficient of variation error model was chosen and the iteratively reweighted, least squares method has been used. In this method, the first estimation of the parameter is achieved by a regression and this estimation is weighted and then re-estimated by the weighted least squares method (Bonate, 2006).

For each concentration, an additive error was assumed arising from a zero mean Gaussian distribution, and the standard deviation of the residual error was best described by a combined additive and proportional structure. Errors on two different concentrations were assumed to be uncorrelated. The error included analytical assay errors and model mis-specification errors. Quality control samples used during pralidoxime quantification in subject samples, showed that a constant coefficient of variation error model was appropriate for assay error. It was assumed that such a model could also well describe error due to the pharmacokinetic model. Actually, it is reasonable to assume that this kind of error is more important during the absorption and the distribution phases rather than at the end of the kinetics. Otherwise, there was no reason to assume that the variance parameters could be different among the subjects. The Akaike criterion was used to select the combination of models that included the best absorption model. In addition, plots of predicted and observed concentration versus time, parameters estimation coefficient of variation, were also examined and their evaluation was considered in order to choose the best fit model.

The population pharmacokinetic analysis showed that the pharmacokinetics of pralidoxime administered intramuscularly followed a two-compartment model with zero-order absorption. This model was chosen although the AIC of the model with first-order absorption was lower (3607 vs. 3645 for first-order and zero-order absorption respectively). As a matter of fact, the estimation coefficients of variation of several estimated and derived parameters were high when data were fitted using the first-order absorption. By contrast, under a zero-order absorption process, they were always lower than those obtained assuming a first-order absorption process (highest value of CV% with zero-order absorption around 25%). In addition, the combined model with first-order absorption seemed to underestimate the maximal concentration.

When pralidoxime was administered with atropine and avizafone using AIBC, a two-compartment model with first-order absorption was identified to be the best model. For these data, AIC, coefficients of variation of derived and estimated parameters and plots of goodness of fit indicated that the model with first-order absorption provided the best fit and the best estimates of the pharmacokinetic parameters.

The distribution parameters (K₁₂ and K₂₁), were estimated by the model and the goodness of fit varied from one subject to another, as it is driven by the number of points taken into account by the model. Transfer constants are part of the mathematical model, which is composed of five parameters in first-order absorption and four parameters only, in zero-order absorption. Although the population value of K₂₁ appeared to be higher than K₁₂ after the administration of pralidoxime with atropine and avizafone using AIBC, the effect of this on the pharmacokinetics of pralidoxime seemed to be moderate. Indeed the derived parameters related to the total drug exposure and absorption are comparable with those obtained by the non-compartmental approach. This further supports the observation of the faster absorption of pralidoxime after the injection of the combination.

When pralidoxime was injected with avizafone and atropine, earlier absorption, accompanied by higher maximal concentration, occurred. This phenomenon was accompanied with a shift of the best mathematical model fitting this process from zero-order to first-order rate one. From a pharmacokinetic point of view, zero-order absorption is known to occur when a limiting step exists in the absorption process or when a zero-order controlled release delivery system is used. Hence, the results we observed could suggest the existence of active transport processes, or a temporary ‘storage’ of the drug at the site of administration with a constant diffusion into the systemic circulation.

Finally, the accelerated absorption of pralidoxime, when combined with avizafone and atropine, is likely to reflect a consequence of a modification of absorption processes, because of changes in blood flow at the site of injection (Hardman and Limbird, 2001). Avizafone is not known to exhibit pharmacological properties suggesting any modification of blood flow or other absorption mechanisms. Nevertheless, when atropine is administered at clinical doses that induce anticholinergic effects, avizafone counteracts the peripheral effects, that is, vasodilatation, leading to modification of blood flow rate at the site of injection (Hardman and Limbird, 2001). Therefore, this pharmacological property of avizafone could explain, at least partially, the faster absorption process for the co-administered compounds.

In summary, the non-compartmental analysis followed by the confidence interval approach allowed us to determine the differences between pharmacokinetic parameters regarding the bioavailability (higher C_max when pralidoxime was given in combination with atropine and avizafone), while the compartmental approach allowed the characterization of the best absorption model and provided several pharmacokinetic parameters that could not be obtained with a model-independent analysis. Our results have contributed to the understanding of various processes affecting the pharmacokinetics of pralidoxime.

Glossary

Abbreviations

AIBC

auto-injector bi-compartmental

AIC

Akaike information criterion

AUC

area under the curve

C_max

maximal concentration

K_a

absorption constant

K_e

elimination constant

K₁₂

K₂₁ transfer constants between compartments 1 and 2

t_max

time to reach maximal concentration

Vz

distribution volume

Conflict of interest

The study had been sponsored by the Service de Santé des Armées, France.

JM Rouseau, G Lallement, and I Bardot are employees of the Service de Santé des Armées, France.

Supporting Information

Teaching Materials; Figs 1–3 as PowerPoint slide.