Spatial Analysis of Feline Immunodeficiency Virus Infection in Cougars

Abstract

The cougar (Puma concolor) is a large predatory feline found widely in the Americas that is susceptible to feline immunodeficiency virus (FIV), a fast-evolving lentivirus found in wild feline species that is analogous to simian immunodeficiency viruses in wild primates and belongs to the same family of viruses as human immunodeficiency virus. FIV infection in cougars can lead to a weakened immune system that creates opportunities for other infecting agents. FIV prevalence and lineages have been studied previously in several areas in the western United States, but typically without spatially explicit statistical techniques. To describe the distribution of FIV in a sample of cougars located in the northern Rocky Mountain region of North America, we first used kernel density ratio estimation to map the log relative risk of FIV. The risk surface showed a significant cluster of FIV in northwestern Montana. We also used Bayesian cluster models for genetic data to investigate the spatial structure of the feline immunodeficiency virus with virus genetic sequence data. A result of the models was two spatially distinct FIV lineages that aligned considerably with an interstate highway in Montana. Our results suggest that the use of spatial information and models adds novel insight when investigating an infectious animal disease. The results also suggest that the influence of landscape features likely plays an important role in the spatiotemporal spread of an infectious disease within wildlife populations.

1. Introduction

Diseases such as SARS, monkeypox, avian influenza, West Nile virus, Lyme disease, and human immunodeficiency virus (HIV) represent examples of infectious diseases which have crossed or are crossing over to humans from contemporary or historical animal reservoirs. Recent outbreaks of such diseases capture the attention of both the general public and the scientific community with respect to the interaction of population, landscape, and inter- and intra-species factors in defining outbreaks and sustained reservoirs of infectious disease. Some of these diseases evolve to allow direct human-to-human transmission (e.g., HIV, H1N1 influenza, and feared mutations of H5N1 influenza), but considerable health impacts exist even in the absence of such transmission.

In order to understand effective prevention and treatment of human cases of such diseases, the comments above suggest that it is critical to understand the entire disease system, i.e., the ecology of the disease. Research in disease ecology seeks to quantify and describe the complex interactions between disease incidence in a specific host and a variety of ecological/environmental processes. Research often focuses on infectious diseases, where investigators attempt to summarize the virulence of the pathogen, the primary route of infection, the role of any vectors, reservoir hosts, and environmental impacts on the disease transmission process. One can consider the term “environmental” very broadly, here, possibly including social contact networks, healthcare utilization, species interaction, as well as more familiar measures of climate, physical features, and land use.

The fundamental theory of disease ecology is well-established and the idea of studying interactions between animals, humans, pathogens, and environment appear throughout the literature in several forms and across several disciplines. Some relevant fields related to disease ecology include landscape ecology or landscape epidemiology, landscape genetics, conservation medicine, and conservation ecology. Landscape epidemiology is the study of the influence of the physical landscape on the spread and pattern of infectious disease (Paulousky 1966). Landscape genetics focuses on the genetic differentiation of species into subpopulations and the influence that landscape features has on the formation of subpopulations (Manel et al. 2003, Storfer et al. 2007). The notion of geographic structure among genetic subpopulations has been the subject of recent work in population structure and selection by Rousset (2004) and in phylogeography by Avise (2000), building on early work by Wright (1943, 1946). Recent efforts also attempt to expand empirical methods to use spatial pattern to describe population genetics (Epperson 2003, Guillot et al. 2009a). Conservation medicine addresses the intersection of animal health, human health, and ecosystem health (Aguire et al. 2002, Weinhold 2003). Conservation ecology is primarily concerned with the preservation of suitable habitats of interest. These individual fields of study interrelate with each other within disease ecology. Landscape genetics is related to conservation medicine and conservation ecology, where understanding the role that landscape has on species differentiation is also important for managing the health of animal populations and preserving habitat that ensures genetic diversity in animal populations. Landscape genetics and landscape epidemiology are related, as several studies have shown an association between population genetic diversity and infection dynamics (Barone et al. 1994, Ernest et al. 2003, Heeney et al. 1990, Wildt et al. 1987).

The concepts of landscape epidemiology and landscape genetics are particularly relevant branches of disease ecology motivating the analysis below, which explores the spatial distribution of feline immunodeficiency virus (FIV) and the spatial structure of this virus within a sample of cougars. FIV is a fast-evolving lentivirus that is analogous to simian immunodeficiency viruses in wild primates (Biek et al. 2003, Troyer et al. 2005), belonging to the same family of viruses as HIV. Strains of FIV are species-specific in the family Felidae, and cougars have their own type of FIV, called FIV_PCO. For convenience in notation, we will refer to the disease in the cougar data as FIV. FIV is spread through horizontal transmission through saliva, typically through bites or scratches during mating or territorial fights, and through vertical transmission from an infected dam to offspring (Biek et al. 2003). An FIV infection in cougars can result in a similar disease state as an HIV infection in humans, characterized by a weakened immune system that creates opportunities for other infecting agents, which can lead to a fatality in the host organism. However, reaction to FIV infection is stronger in domestic cats than in wild felines, and cougars infected with FIV generally remain asymptomatic (Blake et al. 2006). The overall prevalence of FIV in cougars is estimated to be 30% in North and South America, or 31% when limited to North America (Carpenter et al. 1996, Blake et al. 2006). The relatively fast rate of evolution of the virus makes it useful in studying its host population dynamics (Biek et al. 2006), where population patterns not evident in the host genetic data may be revealed.

The cougar (Puma concolor) is a large predatory feline distributed throughout South America and parts of North America. Cougars prefer habitats rich with vegetation and land cover due to their hunting technique of stalking prey. While cougars have a preferred habitat, they are fairly mobile and will move within a home range to find prey. Estimates for home ranges for cougars fall between 10 and 500 square miles, depending on sex (Cougar Discussion Group 2009). Cougar movement is believed to be influenced by both natural and manmade landscape barriers. Over time this restriction of movement could lead to spatial structure in both population genetic structure and FIV lineages that aligns with landscape features. In fact, there are several examples in the literature of cougar genetic diversity aligning with various landscape barriers (Ernest et al. 2003, Loxterman 2001, McRae et al. 2005, Walker et al. 2000). There has been no previous work to investigate whether any spatial structure in the feline immunodeficiency virus within infected cougars is associated with landscape features.

There are several objectives for this paper. We first seek to describe the spatial distribution of cougar FIV in the northern Rocky Mountain region in a population of free-ranging cougars, and then determine the number and composition of genetically distinct clusters of the virus. We also wish to assess whether spatial structure in FIV aligns with landscape barriers and previously identified genetic population structure in cougars. We describe the spatial distribution of FIV using kernel density estimation and the FIV status for each of the sampled cougars. We investigate spatial structure in the feline immunodeficiency virus itself using the virus sequence data for FIV infected cougars and Bayesian cluster models. We then assess whether spatial structure in FIV aligns with landscape features that may impact host movement using a geographic information system (GIS).

2. Distribution of FIV

2.1 Data

Our data contain the geographic coordinates for the sample location of each of 354 cougars caught for research purposes or killed by hunters in the northern Rocky Mountain regions of Idaho and Montana and extending into Alberta and British Columbia, Canada during 1990-2004. The data also include FIV infection status (positive: n = 100, negative: n = 254) for each cougar and virus sequence data for most FIV infected cougars (n = 85). The virus sequence data consists of a 1423 nucleotide sequence (A, C, G, T) for each cougar. FIV infection and the virus sequence data were derived using standard techniques and protocols in a previous lab analysis of DNA from blood and tissue samples (Biek et al. 2006). Detection of FIV was done through polymerase chain reaction with amplification of the pol and env genes (Biek et al. 2006). Biek et al. (2006) previously analyzed the virus sequence data independently of geographic locations of the sampled cougars to determine FIV lineage (aspatially).

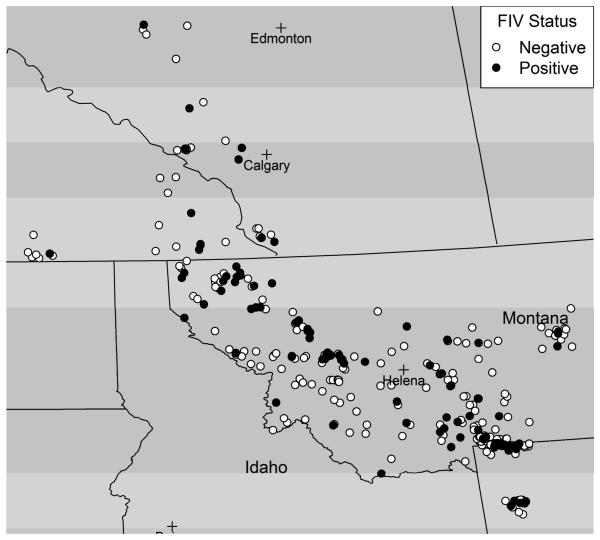
The estimate of crude prevalence of FIV in this area from 1990-2004 is 0.28 (100/354), consistent with the referenced prevalence estimates above. To initially explore the spatial distribution of FIV infection in this sample of infected and uninfected cougars, we first mapped the sampled cougars according to FIV infection status in a geographic information system (Figure 1). There is an uneven distribution of FIV cases in the study area. For example, there is an area in northwestern Montana with many FIV cases, as well as area in south-central Montana with several cases. There is a nearly linear swath of mostly non-cases, with very few cases, located between these two areas, parallel to the southwestern border of Montana.

Figure 1.

FIV infected and uninfected for sampled cougars in Rocky Mountain region

2.2 Spatial Log Relative Risk of FIV Infection

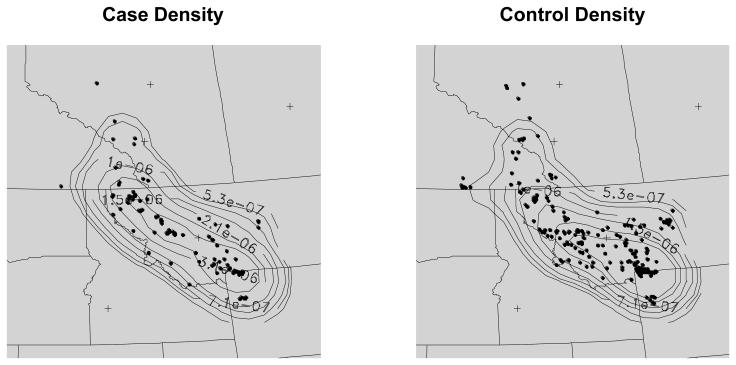
To investigate whether there are any variations in spatial patterns between FIV infected and non-infected cougars, we treated the two data sets as realizations of two spatial point processes over the same study area and sought to determine where the local intensities (number of data locations per unit area) appeared to differ. Note that the spatial sampling is not uniform but we assumed there is no difference in sampling between FIV-positive and FIV-negative cougars, i.e., we assumed FIV status does not impact behavior of either cougars or hunters. For this analysis, we first estimated the densities of infected and uninfected cougars using kernel density estimation (Kelsall and Diggle 1995; Waller and Gotway 2004). We performed kernel density estimation in R using the KernSmooth package. The kernel density function method estimates the probability of an event occurring at a location s in space, using a kernel function to count events over space. We defined a 51×51 regular grid to cover the study area and then estimate the density at each grid point. We limited the spatial extent of the analysis area to exclude two uninfected observations on the far eastern edge of the study area that we considered spatial outliers. The kernel function uses a bandwidth that determines the extent of the kernel and the overall smoothness of the resulting estimated density surface. We used Scott's (1992) rule for optimal bandwidth selection in a Gaussian kernel, where there are kernel bandwidths in both the x and y direction in spatial coordinates recorded as (x, y). Scott's rule considers the number of events and spatial variance of events in a point pattern when calculating the kernel bandwidth. We used kernel bandwidths of approximately 48 miles in the x and y directions for both FIV positive and uninfected cougars. The patterns of probability of FIV infected and non-infected cougars over space are somewhat different, especially in a north-central portion of the study area, in northwestern Montana, where the probability of cases is higher than the probability of controls (Figure 2). These patterns suggest a relatively higher risk of FIV in northwestern Montana than elsewhere in the study area.

Figure 2.

Density of cases and non-cases of FIV

To estimate the risk of FIV throughout the study area, we estimated the log relative risk at each grid point as the log ratio of the kernel density for infected cougars to the kernel density of uninfected cougars, with the same bandwidth, approximately 44 miles, used in both directions for each kernel (Kelsall and Diggle 1995). The log relative risk surface and log relative risk contour lines (Figure 3) show that the risk for FIV is largest near the center of the study area, in northwestern Montana. The largest relative risk in this area just exceeds 3, suggesting that cougars sampled in this area were approximately 3 times more likely to be FIV-positive than FIV-negative. We assessed statistical significance of local deviations in the surface through Monte Carlo “random labeling” wherein the labels of “infected” or “non-infected” are permuted over the observed study locations, thereby providing tolerance bands around the null value of zero and inference regarding local maxima and minima. The log relative risk contour plot shows the statistically significant areas of log relative risk using the 97.5% upper tolerance limits from 999 Monte Carlo randomizations of the case labels with hatched symbols (“+”). These significant local clusters of elevated log relative risk correspond to the higher points on the log relative risk surface map.

Figure 3.

Log relative risk surface for FIV (left) and log relative risk contour lines (right) calculated from the ratio of FIV infected cougar density to FIV uninfected cougar density. Hatches (“+”) indicate significantly elevated log relative risk based on Monte Carlo randomization of case labels

3. Spatial Structure of FIV Sequence Data

3.1 Methods

In addition to analyzing the pattern of FIV infection, it is also possible to investigate the spatial genetic pattern of the feline immunodeficiency virus through analysis of the geolocated virus sequence data. One possible analytical approach is to analyze the virus sequence data as genetic data (e.g. microsatellite, single nucleotide polymorphisms) typically used when assessing genetic population structure with Bayesian cluster models. Bayesian clustering models are now popular tools in population genetics to delineate genetic structure in populations and detect factors influencing gene flow (see, for example, Frantz et al. 2009, McCairns and Bernatchez 2008). The Bayesian clustering models used in population genetics are more complicated than the traditional clustering methods found in the unsupervised learning literature (see Berk 2008, Hastie et al. 2001) because they are designed for outcome (genetic) data that are multivariate and categorical. The approach of applying these models to virus sequence data would allow one to classify virus lineage, an indication of differentiation in virus strain, from virus sequence data and spatial information. We explore this potentially useful technique to study spatial structure in cougar FIV lineage.

There are several types of Bayesian clustering models designed for analyzing genetic population structure in genetic data. Bayesian cluster models designed for genetic data seek to answer several questions, such as how many subpopulations exist in a population, what is the composition of each subpopulation, and what is the posterior probability of each individual belonging to each subpopulation. Bayesian spatial cluster models seek to identify spatial structure in the subpopulations. The structure found may then be overlaid with landscape features to identify features that may represent physical barriers to genetic flow. In applying these models to the feline immunodeficiency virus, we seek to identify the number of and membership of distinct clusters of the virus. Several Bayesian cluster models for genetic data have been implemented in freely available software. Two popular software packages are STRUCTURE (Pritchard et al. 2000) and GENELAND (Guillot et al. 2005b), where STRUCTURE implements non-spatial models and GENELAND implements both spatial and non-spatial models. Excoffier and Heckel (2006) provide a comprehensive review of many software packages for analyzing genetic data, including those specialized for studying population genetic structure with individual-level data, such as GENELAND. There are also reviews of methods appropriate for analysis of genetic data, in particular when the impact of landscape features on genetic structure is of interest (Manel et al. 2003, Storfer et al. 2007).

The virus sequence data do not neatly fit into the data structures assumed by some software implementations. In our case, in order to apply the Bayesian cluster models in GENELAND to virus sequence data, one would have to first recode the bases to integers to mimic alleles (Guillot et al. 2009b). Therefore, we recoded the FIV sequence bases in a manner similar to alleles for a haploid organism. There is one allele per locus in a haploid organism, hence we began with 1423 loci per infected cougar. We next removed any locus where there was no variation expressed across the sample of cougars, i.e. no polymorphism. This step reduced the dimension of the data to 572 loci per cougar. This is still a relatively large number of loci and can lead to computational challenges in using the Bayesian cluster models.

The Bayesian classification models in GENELAND are based on work by Guillot et al. (2005a, 2005b) and we briefly review relevant model details now, while also drawing from Guillot (2009). The spatial locations are denoted as s = (s₁, …, s_n) for n sampling locations, where s_i is a two-dimensional vector of coordinates. The genotypes are denoted as s_i, where z_i is a vector of L alleles for each cougar. The genotype Z_il at locus l for individual i is denoted by the allele α_il for haploid organisms. The n individuals can be grouped to form K populations, where K is either estimated in the model or fixed a priori. When K is estimated in the model, it is assumed to follow a uniform distribution on 1 and a user-defined maximum. The allele frequency of allele j in locus l in population k is f_klj. The allele frequencies are assumed to vary across subpopulations and for haploid organisms are assumed to be uncorrelated across populations in GENELAND. The uncorrelated allele frequency assumption is a common one in population genetics (Guillot et al. 2005a). For haploid organisms, the model assumes the genotypes follow a multinomial distribution conditional on allele frequencies and population membership. The model assumes Hardy-Weinberg equilibrium (HWE) holds in each subpopulation for each locus and that there is linkage equilibrium. The HWE assumption equates to assuming that alleles in each subpopulation are sampled independently from a shared vector of allele frequencies f_klj. The HWE assumption for haploid organisms is written as

$$\pi (z_{1l},\dots ,z_{\mathit{nl}}\mid f_{\mathit{kl}.},\mathrm{p})=\prod _{i=1}^n{f}_{\mathit{kl}{\alpha }_{\mathit{il}}},$$ (1)

where p = (p₁, …, p_n) is a vector of subpopulation membership for individuals. The likelihood of observing the genotypic data given the parameters θ is written

$$\pi (\mathrm{z}\mid \mathrm{\theta })=\prod _{i=1}^n\prod _{l=1}^L\pi (z_{\mathit{il}}\mid \mathrm{\theta }).$$ (2)

The distinguishing feature between the spatial model and the non-spatial model in GENELAND is the assumption of spatial correlation of genotypes in the spatial model. This assumption is realized in the spatial model through a marked Poisson-Voronoi tessellation process. The model assumes that the K subpopulations partition the study area into non-overlapping areas Δ₁,…,Δ_K. There are m Voronoi polygons in the tessellation that are combined to form K the subpopulations. The polygons have nuclei (u₁,…,u_m), which are random and uniformly distributed, $(u_1,\dots ,u_m)\stackrel{i.i.d.}{~}U\left(D\right)$. The number of polygons is assumed to follow a Poisson distribution, m ~ Poisson(λ). The mark, or “color”, (c₁,…,c_m) for each polygon defines the subpopulation membership and is sampled from a uniform distribution, $(c_1,\dots ,c_m)\stackrel{i.i.d.}{~}U\{1,\dots ,K\}$. The subpopulation membership for each individual, p_i, is determined from the Voronoi polygon that contains the individual. The level of spatial organization in the process is controlled by the parameter λ, which has a uniform distribution with a maximum taken as the number of sampled individuals, λ ~ U(0, n). A small λ, and therefore m, results in strong spatial organization and hence clearer spatial boundaries between groups. For a very large λ, each Voronoi polygon would contain at most one observation and the tessellation model would produce results similar to that from an independent and identically distributed (i.i.d.) mixture model. In the non-spatial model in GENELAND, the prior for the vector of individual population membership, p=(c₁,…,c_n), is an i.i.d. prior, π (p | K) = 1/Kⁿ. The choice of prior is determined from an a priori belief of whether or not landscape features influence genetic differentiation, where one would select the spatial prior if one believed that landscape features indeed influenced genetic structure.

Parameter inference for the Bayesian cluster models in GENELAND comes from a reversible-jump Markov chain Monte Carlo (MCMC) algorithm, which samples from the joint posterior distribution of the parameters, π(θ|s,z). The model parameters are denoted by the vector σ = (K,m,u,c,f) for the spatial model assuming uncorrelated allele frequencies. In addition to the subpopulation memberships, GENELAND provides the posterior probabilities of membership in each of the K subpopulations for each individual through results of the MCMC algorithm.

For the following analysis, we used the library GENELAND in R. As a comparison, we used both the non-spatial and spatial models in GENELAND to determine the number and composition of FIV clusters under the two different modeling assumptions. We followed the suggestion of Guillot et al. (2009b) and used an iterative estimation approach, first estimating K in one MCMC run and then estimating the other model parameters in another MCMC run with K fixed at the previously estimated value. We repeated this process for both the non-spatial and spatial models. For each model, we used 500,000 iterations of the MCMC algorithm to sample from the joint posterior distribution, thinning every 100^th iteration, with a burn-in of 100,000 iterations. We visually inspected the MCMC results for convergence to the joint posterior distribution. We used R and ArcGIS (ESRI 2005) to map the estimated FIV clusters.

In addition to the non-spatial and spatial models, we also fitted a spatial model with uncertainty in the spatial sampling coordinates to represent a home range for each cougar. GENELAND models a home range by treating each true coordinate t_i as a sum of the sampled location coordinates and a random noise, t_i = s_i +δ_i. The additive noise term is δ_i sampled uniformly from a square centered on (0,0). As a first step in including spatial uncertainty, we selected a square with 25 mile sides for a representation of a very large home range for a male cougar. We chose a large home range to account for additional uncertainty in sampling location that could come from the hunting of cougars.

3.2 Results

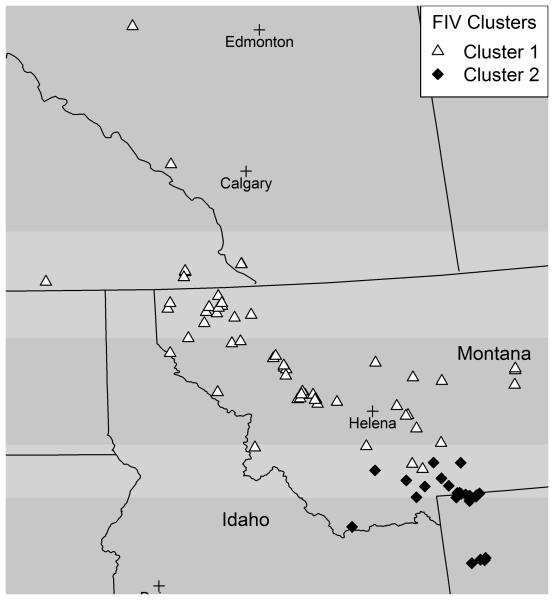
Both the spatial and non-spatial models found two differentiated FIV clusters. A finding of one FIV cluster would indicate there is no differentiation in the virus sequence data, and would suggest that there are no barriers to transfer of FIV in the population. In fact, the two models identified the same two spatially distinguishable FIV clusters, i.e. the cluster membership is the same for both models (Figure 4). The cluster membership assignments, 1 or 2, for each cougar are based on the posterior probabilities of cluster membership. There is no spatial overlap in the clusters, as a curved line drawn would separate the clusters. Contour lines of the posterior probabilities of cluster membership based on calculating the probability of being in each cluster for each cell in a grid placed over the study area give an approximation of the boundary separating the two clusters. The approximation is especially rough where there are few data points. The contours of posterior probabilities of membership in FIV cluster 2 show a fairly steep decline in the probability of belonging to cluster 2 (Figure 5), with a decrease from a probability of 0.9 to 0.1 over a relatively small distance. Only a few cougars in cluster 1 have a probability > 0.1 of being in cluster 2, and these are located in the immediate border area. We assessed the level of differentiation in FIV clusters using the F_ST value (Weir and Cockerham 1984), which is a commonly used measure in landscape genetics to measure population differentiation. The F_ST value of 0.21 for the two clusters indicates there is limited flow of FIV between the two clusters.

Figure 4.

FIV cluster membership from the spatial model

Figure 5.

Contours for probability of membership in FIV cluster 2

The adjustment for uncertain location within cougar home ranges in the spatial model changed the subpopulation assignment for three cougars along the boundary area between the two clusters (Figure 6). The boundary between the two FIV clusters in the model that adjusts for home range is now effectively a straight horizontal line, indicating a clear boundary dividing the study area into a northern area and a southern area. Two cougars in cluster 2 switched to cluster 1 and one cougar from cluster 1 changed to cluster 2 when adjusting for spatial uncertainty. This result is sensible if the locations of these three cougars were moved from the north of the barrier to the south of the barrier, or vice versa, when adjusting for home range, while the rest of the data were influential in demarcating the same barrier location as previously determined. One might expect that the location of the barrier between the clusters may become spatially fuzzier when adding spatial uncertainty to the sampling locations, but in this case the barrier is effectively unchanged, as determined from the majority of the data. The overall consistency in the composition of the FIV clusters from the three different models provides a degree of confidence in the clusters found by the Bayesian spatial cluster model, and strongly suggests that the spatial prior is not overly influential in the delineation of FIV clusters.

Figure 6.

FIV clusters for spatial model (left) and spatial model with home range adjustment (right)

Biek et al. (2003) noted that different FIV subtypes should be expected with a mobile host such as free-ranging cougars and that intermixing of distinct subtypes indicates extensive cougar movement. Biek et al. (2006) observed spatial structure in FIV, but did not quantify it, and hypothesized that it was a temporary phenomenon related to cougar populations rebounding from a recent bottleneck. Spatially distinct FIV subtypes suggest some physical barrier to host intermixing. Given the obvious boundary between the FIV clusters estimated from the Bayesian cluster models, we next investigated the correspondence between the FIV clusters and certain relevant landscape features to determine the plausibility of a landscape barrier effect on FIV flow in this sample of cougars. It is not possible in the Bayesian clustering models in GENELAND to adjust cluster membership probabilities for covariates, such as potential landscape barriers. Instead, we overlaid predicted cluster membership from the spatial model with the landscape layers of average annual precipitation, major rivers, and major roads and assessed their spatial alignment. We selected these landscape variables in advance because they were thought to impact the movement of cougars over space. Previous work suggests landscape barriers to genetic flow in cougars and other carnivores in the form of roads (Riley et al. 2006), water bodies (Ernest et al. 2003), and habitat barriers (Walker et al. 2000, McRae et al. 2005). We used ArcGIS to map FIV cluster membership and landscape thematic layers. The landscape thematic layers for major roads and major rivers are from ESRI. The thematic layer for average annual precipitation during 1961-1990 is from the Spatial Climate Analysis Service at Oregon State University.

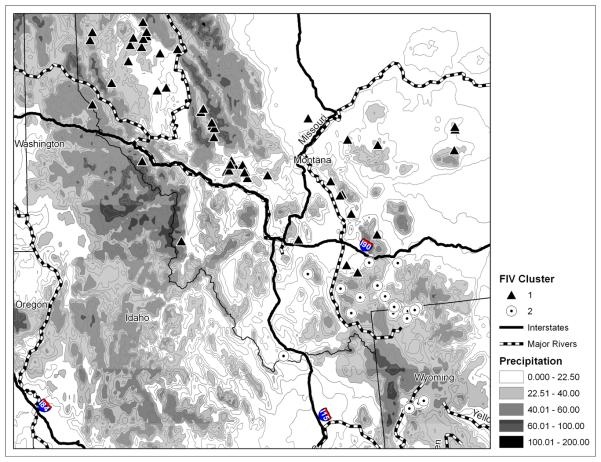
The map of FIV clusters and landscape features suggests that Interstate Highway 90 has influenced FIV structure in this cougar population (Figure 7). The map was constructed to focus on the border area dividing the two FIV clusters. Interstate Highway 90 predicts the membership for all but two cougars in the area of cluster separation. North of the highway is generally cluster 1 and south of the highway is cluster 2. This interstate highway has existed for decades and it is a plausible biological barrier (or at least impediment) to cougar movement and FIV flow in this area. The other landscape features considered (major rivers and average annual precipitation) do not align well with the structure in FIV.

Figure 7.

FIV cluster membership and landscape features

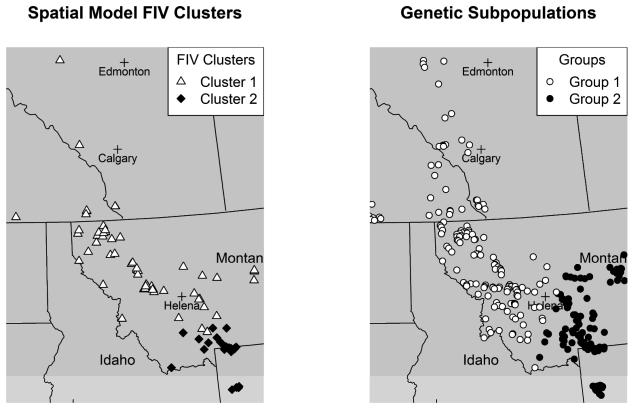
In addition to association between virus clusters and landscape features, we were interested in whether spatial structure in FIV aligned with previously determined genetic population structure in this sample of cougars (Biek et al. 2006, Wheeler and Waller 2010). One hypothesis is that there could be some alignment in disease prevalence and genetic population structure, as the flow of host genes and virus among subpopulations may be correlated. The map of genetic subpopulations found by Wheeler and Waller (2010) and FIV clusters (Figure 8) shows that the genetic subpopulations and FIV clusters do not align spatially. FIV cluster 2 is effectively a subset of the cougar genetic subpopulation in the eastern portion of the area. There are two prominent north-south landscape barriers, a major highway and a major river, for the genetic subpopulations, but one east-west landscape barrier for the FIV clusters. While both genetic population structure and FIV structure are aligned with interstate highways, they do not align with the same highways. One possible scenario to explain this pattern is that a relatively new lineage of FIV entered into the study area from the south and has not had adequate time to cross the highway landscape barrier. Biek et al. (2006) found that FIV lineages are spatially expanding over time and this, combined with the thought that recovery of cougar populations from sharp population declines during the early 20^th century happened earlier in Alberta than in southern locations, could explain the smaller geographic area occupied by FIV cluster 2. The temporal dynamics of FIV, unmeasured here, are likely very influential on the observed FIV structure. It is reasonable to expect that in the future, the structure of FIV lineages will be similar to the genetic population structure of cougars (Biek et al. 2006). Nevertheless, it is also not entirely surprising that the genetic population structure does not align exactly with the FIV structure. Each outcome represents a different process taking place over the landscape. FIV is a fast-evolving virus and its pattern can reveal recent demographic history about its host that genetic population structure of the host cannot (Biek et al. 2006).

Figure 8.

FIV cluster membership and genetic subpopulation membership

4. Discussion

In this analysis, we found a non-uniform spatial distribution of FIV prevalence in cougars and an overall prevalence of 0.28 and evidence for spatial structuring of FIV that aligned with an interstate highway in Montana. While our results are interesting and motivating, there are several limitations to our analyses. One limitation is that while we found a correspondence with FIV structure and a landscape feature, we have not formally quantified how this landscape feature has affected virus differentiation. While there is a clear spatial boundary in the FIV structure, we cannot formally explain this structure using the landscape with confidence. Ideally, one would include suspected landscape barriers to host movement in a Bayesian cluster model and quantify the effect of these landscape variables on the pattern of virus differentiation.

Another limitation of our analysis is that the sample of cougars we analyzed may not be spatially representative of the larger cougar population in this region of North America. Some of the cougars were collected by hunters, and since there are geographic areas where cougar hunting is prohibited, cougar populations from these areas will likely be underrepresented. This could potentially distort the pattern of FIV structure we found if FIV structure is related to landscape features in areas with no observations. There are some discontinuities in the sampling distribution of cougars (Figure 1), and we would obviously fail to capture any FIV structuring in unsampled areas. Similarity in FIV sequences on different sides of sampling discontinuities, however, suggests a lack of unmeasured FIV structure. We also assumed the sample was representative in terms of FIV status, such that cougar behavior was not altered significantly by FIV-positive status to result in different hunted rates by FIV status. There is no way to verify this assumption, but the fact that the crude FIV prevalence for the sample (28%) is very similar to the overall estimated prevalence in the Americas (30%) gives some measure of confidence that this is not a major issue with these data. While we do not have a spatially uniform sampling plan, due to local variations in cougar presence and hunting regulations as noted above, we do not anticipate differential effects between FIV positive and FIV negative groups. As a result, local comparisons are valid, but may vary in local power to detect differences depending on the local sample sizes relative to sample sizes from other areas. Our goal in the descriptive analysis of FIV was to determine whether the patterns of FIV positive and FIV negative cougars differ from one another, not to determine whether either provides an unbiased estimate of the spatial distribution of cougars. Another drawback of this study is not having temporal data to supplement the geographic data. Without temporal information for each cougar, our spatial analysis cannot capture variation in FIV distribution over time. This temporal information is especially critical for studying the spatial spread of FIV over time (Biek et al. 2006).

One ambiguity in this analysis is how the assumptions of Hardy-Weinberg equilibrium within populations and linkage equilibrium among loci in genetic data hold with high-dimensional virus sequence data. With so many loci (recoded nucleotide bases), it is likely there is some linkage disequilibrium, or dependence in pairs of loci. One naïve way to diminish this potential situation is to decrease the number of loci used in the Bayesian cluster model. In a secondary analysis, we used random samples of 10%, 20%, and 50% of the loci in spatial models in GENELAND and in each case found cluster membership results consistent with the spatial model with 100% of the loci. This suggests that if there is a violation of the linkage equilibrium assumption, it is not influential on the model results. In another sensitivity analysis, we used the eight virus lineages defined by Biek et al. (2006) as the outcome variable to be modeled in GENELAND and found essentially the same FIV cluster membership pattern when there were two clusters. Both sensitivity analyses suggest robustness of results with respect to these underlying issues.

There are several public health implications from this research. Public health focuses on prevention and populations, and there is considerable interest in public heath in infectious diseases and zoonoses, such as rabies, West Nile Virus, SARS, avian influenza, Lyme disease, and Ebola virus. Disease ecology and landscape genetics involve studying the complex interactions in how disease spreads through a population, whether looking at the movement of the virus or disease host, often with the hope of controlling or preventing future disease spread. The relevance of investigating landscape features is that the landscape can influence the spread of an emerging disease, and understanding this influence enables more accurate predictions of disease spread, enhanced planning of appropriate responses, and improved design of intervention strategies. The methods and types of data utilized in this study should be applicable to a wide range of systems and species in public health analysis. One immediate example of a potential application of these methods is in modeling the spread of raccoon rabies, where the identification of landscape features that slow or prevent spread could be used to allocate scarce vaccine resources in areas of forecasted high-spread potential (Biek et al. 2007, Wheeler and Waller 2008). Analyzing virus structure could assist in predicting direction and time of disease spread. Combining this information about spread with landscape feature influence should improve predictive models of disease transmission.

Taking into account spatial correlation when considering an infectious disease seems particularly important, especially in an animal population where long-distance contact is less likely than in human populations and clustering in the genetic host is likely. This is particularly relevant for public health implications in a zoonosis. However, many currently utilized methods in disease ecology to determine virus lineage (of which we are aware) do not make explicit use of spatial correlation. Hence, there are many opportunities for further methodological research developments in this area.