Implications of Three-Step Swimming Patterns in Bacterial Chemotaxis

Abstract

We recently found that marine bacteria Vibrio alginolyticus execute a cyclic three-step (run-reverse-flick) motility pattern that is distinctively different from the two-step (run-tumble) pattern of Escherichia coli. How this novel, to our knowledge, swimming pattern is regulated by cells of V. alginolyticus is not currently known, but its significance for bacterial chemotaxis is self-evident and will be delineated herein. Using a statistical approach, we calculated the migration speed of a cell executing the three-step pattern in a linear chemical gradient, and found that a biphasic chemotactic response arises naturally. The implication of such a response for the cells to adapt to ocean environments and its possible connection to E. coli's response are also discussed.

Introduction

Existing observations made in Escherichia coli have shown that sensing and motility impose different requirements on bacterial chemotactic response (1,2). The debate on this interesting issue was initiated by the observation of Block et al. (3), who discovered that the experimentally measured chemotactic response function R(t) integrated over time t is zero. In physical terms, R(t) can be thought of as the Green's function of the chemotactic network when subjected to an impulsive or a δ-in-time perturbation. The importance of this null integrated effect goes without saying, and was immediately recognized by the investigators as the bacterium's means of sensing. In their words (3), “the bacterium compares the information received in the past one second with that received over the previous three seconds.” In effect, the double-lobe response function, which is displayed in Fig. 1 c, allows the bacterium to react to fast temporal variations of a chemical signal c(t) but not to its direct-current component, enabling the cell to adapt to a wide range of chemical concentrations.

Figure 1.

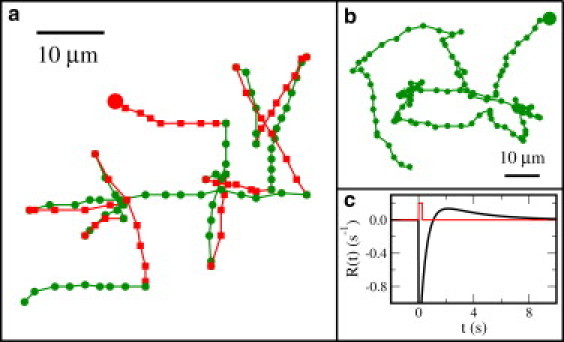
Bacterial swimming trajectories of V. alginolyticus (a) and E. coli (b). The cells have been selected among many because they are more or less swimming in the focal plane, 50–100 μm above the glass coverslip. The starting points for both trajectories are indicated by the two large solid dots. The time lapse between adjacent dots are 0.067 s and 0.13 s for panels a and b. The red and green segments in panel a designate the backward and forward swimming intervals, and transitions from backward to forward cause flicking, randomizing the swimming direction. Unlike a transition from forward to backward, which has a directional change Δθ ≃ π (or backtracking), a backward to forward transition is random with Δθ uniformly distributed between 0 and 180°. (c) A hypothetical response function R(t) of E. coli based on the model of Tu et al. (13) is plotted as the dark curve, and the cell is stimulated at t = 0 with a brief pulse of attractant (red curve). Here, $R\left(t\right)=R_0\left[\frac{1}{{\tau }_m}\exp \left(-\frac{t}{{\tau }_m}\right)-\frac{1}{{\tau }_z}\exp \left(-\frac{t}{{\tau }_z}\right)\right]$, where we set R₀ = 1, and used the typical E. coli methylation time (τ_m = 3 s) and phosphorylation time (τ_z = 0.5 s) (13,14).

Using a macroscopic diffusion argument, it was suggested by Schnitzer et al. (4) that a finite memory time is required for a bacterium to migrate in a linear chemical gradient; without the memory effect (or R(t) ≃ δ(t)), it was concluded that the chemotactic coefficient κ = V/∇c or the drift velocity V would be zero, where V is in the direction of the chemical gradient ∇c. However, de Gennes (5) pointed out that the macroscopic diffusion approach ignored important correlations between bacterial swimming and the underlying chemical gradient. By taking into account such correlations, de Gennes showed that the optimal (or a fast) response for migration in a linear gradient is an exponential function with a decay rate determined by the cell's memory time τ. He further pointed out that the double-lobe response function observed in E. coli could only reduce the migration speed in the gradient.

Contributing to this stimulating debate is the finding of Clark and Grant (1), who argued that whereas a cell needs a fast drift speed in a concentration gradient, it is equally important for the cell to localize once the top of the gradient is reached. They showed that the single-lobe function proposed by de Gennes is inadequate for cell localization. By imposing the corequirements of being able to localize as well as to migrate, they demonstrated that the optimal response function is biphasic, which is in remarkably good agreement with the one measured in the experiment (3). This observation led Clark and Grant to conclude that the biphasic response in E. coli perhaps reflects a compromised need of the cells in different environments. A recent study also suggested that the laboratory observed bacterial response corresponds to the maximin strategy that ensures the highest minimum uptake of nutrient for any profile of concentration (2).

Recently, we found that the swimming pattern of the marine bacterium Vibrio alginolyticus is a cyclic three-step process (6), where a cell swims forward for a time interval Δ_f and it then backtracks by reversing the motor direction for a time Δ_b. However, upon resuming forward swimming, the bacterial flagellum flicks, causing the cell body to veer in a new direction. This type of motility pattern is very different from that of E. coli, which exhibit a run-tumble pattern.

By way of introduction, a typical trajectory of V. alginolyticus and that of E. coli are presented, respectively, in Fig. 1, a and b. For the V. alginolyticus' trajectory (Fig. 1 a), the forward and the backward segments are designated by green and red, respectively, for clarity. We termed this novel, to our knowledge, swimming pattern a run-reverse-flick process.

The last (flicking) step is functionally equivalent to a tumble in E. coli, allowing the bacterium to randomly select a direction, and a new cycle ensues. Despite the fact that run and reverse intervals, Δ_f and Δ_b, as well as the flicking angle Δθ are stochastic, the three-step cycle is deterministic and has been observed in different V. alginolyticus strains and in a swimming buffer with and without a chemical gradient (6). In a steady state without a chemical gradient, we found that the probability density functions P(Δ_b) and P(Δ_f) are statistically independent and have long exponential tails (or a Poissonian-like behavior) with the mean intervals τ_b ≃ τ_f ≃ 0.3 s. However, when a point source of chemoattractant is present, the cells can quickly migrate along the gradient and form a tight pack around the source.

The biochemical network that regulates the activity of E. coli motor is reasonably well understood (7). Although this is not the case for V. alginolyticus, it cannot deter our progress because we know that even for very diverse microorganisms, such as E. coli and Bacillus subtilis that are roughly one billion years apart according to the recently constructed phylogenetic tree (8), the fundamental mechanism of regulation is still similar, i.e., a ligand binding to a receptor triggers a cascade of chemical reactions. The end-product of the reaction is a chemically modified protein, called the response regulator (CheY-P), that binds to the motor, causing it either to rotate counterclockwise (B. subtilis) or clockwise (E. coli). The basic aim of different microorganisms is also the same, namely guided by chemical signals—the cell is directed toward the source of chemoattractant and away from chemorepellent. According to the phylogenetic tree (8), V. alginolyticus appears to be much closer to E. coli than B. subtilis, suggesting that there is much in common between these two bacterial species. Indeed, in V. alginolyticus, one can identify chemotaxis genes that are largely homologous to E. coli with the exception of cheV that is absent in E. coli but is present in B. subtilis. A recent study moreover showed that the phosphorylated CheY in V. alginolyticus causes the polar flagellar motor to reverse the direction from counterclockwise (CCW) to clockwise (CW), similar to E. coli (9).

It is clear that the three-step swimming pattern is significantly different from the well-studied two-step swimming pattern of run-and-tumble, and it has strong implications for bacterial chemotaxis, which can be characterized by an effective diffusion coefficient D and a drift velocity V in the presence or absence of a chemical gradient. The calculation below illustrates that cells executing the three-step swimming pattern can exhibit rich chemotactic behaviors, and the variations can be acted on by natural selection so that a particular response emerges. Below we will illustrate these new aspects of bacterial chemotaxis based on our findings of the three-step process.

Similar to cells of E. coli, the flagellar motor of V. alginolyticus has two lifetimes for the state of rotations: one (τ_f) for the CCW interval and one (τ_b) for the CW interval, where the subscripts f and b stand for forward and backward swimming, respectively. To modulate their chemotactic behaviors, these lifetimes are affected by the local concentration of chemoeffectors and cells' adaptation mechanism. Unlike E. coli, however, CW rotation in V. alginolyticus causes the cell to backtrack. Both swimming intervals are expected to depend on the ligand concentration c(t), which we assume to be chemoattractant. For small c(t), we assume that a linear response is applicable and hence,

$$\frac{1}{{\tau }_f\left(t\right)}=\frac{1}{{\tau }_f}\left[1-\stackrel{t}{\underset{-\infty }{\int }}d{t}^{\prime }{R}_f\left(t-t^{\prime }\right)c\left(t^{\prime }\right)\right],$$ (1)

$$\frac{1}{{\tau }_b\left(t\right)}=\frac{1}{{\tau }_b}\left[1-\stackrel{t}{\underset{-\infty }{\int }}d{t}^{\prime }{R}_b\left(t-t^{\prime }\right)c\left(t^{\prime }\right)\right],$$ (2)

where τ_f and τ_b are the steady-state values, and R_f(t) and R_b(t) are the memory (or the response) functions, which are not necessarily the same for the two swimming intervals. In the above, an exposure to the ligand causes the forward lifetime to increase, and is consistent with our observations in V. alginolyticus (6). Linearity of Eqs. 1 and 2 suggests that it is possible to examine one delay time θ at a time and sum up all possible delays at the end.

Following de Gennes, we write R_s(t) = α_sδ(t – θ), where the strength of the response α_s(s = f, b) has the dimension of volume. Next, we consider a cell moving in a chemical gradient as depicted in Fig. 2. Our aim is to calculate the displacement x_i along the gradient in one cycle, Δ_f + Δ_b, which leads to a mean drift velocity $V={\overline{x}}_i/({\tau }_f+{\tau }_b)$ after averaging over Δ_f and Δ_b. Because a cell randomizes its swimming direction at the end of the backward interval by a flick, the motions in two consecutive cycles are uncorrelated. This allows us to place the origin of time (t = 0) at the beginning of the forward run. Assuming that the forward run time is Poisson-distributed, the surviving probability of a cell swimming forward up to Δ_f is given by

$$P_f\left({\Delta }_f\right)=\exp \left[-\stackrel{{\Delta }_f}{\underset{0}{\int }}d{t}^{\prime }\frac{1}{{\tau }_f\left(t^{\prime }\right)}\right]\simeq \exp \left(-\frac{{\Delta }_f}{{\tau }_f}\right)\left[1+\frac{{\alpha }_f}{{\tau }_f}\stackrel{{\Delta }_f-\theta }{\underset{-\theta }{\int }}d{t}^{\prime }c\left(t^{\prime }\right)\right],$$ (3)

and the probability that it stops immediately after Δ_f is –∂P_f(Δ_f)/∂Δ_f. Likewise, the surviving probability of a cell swimming backward from Δ_f to Δ_f +Δ_b is given by

$$P_b\left({\Delta }_b,{\Delta }_f\right)=\exp \left[-\stackrel{{\Delta }_f+{\Delta }_b}{\underset{{\Delta }_f}{\int }}d{t}^{\prime }\frac{1}{{\tau }_b\left(t^{\prime }\right)}\right]\simeq \exp \left(-\frac{{\Delta }_b}{{\tau }_b}\right)\left[1+\frac{{\alpha }_b}{{\tau }_b}\stackrel{{\Delta }_f+{\Delta }_b-\theta }{\underset{{\Delta }_f-\theta }{\int }}d{t}^{\prime }c\left(t^{\prime }\right)\right],$$ (4)

and the stopping probability at the end of the backward run is $-\partial P_b\left({\Delta }_b,{\Delta }_f\right)/\partial {\Delta }_b.$

Figure 2.

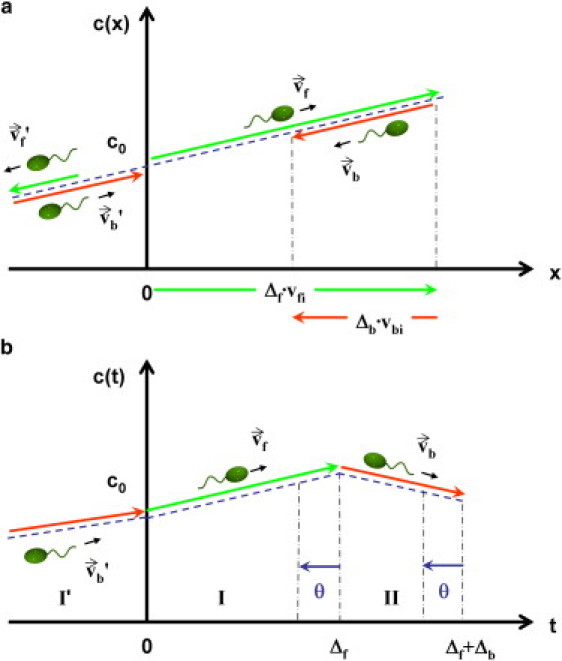
Migration of V. alginolyticus in a linear chemical gradient. (a) (Dashed blue line) In the spatial domain, the chemical gradient is specified. (Green and the red arrows) Forward and backward swimming segments along the gradient. (The color usage in the arrows is consistent with that in Fig. 1.) The values Δ_f and Δ_b are, respectively, the forward and backward swimming time intervals, and v_fi and v_bi are, respectively, the forward and backward velocity components along the chemical gradient. Note that backtracking means $\overrightarrow{v_b}=-\overrightarrow{v_f}$. (b) The bacterial chemotactic network processes the chemical information in the temporal domain, and the concentration detected by the cell is depicted in panel b, where θ is the memory time of the bacterium. I and II are chemosensing in the current cycle, and I′ is due to the previous cycle.

It follows that the net mean displacement in one cycle is given by

$${\overline{x}}_i\equiv {\overline{x}}_{fi}+{\overline{x}}_{bi}=\langle \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\left(-\frac{\partial P_f\left({\Delta }_f\right)}{\partial {\Delta }_f}\right)v_{fi}{\Delta }_f\rangle +\langle \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\left(-\frac{\partial P_f\left({\Delta }_f\right)}{\partial {\Delta }_f}\right)\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_b\left(-\frac{\partial P_b\left({\Delta }_b,{\Delta }_f\right)}{\partial {\Delta }_b}\right)v_{bi}{\Delta }_b\rangle ,$$ (5)

where ${\overline{x}}_{fi}$ and ${\overline{x}}_{bi}$ represent, respectively, the mean displacement during the forward (Δ_f) and the backward (Δ_b) swimming interval, and 〈…〉 designates the angular average for v_fi and v_bi. For the linear gradient depicted in Fig. 2, the concentration experienced by the cell can be represented as

$$c\left(t\right)=c_0+\nabla c·v_{fi}·t\text{for}0\le t<{\Delta }_f$$

and

$$c\left(t\right)=c_0+\nabla c·v_{fi}·{\Delta }_f+\nabla c·v_{bi}·(t-{\Delta }_f)\text{for}{\Delta }_f\le t<{\Delta }_f+{\Delta }_b.$$

Because c₀ is determined by the velocity in the previous cycle, it does not contribute to the above integrations after angular averaging. Although the calculation of Eq. 5 is tedious, which is given in Appendix A, the final result is straightforward:

$${\overline{x}}_i=\{{\alpha }_f{\tau }_f^2\langle v_{fi}^2\rangle \exp \left(-\frac{\theta }{{\tau }_f}\right)+{\alpha }_b\left[\frac{{\tau }_f^2{\tau }_b^2}{{\tau }_f-{\tau }_b}\langle v_{fi}{v}_{bi}\rangle \left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right)+{\tau }_b^2\langle v_{bi}^2\rangle \exp \left(-\frac{\theta }{{\tau }_b}\right)\right]\}\nabla c.$$ (6)

The first term in the curly brackets of Eq. 6 is the displacement during the forward interval, and the second term is the displacement during the backward interval. It is noteworthy that during the second interval, there is a cross term proportional to

$$\frac{{\tau }_f^2{\tau }_b^2}{{\tau }_f-{\tau }_b}\langle v_{fi}{v}_{bi}\rangle \left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right),$$

which results from the delay, i.e., even though the cell is moving backward, in the early episode of that interval, the cell still remembers the concentration sensed during the previous forward swimming. This gives rise to anticorrelation, because 〈v_fi v_bi〉 < 0, which contributes to a negative displacement. This important correlated motion adds richness to bacterial chemotaxis and is what makes V. alginolyticus behave differently from E. coli. We noted that Eq. 6 yields the result

$${\overline{x}}_i=\left[{\alpha }_f{\tau }_f^2\langle v_{fi}^2\rangle +{\alpha }_b{\tau }_b\left({\tau }_b\langle v_{bi}^2\rangle +{\tau }_f\langle v_{fi}{v}_{bi}\rangle \right)\right]\nabla c$$

in the limit of no memory, θ → 0. It is interesting that even when there is no memory, the cross term survives because there is no direction randomization after a forward run. Moreover, the displacement during the backward interval can contribute positively or negatively to the net mean displacement, depending on the mean lifetimes τ_f and τ_b, and the swimming velocities ${\overrightarrow{v}}_f$ and ${\overrightarrow{v}}_b$. We found the swimming pattern of V. alginolyticus is approximately symmetric with τ_f ≃ τ_b and $\left|{\overrightarrow{v}}_f\right|\simeq \left|{\overrightarrow{v}}_b\right|$ (6), and hence

$${\overline{x}}_i\simeq {\alpha }_f{\tau }_f^2\langle v_{fi}^2\rangle \nabla c.$$

The corresponding quantity for E. coli is

$${\overline{x}}_i={\alpha }_f{\tau }_f^2\langle v_{fi}^2\rangle {\varphi }_0\nabla c$$

when θ → 0, where the subscript f stands for the forward run (or CCW rotation) and

$${\varphi }_0={\tau }_{CCW}/\left({\tau }_{CCW}+{\tau }_{CW}\right)$$

is the CCW bias. Because near a steady state ϕ₀ ≃ 0.5 or ∼0.8 according to Block et al. (3) and Korobkova et al. (10), respectively, E. coli cells produce a smaller displacement than V. alginolyticus within one swimming cycle if everything else is equal. Using v_fi = −v_bi = v_i and summing up all possible delays in Eq. 6, we found that the mean displacement is given by

$${\overline{x}}_i=\{{\tau }_f^2\underset{0}{\overset{\infty }{\int }}d\theta R_f\left(\theta \right)\exp \left(-\frac{\theta }{{\tau }_f}\right)+{\tau }_b^2\underset{0}{\overset{\infty }{\int }}d\theta R_b\left(\theta \right)\times \left[\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{{\tau }_f^2}{{\tau }_f-{\tau }_b}\left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right)\right]\}\langle v_i^2\rangle \nabla c.$$ (7)

The average drift speed in the gradient is

$$V\left(\equiv \kappa \nabla c\right)={\overline{x}}_i/\left({\tau }_f+{\tau }_b\right),$$

which allows the chemotactic coefficient κ to be calculated. In E. coli, κ is proportional to the diffusion coefficient

$$D\simeq \frac{1}{3}{\varphi }_0\langle v^2\rangle {\tau }_f,$$

and one finds

$$\kappa =D{\int }_0^{\infty }{R}_f\left(\theta \right)\exp \left(-\frac{\theta }{{\tau }_f}\right)d\theta .$$

For an organism exhibiting the three-step swimming pattern, the diffusivity is given by

$$D=\langle v_i^2\rangle \frac{{\left({\tau }_f-{\tau }_b\right)}^2}{{\tau }_f+{\tau }_b}=\frac{1}{3}\langle v^2\rangle \frac{{\left({\tau }_f-{\tau }_b\right)}^2}{{\tau }_f+{\tau }_b},$$ (8)

and the chemotaxis coefficient can be written as

$$\kappa =\frac{D}{{\left({\tau }_f-{\tau }_b\right)}^2}\{{\tau }_f^2\underset{0}{\overset{\infty }{\int }}d\theta R_f\left(\theta \right)\exp \left(-\frac{\theta }{{\tau }_f}\right)+{\tau }_b^2\underset{0}{\overset{\infty }{\int }}d\theta R_b\left(\theta \right)\left[\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{{\tau }_f^2}{{\tau }_f-{\tau }_b}\left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right)\right]\}.$$ (9)

This calculation leads to two possible scenarios (or fundamental hypotheses) for bacterial chemotaxis: 1), independent and 2), shared chemosensing.

In the first case, the response functions in the forward and backward intervals are uncorrelated, i.e., R_f(θ) and R_b(θ) have different functional forms, so that the sensing system breaks the time reversal symmetry. To achieve such a control, the flagellar motor cannot only passively receive signals from the chemotaxis network; the status of the motor must also be made known to the chemotaxis regulatory network. This may be attained either by the flagellar motor being a part of the regulatory network or by a feedback signal via a protein that can reset the chemotactic response. In short, there will be a backflow of information from the motor to the chemotaxis network in addition to the normal chemotaxis regulation. To optimize the drifting velocity, we applied a variational principle to Eq. 9, which is delineated in Appendix B. We used the constraints that R_f(θ) and R_b(θ) have constant variances ${\sigma }_s^2/{\tau }_s(s=f,b)$ (1), yielding

$$R_f\left(\theta \right)\propto \frac{{\sigma }_f}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_f}\right),$$ (10)

$$R_b\left(\theta \right)\propto \frac{{\sigma }_b}{{\tau }_b}\left[\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{{\tau }_f^2}{{\tau }_f-{\tau }_b}\left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right)\right].$$ (11)

It is evident from the optimization procedure that, to attain the maximum possible drifting speed, the forward response function R_f(θ) should be monophasic but the backward response function R_b(θ) can be either monophasic or biphasic, depending on the ratio of the two lifetimes, β ≡ τ_b/τ_f. Fig. 3 displays (τ_f/σ_f)R_f(θ) and (τ_b/σ_b)R_b(θ) for different values of β = 0.8, 1.2, 1.5, 1.8, and 2.4. The figure shows that the biphasic character of R_b(θ) becomes more pronounced as β decreases toward unity but disappears altogether for β < 1, where the response is negative for all θ. An analysis shows that the biphasic response occurs in a narrow range of β (1 ≤ β ≤ 2), and outside this range the response is always monophasic.

Figure 3.

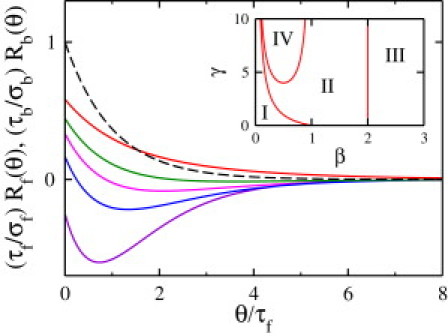
Chemotactic Strategy I. The bacterium uses separate response functions, R_f(θ) and R_b(θ), for chemosensing. The figure shows the dimensionless forms of the response functions. (Black curve) R_f(θ). (Purple, blue, pink, green, and red curves) R_b(θ) with β (≡ τ_b/τ_f) = 0.8, 1.2, 1.5, 1.8, and 2.4, respectively. (Inset) Phase diagram for Chemotactic Strategy II. It displays the phase boundaries between monophasic (I, III, IV) and biphasic (II) response regimes when the chemotaxis response obeys the relation R(θ) = R_f(θ) = R_b(θ)/γ.

This behavior is understandable because when τ_b is shorter than τ_f, the backward interval is strongly influenced by the signal sensed in the previous forward interval due to the memory effect. To deal with this inconsistency between sensing and motility, the optimal strategy is a negative monophasic response, as depicted by the purple curve (β = 0.8) in Fig. 3. On the other hand, when τ_b is longer than τ_f, the cell would have consistent sensing and motility so that a monophasic positive response is more favorable, which is shown by the red curve (β = 2.4) in Fig. 3. In the limiting case where τ_b >> τ_f or τ_b << τ_f , Eqs. 9–11 make it clear that the chemotactic coefficient κ is dominated, respectively, by the backward or the forward swimming interval. The situation is formally equivalent to E. coli chemotaxis, where the monophasic response is optimal for a fast migration in a linear chemical gradient, as was concluded by de Gennes (5).

In case 2, that of shared chemosensing, the bacterium uses a single response function R(θ), albeit the amplitudes of the responses may be different in the two directions, R_f(θ) = R_b(θ)/γ = R(θ). A simple reason for γ ≠ 1 could be due to different swimming speeds v_f and v_b, but other possibilities may also exist. For this type of sensing, there is no breaking of time reversal symmetry because the chemotaxis network processes information received during the forward and the backward interval equally, and there is no need for a backflow of information. Using Eq. 9, we found

$$\kappa =\frac{D}{{\left({\tau }_f-{\tau }_b\right)}^2}\underset{0}{\overset{\infty }{\int }}d\theta R\left(\theta \right)\{{\tau }_f^2\exp \left(-\frac{\theta }{{\tau }_f}\right)+\gamma {\tau }_b^2\left[\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{{\tau }_f^2}{{\tau }_f-{\tau }_b}\left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right)\right]\}.$$ (12)

Applying the variational principle again (see Appendix B), we found that the drift velocity is optimized by the following response function

$$R\left(\theta \right)\propto \frac{\sigma }{{\tau }_f+{\tau }_b}\{\exp \left(-\frac{\theta }{{\tau }_f}\right)+\gamma {\left(\frac{{\tau }_b}{{\tau }_f}\right)}^2\left[\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{{\tau }_f^2}{{\tau }_f-{\tau }_b}\left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right)\right]\}.$$ (13)

As displayed in Fig. 4, R(θ) can be monophasic or biphasic, depending on γ as well as the time ratio β ≡ τ_b/τ_f. The biphasic regime is bounded by

$$\frac{1-\beta }{\beta }\le \gamma <\frac{1}{\beta \left(1-\beta \right)}\text{for}0\le \beta <1$$

and

$$\gamma \ge 0\text{for}1<\beta \le 2,$$

which is displayed in the inset of Fig. 3. The inset shows that the parameter space (γ, β) consists of four different regimes with I, III, and IV being monophasic and II, biphasic. Our theory hence predicts that if a bacterium uses a single response function, for very short (β << 1) or very long (β >> 1) backward swimming intervals, the biphasic response is not a good chemotactic strategy for migration in a linear chemical gradient. The biphasic response emerges only when τ_f and τ_b are close (or β ≃ 1), which is the case in V. alginolyticus (6). It is conspicuous that in the limits β → 1 and γ → 1, R(θ) calculated using Eq. 13 is identical to the solution of a critically damped harmonic oscillator, which has the interesting property of

$${\int }_0^{\infty }\left(1-\theta /\tau \right)\exp \left(-\theta /\tau \right)d\theta =0,$$

i.e., the response is precisely adaptive.

Figure 4.

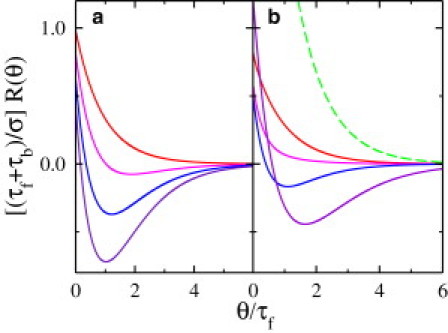
Chemotactic Strategy II. The bacterium shared the same response function R(θ) = R_f(θ) = R_b(θ)/γ for the forward and backward swimming intervals. (a) β = 0.75 and γ = 0.1 (red), 1.0 (pink), 2.0 (blue), and 3.0 (purple). (b) γ = 2 and β = 0.1 (red), 0.3 (pink), 0.5 (blue), 1.0 (purple), and 2.0 (green). As can be seen, for fixed β ≃ 0.75, the response becomes strongly biphasic as γ increases. On the other hand, for fixed γ = 2, the response is monophasic for small β, and becomes biphasic for intermediate values of β, and returns to monophasic for β ≥ 2.

The above two hypotheses are testable by laboratory experiments where the bacteria are subject to a defined chemical stimulation, and one measures the switching rate

$$s\left(t\right)=2/\left({\tau }_f\left(t\right)+{\tau }_b\left(t\right)\right)$$

and the forward swimming bias

$$\varphi \left(t\right)={\tau }_f\left(t\right)/\left({\tau }_f\left(t\right)+{\tau }_b\left(t\right)\right)$$

as a function of time. For a weak stimulation, the above calculation allows us to find

$$s\left(t\right)=s_0\left[1-{\varphi }_0\stackrel{t}{\underset{-\infty }{\int }}{R}_f\left(t-t^{\prime }\right)c\left(t^{\prime }\right)d{t}^{\prime }-\left(1-{\varphi }_0\right)\stackrel{t}{\underset{-\infty }{\int }}{R}_b\left(t-t^{\prime }\right)c\left(t^{\prime }\right)d{t}^{\prime }\right],$$ (14)

$$\varphi \left(t\right)={\varphi }_0\left[1+\left(1-{\varphi }_0\right)\stackrel{t}{\underset{-\infty }{\int }}\left(R_f\left(t-t^{\prime }\right)-R_b\left(t-t^{\prime }\right)\right)c\left(t^{\prime }\right)d{t}^{\prime }\right],$$ (15)

where

$$s_0\equiv 2/\left({\tau }_f+{\tau }_b\right)\text{and}{\varphi }_0\equiv {\tau }_f/\left({\tau }_f+{\tau }_b\right)$$

are the steady-state switching rate and the forward bias, respectively. The expressions are significantly simplified if the perturbation is δ-in-time, c(t) = c′δ(t), and they are given by

$$s\left(t\right)=s_0\left[1-c^{\prime }\left({\varphi }_0{R}_f\left(t\right)+\left(1-{\varphi }_0\right)R_b\left(t\right)\right)\right],$$ (16)

$$\varphi \left(t\right)={\varphi }_0\left[1+c^{\prime }\left(1-{\varphi }_0\right)\left(R_f\left(t\right)-R_b\left(t\right)\right)\right].$$ (17)

The calculation shows that if the second scenario is true and R_f(t) ≃ R_b(t), the forward bias will be weakly dependent on time t, and the switching rate is simply given by

$$s\left(t\right)\simeq s_0\left[1-c^{\prime }{R}_f\left(t\right)\right].$$

However, if the first scenario is true, the measured s(t) and ϕ(t) can be used to find the response function R_f(t) and R_b(t) using Eqs. 16 and 17. In this case, the following simple relations result:

$$R_f\left(t\right)=\frac{1}{c^{\prime }}\left[\frac{\varphi \left(t\right)}{{\varphi }_0}-\frac{s\left(t\right)}{s_0}\right],$$ (18)

$$R_b\left(t\right)=\frac{1}{c^{\prime }}\left[\frac{1-\varphi \left(t\right)}{1-{\varphi }_0}-\frac{s\left(t\right)}{s_0}\right].$$ (19)

An alternative and perhaps more direct way to find R_f(t) and R_b(t) is to perform conditional stimulation for individual cells. The bacterium can be either tethered to a surface, such as in the experiment of Block et al. (3), or freely swimming, as in the experiment of Khan et al. (11). For tethered cells, one can apply a pulse of chemoattractant at the moment the motor switches from CW (CCW) to CCW (CW), and record the subsequent swimming interval Δ_1f (Δ_1b), where the subscript 1 emphasizes the interval before the first switch. By counting the switching events up to time t, one can construct a cumulative probability density function (normalized by the total number of cells) Ψ_s(t), and the time-dependent switching rate can be obtained according to

$${\tau }_s^{-1}\left(t\right)=-\frac{d}{dt}\ln \left(1-{\Psi }_s\left(t\right)\right),$$

where s = f or b. For freely swimming cells, one can use photoactive serine, which is an attractant to V. alginolyticus, to stimulate cells. If the first scenario is true, one should find that τ_f⁻¹(t) and τ_b⁻¹(t) have different time dependence, or equivalently, R_f(t) and R_b(t) have different functional forms. However, if the second scenario is true, there should be not much difference between τ_f⁻¹(t) and τ_b⁻¹(t) or R_f(t) ∝ R_b(t).

To conclude, the three-step motility pattern of V. alginolyticus discovered in our recent experiment (6) allows significant variations in bacterial chemotactic behaviors. These variations can be acted on by natural selection and give rise to distinct phenotypes observed in the wild. Compared to the two-step swimming pattern of E. coli, cells of V. alginolyticus can engage in chemosensing and migration in both the forward and the backward swimming intervals, and hence their duty cycle is ∼100% as compared to ∼50–80% in E. coli (3,10). An important aspect in three-step chemotaxis is backtracking that gives those bacteria heading down a gradient an opportunity to reexploit what they find a moment earlier. In our opinion, the full duty cycle, backtracking, and flicking are defining characteristics of V. alginolyticus. These significant niches are likely selected for by the ocean environment where a quick response to transitory signals is important.

We showed that for a swimmer executing the cyclic three-step motility pattern, a biphasic response arises naturally without the need to invoke cell localization as suggested for E. coli (1). Moreover, we showed that the biphasic response is most effective when the forward τ_f and the backward τ_b swimming intervals are comparable. This makes biological sense, inasmuch as a brief forward or a brief backward interval contributes little to motility, and consequently a monophasic response is sufficient for migration.

This also raises the interesting question why the nonmotile CW interval in E. coli is so long, taking up at least 20% of the duty cycle. If tumbling is just to change the direction, would not it be better if the CW interval is shorter?

An interesting possibility is that the ancestral cell that gave birth to E. coli and V. alginolyticus was a three-step swimmer. However, when E. coli became specialized in a different environment, which favored multiple flagella for motility, they gave up backtracking and flicking, resulting in a tumbling movement. In this view, then, it is not surprising that E. coli's tumbling interval is long and its chemotactic response is biphasic.

Based on motility alone, we propose two different mechanisms—independent and shared chemosensing—by which cells of V. alginolyticus can optimize their migration speed in a linear gradient. Interestingly, the biphasic response appears in both types of chemotactic strategies. We know very little at present how the chemotaxis network of V. alginolyticus regulates the three-step motility pattern. However, based on our calculation, it is likely that a biphasic response is also adopted by V. alginolyticus, and awaits verification in future experiments. Finally, it would be interesting to generalize the above calculation to situations where the chemical landscape is constantly changing, such as chemical waves (12).

Appendix A: Calculation of the Mean Displacement

In the following, we provide a more detailed derivation of the mean displacement ${\overline{x}}_i={\overline{x}}_{fi}+{\overline{x}}_{bi}$ in a single three-step cycle. The displacement is made in the two time intervals, Δ_f and Δ_b, and is represented by Eq. 5. The concentration sensed by the bacterium is piecewise continuous according to Fig. 2 and is given by

$$c\left(t\right)=\{\begin{array}{c}{c}_0+\nabla c{v^{\prime }}_{bi}t,\\ c_0+\nabla c{v}_{fi}t,\\ c_0+\nabla c{v}_{fi}{\Delta }_f+\nabla c{v}_{bi}\left(t-{\Delta }_f\right),\end{array}\begin{array}{c}t<0\\ 0\le t<{\Delta }_f\\ {\Delta }_f\le t<{\Delta }_f+{\Delta }_b\end{array},$$

where the subscript i designates the component of the velocity along the gradient direction. The primed and unprimed velocities correspond to t < 0 (regime I′) and t ≥ 0 (regimes I and II), respectively.

The first part of Eq. 5 is readily calculated by integration by parts,

$${\overline{x}}_{fi}\equiv \langle \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\left(-\frac{\partial P_f\left({\Delta }_f\right)}{\partial {\Delta }_f}\right)v_{fi}{\Delta }_f\rangle =\langle \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f{P}_f\left({\Delta }_f\right)v_{fi}\rangle ,$$ (20)

where P_f(Δ_f) is given by Eq. 3, which contains an integration in time t over the range

$$-\theta \le t\le {\Delta }_f-\theta .$$

Because Δ_f varies from 0 to ∞, we have to distinguish two cases in the integration:

$$\left(\mathrm{i}\right){\Delta }_f-\theta <0\text{and}$$

$$\left(\mathrm{ii}\right){\Delta }_f-\theta >0.$$

One can deal with these two mutually exclusive cases by the use of Heaviside functions H(x), i.e., we write

$$\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f(\dots )\equiv \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\left[H\left(\theta -{\Delta }_f\right)+H\left({\Delta }_f-\theta \right)\right](\dots ).$$ (21)

The first Heaviside function confines the integral to t < 0, and because $\langle v_{bi}^{\prime }{v}_{fi}\rangle =0$, there is no contribution from this term. The integration constrained by the second Heaviside function yields

$${\overline{x}}_{fi}={\alpha }_f\nabla c\langle v_{fi}^2\rangle {\tau }_f^2\exp \left(-\frac{\theta }{{\tau }_f}\right).$$ (22)

This equation is identical to that found by de Gennes when he calculated the drift velocity for E. coli cells (5).

The second part of Eq. 5 is more complicated because one has to take into account more possibilities. Again, we used integration by parts to obtain

$${\overline{x}}_{bi}\equiv \langle \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_b\left(-\frac{\partial P_f\left({\Delta }_f\right)}{\partial {\Delta }_f}\right)\left(-\frac{\partial P_b\left({\Delta }_b,{\Delta }_f\right)}{\partial {\Delta }_b}\right)v_{bi}{\Delta }_b\rangle =\langle P_f\left(0\right)\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_b{P}_b\left({\Delta }_b,0\right)v_{bi}\rangle +\langle \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_b{P}_f\left({\Delta }_f\right)\frac{\partial P_b\left({\Delta }_b,{\Delta }_f\right)}{\partial {\Delta }_f}{v}_{bi}\rangle .$$ (23)

Let the first term in the above equation be ${\overline{x}}_{bi}^{\langle bb\rangle }$ and the second term be ${\overline{x}}_{bi}^{\langle bf\rangle }$. Because P_f(0) = 1 and P_b(Δ_b, 0) = P_f(Δ_b), it follows that the integration in the first term is identical to Eq. 20 with the replacement of the subscript f by b. This yields

$${\overline{x}}_{bi}^{\langle bb\rangle }={\alpha }_b\nabla c\langle v_{bi}^2\rangle {\tau }_b^2\exp \left(-\frac{\theta }{{\tau }_b}\right).$$ (24)

Now, let us examine the anticorrelation term ${\overline{x}}_{bi}^{\langle bf\rangle }$, which corresponds to the situation when the bacterium swims down the gradient but it still keeps its “old good memory”. Dropping the nonlinear terms in concentration c, we found

$${\overline{x}}_{bi}^{\langle bf\rangle }=\frac{{\alpha }_b}{{\tau }_b}\langle \stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_b\exp \left(-\frac{{\Delta }_f}{{\tau }_f}\right)\exp \left(-\frac{{\Delta }_b}{{\tau }_b}\right)\frac{\partial }{\partial {\Delta }_f}\stackrel{{\Delta }_f+{\Delta }_b-\theta }{\underset{{\Delta }_f-\theta }{\int }}dtc\left(t\right)v_{bi}\rangle .$$ (25)

When integrating over Δ_f, there are two possibilities for the lower limit of the t-integration, i.e., either Δ_f – θ < 0 or Δ_f – θ ≥ 0. These will be delimited by the Heaviside functions as before. For each of these cases, while integrating over Δ_b, there are additional possibilities for the upper limit of the t-integration. For the first case, when Δ_f − θ <0, there are three possibilities,

$$\left(\text{i}\right){\Delta }_f-\theta \le {\Delta }_f+{\Delta }_b-\theta \le 0,$$

$$\left(\text{ii}\right)0\le {\Delta }_f+{\Delta }_b-\theta \le {\Delta }_f,$$

and

$$\left(\text{iii}\right){\Delta }_f\le {\Delta }_f+{\Delta }_b-\theta \le {\Delta }_f+{\Delta }_b,$$

corresponding to the regimes I′, I, and II in Fig. 2, respectively. However, because motion is uncorrelated after a flick or $\langle v_{bi}^{\prime }{v}_{bi}\rangle =0$, the first possibility does not contribute to the displacement. In the second case, when Δ_f − θ ≥ 0, there are two additional possibilities,

$$\left(\text{iv}\right){\Delta }_f-\theta \le {\Delta }_f+{\Delta }_b-\theta \le {\Delta }_f$$

and

$$\left(\text{v}\right){\Delta }_f\le {\Delta }_f+{\Delta }_b-\theta \le {\Delta }_f+{\Delta }_b,$$

corresponding to the regimes I and II in Fig. 2, respectively. The corresponding time integrals for the above four possibilities (ii–v) are given by

$$\stackrel{{\Delta }_f+{\Delta }_b-\theta }{\underset{{\Delta }_f-\theta }{\int }}dtc\left(t\right)=\{\begin{array}{c}{c}_0\left({\Delta }_f+{\Delta }_b-\theta \right)+\frac{1}{2}\nabla c{v}_{fi}{\left({\Delta }_f+{\Delta }_b-\theta \right)}^2,\\ c_0{\Delta }_f+\frac{1}{2}\nabla c{v}_{fi}{\Delta }_f^2+c_1\left({\Delta }_b-\theta \right)+\frac{1}{2}\nabla c{v}_{bi}{\left({\Delta }_b-\theta \right)}^2,\\ c_0{\Delta }_b+\nabla c{v}_{fi}{\Delta }_b\left({\Delta }_f+\frac{1}{2}{\Delta }_b-\theta \right),\\ c_0\theta +\nabla c{v}_{fi}\theta \left({\Delta }_f-\frac{\theta }{2}\right)+c_1\left({\Delta }_b-\theta \right)+\frac{1}{2}\nabla c{v}_{bi}{\left({\Delta }_b-\theta \right)}^2,\end{array}\begin{array}{c}\left(ii\right)\\ \left(iii\right)\\ \left(iv\right)\\ \left(v\right)\end{array}$$ (26)

where c₁ ≡ c₀ + ∇cv_fiΔ_f. Using the above expressions, we take the derivative with respect to Δ_f to obtain

$$\frac{\partial }{\partial {\Delta }_f}\stackrel{{\Delta }_f+{\Delta }_b-\theta }{\underset{{\Delta }_f-\theta }{\int }}dtc\left(t\right)=\{\begin{array}{c}{c}_0+\nabla c{v}_{fi}\left({\Delta }_f+{\Delta }_b-\theta \right),\\ c_0+\nabla c{v}_{fi}\left({\Delta }_f+{\Delta }_b-\theta \right),\\ \nabla c{v}_{fi}{\Delta }_b,\\ \nabla c{v}_{fi}{\Delta }_b.\end{array}\begin{array}{c}\left(ii\right)\\ \left(iii\right)\\ \left(iv\right)\\ \left(v\right)\end{array}$$ (27)

Again, using the Heaviside functions to represent these four nontrivial possibilities, we have the identity

$$\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_b(\dots )=\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_f\stackrel{\infty }{\underset{0}{\int }}d{\Delta }_b\{H\left(\theta -{\Delta }_f\right)\left[H\left({\Delta }_f+{\Delta }_b-\theta \right)H\left(\theta -{\Delta }_b\right)+H\left({\Delta }_b-\theta \right)H\left(\theta \right)\right]+H\left({\Delta }_f-\theta \right)\left[H\left({\Delta }_b\right)H\left(\theta -{\Delta }_b\right)+H\left({\Delta }_b-\theta \right)H\left(\theta \right)\right]\}(\dots ).$$ (28)

Substituting this equation into Eq. 25, we found

$${\overline{x}}_{bi}^{\langle bf\rangle }=\frac{{\alpha }_b}{{\tau }_b}\langle \underset{0}{\overset{\infty }{\int }}d{\Delta }_f\underset{0}{\overset{\infty }{\int }}d{\Delta }_b\exp \left(-\frac{{\Delta }_f}{{\tau }_f}\right)\exp \left(-\frac{{\Delta }_b}{{\tau }_b}\right)\times \{H\left(\theta -{\Delta }_f\right)\left[H\left({\Delta }_f+{\Delta }_b-\theta \right)H\left(\theta -{\Delta }_b\right)\left(ii\right)+H\left({\Delta }_b-\theta \right)H\left(\theta \right)\left(iii\right)\right]+H\left({\Delta }_f-\theta \right)\left[H\left({\Delta }_b\right)H\left(\theta -{\Delta }_b\right)\left(iv\right)+H\left({\Delta }_b-\theta \right)H\left(\theta \right)\left(v\right)\right]\}{v}_{bi}\rangle ,$$ (29)

where (ii), (iii), (iv), and (v) are the terms given in Eq. 27. The four integrations in the above equation are delimited by different combinations of Heaviside functions, yielding different lower and upper integration limits for each integral. Designating these integrals as

$${\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{ii},{\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{iii},{\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{iv},\text{and}{\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_v,$$

we found

$${\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{ii}=\frac{{\alpha }_b}{{\tau }_b}\nabla c\langle v_{fi}{v}_{bi}\rangle \stackrel{\theta }{\underset{0}{\int }}d{\Delta }_f\stackrel{\theta }{\underset{\theta -{\Delta }_f}{\int }}d{\Delta }_b\exp \left(-\frac{{\Delta }_f}{{\tau }_f}\right)\exp \left(-\frac{{\Delta }_b}{{\tau }_b}\right)\left({\Delta }_f+{\Delta }_b-\theta \right)={\alpha }_b\nabla c\langle v_{fi}{v}_{bi}\rangle \frac{{\tau }_f}{{\tau }_f-{\tau }_b}\exp \left[-\theta \left(\frac{1}{{\tau }_b}+\frac{1}{{\tau }_f}\right)\right]\times \left\{{\tau }_b^2\left[\exp \left(\frac{\theta }{{\tau }_b}\right)-1\right]-{\tau }_f^2\left[\exp \left(\frac{\theta }{{\tau }_f}\right)-1\right]+\theta \left({\tau }_f-{\tau }_b\right)\right\},$$ (30)

$${\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{iii}=\frac{{\alpha }_b}{{\tau }_b}\nabla c\langle v_{fi}{v}_{bi}\rangle \stackrel{\theta }{\underset{0}{\int }}d{\Delta }_f\stackrel{\infty }{\underset{\theta }{\int }}d{\Delta }_b\exp \left(-\frac{{\Delta }_f}{{\tau }_f}\right)\exp \left(-\frac{{\Delta }_b}{{\tau }_b}\right)\left({\Delta }_f+{\Delta }_b-\theta \right)={\alpha }_b\nabla c\langle v_{fi}{v}_{bi}\rangle {\tau }_f\left[{\tau }_f+{\tau }_b-\left({\tau }_f+{\tau }_b+\theta \right)\exp \left(-\frac{\theta }{{\tau }_f}\right)\right]\exp \left(-\frac{\theta }{{\tau }_b}\right),$$ (31)

$${\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{iv}=\frac{{\alpha }_b}{{\tau }_b}\nabla c\langle v_{fi}{v}_{bi}\rangle \stackrel{\infty }{\underset{\theta }{\int }}d{\Delta }_f\stackrel{\theta }{\underset{0}{\int }}d{\Delta }_b\exp \left(-\frac{{\Delta }_f}{{\tau }_f}\right)\exp \left(-\frac{{\Delta }_b}{{\tau }_b}\right){\Delta }_b={\alpha }_b\nabla c\langle v_{fi}{v}_{bi}\rangle {\tau }_f\left[{\tau }_b-\left(\theta +{\tau }_b\right)\exp \left(-\frac{\theta }{{\tau }_b}\right)\right]\exp \left(-\frac{\theta }{{\tau }_f}\right),$$ (32)

$${\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_v=\frac{{\alpha }_b}{{\tau }_b}\nabla c\langle v_{fi}{v}_{bi}\rangle \stackrel{\infty }{\underset{\theta }{\int }}d{\Delta }_f\stackrel{\infty }{\underset{\theta }{\int }}d{\Delta }_b\exp \left(-\frac{{\Delta }_f}{{\tau }_f}\right)\exp \left(-\frac{{\Delta }_b}{{\tau }_b}\right){\Delta }_b={\alpha }_b\nabla c\langle v_{fi}{v}_{bi}\rangle {\tau }_f\left({\tau }_b+\theta \right)\exp \left(-\frac{\theta }{{\tau }_f}\right)\exp \left(-\frac{\theta }{{\tau }_b}\right).$$ (33)

In the above calculation, the terms involving c₀ do not contribute because 〈v_bi〉 = 0. The anticorrelation term due to all the above contributions is then given by

$${\overline{x}}_{bi}^{\langle bf\rangle }={\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{ii}+{\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{iii}+{\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_{iv}+{\left({\overline{x}}_{bi}^{\langle bf\rangle }\right)}_v={\alpha }_b\nabla c\langle v_{fi}{v}_{bi}\rangle \frac{{\tau }_f^2{\tau }_b^2}{{\tau }_b-{\tau }_f}\left[\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)\right].$$ (34)

Combining Eqs. 22, 24, and 34, we finally obtain the mean displacement in a given cycle for the three-step swimmer,

$${\overline{x}}_i={\alpha }_f\nabla c\langle v_{fi}^2\rangle {\tau }_f^2\exp \left(-\frac{\theta }{{\tau }_f}\right)+{\alpha }_b\nabla c\langle v_{bi}^2\rangle {\tau }_b^2\exp \left(-\frac{\theta }{{\tau }_b}\right)+{\alpha }_b\nabla c\langle v_{fi}{v}_{bi}\rangle \frac{{\tau }_f^2{\tau }_b^2}{{\tau }_b-{\tau }_f}\left[\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)\right].$$ (35)

Appendix B: Drifting Velocity Optimization

For the first chemotactic strategy, R_f(t) and R_b(t) in Eq. 9 are independently optimized. The procedure requires us to constrain a family of response functions R_s(t), where s = f, b. We followed Clark and Grant's approach (1) and assumed that R_s(t) is finite, continuous, and decays to zero for large t. The simplest way to impose the constraint is to assume a finite variance

$$\stackrel{\infty }{\underset{0}{\int }}{R}_s^2\left(t\right)dt={\sigma }_s^2/{\tau }_s$$ (36)

that is to be satisfied by all curves in the family. Optimizing κ with the above constraint is equivalent to

$$\frac{\delta }{\delta R_s\left(t\right)}\stackrel{\infty }{\underset{0}{\int }}dt\left[R_s\left(t\right)K_s\left(t\right)-\lambda \left(R_s^2\left(t\right)-\frac{{\sigma }_s^2}{{\tau }_s}\right)\right]=0,$$ (37)

where K_s(t) is the kernel that weights the forward (s = f) and the backward (s = b) response functions,

$$K_f\left(t\right)=\exp \left(-\frac{t}{{\tau }_f}\right),$$ (38)

$$K_b\left(t\right)=\exp \left(-\frac{\theta }{{\tau }_b}\right)-\frac{{\tau }_f^2}{{\tau }_f-{\tau }_b}\left(\frac{1}{{\tau }_b}\exp \left(-\frac{\theta }{{\tau }_f}\right)-\frac{1}{{\tau }_f}\exp \left(-\frac{\theta }{{\tau }_b}\right)\right).$$ (39)

Aside from normalization constants, the optimized response functions are given in Eqs. 10 and 11.

The similar procedure can also be applied to the second chemotactic strategy, resulting in the optimized response function given by Eq. 13.