Abstract
The regulated ability of integrin αIIbβ3 to bind fibrinogen plays a crucial role in platelet aggregation, adhesion, and hemostasis. Employing an optical-trap-based electronic force clamp, we studied the thermodynamics and kinetics of αIIbβ3-fibrinogen bond formation and dissociation under constant unbinding forces, mimicking the forces of physiologic blood shear on a thrombus. The distribution of bond lifetimes was bimodal, indicating that the αIIbβ3-fibrinogen complex exists in two bound states with different mechanical stability. The αIIbβ3 antagonist, abciximab, inhibited binding without affecting the unbinding kinetics, whereas Mn2+ biased the αIIbβ3-fibrinogen complex to the strong bound state with reduced off-rate. The average bond lifetimes decreased exponentially with increasing pulling force from ∼5 pN to 50 pN, suggesting that in this force range the αIIbβ3-fibrinogen interactions are classical slip bonds. We found no evidence for catch bonds, which is consistent with the known lack of shear-enhanced platelet adhesion on fibrinogen-coated surfaces. Taken together, these data provide important quantitative and qualitative characteristics of αIIbβ3-fibrinogen binding and unbinding that underlie the dynamics of platelet adhesion and aggregation in blood flow.
Introduction
Integrins are ubiquitous transmembrane heterodimers that mediate cell-matrix and cell-cell interactions (1). In platelets, the most abundant integrin is αIIbβ3 (GPIIb-IIIa or CD41/CD61), a receptor for fibrinogen, von Willebrand factor, fibronectin, and vitronectin that is required for platelet aggregation (2). There are 60,000–80,000 copies of αIIbβ3 on the surface of unstimulated platelets (3), and an additional intracellular granular pool of αIIbβ3 becomes available after platelet activation (4). The presence of a sufficient number of αIIbβ3 molecules on the platelet surface is necessary to prevent hemorrhage, so congenital deficiency of functional αIIbβ3 results in the hemorrhagic disorder Glanzmann's thrombasthenia. Conversely, the formation of αIIbβ3-mediated intravascular platelet aggregates causes myocardial infarction and stroke, so the ligand-binding activity of αIIbβ3 is strongly regulated (5,6).
To form hemostatically effective platelet plugs, αIIbβ3-ligand interactions must be sufficiently strong to withstand the mechanical loads of blood flow, vascular wall stretching, and clot retraction. Previous studies of the strength of αIIbβ3-ligand bonds using single-molecule forced unbinding studies have suggested that there is mechanical regulation of αIIbβ3 structure and ligand-binding activity (7–14). Steered molecular dynamics simulations also have shown that αIIbβ3 activation or deactivation is likely preceded by a force-induced conformational rearrangement (15–17). Further, αIIbβ3 and other integrins are thought to play a central role in sensing and converting external mechanical forces into intracellular perturbations, a process termed molecular mechanotransduction (18–20).
A number of molecular complexes, including P-selectin-PSGL-1 (21), GP1bα-von Willebrand factor (22), myosin-actin (23), and FimH-mannose (24) display catch-bond behavior, where bond stability increases with increasing mechanical tension (25–27). This may also be the case for integrins, since the integrin α5β1 was recently found to display catch-bond behavior during its interaction with a fragment of fibronectin (28). Nonetheless, there is as yet no direct evidence that this is the case for integrins in general.
Previously, we used optical-trap force spectroscopy to show that the distribution of rupture forces between individual αIIbβ3 and fibrinogen molecules displays at least two components that differ in kinetics, loading-rate dependence, and susceptibility to αIIbβ3 activation and inhibition (11). Thus, the interaction of αIIbβ3 and fibrinogen appears to be a complex, multistep process that depends on the conformational state of both αIIbβ3 and fibrinogen, the duration of their interaction, and environmental factors such as externally applied shear force.
Here, we studied the factors responsible for the formation of stable αIIbβ3-fibrinogen complexes and tested the possibility that αIIbβ3 displays catch-bond behavior by quantifying the lifetime of bonds between individual αIIbβ3 and fibrinogen molecules using an upgraded optical trap setup that applies constant unbinding force to single-molecule protein-protein complexes. We found that the distribution of αIIbβ3-fibrinogen bond lifetimes was bimodal, reflecting the heterogeneous nature of the interactions and the presence of multistep binding/unbinding pathways. Furthermore, αIIbβ3-fibrinogen complexes displayed classical slip-bond behavior in a force range up to 50 pN without signs of catch-bond formation. These data provide new mechanistic insights into the dynamics of αIIbβ3-fibrinogen interactions that underlie the formation of platelet aggregates in the bloodstream.
Materials and Methods
Modification of an optical trap to measure receptor-ligand interactions at constant tensile force
A custom-built optical trap, previously described in detail (11), was modified to measure individual ligand-receptor interactions under constant force (Fig. 1). This system makes it possible to control the duration of compressive contact between interacting surfaces, the magnitude of compressive force, and the magnitude of the tensile force during bond rupture. The maximum tensile force is limited to ∼100 pN. All experiments are conducted at an average trap stiffness of 0.10 ± 0.02 pN/nm. Force calibration and trap stiffness are routinely confirmed by the Stokes’ force method (29). LabVIEW software is used to control and record laser-beam deflection, move the piezoelectric stage, and analyze data off-line.
Figure 1.
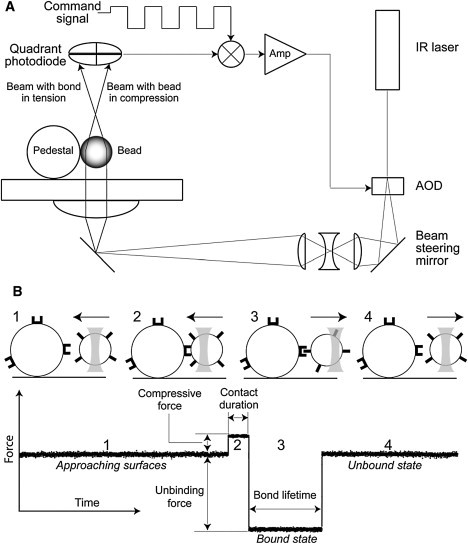
(A) Simplified schematic drawing of the optical trap setup equipped with a force clamp. Briefly, the core of the optical trap is a Nikon Diaphot 300 inverted microscope and a 100× 1.3 NA Fluor lens combined with an FCBar Nd/YAG laser (λ = 1064 nm) with 4 W power in continuous TEM-00 mode. A computer-operated two-dimensional acousto-optical deflector (AOD) is used to control the tilt of the incoming laser beam at the back focal plane of the microscope objective, thereby altering the trap position. Displacement of a latex bead from the trap center, and consequently the force exerted by the trap on the displaced bead, is measured with a back focal plane quadrant detector. The voltage signal produced by the photodiode can be calibrated in force units using the power spectrum of Brownian motion of a trapped bead. The force clamp consists of an analog feedback loop that adjusts the trap position (AOD) relative to the center of the ligand-coated latex bead so that the difference between the quadrant detector voltage (bead force) and a command signal is kept nearly zero. The command signal is generated by a digital-to-analog board under the control of a LabVIEW program (National Instruments, Austin, TX). The command is normally a square-wave voltage adjusted to give positive and negative force amplitudes, frequency, and duty cycle. (B) A bead oscillation cycle and portion of a typical data trace of αIIbβ3-fibrinogen interactions under a constant tensile force. The bead motion cycle has four parts: 1), approach of a bead to a pedestal; 2), bead-pedestal contact; 3), bonding under tensile force (if a bond formed); and 4), the bead moving away. When the command is positive, the ligand-coated bead is compressed at constant force against a silica pedestal coated with receptor protein. When the command is negative and no bond has formed during the compression, the trap is stopped at a fixed distance from the pedestal. If, however, a bond has formed, the trap maintains constant tension throughout the lifetime of the ligand-receptor bond (Fig. 1B and Fig. S2).
Measurement of αIIbβ3-fibrinogen bond lifetimes
To measure the lifetime of αIIbβ3-fibrinogen bonds, purified αIIbβ3 dissolved in 20 mM HEPES buffer, pH 7.4 (150 mM NaCl, 30 mM n-octyl-β-D-glucoside, and 1 mM CaCl2) was immobilized on stationary silica pedestals 5 μm in diameter (Bangs Laboratories, Fishers, IN) anchored with a thin layer of polyacrylamide to the bottom of a flow-through chamber, as previously described (8,11). When Mn2+ was used to activate αIIbβ3, the integrin was pretreated with 1 mM MnCl2 for 30 min at 37°C before it was immobilized in the presence of 1 mM MnCl2. Purified human fibrinogen was covalently coupled to suspended carboxylate-modified 1.75-μm latex beads (Bangs Laboratories, Fishers, IN) using water-soluble carbodiimide. Bovine serum albumin (BSA) was then used to block potential unoccupied protein-binding sites on the silica pedestals and latex beads.
Before each experiment, the flow-through chamber was equilibrated with the working buffer (0.1 M HEPES buffer, pH 7.4, with 2 mg/ml BSA, 0.1% Triton X-100, and 1 mM CaCl2 or 1 mM MnCl2) at room temperature. Then, 1 μl of the fibrinogen-coated latex bead suspension (107 beads/ml) in 50 μl of working buffer was flowed into the chamber containing αIIbβ3-coated pedestals. In control experiments, inhibitors of ligand binding to αIIbβ3 were added to the bead suspension before it was introduced into the chamber.
The chamber containing fibrinogen-coated beads was then placed on a microscope stage, a single bead was trapped by the laser, and the stage was moved manually to bring an αIIbβ3-coated pedestal within 1–2 μm of the trapped bead. The microscope focus was adjusted so that the bead and pedestal centers were the same distance from the coverslip surface. Then, using the piezostage, the separation of pedestal and bead was reduced in 100-nm or 10-nm steps until they touched each other. For measurements of fibrinogen-αIIbβ3 bonds with force spectroscopy, the position of the optical trap was oscillated in a triangular waveform with oscillation frequencies of 10 Hz and constant peak-to-peak amplitude of 800 nm. For measurement of the bond lifetimes under a constant force, the feedback loop controlled the bead force as a square wave with independent control of the magnitude and duration of bead compression and tension. The compressive force (both in force-clamp and ramp-force measurements) was in the range 10–20 pN and the duration of contact in the constant-force experiments was 0.5 s. The data were recorded from first contact and were digitized at the rate of 2000 samples/s.
Several tens of pedestal-bead pairs, using αIIbβ3 and fibrinogen from different batches, were analyzed for each experimental condition. The number of contacts recorded for each pedestal and bead pair depended on the oscillation frequency and the incidence of binding events and was collected for ∼10 min to obtain a manageable file size. The binding/unbinding events from individual files were summarized so that the total number of bond-lifetime values observed at each experimental condition varied from ∼102 to 103. Bond lifetimes of <40 ms represented weak, nonspecific interactions and were not susceptible to inhibition by eptifibatide or abciximab or enhancement by Mn2+. Bond-lifetime values were sorted into a histogram and normalized by the total number of contacts. The percentage of events in a particular bond-lifetime range (bin) represents the probability density of a bond rupture in that range.
Purification of functional αIIbβ3 and fibrinogen
αIIbβ3 was purified from detergent extracts of human platelets by affinity chromatography, as described previously (30). Purified human fibrinogen was purchased from HYPHEN BioMed (France). The polypeptide composition, purity, and potential oligomerization of the purified proteins were assessed by SDS-polyacrylamide gel electrophoresis and transmission electron microscopy using rotary shadowing with tungsten (31). The purified fibrinogen was 97% clottable with thrombin, confirming its purity and activity. The ability of the purified fibrinogen to bind to αIIbβ3 was confirmed using rupture-force spectroscopy (8,11). The distribution of rupture forces for fibrinogen bound to αIIbβ3 corresponds to our previously observed force spectra and demonstrates that at least 80% of the interactions stronger than 20 pN were sensitive to the αIIbβ3-specific inhibitor eptifibatide (Fig. S4 in the Supporting Material) and therefore represent specific αIIbβ3-fibrinogen binding.
Analysis of αIIbβ3-fibrinogen bond lifetimes and mapping the free energy landscape for αIIbβ3-fibrinogen bond rupture
The distribution of experimental bond lifetimes in this study was bimodal, suggesting that the unbinding process can be modeled as multistep dissociations that follow complex paths through the free-energy landscape of the interaction (32). Because the first portion of the bond-lifetime distribution appeared to be a spontaneous and stochastic process, it was described using a single-step kinetic model: , with an unbinding rate constant, , where denotes the fibrinogen-αIIbβ3 (ligand-receptor) complex, and L and R stand for fibrinogen and αIIbβ3, respectively. Corresponding to this process, an exponential probability density function of the bond lifetimes pu(t) is given by
| (1) |
To analyze the second portion of the bond-lifetime distribution, we applied a simple analytical model that provided reasonable fits for the αIIbβ3-fibrinogen dissociation data and modeled the conformational rearrangement of molecules during bond rupture with three phenomenological parameters (33,34). This model was recently used successfully to describe the mechanical unfolding of the all-β-sheet WW domain (33).
The major assumption underlying this model, an assumption consistent with our previous experimental data (11), is that the external mechanical force, , experienced by the αIIbβ3-fibrinogen system increases linearly with the elongation of the complex, , where is a lumped spring constant corresponding to the mechanical deformations of the αIIbβ3-fibrinogen complex. Here, x is a collective reaction coordinate, quantifying the extent of the mechanochemical unbinding reaction for the αIIbβ3-fibrinogen complex and reflects the sum of the force-induced αIIbβ3-fibrinogen bond extension, as well as conformational changes, including straightening and partial elongation of the integrin and fibrinogen molecules. Based on these assumptions, the lifetime of more prolonged αIIbβ3-fibrinogen interactions can be described using a Brownian oscillator model (a harmonic oscillator coupled to a stochastic environment). In this model, the force-induced dissociation of the αIIbβ3-fibrinogen complex can be described by the one-dimensional Brownian motion of the extension of the αIIbβ3-fibrinogen complex, x, in a harmonic potential, (34), undergoing gradual diffusion in the direction of pulling force. The extension, x, is assumed to follow the Langevin equation, , where ζ is the friction constant, is the pulling force, and is the Gaussian random force, which represents the influence of the thermal environment surrounding the αIIbβ3-fibrinogen complex ( is the Boltzmann constant and T is the temperature). Bond rupture is assumed to occur when x reaches the critical elongation of the complex, . The corresponding cumulative distribution function of bond lifetimes is given by (33)
| (2) |
where Erfc[y] is the complementary error function (35), is the average extension of the complex, is the width of the distribution and is the unbinding rate constant. The probability density function of bond lifetimes is given by . We used these equations to describe strong αIIbβ3-fibrinogen interactions in the absence and in the presence of a specific αIIbβ3 inhibitor, abciximab, or of the αIIbβ3 activator Mn2+ (Fig. 2), and to resolve the critical extension of the receptor-ligand complex, , the spring constant, , and the unbinding rate, (see Tables 2 and 3). Statistical analysis of the extracted parameters was performed using the bootstrapping method (36).
Figure 2.
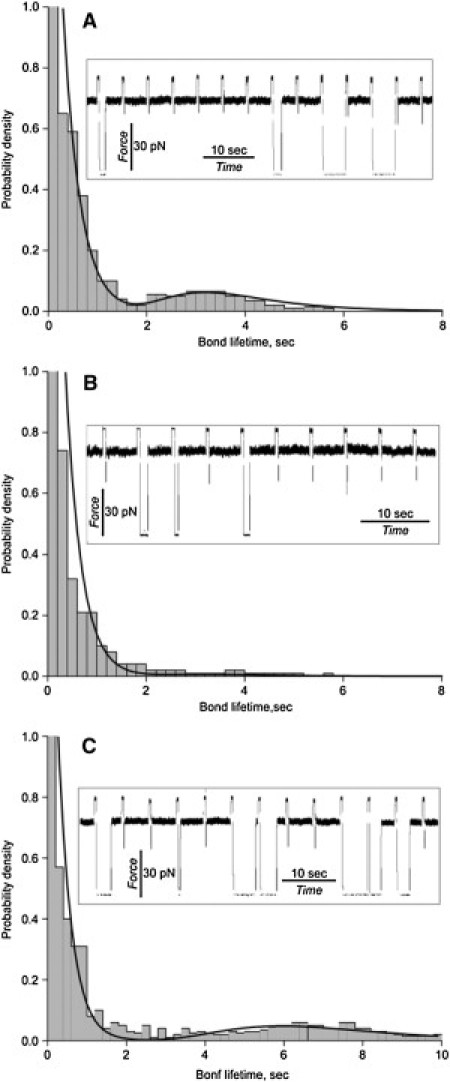
Histograms of bond lifetimes for the αIIbβ3-fibrinogen interactions measured under a constant tensile force of fext = 50 pN and contact duration (interaction) T = 0.5 s. The bond lifetimes in the absence (A) and presence of 200 μg/ml abciximab, a specific αIIbβ3 antagonist (B), or 1 mM Mn2+, an integrin activator (C), are compared with the theoretically derived probability density functions of bond lifetimes (fitting curves) obtained using Eq. 6. In the histograms, the bin size is obtained using an adaptive approach to the optimal bandwidth selection (52). (Insets) Raw data traces typical for each experimental condition represented in the figure.
Table 2.
Average forced unbinding characteristics from the Brownian oscillator model for the weak (LR1) and strong (LR2) bound states of the αIIbβ3-fibrinogen complex
| Control |
With abciximab |
With Mn2+ |
||||
|---|---|---|---|---|---|---|
| LR1 | LR2 | LR1 | LR2 | LR1 | LR2 | |
| Populations, λ1 and λ2 | 0.83 (0.04) | 0.17 (0.04) | 0.97 (0.03) | 0.03 (0.03) | 0.71 (0.03) | 0.29 (0.03) |
| Unbinding rate constants, ku1 and ku2 (s−1) | 3.06 (0.11) | 0.25 (0.01) | 3.38 (0.33) | 0.25 (0.01) | 2.84 (0.17) | 0.189 (0.002) |
| Spring constant, ksp (pN/nm) | — | 12.00 (0.07) | — | 12.02 (0.08) | — | 13.58 (0.08) |
| Critical extension, x∗ (nm) | — | 2.46 (0.05) | — | 2.52 (0.04) | — | 2.86 (0.05) |
| Unbinding energy, kBT | — | 8.78 (0.41) | — | 9.20 (0.28) | — | 12.42 (0.53) |
Analytical estimates of the mechanical, kinetic, and equilibrium parameters correspond to a tensile force of fext = 50 pN. The model and parameters are introduced in the Materials and Methods section. Numbers in parentheses are standard deviations.
Table 3.
Kinetic and thermodynamic characteristics for the weak (LR1) and strong (LR2) bound states of the αIIbβ3-fibrinogen complex at different tensile forces (fext)
|
fext = 50 pN |
fext = 20–40 pN |
fext = 10–20 pN |
fext = 0 pN∗ |
|||||
|---|---|---|---|---|---|---|---|---|
| LR1 | LR2 | LR1 | LR2 | LR1 | LR2 | LR1 | LR2 | |
| Populations, λ1 and λ2 | 0.83 (0.04) | 0.17 (0.04) | 0.72 (0.03) | 0.28 (0.03) | 0.62 (0.02) | 0.38 (0.02) | 0.58 | 0.42 |
| Unbinding rate constants, ku1 and ku2 (s−1) | 3.06 (0.11) | 0.25 (0.01) | 1.64 (0.11) | 0.207 (0.008) | 1.28 (0.08) | 0.16 (0.01) | 1.1 | 0.15 |
| Spring constant, ksp (pN/nm) | — | 12.00 (0.07) | — | 9.30 (0.45) | — | 8.00 (0.71) | — | 7.5 |
| Critical extension, x∗ (nm) | — | 2.46 (0.05) | — | 2.26 (0.09) | — | 1.98 (0.13) | — | 1.78 |
| Unbinding energy, kBT | — | 8.78 (0.41) | — | 5.73 (0.37) | — | 3.78 (0.41) | — | 2.9 |
Parameters are introduced in the Materials and Methods section. Numbers in parentheses are standard deviations.
The parameters for fext = 0 pN were determined by linear extrapolation.
In addition to an analysis of bond-lifetime distributions, we mapped the average free-energy landscape for the force-induced dissociation of the αIIbβ3-fibrinogen complex using the Bell model (37) for the force dependence of the average unbinding rate ,
| (3) |
where is the average force-free rate constant for unbinding, and is the distance from the bound state () to the ensemble average transition state for unbinding (the average interaction range). It is noteworthy that there can be several bound states (, , etc.) or the forced unbinding might occur through multiple unbinding pathways or might involve formation of intermediate species. Therefore, ku and values for different bound states or unbinding pathways might not be equal to their ensemble averages, and , respectively. The phenomenological parameters and were determined from least-squares fits to the average bond-lifetime data. The obtained value of can be used to estimate the ensemble average energy of unbinding, ,
| (4) |
where is the diffusion constant.
Results
Distribution of the αIIbβ3-fibrinogen bond lifetimes
When pedestals coated with αIIbβ3 and beads coated with fibrinogen were allowed to interact for 0.5 s, followed by forced unbinding under a constant 50-pN tension, a wide range of dissociation times (t), varying from milliseconds to seconds, was observed (Fig. 2 A). In a series of control experiments performed using untreated beads and pedestals or replacing αIIbβ3, fibrinogen, or both with inert compounds, the durations of interactions were substantially briefer (Table S1). The cumulative probability of αIIbβ3-fibrinogen interactions with bond lifetimes >0.04 s was ∼20% (Table 1), and the probability of nonspecific interactions in the control experiments was in the range 0.3–5.3% (Table S1). In all cases, the low probability of events suggests that the majority of the observed binding events were bimolecular. Bond lifetimes of t < 0.04 s were likely due to nonspecific interactions, since they were insensitive to αIIbβ3 inhibitors and activators. For bond lifetimes between t > 0.04 s and t < 2 s, there was an exponentially decreasing probability density, whereas for lifetimes of t > 2 s, there was a peak probability density at ∼3 s. Thus, these results indicate that there are two distinct αIIbβ3-fibrinogen binding states, one with lower and one with higher mechanical stability.
Table 1.
Differential effects of abciximab and Mn2+ on the cumulative probabilities of short (t < 2s) and long (t > 2s) interactions between αIIbβ3 and fibrinogen
| Probability of short interactions lasting <2 s | Probability of long interactions lasting >2 s | |
|---|---|---|
| Fibrinogen + Integrin (n = 56) | 0.19 ± 0.12 | 0.020 ± 0.016 |
| Fibrinogen + Integrin + Abciximab (n = 26) | 0.08 ± 0.06 | 0.0032 ± 0.0054 |
| Fibrinogen + Integrin + Mn2+ (n = 28) | 0.28 ± 0.18 | 0.080 ± 0.074 |
Numbers within a column are significantly different (p < 0.01).
To evaluate the specificity of fibrinogen binding to αIIbβ3, the system was perturbed by adding either abciximab, the Fab fragment of a murine-human chimeric monoclonal antibody that inhibits fibrinogen binding to αIIbβ3 (38), or Mn2+, which shifts inactive integrins to their active states by perturbing the conformation of their extracellular domains (39). The detailed analysis of the cumulative binding probabilities in the presence of abciximab shown in Fig. 2 indicates that although abciximab reduced the number of interactions lasting >2 s by sixfold, it only inhibited interactions lasting <2 s by ∼40% (Table 1). These experiments thus confirm that the longer- and shorter-duration interactions we measured result from the specific interaction of αIIbβ3 with fibrinogen. However, they also demonstrate that these interactions are differentially sensitive to the inhibitory effect of abciximab.
To test whether Mn2+-induced αIIbβ3 activation alters the fibrinogen-binding characteristics of individual αIIbβ3 molecules, we measured αIIbβ3-fibrinogen bond lifetimes in the presence of 1 mM MnCl2. In the presence of Mn2+, the peak of the longer bond lifetimes shifted from ∼3 s to ∼6 s (Fig. 2 C). Further, Mn2+ also increased the cumulative probability of interactions lasting <2 s by ∼30% and the number of interactions lasting >2 s by fourfold (Table 1). It is noteworthy that in the presence of Mn2+, the fraction of active αIIbβ3 molecules became substantially greater, consistent with the notion that Mn2+ induces a structural rearrangement of αIIbβ3 that enables it to bind fibrinogen. Our results indicate that Mn2+ increases the mechanical stability of the αIIbβ3-fibrinogen complex as well.
Kinetic and thermodynamic characteristics of the force-induced dissociation of αIIbβ3-fibrinogen complexes
To obtain kinetic and thermodynamic parameters of the αIIbβ3-fibrinogen interaction, the dynamics of unbinding were modeled using a two-state kinetic scheme,
| (5) |
where is the rate constant for unbinding for the short-duration interactions (), is the rate constant for unbinding for the long-duration interactions (), and is the rate constant for the conformational transition →. The probability density function of the αIIbβ3-fibrinogen bond lifetimes corresponding to the kinetic scheme (Eq. 5) is given by
| (6) |
where and are the populations of the bound-state and , respectively (). As discussed in detail in Materials and Methods, an exponential probability density function was used to model , dissociation from the short-duration state , and the Brownian oscillator model was used to model , dissociation from the long-duration state . We were able to estimate the kinetic parameters of the model using Eq. 6 and numerically fit the computationally derived distributions of bond lifetimes to the experimentally obtained histograms of αIIbβ3-fibrinogen bond lifetimes in the absence or presence of abciximab as well as in the absence or presence of Mn2+ (Fig. 2).
Using the two-step kinetic scheme to model the constant-force experiments indicated that when αIIbβ3 and fibrinogen were allowed to interact for 0.5 s, the resulting complex was found to be predominantly in the short-duration state, , 0.83 vs. λ2 = 0.17 for the long-duration state, LR2, and with unbinding rate constants = 3.06 s−1 and = 0.25 s−1, respectively (Table 2). This result is similar to the experimentally determined prevalence of shorter (t < 2 s) and longer (t > 2 s) bond lifetimes shown in Table 1. Further, the force-induced rupture of the long-duration state, , was characterized by a stiff molecular spring (= 12 pN/nm) and a large critical extension of the complex (= 2.46 nm) at which point the complex falls apart (Table 2). This implies that dissociation of the long-duration state, , is associated with partial straightening and/or extension of the αIIbβ3 and/or fibrinogen molecules. The presence of abciximab did not affect the kinetics of αIIbβ3-fibrinogen bond rupture, but rather blocked formation of the long-duration state , i.e., 0.97 for versus 0.03 for (Table 2). Mn2+ destabilized the short-duration state ( 0.71 vs. 0.83 for control, p < 0.01) without significantly affecting the kinetics of the αIIbβ3-fibrinogen bond rupture from ( = 2.84 s−1 vs. 3.06 s−1, p > 0.05). By contrast, it enhanced the stability of long-duration binding ( 0.29 vs. 0.17 in control, p < 0.001) and altered the kinetics of the αIIbβ3-fibrinogen bond rupture from this state by increasing the critical extension of the complex, , from 2.46 nm to 2.86 nm (p < 0.01) and by decreasing the kinetic rate constant, , from 0.25 s−1 to 0.189 s−1 (p < 0.05) (Table 2).
Model parameters, i.e., the molecular spring constants () and the critical extensions (), were then used to estimate the energy needed to dissociate αIIbβ3 from fibrinogen in the long-duration state, . This energy must be supplied to the complex to overcome the transition-state barrier for unbinding. We found that at room temperature (T = 300 K), abciximab had no significant effect on the energy required to dissociate αIIbβ3 and fibrinogen: or 21.9 kJ/mol in the absence of abciximab, and 9.2kBT or 23.2 kJ/mol in the presence of abciximab (p > 0.05). However, Mn2+ ions increased the unbinding energy to or 30.8 kJ/mol (p < 0.05) (Table 2).
Force dependence of the force-induced dissociation
The distribution of dissociation times for αIIbβ3-fibrinogen bonds is strongly dependent on the applied constant tension (Fig. 3 and Fig. S6). The weighted average of the lifetimes of αIIbβ3-fibrinogen bonds decreased exponentially as tensile force was increased in the range 5–50 pN (Fig. 3). The average lifetimes were fit using the Bell model (Eq. 3 and Fig. 3, solid line) with = 0.052 s−1 and = 0.28 nm. Because the force-induced dissociation of the αIIbβ3-fibrinogen complex is dominated by the rupture of the αIIbβ3-fibrinogen bond from the weaker bound state, (Fig. 2 A), these values are more characteristic of the force-free unbinding rate constant () and the critical extension () for the weak bound (short-duration) state (), i.e., = 0.052 s−1 and = 0.28 nm. Using Eq. 4, we also estimated the ensemble average energy of dissociation of the αIIbβ3-fibrinogen complex, which is roughly equal to the energy of dissociation of the weak bound state, , i.e., . We found that (0.75 kJ/mol), confirming the weak binding of αIIbβ3 and fibrinogen in .
Figure 3.
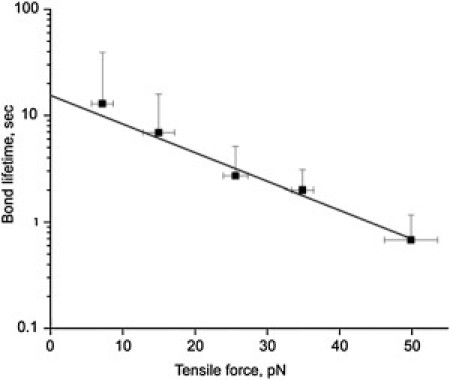
The effect of tensile force on the weighted average of αIIbβ3-fibrinogen bond lifetimes, t, shown on a semilogarithmic scale. The least-squares fit of the experimental data points for the αIIbβ3-fibrinogen bond lifetimes (black squares) with the theoretical dependence of the bond lifetimes on pulling force, (solid line), was used to estimate the kinetic parameters underlying the force-induced rupture of single bonds between the fibrinogen ligands and the αIIbβ3 receptors summarized in the main text.
To test whether the bimodal nature of bond lifetimes persists at different unbinding forces and to quantitatively assess the mechanical compliance of the αIIbβ3-fibrinogen complex in response to variable tension, we used the two-state kinetic scheme to analyze the bond-lifetime distributions obtained at the different tensile forces 10–20 pN, 20–40 pN, and 50 pN (Fig. S6). The model parameters obtained for the different values of fext are summarized in Table 3. These were also extrapolated linearly to fext = 0. Several clear trends in the force dependence of the model parameters are apparent. First, the population increases ( = 0.17 < 0.28 < 0.38 < 0.42) and the population decreases ( = 0.83 > 0.72 > 0.62 > 0.58) with decreasing force. This implies that at lower forces, the αIIbβ3-fibrinogen complex in state LR2 is more stable than at higher forces and that the conformational transition, LR1→LR2, occurs on an experimental timescale of a few seconds. Using the contact duration of 0.5 s, we can estimate the rate constant as ∼1/T = 2.0 s−1. Second, the unbinding rate constants for LR1 and LR2 increase with unbinding force (ku1 = 1.1 < 1.28 < 1.64 < 3.06 s−1 and ku2 = 0.15 < 0.16 < 0.207 < 0.25 s−1, respectively), implying that both the weaker and stronger αIIbβ3-fibrinogen interactions represent classical slip bonds without a catch-to-slip bond transition. Third, the molecular spring constant ksp for the LR2 complex increases with force (7.5 < 8.0 < 9.3 < 12.0 pN/nm), implying that the αIIbβ3-fibrinogen complex becomes stiffer when pulled harder. Last, the critical extension, x∗, for the LR2 state increases with force (1.78 < 1.98 < 2.26 < 2.46 nm), indicating that the position of the transition state for the force-driven dissociation shifts toward the unbound state. Thus, the forced unbinding reactions at higher forces are likely coupled to short-scale conformational transitions, presumably partial elongation of the interacting species, molecular straightening, and alignment along the direction of pulling force. This is consistent with the observed increase of the unbinding energy with force (2.9 < 3.78 < 5.73 < 8.78 kBT).
Discussion
Fibrinogen binding to the integrin αIIbβ3 is essential for the platelet-matrix and platelet-platelet cohesion that occurs in dynamic high-shear conditions in vivo. Thus, studies of αIIbβ3-fibrinogen forced unbinding are physiologically relevant (40,41). Previously, we studied fibrinogen binding to αIIbβ3 using optical-trap-based rupture-force spectroscopy where the rupture force is ramped to quantify the binding strength of individual αIIbβ3 and fibrinogen molecules under different experimental conditions, using either purified proteins or immobilized living platelets (8,11,13). We found that fibrinogen binding to αIIbβ3 is a complex, time-dependent, multistep process during which the strength of the bond between αIIbβ3 and fibrinogen appears to progressively increase. Here, we employed an optical-trap-based force clamp to study the interaction of purified αIIbβ3 with fibrinogen under constant tensile force. This enabled us to derive equilibrium thermodynamic and kinetic parameters directly from the bond-lifetime measurements.
To ensure that the majority of the observed rupture events were due to single αIIbβ3-fibrinogen bonds, surface-coating conditions were tuned to keep protein density low. Thus, the frequency of binding events comprised <30% of total interface contacts (Fig. S4 A), and <90% of the rupture events occurred in a single step. Further, we found that eptifibatide, a small-molecule αIIbβ3-specific inhibitor of fibrinogen binding to platelets, reduced the binding probability sixfold, indicating that most rupture-force events resulted from αIIbβ3-fibrinogen binding (Fig. S4 B).
Most rupture force measurements were performed at a tensile force = 50 pN, which is within the range of hydrodynamic forces exerted on single integrin-fibrinogen bonds during arterial thrombosis (42). We found that the bond-lifetime histograms for fibrinogen bound to αIIbβ3 (Fig. 2 A) had a bimodal distribution, implying two bound states of the αIIbβ3-fibrinogen complex. The first state was composed of shorter-lifetime interactions, t < 2 s, with an unbinding rate constant = 3.06 s−1 and was associated with an exponential probability distribution. The second state had a broader Gaussian-like distribution and was composed of interactions with prolonged lifetimes, t > 2 s, and an ∼10-fold-lower unbinding rate constant, = 0.25 s−1.
The two bound states, designated LR1 and LR2, also differed in their dissociation energy, their stability against the mechanical perturbation, and their susceptibility to inhibition and activation, suggesting that they correspond to the low- and high-affinity αIIbβ3-fibrinogen interactions discovered earlier in bulk experiments (43). Bond lifetimes of <2 s were found to be less perturbed by abciximab, a specific αIIbβ3 antagonist, whereas bond lifetimes >2 s were suppressed severalfold. Moreover, the longer-duration interactions were found to be more sensitive to activation with Mn2+ ions (Table 1). This resulted in a substantial increase in the frequency of fibrinogen binding to αIIbβ3, likely due to an increased fraction of molecules in the high-affinity form, as well as increased stability of the αIIbβ3-fibrinogen complex. Indeed, in the presence of Mn2+, the population of LR2 increased from = 0.17 to = 0.29 (p < 0.001) and the unbinding rate constant for the high-affinity αIIbβ3-fibrinogen interactions decreased from = 0.25 s−1 to = 0.189 s−1 (p < 0.05).
These results suggest that the short-duration interactions are relatively weak and brittle, since bond rupture was accompanied by a short critical extension of the αIIbβ3-fibrinogen complex ( 0.28 nm). By contrast, the longer-duration interactions were more ductile and were associated with an ∼10-fold longer critical extension (= 2.46 nm), albeit with a stiff molecular spring (= 12 pN/nm). Nonetheless, the αIIbβ3-fibrinogen complex existed predominantly in the weaker form and the overall unbinding scenario was similar to unbinding from the weaker state. Because kinetic constants determined from single-molecule unbinding assays and from bulk experiments are different by nature, it is not possible to compare them directly. Indeed, the kinetic parameters of forced dissociation of the surface-bound molecules include their surface density, steric limitations, and spatial orientation and should be considered as pseudokinetic rate constants. However, the parameters determined here may be more physiologically relevant for in vivo platelet-matrix or platelet-platelet adhesion mediated by fibrinogen and fibrin, where both the receptor and the ligand are attached to a surface.
There are several potential explanations for the bimodal mechanism of fibrinogen binding to αIIbβ3. First, the weaker and stronger binding states may correspond to two different interconvertible functional states of the αIIbβ3 molecule. This possibility is supported by the observation that Mn2+, a potent allosteric activator of αIIbβ3, increases the binding probability by shifting the αIIbβ3 population from the LR1 state to the LR2 state, as well as by recruiting new αIIbβ3 molecules from the available pool. Second, LR1 and LR2 may reflect sequential binding steps that differ in the completeness of association and the depth of the receptor-ligand docking. This possibility is corroborated by our previous observation that the strength of integrin-fibrinogen bonding is time-dependent (11), and by ligand-induced binding-site remodeling in αIIbβ3 (44). Based on crystallographic observations (45), it is possible that the fibrinogen γC-peptide initially binds to either αIIb or β3 as part of a ligand-binding claw (LR1), followed by attachment to the rest of the αIIbβ3 binding surface (LR2). Third, it is possible that there is more than one αIIbβ3 binding site on fibrinogen and that these binding sites interact cooperatively or synergistically (46). Thus, one of the two RGD motifs in the fibrinogen Aα chain may form a transient weak bond (LR1) that is reinforced by additional strong bonds by the γC-peptide (LR2). The latter possibility can be tested experimentally by using RGD- and AGDV-containing peptides and/or a recombinant fibrinogen variant with mutated potential αIIbβ3-binding motifs.
Irrespective of the mechanisms underlying the existence of two types of fibrinogen-αIIbβ3 interactions, this finding may have substantial physiological relevance. The short or weak interactions may correspond to the so-called low-affinity state of the αIIbβ3 found on resting platelets. Resting platelets adhere weakly and reversibly to fibrinogen-coated surfaces, perhaps as a result of the short and brittle αIIbβ3-fibrinogen binding events we observed and characterized in this study. However, when platelets, and consequently αIIbβ3, are activated and/or allowed to stay in contact with fibrinogen for longer periods of time, fibrinogen binding becomes strong and irreversible, perhaps a reflection of the formation of a mechanically stable αIIbβ3-fibrinogen complex that is resistant to the pulling forces generated by hydrodynamic shear. Remaining open questions include whether the two types of αIIbβ3-fibrinogen interaction are interconvertible and what are the driving forces for the strengthening of the interaction.
It has been hypothesized that integrin-ligand affinity and unbinding kinetics could be modulated by an applied pulling force, resulting in an initial increase in ligand-binding affinity and bond lifetime at low forces (catch bonds) followed by a decrease in affinity and bond lifetime at higher forces (slip bonds). This hypothesis was based on a structural model in which an applied force, by pulling on an inactive integrin, opens its bent conformation and is followed by a switchbladelike extension of the integrin into its active form (25).
The only integrin shown to form bimolecular catch bonds is α5β1 (28). We asked whether a catch-bond/slip-bond mechanism could explain the interaction of αIIbβ3 with fibrinogen, as has been proposed by others (25–27). Because the catch-bond regime occurs at tensile forces <30 pN (21–23,47,48), we carried out constant-force measurements of bond lifetimes for fibrinogen bound to αIIbβ3 at several pulling forces in the range 5–50 pN. We found that average αIIbβ3-fibrinogen bond lifetimes decreased monotonically with increasing tensile force and did not exhibit biphasic behavior indicative of pure slip-bond dissociation. More complex model fitting also showed a gradual, monotonic increase of the unbinding rate constants in response to increasing unbinding force. Thus, within the 5–50 pN range of constant pulling force, the αIIbβ3-fibrinogen complex does not form catch bonds, consistent with the lack of shear-induced platelet adhesion on the fibrinogen-coated surface over a wide range of shear forces (49). The results also indicate that although the existence of two bound states and/or two unbinding pathways is necessary for the emergence of a catch regime of unbinding for biomolecular complexes (50,51), this might not be sufficient for the bond lifetimes to exhibit nonmonotonic biphasic dependence on the applied pulling force.
In conclusion, we employed an optical-trap-based electronic force clamp and detected two types of αIIbβ3-fibrinogen complexes that differed in their mechanical stability, as well as in their binding and unbinding kinetic pathways. We found no evidence for catch bonds, consistent with the lack of shear-enhanced platelet adhesion to fibrinogen-coated surfaces. These observations provide important quantitative and qualitative characteristics of fibrinogen binding and unbinding to αIIbβ3, events that underlie the dynamics of fibrinogen-mediated platelet adhesion and aggregation in flowing blood.
Acknowledgments
The authors thank Hua Zhu for providing an integrin preparation, Justin Vranic for valuable technical assistance, and Serapion Pyrpassopoulos for providing software for the bootstrap analysis. This work was supported by National Institutes of Health grants HL40387 and HL81012, as well as by a Scientist Development Grant (09SDG2460023) from the American Heart Association (V.B.).
Footnotes
Andrew J. Schissler is currently a student at Harvard Medical School, Boston, MA
Andrew R. Fisher is currently a student at the University of Pennsylvania School of Medicine, Philadelphia, PA.
Supporting Material
References
- 1.Hynes R.O. Integrins: bidirectional, allosteric signaling machines. Cell. 2002;110:673–687. doi: 10.1016/s0092-8674(02)00971-6. [DOI] [PubMed] [Google Scholar]
- 2.Coller B.S., Shattil S.J. The GPIIb/IIIa (integrin αIIbβ3) odyssey: a technology-driven saga of a receptor with twists, turns, and even a bend. Blood. 2008;112:3011–3025. doi: 10.1182/blood-2008-06-077891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Shattil S.J., Kashiwagi H., Pampori N. Integrin signaling: the platelet paradigm. Blood. 1998;91:2645–2657. [PubMed] [Google Scholar]
- 4.Suzuki H., Kaneko T., Tanoue K. Redistribution of α-granule membrane glycoprotein IIb/IIIa (integrin αIIbβ3) to the surface membrane of human platelets during the release reaction. J. Electron Microsc. (Tokyo) 1994;43:282–289. [PubMed] [Google Scholar]
- 5.George J.N., Caen J.P., Nurden A.T. Glanzmann's thrombasthenia: the spectrum of clinical disease. Blood. 1990;75:1383–1395. [PubMed] [Google Scholar]
- 6.Lefkovits J., Plow E.F., Topol E.J. Platelet glycoprotein IIb/IIIa receptors in cardiovascular medicine. N. Engl. J. Med. 1995;332:1553–1559. doi: 10.1056/NEJM199506083322306. [DOI] [PubMed] [Google Scholar]
- 7.Lee I., Marchant R.E. Force measurements on the molecular interactions between ligand (RGD) and human platelet αIIbβ3 receptor system. Surf. Sci. 2001;491:433–443. [Google Scholar]
- 8.Litvinov R.I., Shuman H., Weisel J.W. Binding strength and activation state of single fibrinogen-integrin pairs on living cells. Proc. Natl. Acad. Sci. USA. 2002;99:7426–7431. doi: 10.1073/pnas.112194999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Arya M., López J.A., Anvari B. Glycoprotein Ib-IX-mediated activation of integrin α(IIb)β(3): effects of receptor clustering and von Willebrand factor adhesion. J. Thromb. Haemost. 2003;1:1150–1157. doi: 10.1046/j.1538-7836.2003.00295.x. [DOI] [PubMed] [Google Scholar]
- 10.Lee I., Marchant R.E. Molecular interaction studies of hemostasis: fibrinogen ligand-human platelet receptor interactions. Ultramicroscopy. 2003;97:341–352. doi: 10.1016/S0304-3991(03)00059-7. [DOI] [PubMed] [Google Scholar]
- 11.Litvinov R.I., Bennett J.S., Shuman H. Multi-step fibrinogen binding to the integrin αIIbβ3 detected using force spectroscopy. Biophys. J. 2005;89:2824–2834. doi: 10.1529/biophysj.105.061887. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Hussain M.A., Agnihotri A., Siedlecki C.A. AFM imaging of ligand binding to platelet integrin αIIbβ3 receptors reconstituted into planar lipid bilayers. Langmuir. 2005;21:6979–6986. doi: 10.1021/la046943h. [DOI] [PubMed] [Google Scholar]
- 13.Litvinov R.I., Vilaire G., Bennett J.S. Activation of individual αIIbβ3 integrin molecules by disruption of transmembrane domain interactions in the absence of clustering. Biochemistry. 2006;45:4957–4964. doi: 10.1021/bi0526581. [DOI] [PubMed] [Google Scholar]
- 14.Agnihotri A., Soman P., Siedlecki C.A. AFM measurements of interactions between the platelet integrin receptor GPIIbIIIa and fibrinogen. Colloids Surf. B Biointerfaces. 2009;71:138–147. doi: 10.1016/j.colsurfb.2009.01.019. [DOI] [PubMed] [Google Scholar]
- 15.Jin M., Andricioaei I., Springer T.A. Conversion between three conformational states of integrin I domains with a C-terminal pull spring studied with molecular dynamics. Structure. 2004;12:2137–2147. doi: 10.1016/j.str.2004.10.005. [DOI] [PubMed] [Google Scholar]
- 16.Puklin-Faucher E., Gao M., Vogel V. How the headpiece hinge angle is opened: New insights into the dynamics of integrin activation. J. Cell Biol. 2006;175:349–360. doi: 10.1083/jcb.200602071. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Zhu J., Luo B.H., Springer T.A. Structure of a complete integrin ectodomain in a physiologic resting state and activation and deactivation by applied forces. Mol. Cell. 2008;32:849–861. doi: 10.1016/j.molcel.2008.11.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Goncalves I., Nesbitt W.S., Jackson S.P. Importance of temporal flow gradients and integrin αIIbβ3 mechanotransduction for shear activation of platelets. J. Biol. Chem. 2005;280:15430–15437. doi: 10.1074/jbc.M410235200. [DOI] [PubMed] [Google Scholar]
- 19.Puklin-Faucher E., Sheetz M.P. The mechanical integrin cycle. J. Cell Sci. 2009;122:179–186. doi: 10.1242/jcs.042127. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Podolnikova N.P., Yermolenko I.S., Ugarova T.P. Control of integrin αIIb β3 outside-in signaling and platelet adhesion by sensing the physical properties of fibrin(ogen) substrates. Biochemistry. 2010;49:68–77. doi: 10.1021/bi9016022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Marshall B.T., Long M., Zhu C. Direct observation of catch bonds involving cell-adhesion molecules. Nature. 2003;423:190–193. doi: 10.1038/nature01605. [DOI] [PubMed] [Google Scholar]
- 22.Yago T., Lou J., Zhu C. Platelet glycoprotein Ibα forms catch bonds with human WT vWF but not with type 2B von Willebrand disease vWF. J. Clin. Invest. 2008;118:3195–3207. doi: 10.1172/JCI35754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Guo B., Guilford W.H. Mechanics of actomyosin bonds in different nucleotide states are tuned to muscle contraction. Proc. Natl. Acad. Sci. USA. 2006;103:9844–9849. doi: 10.1073/pnas.0601255103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Yakovenko O., Sharma S., Thomas W.E. FimH forms catch bonds that are enhanced by mechanical force due to allosteric regulation. J. Biol. Chem. 2008;283:11596–11605. doi: 10.1074/jbc.M707815200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Zhu C., Lou J., McEver R.P. Catch bonds: physical models, structural bases, biological function and rheological relevance. Biorheology. 2005;42:443–462. [PubMed] [Google Scholar]
- 26.Luo B.H., Carman C.V., Springer T.A. Structural basis of integrin regulation and signaling. Annu. Rev. Immunol. 2007;25:619–647. doi: 10.1146/annurev.immunol.25.022106.141618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.McEver R.P., Zhu C. A catch to integrin activation. Nat. Immunol. 2007;8:1035–1037. doi: 10.1038/ni1007-1035. [DOI] [PubMed] [Google Scholar]
- 28.Kong F., García A.J., Zhu C. Demonstration of catch bonds between an integrin and its ligand. J. Cell Biol. 2009;185:1275–1284. doi: 10.1083/jcb.200810002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Visscher K., Gross S.P., Block S.M. Construction of multiple-beam optical traps with nanometer-resolution position sensing. IEEE J. Sel. Top. Quantum Electron. 1996;2:1066–1076. [Google Scholar]
- 30.Bennett J.S., Hoxie J.A., Cines D.B. Inhibition of fibrinogen binding to stimulated human platelets by a monoclonal antibody. Proc. Natl. Acad. Sci. USA. 1983;80:2417–2421. doi: 10.1073/pnas.80.9.2417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Weisel J.W., Nagaswami C., Bennett J.S. Examination of the platelet membrane glycoprotein IIb-IIIa complex and its interaction with fibrinogen and other ligands by electron microscopy. J. Biol. Chem. 1992;267:16637–16643. [PubMed] [Google Scholar]
- 32.Barsegov V., Morrison G., Thirumalai D. Role of internal chain dynamics on the rupture kinetic of adhesive contacts. Phys. Rev. Lett. 2008;100:248102. doi: 10.1103/PhysRevLett.100.248102. [DOI] [PubMed] [Google Scholar]
- 33.Zhmurov A., Dima R.I., Barsegov V. Order statistics theory of unfolding of multimeric proteins. Biophys. J. 2010;99:1959–1968. doi: 10.1016/j.bpj.2010.07.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Doi M., Edwards S.F. Oxford University Press; New York: 1994. The Theory of Polymer Dynamics. [Google Scholar]
- 35.Abramowitz M., Stegun I.A. Dover Publications; New York: 1972. Handbook of Mathematical Functions. [Google Scholar]
- 36.Press, W. H., S. A. Teukolsky, …, B. P. Flannery, editors. 2005. Numerical Recipes in C++: The Art of Scientific Computing, 2nd ed. Cambridge University Press, New York.
- 37.Bell G.I. Models for the specific adhesion of cells to cells. Science. 1978;200:618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 38.Coller B.S. A new murine monoclonal antibody reports an activation-dependent change in the conformation and/or microenvironment of the platelet glycoprotein IIb/IIIa complex. J. Clin. Invest. 1985;76:101–108. doi: 10.1172/JCI111931. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Litvinov R.I., Nagaswami C., Weisel J.W. Functional and structural correlations of individual αIIbβ3 molecules. Blood. 2004;104:3979–3985. doi: 10.1182/blood-2004-04-1411. [DOI] [PubMed] [Google Scholar]
- 40.Bennett J.S. Structure and function of the platelet integrin αIIbβ3. J. Clin. Invest. 2005;115:3363–3369. doi: 10.1172/JCI26989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bennett J.S., Berger B.W., Billings P.C. The structure and function of platelet integrins. J. Thromb. Haemost. 2009;7(Suppl 1):200–205. doi: 10.1111/j.1538-7836.2009.03378.x. [DOI] [PubMed] [Google Scholar]
- 42.Shankaran H., Neelamegham S. Hydrodynamic forces applied on intercellular bonds, soluble molecules, and cell-surface receptors. Biophys. J. 2004;86:576–588. doi: 10.1016/S0006-3495(04)74136-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bennett J.S. Platelet-fibrinogen interactions. Ann. N. Y. Acad. Sci. 2001;936:340–354. doi: 10.1111/j.1749-6632.2001.tb03521.x. [DOI] [PubMed] [Google Scholar]
- 44.Hantgan R.R., Stahle M.C., Medved L. Integrin αIIbβ3:ligand interactions are linked to binding-site remodeling. Protein Sci. 2006;15:1893–1906. doi: 10.1110/ps.052049506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Springer T.A., Zhu J., Xiao T. Structural basis for distinctive recognition of fibrinogen γC peptide by the platelet integrin αIIbβ3. J. Cell Biol. 2008;182:791–800. doi: 10.1083/jcb.200801146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Sánchez-Cortés J., Mrksich M. The platelet integrin αIIbβ3 binds to the RGD and AGD motifs in fibrinogen. Chem. Biol. 2009;16:990–1000. doi: 10.1016/j.chembiol.2009.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Laakso J.M., Lewis J.H., Ostap E.M. Myosin I can act as a molecular force sensor. Science. 2008;321:133–136. doi: 10.1126/science.1159419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Auton M., Sedlák E., Cruz M.A. Changes in thermodynamic stability of von Willebrand factor differentially affect the force-dependent binding to platelet GPIbα. Biophys. J. 2009;97:618–627. doi: 10.1016/j.bpj.2009.05.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Savage B., Saldívar E., Ruggeri Z.M. Initiation of platelet adhesion by arrest onto fibrinogen or translocation on von Willebrand factor. Cell. 1996;84:289–297. doi: 10.1016/s0092-8674(00)80983-6. [DOI] [PubMed] [Google Scholar]
- 50.Barsegov V., Thirumalai D. Dynamics of unbinding of cell adhesion molecules: transition from catch to slip bonds. Proc. Natl. Acad. Sci. USA. 2005;102:1835–1839. doi: 10.1073/pnas.0406938102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Barsegov V., Thirumalai D. Dynamic competition between catch and slip bonds in selectins bound to ligands. J. Phys. Chem. B. 2006;110:26403–26412. doi: 10.1021/jp0653306. [DOI] [PubMed] [Google Scholar]
- 52.Bura E., Zhmurov A., Barsegov V. Nonparametric density estimation and optimal bandwidth selection for protein unfolding and unbinding data. J. Chem. Phys. 2009;130:015102. doi: 10.1063/1.3050095. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


