Progressive EPR imaging with adaptive projection acquisition

Abstract

Continuous wave electron paramagnetic resonance imaging (EPRI) of living biological systems requires rapid acquisition and visualization of free radical images. In the commonly used multiple-stage back-projection image reconstruction algorithm, the EPR image cannot be reconstructed until a complete set of projections is collected. If the data acquisition is incomplete, the previously acquired incomplete data set is no longer useful. In this work, a 3-dimensional progressive EPRI technique was implemented based on inverse Radon transform in which a 3-dimensional EPR image is acquired and reconstructed gradually from low resolution to high resolution. An adaptive data acquisition strategy is proposed to determine the significance of projections and acquire them in an order from the most significant to the least significant. The image acquisition can be terminated at any time if further collection of projections does not improve the image resolution distinctly, providing flexibility to trade image quality with imaging time. The progressive imaging technique was validated using computer simulations as well as imaging experiments. The adaptive acquisition uses 50–70% less projections as compared to the regular acquisition. In conclusion, adaptive data acquisition with progressive image reconstruction should be very useful for the accelerated acquisition and visualization of free radical distribution.

1. Introduction

In the last two decades, electron paramagnetic resonance imaging (EPRI) has made rapid progress [1–3] and demonstrated its unique usefulness in many branches of science including biology and medicine [4–12]. Several review articles on the development of EPRI methods and their application to biological systems have appeared in recent years [3,13–15]. While the time-domain EPRI technique has emerged recently with the advantage of significantly reduced imaging time [16,17], the continuous wave (CW) EPRI technique still dominates current applications because of its higher sensitivity and applicability to a large variety of spin probes of varied linewidths [17]. The filtered back-projection (FBP) method is commonly used for image reconstruction in CW EPRI in which an n-dimensional EPR image is reconstructed through (n − 1)-stage back-projection operations [2,18,19]. For instance, a 3-dimensional EPR image is reconstructed in two stages, with each stage consisting of the reconstruction of a set of 2-dimensional images. The multi-stage reconstruction algorithm is easy to implement and very fast in computation speed. The use of low-computation approaches was important when advanced computational facilities (speed and memory) were not available. Despite its low requirements for computational facilities, the multi-stage image reconstruction algorithm has several limitations. First, it requires an equal-angle increment in stepping the gradient vector. The uniform angular sampling of the object space causes a non-uniform gradient density distribution on the surface of the object which considerably decreases the data acquisition efficiency [20,21]. Second, the image reconstruction can be performed only after all the projections are collected. During the data acquisition period, however, no information is available about the image. If the data acquisition terminates due to unexpected reasons such as a change in animal physiology, position, or environment, the previously acquired incomplete data set is no longer useful. Additionally, all the projections are by default assigned with equal importance and acquired in a nested-loop order. This content-insensitive acquisition method is not optimal in data acquisition time and/or image resolution [22].

In this work, a novel 3-dimensional progressive EPRI method with content-sensitive acquisition was developed. The inverse Radon transform [21,23] was implemented and applied to reconstruct EPR images from projections in a single stage, in which all the filtered projections are back-projected directly on to the 3-dimensional goal image. Since the image reconstruction can be done during the data acquisition process, it enables progressive reconstruction and visualization of the EPR image. The uniform gradient scanning approach [20,21] was adapted to replace the uniform angular sampling (non-uniform gradient scanning) and it was shown the data acquisition efficiency could be considerably increased. We proposed an adaptive data acquisition strategy in which all the projections are acquired in a sorted order according to their significance values derived from the previously acquired projections. The proposed progressive imaging technique with adaptive projection acquisition was implemented and tested through simulations and imaging experiments. Compared with the regular EPRI data acquisition, marked performance improvements have been realized.

2. Theory

2.1. Progressive image reconstruction using inverse Radon transform

The Radon transform of a 3-dimensional object f (x,y, z) is expressed by the following equation [21,23].

$$p(s,\alpha ,\theta )={\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x,y,z)\delta (x\text{sin}\theta \text{cos}\alpha +y\text{sin}\theta \text{sin}\alpha +z\text{cos}\theta -s)\mathrm{d}x\mathrm{d}y\mathrm{d}z.}}}$$ (1)

The inverse Radon transform of Eq. (1) is given by

$$f(x,y,z)={\displaystyle {\int }_0^{\mathrm{\pi }/2}{\displaystyle {\int }_0^{2\mathrm{\pi }}\widehat{p}(x\text{sin}\theta \text{cos}\alpha +y\text{sin}\theta \text{sin}\alpha +z\text{cos}\theta ,\alpha ,\theta )\text{sin}\theta \mathrm{d}\alpha \mathrm{d}\theta ,}}$$ (2)

where

$$\widehat{p}(s,\alpha ,\theta )=-\frac{1}{8{\mathrm{\pi }}^2}\frac{{\partial }^{2}p(s,\alpha ,\theta )}{\partial s^2}.$$ (3)

Refer to Fig. 1 for a definition of projection geometry. Image reconstruction in 3-dimensional EPRI is mathematically a 3-dimensional inverse Radon transform descried above but operated in digital domain. Therefore, the second partial derivative in the filtering operation, Eq. (3), can be approximated using a three-point digital filter [21], as

$$\widehat{p}(s_i,{\alpha }_j,{\theta }_k)=-\frac{1}{8{\mathrm{\pi }}^2}[2p(s_i,{\alpha }_j,{\theta }_k)-p(s_{i-1},{\alpha }_j,{\theta }_k)-p(s_{i+1},{\alpha }_j,{\theta }_k)],$$ (4)

where 0 ⩽ i ⩽ I − 1, 0 ⩽ j ⩽ J − 1, and 0 ⩽ k ⩽ K − 1. I is the number of data points for each projection. J and K are the sample number of the azimuth angle α and elevation angle θ, respectively. Similar to Eq. (4), the integration in Eq. (2) is approximated using summation [21],

$$\widehat{f}(x,y,z)=\frac{2{\mathrm{\pi }}^2}{K}{\displaystyle \sum _{k=0}^{K-1}\text{sin}{\theta }_k\frac{1}{J}}{\displaystyle \sum _{j=0}^{J-1}\widehat{p}(x\text{sin}{\theta }_k\text{cos}{\alpha }_j+y\text{sin}{\theta }_k\text{sin}{\alpha }_j+z\text{cos}{\theta }_k,{\alpha }_j,{\theta }_k).}$$ (5)

Eq. (5) states that, given the sample number of α and θ as J and K (then the total projection number as JK), each projection is reconstructed independent of others to obtain a 3-dimensional “basis” image. All the JK “basis” images are accumulated to obtain the final reconstruction result. Apparently, in the beginning, when only a few projections are acquired, a few “basis” images will be accumulated to obtain a low-resolution image. As more projections are collected, more “basis” images will be added to the low-resolution image to obtain a high-resolution image. Thus, a progressive image acquisition scheme is implemented based on the inverse Radon transform.

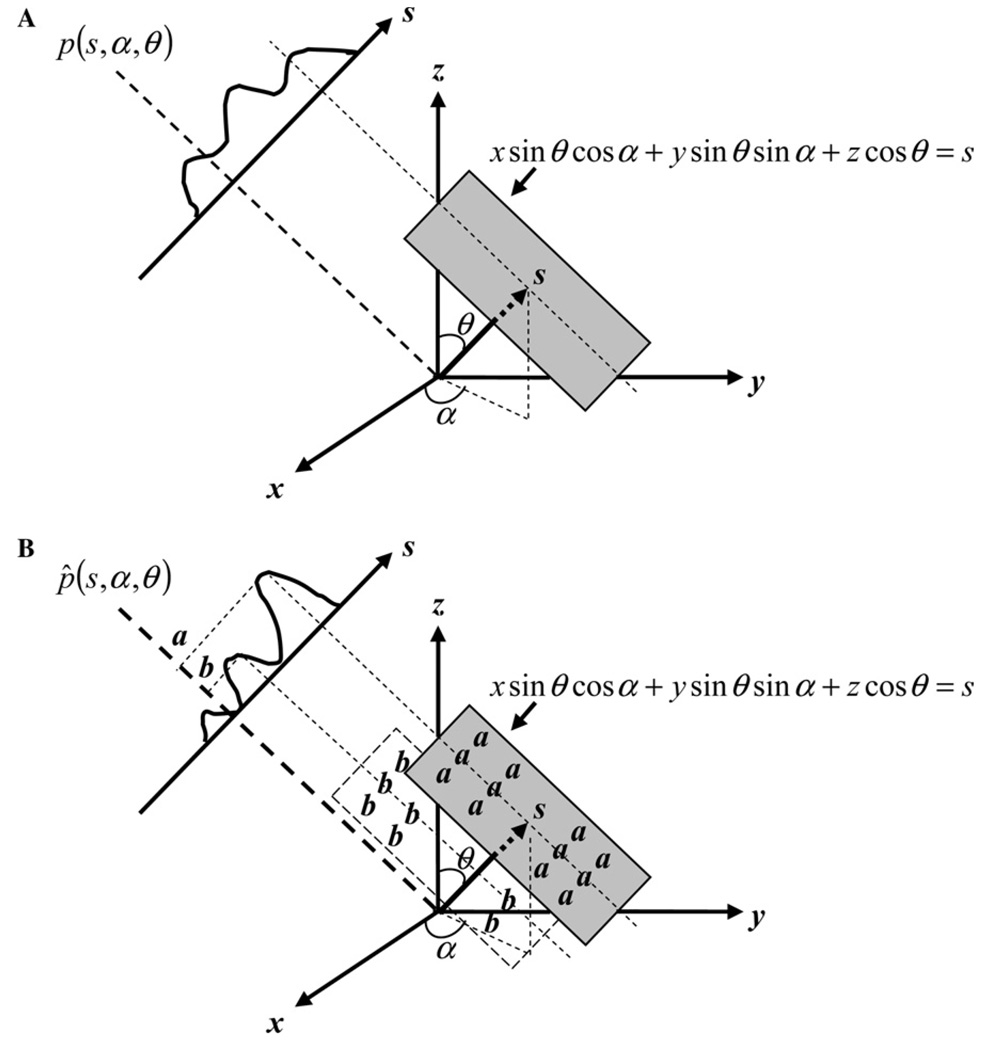
Fig. 1.

Image reconstruction using Radon transform. A: Acquisition of projections in 3-dimensional EPRI. Each point of the projection p(s,θ,α) is a plane integral of the object f(x,y,z) on the plane defined by x sin θ cos α + y sin θ sin α + z cos θ = s. (B) 3-dimensional image reconstruction using inverse Radon transform. Each point of the filtered projection p̂ (s, θ, α) is back-projected on to a 2-dimensional plane defined by x sin θ cos α + y sin θ sin α + z cos θ = s. Such a plane is a slice of the 3-dimensional object being reconstructed. Thus, the entire projection (after filtering) is directly back-projected to obtain a 3-dimensional “basis” image. All the “basis” images are accumulated to obtain the final reconstruction result. This method is also called single stage image reconstruction.

2.2. Uniform magnetic field gradient scanning

In Eq. (5), α and θ are sampled uniformly, i.e., α_j = j2π/J and θ_k = kπ/2K + π/4K. This is required in principle by the two-stage back-projection image reconstruction algorithm (otherwise interpolation is needed). However, the equal-increment of α and θ will result in a non-uniform gradient density distribution over the surface of the 3-dimensional object [20,21]. As shown in Fig. 2A, the gradient density near the pole (θ close to 0) is much higher than that near the equator (θ close to π/2). As will be seen later, the over-sampling near the pole seriously decreases the data acquisition efficiency. In this study, since the single stage image reconstruction algorithm is used, we will be able to implement a uniform gradient scanning path to improve the data acquisition efficiency, as reported previously.

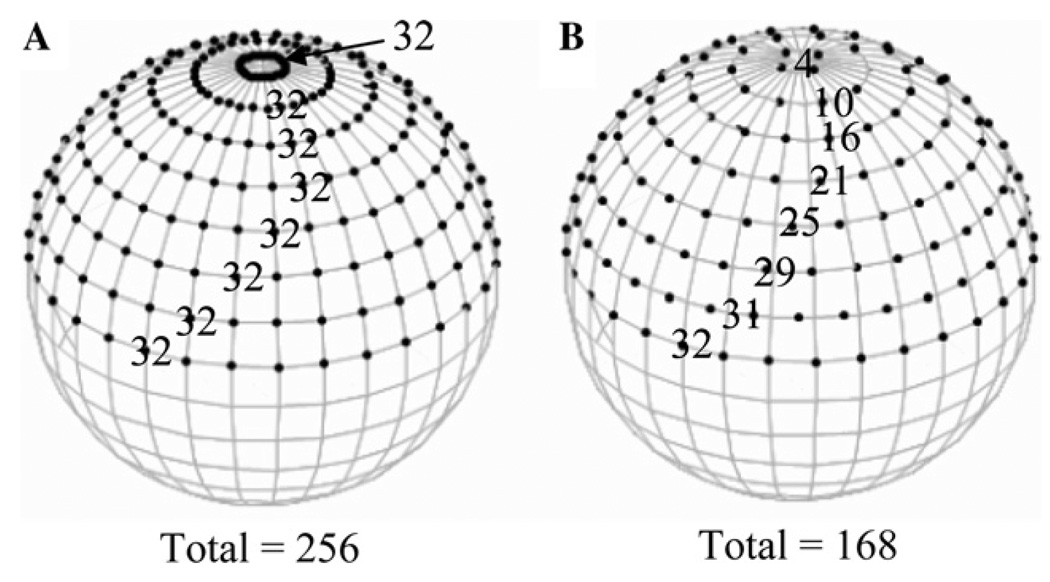
Fig. 2.

Two different gradient scanning modes. (A) Non-uniform gradient scanning mode (also called uniform angular sampling mode). In this mode, the elevation angle θ and azimuth angle α are uniformly sampled. The gradient density near the pole is much higher than that near the equator. The over-sampling near the pole area seriously decreases the data acquisition efficiency. (B) Uniform gradient scanning mode. In this mode, only the elevation angle θ is uniformly sampled. The number of samples for α is determined by Eq. (6). The gradient density is approximately uniform and the data acquisition efficiency is increased by avoiding over-sampling.

In the uniform gradient scanning scheme, the elevation angle θ is still uniformly sampled but the sampling of the azimuth angle α is different: the increment step size of α is calculated according to the current elevation angle θ_k. The number of samples for α at θ_k is

$$J_k=\text{round}(J\text{sin}{\theta }_k).$$ (6)

Consequently, Eq. (5) is rewritten as

$$f(x,y,z)=\frac{2{\mathrm{\pi }}^2}{K}{\displaystyle \sum _{k=0}^{K-1}\text{sin}{\theta }_k\frac{1}{J_k}}{\displaystyle \sum _{j=0}^{J_k-1}\widehat{p}(x\text{sin}{\theta }_k\text{cos}{\alpha }_j+y\text{sin}{\theta }_k\text{sin}{\alpha }_j+z\text{cos}{\theta }_k,{\alpha }_j,{\theta }_k).}$$ (7)

Obviously, when θ_k = π/2, the number of samples for α reaches the maximum value, i.e., J, and when θ_k → 0, it reaches the minimum value. At other θ_k, the number of samples for α is less than J. In this way, the gradient density is uniformly distributed and the over-sampling near the pole is avoided, as shown in Fig. 2B. The improvement of data acquisition efficiency by the uniform gradient scanning can be estimated as

$$\eta =1-\frac{{\displaystyle {\sum }_{k=0}^{K-1}{J}_k}}{J·K}.$$ (8)

In the above estimation, it is assumed that the signal-to-noise ratio of the projections is high enough so that the signal averaging through over-sampling is not necessary. In a typical case of J = 64 and K = 16 (equivalent as J = 32 and K = 32 for 180°–180° regular 3-dimensional EPRI data acquisition), 660 projections, instead of 1024, need to be acquired. Thus, the data acquisition efficiency is increased by one-third by using the uniform gradient scanning mode.

3. Adaptive data acquisition

So far, in both single-stage and two-stage image reconstruction algorithms, all the projections are acquired in a nested-loop order spanning the entire object space. The acquisition process is blind to the nature of the sample structure. While this conservative data collection strategy is unbiased and suitable for arbitrary sample structure, it is not optimized for objects with non-uniform structures [22]. If the spins are concentrated only in some locations within the object, not all the projections are equally important in image reconstruction. For example, if the spins are distributed as a narrow-line strip-shape, then the projection acquired with the gradient vector parallel to the long axis of the strip carries relatively more information about the spin distribution than the projection acquired with the gradient perpendicular to the long axis because the former will have a much wider band width. The information content of each projection (or the significance of each projection) will determine the contribution from the current projection to the reconstruction result and therefore the convergence speed of the reconstruction error. In the following, we will develop an adaptive data acquisition algorithm capable of optimizing the data collection time and the image resolution.

Placidi et al. [22] proposed an adaptive technique in which the “entropy” was used to measure the information content of projections and to determine their acquisition order. Their preliminary results of 2-dimensional EPRI experiments showed that about 30% of the projections can be saved using the adaptive algorithm compared with the regular nested-loop data acquisition method. While the “entropy” is an effective measure of projection information content, it is not intuitive how the measured “entropy” of a projection is directly related to the image reconstruction error. Recall that in the 3-dimensional single stage image reconstruction algorithm, every value of a filtered projection is back-projected onto a 2-dimensional plane which is a slice of the 3-dimensional goal image being reconstructed (Fig. 1B). The larger the amplitude of the filtered projection, the bigger is that projection’s contribution to the goal image. For example, assuming that there are two filtered projections whose values are 100 and 10, respectively, then a 3-dimensional “basis” image of value 100 will be added to the reconstruction result after the first projection is back-projected. When the second projection is back-projected, however, a constant 3-dimensional “basis” image of value 10 will be added to the reconstructed result. Obviously, the first projection will decrease the reconstruction error much faster than the second one if the mean square error (MSE) criterion is used. Therefore, we can conclude that the first projection is more important and should be acquired prior to the second one. Based on the above analysis, in this work, the mean-square amplitude of the filtered projection is used to evaluate the significance for each projection, as

$${\lambda }_{j,k}=\frac{1}{I}{\displaystyle \sum _{i=0}^{I-1}{\widehat{p}}^2(s_i,{\alpha }_j,{\theta }_k).}$$ (9)

Since in experiments a projection is not available until it is acquired, a linear interpolation method is used to predict the significance value from the previously acquired projections.

We propose the following algorithm to acquire projections in an order according to their significance values: (i) Given the imaging parameters, calculate the uniform gradient scanning path (see Fig. 2B). (ii) Acquire a pre-defined number of projections, say, 10 percent of the entire projections. These projections will be used as “seeds” to determine the acquisition order for other projections through prediction, as in step (iii). To shorten the time within which all the important projections will be covered, these “seed” projections should be distributed evenly in the pre-calculated gradient scanning path. (iii) Calculate the significance values for all the acquired projections and predict the significance values for all other uncollected projections using linear interpolation. Acquire the projection with the highest significance value in the prediction. (iv) Filter and back-project the projection acquired in step (iii) and update the reconstruction result and image display. (v) Repeat steps (iii) and (iv) until all the projections are collected or the data acquisition is stopped.

4. Results

4.1. Simulation results

The progressive image reconstruction algorithm and the adaptive acquisition method were first tested by simulation on two different digital phantoms (64 × 64 × 64). The imaging parameters were chosen to simulate EPRI experiments at 300 MHz. All the projections were calculated from the phantom using our EPRI simulation program written in Matlab language. The calculated projections were reconstructed to obtain the goal image through either the single stage or the two-stage image reconstruction algorithm. The imaging parameters in the simulation were as follows: central field, 10 mT; sweep width, 0.75 mT; data points, 128; field of view (FOV), 50 × 50 × 50 mm³. The Lorentzian absorption line shape was used with full-width at half-height (FWHH) as 0.02 mT. The gradient strength was 15 mT/m. No deconvolution was performed. The image resolution was approximately 1.3 mm [24]. The uniform gradient scanning strategy was used in the simulation which saved about one third of data acquisition time as discussed above. For each phantom, both the regular acquisition (in a nested-loop order) and the adaptive acquisition were tested.

4.2. “Tubes” phantom

The “Tubes” phantom consisted of a bunch of tubes with diameter of either 3.9 or 6.2 mm and length of about 30 mm. Two tubes have been intentionally made smaller than the others for identification of orientation. Fig. 3A shows the progressive image reconstruction results as the projections were acquired in a nested-loop order. The original digital phantom is also shown in the same figure. When a few projections were collected, a low resolution image was obtained. As more projections were accumulated, the image resolution increased correspondingly. Since all the projections were treated with equal importance and, therefore, acquired in a nested-loop order, the reconstructed images converged very slowly to the original phantom. Fig. 3B is the reconstruction results of the same phantom but acquired using the adaptive acquisition algorithm. In the adaptive acquisition, 66 projections were acquired as “seeds,” which were uniformly distributed in the predefined gradient scanning path. The algorithm discussed in the Theory section was used to determine the projection with the largest significance value. So, all the remaining 90% of the projections were acquired in an order from the most important to the least important. Fig. 3B clearly shows that the data acquisition efficiency was significantly improved by the adaptive acquisition algorithm. For example, after only 200 projections were acquired, the image quality was reasonably good. It was further improved after 300 projections were acquired. In both cases, the images with adaptive acquisition were much better than the corresponding ones with the same number of projections acquired using the regular data acquisition. Fig. 4 shows the significance distribution of the projections and the reconstruction error curve. From Fig. 4A, it is very interesting to note that, with the “Tubes” phantom, almost all the important projections are located at the end (projection index number >500) if the projections were acquired in a nested-loop order. Thus, the reconstruction error converges very slowly in the regular acquisition (see Fig. 4C). On the contrast, the adaptive data acquisition scheme worked very well and was able to identify and acquire all the important projections within the first 250 projections (Fig. 4B). Fig. 4 also clearly shows that the significance distribution of the projections, given in Eq. (9), is consistent with the reconstruction error curve. For example, with the adaptive acquisition, the significance distribution curve shows that there are no important projections with the projection index number >300. This is clearly supported by the reconstruction error curve which converges at 300. Thus, with the “Tubes” phantom, at most 70% of the projections could be saved using the adaptive acquisition algorithm combined with the uniform gradient scanning strategy.

Fig. 3.

Demonstration of regular versus progressive image reconstruction using a simulated “Tubes” phantom. The details of the phantom and image acquisition are described in the text. (A) Image reconstruction results using regular data acquisition (projections were acquired in a nested-loop order). The reconstructed images converged slowly to the original phantom as more projections were collected. (B) Image reconstruction results using adaptive projection acquisition algorithm. Sixty-six projections were pre-acquired as “seeds” and all other projections were acquired in an order from the most important to the least important. The convergence speed of the reconstructed images is faster than that in the regular data acquisition.

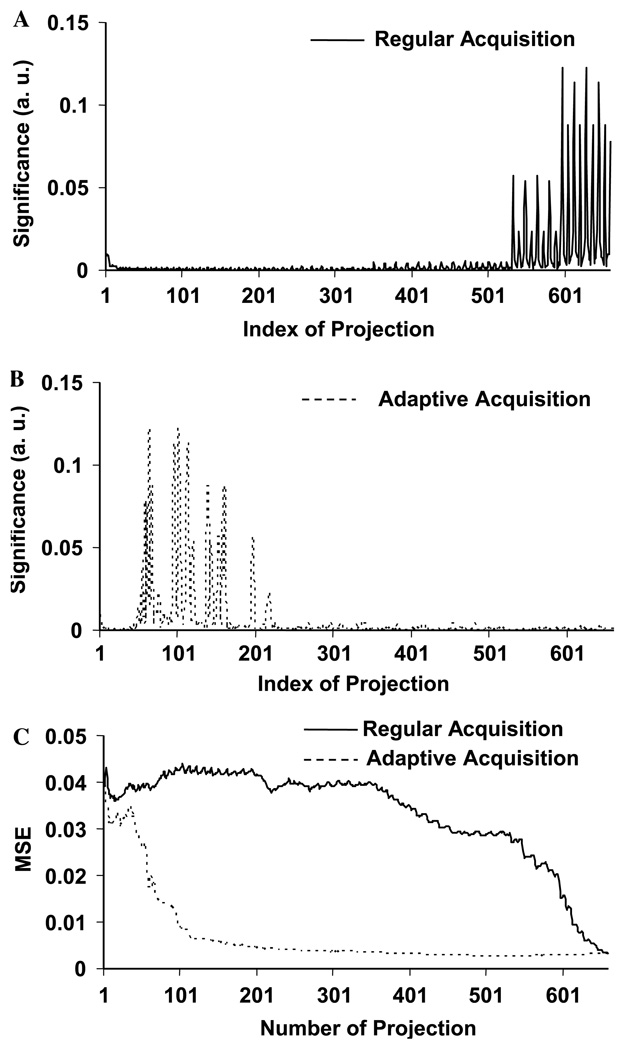
Fig. 4.

Significance distribution of projections and reconstruction error. (A) and (B) Significance distribution of projections. The significance of a projection (also in Figs. 6 and 8) is defined in Eq. (9) as the mean-square amplitude of the projection after filtering. In the regular data acquisition, all the projections were acquired in a nested-loop order. With this phantom, all the important projections were actually located at the end. In the adaptive acquisition, all the projections (except the first 10%) were acquired according to their significance values, from the most important to the least important. The adaptive algorithm was able to determine all the most important projections and acquire them within the first 250 projections. (C) Reconstruction error. In the regular data acquisition, since the important projections were located at the end, the reconstruction error converges very slowly. With the adaptive algorithm, all the important projections were identified and acquired prior to the less important projections. The construction error converges roughly at the number of 300. The improvement of the data acquisition efficiency is clearly seen.

4.3. “EPR” phantom

A second phantom made up of three letters “E,” “P,” and “R” was also tested in the simulation. The image reconstruction results from the regular and adaptive acquisitions are shown in Figs. 5A and B, respectively. The significance distribution of the projections and the reconstruction error are shown in Figs. 6A–C, respectively. Similar to Fig. 3, the progressive image reconstruction process is demonstrated in Fig. 5 in which the convergence speed of the reconstruction results has been remarkably accelerated by the adaptive acquisition algorithm. Since the “EPR” phantom has more complex structures throughout than the “Tubes” phantom, its important projections are located in a wide range (basically at the both end sides, see Fig. 6A), rather than only at the end (Fig. 4A). However, the proposed adaptive acquisition algorithm was still able to locate all the most important projections and acquire them within the first 300 projections. From the reconstruction error curve (Fig. 6C), it can be seen that after acquiring 400 projections, the reconstruction error curve converges. Thus, with the “EPR” phantom, at most 60% of projections could be saved using the adaptive acquisition algorithm combined with the uniform gradient scanning strategy.

Fig. 5.

Demonstration of regular versus adaptive acquisition methods using a simulated “EPR” phantom. (A) Image reconstruction results using regular data acquisition. A progressive image reconstruction process is clearly demonstrated but the reconstructed images converged slowly to the original phantom in regular acquisition. (B) Image reconstruction results using adaptive acquisition algorithm. Ten percent of projections (66 projections) were pre-acquired as “seeds” and all other projections were acquired in an order from the most important to the least important. The convergence speed of the reconstructed images is faster in adaptive data acquisition than in the regular data acquisition.

Fig. 6.

Significance distribution of projections and reconstruction error. (A) and (B) Significance distribution of projections. The most significant projections are located at both ends. The adaptive algorithm was able to determine all the most important projections and acquire them within the first 300 projections. (C) Reconstruction error. In the regular data acquisition, since the important projections were located at both ends, the reconstruction error converges very slowly. With the adaptive algorithm, all the important projections were identified and acquired prior to the less important projections, thus, the construction error converges fast (roughly at the number of 400).

4.4. Experimental phantom

The proposed adaptive acquisition algorithm was also tested by imaging a phantom constructed by machining the letters “E,” “P,” and “R” on three plastic bricks (35 × 27 mm²). Each letter was filled with DPPH (2,2-diphenyl-1-picrylhydrazyl) powder diluted five times with Agar (Aldrich Chemical). The imaging measurement was performed using our home-built 300 MHz EPRI system [25]. Further detailed information about the system will be reported in the future. The imaging parameters used for both the regular and adaptive acquisition were as follows: scan width, 2.4 mT; FOV, 60 × 60 × 60 mm³; modulation amplitude, 0.05 mT, scan time, 3.9 s; and time constant, 10 ms. The peak–peak line width of the DPPH spectrum measured at 300 MHz was 0.12 mT. The gradient strength was 40 mT/m. The image resolution was calculated to be 5.2 mm before deconvolution and 2 mm [24] after the automatic deconvolution algorithm was applied [26].

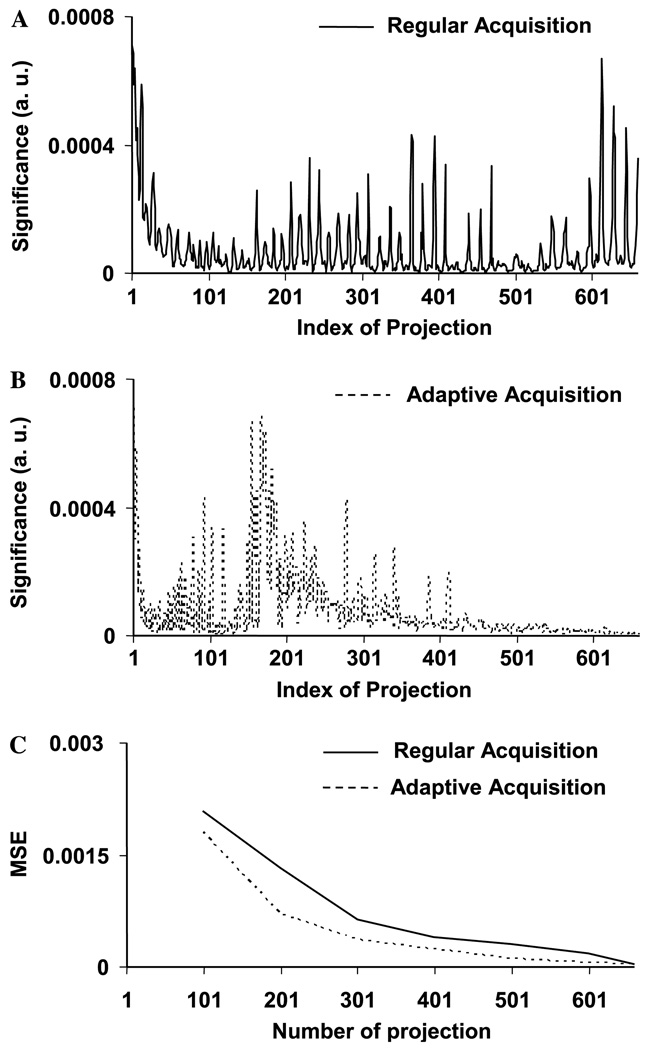
The imaging results from the regular and adaptive data acquisitions are shown in Fig. 7. The significance distribution of projections and the reconstruction error curve are shown in Fig. 8. A 3-dimensional regular EPR image was acquired (32 × 32 = 1024 projections with uniform angle sampling) as the reference image. Fig. 7 shows that the imaging results from the adaptive acquisition algorithm converged much faster than that from the regular data acquisition. Figs. 8A and B are consistent with the simulation results (see Figs. 5A and B) except that there are a few important projections distributed in the middle. Because of the complexity of the phantom structure as well as the noise induced during data acquisition, the adaptive acquisition algorithm took longer time in the experiments than in simulation (although 20% projections were pre-acquired as “seeds” in the experiment) to determine and acquire all the important projections. Therefore, the reconstruction error (Fig. 8C) converges at 500 projections, demonstrating that 50% of projections could be saved using the adaptive acquisition algorithm combined with the uniform gradient scanning strategy.

Fig. 7.

Imaging results of the “EPR” phantom. The imaging measurements were performed using a home-built 300 MHz EPRI system. (A) Image reconstruction results using regular data acquisition. A progressive image reconstruction process is clearly demonstrated but the reconstructed images converged slowly to the original phantom. (B) Image reconstruction results using adaptive projection acquisition algorithm. Twenty percent of projections (132 projections) were pre-acquired as “seeds” and all other projections were acquired in an order from the most important to the least important. The convergence speed of the reconstructed images is faster in adaptive data acquisition than in regular data acquisition.

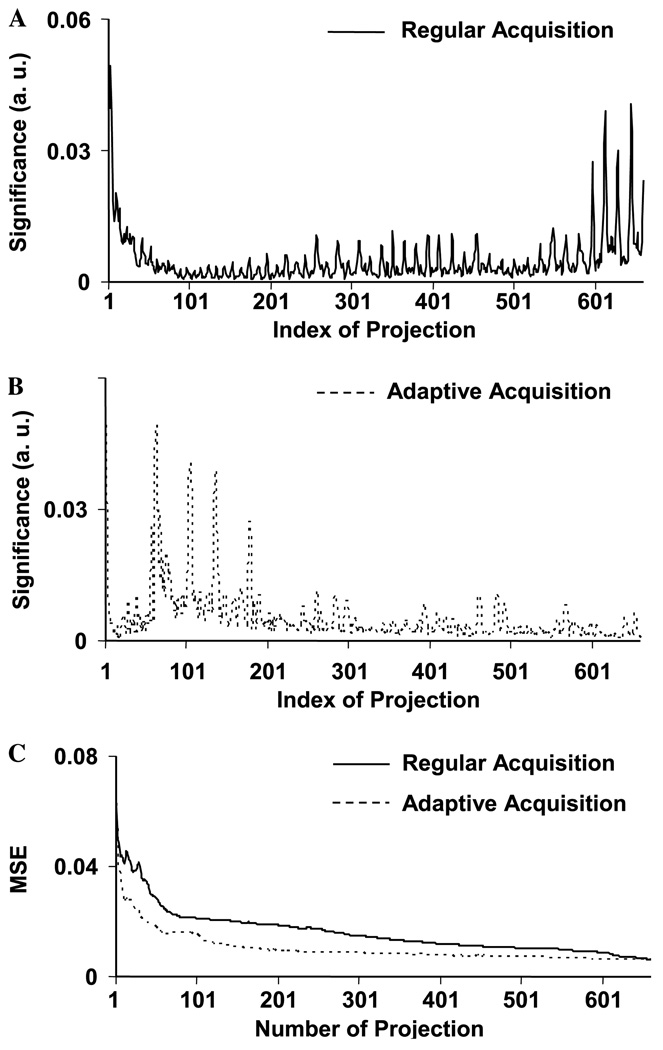
Fig. 8.

Significance distribution of projections and reconstruction error. (A) and (B) Significance distribution of projections. The real “EPR” phantom has more structures than the simulated phantoms. Its important projections were located almost everywhere. The adaptive algorithm determined and acquired all the most important projections within the first 410 projections. (C) Reconstruction error. In the regular data acquisition, since the important projections were located more evenly, the reconstruction error converges very slowly. With the adaptive algorithm, all the important projections were identified and acquired prior to the less important projections, thus, the construction error converges fast (roughly at the number of 500).

5. Discussion

While the two-stage image reconstruction algorithm is fast in computational speed, it requires the complete set of projections to be collected before the image reconstruction can proceed. On the other hand, the single-stage image reconstruction algorithm allows progressive image reconstruction in which the back-projection operation is done “on-the-fly,” but it involves extensive computation. In the following, we will compare the computation amount in both algorithms. Assume 32 × 32 = 1024 projections are acquired and the goal image size is 64 × 64 × 64. With the two-stage image reconstruction algorithm, since each projection is back-projected to a 2-dimensional 64 × 64 image, the number of back-projection operations is 32 × 32 × 64 × 64 + 32 × 64 × 64 × 64, assuming that the projection number is doubled from 32 × 32 to 32 × 64 after the first stage back-projection operation. In the single-stage image reconstruction algorithm, however, each projection is directly back-projected to a 3-dimensional 64 × 64 × 64 “basis” image, so the number of back-projection operations is 32 × 32 × 64 × 64 × 64. The computational amount in the single stage image reconstruction algorithm is therefore approximately 20 times higher than that in the two-stage image reconstruction algorithm, given the above reconstruction parameters. The 20-fold computational efficiency was critical when the fast-speed computation facilities such as fast personal computers (PCs) were not available in the past. Fortunately, in recent years, the performance of PCs has been improved dramatically. For example, the CPU speed has been increased by about 30 times between 1993 (Pentium 150 MHz, 20 millions of additions per second) and 2004 (Pentium IV 3.2 GHz, 680 millions of additions per second). This dramatic increase of CPU speed offers us the opportunity to readily apply the single stage image reconstruction algorithm for EPRI. We have demonstrated that the reconstruction of a 3-dimensional image from 660 projections using single stage reconstruction algorithm took only 2.5 min (Matlab 6.1 on Pentium 4 with 3.06 GHz CPU). However, the speed can be accelerated by one order of magnitude by transferring the Matlab codes to C++ implementation. Thus, it is very practical to implement and apply the proposed method for EPRI applications.

We have shown that about 50–70% of projection acquisition time has been saved with negligible lose of image quality in both simulations and experiments. The increase of data acquisition efficiency is benefited from the following two aspects. First, the uniform gradient scanning strategy improves the data acquisition efficiency (typically by one-third) by avoiding over-sampling. It should be noted that the uniform gradient scanning may result in different image quality, depending on the signal-to-noise ratio of the projections. In both our simulation and experiments, the signal-to-noise ratio of the projections was high enough so that the reduction of projection number by avoiding over-sampling (from 1024 to 660, typically) did not cause noticeable decrease of image quality. Second, the adaptive acquisition algorithm is capable of preserving all the important projections and discarding all other less important ones. As previously discussed, when a sample is non-uniformly distributed, the significance of projection varies one from the other. In this case, the proposed adaptive acquisition algorithm is able to evaluate all the projections and determine all the important projections first. The data acquisition time is therefore saved by acquiring all the important projections and skipping all other less important ones. However, if the sample has a uniform distribution, each projection will have equal importance. Then both regular and adaptive algorithms have to acquire all the projections and no gains will be achieved by the proposed adaptive algorithm.

6. Conclusion

We implemented a 3-dimensional progressive EPR imaging technique based on the inverse Radon transform. We proposed an adaptive data acquisition strategy in which all the projections are sorted according to their predicted significance and acquired in an order from the most important to the least important. The significance of a projection is measured as the mean-square amplitude of the filtered projection. Since it is derived from the filtered projections, it correlates with the reconstruction image quality. The imaging process can be terminated at any time if further collection of projections does not improve the image resolution distinctly or the acquisition can not continue due to hardware or other problems. The uniform gradient scanning scheme was also adapted to improve the data acquisition efficiency by avoiding over-sampling as occurred in the conventional EPRI experiments. The validation of the proposed scheme was tested by simulations and imaging experiments. Compared with the regular EPRI data acquisition, 50–70% data acquisition time could be saved with negligible loss of image quality. This technique should be very useful for accelerated acquisition and visualization of free radical distribution.