The Importance of Dielectric Constant for Drug Solubility Prediction in Binary Solvent Mixtures: Electrolytes and Zwitterions in Water + Ethanol

INTRODUCTION

In drug discovery and formulation, drug solubility in water and organic solvent plays an important role and affects many pharmaceutical processes including design, synthesis, extraction, purification, formulation, absorption, and distribution in body fluids (1). In most cases, aqueous solubility of a chemical compound as a medicine is not enough to be applicable in pharmaceutical formulations and clinical administration. Hence, different kinds of solubilization techniques including cosolvency, complexation, micellization, and salt formation have been applied to increase the solubility (1,2). However, in some cases, it is required to reduce solubility in the medium, for example, in crystallization process (3). These methods not only influence the solubility of a compound, but can also alter its stability in the liquid medium (1). Cosolvency is the most feasible method for this purpose, and the most common pharmaceutical cosolvent is ethanol. Another useful and more employed method is salt formation, and an accountable proportion of the available medicinal compounds is in salt form. For developing liquid formulations of these compounds or crystallization process design, the use of cosolvents might be necessary to influence their solubility/stability.

To speed up the development processes in the pharmaceutical industry, calculative models for solubility prediction in mixture of solvents have been proposed in recent decades (1,2). Almost all of the proposed models were designed for solubility correlation/prediction of the non-electrolytes in the solvent mixtures (1,2). The main pattern of solubility behavior in water + ethanol mixture has a maximum of solubility in ethanol-rich area for most of the non-electrolyte solutes (1,2). This pattern is not the same for ionizable compounds in water such as sodium salts of medicines and amino acids where the solubility value in water is more than solubility value in neat ethanol (4).

Maybe changes in dielectric constant of the medium have a dominant effect on the solubility of the ionizable solute in which higher dielectric constant can cause more ionization of the solute and results in more solubilization (5). As an example, water (D_W,298 = 78.5) has higher dissociation strength on ions in comparison with ethanol (D_E,298 = 24.2) which is resulted in more solubilization power of ions in water. Born has proposed a theoretical model for solubility correlation in two different phases as following equation (6):

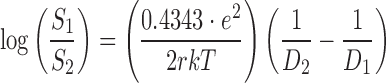1

where S₁ and S₂ are the solubilities of the solute in media 1 and 2; e is the charge of an electron; r is the effective radius of the ion in the medium; k is the Boltzmann constant; T is the absolute temperature; and D₁ and D₂ are the dielectric constants of the media 1 and 2, respectively. Unfortunately, by using this equation, the predicted solubility values (when r values are known) or predicted r values (when solubility values are known) based on experimental data do not seem to be meaningful (7). However, one can consider the constant value of 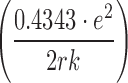as A_T for a specific solute and obtain:

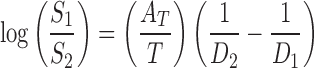2

where A_T is a slope which can be calculated using two experimental solubility data points (e.g., solubility values in water and ethanol).

In this technical note, the predictability of Eq. 2 for solubility data of ionizable solutes in water + ethanol mixtures with acceptable prediction error is reported.

DATA AND COMPUTATIONAL METHODS

Available solubility data for electrolytes and zwitterions in water + ethanol mixtures were extracted from the literature (1,4,8). The criterion for inclusion in selected data was the availability of solubility data in water and ethanol, where S_W > S_E.

Dielectric constants of water and ethanol at different temperatures were collected from the literature (9). For calculating dielectric constant of water and ethanol at different temperatures other than those reported by Akerlof, we interpolated the data with following equation described by Akerlof:

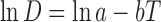3

where lna and b are the intercept and coefficient of the regression, respectively. The calculated values of dielectric constant for water and ethanol at different temperatures were used in a previously trained version of the Jouyban-Acree model for prediction of dielectric constant of the water + ethanol at different temperatures (10):

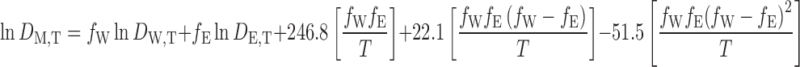4

where D_M,T, D_W,T, and D_E,T are dielectric constants of the solvent mixture, water, and ethanol at temperature T (Kelvin); f_W and f_E are the volume fractions of water and ethanol, respectively.

For solubility prediction using Eq. 2, the A_T values were calculated using only two solubility data points in mono-solvents, i.e., S_W,T and S_E,T, as:

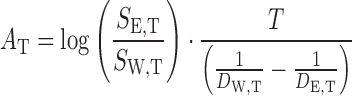5

After calculation of the A_T values for each solute at the temperature of interest and calculation of the dielectric constants of water + ethanol mixture at related temperature, the solubility amount in mixed solvents were calculated using:

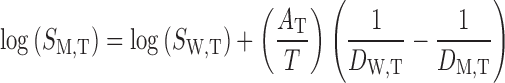6

The mean relative deviation (MRD) is used as an error criterion:

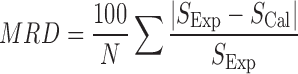7

where N is the number of data in each set, and S_Exp and S_Cal are experimental and calculated solubility values.

RESULTS

The resulted equations for dielectric constant prediction of water and ethanol at different temperatures are as follows, respectively:

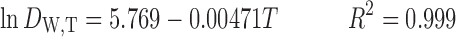8

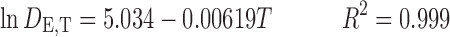9

List of extracted data sets, their related A_T values calculated by Eq. 5, and produced MRD values are tabulated in Table I. For total 400 data points of 45 sets of 14 compounds, the overall MRD value is 23.8 ± 25.4%, with the highest and the lowest MRD values of 46.3% and 7.0% for clindamycin phosphate (at 283 K) and sodium sulfamethazine (at 283 K), respectively. By excluding clindamycin phosphate data sets which produce high errors in prediction, for 302 data points of 31 sets of 13 compounds, the overall MRD value is 18.8 ± 18.8%, with the highest MRD value of 40.2% for glycyl glycine. The expected prediction error (23.8% or 18.8%) is within an acceptable range, where 30% error is accepted for correlating the solubility data in the pharmaceutical area (11,12). The prediction error for solubility of drugs in water + ethanol mixtures employing experimental data in mono-solvents using previously trained versions of the cosolvency models are 52.9% (13) and 40.7% (14), and the produced prediction error for the method proposed in this work is less than these errors.

Table I.

List of Studied Data Sets in Calculations and Related Properties

Set	Solute	T	A T	MRD	N	logS W	logS E	logS W–logS E	Ref.
1	Alanine (Beta)	298	32882.36	38.2	7	−0.816	−3.955	3.139	8
2	Alanine (DL)	298	29935.18	20.3	7	−1.490	−4.347	2.858	8
3	Asparagine (L)	298	35637.41	22.6	5	−2.468	−5.870	3.402	8
4	Aspartic acid (L)	298	31415.81	35.2	7	−3.168	−6.167	2.999	8
5	Clindamycin phosphate	278	50080.77	45.6	7	−0.754	−5.222	4.468	1
6	Clindamycin phosphate	283	36393.46	46.3	7	−0.745	−4.046	3.301	1
7	Clindamycin phosphate	288	35941.97	37.7	7	−0.731	−4.046	3.315	1
8	Clindamycin phosphate	293	34733.16	35.8	7	−0.700	−3.959	3.259	1
9	Clindamycin phosphate	298	33114.89	34.0	7	−0.693	−3.854	3.161	1
10	Clindamycin phosphate	303	30269.38	32.2	7	−0.679	−3.620	2.941	1
11	Clindamycin phosphate	308	28760.03	32.6	7	−0.664	−3.509	2.844	1
12	Clindamycin phosphate	313	27969.18	33.8	7	−0.652	−3.469	2.817	1
13	Clindamycin phosphate	318	26662.22	36.2	7	−0.642	−3.377	2.734	1
14	Clindamycin phosphate	323	25957.73	41.7	7	−0.635	−3.347	2.712	1
15	Clindamycin phosphate	328	25355.32	43.7	7	−0.629	−3.328	2.699	1
16	Clindamycin phosphate	333	24276.41	43.1	7	−0.619	−3.252	2.633	1
17	Clindamycin phosphate	338	22900.79	42.1	7	−0.599	−3.131	2.532	1
18	Clindamycin phosphate	343	21441.68	39.5	7	−0.534	−2.951	2.417	1
19	Dexamethasone sodium phosphate	298	22617.99	31.0	10	−1.598	−3.757	2.159	1
20	Glycine	298	35530.97	27.9	7	−1.246	−4.638	3.392	8
21	Glycyl glycine	298	45746.19	40.2	7	−1.522	−5.889	4.367	8
22	Leucine (L)	298	16991.14	25.2	7	−2.503	−4.125	1.622	8
23	Norleucine (DL)	298	14812.25	24.8	7	−2.801	−4.215	1.414	8
24	Sodium sulfadiazine	278	30661.88	17.8	11	−1.389	−4.124	2.735	4
25	Sodium sulfadiazine	283	30178.20	16.9	11	−1.371	−4.108	2.737	4
26	Sodium sulfadiazine	288	29687.43	17.0	11	−1.354	−4.092	2.738	4
27	Sodium sulfadiazine	293	29200.49	17.2	11	−1.337	−4.076	2.740	4
28	Sodium sulfadiazine	298	28714.22	18.1	11	−1.321	−4.062	2.741	4
29	Sodium sulfadiazine	303	28244.33	19.0	11	−1.304	−4.048	2.744	4
30	Sodium sulfadiazine	308	27752.49	20.6	11	−1.288	−4.033	2.745	4
31	Sodium sulfamerazine	278	22493.65	10.1	11	−1.936	−3.943	2.007	4
32	Sodium sulfamerazine	283	22293.56	10.9	11	−1.884	−3.906	2.022	4
33	Sodium sulfamerazine	288	21972.89	11.7	11	−1.831	−3.858	2.027	4
34	Sodium sulfamerazine	293	21728.39	13.6	11	−1.790	−3.829	2.039	4
35	Sodium sulfamerazine	298	21551.10	16.0	11	−1.736	−3.793	2.057	4
36	Sodium sulfamerazine	303	21371.01	18.9	11	−1.687	−3.763	2.076	4
37	Sodium sulfamerazine	308	21064.28	21.5	11	−1.642	−3.725	2.083	4
38	Sodium sulfamethazine	278	14728.76	8.5	11	−1.699	−3.013	1.314	4
39	Sodium sulfamethazine	283	14311.38	7.0	11	−1.656	−2.954	1.298	4
40	Sodium sulfamethazine	288	13810.28	9.3	11	−1.611	−2.885	1.274	4
41	Sodium sulfamethazine	293	13488.69	13.9	11	−1.568	−2.833	1.266	4
42	Sodium sulfamethazine	298	13211.81	17.7	11	−1.524	−2.785	1.261	4
43	Sodium sulfamethazine	303	12942.27	21.1	11	−1.479	−2.737	1.257	4
44	Sodium sulfamethazine	308	12938.35	23.7	11	−1.430	−2.709	1.280	4
45	Valine (DL)	298	22610.62	21.2	7	−1.967	−4.126	2.158	8

MRD mean relative deviation, DL mean racemic mixture of the solute, L mean L-enantiomer of the solute

DISCUSSION

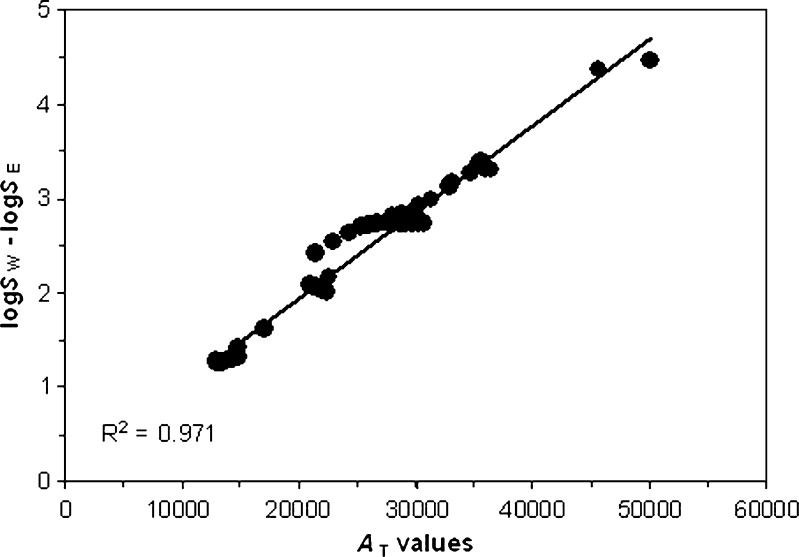
The resulted A_T values show indirect relation with temperature. This is expected, as it has indirect correlation with r of Eq. 1 which has direct correlation with temperature. Also, it seems that A_T values are not mainly affected by the structure of the solutes under study. For example, the structural difference between three studied sulfonamides is just on two methyl groups. But, their A_T values are rather different values. On the other hand, there is a good correlation between A_T values and logS_W–logS_E of the solutes (Fig. 1). This might suggest the effect of the difference among solubilities in water and ethanol on the solubility behavior of drugs in their mixture.

Fig. 1.

The correlation between A _T values and logS _W–logS _E of the solutes

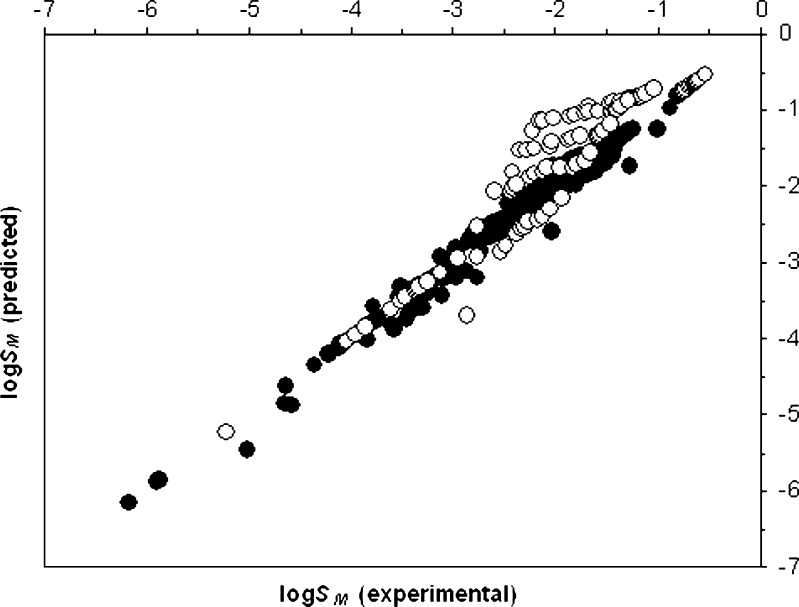
The main advantage of the proposed model is that it does not require any experimental solubility data in mixed solvents. Just two experimental solubility data points in mono-solvents and dielectric constants of solvent systems under consideration are employed in the prediction process. It almost provides good results which might show its applicability in solubility prediction (Fig. 2). These characteristics make it a suitable model for solubility prediction of electrolyte and zwitterionic solutes in water + ethanol mixtures.

Fig. 2.

Logarithm of experimental solubility data versus logarithm of predicted solubility data for 400 studied solubility data points (closed circle: solubility data for drugs except clindamycin phosphate; open circle: data for clindamycin phosphate)

The proposed model is tested on the solubility of electrolytes or zwitterions in water + ethanol mixtures in which the ionization is a dominant parameter in the solubility phenomenon. We expect more solubility in higher dielectric constants (water-rich area) and considered S_W > S_E as an inclusion criteria.

The main disadvantage of the proposed prediction method is that it is applicable only for the solubility prediction of electrolytes or zwitterions in which the ionization is the dominant parameter and the phenomenon could be represented using Born model.

SUMMARY AND CONCLUSIONS

Improving solubility prediction methods or making them easy to use is highly demanded in the pharmaceutical industries. It can be used in formulation design and pharmaceutically related processes such as crystallization. In this work, we have showed that dielectric constants of solvents and their mixtures might be helpful in solubility prediction of electrolytes and zwitterions with acceptable error in water + ethanol mixtures.