Transport properties of glass-forming liquids suggest that dynamic crossover temperature is as important as the glass transition temperature

Abstract

It is becoming common practice to partition glass-forming liquids into two classes based on the dependence of the shear viscosity η on temperature T. In an Arrhenius plot, ln η vs 1/T, a strong liquid shows linear behavior whereas a fragile liquid exhibits an upward curvature [super-Arrhenius (SA) behavior], a situation customarily described by using the Vogel–Fulcher–Tammann law. Here we analyze existing data of the transport coefficients of 84 glass-forming liquids. We show the data are consistent, on decreasing temperature, with the onset of a well-defined dynamical crossover η_×, where η_× has the same value, η_× ≈ 10³ Poise, for all 84 liquids. The crossover temperature, T_×, located well above the calorimetric glass transition temperature T_g, marks significant variations in the system thermodynamics, evidenced by the change of the SA-like T dependence above T_× to Arrhenius behavior below T_×. We also show that below T_× the familiar Stokes–Einstein relation D/T ∼ η^-1 breaks down and is replaced by a fractional form D/T ∼ η^-ζ, with ζ ≈ 0.85.

The glass transition, attained by decreasing temperature or increasing the system density, is one facet of the more general dynamical arrest (jamming) phenomenon that impacts many areas of science, representing today an intriguing topic that is far from being completely clarified (1, 2). The phenomenon of dynamic arrest, accompanied by a remarkable dynamic slowing down, marks a dramatic change in the physical properties of the system. The clarification of the underlying microscopic origin of this slowing down represents a topic of much current research in condensed matter physics. One approach to study this phenomenon is offered by the exploration of the temperature dependence of transport coefficients (e.g., viscosity η, self-diffusion constant D_s, and relaxation time τ) of a liquid supercooled into a metastable state below its melting temperature T_M, until it either crystallizes or vitrifies. The manner in which η, D_s, and τ approach their limiting values can provide information about the nature of the arrest phenomenon. As T decreases below T_M, τ changes by several orders of magnitude, surpassing the time required for experimental accessibility. An open question, triggered by this marked change, is whether transport parameters reflect an underlying phase transition to a state in which quantities become infinite (a “dynamic divergence”) (3). In the presence of conflicting opinions (4–9), many models and theories have been developed that focus on the temperature dependence of transport parameters of liquids in their supercooled phase in particular, η(T). The corresponding behaviors are often characterized by a super-Arrhenius (SA) behavior, which differs from the well-known Arrhenius equation (AE: ln η/η₀ = E/k_BT) by the presence of an upward curvature in the T dependence. To describe these SA glass-forming materials near dynamical arrest, the Vogel–Fulcher–Tammann (VFT) equation,

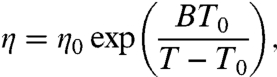[1]

has been widely used, where B and T₀ are material-dependent parameters. It must be stressed that such a form, contrary to the AE one, predicts divergence at a nonzero temperature T₀. The diverging scales of τ, D_s, η contained within Eq. 1 are considered important for understanding the nature of the glass transition and arrested matter (10, 11). The temperature T₀ has been associated with the Kauzmann temperature T_K (linked to an ideal glass temperature) (1, 2), and a large class of experiments have used the VFT formalism to relate T₀ to the calorimetric glass transition temperature T_g. In particular, Angell (12) has offered a classification of the glass-forming liquids by using the concept of “fragility”: “fragile” liquids obey Eq. 1 with T₀ = T₀(T), whereas “strong” liquids exhibit a pure AE behavior T₀ = const. From the analyses of the thermal behavior of η(T), it has been conjectured that some supercooled liquids can display a fragile-to-strong (FS) crossover temperature T_g < T_× < T_M (see ref. 13 and references therein). An analogous situation has been hypothesized for water at T_× ∼ 228 K (just to explain water anomalies such as the isothermal compressibility K_T) by assuming that the crossover corresponds to a change in the liquid structure (14). Note that T_× and T_M are material-dependent properties.

Another feature of fluids near the arrest is that their dynamics result from microscopic cooperative processes. There is a growing body of evidence that, upon cooling, a liquid does not become a glass in a spatially homogeneous fashion (15–19). The system becomes increasingly spatially correlated due to the growing of characteristic length and time scales of dynamically correlated regions of space as T decreases (9, 15, 20–24). For example, there is an explicit dependence of the α-relaxation time τ on the typical length scale ξ, τ = exp[μξ(T)/T], where μ represents a typical free energy per unit length (9). This phenomenon is often called “spatially heterogeneous dynamics” (20, 25–27), because there are spatial regions in which the structural relaxation time can differ by orders of magnitude from the average over the entire system. Furthermore, the presence of these dynamic heterogeneities has been argued to give rise to the breakdown of the Stokes–Einstein (SE) relation and to the dynamic FS crossover (16–19) in a region located inside the supercooled phase at some temperature in the interval from T_g to T_M. Because the derivation of the SE relation assumes uncorrelated motion of particles, it is reasonable that the onset of correlations could result in its breakdown. On these bases, the SE violation represents a useful element to study deeper aspects of the glass transition (17, 28) and other relevant phenomena observed in the interval T_M - T_g. A recent example is the study of the SE violation using a mode coupling theory (MCT) approach incorporating activated hopping processes (29). Experimental (30–32) and molecular dynamic simulation (33–35) studies made in confined and bulk supercooled water show that the SE violation is accompanied by a dynamic FS crossover at the same temperature T_× ∼ 225 K, with T_g < T_× < T_M.

The existence of a temperature T_×, marking dynamical changes of fragile supercooled liquids below T_M, has been already considered in the past (5, 13, 36–42). This is due to problems such as the existence of the dynamical divergence associated with the VFT form and the possibility that neither T₀ nor T_g is relevant to describe and understand slowing down in transport parameters of supercooled liquids.

Belonging to this scenario is also the idea that the VFT approach lacks physical meaning. Very recently, by considering a glass-forming system composed of particles interacting via soft potentials, Eckmann and Procaccia explicitly demonstrated that the configurational entropy is finite at any temperature (9); i.e., a Kauzmann temperature T_K, where the liquid is out of the equilibrium, does not exist and thus the VFT may be considered only a fitting formula. Furthermore, a recent study (40) of the dielectric relaxation times τ(T), nearly simultaneous with ref. 9, confirms the suggestion that there is no compelling evidence for the VFT prediction that transport parameters diverge at a finite T and provides a demonstration, in terms of an Avramov form τ(T) = τ₀ exp(B/Tⁿ), that the use of the VFT does not represent a fruitful route to explain supercooled liquid dynamics by analyzing τ(T) for 42 ultraviscous glass-forming fluids. The scenario proposed in this work agrees with the main findings of ref. 9, and its validity has been proved by considering the segmental relaxation data of glass-forming polymers as T → T₀ (43): The time scales related to the arrest may not diverge at nonzero temperature. Similar findings have been reported also for polymers and small molecule glass formers (see, e.g., references 7–9 of ref. 43), suggesting that the main finding of the model proposed for soft systems can have a larger generality.

A common theme of many works on glass-forming liquids is that, inside the region of the supercooled phase limited by such a crossover temperature T_×, their transport parameters such as viscosity (5, 13, 39) and dielectric relaxation time (38, 40, 41) can have universal features. For example, using for η a 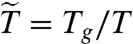representation (39), one obtains a master curve only for 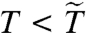, whereas for 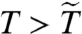deviations occur and the highest T data are fit using the VFT formula.

In a very recent case, the analysis of the relaxation times and the viscosities (of 58 liquids) in terms of the parabolic form [(T_o/T) - 1]² exhibits a degree of universality inside the interval T_× < T < T_o (41), where T_o is defined as an onset temperature where the liquid dynamics crosses over from that of a simple liquid to that of a strongly correlated material like a glass former. As with T_×, also T_o depends on the material. The result is that above T_o liquid transport has a weak T dependence, whereas in a region inside the SA liquid behavior all the transport data appear to collapse into one parabola. However, such an approach holds only inside the range T_× < T < T_o (41).

The conclusions of (40–42), the theoretical indication (9), together with the finding of cited works invocating the existence of a crossover temperature (5, 13, 36–41) propose that VFT must be reconsidered for the explanation of the dynamical arrest. We have examined the temperature behavior of the viscosity and the other transport coefficients of many liquids. Our aim is to demonstrate that the dynamical FS crossover represents a general property of glass-forming liquids. For this, we have used the power law that originally predicted the dynamical FS crossover in glass-forming materials (13),

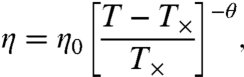[2]

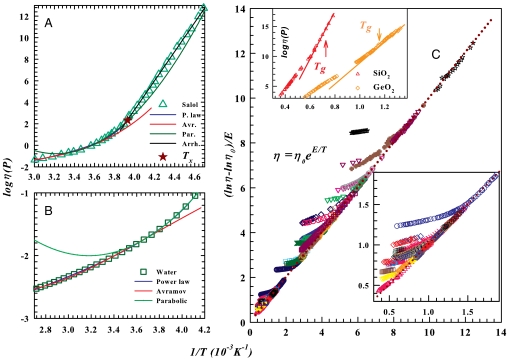
to analyze the viscosity [and also D_s(T) and τ(T)] of a larger number of diverse systems (Table 1) and to have an estimation of the FS crossover temperature T_×. Fig. 1 A and B, plotting log η vs 1/T, report for salol and bulk water, respectively, a comparison between this form, the parabolic and the Avramov ones. The power-law approach works better than the others. In the salol case these simple data plotting evidence directly the two strong and fragile η(T) behaviors and thus the dynamical FS crossover located at T_× ≃ 256 K; the FS crossover is not observable in bulk water [unlike confined water (30–32)] because the system can be supercooled only for a limited T range. The power-law form originally proposed to study the η(T) behavior of supercooled liquids (13) is the same used to study water compressibility (14). We must mention the agreement among the viscosity crossover temperature value obtained for salol, directly from Fig. 1A, by means of Eq. 2 (T_× ≃ 262 K) and by the MCT analysis of the light scattering α and β relaxation times (256 < T_c < 266 K) (36, 37).

Table_1.

Glass-forming liquids included in the present analysis. The symbols are those used in Figs. 1–3. More details (including references, temperatures, fitting data, and some further information) are provided in Supporting Information.

Fig. 1.

(A) The shear viscosity of salol, which displays a dynamical crossover (star) from super-Arrhenius to Arrhenius at 1/T_× ≈ 3.91 × 10^-3 K^-1 (256 K). For T > T_×, we fit the data using three approaches: power law (13), Avramov (40), and parabolic (41). For T < T_×, we fit the data by an Arrhenius form function. (B) The shear viscosity of water in a region T > T_× studied by means of the same functional forms as in A. The viscosity literature data for bulk water are available only for a limited temperature range above the crossover that has been observed only for confined water (30). In both A and B, the power law well fits the data in all the interval T > T_X better than the other forms that work only in opposite regions of that interval (the Avramov works for the highest T, and the parabolic holds only for the lowest). The power-law fitting gives for water: η₀ = 0.138cP, T_× = 225 ± 5 K, and θ = 1.67 ± 0.04. (C) Shear viscosity η for 48 different glass-forming liquids, showing Arrhenius behavior at the lowest temperatures. A dynamical crossover is displayed by all 48 liquids. (Lower Inset) Enlargement of the low coordinate region, including 15 glass-forming liquids. (Higher Inset) Arrhenius plot of η for SiO₂ and GeO₂: The behavior of both liquids is not purely that of strong glass formers. The crossing of the glass transition temperature T_g does not correspond to any change in η behavior; in particular, its behavior is continuous and regular. Table 1 defines the symbols for each liquid.

Fig. 1C is a reduced AE plot (ln η - ln η₀)/E vs. 1/T and provides, as in the salol case (Fig. 1A), direct evidence of the dynamical FS crossover for 48 glass-forming liquids. Because the dynamical crossover in the transport parameters is observed in a large set, 51, of the liquids considered here, it is natural to inquire whether the behavior illustrated for these liquids is typical of all liquids. Fig. 1C, Upper Inset, displays the viscosity of SiO₂ and GeO₂. For both glass formers, we observe differences from a pure strong liquid, and a continuity in η(T) on crossing the calorimetric T_g. Such a situation, observable in many materials, is intriguing: The dynamical arrest at T_g appears to have no influence on dynamical quantities. However with respect to the measured C_P, strong and fragile liquids have different behaviors. The SA T dependence often coincides, on approaching T_g, with a relatively large change in C_P, whereas Arrhenius strong liquids often display very small changes.

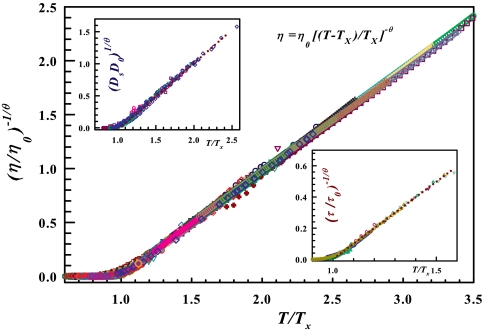
Fig. 2 plots (η/η₀)^-1/θ vs. T/T_× in a single master curve for 80 liquids. In the insets, analogous master curves for D_s (12 liquids) and τ (8 liquids) are reported. We stress that the master curve, a scaled representation of Eq. 2, makes sense only for T > T_×, where the three master curves can be superposed.

Fig. 2.

Data collapse for the shear viscosity η for 80 different liquids (including the 48 liquids of Fig. 1C, displaying Arrhenius behavior at the lowest T). Shown is the scaled viscosity (η/η₀)^-1/θ as a function of the scaled temperature T/T_×, where T_× is the crossover temperature. Whereas 48 liquids of Fig. 1C display an evident crossover, for the remaining 32 liquids (including water of Fig. 1B) we estimate T_× using Eq. 2; all fluids are characterized by viscosity values covering at least four orders of magnitude. The scaling exponent θ takes on slightly different values for each of the 80 liquids we studied, with θ ≈ 2 ± 0.3. (Insets) Self-diffusion constant D_s for 12 different liquids, and the characteristic structural relaxation time τ for 8 liquids.

The relevant indication from our present results is that the crossover temperature T_× is more significant for classifying the flow properties of liquids approaching the dynamical arrest temperature than the temperature T₀ of the VFT equation (i.e., T_K) or the glass transition temperature T_g. In fact, many believe that the VFT is only a convenient fitting formula (9, 40–42), whereas for T_g there is no compelling evidence of any singular characteristic in the fluid transport properties around it. Rather it appears that when T decreases, the transport coefficients do not diverge but on crossing T_× alter their temperature dependence and reassume an AE form.

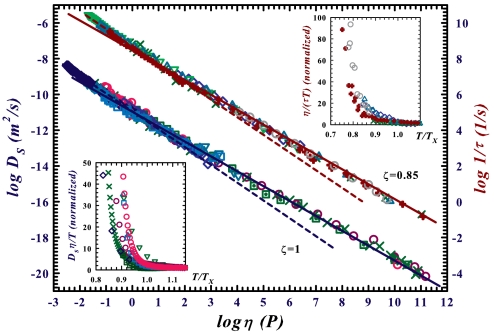
In order to further examine our crossover temperature results, we evaluate (Fig. 3 insets) the Stokes–Einstein ratio R_SE ≡ D_sη/T and the Debye–Stokes–Einstein (DSE) ratio R_DSE ≡ η/τT. We see in both these quantities a breakdown very close to T_×. A recent study in terms of the extended MCT (44) demonstrates, in agreement with other experimental observations in some glass-forming liquids (18, 19, 45–47), that these SE and DSE violations occur very close to T_× and are a manifestation of the decoupling of transport coefficients (35) whose microscopic origins can be due to the onset of typical length scales that increase rapidly as T decreases (6, 9). In particular, the dynamical heterogeneity picture implies correlations between time scale and length scale: The increase in the time scale, as arrest is approached, leads to a growing length scale of dynamically correlated regions in space (20, 24), suggesting that supercooled liquids might display dynamical scaling. In these conditions, the supercooling imposes that below a certain temperature the SE (and the DSE) relation gives way to the fractional SE relation D_s ∼ τ^-ζ, where the index ζ is related with the characteristic spatial-temporal length scales of the “spatially” heterogeneous dynamics (18, 19, 45–47). The following has been proposed (28): ζ = α(T)/β(T) with α and β being temperature-dependent scaling exponents of D_s and τ, respectively. Analogous arguments hold for the viscosity η.

Fig. 3.

(Lower Inset) Onset of the breakdown of the SE law for nine liquids analyzed. (Upper Inset) Breakdown of the DSE law for six liquids. In both cases the breakdowns occur just below the corresponding crossover temperature, identified using the power-law approach of Eq. 2. The main plot shows a scaled representation of the fractional SE and of the fractional DSE, lower and upper data, respectively. In both cases, for all the liquids studied, the scaling exponent ζ takes almost the same value, ζ = 0.85 ± 0.02. We note that the onset of the breakdown of the fractional SE and DSE takes place at the same value of viscosity, η_× ≈ 10³ Poise. These data demonstrate a remarkable degree of universality in the temperature behavior of the transport properties of supercooled liquids.

Fig. 3 represents the liquid transport parameters in terms of our scaling approach. For all the liquids we studied, the onset of the breakdown takes place at the same value of viscosity, η_× ∼ 10³ Poise, a value that is 8–10 decades lower than the value generally found near T_g. However, the main finding is that the two obtained master curves are consistent with a remarkable degree of universality. It is certainly relevant that this result emerges directly from the values of two transport parameters measured independently. The crossover temperature arises from a universal behavior rather than a definition linked to a specific cooling rate like the calorimetric T_g. In both the fractional SE and the DSE, the decoupling in transport properties takes place at the crossover temperature T_x where the system recovers Arrhenius behavior.

From the two scaled plots we calculate an exponent ζ with almost the same value, ζ = 0.85 ± 0.02. Fig. 3 highlights a precise correspondence at T_× among (i) the dynamical FS crossover, (ii) the breakdown of the Stokes–Einstein and the Debye–Stokes–Einstein relations, and (iii) the dynamical heterogeneities. In addition, the measured ζ value (ζ = 0.85 ± 0.02) agrees with the finding of other experimental (18, 19, 32, 47) and theoretical studies predicting the presence of a crossover from hierarchical SA dynamics for short length scales to pure Arrhenius at larger ones (6, 28) and that of the extended MCT approach for which the crossover is caused by the change in the dynamics from the one determined by the cage effect to that dominated by hopping processes (44).

A common suggestion of these approaches is that the observed dynamical changes of the SA glass-forming liquids have a structural origin–a situation that can be easily understood by recognizing that the SE relation defines an effective hydrodynamic radius (correlation length). The temperature decreasing determines a growth of these correlated regions whose length can in principle diverge originating the slowing-down characteristic of the critical processes (i.e., the invoked η(T) divergence at a finite temperature). A phenomenon not observed here because at a certain temperature this “apparent” criticality evolves toward a nondivergent behavior. The reason of this may be that in supercooled liquids the growth process originates solely disordered and finite regions of correlations (a sort of finite polydisperse dynamical clustering) whose molecules are more “sluggish” than the less correlated. The internal motions of such clusters are dynamical and strongly dependent on the temperature; a T decreasing causes their progressive slowing down up to a temperature at which they are practically frozen and an intercluster dynamics results more favored. Such a temperature is the crossover one: Above it the molecular motion, identified by D_S (and thus reflected in τ and η), depends essentially on the clusters dynamics. It is just the cluster polydispersity and the interaction between each other that give rise to hierarchical relaxation times that are reflected in the time dependence of the density–density correlation functions F(q,t) as the well-known superexponential decays and in the transport parameters like η as the SA behavior.

These two dynamics, intracluster and intercluster, have a different physical scenario: The first assumes the existence of a multibasins energy landscape with a corresponding large frequency (and thus correlation time) distribution and the second of a two-state basin with a single frequency permitted. At the highest temperatures the multibasins dynamics, i.e., the SA behavior, is clearly favored. Each of these basins is characterized by a temperature-dependent weight factor, and the T decreasing implies not only their progressive numerical reduction but also a decreasing of their weight up to negligible values. At this stage the only relevant dynamics is the molecule migration from a cluster to another one, i.e., a process with only one typical energy scale: the Arrhenius energy.

On considering the above reported results, we consider that the arrested process may be characterized by a crossover in the dynamical properties (13, 14, 39, 41). In addition, we have already the demonstration that the singularity implied by a genuine structural arrest appears not to be supported by the existing experimental data (40, 41), and the VFT equation seems to lose any physical basis (40). We showed, from analyses of the temperature dependence of transport coefficients of many liquids (84), using a scaling law approach (13), the existence of a well-defined fragile-to-strong dynamic crossover temperature T_× in the supercooled liquid regime. We thus conclusively demonstrated that this phenomenon is a general property of all glass-forming liquids. Based on these considerations, we propose the following:

1. The FS crossover phenomenon has a larger generality than the traditional Angell classification of liquids into two separate classes of glass formers: fragile and strong;

2. Transport coefficients [and the isothermal compressibility K(T)] show significant change of behavior but only near T_×;

3. The FS crossover, the appearance of the fractional Stokes–Einstein violation, the Debye–Stokes–Einstein violation, and the dynamical heterogeneities are directly linked with T_×.

Thus we conclude that (a) T_× appears to be more relevant than T_g or T₀ for understanding the physics of dynamical arrest phenomena and (b) the universality attained in the master curves from the scaled description of the Stokes–Einstein and of the Debye–Stokes–Einstein violations appears as a “ground-breaking” reality indicating a previously undescribed route to explore arrested processes.

Methods

We considered three thermodynamical coefficients—viscosity, self-diffusion, and relaxation time—of 84 glass-forming liquids. The majority we studied in both the stable and the supercooled temperature phase. Fig. 1 A and B report the η(T) data fitting for salol and bulk water, respectively, by using the three different approaches discussed in the text. For the salol data we note both the Arrhenius and SA behaviors, with a crossover at T_× ∼ 256 K, but for bulk water there are available data only in the SA region up to 237 K. The situation illustrated in Fig. 1 A and B is representative of what we observe for all the studied liquids, and from the corresponding analysis we obtain η₀, T_×, T_o, and the exponent θ. For T_× we observe that the values we obtain are nearly coincident with those arising from Fig. 1C (the T value at which the straight line representing the AE behavior crosses the SA data points). The T_o values obtained in the present study agree well with those of ref. 41.

The literature gives η(T) for 80 liquids. Among them, 48 give direct evidence, by means of the AE law, of the FS crossover (see Fig. 1C). Such an approach allows a direct estimation of T_×. Of the remaining 32 liquids, 7 liquids exhibit data in the supercooled region (i.e., for T lower than T_M), and 25 liquids exhibit data in the stable liquid phase.

For a wide T range, including the supercooled region, we have also analyzed the self-diffusion coefficient D_s for 12 liquids and the relaxation time τ for 8 liquids. Of these liquids, 9 have both η and D_s, and 6 have the measured η and τ. We took all the liquid data from the literature, and the corresponding details are reported in Supporting Information. After the direct estimation of T_× for the 48 liquids that clearly show the FS crossover (Fig. 1C), we have used Eq. 2 to evaluate η₀, T_×, and θ for all 84 fluids. A comparison between the temperatures T_×, separately obtained for the 48 liquids of Fig. 1C by means of this procedure and by direct evaluation, shows that these are approximately the same.

We use the parameters η₀, T_×, and θ, evaluated according to the above described procedures (for η, D_s, and τ), to generate Fig. 2, which shows the scaled viscosity (η/η₀)^-1/θ as a function of the reduced temperature T/T_×. We obtain a single master curve that represents the viscosity of all 80 liquids. We find T_M > T_×, and that the exponent θ takes slightly different values for each of the liquids, with θ ≃ 2.0 ± 0.3. From Fig. 2 it is evident how T_× marks the border point between the two dynamical regimes, the fragile and the strong. The same situation is represented in the two insets for D_s (12 liquids) and τ (8 liquids).

Fig. 3 analyzes the data in terms of the scaling law approach for the SE and DSE violations. More precisely D_s vs. η (lower data) and 1/τ vs. η (upper data) are plotted in a log–log scale to detect the “fractional” SE and the DSE violations, respectively (6, 28). The data clearly show two different scaling behaviors above (dashed lines) and below (solid lines) the fragile-to-strong crossover temperature T_×. From both the figures it is evident that, for all liquids studied, the onset of the breakdown takes place at approximately the same viscosity η_× ≈ 10³ Poise and that the curves are universal in the sense that the data for different fluids superpose.