Inferring social ties from geographic coincidences

Abstract

We investigate the extent to which social ties between people can be inferred from co-occurrence in time and space: Given that two people have been in approximately the same geographic locale at approximately the same time, on multiple occasions, how likely are they to know each other? Furthermore, how does this likelihood depend on the spatial and temporal proximity of the co-occurrences? Such issues arise in data originating in both online and offline domains as well as settings that capture interfaces between online and offline behavior. Here we develop a framework for quantifying the answers to such questions, and we apply this framework to publicly available data from a social media site, finding that even a very small number of co-occurrences can result in a high empirical likelihood of a social tie. We then present probabilistic models showing how such large probabilities can arise from a natural model of proximity and co-occurrence in the presence of social ties. In addition to providing a method for establishing some of the first quantifiable estimates of these measures, our findings have potential privacy implications, particularly for the ways in which social structures can be inferred from public online records that capture individuals’ physical locations over time.

Every day, we make inferences about the social world from incomplete observations of events around us. A particular category of such inferences draws on co-occurrences in space and time—basing estimates of a social tie between two people on the fact that they were in the same geographic locale at roughly the same time. In addition to its intuitive accessibility, such reasoning has been employed in psychological studies of urban life (1) and legal analyses of the dangers of “guilt by association” (2, 3). These issues also arise naturally in online domains, including those that reflect spatio-temporal traces of their users’ activities in the physical world. Despite the broad relevance of the underlying questions, however, there has been essentially no precise basis for quantifying the significance of these effects. Here we study this issue in an online setting and find that geographic co-occurrences can in fact have significant power in forming inferences about social ties: The knowledge that two people were proximate at just a few distinct locations at roughly the same times can indicate a high conditional probability that they are directly linked in the underlying social network, in the data we consider. Our results use publicly accessible spatial and temporal information from a large social media site to derive estimates of links in the online social network of the site. We also develop a probabilistic model to account for the high probabilities that are observed. In addition to providing a quantitative basis for the power of these inferences, our results have implications for the unintended leakage of private information via participation in such sites.

Our analysis uses data in which individuals engage in activities at known places and times. There are many potential sources of such data, including transaction records from cell phones, public transit systems, and credit-card providers. We use a source where analogous activities are recorded publicly and online: a large-scale dataset from the popular photo-sharing site Flickr. Most photos uploaded to Flickr include the time at which the photo was taken, as reported by a clock in the digital camera, and many photos are also geo-tagged with a latitude–longitude coordinate indicating where on Earth the photograph was taken. These geo-tags either are specified by the photographer by clicking on a map in the Flickr web site, or (increasingly) are produced by a global positioning system (GPS) receiver in the camera or cell phone. Flickr also contains a public social network, in which users specify social ties to other users.

Results

Spatio-Temporal Co-occurrences and Social Ties

We define a spatio-temporal co-occurrence between two Flickr users as an instance in which they both took photos at approximately the same place and at approximately the same time. Specifically, we divide the surface of the earth into grid-like cells, each of whose side lengths span s degrees of latitude and longitude. We say that two people A and B co-occurred in a given s × s cell C, at temporal range t, if both A and B took photos geo-tagged with a location in cell C within t days of each other. Then, for a given pair of people, we count the number of distinct cells in which they had a co-occurrence at temporal range t. For example, in Fig. 1, A and B have three co-occurrences at a temporal range of 2, and four co-occurrences at a temporal range of 7.

Fig. 1.

Illustration of how spatio-temporal co-occurrences are counted, for some sample time-stamped observations of individuals A and B. The world is divided into discrete cells of size s × s, and we count the number of cells k in which the two individuals have been observed within a time threshold of t days—in this case, k = 3 when t is 2.

Our central question is the following: What is the probability that two people have a social tie, given that they have co-occurrences in k distinct cells at a temporal range of t? This is a question that is relevant in any setting where co-occurrences may be indicative of social ties, and we emphasize that our methodology for exploring it is a general one; because Flickr in particular provides spatio-temporal information and also an explicit listing of social ties among its users, it is a natural domain in which to compute concrete numerical answers to the question. The answers depend on three parameters: the number of co-occurrences k (indicating the amount of evidence for a social tie), together with the cell size s and temporal range t (indicating the precision of the evidence). We compute the probability as a function of these parameters by first constructing the social network of Flickr using all friendship links declared up through April 2008 and then identifying spatio-temporal co-occurrences that occurred after April 2008. In this way, and in keeping with our initial motivation, we are only identifying social ties that existed prior to the accumulation of the evidence via co-occurrences (this is explained in more detail in Discussion).

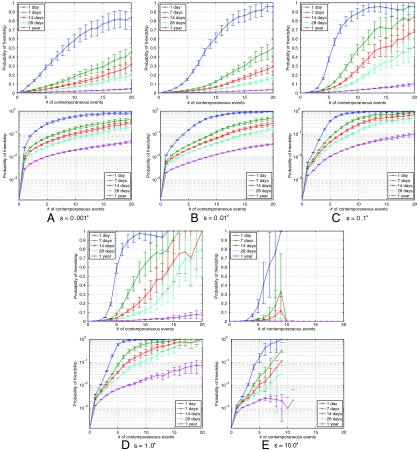
Using a dataset of 38 million geo-tagged photos from Flickr (see Materials and Methods for more detail), we find (Fig. 2) that the probability of a social tie increases sharply as the number of co-occurrences k increases and the temporal range t decreases. What is perhaps most striking is not the direction of this dependence but rather the large values of the probabilities themselves relative to the baseline probability of having a social tie. Two randomly selected Flickr users have a 0.0134% chance of having a social tie, but when two users have multiple spatio-temporal co-occurrences, this probability grows significantly. For example, two people have almost a 60% chance—nearly 5,000 times the baseline probability—of having a social tie on Flickr when they have five co-occurrences at a temporal range of a day in distinct cells of side length equal to 1 latitude-longitude degree (about 80 km on a side at the mid latitudes). Moreover, this number is likely an underestimate of the true probability, because many Flickr users choose to keep their contact list private or do not use the social networking features of the site at all (and hence those social ties are missing from our ground truth data). Even with just three co-occurrences for this value of s and t, the probability is roughly 5%, which is more than 300 times greater than the prior probability of having a social tie in our dataset.

Fig. 2.

The probability that two Flickr users have formed a social contact on the site, as a function of the number of times they have taken pictures at approximately the same place and time. A shows the probabilities for a spatial cell size of s = 0.001° (or around 80 meters in the middle latitudes) for time periods ranging from a day to a year. The lower plot is the same as the upper plot but with a log scale on the y-axis. Also shown are plots for cell size s equal to (B) 0.01°, (C) 0.1°, (D) 1.0°, and (E) 10.0°.

The dependence of the probability on the cell size s is more subtle: Because the co-occurrences are required to be in distinct cells, it is possible for k co-occurrences at a small value of s to all take place inside the same cell at a larger value of s. As a result, k co-occurrences in distinct 1° cells may be more or less informative than k co-occurrences in distinct .01° cells, because the latter may all take place close together. (For example, three co-occurrences that each take place within .01° of each other in New York City represent closer spatial proximity, but the fact that there are three of them may be less significant because they all take place within the same city; on the other hand, three co-occurrences that each take place within 1° of each other at points spread out across the United States represent less spatial proximity per co-occurrence, but collectively they may be more significant because they are taking place far apart from each other.) The presence of these counteracting forces is borne out in Fig. 2, in which we see that the probabilities of friendship do not necessarily increase as the cell size decreases.

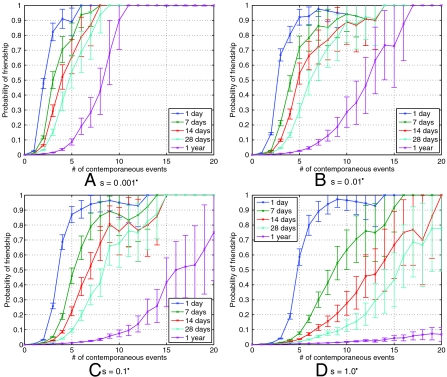
In Fig. 3 we correct for this effect by counting at most one co-occurrence in any 1° cell, regardless of the value of s; this forces the total possible number of co-occurrences between two people to be 180 × 360 = 64,800 regardless of the spatial cell size s. With this correction in place, the probability of a social tie grows monotonically as the cell size s decreases; for example, with k = 3 and t equal to a day, the probability increases from about 5% for s = 1° to over 80% for s = 0.001°.

Fig. 3.

(A–D) A variant of the analysis in Fig. 2, with the modification that at most one co-occurrence is counted per 1° spatial bin. This makes the scales on the x axes directly comparable.

Another source of subtlety arises from the fact that the area of the spatial cells varies significantly over the surface of the globe, because degrees of longitude become closer together as one traverses the globe from the equator to the poles. To address this issue, we also performed our analysis using equal-area partitionings of the globe computed via HEALPix (4). We found that the results did not differ significantly, and hence in what follows we use the conceptually simpler cells measured in degrees.

A Model of Spatio-Temporal Co-occurrences.

The fact that a very small number of co-occurrences can lead to orders-of-magnitude greater probabilities of a social tie suggests the need for a deeper investigation of the underlying phenomenon. We show that the basic effect is a robust one, in that it can arise even on very simple models of social networks, provided we have an appropriate probabilistic model for how activity is correlated across social ties. We begin with a simple model, followed by a richer one that matches the observed data more closely.

To formulate the simpler model, we suppose that the world is divided into N geographic cells (like those pictured in Fig. 1). There are M people, each having one social tie, so that the social network consists of M/2 disjoint edges. Each day, each pair of friends chooses to visit a place jointly with probability β and independently with probability 1 - β; in either case the choice of location(s) is made uniformly at random. Using Bayes’ Law, the probability that two people are friends (event F) given that they visit exactly the same cells on k consecutive days (event C_k) is

The prior probability that two people are friends, P(F), is , while the likelihood function P(C_k|F) in the numerator is , where p₁ is the probability of two friends being at the same place on a given day,

The prior probability on observing k co-occurrences of two random people is

where denotes the event that the two people are not friends, and is the probability of a co-occurrence between two nonfriends. By substituting and simplifying into the Bayes’ Law equation, we have,

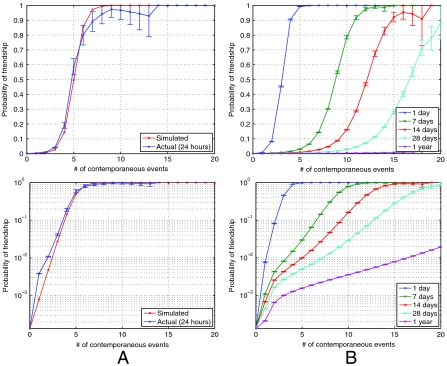
Fig. 4A presents a plot of this probability as a function of k (with parameters M = 7,500, N = 100, β = 0.05), showing a strong resemblance to the observed t = 1, s = 1 plot of Fig. 2D. Note that with M large and k small, this function simplifies to an exponential distribution,

which explains the near-linear curve in the semilog plot in Fig. 4A, in which N and β jointly control the growth rate of the exponential function, and M controls the probability at k = 0.

Fig. 4.

Simulation results for 1° spatial bins, using (A) a Bayesian probabilistic model and (B) a more detailed model incorporating richer spatial structure. These simulation results approximately match the shape of the plots based on actual Flickr data in Fig. 2D.

While this basic probabilistic model explains the major features of Fig. 2, it is too simple to capture all of the details, including the rapid probability increase between k = 0 and k = 1. To model the significance of a single co-occurrence, we take into account the principle of homophily: the fact that people connected by a social tie are more likely to engage in related activities, due to their inherent similarity, even when they are choosing independently. For example, two people who know each other are more likely to live close together and hence to visit places that are near each of them. To incorporate this notion, we extend the model to give each individual an attribute that is shared across social ties. As before, we assume that there are M people, each with exactly one social tie. The N geographic cells are arranged in a grid, and each pair of friends (A, B) has a randomly chosen “home” cell, drawn from the two-dimensional empirical distribution of Flickr photograhs (used here as a proxy because we do not know actual home cities of Flickr users), which approximately follows a power law with exponent 2.45. When A or B chooses a place on a given day, they sample from a distribution D_(A,B), which is peaked around the home cell and decays with distance according to another power law distribution (with exponent γ) (5, 6). On each day, each person independently decides whether to visit a cell, with probability α, or to do nothing (and hence not be observed that day). If two friends each choose to visit a cell (an event with probability α²), then with probability β they visit the same cell, and with probability 1 - β their selections are independent. In all cases, they select cells from the distribution D_(A,B).

The probabilities of friendship as a function of co-occurrence produced by this model (Fig. 4B) qualitatively approximate the distributions observed in the actual Flickr data (Fig. 2D) across the five time ranges we study (1 day, 7 days, 14 days, 28 days, and 1 year). (In contrast, multiple simplifications of this model that we investigated, including sampling home cells independent of the social network and substituting uniform or Gaussian distributions for the home cell and travel distributions, did not match the empirical observations well.) The values for the model parameters (M = 7,500, N = 64,800, α = 0.29, β = 0.12, γ = 1.8) were found by minimizing the Kolmogorov–Smirnov statistics between the distributions predicted by the model and those observed in the data, across all five time ranges, using a brute-force search over a grid of quantized parameter values. Better quantitative fits to the model are possible if the parameters are adjusted for each of the five temporal distributions separately; for example setting α = 0.55 and β = 0.05 gives a very good fit for the distribution corresponding to temporal range 1. A better fit for all time periods with a single set of model parameters could likely be achieved by explicitly modeling correlation of user activities across time, instead of assuming that all decisions are made on a day-by-day basis as our model currently does.

The analyses from these models thus indicate how very few co-occurrences can lead to a sharp increase in the probability of a social tie, even with an extremely simple underlying network structure. More complex frameworks could be used to study the analogous effect on realistic network structures, via models such as Markov random fields (MRFs) (7) in which the behavior of each node is correlated with that of its neighbors. While the inference problem for such models is computationally difficult on arbitrary networks, there exist good approximation algorithms such as Loopy Belief Propagation (8) and methods based on graph cuts (9).

Discussion

One can view our results as playing a role similar in spirit to that of studies quantifying the power of “coincidences” (10, 11). Indeed, our analysis could be considered as connecting two distinct notions of “coincidence”—the literal sense of two entities coinciding (in our case in space and time) and the colloquial sense of a surprising and seemingly random juxtaposition of events. Both our empirical results and our models suggest a way to quantify the significance of such juxtapositions.

Our results have potential implications for the privacy of users on social media sites. Earlier work on privacy breaches has shown how people can be uniquely identified using information such as postal codes, gender, and dates and places of birth (12–14), as well as the contents of search engine queries and online reviews and discussion (15–17). Other work has shown how social network structure can be exposed by analyzing anonymized versions of it (18, 19) or by looking for commonalities in online behavior, such as covisitations to web sites (20) and tagging shared content with similar textual keywords (21). Our findings here differ from these studies by establishing a strong form of leakage from sparse individual information about activities in the physical world into pairwise information about links in the underlying social network. Recent work in the geo-science community has studied how to aggregate and visualize the geo-spatial movement of people (22), including how to summarize movement in a way that preserves individual privacy (23), but has not studied the correlation of this data across links in a social network. Our results also address a substantively different issue from recent work on inferring social network structure from detailed time series of physical copresence (24): Rather than basing estimates on extensive high-resolution traces of individual behavior, we ask what can be learned from an extremely small number of instances in which two people were proximate in time and space. This latter type of inference is arguably a greater privacy risk, because small quantities of such data are more easily exposed than detailed traces of physical copresence.

The conclusion is that individuals who choose to reveal small amounts of public information about the times and locations of their activities may be inadvertently sending strong signals about certain of their social ties as well. Similar risks arise even when individuals are not publicly disclosing information about activities, but instead when this information is logged through transactions with financial, communication, or transportation systems. The framework and models we introduce here could be used to analyze information leakage from these other sources of sparse geo-temporal observations.

It is important to note that our results do not suggest that most friendships reveal themselves through a pattern of repeated spatio-temporal co-occurrences; indeed, most pairs of friends in the data are never in the same place at approximately the same time. Rather, the point is the strength of the opposite implication: that when two people exhibit multiple spatio-temporal co-occurrences, this is a strong indicator of a social tie, relative to the baseline frequency of such ties. In order to assess the scope of such results, however—for example, to understand the breadth of the privacy implications—it is of interest to determine how numerous such co-occurrences are and how many individuals in the data are involved in them. Note that especially in the context of privacy concerns, a moderately large absolute number of affected individuals can represent a significant effect, even if most of the population is not implicated.

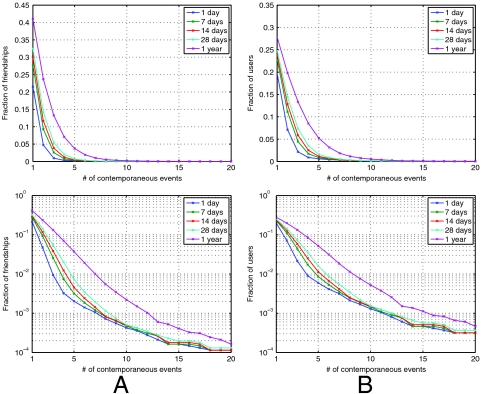
To analyze these issues, we begin by observing that most Flickr users in our dataset have very little opportunity to be involved in co-occurrences, because the median user in the dataset has uploaded fewer than 15 photos. Thus, for the sake of nontriviality, we focus our discussion of this issue on the 10% of the Flickr population consisting of the most active users (corresponding at this percentile to users who have uploaded at least 189 geo-tagged photos). Here we find, in Fig. 5A, that a significant number of friendships involving these high-activity users exhibit spatio-temporal co-occurrences; for example, approximately 22% of all such friendships have one co-occurrence in a 1° cell at a temporal range of a day, and approximately 1% of all such friendships have three co-occurrences at this spatio-temporal range. Viewing these same results in terms of the number of individuals involved (rather than the number of friendships involved), we find, in Fig. 5B, that 19% of all high-activity users have at least one friendship with one co-occurrence in a 1° cell at a temporal range of a day, and approximately 2.5% of all high-activity users have at least one friendship with three such co-occurrences. (The percentage of users affected is not necessarily larger than the percentage of friendships affected, primarily because nearly 40% of the users in this population do not have any social connections or choose to keep their social connections private; thus the maximum possible percentage of affected friendships is 100% while only 60% of users could possibly be affected.) Finally, reflecting the fact that the full population contains a large fraction of users with very few photos and hence very few spatio-temporal appearances overall, we find lower rates of co-occurrences across this full population: On log-linear scales, the curves for the full population are very similar in shape to Fig. 5A but scaled down, and we find, for example, that approximately 1.5% of all friendships have one co-occurrence in a 1° cell at a temporal range of a day (involving approximately 12% of all users), and approximately 0.03% of all friendships have three such co-occurrences (involving approximately 0.7% of all users).

Fig. 5.

The fraction of social links that exhibit co-occurrences at a spatial threshold of s = 1°, expressed in terms of (A) the fraction of friendships and (B) the fraction of users having at least one such friend.

Ultimately, our analysis—both in the models and in the hypothesized mechanism underlying the empirical observations—is exploiting the fact that a social tie among two people biases them to engage in similar activities at similar times and places. We expect this effect to be present in a wide range of datasets where activities are recorded with spatio-temporal precision, including travel, communication, commercial transactions, and other settings. In quantifying this effect, however, we need to be careful to control for other sources of bias that may be specific to Flickr as a source of data. Clearly in using Flickr as a dataset, we have access by definition only to the behavior of its users, who are a small and not necessarily representative sample of broader populations. For example, the conditional probabilities of friendship given geo-spatial co-occurrences are likely to be higher in the Flickr community than in the population at large, because two Flickr users are likely to be more similar (and hence more likely to be friends) than two people chosen at random from the world’s population. However, this sparsity affects the baseline probability of a social tie as well, and the crux of our analysis is concerned with the comparison between this baseline probability and the conditional probability given a set of co-occurrences. Thus, while we expect the absolute conditional probabilities to change according to the sampling properties of a particular dataset, the high conditional probabilities relative to the baseline are likely to be a general feature that is observable in a wide range of settings.

In conducting our experiments, we also have identified and attempted to mitigate several further sources of bias arising from the ways in which the design of a social media site may influence its users’ behavior. These include the following:

1. Users may seek contacts on Flickr by explicitly searching for people who have geo-temporally co-occurred with them. To control for this, we look for co-occurrences occurring after a fixed date (April 2008), using the social ties that were declared before that date. The results are similar even without this partitioning of the time ranges used to define the social network and the co-occurrences, perhaps because the publicly available Flickr search interface does not offer an easy way to find such co-occurring users.

2. Some co-occurrences in Flickr may be caused by social contacts uploading exactly the same photo. To prevent this from affecting our analysis, we ignored photos that were duplicated across users. This changed the results very little, probably because the Flickr user interface does not provide an easy way for a user to repost another user’s photos.

3. Users with many contacts on Flickr also have many photos and are more likely to geo-tag (21, 25). In other words, the relation between a person’s geo-tagging and social activity on Flickr may not align well with the corresponding relationship in the physical world, between the number of places a person visits and the size of his or her social neighborhood. To address this bias, we conducted a randomization test in which we kept the structure of the social network but shuffled the geo-temporal observations across users. We found that the correlation between number of co-occurrences and probability of friendship disappeared entirely, thus confirming that this source of bias was not causing the empirical effects we observe in the Flickr data.

Finally, the nature of photography as an activity introduces further complications into the interpretation of the results. Opposing forces are likely at work here: People often take pictures when they are with friends, which may increase the proportion of social ties among observed co-occurrences; but they also often take pictures at massively popular public events in which they are members of large crowds, which may correspondingly decrease the proportion of social ties among observed co-occurrences. Such counterbalancing forces may also be observed in spatio-temporal records of other social activities, including traces of communication and purchasing as well as diary-style records such as blogs. The point is that all these types of records tend not to be simply random samplings of a person’s complete stream of activities but rather are modulated by the activities themselves. Controlling for such subtle effects on the rate of co-occurrences is an interesting open question.

Despite these caveats concerning the data used in our experiments, the general analytic framework and models we present could provide insight into a set of basic facts arising from the intersection of human social behavior and the detailed recording of human activities. As people go about their lives, they carve out paths through time and space; sometimes these intersect with the paths of friends, and sometimes with the paths of strangers. Our study suggests a way to differentiate between these two kinds of intersections: After a relatively small number of such co-occurrences between two people at distinct locations, the probability that they are in fact socially connected rapidly increases. Such inferences have long been supported informally by intuition and anecdote but have been difficult to make precise. The fact that probabilities of social ties can depend so strongly on a handful of observations underscores the power of co-occurrences and highlights the extent to which our social networks are embedded in the trails we leave through the world.

Materials and Methods

We collected the dataset of geo-tagged photographs using Flickr’s public API interface. To do this we repeatedly searched for public photos taken at random geographic coordinates and at random points in time until we had covered the entire surface of the earth and most of the history of Flickr. This crawling process resulted in about 85 million geo-tagged photographs. We then filtered this set to remove photos with imprecise geo-tags and/or missing timestamps. For the geo-tags, we removed photos having a geo-tag precision less specific than about the size of a city block (according to the geo-tag precision reported by Flickr). For the timestamps, we removed photographs having infeasible timestamps (including dates in the future and in the distant past), as well as photographs whose upload timestamp is identical to the photograph timestamp (which indicates that Flickr assigned a default timestamp because the camera had not recorded one). About 38 million photos taken by about 490,000 users remained after these filters. We then collected the public social contacts for each of these users.