Thalamocortical model for a propofol-induced α-rhythm associated with loss of consciousness

Abstract

Recent data reveal that the general anesthetic propofol gives rise to a frontal α-rhythm at dose levels sufficient to induce loss of consciousness. In this work, a computational model is developed that suggests the network mechanisms responsible for such a rhythm. It is shown that propofol can alter the dynamics in thalamocortical loops, leading to persistent and synchronous α-activity. The synchrony that forms in the cortex by virtue of the involvement of the thalamus may impede responsiveness to external stimuli, thus providing a correlate for the unconscious state.

The anesthetic agent propofol (2,6-di-isopropylphenol) is known to elicit frontal α-rhythms (10–13 Hz) in the EEG (1). Recent data analyses (2, 3) suggest that this rhythm, which is spatially distinct from the classic occipital α-rhythm, is highly coherent across electrodes. Moreover, its appearance is well correlated with the anesthetic-induced loss of consciousness. Although much is known about the molecular actions of propofol, an understanding of the network mechanisms that lead to such EEG-level phenomena remains absent. The present work uses computational models to elucidate some of these mechanisms. It builds on the work of McCarthy et al. (4), in which a model of cortical networks was used to reveal dynamic changes that may underlie the paradoxical excitation associated with low doses of propofol. Here, these mechanisms are incorporated into a broader thalamocortical model that accounts for the aforementioned EEG features associated with the administration of higher anesthetic doses.

The model suggests that propofol, via its potentiation of the GABA_A synaptic current, effectively enhances the strength of projections from the cortex to thalamus, resulting in a well-coordinated thalamocortical α-oscillation. We consider a network of cortical pyramidal (E) cells and interneurons (INs), coupled with thalamocortical relay (TC) and thalamic reticular (RE) neurons. Reciprocal projections between the E and TC cells form an excitatory thalamocortical loop. Propofol enters the model as an increase in the conductance and decay time of the GABA_A inhibitory current. At low levels of the drug, the cortical part of the model produces the expected paradoxical excitation, whereas the thalamic part fires at a slower irregular rate. Increasing the inhibition to a level commensurate with a higher dose of the drug causes cortical cell firing to slow into the α-range. Importantly, this also changes the thalamic substrate by increasing the inhibition delivered by the RE neurons to the TC neurons, producing rebound spiking. Thus, the cortical input to the thalamus is effectively enhanced, enabling the latter to be recruited into the same α-frequency. Because the reticular nucleus innervates widely, it has the capacity to synchronize thalamic oscillations. These oscillations then manifest coherently at the cortex through the thalamocortical loop. Thus, the model produces a coherent propofol-induced α-rhythm that is consistent with experimental data.

Recent theories have pointed to a deactivation of the thalamus during deep levels of general anesthesia (i.e., the notion of a thalamic “off-switch”) (5, 6). In contrast, the model developed here suggests that the thalamus is engaged in rhythmic activity at deep anesthetic levels. The intracortical synchrony may limit the efficacy of the thalamus in propagating specific signals upward, thus promoting loss of consciousness. The phenomenology, model details, and simulation studies are presented in the subsequent sections.

Phenomenology

Data and Analysis.

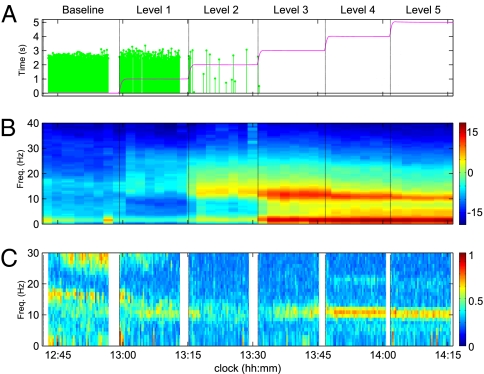
Experiments were conducted at the Massachusetts General Hospital to assess the electroencephalographic markers associated with loss of consciousness under general anesthesia. Subjects were given a controlled infusion of the drug propofol, and a 64-channel EEG was recorded from the scalp. Throughout the infusion, subjects were required to respond to a series of auditory stimuli, the latency of which serves as a measure of loss of consciousness. Fig. 1 illustrates the time course of the infusion for a single subject along with the EEG analysis. The dose level is increased in five discrete levels. For the subject shown, cessation of responses occurs soon after the second infusion. After dose level five, the infusion is gradually decreased, at which time the subject regains consciousness and resumes the task.

Fig. 1.

Results from propofol infusion in a single representative subject. (A) Time course of propofol infusion and behavioral response. The green traces indicate the latency of correct responses to auditory stimuli. Cessation of response indicates anesthetic-induced loss of consciousness. The red trace describes the estimated propofol blood concentration. (B) Whole-study spectrogram from a frontal electrode. Loss of consciousness coincides with the emergence of broadband β-activity, which strengthens and slows into the α-range as the infusion increases. (C) Coherent EEG activity. At the deepest levels of general anesthesia the α-band exhibits high global coherence (2); being frontal, it is distinct from the classic occipital α in anatomical location.

The EEG spectrogram exhibits distinct features that coincide with transitions in subject behavior (Fig. 1B). The initial onset of loss of consciousness is correlated with a diffuse increase in low β/high α-band power, which gradually slows into the α-range as the level progresses. The next level of the infusion strengthens this α-power in frontal electrodes. Such an “anteriorization” of EEG power under general anesthesia has been noted in other studies (7, 8) with different anesthetic agents. Slower activity in the <2-Hz band also increases in intensity at this time. When the subject emerges from loss of consciousness (i.e., resumes responding to the task), the α- and slow activity lift and the EEG returns to the baseline pattern. Note that, as expected, this frontal electrode does not exhibit the classic posterior α-rhythm (9) (subjects’ eyes were closed during all levels).

To ascertain the spatiotemporal properties of this activity, a global coherence analysis was performed over all electrodes (2, 3) (Fig. 1C). Here, the coherence within each frequency band is measured by the energy contained in the first principal component of the cross-spectral matrix. The analysis shows coherent activity in the α-band at deep levels, primarily in frontal electrodes. This coincides with the frontally dominant α seen in the power spectrum. We interpret these results as an indication of increased α-synchrony in frontal regions, suggesting that this rhythm is mechanistically distinct from the occipital α.

Modeling Objectives.

We note three main features of the above analysis: (i) early loss of consciousness is associated with diffuse β-activity; (ii) deeper general anesthesia is associated with α- and slow activity; and (iii) the α-activity exhibits a high spatial coherence, predominantly in the frontal electrodes.

Many studies of the EEG at deeper planes of general anesthesia have focused on describing activity in the slower frequency bands (e.g., refs. 10 and 11, and the references therein). The α-band activity, conversely, is a recent finding (1), and its coherence is a newly described result. Thus, in this paper, the modeling is directed toward the α-EEG activity. Possible mechanisms for the slow oscillation are addressed elsewhere in this paper (Discussion).

Approach.

To investigate the α-activity, we construct a model with the smallest set of features necessary to exhibit the spatial and temporal properties outlined above. A study of the spatial coherence requires an extension to the purely cortical model of McCarthy et al. (4). The high level of synchrony in the frontal electrodes is particularly indicative of subcortical participation in the α-activity. The thalamus, with its connectivity to prefrontal areas (12, 13) and its propensity to produce α-type rhythms (14–18), is a likely candidate.

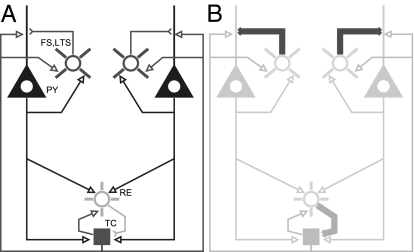
We construct a thalamocortical model, combining known cortical dynamics (4) with models of the thalamus (15). The model, illustrated schematically in Fig. 2, is based on biophysical equations that allow for the manipulation GABA_A, thus mimicking the effects of propofol in a physiologically relevant way. We consider two distinct cortical cell populations coupled to a mutual population of thalamic cells. The cortical populations have the capacity to produce synchronous behavior via their thalamic connections. Below, we demonstrate how such a network, through the actions of propofol, can manifest coherent oscillations in the α-band.

Fig. 2.

Schema of model network and mechanism. (A) Network consists of separate populations of pyramidal cells (denoted PY) and INs (here, both FS and LTS are lumped into a single icon) that interact with a mutual population of RE and TC cells. (B) Propofol perturbs the network by potentiating the GABA_A synaptic current and decay time from INs onto PY cells and from RE neurons onto TC cells. Note that all model cells are single compartments.

Results

Model Reproduces Propofol-Induced α-Rhythm.

The network displays a switch in coherence as the GABA_A receptor dynamics are modified according to the actions of propofol.

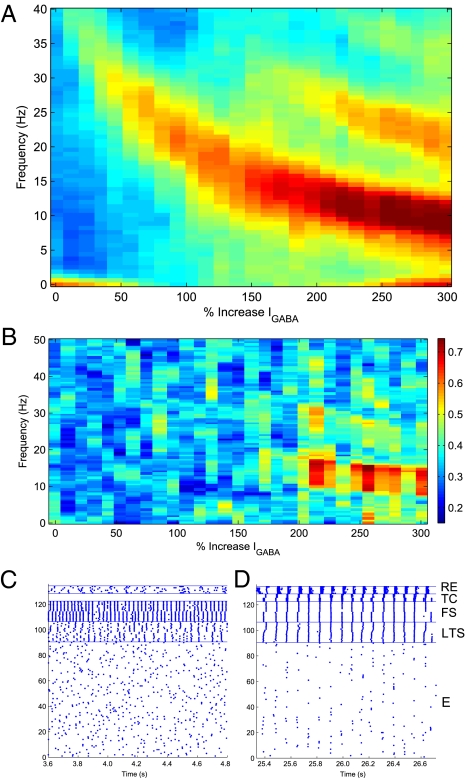
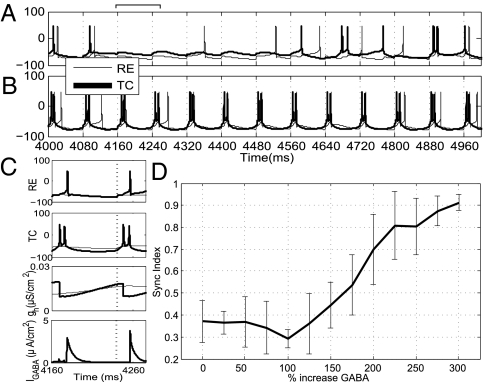
Fig. 3 illustrates the behavior of the model network as a function of the percent increase in both the GABA_A conductance and decay time. As shown in Fig. 3A, the dominant EEG rhythm decreases from a baseline frequency in the γ-range (see Methods) to a β-rhythm associated with low doses, and finally to a 10- to 13-Hz α when the current increases 200% (i.e., threefold the baseline level). As described in the Methods, such an increase in GABA_A inhibition is consistent with the effects of an anesthetic dose of propofol. Fig. 3B shows the coherence between the two cortical populations over the same range of GABA_A synaptic strength. The network does not exhibit coherence at baseline and low-dose levels. As the rhythm slows into the α-range (i.e., when the dose reaches the anesthetic level), the cortical populations synchronize and the coherence shows a strong peak between 10 and 13 Hz (Fig. 3B, indicated by red in the color bar).

Fig. 3.

Mean simulated EEG spectrogram and coherence (n = 10) as a function of GABA _A synaptic strength. (A) At baseline, the EEG reflects γ-activity in the 40-Hz range. As the inhibition increases to threefold the baseline level, the frequency decreases to a 10- to 13-Hz α-rhythm. (B) Coherence (0–50 Hz) between thalamic and cortical spiking is shown as a function of dose level (color bar indicates strength of coherence). High coherence is observed from 10 to 13 Hz when propofol increases to threefold the baseline level. (C) Raster of spiking activity in the model near baseline level of propofol. The cortical cells are divided into two populations (E: 1–45, 46–90; LTS: 91–98, 99–106; FS: 107–114, 115–122). RE cell activity is sparse and irregular, whereas TC cells do not spike at all. (D) At 250% of baseline, both thalamic cell types participate in the spiking activity at α-frequency.

The raster plots of the activity at baseline and anesthetic levels (Fig. 3 C and D, respectively) demonstrate the mechanisms that lead to coherence. At baseline, the fast-spiking (FS) cells drive network activity in the γ-range through the pyramidal–interneuron mechanism described by Börgers et al. (19). Individual cortical pyramidal (E)-cell participation is irregular and infrequent. RE cells fire sparsely. TC relay cells are simulated with no exogenous drive and do not exhibit spiking at baseline, consistent with a lack of sensory stimuli. Sparse TC baseline activity would not affect high-dose behavior.

When propofol is increased to a high dose (Fig. 3D), the spiking in cortical cells slows into an α-rhythm, again attributable to the increased decay time of inhibition from both FS and low-threshold spiking (LTS) cells. Importantly, the RE cells and TC cells are now recruited into the rhythm, resulting in an increased functional coupling between the thalamus and cortex. The common thalamic drive serves to synchronize the spiking between both cortical populations, leading to the increased coherence in the model EEG.

Increase in GABA_A Conductance Facilitates Thalamocortical Feedback.

As shown, the increase in GABA_A inhibition appears to recruit and couple the thalamic cells into the cortical rhythm.

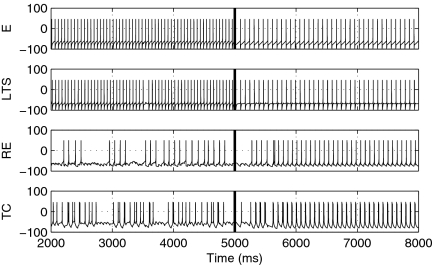
To investigate the behavior of this dynamic switch, we construct a small model involving single E, LTS, RE, and TC cells. Although an FS cell is omitted from this minimal configuration, it could alternatively have been used in place of the LTS cell without changing the result (SI Text). Fig. 4 shows time traces of the voltage for each cell in the network at both low and high doses of propofol. At a low dose (t < 5 s) the E and LTS cells spike at β-frequency, whereas the RE and TC cells fire irregularly. A high dose of propofol is introduced at t = 5 s, at which time the cortical rhythm slows into the α-range. Simultaneously, the thalamic cells begin responding regularly to excitation from the E cells. The reciprocal excitatory feedback from the TC cells onto the E and LTS cells completes the oscillatory loop.

Fig. 4.

Voltage traces for a four-cell model. Propofol changes from a low to high dose at t = 5 s; at that time, cortical cells transition from a β- to α-spiking frequency. Simultaneously, thalamic cells are recruited into the cortical activity, thus engaging a rhythmic thalamocortical loop.

This dynamic switch, from low to high thalamocortical synchrony, is induced by postinhibitory facilitation, which makes the TC cells more responsive to cortical excitation. The increased inhibition delivered by the RE cell to the TC cell causes the latter to respond to cortical excitation with regular predictable bursts. The RE cell, in turn, responds to this burst from the TC cell, thus promoting a thalamic inhibitory-excitatory rhythm that locks to the cortical pace. As described in the next section, this locking is specific to the α-frequency. The phenomenon of thalamic entrainment is exhibited in Fig. 5 A–C, which shows the response of an isolated RE-TC pair to a 12-Hz stimulus over a 1-s time window. In Fig. 5A, the GABA conductance (g_GABA) and decay time are set to baseline (i.e., unanesthetized) values, whereas in Fig. 5B, they are set at the threefold efficacy associated with a high dose. Fig. 5C illustrates the role of increased inhibition and, consequently, of the hyperpolarization-activated current (I_h) in promoting the rhythm: As the RE cell spikes, increased GABA_A inhibition leads to hyperpolarization of the TC cell, which, in turn, yields a slow build-up in the h-current conductance (g_h). The consequent activation of I_h makes the cell receptive to the next incoming cortical excitation, resulting in a burst. The depolarization of the TC cell causes g_h to reset and the RE cell to fire, thus beginning another cycle. In comparison, at baseline, g_h builds much more slowly and the smaller hyperpolarization of the TC cell means that I_h is less active. Thus, cortical excitation does not reliably evoke a burst response.

Fig. 5.

Response of TC-RE pair to cortical drive. (A) TC-RE model cell spiking at the baseline (g_GABA = 0.04). Spiking is sparse and uncorrelated. (B) TC-RE model cell spiking at a high-dose level (g_GABA = 0.14). Spiking is entrained to the 12-Hz drive (the drive arrives at the dashed vertical lines). (C) Detail of activity from 4,160–4,260 ms. (Top to Bottom) RE voltage, TC voltage, g_h (in TC cell), and I_GABA (in TC cell) for baseline (thin line) and propofol (thick line) conditions. The increased I_GABA and, consequently, the I_h are important in promoting the rhythmic thalamic response. (D) Mean Synchronization (Sync) Index obtained over different noise realizations for the single TC-RE pair with a 12-Hz cortical drive (n = 20). As GABA increases beyond twofold the baseline value, the SI increases, reflecting entrainment of the thalamic cells to the cortical excitation.

Fig. 5D shows the Synchronization Index of the RE-TC pair in relation to the 12-Hz stimulus, evaluated over a range of g_GABA and with multiple realizations of background noise. This index provides a measure of synchrony based on the relative phase difference between TC spikes and the cortical drive (SI Text). The decay time of inhibition is held constant at a high-dose level. As the conductance increases beyond a low dose, the index increases to a value close to 1, indicating that the thalamic cells become highly entrained to the cortical α.

Thalamic Entrainment Occurs Only at α.

Fig. 5C indicates the importance of increased GABA_A conductance and decay time, in combination with the intrinsic currents, in entraining the TC and RE cells to the cortical drive. Moreover, this entrainment is constrained to the α-range.

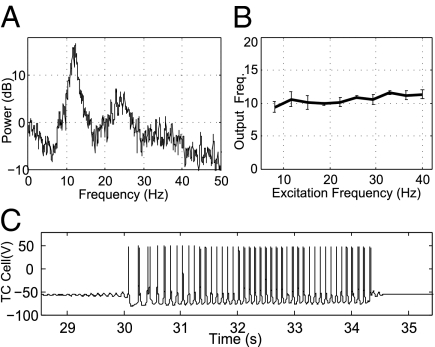
As a demonstration, consider the response, shown in Fig. 6A, of a single RE-TC pair to excitation by a random spike train, with propofol set to high-dose levels. The random train is constructed by drawing interspike intervals from a uniform probability distribution over the range of 25–120 ms. The power spectrum of such an excitation is flat over the range of 8–40 Hz (i.e., it does not have a spectral peak). In contrast, as shown in Fig. 6A, the power spectrum of the thalamic cell activity clearly exhibits a peak at 11–13 Hz, implying that the network naturally favors spiking in the α-range (voltage trace shown in Fig. S1). Indeed, we note that at high-dose levels, in the absence of all excitation, the TC-RE pair produces sporadic waxing and waning oscillations [Fig. 6C, similar to the spindles shown in work of Destexhe et al. (15, 20)] at similar α-frequencies. In another simulation, we subject the thalamic cells to periodic cortical excitation of different frequencies, again with a high-propofol parameterization. As shown in Fig. 6B, the thalamic cells always respond at around 11 Hz, even when excitation extends into the θ- or γ-range (voltage traces and details are shown in Figs. S2 and S3). Thus, the excitation is sufficient to make the thalamic activity persistent but will not evoke faster spiking.

Fig. 6.

Frequency response of thalamic cells at high-dose levels shows that entrainment is constrained to the α-range. (A) Power spectrum of thalamic cell spiking in response to random excitation. The interspike intervals of the excitation are drawn from a uniform distribution. (B) Thalamic cell spiking frequency in response to periodic excitation at different frequencies (n = 20). As a result of the time scales of the inhibition and intrinsic currents, the thalamus always responds near 11 Hz. (C) In the absence of cortical excitation, TC-RE cells produce waxing and waning oscillations similar to the thalamic spindles modeled by Destexhe et al. (15, 20).

The above analysis, combined with that of the previous section, suggests why propofol-induced thalamocortical synchronization occurs at α. At baseline levels, when cortical activity occurs at γ, the amplitude of the RE-TC inhibition is insufficient to facilitate a regular thalamic response (however, other dynamic regimes are discussed below). At high doses, when facilitation is enabled, the time constants in the thalamus are such that any response to excitation occurs at 11–13 Hz. The excitation sustains and “uniformizes” the intrinsic thalamic behavior (Fig. S3) but does not significantly alter the spiking frequency. Indeed, any excess input is effectively shunted, leaving a persistent α-rhythm. Recall that the cortical oscillations themselves slow into α at high doses. Thus, they coalesce with the thalamus in its naturally preferred frequency, and synchrony is achieved.

RE Cells Promote Synchrony Between Cortical Populations.

We have attributed the propofol-induced coherence to increased thalamic participation, which effectively connects otherwise isolated cortical populations. The RE cells are particularly important in this mechanism because they facilitate rebound excitation in thalamic relay cells. Although the thalamus is clearly not a monolithic entity, the reticular nucleus forms an inhibitory shell that innervates many relay nuclei. As such, it alone may promote synchrony over spatially distinct cortical areas.

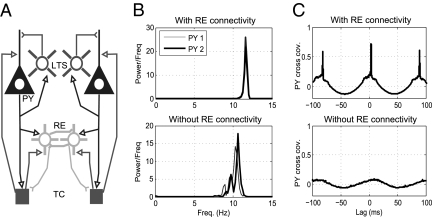
To demonstrate the capacity of RE cells to synchronize cortical cells, we consider the small eight-cell model shown in Fig. 7A, each cortical cell receives excitation from a different relay cell. The two RE cells are reciprocally connected, constituting the only means of coupling between the cortical modules. The network is parameterized heterogeneously such that, in the absence of RE coupling, each cortical cell would spike at a slightly different intrinsic frequency (Fig. 7B Lower). Here, GABA_A conductance and decay time are set to the high-dose levels, resulting in the predicted 10- to 12-Hz α-activity. Clearly, there is no correlation between the two spike trains, as indicated by a flat cross-covariance (Fig. 7C Lower). Mutual inhibition between the RE cells is sufficient to synchronize the entire network, as reflected by identical power spectra (Fig. 7B Upper) and a well-defined cross-covariance peak (Fig. 7C Upper). This is consistent with previous detailed modeling studies, such as that by Börgers and Kopell (21), which have shown the capacity of inhibitory networks to synchronize sparsely coupled cortical populations.

Fig. 7.

Simulation of small network with connectivity between RE cells. (A) Network connectivity. (B) Power spectra of cortical spiking activity with (Upper) and without (Lower) RE cell coupling. In the latter case, as a result of different parameterizations and noise, the activity displays disparate frequencies. (C) Cross-covariance between E-cell spiking showing clear synchrony in the case of RE coupling (Upper) and a lack of synchrony otherwise (Lower).

Model Properties Are Compatible with Active Regimes.

The model developed herein has focused on the role of thalamocortical networks in perpetuating a propofol-mediated α-oscillation. We have not elaborated on the multitude of potential behaviors of the network in a more “active” behavioral state. We can, however, establish that the dynamic range of the model is compatible with other such functional modes (details presented in SI Text).

Discussion

Cellular Mechanisms for Propofol-Induced EEG.

The scalp EEG is a measure of the average activity in large populations of cortical neurons. Propofol, as we have seen, appears to induce synchronous α-rhythms in such populations. In this work, we have used biophysical modeling to suggest the cellular mechanisms responsible for this phenomenon. Our model shows that (i) propofol induces α-activity by increasing GABA_A conductance and decay time; (ii) an increase in GABA_A conductance facilitates involvement of the thalamus, yielding cortical synchrony; (iii) this synchrony is specific to the α-frequency range; and (iv) cells of the reticular nucleus can synchronize disparate relay nuclei, thus enabling synchrony over larger cortical regions.

Features Not Included.

A number of features were not explicitly included in the present model, including GABA_B currents within the thalamic model. Inclusion of GABA_B within the RE population of our model leads to a decrease in the firing rate of individual cells but no change in the population frequency and cortical coherence. An expanded thalamic model could also include propofol-induced effects on intrinsic currents (e.g., I_h) that may be important for other phenomena, such as burst suppression EEG patterns.

The synaptic connectivity within the LTS population is higher than reported in some literature (22). In our model, we have not included IN electrical connectivity via gap junctions (23). Thus, each cell describes the behavior of a lumped population of electrically coupled INs. In addition, LTS cells are known to exhibit an h-current that may lead to such features as sag and rebound depolarization. We find that addition of such a current does not appreciably change the network behavior at high propofol levels, where the GABA_A dynamics dictate cortical activity (SI Text).

Finally, this work does not model the occipital α-rhythm in posterior cortex. The occipital α is thought to involve thalamic nuclei with projections to occipital cortex, such as lateral geniculate nucleus (16), and may be mechanistically distinct from the frontal corticothalamic activity studied herein.

Mechanisms for the Slow Oscillations.

The model developed herein does not account for the slow (<2 Hz) oscillations present in the EEG. In the context of sleep, the prevailing hypothesis is that these frequencies also have a thalamic generator (24, 25). Analysis of the data used here suggests that the anesthesia-induced slow oscillations lack the spatial coherence that would be characteristic of a subcortically driven rhythm. The slow activity may thus be a cortical phenomenon, such as described by Compte et al. (26) and Cunningham et al. (27), which involves anesthetic effects on activity-dependent potassium channels. The relationship between such a mechanism and that of the α is presently unclear, however, and further analysis is required to inform a detailed model that exhibits both rhythms.

Mechanisms for Other Cortical α-Oscillations.

The cortical α-mechanism presented here is created by a potentiated GABA_A response. Models of cortical α in other contexts include work of Jones et al. (28, 29), which suggested a role for h- and T-currents. These mechanisms are less reliant on GABA_A and may be additional contributors to α-rhythmicity in high propofol conditions. Certain in vivo studies, combined with modeling, have suggested a differential role for FS and LTS populations in creating high- and low-frequency rhythms, including α, in response to exogenous periodic drive (30). Our model suggests that propofol would alter these mechanisms by slowing the response of both INs, particularly leading to a lowering of FS-cell rhythmic activity. We emphasize the likely importance of feedforward and feedback dynamics from the thalamus in synchronizing α in this increased GABA_A state.

Predictions of Thalamic Activity Under General Anesthesia.

Previous studies of anesthesia-induced loss of consciousness have centered on the use of slow imaging modalities, such as PET or functional MRI, to characterize large changes that occur in brain activity. This has led to the idea of a so-called “thalamic switch of consciousness” (5, 6), in which the thalamus becomes relatively inactive during general anesthesia. In contrast, our model predicts that some subset of the thalamic network would actually consolidate its activity into a highly structured α-rhythm. Evidence suggests that the blood oxygenation level-dependent signal is closely related to activity in higher frequency bands (31), which could explain why such a behavior has not been seen in these other works. Alternatively, more refined source localization techniques may reveal this increased thalamic activity in nuclei, such as the mediodorsal (12), with dense connections to frontal cortex.

The model also makes predictions of activity in smaller thalamocortical networks that could be validated by suitably designed in vivo experiments. For instance, we would anticipate that adding propofol to a thalamocortical slice preparation, such as in the work of Tancredi et al. (32), could induce persistent and synchronous activity in the α-frequency range.

Because the mechanism for the propofol α-rhythm is a potentiation of GABA_A, we would anticipate that other GABA agonists may elicit similar effects. Indeed, the volatile agent isoflurane has also been shown to yield increased thalamocortical coherence (33). Thus, our model may not be limited to propofol and predicts an important role of GABAergic pathways in propagating more general anesthetic-induced rhythms.

Thalamocortical Coherence as a Mechanism for Loss of Consciousness.

In addition to the cellular mechanisms, this work suggests a functional significance of the observed phenomenology. Recall that the onset of the α-rhythm coincides with the cessation of all responses to the auditory stimuli in the experiment. We have shown that this rhythm is caused in the model by a slowing of cortical activity that subsequently synchronizes within the α-band in thalamocortical loops. An interpretation is that under anesthesia, the dimensionality of the thalamocortical network is reduced by means of synchrony. It is interesting to note that other states of reduced arousal, most notably seizure, are similarly characterized by hypersynchrony. Additionally, α-rhythms have been shown to manifest during selective attention in those regions not relevant to the perceptual task (34, 35). In the case of propofol anesthesia, by engaging in what amounts to a pathologically synchronous α-oscillation, the thalamus loses freedom to project exogenous input. This insensitivity to specific excitation would be consistent with a decrease in task responsiveness, thus relating directly to loss of consciousness.

Methods

Model Structure.

We consider the model structure shown in Fig. 2A, consisting of two isolated cortical patches connected indirectly through a mutual thalamic cell population. Five cell types are considered: E cells, LTS cells, FS cells, RE cells, and TC cells.

The circuit within each cortical patch consists of E→I AMPA connections, with reciprocal I→E inhibition. I→I connectivity is all-to-all within the LTS- and FS-cell populations. Inhibition between the FS- and LTS-cell populations is sparse and random. Both LTS and FS cells are GABA_A-ergic (i.e., the slower GABA_B synaptic current is not considered in this model).

The thalamic part of the model consists of TC cells that form a closed all-to-all excitatory-inhibitory loop with the same number of RE cells. RE-cell inhibition is also via GABA_A. To form the complete network, we introduce thalamocortical and corticothalamic connectivity. Here, TC cells make excitatory connections onto all cortical cell types, whereas E cells provide reciprocal excitation onto both TC and RE cells.

The largest network studied in this work considers 80 E, 16 LTS, 16 FS, 6 RE, and 6 TC cells. The cortical cells are divided evenly in the two isolated populations. Smaller networks, consisting of a few cells of each type, are used to illustrate the cellular mechanisms behind the overall phenomenology.

Model Neurons.

Each individual cell is simulated using a single compartment conductance-based model. The time evolution of the neuronal voltage is governed by a differential equation of the form:

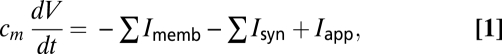where I_memb, I_syn, and I_app denote, respectively, the membrane, synaptic, and external applied currents specific to each cell. Each current is itself governed by differential equations in the biophysically based Hodgkin–Huxley formalism (36), wherein the particular transmembrane currents for a given cell determine its dynamic behavior. The following subsections provide an overview of these currents. Further details and equations are provided in SI Text.

Cortical cells.

Cortical cells contain the fast sodium (I_Na), potassium (I_K), and leak (I_Leak) currents required to elicit spiking. A slow potassium current (I_M) is included in the model of the E and LTS cells. This current is important in the generation of β-rhythms under low doses of propofol (4) (SI Text). FS cells do not contain I_M and are responsible for the generation of γ-activity in the baseline (i.e., unanesthetized) state (19). The applied current (I_app) determines the specific baseline firing rate of a given cell.

Thalamic cells.

Thalamic cells also contain the currents required for spiking. Additionally, TC cells have a T-type calcium current (I_T) and an I_h. As a result, these cells exhibit bursting and postinhibitory (rebound) spikes. The RE cells also contain I_T. The models for both RE and TC cells are derived from the work of Destexhe and colleagues (14, 15, 20), which examined mechanisms for α-spindle rhythms in an isolated thalamus.

Synaptic connectivity.

Connectivity between cells is established through the synaptic currents (I_syn). Two such currents are considered herein: excitatory AMPA (I_AMPA) and inhibitory (). As illustrated schematically in Fig. 2B, propofol, a GABA_A-agonist, perturbs the system dynamics through an increase in the inhibitory conductance and decay time.

Applied current and noise.

The applied current simulates all exogenous inputs to each cell not explicitly included in the model. It consists of a constant drive plus a train of excitatory postsynaptic potentials generated from a Poisson process. The constant drive is chosen randomly from a uniform distribution, which provides a measure of model robustness. In the large network, the background drive is applied only to cortical cells. The Poisson rate parameters are chosen in a manner consistent with the work of Börgers et al. (19) to produce a γ-rhythm in the absence of propofol. We note that although this rhythm is not explicitly seen in Fig. 1A, it is frequently associated with a general state of attention. Thus, given the task being performed, we will infer such a γ as the baseline for our simulations, ensuring that our network has the ability to produce higher frequency rhythms.

Propofol.

Baseline values of the GABA_A current parameters are chosen to be consistent with those of McCarthy et al. (4), which matched experimental data (37). There, a low (nonanesthetic) dose of propofol was modeled as a twofold increase in both the synaptic conductance and decay time. As suggested by McCarthy et al. (4), we will extend this further by modeling a high dose as a 200–300% increase from baseline levels.

EEG.

The EEG is modeled as the mean of AMPA currents emanating from the E-cell population (38), that is:

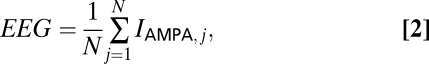where n = 40 for each of the cortical populations in the large network.

Numerics.

Models are simulated and analyzed using C++ and MATLAB with fixed-step solvers, with a maximum time step of 0.02 ms (additional details provided in SI Text).