Dynamic self-assembly and control of microfluidic particle crystals

Abstract

Engineered two-phase microfluidic systems have recently shown promise for computation, encryption, and biological processing. For many of these systems, complex control of dispersed-phase frequency and switching is enabled by nonlinearities associated with interfacial stresses. Introducing nonlinearity associated with fluid inertia has recently been identified as an easy to implement strategy to control two-phase (solid-liquid) microscale flows. By taking advantage of inertial effects we demonstrate controllable self-assembling particle systems, uncover dynamics suggesting a unique mechanism of dynamic self-assembly, and establish a framework for engineering microfluidic structures with the possibility of spatial frequency filtering. Focusing on the dynamics of the particle–particle interactions reveals a mechanism for the dynamic self-assembly process; inertial lift forces and a parabolic flow field act together to stabilize interparticle spacings that otherwise would diverge to infinity due to viscous disturbance flows. The interplay of the repulsive viscous interaction and inertial lift also allow us to design and implement microfluidic structures that irreversibly change interparticle spacing, similar to a low-pass filter. Although often not considered at the microscale, nonlinearity due to inertia can provide a platform for high-throughput passive control of particle positions in all directions, which will be useful for applications in flow cytometry, tissue engineering, and metamaterial synthesis.

Precision and programmable control of microscale droplets and particles is poised to facilitate new capabilities in biomedicine (1), materials synthesis (2), and computation (3–5), similar to how robust control of electrons enabled a myriad of applications in computation and communication. Control of the positions of microscale bioparticles, such as cells in flowing channels, is of great importance for flow cytometry (6), cell separation (7, 8), and cell diagnostics (9). In addition, improving the uniformity of local bioparticle concentrations at the microscale, by countering large statistical fluctuations away from the average bulk value can enable burgeoning fields such as “tissue printing” (10). Complete control of lattices of particles may also allow tunable fabrication of optical or acoustic metamaterials with controlled bandgaps (11, 12).

Recent progress in high-throughput control of particle positioning has taken advantage of inertial effects in microfluidic systems. Although a Stokes flow (i.e., Re = 0) assumption is a widely accepted concept in the microfluidics community, Reynolds numbers in microfluidic channels often reach ∼1 and even ∼100 in some extreme cases (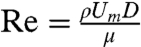, where ρ is the density of the fluid, U_m is the maximum flow speed, D is the hydraulic diameter, and μ is the dynamic viscosity of the fluid). As a consequence, many interesting inertial effects have been observed in microfluidic devices at this finite Reynolds number regime (13). One relevant example is inertial migration of particles in square and rectangular channels (14–16). Conventionally, control of particle position at the microfluidic scale is considered only possible with external force fields (e.g., dielectrophoresis and optical traps). However, fluid inertia has been used to manipulate the transverse position of particles in flow with exceptionally high throughput (15). In addition to transverse migration, particles are observed to self-assemble into uniformly spaced flowing “lattices” with no external force fields (14). This dynamic self-assembly phenomenon suggests the possibility of also manipulating particle position in the flow direction, which can lead to a platform for complete control of particle position in flow. Although studies to date have provided simple descriptions of the phenomenon, the mechanism of self-assembly in these two-phase solid-fluid systems is not well understood, and therefore cannot be engineered effectively.

Self-assembling systems, in general, require multiple interactions that include positive and negative feedback, which for particle systems are realized as attractive and repulsive forces (17–19). To better understand and therefore make use of the above described dynamic self-assembly in engineered microfluidic systems it is important to identify the underlying interactions that yield self-assembly (20–23). We hypothesized that viscous disturbance flows induced by rotating particles under confinement would repel neighboring particles to infinity whereas fluid inertia in the form of lift forces would act to maintain the particles at finite distances. Here we present data that supports this mechanism of dynamic self-assembly, provide a system with easily controlled parameters to study a new class of dynamic self-assembling systems, and demonstrate experimental implications of our increased mechanistic understanding by expanding the limits on passive particle control in microchannel systems.

Results and Discussion

Lateral Inertial Focusing of Particles and Longitudinal Self-Assembly in 1D Trains in Microchannel Flows.

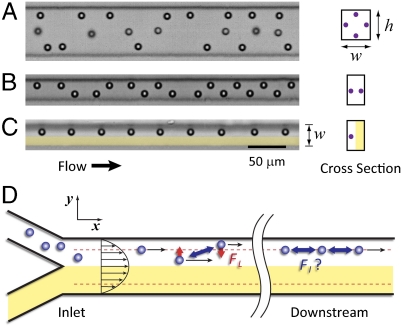
In finite-Reynolds-number channel flows, randomly distributed particles migrate across streamlines due to inertial lift forces (F_L), which is a combination of shear gradient lift that pushes particles toward walls and wall effect lift that pushes particles toward the center of a channel (Fig. 1D) (24). These inertial lift forces focus particles to four (Fig. 1A) or two (Fig. 1B) dynamic “transverse equilibrium positions” that are determined by channel symmetry. The system is a nonequilibrium system that constantly dissipates energy and the transverse equilibrium position is where the inertial lift forces become zero in the cross-section of the channel. We will use “focusing position” to refer to these transverse equilibrium positions to avoid confusion.

Fig. 1.

Particles are dynamically self-assembled in finite-Reynolds number flow. Inertial migration focuses particles to transverse equilibrium positions; particles migrate to predefined equilibrium positions, typically four in a square channel (A) and two in a rectangular channel (B). Particles are not only laterally focused (in the y-z plane) but also longitudinally ordered (in the x-direction). (C) Coflow with particle-free fluid can confine particles on one side of a channel resulting in a single line of particles with regular spacing. (D) Schematic of the dynamic self-assembling particle system in a two-inlet microfluidic channel. Randomly distributed particles are self-assembled through inertial lift forces (F_L) and hydrodynamic particle–particle interactions (F_I).

While traveling down the channel, the particles are laterally (y and z direction) focused by inertial lift forces (F_L) and simultaneously longitudinally (x direction) ordered by particle–particle interactions (F_I). In the final organized state, the system of particles has two degrees of freedom: interparticle spacing (l) and choice of focusing position. The interparticle spacing is determined by flow parameters (U_m, ρ, μ) and geometric parameters [particle diameter (a), channel width (w), and height (h)]. These parameters make up a particle Reynolds number (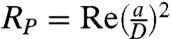) based on the shear rate at the particle scale, and interparticle spacing was previously found to decrease with increasing R_P (25). In this previous work, Morris and coworkers provided a general scaling for interparticle spacing and suggested that reversing streamlines may act as part of the mechanism of train formation; however, a more systematic study has not been possible with cylindrical channel systems.

Microfluidic systems can provide improved measurements of interparticle positions (14–16). We are currently investigating the scaling with microfluidic channels in more detail. For a set of parameters the interparticle spacing has a preferred value if the particles are aligned in the same focusing position. However, different cross-channel spacing and single-stream spacing appear to be preferred (Fig. 1 A and B). Interparticle spacing did not show a strong dependence on channel aspect ratio (16). Note that the selection of a focusing position for particles is intrinsically a random event, which makes diverse patterns in the organized structure. However, additional degrees of freedom in the form of additional focusing positions make the system more complicated to analyze. To study the mechanism of dynamic self-assembly in the simplest possible system, we used two-inlet coflow within a rectangular channel, which reduced the degrees of freedom by focusing the particles in a single line (Fig. 1 C and D). Particle-free fluid was flowed in the lower half of the channel and particles were confined to the upper half of the channel so that only one focusing position becomes accessible. The organized state becomes a 1D system with interparticle spacing as a dependent variable.

Pair Dynamics of Self-Assembly.

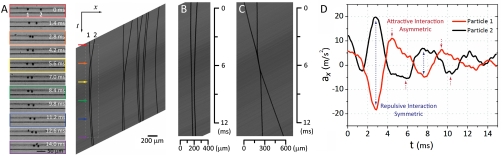
Details of the self-assembly process can be observed from the dynamics of pair and multiparticle interactions. Fig. 2 shows dynamics of interactions between two spherical particles. The channel dimensions with which these results were obtained were 25 μm × 90 μm (w × h) and the particle diameter was 9.9 μm. Movies of individual experiments were analyzed and transformed to x-t graphs to visualize the dynamics of the particle–particle interaction (Fig. S1). The transformed x-t graph represents the particles’ positions (x axis) in a translating reference frame over time (t axis). Image processing is described in detail in the supporting information. Initially, particles at the inlet move with different speeds because they are randomly distributed over a parabolic velocity profile. Due to differences in speed, a faster particle approaches a slower particle and forms a particle pair that moves downstream together. Particle pairs show various dynamics when the distance between the two particles is small enough for the particle–particle interaction to become significant (<  ∼ 10·a). In Fig. 2A, four particle pairs and a single particle are shown. Surprisingly, particle pairs undergo a variety of behaviors including oscillatory motion in the x direction before they achieve an organized (i.e., focused and ordered) state.

Fig. 2.

Snapshots of the high-speed movie and the reconstructed images show particle positions in translating reference frames over time. Different initial conditions result in diverse type of dynamics: oscillation (A), slow converging (B), and passing (C). (A) In many cases, two particles undergo oscillatory movement before settling to a stable pair configuration. (B) Analogous to a critical damped oscillation, particles can settle to an ordered pair without oscillation. (C) Particles can pass each other when their z-position difference is large. (D) The second derivative of particle positions, from (A). Amplitude of peak acceleration decreases in consecutive interactions. Repulsive interaction peaks coincide with each other whereas attractive interaction peaks are asynchronous.

Dynamics of pairwise particle interactions suggest irreversibility of self-assembly with distinct nonsymmetric attractive and symmetric repulsive interactions. Particles entering the system have slightly different speeds, as evidenced by different slopes of the lines in Fig. 2. These different initial conditions (e.g., speed and transverse positions) are observed to lead to differences in dynamics including the amplitude and frequency of oscillation but yield identical final ordered conditions. Note that the oscillation in interparticle spacing contains similar features to a particle oscillating in a potential well. Detailed features of the dynamics become apparent when observing the acceleration (Fig. 2D) of a particle pair marked with the dotted line in Fig. 2A (Movie S1). There are two important aspects of the interaction that can be found from this graph. First, the peak heights decrease over time indicating dissipation of energy and irreversibility. Once particles settle to an organized state with finite interparticle spacing, this condition is maintained without additional disturbance. Importantly, this organized state is only achievable within a moving fluid that requires a constant external energy source (pressure gradient across the resistive channel), which is an important aspect of dynamic self-assembly that differs from traditional self-assembly toward thermodynamic equilibrium. Secondly, acceleration patterns for repulsion and attraction are different. The first acceleration peak of particle 1 (lagging particle) and particle 2 (leading particle) are synchronous and correspond to a repulsive interaction. However, the second peaks, corresponding to attractive interactions, are asynchronous. This offset can be interpreted as the lagging particle first catching up followed by the leading particle slowing down. Note that this acceleration pattern repeats in the following peaks as well (Fig. 2D).

We can conjecture from these results that there are separate origins for attractive and repulsive interactions. Another feature observable in Fig. 2D is that there is an offset for the baseline of the acceleration curves, which means there is an overall acceleration in the positive x-direction. A slow change in the slope (i.e., overall curvature as seen in Fig. 2A) indicates continued particle migration toward focusing positions. This curvature is also observed for single particle traces, which implies that particle-particle interactions can be isolated from the overall acceleration. Another contribution to this overall acceleration is the flow speed change due to channel expansion. High flow speed (0.1–1 m/s) results in high pressure at the inlet, which in turn leads to a slight expansion of the channel. The channel cross-section gradually decreases and the average flow speed correspondingly increases downstream.

Fig. 2 B and C show different types of possible interactions that can lead to a consistent self-assembled state. In Fig. 2B, particles are self-assembled without oscillations analogous to a critically damped oscillation. In Fig. 2C, particles do not form a self-assembled pair but pass by each other. Nevertheless, particles interact; the speed of each particle changes during the interaction (∼4.5–7 ms) and the speed before the interaction and after the interaction are different and not symmetric. Time reversal symmetry is broken in all cases due to finite inertia.

Origin of Repulsive Interactions and the Mechanism of Dynamic Self-Assembly.

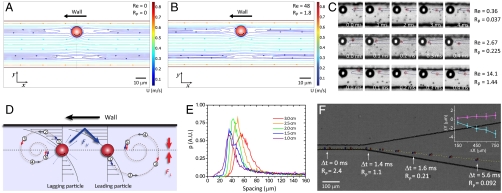
Reversing streamlines accompanying rotating particles have been suggested as a unique and unexpected aspect of flow around a sphere in finite-Reynolds-number shear flow (26–28) and pressure-driven channel flow (16). However, recently it was shown theoretically that reversing streamlines and swapping trajectory particle motion do not necessarily require fluid inertia but can occur in Stokes flow in a confined channel geometry (29). The symmetric reversing streamlines in Stokes flow thus arise from the reflection of the disturbance flow off the channel boundary and does not require inertia. Here we extend these results, shown in linear shear flows, to parabolic channel flows. We have simulated numerically a flow around a sphere at zero-Reynolds number and finite-Reynolds number using previously described numerical methods (24) (SI Text). Zero-Reynolds number simulations are performed by setting the fluid density equal to zero while keeping the flow rate at 100 μL/ min. The simulation results at Re = 0 (Fig. 3A) confirm that recirculation occurs from channel confinement in rectangular channel flow (parabolic shear). The viscous disturbance flow reflected off the adjacent wall generates a secondary flow in the y-direction and this effect does not require fluid inertia, which yields a similar flow field (Fig. 3B, Re = 48). A small difference between the Stokes flow case and finite-inertia case is that there is a slight asymmetry in finite-Reynolds-number flow streamlines due to inertial effects, such that the stagnation point seen on the lower half of the channel is shifted in the flow direction. We have also experimentally observed the existence of these reversing flows for the first time (Fig. 3C and Movie S2). To visualize the streamlines, 1 μm tracer particles were added to the suspension of 10 μm particles. In the frame of reference of and near larger particles, tracer particles are observed to reverse direction. This behavior was observed regardless of particle Reynolds number, in agreement with reversing streamlines present in all of the simulation results and suggesting the reversing flow is predominantly due to the confinement effect.

Fig. 3.

Mechanism of dynamic self-assembly involves inertial lift forces and viscous disturbance flows induced by rotating particles. Simulated streamlines for Stokes flow (Re = 0) (A) and finite-Reynolds number flow (Re = 48) (B) are not significantly different from each other. Reversing flow can occur solely from confinement effects. The channel dimension in the simulation is 45 μm × 60 μm and particle diameter is 9.9 μm. (C) Existence of this reversing flow was experimentally observed over a range of Reynolds numbers. Tracer particles (1 μm diameter) are observed to follow reversing streamlines with little disturbance. In agreement with simulation, reversing flow appears at near-zero-Reynolds number. Larger particle size is 9.9 μm in diameter. (D) Schematic of two particle interactions. Major components are (i) viscous disturbance flows reflected off the side wall (F_V), (ii) inertial lift force (F_L), and (iii) flow speed distribution (gray arrows). Particles are repelled by F_V and stabilized by F_L. Flow speed distribution fine-tunes the balance of the interactions. The oscillation is initiated by strong F_V when two particles approach close enough for F_V > F_L. (E) Histograms of interparticle distances show that there are preferred spacings. The interparticle spacings shift to larger distances with increasing distance from the inlet, which indicates that small repulsive interactions remain whereas attractive interactions vanish. (F) Time-sequential capture shows defocusing dynamics of two particles entering the expanding region. Average defocusing trajectory ± standard deviation (N = 8) is shown (Inset). Decreasing R_P indicates decreasing inertial interaction.

These results show that fluid inertia has little effect in the repulsive interaction suggesting a unique mechanism for dynamic self-assembly consistent with the data. The repulsive interaction initiated by a viscous disturbance flow (F_V), becomes strong at small interparticle spacings (O(1/l²)) (29, 30), (Fig. 3D). This viscous disturbance flow reflected from the nearby channel wall pushes particles off their focusing positions into staggered y-positions ①. The parabolic flow distribution (gray arrows in Fig. 3D) across different y-positions next magnifies interparticle spacings ②. That is, particles are pushed apart due to the parabolic velocity distribution (moving in different flow directions in the moving reference frame). Experimental results agree with this description—Fig. 2A shows that the leading particle moves closer to the center of the channel when it interacts in this repulsive phase. Particles however do not move off to infinity but are pushed back toward focusing positions and trajectories are stabilized by inertial lift (F_L) ③. Multiple oscillation cycles to reach focusing positions can be explained by overshooting (③→④). Further experimental results showing an asynchronous attractive interaction in Fig. 2D suggest that the lagging particle (particle 1) returns back to the focusing position before the leading particle (particle 2). This observation is consistent with the difference in magnitude of the inertial lift force on different sides of the inertial focusing position (transverse equilibrium position) (24). The lift force becomes larger—nearer to the channel wall (24) where the lagging particle is pushed than near to the channel centerline corresponding to the position of the leading particle.

We investigated the stability of self-assembled pairs. Yan et al. (31) have shown numerically that particle pairs can have limiting cycles, and thus the possibility of trains of particles with stable uniform spacings. However, in this theoretical work they used periodic boundary conditions that are more suitable for long trains of particles, where particles can be stabilized with only symmetric repulsive interactions from neighboring particles in the train. The symmetry is broken for the particles at the end of trains (i.e., boundary of the crystal) or for particle pairs. This leads to the question of what is responsible for maintaining particle pair spacings as both particles settle to their focused position in the presence of repulsive viscous interactions. In this case attractive interactions arising from the parabolic base flow and staggered particle positions have become vanishingly small. One possible explanation for observations of stable particle positions is that the repulsive interaction quickly decreases with interparticle spacing, In our high aspect ratio channel system the viscous interactions decay quickly with interparticle spacing; the interactions will decay in a manner similar to that due to a force dipole near a single wall (∼1/l²), when l is comparable to w, and will decay exponentially beyond that as in quasi-1D systems (30, 32, 33). In agreement with the strong decay in repulsive viscous interactions, data from particle pair trajectories do not show significant changes in interparticle spacings after they assemble (Figs. 2 and 4) when observed over intermediate distances (< 500·a). However, because of the limitation of the microscope field of view, individual particle pairs cannot be tracked for longer distances. Thus, we measured interparticle spacings at different downstream positions of the flow channel and plotted histograms (Fig. 3E). For longer distances we would expect small increases in interparticle spacing if no additional attractive interaction was present. Interestingly, the peak in interparticle spacing continuously shifts to larger distances further downstream. The larger particle spacings become noticeable (∼2·a) if particles travel long distances (∼2000·a). Overall, these experiments suggest that once particle pairs are self-assembled, whereas attractive interactions due to variations in y-position in the flow vanish, small repulsive interactions remain and further push particles apart as they travel downstream. However, interparticle spacings have been measured consistently (16, 25) and are stable for most practical applications that do not require long travel length.

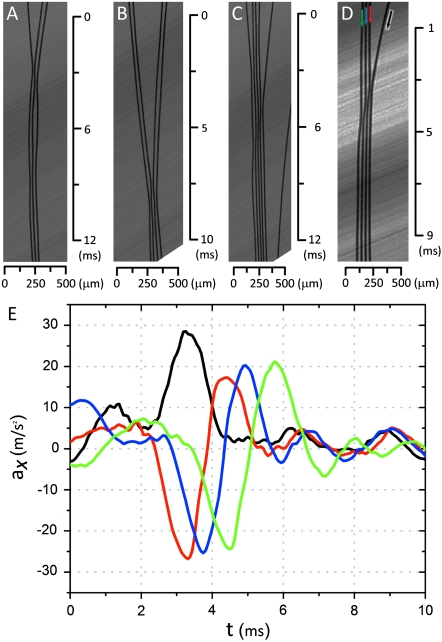
Fig. 4.

Randomly distributed particles develop into a long train of particles through a series of interactions. (A) A single particle joins a particle pair. (B) Two particle pairs join to make a four-particle train. (C) Train elongation. First, a faster single particle catches up to a three particle train, then, a slower particle joins the other particles. (D) A first particle (black arrow) joins a three-particle train. The impact is transferred down the train. (E) Particle acceleration from (D). Accelerations of the last three particles (red, blue, green) are nearly identical but translated in time displaying an aspect of wave propagation.

We used expanding channels to isolate the repulsive viscous interaction from inertial interactions and analyze the balance of these interactions (Fig. 3F). Fig. 3F shows a particle pair entering an expanding channel experiencing defocusing due to the viscous disturbance flow. In the expanding region particles slow down and move closer due to expanding streamlines. Interestingly, particles, when in pairs, also move away from the trajectory line of single particles. This can be explained due to the changing balance between inertial lift and viscous disturbance flow effects. At the expanding region, stabilizing inertial lift effects (scaling with R_P) decay monotonically, whereas the viscous swapping interactions initially increase due to decreasing interparticle spacing. The balance between the interactions is broken and the lagging particle is pushed toward the wall, and the leading particle is pushed away from the wall. This result is in agreement with the explanation of pair dynamics (Fig. 3C) and has important practical ramifications for continuous flow particle separation systems that also operate at low Reynolds number. Particle focusing near walls or in expanding channel geometries (13, 34–36) is used in many microfluidic particle-separation devices. However, for example in expansion channels, the phenomenon described here results in broadening of focused particle or cell streams (Fig. S2). Particle–particle interactions in high concentration particle suspensions result in defocusing in regions near channel walls, which adversely affects particle separation in microfluidic devices. We have identified that this defocusing is deterministic in origin (Fig. 3F, Inset) and is caused by viscous disturbance flows reflected from channel walls. The mechanism we propose implies engineering solutions (e.g., quickly expanding channels such that particles can be positioned away from channel walls) to address this issue. Particles with an appropriate concentration develop unique patterns at the expanding channel due to the deterministic defocusing (Fig. S3 and Movie S3). This pattern formation could also be used for two-dimensional self-assembly of microparticles. Besides implications for improvement of particle control in microfluidic systems, these results also have implications for blood flow near vessel walls (37, 38), suggesting limits to the dimensions of “cell-free layers” (39), and cell and particle diffusion in concentrated suspensions (40).

Multiparticle Dynamics: Formation of Trains and Wave Propagation.

Dynamics for more than two particles follows the same mechanism described for two particles with additional unexpected features. Particles develop into trains through a series of self-assembly processes at the particle pair level (Fig. 4). The particle trains elongate through additional particles joining already organized particle pairs or trains of particles. Particle–particle interactions are essentially the same as in two particle interactions (as evidenced by oscillations and acceleration patterns during interaction). It is worth noting that the “impact” of a particle joining a train is transferred down the train in these multiparticle systems (Fig. 4D and Movie S4). As shown in Fig. 4E, particle acceleration patterns are mostly identical for particles in the middle of the train during momentum transfer. The result suggests that middle particles dissipate little momentum of the first particle, which again suggests a prominent role for reversible viscous interactions in the initial repulsive transfer of momentum down the particle train. Potentially, this unique wave-like momentum transfer can be used to reveal nonequilibrium phenomena in self-assembled 1D particle systems as shown with microfluidic crystals (41, 42). The system shown here is unique in the sense that stable crystals are formed by dynamic self-assembly. Notably, particle self-assembly into longer trains requires differences in initial velocities. That is, our findings indicate that there is no long-range attractive interaction, only local overshooting of the equilibrium position leading to short-range attraction. This mechanistic understanding leads directly to engineering solutions to control particle spacing without dependence on R_p. If we can introduce perturbations in the flow to push particles apart our mechanism suggests that we would be able to maintain this configuration.

Modulation of Spatial Frequency of Particle Trains Using Locally Structured Microchannels.

One of many aspects characterizing Stokes flow is reversibility. In a channel with symmetric changes in geometry (e.g., expansion and contraction), the relative spacing between particles should return to the same value upstream versus downstream of the geometry change (assuming no collisions occur). We observed changes in particle spacing in a channel with a symmetric expansion and contraction shown in Fig. 5A. The channel width is 25 μm in the narrow region and 45 μm in the expansion region. The channel height is 85 μm and the length of the expansion region is 2 mm. Unlike the expectation for Stokes flow conditions, interparticle spacing downstream did not return to its original value. A histogram of interparticle spacing clearly shows a cutoff and shift of small interparticle spacings to significantly larger values (Fig. 5C). It should be noted that this shift is possible because whereas sequences of particle trains exist upstream, there are also large regions with no particles (i.e., “voids”). A shift in particle spacing spreads the localized trains and distributes particles more uniformly to fill in these voids.

Fig. 5.

Interparticle spacing can be manipulated by altering channel width. (A) Unlike in simple Stokes flow, the spatial frequency of ordered particle trains changes when the particles pass through a symmetric expansion-contraction geometry. (B) Pair dynamics in the expansion-contraction geometry show the dynamics leading to interparticle spacing changes. (C) A histogram of interparticle spacing before and after particles pass through the expansion region. A suspension of 0.05% v/v with 9.9 μm (diameter) beads was flowed at rate of 60 μL/ min. (D) Interparticle spacings after the expansion (d_a) are plotted as function of interparticle spacings before the contraction (d_a) demonstrating irreversibility.

Individual particle pairs were tracked to investigate the changes in interparticle spacing within the microchannel expansion (Fig. 5 B and D and Movie S5). Fig. 5B shows three representative plots of particle pairs with different initial spacings (d_b). The large negative slope indicates that the particles entering the expansion region slowed down as expected by conservation of mass. Interparticle spacing also initially becomes smaller in this region (d_b > d_m1). Particle pairs with d_b smaller than a threshold value experience a viscous repulsive interaction as described in Fig. 3D. The increasing interparticle spacing that follows supports this mechanism (d_m2 > d_m1). Finally interparticle spacing becomes larger when particles exit the expansion region consistent with conservation of mass. This entire process is reversible (d_a = d_b) for a particle pair with d_b larger than a threshold value (∼100 μm for this specific geometry), whereas the spacing irreversibly increases (d_a > d_b) for particle pairs that experience repulsion and reorganization, because of the absence of long-range attraction in the self-assembly process. Unexpectedly, below the threshold value d_b and d_a have a negative correlation (Fig. 5D). We believe that smaller d_b, thus smaller d_m1, results in a stronger repulsion in the expansion region that leads to a larger d_a. Together these results show that a short change in channel dimensions can be utilized for modulation of the spatial frequency of particles, ideally working as a passive frequency selective filter. Although we have only presented one design, modified dimensions of the expansion region are expected to result in a range of tunable spatial cutoff frequencies. A microfluidic device capable of particle spatial frequency tuning can be used in many practical applications. For example more uniform and controlled particle distributions (as opposed to Poisson distributions) improve efficiency of flow cytometry (6) and single cell encapsulation applications (43) by reducing particle coincidences and zeros. Additionally, the ability to consider particle trains as “signals” that can be sequentially modulated provides a strong analogy suggesting information processing and computation functions, such as have been demonstrated with bubbles and droplets in microfluidic networks (3–5).

In conclusion, we have investigated dynamics of particle–particle interactions in finite-Reynolds-number channel flow, identified mechanisms of self-assembly, and developed a framework for complete control of particle positions. High-speed imaging revealed diverse particle dynamics, including oscillatory motion, through which stable self-assembled pairs are formed. Normally the particles in the channel flow simply bypass one another or interact unstably (i.e., repelled to infinity) due to viscous disturbance flows reflected off nearby walls. Fluid inertia acts to stabilize the system keeping the particles organized at finite and precise spacings, but not providing a long-range attractive interaction. Reversing streamlines were found to be a critical component of particle–particle interactions leading to cross-streamline movement near microscale channel walls with key implications across various fields concerned with particle-laden flows. Finally, the self-organized particle system described here displays newly discovered characteristics such as wave propagation and irreversible frequency tuning, which have scientific and practical significance.

Materials and Methods

Particles used in this study were polystyrene beads with ∼9.9 μm diameters (Thermo scientific). The particles were dispersed in water with 0.05% w/v of Polyoxyethylene (20) sorbitan monooleate (Tween 80, Fisher Scientific) to prevent aggregation. Microfluidic channels were made by bonding molded polydimethylsiloxane channels (44) to glass slides. Channel widths were 25–45 μm and heights were 50–110 μm with h/w≥2. We have not found significant differences in the overall dynamics for different-sized channels as long as h > w. The concentration of particles in the fluid was ∼0.05–0.5%. Particles are dispersed far enough to see pair interaction at this concentration. A syringe pump (Harvard PHD 22/2000) was used to control volumetric flow rate. Typical flow rate was 40–80 μL/ min.