Limits to the evolution of assortative mating by female choice under restricted gene flow

Abstract

The evolution of assortative mating is a key component of the process of speciation with gene flow. Several recent theoretical studies have pointed out, however, that sexual selection which can result from assortative mating may cause it to plateau at an intermediate level; this is primarily owing to search costs of individuals with extreme phenotypes and to assortative preferences developed by individuals with intermediate phenotypes. I explore the limitations of assortative mating further by analysing a simple model in which these factors have been removed. Specifically, I use a haploid two-population model to ask whether the existence of assortative mating is sufficient to drive the further evolution of assortative mating. I find that a weakening in the effective strength of sexual selection with strong assortment leads to the existence of both a peak level of trait differentiation and the evolution of an intermediate level of assortative mating that will cause that peak. This result is robust to the inclusion of local adaptation and different genetic architecture of the trait. The results imply the existence of fundamental limits to the evolution of assortment via sexual selection in this situation, with which other factors, such as search costs, may interact.

1. Introduction

The majority of species concepts, implicitly or explicitly, stress the importance of reproductive isolation between species [1]. A strict interpretation of many of these definitions, including the Biological Species Concept, would require no gene flow between two populations in order for them to be labelled ‘species’ (e.g. [2,3]). In practice, however, taxa are often considered ‘good species’ even when there is a significant amount of successful hybridization between them. Many theoretical models of speciation have implicitly taken advantage of this more casual definition by describing their results as speciation even when reproductive isolation is merely initiated or strengthened, not completed (e.g. see [4]).

The issue of incomplete premating isolation between species arises any time that there is the potential for gene flow. The process of reinforcement has long been of interest as a possible step to complete the speciation process when there is secondary contact between incipient species that are still able to exchange genes. One of the early, influential objections to the importance of reinforcement was that as it led to the evolution of increasingly strong premating isolation fewer and fewer hybrids would be produced, thus removing the selection pressure (selection against low-fitness hybrids) that drove the process in the first place; the evolution of premating isolation therefore could not be completed [5]. To many, this emphasis on the strict completion of speciation seems semantic and misplaced. It is still of interest, however, to ask whether processes such as reinforcement and sympatric speciation can lead to strong reproductive isolation, and if so, how strong?

Several previous models of the evolution of assortative mating have found that there may be limits to its evolution in the presence of gene flow, not only because of the effects of gene flow itself, but also because of the action of sexual selection (e.g. [6–12]). Sexual selection in these models generally acts on males, driving changes in allele frequencies, but does not act on females. These models include various forms of divergent selection owing to competition or other forms of frequency-dependent viability selection as a force tending to drive the evolution of assortment. They also include search costs of finding mates. Here I strip a model of assortative mating via female choice down to the basics and ask two questions. First, is the presence of assortative mating sufficient to drive the further evolution of assortment? Second, what, if any, limitations on the evolution of assortative mating are present in such a model? I use a simple haploid model without search costs to address these questions, and then consider the effects of adding biological complexity in the form of selection and changes to the genetic architecture of the trait used for mating.

2. Models and results

First I examine a simple one-locus model in which assortative mating is already established and ask what degree of trait differentiation can be maintained between two populations exchanging migrants. The initial goal is to examine how the strength of assortative mating affects this differentiation. Then I introduce a locus that controls the strength of assortative mating to address the evolution of this parameter. I follow this by exploring two variants of these models, one in which there is viability selection on the mating trait, and another in which the mating trait has a more complex genetic architecture.

(a). Established assortative mating

In this haploid model, individuals in two populations differ in the allele present at a trait locus, T; members of population 1 have predominantly trait allele T₁ and members of population 2 have predominantly trait allele T₂. The use of haploids eliminates intermediate phenotypes. Females are assumed to have an established mating preference for males that share their allele at this trait locus. Specifically females are 1 + α times more likely to mate with a male that they prefer if they encounter one of each type of male. Strict polygyny is assumed, with no costs to choice (all females have equal mating success; the formulation is thus analogous to that in Kirkpatrick [13]). The assumption of established assortative mating yields very different results than a sexual selection model with a preference and a trait (as in Kirkpatrick [13]) in an isolated population; in an isolated population, the only stable equilibria in this model are for the trait T₂ to reach a frequency of 0 or 1, with the frequency of 1/2 being an unstable equilibrium between them (see electronic supplementary material, appendix A). This situation imagined in the two-population model here is secondary contact; traits are assumed to have diverged significantly in frequency before the onset of migration. Standard population genetic recursion equations are built using a life cycle that consists of symmetric migration occurring between the populations at rate m, followed by sexual selection with the mating preferences described above. Exact equations are presented in the electronic supplementary material, appendix A. Many previous models of secondary contact have concentrated on the commencement of assortative mating using relatively weak preferences (e.g. [14,15]); note that in order to examine limits to the evolution of assortment, which may have been missed in these previous models, strong preferences must instead be considered.

Despite its apparent simplicity, further assumptions have to be made to this model to obtain an analytical solution. Because assortative mating of a set strength and symmetric migration are the only evolutionary processes occurring in the model, the heuristic argument can be made that when variation is present at the T locus, the frequency of T₁ in population 1 should be equal to the frequency of T₂ in population 2 at equilibrium. First I will assume this symmetry of the allele frequencies and analyse this version of the model as a special case of the ‘asymmetric’ version. I show below that many of the results of the symmetric version also apply to the asymmetric version.

In the symmetric version of the model described above three equilibria are obtained for the frequency of T₂ in population 2 (t₂):

2.1

(see also [16], electronic supplementary material, appendix). Substitution of the equilibria in expression (2.1) into the system of equations without the symmetry assumption (presented in electronic supplementary material, appendix A) shows that these are also equilibria in the asymmetric case. It should be noted that the second two equilibria sum to one. To put this in the context of the two-island model with secondary contact, the second equilibrium frequency (above 1/2) would represent the frequency of T₂ reached on island 2 (and likewise the frequency of T₁ on island 1), while the third equilibrium frequency (below 1/2) would represent the frequency of T₂ on island 1. The first equilibrium frequency (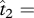1/2) would represent no differentiation between the islands.

In order to see how these equilibria are affected by the strength of assortative mating, I can simply plot these equilibrium points as a function of α (figure 1). This creates a bifurcation diagram that assumes a separation of timescales where the evolution to equilibrium at the trait locus (expression 1) is much faster than the processes that would lead to the evolution of α. Assuming that α evolves by the fixation of successive mutations, this is justified both by an argument that mutations are likely to be rare and by two-locus simulations (discussed further below) that demonstrate that the equilibrium value in the trait locus is reached very quickly in comparison with the spread of a new allele at a locus that changes α. This heuristic of simply allowing α to vary thus serves here as a proxy for a more detailed analysis of the evolution of α, which is conducted below.

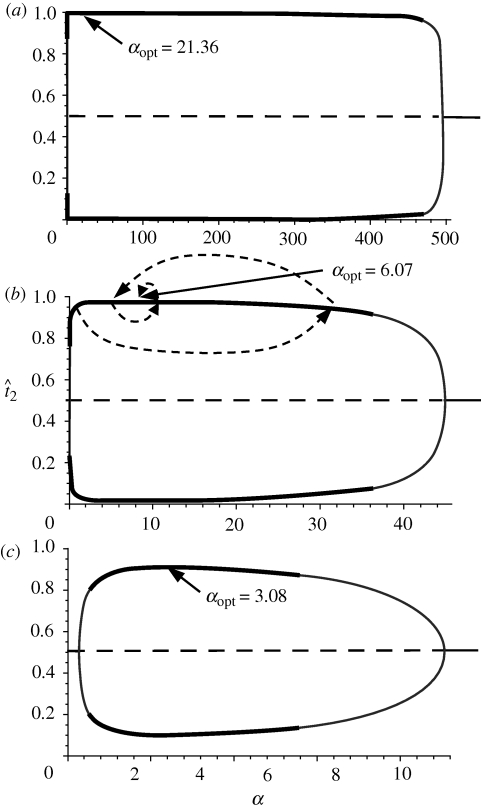
Figure 1.

Equilibrium frequencies of sexually selected traits in population 2 as α increases, from expression (2.1). The top curve corresponds to the frequency of the trait characteristic of this population, while the bottom curve corresponds to the frequency of the trait characteristic of population 1. Solid lines (grey plus black) show stable equilbria and dashed lines show unstable equilibria with the assumption of symmetry. Black solid lines on the curves show the equilibria reached in simulations of the asymmetrical model for that value of α, starting from the assumption of secondary contact (t₂ ≈ 0 in population 1 and t₂ ≈ 1 in population 2 or vice versa, with offsets of 0.001 and 0.002). The values of α_opt are marked in each graph. In (b) the thin dashed arrows show a potential series of steps in the evolution of assortative mating, as described in the text. (a) m = 0.001, (b) m = 0.01, (c) m = 0.03.

The curves shown in figure 1 show that the second and third equilibrium frequencies for t₂ from expression (2.1) appear as α increases from 0, diverge and then converge again, owing to higher order effects. Given a low m (less than approx. 5.5%), these equilibrium values can be shown to be real, not equal to 1/2, and between 0 and 1, under the following conditions:

2.2

Moreover, a linear stability analysis shows that if condition (2.2) holds, these second and third equilibria points are stable (see electronic supplementary material, appendix B for these analyses). When the migration rate is too high, differentiation between the populations cannot be maintained.

Numerical simulations and a numerical bifurcation analysis (using Content) of the asymmetric version of the model also indicate that for a wide range of migration rates and preference strengths the second and third equilibria in expression (2.1) are stable (see figure 1 and electronic supplementary material, appendix C). However, in the asymmetric version of the model, variation is lost at the T locus with extreme values of α and high values of m, even when the symmetric model indicates stable equilibria. For migration rates where stable values exist (m < approx. 4%) in the asymmetric model, the α corresponding to the highest level of divergence between the populations (α_opt below) was always found to be contained within the stable range. In the asymmetric model, variation at the T locus is additionally lost with α outside of the ranges of condition (2.2), instead of the frequency of t₂ = 1/2 being stable as under the assumption of symmetry.

Both with and without the symmetry assumption, there is, therefore, a value of α for which the equilibrium frequency of T₂ in population 2 (the higher of the two curves) will reach a peak; beyond this point less (or no) differentiation is maintained in the trait between the two populations. I will refer to this value of α as α_opt.

It is possible to calculate the value of α_opt for a given migration rate by setting the derivative of the second and third equilibrium points with respect to α equal to zero, yielding

2.3

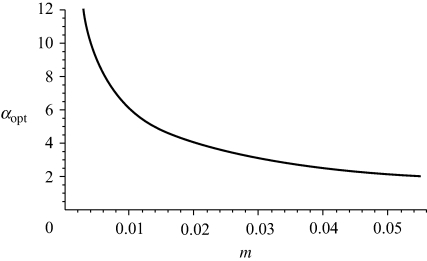
As migration rates increase, the value of α_opt drops (figures 1 and 2). It can be seen that when migration rates are moderate, for example, with 1–5% of individuals migrating each generation, α_opt is surprisingly low. Note that this expression for α_opt matches the values of α_opt found in numerical simulations of the asymmetric version of the model (valid for m < approx. 4%; see fig. C1 in the electronic supplementary material), as described in §2b.

Figure 2.

Change in α_opt with changing migration rate.

Why does α_opt exist? When assortative mating is very weak, it generates weak sexual selection driving the spread of the more common trait allele in a population. As the strength of assortative mating preference starts to increase, so does the sexual selection increasing the frequency of this common trait allele. However, in the extreme case where assortative mating is absolute, sexual selection becomes absent; assuming all females mate, females with the less common trait will always mate with the less common males, and females with the more common trait will always mate with the more common males. The mating success of the males is proportional to their trait frequencies, thus there is no sexual selection. Therefore, with very strong assortative mating (versus weaker assortative mating), there is actually weaker sexual selection favouring the more common allele. This effect can be demonstrated in a single population by extracting the selection coefficients on a trait under assortative mating generated by sexual selection with varying α, using the methodology developed by Barton and Turelli (see appendix A).

When migration is higher, the frequency of the less common allele in each population will tend to be greater. This reduces the sexual selection disadvantage to the rare type when assortative mating is strengthening from low values. This weaker sexual selection leads to a lower α_opt with high migration as argued in the appendix and seen in figures 1 and 2.

(b). Evolution of assortative mating

Why is α_opt important? In order to answer this question, I consider two locus models in which the first locus, T, behaves identically to the model above, while a second locus, A, allows for the evolution of assortative mating. Specifically, alleles A₁ and A₂ at this locus code for different strengths of assortative mating, α₁ and α_2. The value of α_opt is important because it is possible to demonstrate with a mix of analytical and numerical techniques (see electronic supplementary material, appendix D) that when the population is fixed for A₁ with α₁ = α_opt, an allele A₂ coding for any other value of α₂ cannot invade (i.e. α_opt is an evolutionarily stable strategy (ESS), [17]). Furthermore, deterministic simulations consisting of exact iterations of the six population genetic recursion equations that result from these assumptions consistently demonstrate that when a population is fixed for A₁ with α₁ ≠ α_opt, an allele A₂ can invade and will evolve to fixation if and only if α₂ yields a higher amount of divergence in the trait values between the populations (higher T₂ in population 2 and T₁ in population 1) than does α₁ (provided that genetic variation is maintained at the T locus with A₁ fixed; in these simulations A₂ is introduced after migration–selection balance is reached at the T locus). Provided the appropriate genetic variation for α is generated by mutation, populations will thus evolve from any initial α to an α that yields more trait divergence, until α_opt is reached (see figure 1b; hence α_opt is not only an ESS but also a convergence stable strategy (CSS), cf. [18]).

The explanation for this phenomenon lies in the fact that an assortative mating allele leading to a higher equilibrium frequency of the locally common trait allele will form positive linkage disequilibrium with this trait allele. As the trait allele increases in frequency each generation this assortative mating allele will spread to fixation via indirect selection. For example, consider an allele A₂ that leads to stronger sexual selection on allele T₂ in population 2 (note that α₂ can be higher or lower than α₁, see above). This allele will lead to a higher frequency of T₂ than did the previously fixed allele (A₁); thus by definition it has an α that is closer to α_opt. Because it causes stronger sexual selection favouring T₂ in this population, the individuals that carry A₂ and T₂ will increase in frequency. This causes a positive genetic association between the A₂ and T₂ alleles in this population (positive linkage disequilibrium at the A and T loci; note that in population 1, a parallel process is occurring to cause a genetic association between A₂ and T₁, leading to a negative linkage disequilibrium in that population). Each generation T₂ will increase in frequency in population 2 because of sexual selection, increasing the frequency of A₂ through linkage disequilibrium (likewise T₁ increases in population 1, increasing the frequency of A₂ there as well). Each generation migration also occurs, lowering the frequency of T₂ in population 2, but migration does not change the overall frequency of A₂ (or any other allele) across the closed system of both populations. The frequency of A₂ thus continues to increase every generation until it reaches fixation. If, in a different situation, A₂ led to weaker sexual selection on T₂ than did A₁ in population 2, then the signs of linkage disequilibrium in each population would be reversed, and A₂ would be lost. These effects are all readily observable by tracing linkage disequilibrium values and allele frequencies through numerical simulations.

(c). Selection on the trait

Here, I assume that traits that are used as the basis of assortative mating by females may also affect the fitness of individuals that carry them (a ‘magic trait’ model sensu [19]). I incorporate selection on the trait locus T under the assumption that the more common allele in each population is favoured by selection. Selection on the trait is thus modelled by assigning fitness (1 + s) to the trait T₁ in population 1 and to the trait T₂ in population 2 in both males and females.

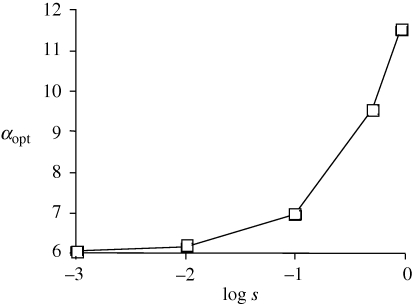
The incorporation of selection still allows analytical solutions to the model with fixed symmetry, but the results are not of sufficient simplicity to be illustrative (even when weak selection is assumed). Numerical simulations, however, indicate that for a fixed value of s, results very similar to those shown in figure 1 above are obtained. The primary difference is that because there is local adaptation based upon the trait, the trait favoured in each population will remain at a frequency above 0.5 even when assortative mating is extremely strong or extremely weak (or absent). The inclusion of selection does change the value of α_opt for a given migration rate, as is seen in figure 3; specifically stronger selection favouring the trait increases the value of α_opt (see also the appendix, figure 5). In the two locus simulations with selection and relaxed symmetry, the results once again indicate that an allele A₂ cannot invade provided that allele A₁ is fixed with α₁ = α_opt. These results appear to be robust to asymmetries in the starting frequencies of the trait in each population. When the selection coefficients favouring the local trait in each population are asymmetrical, the frequency of the trait in each population will peak at different values of α_opt, as determined by simulation, presumably owing to interactions between the frequency of the trait and the strength of sexual selection in each population. In this situation, the value of α that is uninvadable appears from numerical simulation to occur very close to the average of the values of α_opt in each population.

Figure 3.

Change in α_opt with changing selection on the trait. The migration rate m = 0.01.

(d). Changes to the genetic architecture

It is possible that females prefer to mate assortatively with members of their own population based on phenotypes controlled by multiple loci. I assume that there are two loci, M and N, each with alleles 1 and 2, characteristic of populations 1 and 2, respectively. These loci interact epistatically to produce population specific (‘pure’, for example, M₁N₁ in this haploid model) or hybrid (for example, M₁N₂) genotypes. I assume that pure females prefer pure males of the same genotype (e.g. M₁N₁ females prefer M₁N₁ males), but hybrid females have no preference. Females are again assumed to have equal mating success. First, I assumed that there was no selection on the M or N loci, and assumed symmetry both between the N and M loci (i.e. alleles with the same index at these loci have identical effects and thus identical frequencies) and, as described above for the T locus, between the two populations. It is therefore sufficient simply to track the frequency of the allele N₂ (frequency n₂) in one population and the linkage disequilibrium (D) that would occur in that population between the M and N loci.

Under these assumptions, numerical simulations indicate behaviour very similar to the initial model with assortative mating based upon the T locus with no selection. As shown in figure 4a, with very low assortative mating there is a single stable equilibrium at a frequency n̂₂ = 1/2 and no linkage disequilibrium, corresponding to no differentiation between the populations. As assortative mating strengthens (increasing α), stable equilibria appear at lower and higher frequencies of N₂, allowing population differentiation when different equilibrium values are reached in each population (figure 4b). Linkage disequilibrium appears between the M and N alleles. The populations reach a maximum value of difference in frequency between them with assortative mating strength α_opt (figure 4c), and then the differences decline, although because of strong assortative mating based on the combined phenotype of the two loci, the linkage disequilibrium continues to strengthen (figure 4d–f). When assortative mating is strong enough, the system returns to a single stable equilibrium point at n̂₂ = 1/2, now with high linkage disequilibrium (figure 4f). Simulations of a three locus version of this problem, allowing assortative mating to evolve by addition of the A locus described in the earlier models, once again indicate that an intermediate value of α₁ exists that prohibits invasion by an allele A₂ coding for any other value of α. However, the interpretation of this value of α is unclear; correspondence has not been found between it and a maximization of differences in any measure of frequencies tested at the M and N loci (including the equilibrium value in population i of N_i, of M_iN_i, of M_iN_i as a proportion of only pure genotypes, or to any of approximately 15 other values tested). This is potentially owing both to the more complicated architecture and to the fact that not all females express a preference in this version of the model (‘hybrid’ females mate at random).

Figure 4.

Summaries of evolutionary trajectories of the frequency of allele N₂ and the linkage disequilibrium D across various values of α with m = 0.01 and free recombination between the M and N loci. Each line summarizes an evolutionary trajectory by drawing a line from values at the start of a simulation (shown by the regularly spaced dots) to the equilibrium points, seen as the points of convergence. (a) α = 0.01; (b) α = 0.15; (c) α_opt = 9; (d) α = 65; (e) α = 70; (f) α = 75.

Selection against hybrids can be incorporated into this model by assuming lower fitness of the hybrid (M₁N₂ and M₂N₁) genotypes. When this selection is included, the value of α_opt that produces the peak value of N₂ drops as selection increases (not shown, see electronic supplementary material, appendix E for confirmation of this behaviour from the selection coefficients calculated by the methodology of Barton & Turelli [20]).

3. Discussion

The simple model at the core of these analyses asks the question of whether the existence of assortative mating is sufficient to drive the evolution of further assortative mating, and what may limit this process. Although not all forms of assortative mating do so [11,12,19,21,22], the assortative mating in this model, resulting from female preferences for males that share their traits in a polygynous system, generates sexual selection acting on the trait locus. I find that the presence of this sexual selection in this haploid model leads to the existence of a specific degree of assortative mating (α_opt) that determines both the peak value of trait differentiation between populations and the maximal degree to which assortative mating will evolve given sufficient mutational variants.

Specifically, when sexual selection results from assortative mating, all types of females have a preference for the matching type of male. If females are guaranteed to mate (see below), as the strength of assortment becomes very strong both the common and rare males will be increasingly likely to be chosen by a matching female. Sexual selection thus weakens as assortative mating becomes too strong. This leads to an intermediate strength of assortment (α_opt) that corresponds to the strongest effective sexual selection within populations and thus the strongest divergent sexual selection, and the strongest trait differentiation, between populations.

More interestingly, the weakening of sexual selection with strong preference strengths additionally determines the evolution of assortative mating in this situation. Any assortative mating allele that leads to stronger effective sexual selection on the trait, and hence more trait divergence between populations at equilibrium, naturally becomes genetically associated with the trait allele that it is driving to a higher frequency. As the trait allele increase in frequency, the assortative mating allele will thus increase with it by indirect selection, as described in detail above. Populations in this model will thus tend to evolve the degree of assortative mating that leads to the maximal trait variation between them (α_opt is thus a CSS).

The strength of assortment that will tend to evolve in a population is strongly affected by migration, which alters the trait frequencies and hence affects the effective strength of sexual selection because of its frequency-dependent nature. With moderately high migration rates, the level at which assortment will plateau can be quite low. This level can also be altered by local adaptation or other forms of selection acting on the trait allele because these forces also shift trait frequencies. Additionally, if the population cannot evolve to an optimal level of assortment because of a lack of the necessary mutations, the simulations above show that a mutation for any level of assortment will spread, provided that it leads to more trait differentiation at equilibrium.

The implications of these models are that the levels of assortment that will evolve in sets of populations may be fluid, and depend upon both the variants afforded by mutation and by changes in migration rates and selection pressures in populations. In some cases, a very strong level of assortment may evolve by the spread of a single mutation provided that the original level of trait differentiation between the populations was relatively low (e.g. figure 1b). This strong assortment could then be degraded if mutations arose that brought the level of assortment closer to that which caused the maximal amount of trait divergence. Different levels of assortment would thus also be expected if mutations in the strength of assortment were of large effect (causing α_opt to be ‘jumped over’) or of small effect (leading to relatively smooth evolution to α_opt).

When the genetic architecture of the trait under assortative mating is based on two epistatically interacting loci, a stable intermediate level of assortment still exists, although it has not yet been mapped to a corresponding maximization in a feature of the phenotype frequency. Evolution to an intermediate level of assortment occurs in a diploid version of the model (discussed further below) as well. The existence of this optimal level of assortment thus appears to be robust across a variety of model assumptions, although several interacting effects may be operating in more complicated versions of the basic model (see below).

The limitation of the evolution of assortative mating owing to the reduced effective sexual selection that results from very strong preference parameters has most probably been present in previous two-island models of the evolution of reproductive isolation, although it has rarely been noted, owing to a restriction of the exploration of the parameter space to weaker mating strength reflecting the initiation of divergence (e.g. [14,15,23]). Proulx & Servedio [16] point out these effects, which lead to a reduction of the rate of spread of an assortment allele in some of the models they examine (see their appendix). A similar effect to that demonstrated here was also noted by M'Gonigle & FitzJohn [24], who showed that intermediate preference strengths lead to the highest level of mosaic structure in a hybrid zone, again probably owing to rare individuals matching with rare mates.

Sexual selection generated by assortative mating has also been shown to have profound effects towards limiting speciation in models with different geography (e.g. sympatric speciation) or ploidy (diploidy), through a variety of mechanisms. Kirkpatrick & Nuismer [7], for example, demonstrated that assortative mating within one population may generate stabilizing sexual selection owing to rare individuals being at a disadvantage (i.e. positive frequency-dependent selection), making it harder for sympatric speciation to occur. Similarly, Bürger and co-workers [9,10,25] demonstrated that an intermediate level of assortment tends to deplete genetic variation in the trait that is the target of assortative mating, owing to the generation of locally stabilizing selection when rare types find it difficult to find mates (see also [35]). Although they did not study the evolution of assortment per se, they argue that this loss of variation would prevent further progress towards speciation. Using assortative mating by female preferences similar to that used in the current model, Matessi et al. [6] also find that the gradual evolution of assortative mating from random mating, based on a trait under disruptive selection, will stop at an intermediate level that is generally weak, although this could be countered by very strong selection against intermediate types (see also [26]). The mechanism causing the cessation of the evolution of assortative mating is not ascribed to sexual selection in their study.

Otto et al. [11] and Pennings et al. [12] point out that these types of effects imply that if assortative mating is generated by female preferences for a diploid trait under selection, stronger assortment would be much more likely to evolve in a scenario in which significant assortative mating is already established (perhaps secondary contact) than if assortative mating is evolving de novo (as in sympatric speciation). Specifically, these two models ascribe this to the fact that the presence of sexual selection favouring heterozygotes can cause the evolution of assortment to be self-limiting when heterozygotes are common, which is unlikely if strong assortative mating based upon this trait has already evolved. A preliminary analysis of a diploid version of the basic (no viability selection) model in the present paper confirms that once again there are conditions under which an intermediate level of assortment will evolve, although it is hard to know in this case if this is because of sexual selection for heterozygotes or because of the elimination of sexual selection with strong assortment as evidenced in the haploid case. The limitations of the evolution of assortment in the haploid case cannot, of course, be attributed to sexual selection for heterozygotes or other intermediate forms, which are absent in the haploid model. From the summary of these previous models, it is clear that there are several potential mechanisms that can account for the evolution of intermediate levels of assortative mating, and a need for further analyses of the ways in which these may interact.

Search costs are not included in the models in this paper. The assumption of strict polygyny assures that every female will mate, even if she is rare and therefore searching for a rare male. This assumption allows the identification of the effect of weakening sexual selection under strong preferences without the confounding effect of selection on rare types. If this assumption were broken, costs may be expected to be low even for rare females if population densities are high or migration rates are significant (‘rare’ will not be too rare). Whether assortative mating could evolve in this situation may depend on the biology of searching and the assumptions of the model; de Cara et al. [22] found that the spread of an allele for assortative mating was uniformly inhibited by direct selection when they assumed lower mating success of rare individuals (but see, e.g. [9]; interestingly, a version of de Cara et al.'s model that does not induce sexual selection finds that assortment always evolves to completion provided that disruptive viability selection on the trait is present, unlike in, e.g. [12]; intermediate levels of assortment are not found in de Cara et al.'s models). When densities and/or migration rates are very low in the presence of costs, rare females may not mate if assortment is very strong, leading to stronger sexual selection against rare male phenotypes. This would increase the positive frequency dependence that results from assortative mating and, depending on the strength of costs, ameliorate or reverse the reduction in this frequency dependence that is expected from the removal of sexual selection when preference strength becomes very strong. Thus, strong assortative mating would be expected to result in higher population-specific trait frequencies than seen in this paper if this type of cost was included. This would not, however, necessarily be expected to result in the spread of alleles for stronger assortative mating (e.g. [7]), since if mating is not assured, strong assortative mating would incur more direct costs to females than would weak assortative mating (e.g. [27,28] see also [29]). The further evolution of assortative mating may thus be expected to be impeded both without (as in the current version of the model) and with these costs.

The assortative mating studied in this model can best be described by the term ‘self-reference phenotype matching’ (see [30]), in which animals choose mates with matching traits. Similar outcomes could potentially result from animals sexually imprinting on parental phenotypes, although this warrants further study. Because the effective strength of sexual selection is such a critical component of the outcomes described in this paper, maternal imprinting would be expected to yield an outcome closer to the assortment modelled here than would paternal imprinting, which naturally generates stronger sexual selection (see [31,32]).

Bolnick [33] and Pennings et al. [12] point out that the existence of partial reproductive isolation does not necessarily imply that speciation is in the process of occurring. The findings of this paper strengthen the evidence that, in a number of different situations and via multiple possible mechanisms, an intermediate level of assortment may often tend to evolve. The complicated interactions that lead to the evolution of premating isolation, even in situations where it will evolve to a modest value, make this phenomenon of interest in its own right, not just as a proxy for the endpoint of speciation.

Appendix A

(a). Selection coefficients on a trait under assortative mating in a single population

By considering a single population in which a trait is under assortative mating it can be demonstrated that for a given trait frequency, there is a specific level of assortative mating that leads to the strongest directional selection on the trait. Using the notation of Barton & Turelli [20], I write the equation for relative fitness as

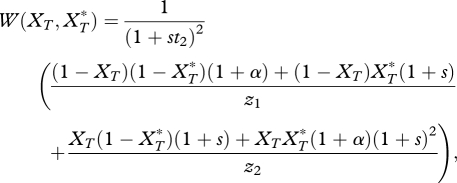A 1

where

Here X_T represents the T allele present in females, where X_T = 0 if T₁ is present and X_T = 1 if T₂ is present. The parallel values in males are denoted by an asterix. Equation (A 1) assumes that there is selection of strength s favouring the trait T₂ in both sexes in this population. By matching terms between equation (A 1) and eq. (6) of Barton & Turelli [20]; see description in appendix B of Kirkpatrick & Servedio [34]) it is possible to extract terms that measure, in each sex, the net strength of selection (caused by both natural and sexual selection) favouring allele T₂. The strength of this selection in males, a_0,T, can be shown to be

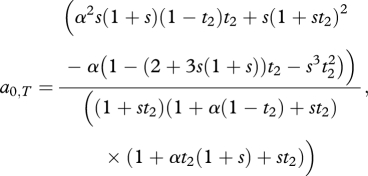A 2

(the strength of selection in females is simply a_T,0 = s/(1 + s t₂)). When s = 0, this is

A 3

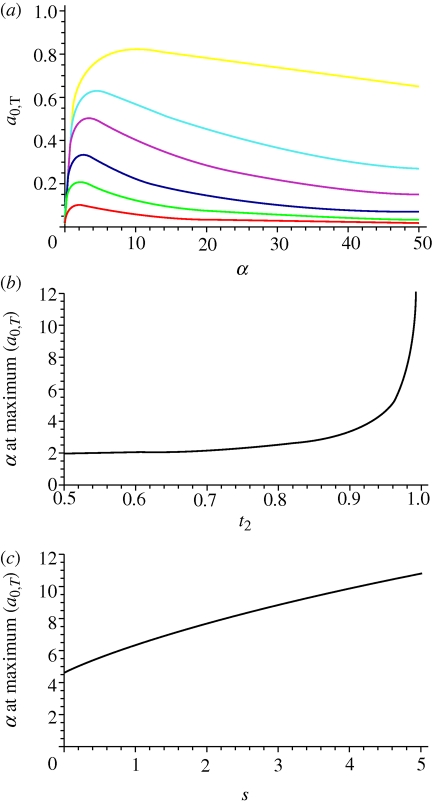
(in females a_T,0 = 0). Figure 5a shows that for a given frequency of t₂, expression (A 3), which is the strength of selection favouring T₂ (in this case solely owing to sexual selection since s = 0), peaks at an intermediate level of α. The position of the peak seems to move as t₂ changes. This can be confirmed by plotting the value of α that leads to the maximum of (A 3) as t₂ increases (figure 5b), demonstrating that for a higher t₂, the α leading to the strongest selection is higher. This can explain why α_opt decreases as migration increases in the model in the main text (figure 1); higher migration causes t₂ to be at a relatively lower level in the population in general, corresponding to a relatively lower expected level for the α that causes the strongest sexual selection on t₂.

Figure 5.

Evaluation of the strength of selection on T₂ in a single population. (a) Strength of selection on T₂ in males (a_0,T) as α changes, for different values of t₂, when s = 0. Black: t₂ = 0.5, red: t₂ = 0.6, green: t₂ = 0.7, blue: t₂ = 0.8, pink: t₂ = 0.9, light blue: t₂ = 0.95, yellow: t₂ = 0.99. (b) The value of α that leads to the peak strength of selection in males (a_0,T) with increasing t₂, with s = 0. (c) The value of α that leads to the peak strength of selection in males (a_0,T) with increasing s, with t₂ = 0.95.

When s ≠ 0, it can also be seen graphically that for a given t₂, the value of α leading to the maximum level for the strength of selection in males, a_0,T, increases as s increases (figure 5c). This is consistent with the results for the two population model in the main text. When t₂ is allowed to vary, higher s will also lead to a generally higher t₂. This will correspond to a relatively higher level of α causing the strongest sexual selection on t₂, in much the same way that lower migration rates lead to a similar effect.