On the coevolution of social responsiveness and behavioural consistency

Abstract

Recent research focuses on animal personalities, that is individual differences in behaviour that are consistent across contexts and over time. From an adaptive perspective, such limited behavioural plasticity is surprising, since a more flexible structure of behaviour should provide a selective advantage. Here, we argue that consistency can be advantageous because it makes individuals predictable. Predictability, however, can only be advantageous if at least some individuals in the population respond to individual differences. Consequently, the evolution of consistency and responsiveness are mutually dependent. We present a general analysis of this coevolutionary feedback for scenarios that can be represented as matrix games with two pure strategies (e.g. hawk-dove game, snowdrift game). We first show that responsive strategies are favoured whenever some individual differences are present in the population (e.g. due to mutation and drift). We then show that the presence of responsive individuals can trigger a coevolutionary process between responsiveness and consistency that gives rise to populations in which responsive individuals coexist with unresponsive individuals who show high levels of adaptive consistency in their behaviour. Next to providing an adaptive explanation for consistency, our results also link two key features associated with personalities, individual differences in responsiveness and behavioural consistency.

1. Introduction

Different behavioural types often coexist within single populations [1,2] and such types often exhibit behavioural consistency over time (e.g. types that are more aggressive as juveniles are also more aggressive as adults) and across contexts (e.g. types that are more aggressive towards conspecifics are also more aggressive towards predators). Both types of consistency indicate limited behavioural plasticity to a degree that, from an adaptive point of view, is often surprising [3–5]. Consider, for example, aggressive fishing spiders that tend to be highly successful in catching prey. Interspecific aggression, however, is correlated with intraspecific aggression, and aggressive females have a low mating success, since they tend to attack and cannibalize males before copulation [6]. In these and many other examples (e.g. [7–11]), one would expect a that a more flexible structure of behaviour that is fine-tuned to the local circumstances (e.g. being highly aggressive when confronted with prey, being only mildly aggressive when confronted with potential mates) should prove advantageous to individuals.

On a proximate level, behavioural consistency can often be understood in terms of the architecture of behaviour, that is, the genetic, physiological, neurobiological and cognitive systems underlying behaviour. This architecture gives rise to behavioural consistency whenever multiple traits are affected by a common underlying mechanism within this architecture. Such mechanisms are ubiquitous; examples include pleiotropic genes [12], hormones [13], neurotransmitters [14], emotions [15] and simple heuristics [16] affecting multiple traits at the same time. In the case of fishing spiders, for example, both inter- and intraspecific aggressiveness might be regulated by the same hormone. This would explain the correlation between inter- and intraspecific aggressiveness, but it would not explain why the dependence of the two traits on a single hormone has not been uncoupled in the course of evolution. In other words, why has natural selection not led to a more flexible architecture of behaviour?

Two types of adaptive explanations for behavioural consistency can be found in the literature [5,17], both of which are based on differences in states in combination with state-dependent behaviour (condition-dependent behaviour, phenotypic plasticity). The term state here refers to those features of the animal (e.g. morphological, physiological, neurobiological or environmental) that affect the cost and benefits of its behavioural actions and thus its optimal behaviour [18–20].

First, consistency in behaviour may reflect inherently stable states, that is, features that are very costly, time-consuming or even impossible to change. Examples include the sex, size or caste of an individual, or those parts of its (micro) environment that are stable over time. Whenever such states affect the optimal behaviour in a given context, the stability of such states can explain adaptive behavioural consistency in that context. It is interesting to note that also less apparent features of animals may act as inherently stable states in the above sense; examples include organ size [21], basal metabolic rates [22,23] and stress-response systems [24,25] with their associated physiological morphology, organizational features of the brain (e.g. strength of cerebral lateralization [26]) and cognitive mechanisms (e.g. learning ability [27]).

Second, consistency in behaviour may reflect states that are potentially much more labile over time but which are stabilized by positive feedback mechanisms between state and behaviour [28]. Rands et al. [29], for example, discuss a model where ‘leaders’ and ‘followers’ emerge as a consequence of differences in energy reserves that are stabilized by a positive feedback between energy reserves and foraging behaviour. Van Doorn et al. [30] develop a model in which domain general risk-prone and risk-averse behavioural types emerge as a consequence of positive feedbacks between the fitness expectations of individuals and their risk-taking behaviour. Several other feedback mechanisms have been described in the literature [17]. For example, an important positive feedback is caused by the fact that individuals often get better with increased experience [31], that is, processes like learning, training and skill formation give rise to lower costs or higher benefits for the same behavioural pattern when repeated, which in turn favours consistency in this behaviour [32].

In this study we focus on a third explanation, which is based on the idea that individuals can benefit from being predictable in particular types of social interactions. Such situations may select for adaptive behavioural consistency. The simplest examples come from situations where the actions of social partners have to be coordinated. Car drivers, for example, could in principle choose to drive on either side of the road, giving rise to inconsistent behaviour over time. Consistently choosing the same side of the road, however, proves advantageous, since it makes individuals predictable and thus helps to solve the coordination problem. As we will show in this paper, predictability can also be beneficial in conflict situations. Individuals might, for example, consistently put little effort into a joint project (e.g. parental care, group-foraging) and thus ‘force’ their partner to put more effort into that project.

Behavioural consistency may thus be advantageous in social interactions because it makes individuals predictable. This argument clearly hinges on the presence of socially responsive individuals which, when choosing their action, take into account the behavioural history of their social partners. Recent studies have shown that the presence of responsive (reactive, socially aware, eavesdropping) individuals can indeed fundamentally change the selective pressures for the traits they respond to. The presence of responsive strategies, for example, promotes increased levels of aggression in the hawk-dove game [33] and is crucial for stabilizing cooperative strategies in the Repeated Prisoner's Dilemma [34], for the build-up of trust and trustworthiness [35], and for the stability of monitoring and policing [36].

But what determines the benefits and therefore the presence of responsive individuals? The benefits of employing a responsive strategy depend on two factors: variation and consistency [33,35,37]. Without variation among individuals, there is no need to be responsive. Whenever there is variation among individuals, responsiveness is beneficial only if individuals are consistent (otherwise past behaviour does not help to ‘predict’ future behaviour).

Consistency may thus select for responsiveness, which, given our above arguments, may favour consistency. We therefore expect a positive, self-reinforcing feedback loop between consistency and responsiveness [3]: the more consistent individuals are, the more beneficial a responsive strategy is, which in turn favours consistency. A potentially small amount of individual differences (e.g. due to mutation or drift) may thus trigger a coevolutionary process that gives rise to polymorphic populations in which responsive individuals coexist with unresponsive individuals who show high levels of adaptive behavioural consistency.

In what follows, we develop a simple evolutionary model to investigate these verbal arguments. We model pairwise interactions between individuals in which the benefits to an individual depend both on its own action and on the action taken by its partner. We focus on those scenarios that can be represented as matrix games with two pure strategies (e.g. aggressive encounters in the hawk-dove game, cooperative interactions in the snowdrift game). Individuals in our model can either adopt a responsive or an unresponsive strategy. When choosing an action, responsive individuals take the behavioural history of their social partners into account, whereas unresponsive individuals do not. We first investigate the conditions under which responsive strategies can spread in a population of unresponsive individuals. We then study whether the presence of responsive individuals does indeed trigger a coevolutionary process between consistency and responsiveness and whether this process gives rise to adaptive behavioural consistency among unresponsive individuals.

2. Model and results

(a). Set-up of basic model

We consider an evolving population in which individuals are engaged in a large number of rounds of pairwise interactions with other individuals in the population. In each round, individuals within the population are randomly matched with a social partner. Within any interaction, individuals can adopt one out of two actions, payoffs are obtained according to the payoff matrix

2.1

where a_ij is the payoff to an individual who adopts action i when matched with an individual who adopts action j. The strategy of an individual is given by a single number p, 0 ≤ p ≤ 1, which corresponds to the probability with which an individual chooses action 1 in any of the interactions.

Behavioural consistency in our model corresponds to the degree to which individuals show the same behaviour in subsequent interactions, the most consistent strategies are thus p = 1 (‘always choose action 1’) and p = 0 (‘always choose action 2’). One of the questions we want to ask is whether the presence of responsive individuals gives rise to high levels of consistency, we will thus focus on scenarios in which, in the absence of responsive individuals, mixed strategies (0 < p < 1) are played at evolutionary equilibrium. In other words, we focus on scenarios in which none of the pure strategies are evolutionarily stable, that is scenarios where action 2 can invade a population of individuals that always adopt action 1 and vice versa:

2.2

A simple calculation shows (electronic supplementary material) that at the evolutionary equilibrium, the frequency at which action 1 is adopted in each round is given by

2.3

(b). Example: aggressive interactions in the hawk-dove game

The classical example with a mixed strategy equilibrium is the hawk-dove game for aggressive interactions [38]. Individuals fight for a resource of value V and can choose between an aggressive ‘hawk’ and a non-aggressive ‘dove’ strategy. The payoff to the row-player is given by

2.4

where D > V is the cost of injury during an aggressive hawk–hawk interaction. The equilibrium frequency (equation 2.3) of hawks is given by f* = V/D.

(c). Evolutionary equilibrium

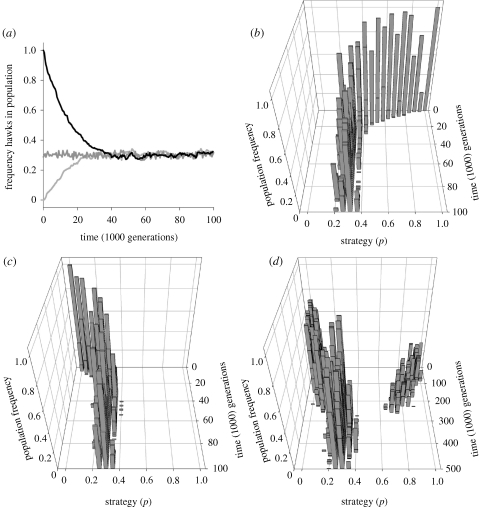
At evolutionary equilibrium, the frequency of action 1 in each of the interactions is given by equation (2.3). Equation (2.3), however, only specifies a population-level equilibrium frequency, and not the full distribution of strategies among individuals in the population [38]. The resulting equilibrium could be monomorphic, meaning that all individuals play the mixed strategy p = f*, but it could also be polymorphic, for example, a fraction f* of the individuals always plays the pure strategy 1 (p = 1) and a fraction (1 − f*) of the individuals always plays the pure strategy 2 (p = 0). Hence, the resulting population can either consist of behaviourally inconsistent individuals (all individuals play same mixture p) or a mixture of consistent individuals. However, as our individual-based simulations show (figure 1), in the absence of responsive individuals there is an evolutionary trend towards behaviourally inconsistent individuals playing p = f* [39].

Figure 1.

Three individual-based simulations for our basic model. Each generation, individuals within a population of size 5000 are engaged in 50 hawk-dove interactions with V = 0.3 and D = 1.0. Reproductive success of individuals is proportional to the sum of the payoff accumulated in these interactions. During clonal reproduction, individuals pass on their strategy to their offspring, mutations occur with probability 0.005, the effects of mutations on the strategy are drawn from a normal distribution with mean 0 and variance 0.005. (a) In all simulations, the average frequency of hawks rapidly converges to the equilibrium value V/D = 0.3. Individuals in the ancestral populations in our simulations are highly consistent. In (b) individuals always choose action 1; in (c) individuals always choose action 2; in (d) we start with a dimorphic population at its equilibrium frequency V/D. Irrespective of their ancestral state, all populations evolve towards the monomorphic equilibrium at which individuals show inconsistent behaviour in repeated interactions. In all cases, variation is maintained in the populations due to mutation and genetic drift.

It can also be seen from figure 1 that at evolutionary equilibrium, mutation and drift give rise to some amount of variation among individuals. As we will now show, responsiveness should be favoured in such a situation since responsive (reactive, socially aware, eavesdropping) individuals, who adapt their behaviour in response to the partner they face, are able to exploit this variation.

(d). Variation favours social responsiveness

Consider first, for the sake of the argument, a responsive individual who has perfect knowledge about the strategy p of its opponent (figure 2). When confronted with an opponent with strategy p, the expected payoffs to action 1 (E₁) and action 2 (E₂) are then given by

2.5

Figure 2.

Variation favours responsiveness. For the special case of a hawk-dove game, (a) illustrates the linear frequency dependence of the payoffs of the pure strategies. Hawks (black line) receive a higher payoff than doves (grey line) against opponents with p < V/D and the converse holds for opponents with p > V/D. (b) Consequently, responsive individuals should play hawk when p < V/D and dove otherwise. (c) By adopting this strategy, responsive individuals (black line) receive a higher payoff than any unresponsive individual (grey line) p_u against all opponents except opponents with p = V/D. U(p_u) = 1/2 · V · (1 + p_u) and L(p_u) = 1/2 · p_u · (V − D).

The payoff difference Δ between actions 1 and 2 is thus given by

2.6

with

2.7

The payoff difference thus strictly decreases in p and changes sign from positive to negative at p = f* (figure 2a). Consequently, depending on the strategy p of its opponent, the best strategy for the responsive individual is to adopt (figure 2b)

2.8

with corresponding payoffs (figure 2c)

2.9

Compare this with any unresponsive individual with strategy p_u that plays against the same opponent. Such an individual obtains the expected payoff (figure 2c)

2.10

The payoff difference between a responsive and an unresponsive individual is thus given by

2.11

which is strictly positive (figure 2c) whenever the opponent does not play p = f*. Consequently, responsive individuals with perfect knowledge obtain a higher payoff than unresponsive individuals whenever the population is not at its monomorphic equilibrium (p = f*).

In natural situations individuals do of course not have perfect knowledge about the strategy of their opponent. Even without perfect information, however, a responsive individual can get some information about the strategy of its opponent by observing its past behaviour. For a long sequence of observations, this information would be close to perfect. We will now show that even a particularly simple responsive strategy that takes into account only the last interaction of its partner, conveys sufficient information about the opponent's strategy to be favoured by selection.

(e). Socially responsive individuals invade whenever sufficient variation is present

To illustrate this point, we now consider our basic model and allow for both unresponsive and responsive strategies. The strategy of unresponsive individuals is, as above, given by a single number p, 0 ≤ p ≤ 1 that determines the probability with which an individual chooses action 1 in each of its interactions. Responsive individuals take into account the last interaction of their partner and choose their behaviour according to a simple eavesdropping strategy [33]: ‘choose action 1 if opponent chose action 2 in its last interaction, otherwise choose action 2’. We assume that being responsive is costly and reduces the payoff of responsive individuals per interaction by c, one might think here, for example, of the cognitive recourses (e.g. memory) needed by responsive individuals.

Let us first investigate the invasion prospects of a responsive individual in a population of unresponsive individuals. Let us assume that the population of unresponsive individuals evolved to their evolutionary equilibrium, that is, the fraction of individuals that choose action 1 per game is given by equation (2.3). As discussed above (figure 1), this equilibrium population will typically not be fully monomorphic. Let denote the variance in the trait p of the unresponsive individuals at that equilibrium. As we show in the electronic supplementary material, the expected payoff difference between a responsive and an unresponsive individual in such a population is given by:

2.12

per interaction, where δ > 0 is given by the above equation (2.7). Responsive individuals can thus invade a population of unresponsive individuals whenever the variation present in this population is large enough, that is

2.13

(f). Coexistence of responsive and unresponsive individuals

If equation (2.13) is satisfied, responsive individuals can invade a population of unresponsive individuals. They will, however, not go to fixation. To see this, consider a population of responsive individuals. Such individuals always respond with action 1 to opponents that adopted action 2 in their last round and vice versa. As a consequence, after sufficiently many rounds, responsive individuals will always adopt action 1 with probability of one-half (see the electronic supplementary material), the corresponding expected payoff is, thus .

In view of the above assumption (equation 2.2), either a₁₂ or a₂₁ is the maximal payoff and this maximal payoff can be obtained by unresponsive individuals. If a₁₂ (a₂₁) is the maximal payoff, unresponsive individuals that play the pure strategy 1 (2) obtain that payoff, since responsive individuals always respond with action 2 (1) to this individual. In fact, as we show in the electronic supplementary material, all unresponsive individuals with can invade a population of responsive individuals.

It follows that at any evolutionary equilibrium, both responsive and unresponsive individuals must be present in the population. This coexistence is maintained by negative frequency dependence: when confronted with an unresponsive individual, responsive individuals do better than unresponsive individuals since they can fine-tune their behaviour to the unresponsive opponent. When confronted with a responsive individual, however, unresponsive individuals do better than responsive individuals since, by choosing the right pure strategy, they can always obtain the maximal payoff in these interactions.

(g). Presence of responsive individuals selects for consistency

Consistency is beneficial whenever an unresponsive individual interacts with a responsive individual. To see this suppose the unresponsive individual has chosen action 1 in its last interaction, the responsive individuals will thus respond with action 2. Since a₁₂ > a₂₂, the unresponsive individual should adopt action 1 again. Conversely, since a₂₁ > a₁₁, unresponsive individuals who chose action 2 in their last interaction should adopt action 2 again. The presence of responsive individuals thus selects for consistency.

To make this point more precise, let us denote the expected payoff of an unresponsive individual p against a responsive individual by W_u,r(p). This payoff is strictly convex in the strategy p of the unresponsive individual (see the electronic supplementary material and figure 3), with a minimum at

In other words, unresponsive individuals obtain the maximal payoff against responsive individuals at either of the highly consistent strategies p = 1 or p = 0, both of which are a local payoff maximum.

Figure 3.

Responsive individuals select for consistency, illustrated for the special case of a hawk-dove game. The payoff that an unresponsive individual obtains in an interaction with a responsive individual is strictly convex in the strategy p of the unresponsive individual. Consequently, consistent strategies are favoured over inconsistent strategies, local payoff maxima occur at p = 0 or p = 1, which selects for highly consistent behaviour.

(h). Evolutionary equilibrium

Two conclusions follow from our analysis so far: first, at any evolutionary equilibrium, unresponsive individuals will coexist with responsive individuals, and second, in interactions with responsive individuals, unresponsive individuals with inconsistent behaviour are outperformed by behaviourally more consistent individuals. This provides the intuition for our result (electronic supplementary material) that, at any evolutionary equilibrium, unresponsive individuals will always employ strategies that give rise to highly consistent behaviour, that is p* = 0 or p* = 1.

As a consequence of this result, there are only three candidate evolutionary equilibria, two dimorphic equilibria in which responsive individuals coexist with one unresponsive type (p = 0 or p = 1) and a trimorphic equilibrium at which responsive individuals coexist with two unresponsive types (p = 0 and p = 1). As we show in the electronic supplementary material, both dimorphic candidates are evolutionarily unstable: the dimorphic equilibrium in which unresponsive individuals always adopt action 1 (p = 1) can be invaded by unresponsive individuals that always adopt action 2 (p = 0) and vice versa. Thus, at evolutionary equilibrium, the population must be composed of three behavioural types: responsive individuals and two unresponsive types who show highly consistent behaviour, that is p* = 0 and p* = 1.

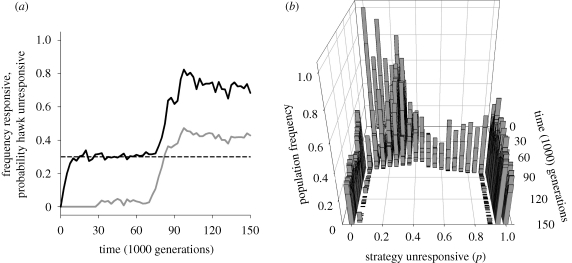
These analytical results are confirmed by our individual-based simulations. Figure 4 shows an example for the case where the interactions correspond to hawk-dove games. To illustrate the effect of responsive individuals, we did not allow for responsive individuals during the first 30 000 generations. During the first few thousand generations, the population frequency of hawks rapidly converges to the predicted equilibrium value for unresponsive individuals (figure 4a), which is indicated by the black hatched line. As we have already seen in figure 1, variation among individuals is a typical feature of such an equilibrium (figure 4b). From 30 000 generations onwards, we allow rare mutations that give rise to responsive individuals. As predicted, these individuals increase in frequency over time (figure 4a, grey line). The presence of responsive individuals, in turn, selects for behavioural consistency among unresponsive individuals (figure 4b): inconsistent behavioural strategies are outperformed by more consistent strategies and, at evolutionary equilibrium, responsive individuals coexist with two types of highly consistent unresponsive individuals that either always adopt the hawk or dove behaviour.

Figure 4.

Evolution of adaptive behavioural consistency. Individual-based simulation with parameter values as in figure 1. After 30 000 generations, we allow rare mutations (mutation rate 0.005) that give rise to responsive individuals. (a) Responsive individuals increase in frequency over time (grey line) and select for an increased frequency of hawks among unresponsive individuals (black line). (b) As predicted from our analysis in the main text and figure 3, the presence of responsive individuals favours high levels of consistency among unresponsive individuals. At evolutionary equilibrium, responsive individuals coexist with unresponsive individuals that either always play hawk (p = 1) or always play dove (p = 0).

In summary, responsiveness and consistency in social interactions may often be coupled by a self-reinforcing feedback loop [3]: the more consistent individuals are, the more beneficial a responsive strategy is. In other words, a mixture of consistent individuals playing different strategies is prone to invasion by responsive individuals. We have seen that a small amount of individual differences (e.g. due to mutation and drift) indeed selects for the presence of responsive individuals [3,35,37]. The presence of responsive individuals, in turn, selects for consistency in behaviour among unresponsive individuals. As a result, evolution gives rise to populations in which inconsistent (responsive) behavioural types coexist with unresponsive behavioural types that show high levels of adaptive behavioural consistency.

3. Discussion

(a). Scope and limitations of results

In this study we focused, for simplicity, on interactions that can be described as matrix games with two pure strategies as, for example, the hawk-dove game. One of the standard models of cooperation, the snowdrift game [40], is also captured by our set-up (equation 2.1) and our results do equally apply in this game. We do not expect, however, that our explanation of behavioural consistency is restricted to these situations. There are two key steps in our arguments.

First, responsiveness is favoured in populations of unresponsive individuals. This will be the case whenever there exists variation (e.g. due to mutations and drift) among unresponsive individuals which fulfils two criteria. First, variation must be consistent, since otherwise, nothing can be gained by taking the past behaviour of social partners into account. Second, the optimal response to different individuals must differ, since otherwise, nothing can be gained by being responsive. Whenever both conditions are fulfilled, responsive strategies should be favoured in populations of unresponsive individuals.

Second, the presence of responsive individuals selects for behavioural consistency among unresponsive individuals. This will certainly not always be the case. Consider, for example, a situation where the pairwise encounters in our model corresponds to a rock-scissors-paper game [38,41]. Individuals have the choice between the three actions ‘rock’, ‘scissors’ and ‘paper’ with intransitive fitness interactions: in any pairwise interaction, rock beats (i.e. obtains a higher payoff than) scissors, scissors beats paper and paper beats rock. As in our model, consistent individual differences should favour the presence of responsive individuals, since the best response to different actions differs. We do, however, not expect that the presence of responsive individuals favours consistency in this situation. Suppose, for example, that individual A played rock in the past, a responsive partner should thus choose the best response to rock, which is paper. As a consequence, A should deviate from its past action and choose scissors. In other words, the presence of responsive individuals in the rock-scissors-paper game does not select for consistent but for inconsistent behaviour among unresponsive individuals. Intuitively, responsive individuals should select for unpredictable behavioural patterns whenever predictable individuals can be exploited. One might think, for example, of (i) prey species trying to avoid the exploitation by predators; (ii) foraging in groups where individuals try to avoid the exploitation of their search effort and information; and (iii) contest situations where individuals try to avoid that rivals develop an effective counter-strategy.

When then, do responsive individuals select for behavioural consistency among unresponsive individuals? Suppose that an individual has chosen action x in its last interaction and that this action has been observed by its current partner, who chooses the best response b(x) to its observation. Consistency is favoured in such a situation whenever x = b(b(x)), that is, whenever x is the best response to the best response of x. This condition is satisfied in games like the hawk-dove game and the snowdrift game: hawk is the best response to dove which is the best response to hawk (and vice versa). Intuitively, predictability is beneficial in at least two types of social interactions. First, whenever the actions of partners have to be coordinated, predictability is beneficial since it promotes this coordination. Examples include cooperative foraging behaviour in groups and collective defensive behaviour. Second, whenever individuals have an incentive to avoid certain outcomes, predictability is favoured since it promotes this avoidance. Examples include aggressive interactions in the hawk-dove game (individuals have an interest to avoid the costly hawk–hawk interactions), cooperative interactions in the snowdrift game (individuals have an interest to avoid the costly defect–defect outcome) and parental care (both parents have an interest to avoid the outcome where none of the parents cares).

In anti-coordination games like the hawk-dove game and the snowdrift game, players benefit from using a different action than their co-player. A traditional idea about such games [42,43] is that there may be a role asymmetry (e.g. ‘owner’ and ‘intruder’) and that players condition their actions on their role (e.g. ‘Bourgeois strategy’: play hawk when owner, play dove when intruder). It is interesting to note that the here discussed polymorphism between responsive and consistent individuals has a similar effect as a role asymmetry by increasing the frequency of interactions where players use different actions.

(b). Testability

On first sight it may seem that our model predicts that responsive and consistent individuals are particularly likely to coexist in social animals. This need not be the case since our model applies only to situations that favour predictability. Social interactions, however, can select for both predictable but also unpredictable behavioural patterns (see above).

As discussed above, predictability should be favoured whenever individuals (i) have to coordinate their actions or (ii) have a mutual interest to avoid certain outcomes. In such situations we would predict a mixture of behaviourally consistent unresponsive individuals, who exhibit stable behavioural patterns over time, and responsive individuals, who adjust their behaviour according to their social partners. Interestingly, recent research suggests that differences in responsiveness might be widespread in the animal kingdom. In rodents, for example, certain individuals adjust their aggressiveness with social context, whereas others do not [24]. Similar differences have been described in several other species including birds [44–46], pigs [47] and humans [48,49]. At present it is not well understood how such differences can be maintained by natural selection. Our model provides a clear-cut and testable explanation for these observations. Responsive individuals are predicted to foster either coordination or avoidance of certain outcomes in social interactions.

(c). Consistency in the absence of responsive strategies

As just discussed, in order for responsiveness to be favoured, the variation present among unresponsive individuals has to be consistent in the sense that the past behaviour of an individual is (to a potentially very small extent) predictive for its future behaviour. In our model, this ‘baseline consistency’ is caused by the assumption that individuals use the same strategy p in all interactions: any potentially small difference in p thus gives rise to a small degree of predictable differences among individuals which, in turn, can be exploited by responsive individuals. In principle, one could envisage an analysis based on a model without this baseline consistency, the strategy of individuals in such a model would then be given by N numbers, where the n-th number gives the behavioural tendency of an individual during its n-th interaction. We do, however, not expect qualitatively different results from such a more complicated model. As in our model, unresponsive individuals would differ due to mutation and drift. At any point in time, owing to chance, these differences might either be consistent or inconsistent, that is there is a positive or a negative correlation among the behavioural actions used in different rounds. In periods where consistency is present, responsiveness should be favoured which, in turn, should trigger the same evolutionary process leading to high levels of adaptive consistency as in our model.

(d). Responsive strategy

In our model we focused on a particularly simple responsive strategy [33] that takes into account only one interaction of its opponent and responds in a very simple manner (‘choose action 1 if opponent chose action 2 in its last interaction, otherwise choose action 2’). In principle, responsiveness can be accomplished with different and potentially much more complex strategies. Responsive individuals may, for example, respond with a mixed strategy 0 < z_i < 1 (i = hawk, dove) to a given observation (responsive individuals in our model always respond with a pure strategy). Alternatively, responsive individuals may take into account more than one behavioural action of their opponent. We do not expect, however, that our results depend on the specific implementation of responsiveness.

Consider first our result that responsive strategies can invade a population of unresponsive individuals. Here, our assumption on responsiveness can be seen as a conservative approach since whenever our simple and behaviourally rigid strategy invades, a more complex and flexible strategy should also be expected to invade.

Consider next our result that an unresponsive strategy can invade a population of responsive individuals. In our model responsive individuals always respond with a pure strategy. As a consequence, after sufficiently many rounds, responsive individuals will adopt action 1 with frequency one-half (see the electronic supplementary material). In other words, because of their constrained behaviour, responsive individuals cannot play the equilibrium frequency (equation (2.3)), favouring the invasion of unresponsive individuals. However, even if responsive individuals employ a more complex strategy that allows them to play the equilibrium frequency, then unresponsive individuals will still outperform responsive individuals provided that there is a cost to responsiveness: unresponsive individuals can play the equilibrium frequency, exactly as responsive individuals do, but without paying a cost of responsiveness.

We also assumed, for simplicity, that responsive individuals have perfect information about their opponent's behaviour in their last interaction. Analogous results, however, can be derived for situations in which this information is imperfect or responsive individuals make errors in responding to this information.

(e). Importance of variation

It has recently been demonstrated that the presence of a potentially small amount of variation in social contexts can trigger coevolutionary processes between responsiveness and the ‘monitored’ traits, that give rise to unexpected evolutionary outcomes. Variation in trustworthiness [35], for example, favours socially aware individuals that trust on the basis of prior trustworthy behaviour. The presence of socially aware individuals, in turn, gives rise to disruptive selection on the trustworthiness of individuals, resulting in the coexistence of trustworthy and untrustworthy individuals. Similarly, variation in cooperativeness favours choosiness among individuals which, in turn, can select for unexpectedly high levels of cooperation in the population [37].

Our results provide yet another example for the drastic effect that a small amount of initial variation can have on the expected evolutionary outcome, in our case, on the behavioural consistency of individuals. In the absence of sufficient variation, individuals in our model evolve a mixed strategy which gives rise to inconsistent behaviour in repeated social interactions. Whenever sufficient variation among individuals is present, however, a coevolutionary process between responsiveness and consistency is triggered which, in turn, gives rise to populations in which responsive individuals coexist with unresponsive individuals who show high levels of adaptive consistency in their behaviour. Interestingly, our explanation for behavioural consistency thus requires the presence of inconsistent (responsive) individuals, since it is precisely the presence of these individuals that makes consistency beneficial.