Running backwards: soft landing–hard takeoff, a less efficient rebound

Abstract

Human running at low and intermediate speeds is characterized by a greater average force exerted after ‘landing’, when muscle–tendon units are stretched (‘hard landing’), and a lower average force exerted before ‘takeoff’, when muscle–tendon units shorten (‘soft takeoff’). This landing–takeoff asymmetry is consistent with the force–velocity relation of the ‘motor’ (i.e. with the basic property of muscle to resist stretching with a force greater than that developed during shortening), but it may also be due to the ‘machine’ (e.g. to the asymmetric lever system of the foot operating during stance). Hard landing and soft takeoff—never the reverse—were found in running, hopping and trotting animals using diverse lever systems, suggesting that the different machines evolved to comply with the basic force–velocity relation of the motor. Here we measure the mechanical energy of the centre of mass of the body in backward running, an exercise where the normal coupling between motor and machine is voluntarily disrupted, in order to see the relevance of the motor–machine interplay in human running. We find that the landing–takeoff asymmetry is reversed. The resulting ‘soft landing’ and ‘hard takeoff’ are associated with a reduced efficiency of positive work production. We conclude that the landing–takeoff asymmetry found in running, hopping and trotting is the expression of a convenient interplay between motor and machine. More metabolic energy must be spent in the opposite case when muscle is forced to work against its basic property (i.e. when it must exert a greater force during shortening and a lower force during stretching).

1. Introduction

Legged terrestrial locomotion results from the coupling of a motor (the muscular system) and a machine (the skeletal lever system of the limbs). The function of the motor is to produce mechanical energy, when muscle shortens and the muscular force performs positive work, and to absorb mechanical energy, when active muscle is forcibly lengthened and the muscular force performs negative work. Primary muscle length changes, similar to the displacement of the pistons in a car engine, are not suitable to sustain locomotion directly. Both during positive and negative work, muscle length changes are applied through tendons to the lever system of the limbs, which interacts appropriately with the different surroundings to promote different kinds of locomotion.

Although the machine (i.e. the skeletal lever system of the limbs) differs widely between animal species according to the diverse kinds of locomotion and surroundings, the motor operating the different machines (i.e. the skeletal muscle) has remained largely the same throughout evolution, maintaining, from frogs to humans, its basic property to resist stretching with a force greater than that developed during shortening, the difference increasing with the velocity of the length change as described by the force–velocity relation of muscle [1].

Recent studies have shown that in humans running at low and intermediate speeds [2], hopping kangaroos and springhares, and running birds, trotting dogs, rams and a monkey [3], where a stretch–shorten cycle of muscle–tendon units takes place each step during the rebound of the body, the different machines act in accordance with the asymmetric response of their motor, allowing a greater force applied for a shorter duration during stretching after landing, and a lower force applied for a longer duration during shortening before takeoff.

This ‘landing–takeoff asymmetry’ appears to be greater the greater the length change of muscle relative to that of tendon during the stretch–shorten cycle [2,4]. If the force were so high and the muscle so stiff as to be kept in a state of isometric contraction, the whole of the length change during stretching would be taken by the elastic structures of tendon, and both duration and force could be equal during stretching and shortening, as in the elastic rebound of a symmetric spring–mass system [5]. From this point of view, therefore, the landing–takeoff asymmetry is the expression of a less economical bounce. In fact, the mechanical efficiency (i.e. the ratio between positive work production and metabolic energy expenditure) was found to be greater in hopping and at high running speeds in humans when the landing–takeoff asymmetry was reduced or absent [6,7].

On the other hand, of course, the difference between the average forces developed during stretching and during shortening depends not only on the difference in force developed by each active muscle fibre when it is forcibly lengthened or allowed to shorten according to the force–velocity relation of its contractile component, but also on the number of fibres activated by the central nervous system during stretching and shortening. Fewer fibres could be activated during stretching and more fibres could be activated during shortening in such a way as to compensate for the different forces exerted by each fibre in the two conditions, resulting in the same average force during stretching and shortening (i.e. in a symmetric rebound). However, this strategy is usually not followed: when muscle length change contributes to the length change of the whole muscle–tendon unit, the asymmetric rebound seems to be the more convenient procedure to follow.

During running on the level at a constant average speed, the absolute amount of negative work done when muscle–tendon units are stretched during the brake equals that of positive work done when muscle–tendon units shorten during the push. Since work is force times displacement, the greater force developed during the brake implies a displacement of the centre of mass of the body in the sagittal plane that is smaller during negative work than during positive work.

We hypothesize that the machine (i.e. the different lever systems of the limbs operating in the different kinds of bouncing gaits), allows the asymmetric rebound by making the displacement of the centre of mass of the body smaller during negative work than during positive work.

In human running, the adaptation of the machine to this goal is, at least qualitatively, consistent with the asymmetric lever system of the human foot, since the moment arm between heel and ankle operating after landing (brake) is shorter than the moment arm between ankle and toe operating before take-off (push [8]), even if other joints may contribute to the asymmetric rebound.

In this study, we measured the landing–takeoff asymmetry in backward running (i.e. in an exercise where the normal coupling between motor and machine, phylogenetically adapted to forward running, is voluntarily disrupted). The dissociation between motor and machine in backward running gives an indication of their relative roles in causing the landing–takeoff asymmetry and shows whether (and, if so, how) the stretch–shorten cycle and the mechanical work and power output differ in the two conditions.

2. Material and methods

(a). Subjects and experimental procedure

Backward running is an unnatural way of locomotion, usually practised for training otherwise unused muscles in normal running and for recovering from injuries occurring in normal running while maintaining training. Scattered results may be obtained when a naive subject begins to practise it. For this reason, the athletes who came to our laboratory from several cities in Italy to serve as subjects for this study had all practised backward running for several years (on average 6 years) of weekly training. Experiments were carried out on seven males (four of whom were elite runners) and two females. Informed, written consent was obtained from each subject. The experiments were carried out in accordance with the Declaration of Helsinki. The characteristics of the nine subjects were: age 43.7 ± 5.8 years, height 1.69 ± 0.07 m and weight 65.9 ± 8.2 kg (mean ± s.d.; n = 9).

The subjects ran at different speeds in an indoor track 56 m long where a strain-gauge force platform sensitive to the forward and vertical component of the force exerted by the feet on the ground was placed at the level of the floor 30 m from one extreme of the track. The force platform dimensions (4 m long and 0.5 m wide) were large enough to avoid subjects altering their stride in an attempt to hit the force plate and allowed records of several complete steps of each run. Other characteristics of the force platform were described previously [9]. Two photocells placed approximately 3 m apart along the side of the platform were used to measure the average running speed, 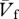. The height of the photocells was set at the level of the neck to prevent interference with the upper limb movements.

The runners were asked to achieve and maintain a constant average speed over the platform. To this end, the subjects started to run at a distance from the platform that increased with the speed to be attained, and were invited to continue running well after the end of the platform. Subsequent runs started from opposite sides of the track.

Subjects begun to run forward or backward at their most comfortable speed. The subjects were then invited to run at speeds lower and/or greater than the freely chosen speed. The speed range in backward running was 3–17 km h⁻¹. The maximal backward running speed was limited by our recommendations to maintain security and feel comfortable. For comparison we analysed runs made by the same subjects during forward running over a similar speed range. When a number of runs considered to be sufficient to adequately cover the whole speed range was acquired during running in one direction (e.g. forward running), the same experimental procedure was adopted for running in the other direction (e.g. backward running).

(b). Data acquisition

The photocells signal and the platform signals, proportional to the ground reaction forces F_v and F_f, were acquired at a rate of 500 Hz through a dedicated DAQ board (PCI MIO 16E, National Instruments, Austin, TX, USA) on a microcomputer. Custom LabVIEW (v. 7.1, National Instruments, Austin, TX, USA) software programs were developed for data acquisition and analysis. The platform signal from the unloaded force platform was measured immediately before each run and subtracted from the platform records of the vertical force, F_v, and fore–aft force, F_f, in order to account for a possible drift of the base line. Only the subset of the F_v and F_f records between photocells crossing were used for subsequent analysis. The time-average of the vertical force platform record 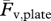was measured after each run over an integer number of steps and compared with the subject weight measured with a balance F_v,scale in order to check the regularity of the acquired steps. We analysed runs where 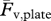/F_v,scale was 1.006 ± 0.015 (mean ± s.d. n = 211). The velocity changes of the centre of mass of the body in the vertical and forward directions were determined after each run by integration of F_v and F_f records, and saved for subsequent analysis along with subject mass, exact photocells distance, plate/balance weight, 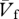and sampling interval.

(c). From velocity changes to mechanical energy of the centre of mass

Previous studies [9,10] describe in detail the procedure followed to determine from the velocity changes recorded during the experiment, the instantaneous vertical velocity V_v(t) and forward velocity V_f(t) of the centre of mass, the kinetic energy of vertical motion E_kv(t) = 0.5M_bV_v(t)² (where M_b is the mass of the body), the kinetic energy of forward motion E_kf(t) = 0.5M_bV_f(t)², the gravitational potential energy E_p(t) = M_b gS_v(t) (where S_v(t) is the vertical displacement of the centre of mass and g is the acceleration of gravity), and the total mechanical energy E_cm(t) = E_kv(t) + E_kf(t) + E_p(t) (figure 1). The work done at each step against gravity, W_v, to sustain the forward velocity changes, W_kf, and the total mechanical energy changes of the centre of mass, W_ext, were measured from the E_p(t), E_kf(t) and E_cm(t) records. Positive values of the energy changes gave positive work and negative values gave negative work. In a perfect steady run on the level, the ratio between the absolute values of positive and negative work done in an integer number of steps should be equal to one. The regularity of the selected steps was therefore assessed from the ratio between positive and negative work: only steps where 0.8 < 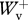/ 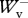< 1.2, 0.6 < 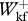/ 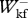< 1.5 and 0.8 < 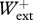/ 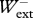< 1.2 were used for analysis, resulting in 107 usable runs in the backward direction and 104 usable runs in the forward direction. Average experimental values were as follows: 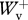/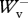=0.987 ± 0.077, 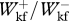= 0.997 ± 0.163, 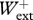/ 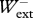= 0.997 ± 0.084 (mean ± s.d.; n = 107) for backward running, and 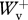/ 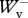= 0.969 ± 0.068, 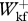/ 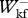= 1.049 ± 0.164, 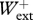/ 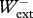= 0.995 ± 0.070 (mean ± s.d.; n = 104) for forward running.

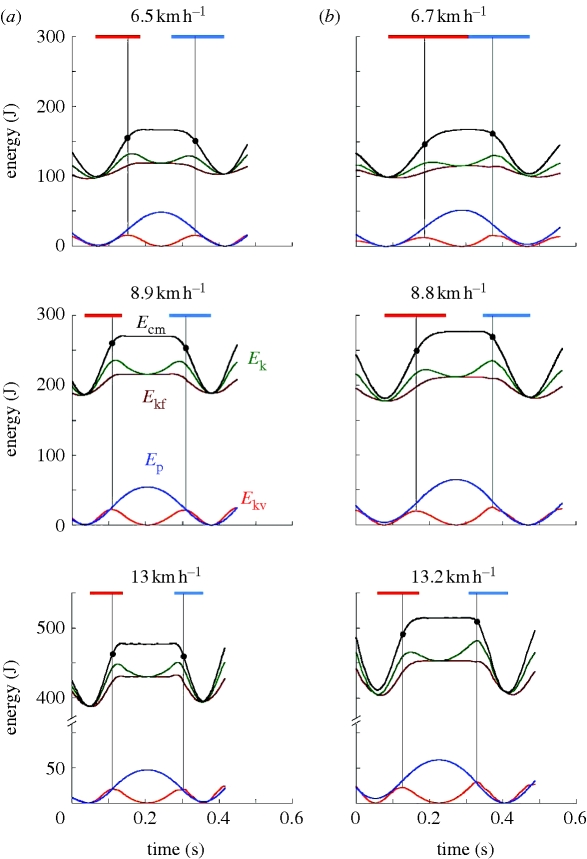
Figure 1.

Mechanical energy of the centre of mass of the body during running steps at the indicated speeds, in a 40-year-old, 65.2 kg mass, 1.72 m height male subject with 10 years of backward running training. (a) Backward running; (b) forward running. In each panel, the curves show the gravitational potential energy (E_p, blue), the kinetic energy of vertical motion (E_kv, red), the kinetic energy of forward motion (E_kf, brown), the kinetic energy of motion in the sagittal plane (E_k = E_kv + E_kf, green) and the total translational energy of the centre of mass of the body in the sagittal plane (E_cm = E_p + E_k, black). The zero line on the ordinate corresponds to the minimum attained by the E_p curve at the beginning or the end of the step. The vertical thin lines through the peaks of E_kv indicate the position of static equilibrium, when the bouncing system is loaded with a vertical force equal to body weight, and the black circles indicate the E_cm level at this position. The red horizontal bars indicate the time during which positive external work is done, t_push (increment of E_cm), whereas the blue horizontal bars indicate the time during which negative external work is done, t_brake (decrement of E_cm). The gap between red and blue bars indicates the duration of the aerial time (when present). Note that whereas in forward running the E_cm level at the equilibrium position is greater during the descent than during the lift, the contrary is true in backward running.

(d). Landing–takeoff asymmetry

The landing–takeoff asymmetry is revealed by the duration of the push, t_push, being greater than that of the brake, t_brake. The ratio t_push/t_brake was therefore taken as a measure of the landing–takeoff asymmetry. Push and brake durations were measured from the increment and the decrement, respectively, of the total mechanical energy of the centre of mass during the step period, E_cm(t) (black curve in figure 1). The difficulty in measuring the increment (t_push) and the decrement (t_brake) of E_cm is mainly due to the blunt attainment of the E_cm plateau. In order to make this transition more sharp, the derivative dE_cm(t)/dt was made. The positive and negative external work durations, t_push and t_brake, were measured as the time intervals where the derivative dE_cm(t)/dt was respectively positive and negative. As described in detail in a previous study [3], two reference levels were set by the user above and below the section of the record, where dE_cm(t)/dt ∼ 0 including the noise of the record. The push and brake durations were measured as the time intervals during which the dE_cm(t)/dt record was respectively above and below the average of the data points comprised between the two reference levels (see electronic supplementary material).

(e). Statistics

The data collected as a function of the running speed (figures 2 and 3) were grouped into speed intervals as follows: 3 to <4, 4 to <5 … 16 to <17 km h⁻¹ for backward running, and 3 to <4, 4 to <5 … 16 to <17.5 km h⁻¹ for forward running. The data points in figures 2 and 3 represent the mean ± s.d. in each of the above speed intervals and the figures near the symbols in figure 2 give the number of items in the mean. When comparing the means of different variables within a subject group with the same number of items at a given running speed, a paired-samples t-test was used to determine when the means are significantly different (figure 2). When comparing the means of different variables between two subject groups having different numbers of items, a two-sample t-test assuming unequal variances was used (figure 3). The values of p refer to the two-tail comparisons (Excel for Mac v. 11.3.5). Asterisks in figures 2 and 3 denote a statistically significant difference (p < 0.05).

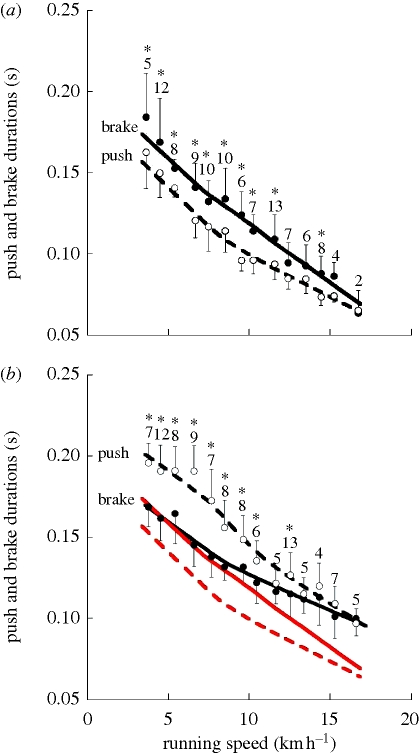
Figure 2.

The positive work duration t_push (dashed line and open circles) and the negative work duration t_brake (continuous line and filled circles) are plotted as a function of the speed of backward running in panel (a), and of forward running in panel (b), with superimposed backward running lines in red for comparison. The vertical bars indicate the standard deviation of the mean, the numbers near the symbols indicate the number of items in the mean and the asterisks indicate a significant difference between t_push and t_brake (p < 0.05). Lines (Kaleidagraph 4.03 weighted fits) are just a guide for the eye and do not describe the underlying physical mechanism. Note that, on average, t_push > t_brake in forward running, whereas t_brake > t_push in backward running, indicating that the landing–takeoff asymmetry is reversed.

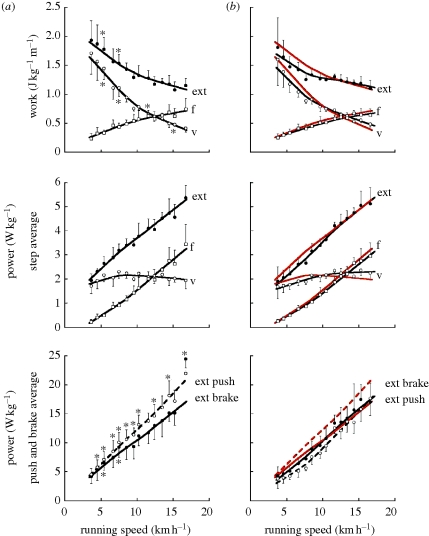
Figure 3.

(a) Backward running. (b) Forward running, with superimposed backward running lines in red for comparison. Upper panels: the external work done per unit distance (ext, filled circles) is plotted with its two components: the work done against gravity (v, open circles) and to sustain the forward velocity changes (f, open squares). Middle panels show the corresponding step-average power (i.e. the positive work done at each step divided by the step period). The bottom panels show the external push-average power (dashed line and open circles) and the external brake-average power (continuous line and closed circles) obtained by dividing the external positive work and the external negative work done at each step by the push and brake durations, respectively (figure 2). Note that at low speeds, the external work done per unit distance (upper panels) tends to be greater in backward running due to a greater work done against gravity with a similar work to sustain the forward velocity changes. Note also that the push power (bottom panels) in backward running is greater than the brake power, whereas the contrary is true in forward running: the difference between backward and forward running is because of a significant increase of the push-average power with a non-significant change in the brake-average power. Asterisks indicate when data obtained in backward running are significantly different from those obtained in forward running (p < 0.05). Other indications as in figure 2.

3. Results

Figure 1 shows several forms (see legend) of the mechanical energy of the centre of mass of the body during steps of running backward (figure 1a) and forward (figure 1b) at the indicated speeds for one subject with 10 years of backward running experience and whose results approached the average of all subjects. As described in §2, the curves in figure 1 derive directly from the computer analysis of the force platform outputs. All of the results described below are deduced from measurements made on records such as those in figure 1.

The vertical force, F_v, applied by the foot on the ground is: F_v = body weight + M_ba_v, where M_b is the body mass and a_v is the vertical acceleration of the centre of mass (i.e. the time-derivative of its vertical velocity, V_v(t)). When the vertical velocity and (as a consequence) E_kv(t) = 0.5M_bV_v(t)² (red curve in figure 1) are at a maximum, the derivative is nil, a_v = 0 and F_v = body weight. The locations of the E_kv(t) peaks attained during the step were therefore used to determine the instants of static equilibrium position, where the vertical force equals body weight (vertical thin lines in figure 1).

(a). Landing–takeoff asymmetry

The landing–takeoff asymmetry described in running humans [2,10] and in running, hopping and trotting of other vertebrates [3] is characterized by: (i) a blunt attainment to the E_cm(t) plateau at the end of the push and a sharp drop off the E_cm(t) plateau at the start of the brake (black curve in figure 1); (ii) a peak of translational kinetic energy in the sagittal plane E_k(t) (green curve in figure 1) that is greater during the descent than during the lift; and (iii) a mechanical energy level of the centre of mass E_cm at the equilibrium position that is greater during the descent than during the lift (black circles on the E_cm(t) curve). These characteristics of the forward running step (clearly visible in figure 1b) tend to be reversed in the backward running step (figure 1a).

As described in previous studies [2,3], the asymmetries shown in the right panels of figure 1 result in a longer duration of the push before ‘takeoff’, t_push, increment of the E_cm(t) curve (red bars in figure 1), and in a shorter duration of the brake after ‘landing’, t_brake, decrement of the E_cm(t) curve (blue bars in figure 1).

Since during running on the level at a constant speed, the momentum gained during positive work equals the momentum lost during negative work (i.e. 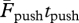= 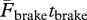), the greater duration of the push (i.e. t_push > t_brake) implies a smaller average force exerted during the push (i.e. ).

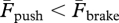Positive and negative work durations are plotted as a function of speed for the two running conditions in figure 2. It can be seen that, on average, t_push > t_brake in forward running [2], whereas t_brake > t_push in backward running. This finding shows that the landing–takeoff asymmetry is reversed in backward running (i.e. 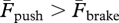—‘hard takeoff’ and ‘soft landing’ in contrast to ‘soft takeoff’ and ‘hard landing’ found in forward running).

Figure 2b shows that the reversal of the landing–takeoff asymmetry in backward running is mainly due to a large decrease of t_push at all running speeds. In both running conditions t_push decreases similarly with speed as shown by the parallel trend of the dashed lines. The negative work duration t_brake is similar in the two conditions at the lowest speeds, but decreases faster with speed in backward running, approaching t_push at the highest speeds, as indicated by the continuous lines.

In backward running, as in forward running, the difference between t_push and t_brake is significant at the lowest speeds (even if larger in forward than in backward running) and not significant at the highest speeds (i.e. in both conditions the landing–takeoff asymmetry decreases with speed), suggesting a more elastic rebound at high speeds [2,4].

Figure 2 shows that at a given speed, the sum t_push + t_brake, which equals the time of foot contact on the ground, is lower in backward running than in forward running [11].

(b). Mechanical work and power

The mass-specific positive external work done per unit distance to move the centre of mass in the sagittal plane and the corresponding step-average power are plotted as function of speed in the upper and middle panels, respectively, of figure 3. In backward running, as in forward running, the gravitational potential energy curve (blue in figure 1) and the kinetic energy curve of forward motion (brown in figure 1) increase and decrease nearly in phase during the step. It follows that the positive external work to move the centre of mass in the sagittal plane (‘ext’ in figure 3) is practically equal to the sum of the positive work done against gravity (‘v’ in figure 3) and to sustain the kinetic energy changes of forward motion (‘f’ in figure 3).

The positive work done per unit distance in forward running is in good agreement with that measured in previous studies (e.g. [12]). It can be seen that in backward running, the work done against gravity (and, as a consequence, the external work) seems to be slightly greater at low speeds, whereas the work done to sustain the kinetic energy changes of forward motion is similar in both conditions.

A more striking difference between backward running and forward running is revealed by the lower panels of figure 3, showing the external power developed during the push and the brake (i.e. the push-average power and the brake-average power). Whereas in the middle panel the positive work done at each step is divided by the duration of the entire step to obtain the step-average power, in the bottom panel the work done at each step, both positive and negative work, is divided by the time intervals during which they are done—respectively, t_push and t_brake (figure 2)—to obtain the much higher push and brake average powers (compare the ordinates of the middle and lower panels).

It can be seen that: (i) in backward running the push power is, on average, greater than the brake power, in contrast to forward running where the brake power is, on average, greater than the push power; (ii) the difference between backward and forward running is due to a significant increase of the push-average power with a non-significant change in the brake-average power.

4. Discussion

It has been found that backward running requires approximately 30 per cent more metabolic energy expenditure than forward running [11,13]. Is this increase in metabolic energy expenditure justified by a corresponding increase in the mechanical work done to maintain locomotion?

The total mass-specific positive work done per unit distance (dashed lines in figure 4) was measured in this study by adding the external work done per unit distance (‘ext’ in the upper panels of figure 3) to the internal work estimated as described in the electronic supplementary material.

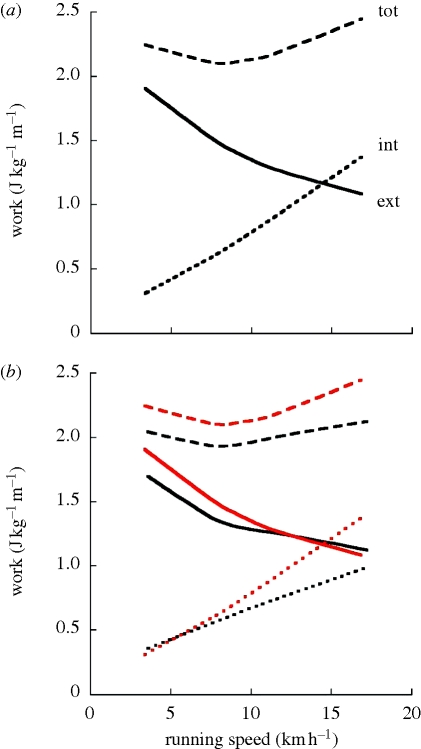
Figure 4.

(a) Backward running. (b) Forward running, with superimposed backward running lines in red for comparison. (a,b) The dotted line (int) indicates the internal positive work done per unit distance to accelerate the limbs relative to the centre of mass calculated as described in the electronic supplementary material; the continuous line (ext) indicates the external work done per unit distance to sustain the motion of the centre of mass of the body in the sagittal plane relative to the surroundings (upper panels of figure 3); and the dashed line (tot) gives the sum of the two. Note that in backward running the total work is approximately 10% greater than in forward running because of a greater external work done against gravity at low speeds and to a greater internal work owing to a higher step frequency at high speeds. Other indications as in figure 2.

It can be seen that the total work done per unit distance is approximately 10 per cent greater in backward running than in forward running, owing to a greater external work done against gravity at low speeds (figure 3) and a greater internal work at high speeds caused by the sharper step frequency increase in backward running [11].

An approximately 30 per cent increment in metabolic energy expenditure for an approximately 10 per cent increment of mechanical work indicates that the mechanical efficiency in running backwards is 1.1/1.3 = 0.85 (i.e. 15 per cent less than in forward running). A possible explanation for the reduced efficiency in backward running is given below.

During the rebound of the body taking place at each step, the negative work phase of the motor precedes in time the positive work phase both in forward and in backward running. In backward running, the machine is reversed when compared with forward running: contact with the ground takes place with the front of the foot and takeoff takes place with the back of the foot (toe–heel versus heel–toe foot contact pattern [14]). It follows that in backward running, negative work is associated with the long-range lever system (toe–ankle), whereas positive work is associated with the short-range lever system (ankle–heel), which is the contrary of what happens in forward running. Note however that the difference between backward and forward running cannot be attributed entirely to the lever system of the foot. In this study, we describe the overall effect of all joints and muscle groups on the timing of positive and negative external work production. We found that this timing is reversed in backward running (figure 2), resulting (as described above) in a lower average force during stretching and a higher average force during shortening.

Since during running on the level at constant speed the negative work done during stretching must equal the positive work done during shortening, and work is force times displacement, the greater force developed during shortening in backward running implies a displacement of the centre of mass in the sagittal plane that is smaller during positive work than during negative work. In other words, in backward running, the positive work performance may not benefit from an appropriate greater distance provided by the lever system as in forward running, but may be constrained to occur over a shorter distance. This is probably the cause of the reversed landing–takeoff asymmetry observed in backward running. The reversed landing–takeoff asymmetry, in turn, may explain the greater energy expenditure measured in backward running. In fact, the landing–takeoff asymmetry measured in forward running has the following advantages relative to the reversed landing–takeoff asymmetry measured in backward running.

During stretching. The greater force developed during stretching allows storage of mechanical energy in tendons and other elastic structures within muscle–tendon units. This storage of mechanical energy is at low cost because: (i) owing to the asymmetric force–velocity relation, each fibre may attain during stretching a force about double that during a maximal isometric contraction, with the consequence that few fibres can be activated to attain a high force; and (ii) the metabolic energy expenditure to maintain a fibre active during stretching is less than the metabolic energy expenditure during an isometric contraction and, particularly, during shortening [15–17].

During shortening. The mechanical energy stored in the tendons during stretching can be recovered with little loss during subsequent shortening because of the small elastic hysteresis of tendons [18]. Furthermore, the recoil of tendon in series with muscle fibres within each muscle–tendon unit decreases the amount of shortening that each fibre must provide, for a given length change of the whole unit, at a higher cost and with a lower force.

On these grounds we conclude that the asymmetric rebound in bouncing gaits is, after all, an energy-saving mechanism when muscle length change must contribute with that of tendons to the total length change of the muscle–tendon unit (i.e. when the force is not high enough to maintain the muscle in a quasi-isometric contraction).

When the landing–takeoff asymmetry is reversed, as in backward running (i.e. when 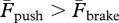), the greater force developed during shortening must require a greater muscle activation during positive work relative to forward running to compensate for (i) the smaller force exerted by each muscle fibre during shortening relative to stretching and (ii) the shorter distance at disposal for positive work production. This greater muscle activation may explain the relatively greater energy expenditure observed in backward running. In other words, the efficiency of the stretch–shorten cycle of muscle–tendon units during the rebound of the body at each running step is favoured in running forwards by the asymmetric response of muscle contractile machinery to stretching and shortening. Apparently for this reason, different machines (skeletal lever systems) in diverse kinds of bouncing gaits result in a greater force during stretching and a lower force during shortening [3]. Reversing the machine, as in backward running, constrains the motor to work against its natural response and this causes a less efficient rebound.