Grandmothering and natural selection

Abstract

Humans are unique among primates in that women regularly outlive their reproductive period by decades. The grandmother hypothesis proposes that natural selection increased the length of the human post-menopausal period—and, thus, extended longevity—as a result of the inclusive fitness benefits of grandmothering. However, it has yet to be demonstrated that the inclusive fitness benefits associated with grandmothering are large enough to warrant this explanation. Here, we show that the inclusive fitness benefits are too small to affect the evolution of longevity under a wide range of conditions in simulated populations. This is due in large part to the relatively weak selection that applies to women near or beyond the end of their reproductive period. However, we find that grandmothers can facilitate the evolution of a shorter reproductive period when their help decreases the weaning age of their matrilineal grandchildren. Because selection favours a shorter reproductive period in the presence of shorter interbirth intervals, this finding holds true for any form of allocare that helps mothers resume cycling more quickly. We conclude that while grandmothering is unlikely to explain human-like longevity, allocare could have played an important role in shaping other unique aspects of human life history, such as a later age at first birth and a shorter female reproductive period.

1. Introduction

For the vast majority of mammals, reproductive and somatic senescence occur simultaneously as part of a gradual, age-related decline in physiological condition. This holds true for most primates. While non-human primates occasionally outlive their reproductive period, their post-reproductive period is relatively short, both in absolute terms and relative to their lifespan [1]. Even among chimpanzees, human's closest living relatives, it is rare for a female to experience a sizable post-menopausal period in the wild [2]. But humans are different: women experience total loss of fertility near middle age, often living for decades in a post-menopausal state [3,4], even though it would seem that natural selection should favour those who extend their reproductive period to more closely match their lifespan. For those interested in explaining why women exhibit an exceptionally long post-menopausal lifespan, empirical evidence suggesting that the age of menopause in humans is the ancestral, not derived, condition [2,5] has largely shifted the focus from the evolution of mid-life menopause (e.g. [6]) to the evolution of our distinctively long lifespan (for review, see [7,8]).

While human longevity may have benefited from relatively recent cultural advancements [9,10], some researchers argue for a considerable increase in longevity much earlier in human evolution [11,12], though just how much earlier is a matter of current debate [13–17]. Proponents of the highly influential ‘grandmother hypothesis’ are among those who argue that an extended lifespan may have appeared in hominins as early as the Late Pliocene [13,16,18,19].

Kristen Hawkes and colleagues first discussed what has become known as the grandmother hypothesis in their interpretation of empirical data from the Hadza, a forager society in Tanzania [20]. They found that mothers who were caring for infants spent less time foraging and contributed less to the nutrition of their weaned children than mothers who were not caring for infants [21]. They also found a positive correlation between the weight of Hadza youngsters and the amount of time the children's grandmothers spent foraging [21]. These observations led to the hypothesis that a grandmother could increase her inclusive fitness by helping her kin in two ways [18,21]. First, a helpful grandmother could decrease the weaning age of her daughter's infant and, ultimately, her daughter's interbirth interval by providing her nursing daughter with food that she would not have been able to obtain otherwise. Second, a helpful grandmother could increase the survival of her young, weaned grandchildren by supplying them with food during periods in which their mother reduced her foraging in response to the presence of a new infant.

Hawkes and colleagues propose that the inclusive fitness benefits generated by grandmothering may have been sufficiently large to relax the selective pressure for women to continue reproducing into old age. Under these conditions, natural selection would favour females who were able to suppress their adult mortality with resources that otherwise would have gone towards their own reproduction [18,19]. A reduction in adult mortality may have had evolutionary consequences for other life-history traits, such as age at maturity [18]. This explanation rests on the as of yet untested assumption that the inclusive fitness benefits associated with grandmothering were large enough to offset the costs of suppressing adult mortality.

The grandmother hypothesis has been as influential as it has been fruitful, serving as the inspiration for numerous studies in a variety of related disciplines [22]. But it has not been without its detractors. Valid objections have been raised about how the proponents of the grandmother hypothesis have applied Charnov's invariants model [23] to human life-history data [7,24]. In addition, empirical research designed to assess the influence of grandmothers using ‘natural fertility’ populations and historical records has yielded mixed results: while some studies find that the presence of grandmothers has a positive effect on the fitness of their kin [25–29], others find no such relationship [30–35]. To date, important assumptions of the grandmother hypothesis remain undemonstrated and important questions remain unanswered. Chief among them is this: in order for human-like longevity to evolve on the backs of helpful grandmothers, just how helpful must they be?

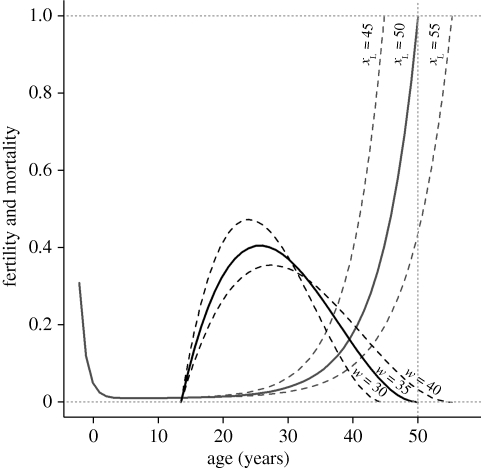
Here, we use an evolutionary agent-based simulation to systematically investigate how selection affects longevity in the presence of grandmothering. More specifically, we use artificial societies to investigate under what conditions the inclusive fitness benefits of grandmothering are large enough for selection to increase longevity via an adaptive post-menopausal lifespan. We model longevity (x_L) and length of the reproductive period (w) as unlinked diploid traits that are subject to mutation and selection (figure 1). We conduct three experiments to assess the evolutionary significance of the benefits associated with two types of helping that are commonly attributed to grandmothers. First, we allow grandmothers to provide help that decreases the weaning age of their daughters' infants. Second, we allow help provided by grandmothers to increase their matrilineal grandchildren's chances of surviving to maturity. In the third experiment, we allow the help provided by grandmothers to have both effects. We test for the effect of grandmothering on the evolution of increased longevity (x_L) and on the length of the reproductive period (w) in females by comparing data collected from simulated populations in which grandmothers provide help to data collected from ‘baseline’ simulations in which grandmothers do not provide help.

Figure 1.

Age-dependent mortality (grey) and fertility (black) trajectories. Male and female mortality is based on Siler's model (μ(x) = a₁e^−b₁x + a₂ + a₃e^b₃x). Female fertility is based on the Brass polynomial (m(x) = c(x − d)(d + w − x)²). Two key life-history parameters—the length of reproductive period (w) and longevity (x_L)—are subject to mutation and selection in our model. Solid lines indicate the shape of trajectories at the start of each simulation, when longevity and age at end of reproduction are both set to 50 years. Dashed lines show how mutations to w and x_L can affect the shape and length of the trajectories.

2. Methods

We use an evolutionary agent-based simulation (run in NetLogo 4.0.2 [36]) to test the effects of grandmothering. Model parameters and values used in our simulations are listed in electronic supplementary material, table S1. The following subsections summarize the main aspects of our model. See electronic supplementary material for a complete model description, which follows the ODD protocol [37]. The commented source code is freely available upon request.

(a). Fertility and mortality

Our simulated populations fluctuate slightly around a target population size of 1000 individuals (s.d. = 6) during the course of each simulation run. Simulated populations include an equal proportion of males and females. In our model, all individuals reach sexual maturity (i.e. adulthood) at 15 years of age. Female age-dependent fertility is based on the Brass polynomial:

2.1

where x is the age, c is the fertility level, d is the age at sexual maturity and w is the length of the reproductive period (figure 1) [38]. The Brass polynomial has been shown to provide the best fit to fertility data for a range of mammals, including humans [39]. The Brass polynomial represents the age-dependent fertility distribution of an ‘average’ female in a heterogeneous population. The integral of the Brass polynomial represents the maximum number of offspring a female can expect to have under idealized conditions (i.e. mortality = 0 and weaning age = 0). We refer to this value as total reproductive potential to reflect the fact that it represents a theoretical expectation. By contrast, we use realized total fertility to refer to the actual number of offspring produced by a female.

We assume that the total reproductive potential of each female is finite and conserved ([40], p. 42). In addition, we assume that all females possess the same total reproductive potential. This requires that we adjust (c) in equation (2.1) (see electronic supplementary material) to ensure that mutations to w only affect the way in which fertility is distributed over a female's lifetime, not the maximum number of offspring she can expect to have under idealized conditions. Holding total reproductive potential constant does not mean that realized total fertility (i.e. the actual number of offspring) does not vary among females. In fact, realized total fertility varies as a function of the age-dependent fertility curve, longevity and grandmothering. Although we hold total reproductive potential constant, daughters who receive help from their mothers have more offspring than females who do not receive help. Adult females are eligible to reproduce only if they are not currently caring for an unweaned child. Thus, by reducing the weaning age of their matrilineal grandchildren, helpful grandmothers allow their adult daughters to return to cycling sooner than ‘unhelped’ females who must wean their offspring at a later age.

An adult male reproduces each time he is randomly chosen to serve as a mate for a reproductive female. Males do not have to wait until their offspring are weaned in order to reproduce again.

Age-dependent mortality for both sexes follows Siler's well-known competing hazards model:

2.2

which is the sum of three components of mortality: immature, residual, and senescent (figure 1) [41,42]. We use empirical data from recent hunter–gatherer populations [12] to parameterize a₁, b₁, a₂ and a₃ (electronic supplementary material, table S1). The probability of dying, q(x), at age x is calculated by transforming the mortality rate provided by Siler's model (μ(x)) as follows:

2.3

To explicitly link age-specific mortality with maximum expected lifespan, we solve equation (2.2) for the age at which μ(x) = 1 for each individual. This is the age we refer to as longevity (x_L). By conservatively using μ(x) = 1 to calculate x_L, the mortality trajectory ensures that agents are highly unlikely to live past x_L. We hold all parameters of the Siler's model constant except b₃, which can be retrieved from x_L. b₃ affects the shape of senescent mortality only.

Life-history theory assumes a trade-off in the amount of energy an individual can invest in somatic maintenance and reproduction, such that increased longevity would entail reduced fertility [23,43]. Likewise, the grandmother hypothesis assumes that decreases in adult mortality are made possible by diverting resources that would have been used for reproduction to enhance somatic maintenance late in life [18,19]. This is the only assumption of the grandmother hypothesis not included in our evolutionary model. Thus, in our model, an increase in longevity does not entail a decrease in reproductive potential. To the extent that this assumption has an effect on evolutionary dynamics, it means that in our model selection will favour increased longevity in the presence of lower inclusive fitness benefits than would be required by the grandmother hypothesis.

(b). Heritable variation

Every individual carries two alleles for each of two diploid traits: longevity (x_L) and length of the reproductive period (w). Alleles are passed via sexual reproduction with segregation and independent assortment. The phenotype of each trait is given by the mean of the two alleles. At birth, each transmitted allele is affected by mutation with probability of 0.05. Each mutation changes the value of the affected allele by an amount given by a real number drawn randomly from a truncated normal distribution with a mean of 0 and a standard deviation of 0.5. Through simulated time, selection acts on heritable variation in longevity (x_L), which affects age-dependent mortality in both sexes, and length of reproductive period (w), which affects the age-dependent fertility distribution in females.

(c). Grandmothering

A grandmother is eligible to help as long as she does not currently have an unweaned offspring of her own. Thus, grandmothers need not be post-menopausal in order to be helpful (unless otherwise stated in the text). We assume that grandmothers help their daughters and matrilineal grandchildren, only. The help provided by grandmothers can have two distinct effects. First, it can decrease the age at which their daughters' infants can be weaned from either 5 or 3 years old to 1 year old. Second, the help provided by grandmothers can decrease their matrilineal grandchildren's mortality each year while the child is aged 1 through υ, the oldest age at which a child can receive help from its maternal grandmother.

(d). Scheduling

We run 25 unique simulations for each experimental setting, collecting data after the 10 000th time step of each to avoid the transient conditions of initialization. At initialization, the age at menopause (d + w) and longevity (x_L) are set to 50 in all agents. There is no genetic variation in the starting population. Simulated time proceeds in annual time steps, during each of which a number of activities can take place in the following order.

First, all individuals age 1 year. As a default, infants are weaned at an age of π. But if the experimental settings allow grandmothers to help their nursing daughters and π > 1, an infant will be weaned when it turns 1 year old if its maternal grandmother is alive and without an unweaned offspring of her own at the time. If an infant's maternal grandmother is dead or caring for her own unweaned offspring when the infant turns 1 year old, the infant will not be weaned until age π. Under experimental conditions in which grandmothering has no effect on weaning age, all infants are weaned at age π.

Second, each adult female without an unweaned offspring compares a real number chosen randomly from a uniform distribution between 0 and 1 with her age-dependent fertility. To maintain a nearly constant population size, age-dependent fertility values are scaled by a coefficient that is sensitive to the difference between the population's expected number of offspring and the discrepancy between the current population size and the target population size (1000 individuals). If the randomly drawn number is less than or equal to a female's scaled age-dependent fertility value, she will produce an offspring (male or female with equal probability) with a randomly chosen adult male. The offspring will receive one allele from its mother and one from its father for each of the traits, w and x_L.

Third, if allowed by the experimental settings, females that are eligible to serve as helpful grandmothers can help their matrilineal grandchildren directly. In cases where helpful grandmothers can affect their grandchildren's survival, the probability of death for any child that has been helped by its grandmother during the current time step is given, not by equation (2.3), but by

2.4

where r is a real number chosen randomly by the grandmother from a uniform distribution between 0 and 1, ι is the importance of grandmothering in the society and n is the total number of grandchildren receiving help from the grandmother during that time step. When ι = a (for ‘absolute help’), q(x) = 0 for any child who received help during that time step.

Fourth, all individuals are exposed to mortality. An individual dies whenever a real number drawn randomly from a uniform distribution between 0 and 1 is less than or equal to its age-dependent mortality, q(x), as provided by equation (2.3) or, if grandmothers are allowed to affect pre-adult mortality, equation (2.4).

3. Results

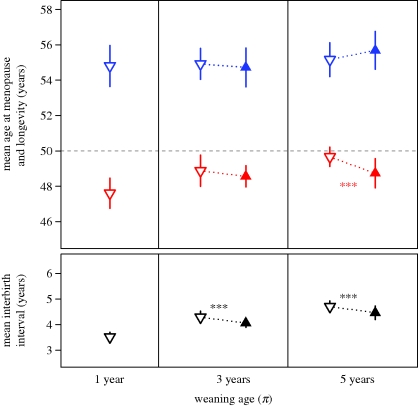
To identify whether the inclusive fitness benefits of grandmothering are large enough for selection to favour increased longevity (x_L) or to affect the length of the reproductive period (w), it is necessary to have an understanding of how selection influences these life-history traits in the absence of grandmothering. For each of three baseline settings, all infants are weaned at the same age (π) regardless of whether their matrilineal grandmother is alive or with infant. In addition, grandmothers have no impact on the survival of their grandchildren in the baseline simulations. We vary π in order to investigate the effect of weaning age on mean interbirth interval, longevity and length of reproductive period in the absence of helpful grandmothers (figure 2). As theory predicts, we find a positive correlation between weaning age and mean interbirth interval (Spearman's ρ = 0.90, p < 0.001). By contrast, weaning age does not affect longevity in baseline simulations (Kruskal–Wallis test: χ² = 1.89, d.f. = 2, p = 0.39). In addition, we find a positive correlation between weaning age and length of the reproductive period (Spearman's ρ = 0.75, p < 0.001).

Figure 2.

The effect of weaning age on mean longevity (x_L, blue), mean age at menopause (d + w, red) and mean interbirth interval (black) in females. Each data point represents the mean ± 1 s.d. of 25 unique simulations. The grey dashed line indicates age at menopause and longevity at the start of all simulations. Empty symbols summarize the results of baseline experiments in which weaning age (π) is identical for all infants. Filled symbols summarize the results of simulations in which grandmothering decreases matrilineal grandchildren's weaning age from π to 1. ***p < 0.001 (Mann–Whitney U tests for the effect of grandmothering on w, x_L and mean interbirth interval).

The first experiment allows for helpful grandmothers to influence the weaning age, but not the survival, of their daughters' infants. As stated above, females who wean their infants earlier enjoy shorter mean interbirth intervals and have more babies. This, in turn, imparts inclusive fitness benefits on the helpful grandmothers who are responsible for decreasing the weaning age of their matrilineal grandchildren. According to the grandmother hypothesis, selection will favour increased longevity when these inclusive fitness benefits are sufficiently large. However, we find that grandmothering has no effect on the evolution of longevity (x_L), regardless of whether helpful grandmothers reduce the weaning age of their grandchildren from 5 years old to 1 year old (Mann–Whitney U test: W = 393, p = 0.12) or from 3 years old to 1 year old (Mann–Whitney U test: W = 286, p = 0.62). However, this form of help does have an effect on the evolution of the length of the female reproductive period. When grandmothering reduces weaning age from 5 years old to 1 year old, selection favours a significantly shorter reproductive period (w) in females than when all children are weaned at the age of 5 (Mann–Whitney U test: W = 110, p < 0.001; figure 2 and the electronic supplementary material, table S2). However, when grandmothering reduces weaning age from just 3 years old to 1 year old, the length of the female reproductive period is not significantly affected relative to the baseline results (Mann–Whitney U test: W = 240, p = 0.16).

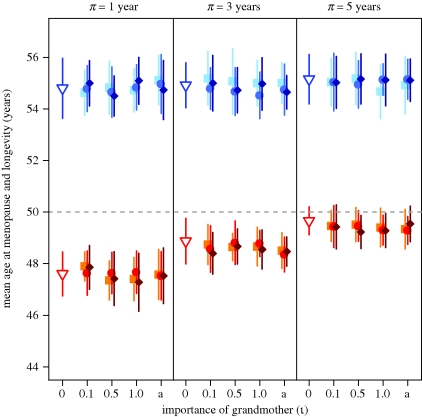
The second experiment allows for helpful grandmothers to influence the survival, but not the weaning age, of their matrilineal grandchildren. We vary ι, a scalar that corresponds to the significance of the help provided by grandmothers, and υ, the oldest age at which a grandchild can receive help from its maternal grandmother, in order to assess whether the importance of grandmothers and/or the duration of grandmothering affect survival to maturity, longevity (x_L) and length of the reproductive period (w). We find that an individual who receives help from his/her grandmother is up to 17.3 per cent more likely to reach maturity than an individual who receives no help (electronic supplementary material, figure S1). This is a large fitness benefit for the child. As expected, the proportion of helped children who reach maturity increases with the importance of grandmothers (ι) and (to a lesser extent) with the age through which help is provided (υ). Despite the large positive effect on survival to maturity, however, this form of grandmothering has no effect on the evolution of longevity or the length of the reproductive period (figure 3 and the electronic supplementary material, table S3). We find that the evolution of longevity is unaffected by the importance of grandmothers (ι) or the oldest age at which a child can receive help (υ) even for the most extreme case tested (ι = a, υ = 10), in which it is possible for helpful grandmothers to render their matrilineal grandchildren immune from mortality through the age of 10.

Figure 3.

The effect of grandmothering on mean longevity (x_L, blue) and mean age at menopause (d + w, red) when help provided by grandmothers affects their matrilineal grandchildren's survival (filled symbols). Each data point represents the mean ± 1 s.d. of 25 unique simulations. The grey dashed line indicates age at menopause and longevity at the start of all simulations. Empty symbols summarize the results of baseline experiments in which weaning age (π) is identical for all infants and grandmothering does not affect grandchildren survival (ι = 0). The results show that w and x_L do not differ significantly (Mann–Whitney U tests for the effect of grandmothering on w and x_L, α corrected for multiple testing) from baseline experiments. Filled squares, ν = 3 years; filled circles, ν = 5 years; filled diamonds, ν = 10 years.

The final experiment allows for the help provided by maternal grandmothers to reduce the weaning age and improve the survival of their matrilineal grandchildren. Despite the fact that grandchildren who receive help are again more likely to reach maturity than those who do not, longevity (x_L) and length of the reproductive period (w) in females do not differ from cases in which grandmothering decreases weaning age, only (electronic supplementary material, figure S2 and table S4). Grandmothering affects the length of the reproductive period in just a single case. The results of this experiment show that the two types of help provided by grandmothers do not have a combined effect on the evolution of x_L or w.

4. Discussion

There is a crucial difference between playing an important role in society and playing a social role with evolutionary significance. The grandmother hypothesis predicts that selection will favour variants that increase longevity when the inclusive fitness benefits accrued by helpful grandmothers are large enough to outweigh the costs of suppressing adult mortality. However, despite the fact that the help provided by grandmothers significantly reduces the mean interbirth intervals of their adult daughters and significantly increases the survival of their matrilineal grandchildren in our model, grandmothering has no effect on the evolution of longevity relative to baseline simulations under any of the conditions tested here. How can this be explained?

Williams' [44] influential paper on senescence considers the natural selection of pleiotropic genes, genes that affect an individual's fitness differently at different ages. His elaboration on a notion first presented by Medawar [45] holds that the strength of selection on an individual weakens as p_x, the proportion of the total reproductive potential that remains after age x, decreases. Williams' ([44], pp. 401–402) model shows that selection favours a variant that provides a slight increase in an individual's fitness early in one's reproductive period, when p_x is larger and selection stronger, even if it incurs a larger decrease in fitness later in one's reproductive period, when p_x is smaller and selection weaker. The prediction that follows from Williams' work is that the inclusive fitness benefits associated with grandmothering must be very large—not merely greater than zero—for the relatively weak selection that applies to peri- and post-menopausal women to favour variants that increase longevity. In speculating that the long post-menopausal period observed in women may have evolved owing to the inclusive fitness benefits of grandmothering, William Hamilton was quick to point out that Williams' finding—that selection is biased towards youth over old age—reduces the likelihood that the hypothesis holds true for humans ([40], p. 37).

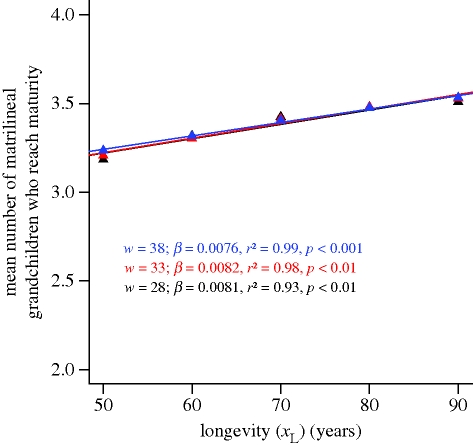
Given this context, it is particularly telling, if not entirely unexpected, that grandmothering does not have an effect on the evolution of longevity in any of our simulations. We conducted an additional test to quantify the lifetime inclusive fitness benefits of grandmothering (ι = a, υ = 10, and helping decreases π from 5 years to 1 year) under different values of x_L, including values far greater than those that evolved in our simulations (figure 4). The magnitude of the effect of x_L on the mean number of matrilineal grandchildren that reach sexual maturity provides a measure of the lifetime inclusive fitness benefits associated with grandmothering. We repeated this test for three values of w (28, 33 and 38). The ordinary least-squares regression coefficients are significantly greater than 0, as to be expected in the presence of grandmothering. However, the regression coefficients range from 0.0076 to just 0.0082, indicating that the fitness effects of grandmothering are relatively weak even with long lives. To illustrate, given w = 33, a female can expect to gain an additional 0.0082 mature matrilineal grandchildren (each of whom shares just one-quarter of her genes) for each 1 year increase in x_L. It would appear that the inclusive fitness benefits associated with grandmothering are not large enough for increased longevity to gain traction under the weak selection operating on females who are old enough to serve as helpful grandmothers.

Figure 4.

The lifetime inclusive fitness effects of grandmothering. Each data point represents the mean of 25 unique simulations in which w and x_L are immutable. Data were collected over the final 1000 times steps of each simulation. Ordinary least-squares regression lines (and results) are presented for each of three values of w: 28 (black), 33 (red), and 38 (blue).

As was found previously for the case of menopause [6,30,46,47], our results suggest that longevity is unlikely to be an evolutionary consequence of grandmothering. The origin of human longevity remains to be explained. Marlowe [48] and Tuljapurkar et al. [49] propose that old-age male fertility may increase the selective pressure against deleterious variants that affect both sexes at ages greater than the age of female menopause. However, the data collected from our two-sex model provide no evidence to support the notion that old-age male reproduction had a large effect on the evolution of increased longevity. Work by Lee [50,51] shows that perhaps the benefits provided by intergenerational resource transfers in extensive social networks may be large enough for selection to favour increased longevity. Lee's work implies that widespread allocare may have important consequences for the mortality trajectory observed in modern humans. We cannot rule out this interesting possibility. Nevertheless, our results are consistent with the idea that the post-menopausal lifespan in humans is a by-product of selection acting on other life-history traits, such as proposed in the reserve capacity hypothesis [24,52] and the embodied capital hypothesis [31,53]. More specifically, our findings strongly support Peccei's [8] conclusion that the presence of a prolonged post-reproductive period in women can be best explained as an epiphenomenon that arises from the intersection where selection for efficient early reproduction meets recent increases in life expectancy. The processes responsible for these increases in life expectancy remain elusive.

Our results also indicate a positive relationship between weaning age and length of the female reproductive period. Weaning age (π) is a key variable because it is positively correlated with the mean interbirth interval. As is widely recognized, the interbirth intervals of humans (3.4–3.6 years) are shorter than those of other large-bodied primates, including wild chimpanzees (5.6 years) [2,24,31,54]. Allocare, which humans use to distribute the costs associated with a relatively long immature period more widely such that genetic parents do not shoulder the entire burden of raising their offspring, plays a role in reducing birth spacing [34,55–57]. Thus, allocare may have enabled ancestral humans to decrease weaning age—and, thus, reduce interbirth intervals—below that of other large-bodied primates. Interestingly, our results suggest that, while such a decrease in the mean interbirth interval would not affect longevity, it could have had serious implications for the length of the female reproductive period. The fact that women and female chimps display similar timing in reproductive senescence [2,5] while women start reproducing at a later age [58] implies that the reproductive period in humans may have been shortened from the front end rather than by ‘stopping early’ (see also [59]).

In conclusion, regardless of whether a human-like longevity was a hallmark of the earliest members of our genus, our species or the consequence of more recent socio-cultural complexity, our results suggest that it probably did not evolve on the backs of helpful grandmothers alone. Even if we assume that helpful grandmothers were present in Pliocene and Pleistocene hominin populations, the relatively weak selection that pertains to females near (or beyond) the end of their reproductive period means that the inclusive fitness benefits associated with grandmothering would need to be very large in order for selection to favour increased longevity. The results of our simulations suggest that the inclusive fitness benefits of grandmothering would not be large enough to explain the evolution of increased longevity, even under conditions that are unrealistically favourable. The origin of human longevity remains an open question. Additional research is needed to better understand how reduced birth spacing may have affected both the onset and the length of the female reproductive period in ancestral humans.