Cross-sectional Geometry of the Femoral Midshaft in Baboons is Heritable

Abstract

A great deal of research into the determinants of bone strength has unequivocally demonstrated that variation in bone strength is highly subject to genetic factors. Increasing attention in skeletal genetic studies is being paid to indicators of bone quality that complement studies of BMD, including studies of the genetic control of bone geometry. The aim of this study is to investigate the degree to which normal population-level variation in femoral midshaft geometry in a population of pedigreed baboons (Papio hamadryas spp.) can be attributed to the additive effect of genes. Using 110 baboons (80 females, 30 males), we 1) characterize normal variation in midshaft geometry of the femur with regard to age and sex, and 2) determine the degree to which the residual variation is attributable to the additive genetic effects. Cross-sectional area (CSA), minimum (I_MIN) and maximum (I_MAX) principal moments of inertia, and polar moment of inertia (J) were calculated from digitized images of transverse midshaft sections. Maximum likelihood-based variance decomposition methods were used to estimate the mean effects of age, sex, and genes. Together age and sex effects account for ~56% of the variance in each property. In each case the effect of female sex is negative and that of age is positive, although of a lower magnitude than the effect of female sex. Increased age is associated with decreased mean cross-sectional geometry measures in the oldest females. Residual h² values range from 0.36–0.50, reflecting genetic effects accounting for 15% to 23% of the total phenotypic variance in individual properties. This study establishes the potential of the baboon model for the identification of genes that regulate bone geometric properties in primates. This model is particularly valuable because it allows for experimental designs, environmental consistency, availability of tissues, and comprehensive assessments of multiple integrated bone phenotypes that are not possible in human populations. The baboon is of particular importance in genetic studies, because it provides results that are likely highly relevant to the human condition due to the phylogenetic proximity of baboons to humans.

Introduction

Cross-sectional geometry is an important contributor to bone strength. Size and shape of the bone reflect and influence loading patterns during weight bearing. It has been repeatedly demonstrated that cross-sectional morphology in long bones, such as the femur, maximizes efficiency of energy expenditure during load bearing, while minimizing risk of fracture [1–4].

Research into determinants of bone strength has unequivocally demonstrated that variation in bone strength is highly subject to genetic factors. Initially most of this work focused on bone mineral density (BMD) because of the relationship between BMD and clinical evaluation of osteoporosis risk. The importance of genetic effects on BMD has been established repeatedly in studies of both nonhuman animal models, including rodents and primates, and human families and populations [5–11].

Increasing attention in skeletal genetic studies is now being paid to indicators of bone quality that complement studies of BMD, including studies of the genetic control of geometric properties of bone. A number of studies in inbred rodents show that geometric properties contribute significantly to bone strength and are strongly influenced by genetic variation [8, 12–21]. Genetic effects have been demonstrated for vertebral cortical area [16], trabecular bone architecture [16]; trabecular bone volume [17] femoral cross-sectional area (CSA) [8, 16, 19], femoral shape [13, 17, 21], femoral bone fragility [12, 22] and bone structure-function relationships [23–24].

Heritability and association studies conducted in humans indicate that the genetic effect on geometric properties that has been detected in inbred rodent strains may translate into an effect of genes on normal population-level variation in humans [25–26]. Published reviews of the osteoporosis genetics (Ralston [26–27] and Liu [9]) describe a series of successes in the detection of genetic effects and localization of quantitative trait loci (QTLs) for bone geometric properties in twin-, family-, and population-based studies. The results show that genes contribute significantly to variation in femoral CSA [17,28–30] and the shape [29] and structure of the femoral neck [28,31]. However, salient differences in the genetic models needed to detect and localize these effects suggest interactions between genes and other variables (e.g. sex, age, and/or hormonal status). For example, Deng et al. [32] report a total of seven femoral neck geometry-related QTLs European-derived pedigrees, two of which are evident only in women and three of which are specific to men. Similarly, Koller et al. detected a femoral neck axis QTL on 5q only evident in premenopausal women [33]. Investigation of the effects of multiple genes and gene-by-environment interactions on bone geometric properties implicated by these results can be complicated by heterogeneity of diet, physical activity, and other important co-variables in humans.

Populations of biologically relevant, genetically characterized animals, such as the baboon, an established and reliable nonhuman primate model for the genetics of many skeletal traits [30, 34–36], whose environmental exposures may be controlled and/or adequately accounted for, may facilitate more accurate detection of these effects and more precise estimation of their magnitudes. Like humans, baboons naturally undergo skeletal remodeling over a relatively long life-span. Similarity in bone composition and microstructure results in fracture properties of bone tissue that are more similar to those of human bone than is true of other popular animal models [37]. Baboons resemble humans in their patterns of skeletal density changes and bone loss with increasing age, experience a natural menopause late in life [38] and show increased skeletal turnover upon ovariectomy [36, 39–40]. Finally, the captive baboon colony at Southwest National Primate Research Center (SNPRC)/Southwest Foundation for Biomedical Research (SFBR) displays a population-wide level of genetic variation that is absent in inbred rodent models.

The aim of this study is to investigate the degree to which normal variation in femoral midshaft geometry in a population of pedigreed baboons can be attributed to the additive effect of genes with the goal of assessing the potential of this valuable animal model for investigating questions of primate skeletal genetics. Specifically, using a sample of 110 baboons we aim to 1) characterize normal variation in midshaft geometry of the femur with regard to age and sex, and 2) determine the degree to which the residual variation is attributable to the additive effects of genes.

Materials and Methods

Midshaft cross-sectional geometry properties were determined using the right femurs of 110 pedigreed baboons, (Papio hamadryas spp.; 80 females and 30 males) from a breeding colony at the SNPRC/SFBR in San Antonio, TX. All the animals included in this study were adults between the ages of 5 and 33 years and were members of a single large extended pedigree.

During life all animals were housed out of doors in social group cages and maintained on commercial monkey diet (SWF Primate Diet, Harlan Teklad, Madison, WI) to which they had ad libitum access. Animal care personnel and staff veterinarians provided daily maintenance and health care to all animals in accordance with the Guide for the Care and Use of Laboratory Animals [41]. All procedures related to their treatment the SNPRC/SFBR were approved by the Institutional Animal Care and Use Committee in accordance with established guidelines. Clinical records for each animal were checked and any animals with medical conditions known to affect bone metabolism were omitted from the sample. Femurs were collected opportunistically at routinely performed necropsies (i.e. no animals were sacrificed for the purpose of this study), wrapped in saline-soaked gauze, placed in air tight plastic bags, and frozen until specimen processing.

Specimens were processed as follows: A 10-mm section of bone was removed from the femoral midshaft using a band saw. A section ~300 microns thick was cut from the center of the 10-mm section using an Isomet 1000 Precision Saw (Buehler Ltd. Lake Bluff, IL). The sections were then ground manually to a thickness of ~100 microns according to a standard protocol [42].

These midshaft transverse sections of the right femur were mounted on slides and digitized using a Zeiss Stemi SVII Microscope with an attached color digital camera. Digital images were then segmented using ImageJ (U. S. National Institutes of Health, Bethesda, MD) to extract the bone data using a combination of iterative thresholding and active contours. Segmented images were registered based on nominal anatomic orientation using Matrix Laboratory (MATLAB) (The Mathworks, Inc. Natick, MA). Cross-sectional area (CSA), minimum (I_MIN) and maximum (I_MAX) principal moments of inertia, and polar moment of inertia (J) were calculated from the segmented/rotated images with the aid of MATLAB to characterize the amount of bone material and its distribution around the neutral axis.

Maximum likelihood-based variance decomposition methods implemented in the computer software SOLAR [43] were used to simultaneously estimate the mean effects of age, sex, sex-specific age effects, body weight, and the additive effects of genes on baboon midshaft cross-sectional geometric properties. Evaluation of the covariance between relative pairs in geometric properties allows for quantification of the contribution of additive genetic effects, heritability (h²), on these traits. This approach is described in detailed elsewhere [43]. Significance of maximum likelihood estimates for heritability and other parameters was assessed by means of likelihood ratio tests in a manner described in detail elsewhere [44–46].

Age, sex and age-by-sex were selected for inclusion as covariates in the final model by means of a Bayesian model averaging procedure implemented in SOLAR. This procedure evaluates all possible covariates alone and in all possible combinations to identify the best set for inclusion based on a Bayesian Information Criterion for each covariate/combination and a posterior probability assigned to each covariate [47].

Results

Age and Sex Effects

Descriptive statistics by sex are displayed in Table 1. Males show higher means and a wider range in absolute values for all properties than females. The higher means are expected in a sexually dimorphic species [48–49] such as the baboon, in which females have an average body mass that is 52% of the average male body mass [50]. It is important to note that although a specific measure of individual body weight was not selected for inclusion in our final model using our Bayesian model averaging procedure, the effect of body size is most certainly a contributor to the effect of the sex covariate.

Table 1.

Descriptive statistics for age and bone geometry measures by sex.

Variable		N	Range	x̄	SD
Females	Age (years)	80	5.84–33.27	18.49	7.14
	CSA	80	106.73–161.23	133.89	12.06
	J	80	2862.83–7614.42	5195.88	978.74
	I_MAX	80	1493.96–3977.33	2762.03	531.91
	I_MIN	80	1368.87–3723.27	2433.85	465.76
Males	Age (years)	30	5.23–25.51	15.44	6.21
	CSA	30	128.54–243.73	188.41	22.05
	J	30	4760.54–15035.58	10498.27	2418.02
	I_MAX	30	2525.83–8162.18	5644.86	1310.20
	I_MIN	30	2234.70–6873.40	4853.40	1129.84

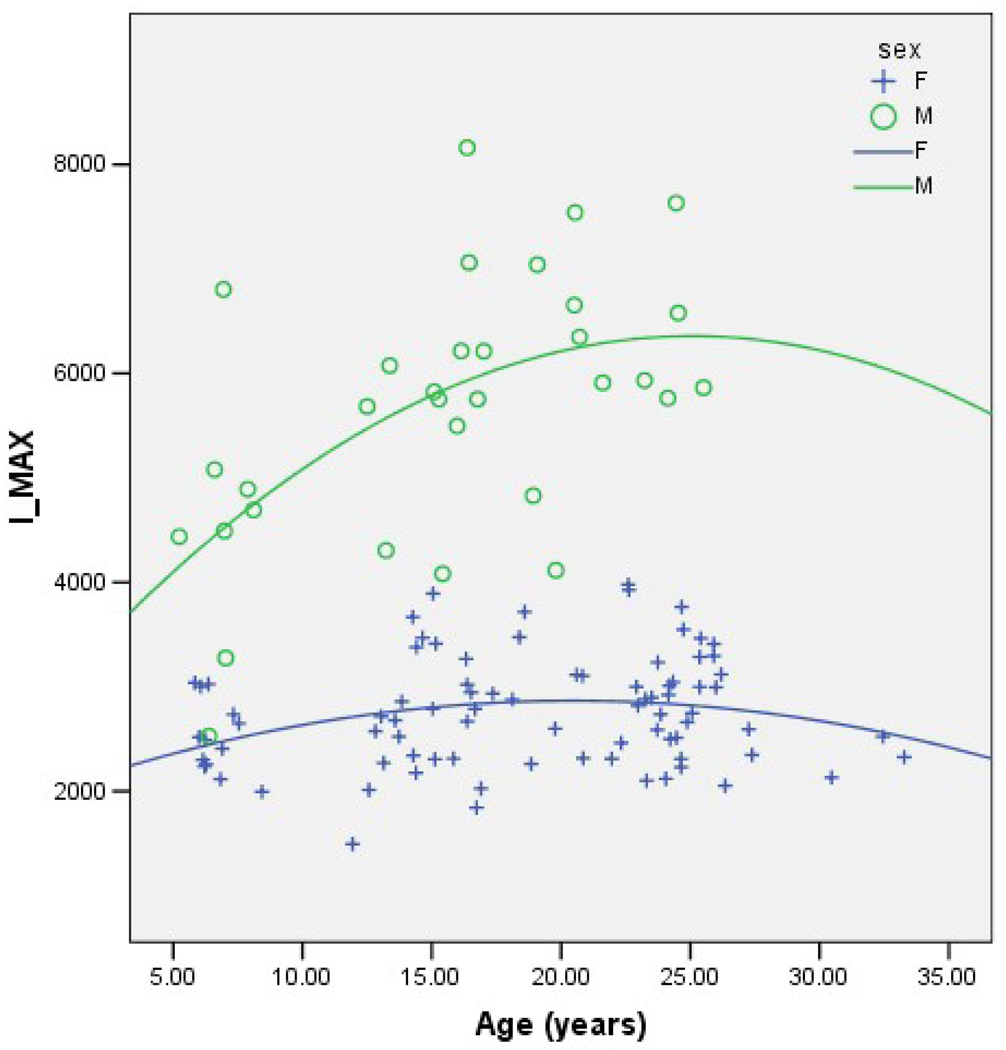
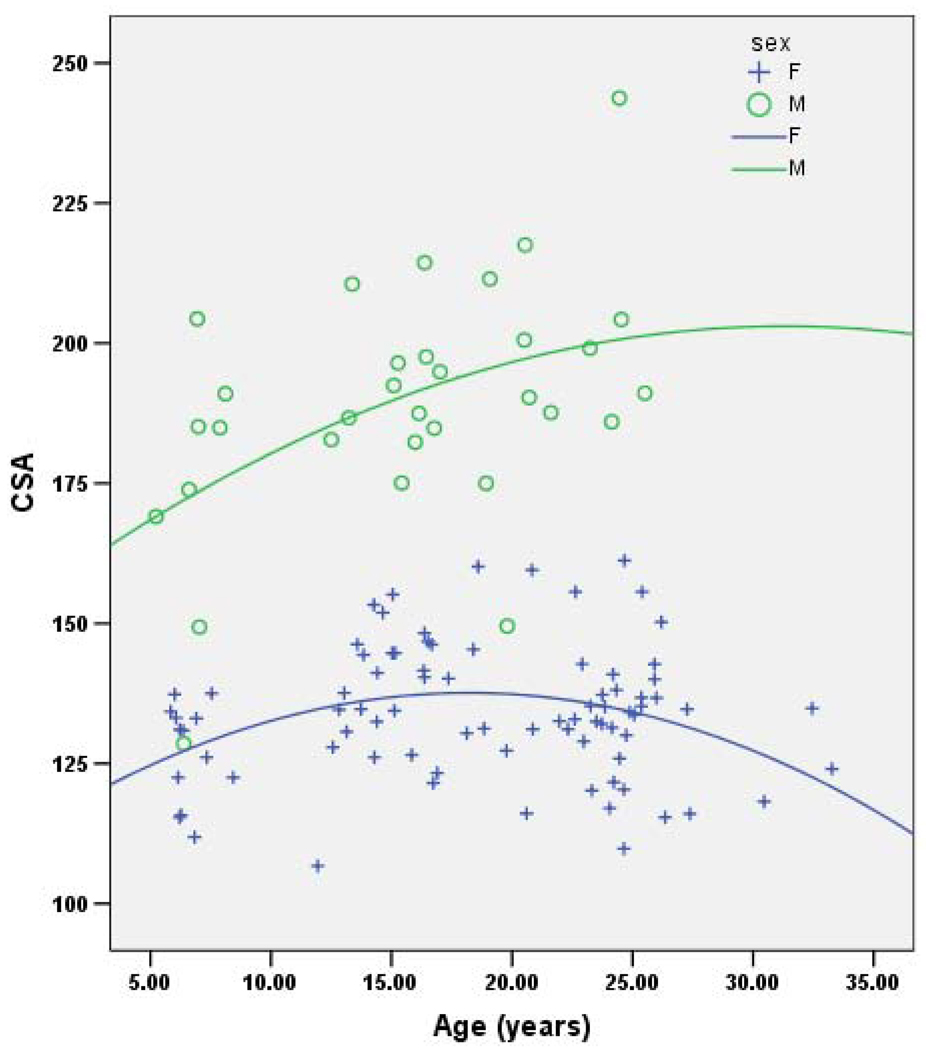
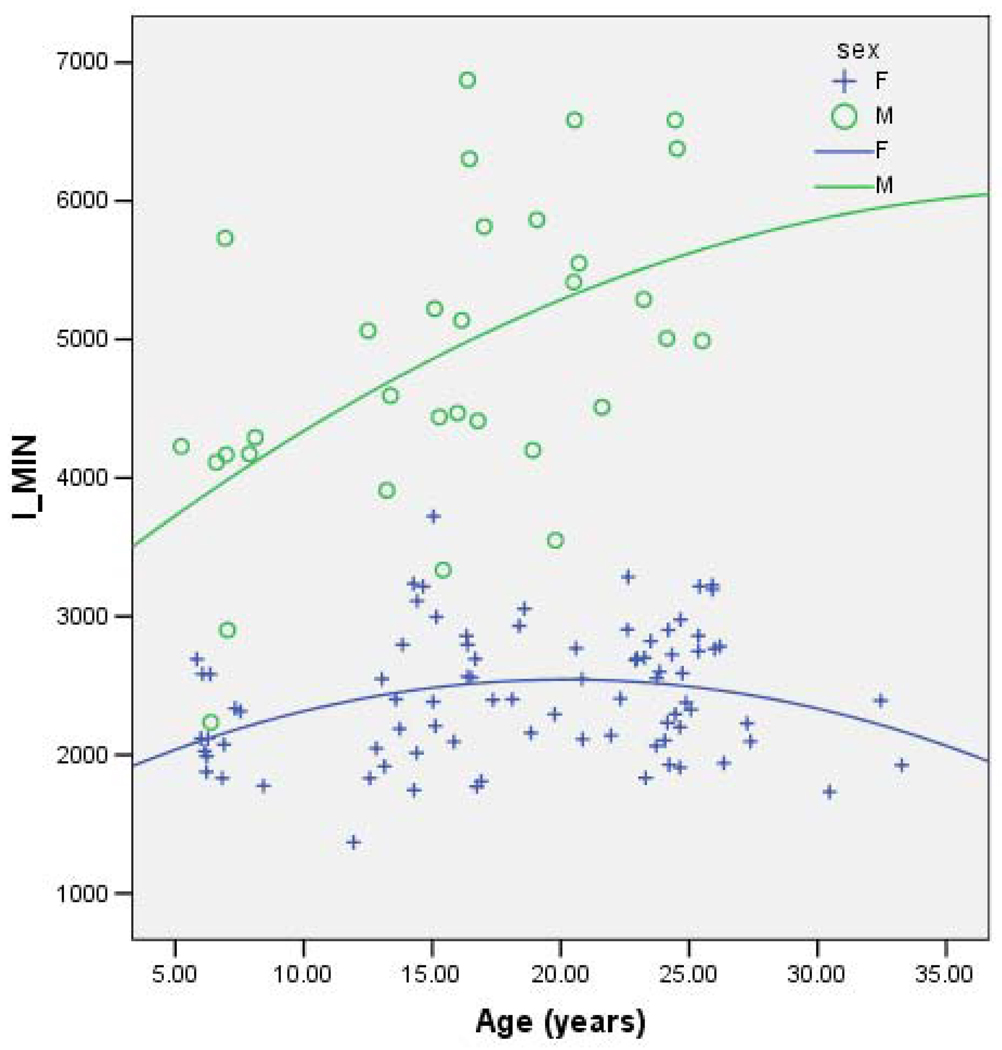
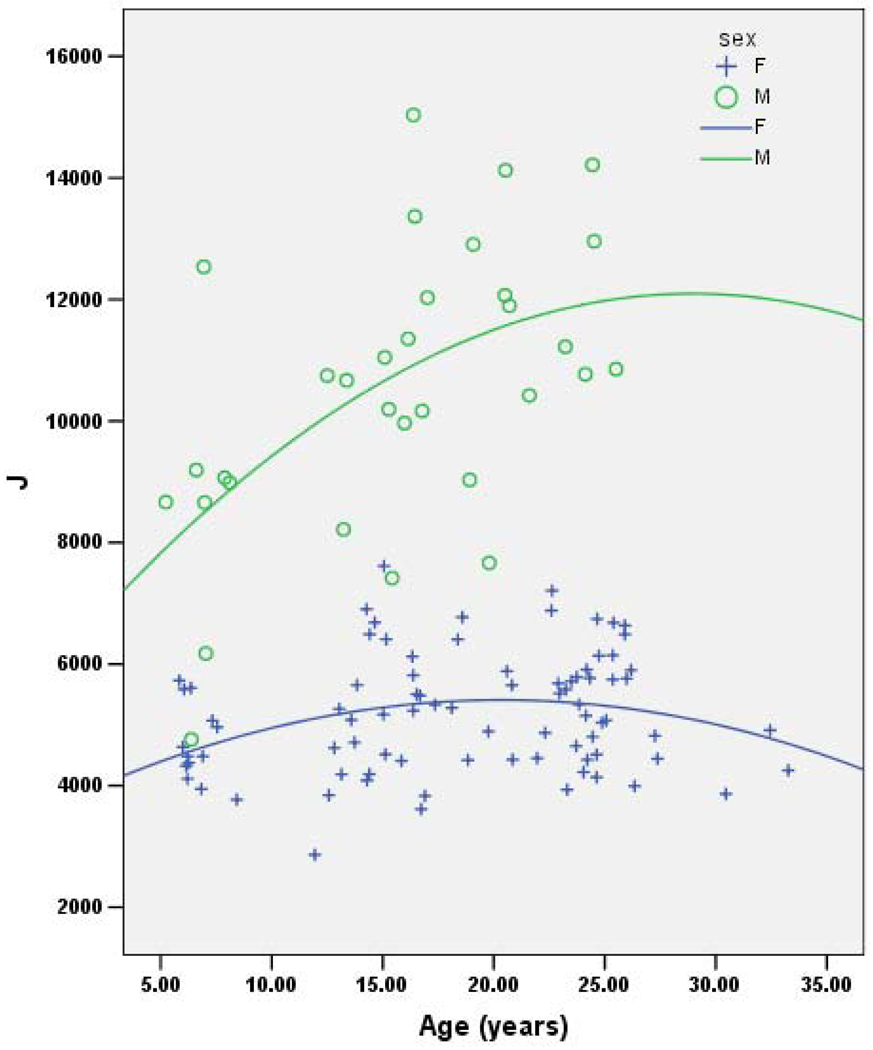
Together, age, sex and age*sex consistently account for ~56% of the variance in each geometric property (Table 2). In each case the effect of female sex is negative and the effect of age is positive, although of a lower magnitude than the effect of female sex. Age-by-sex interaction shows a decrease in the oldest females that is not seen in the oldest males. (Note that this may be due to the lack of older males in the sample.) Figures 1–4 demonstrate the relationship between age by sex for each of the measures of bone geometry and provide the associated r² values. These values indicate that 8–10% of the variation in midshaft geometry is explained by variation in age in females. This percentage is noticeably higher for males, in which 23–36% of the variation in midshaft geometry is explained by variation in age.

Table 2.

Additive genetic effect on bone geometry measures.

Variable	h2	p-value	Variance due to covariates	Total variance due to additive genetic effects
CSA	0.50±0.30	0.0218	54%	23%
IMAX	0.36±0.21	0.0159	59%	15%
IMIN	0.42±0.23	0.0102	59%	17%
J	0.40±0.22	0.0096	59%	16%

h² = heritability estimate = proportion of variance due to the additive effects of genes.

Covariates: age, sex, age*sex

Fig. 1.

I_MAX vs. age for males (r²=0.36) and females (r²=0.08).

I_MAX=Maximum Principal Moment of Inertia

Fig. 4.

CSA vs. age for males (r²=0.225) and females r²=0.08).

CSA=Cross-sectional Area

Additive Genetic Effects

A quantifiable additive genetic effect was detected for each of the geometric properties measured. Table 2 displays the heritability estimate for each variable and indicates the proportion of the total phenotypic variance accounted for by the additive genetic effect. CSA, I__MAX, I__MIN, and J show residual h² values that range from 0.36 to 0.50. Though the standard errors around these estimates are relatively large, all estimates are significant (p=0.02 to 0.01).

Discussion

This study is the first to demonstrate that an additive genetic effect on population-level normal variation in femoral geometry in a non-inbred animal model is detectable and quantifiable, thereby emphasizing that bone geometry is an important potential target of the genetic mediators of bone strength. Residual h² values from 0.36 to 0.50 reflect genetic effects that account for 15% to 23% of the total phenotypic variance in individual geometric properties in this outbred primate population.

The femoral midshaft, though not a common site of fracture, is highly relevant to the study of contributors to variation in bone strength due to the substantial influence of biomechanical forces of the musculature on this region of the femur [51] Our results clearly identify a substantial genetic effect on variation in midshaft femoral geometry; however, we cannot and do not make any claims as to the nature of or the mechanism(s) of action of the genes responsible for this effect based on this particular study. It may be useful, however, to speculate, based on general knowledge about contributors to variation in midshaft femoral morphology, as to how genes might affect geometric variation in this region. Several possibilities involve interaction between genes and biomechanical loading environment including variation in processes involved in muscle growth, mass, or function. It is also possible that the responsible genes may influence musculoskeletal communication or mechnotransduction in bone, or a host of other processes involved in skeletal response to biomechanical forces exerted by the musculature. It is equally possible that the genetic effect we have detected affects variation through mechanisms that have little or nothing to do with the effects of the muscular component. Unfortunately a detailed treatment of this issue requires data we do not have.

The magnitude of the h² estimates of both the size and the shape parameters bode well for the success of subsequent studies to localize the observed genetic effects to specific chromosomal regions and, ultimately, to identify the genes responsible. CSA yielded the strongest heritability (though the significant h² estimates for each of the parameters overlap when the standard errors of the estimates are considered) with an h² value of 0.50±0.30, accounting for 23% of the total phenotypic variance. This result suggests that the strongest genetic effect observed is with regard to bone size; however, genetic effects on bone shape variables are also substantial.

Our data not only show significant heritability of cross-sectional geometry, but also show that increased age is associated with decreased mean cross-sectional geometry measures of bone fracture resistance in the oldest females. This may be related to decreased bone strength in females with age, since proportionately smaller cross-sectional geometries generally will result in decreased bone bending strength. However, as shown by Tommasini et al. [52], biological co-adaptation of morphological and compositional traits contributes to mechanical functionality and skeletal fragility. Bone tissue properties may compensate for variations in bone shape to maintain bone structural integrity under daily loading conditions. Previous research in these baboons shows age related changes in BMD and substantial occurrence of osteopenia in baboon females of advanced age [34, 39, 53]. Future research should focus on the complex interplay between bone geometry, BMD, and bone strength and to what level these changes are under genetic control. To this end, characterization of bone tissue properties in these animals is currently underway. Tissue property data will be integrated with a comprehensive set of data on BMD, cortical bone microstructure, trabecular bone structure, mechanical properties of cortical and trabecular bone, and gross bone geometric properties from the same animals to investigate shared genetic control of these intimately related indicators of bone health.

Our findings are also interesting with regard to the role of genetics vs. sex in variation in bone quality in inbred rodent models [e.g. 13, 15–16, 19–22]. In a study of the effect of genetic loci on mechanically-stimulated bone formation in three congenic mouse strains, Robling et al. [20] report a sex-specific response in which male congenic mice exhibited a higher response vs. controls than did the females vs. controls, independent of bone size. Our results show that the effect of sex on femoral midshaft geometry is minimal after the effect of genes has been removed. Future studies in these baboons to formally test for genotype-by-sex effects (tests that require a much larger sample size than is currently available) are warranted given the clear evidence for sex-specific genetic effects in inbred mice. The results of the study of Robling et al. [20] and ours, taken together, may indicate that the effect of sex on femoral midshaft geometry is largely the result of sex-specific genetic effects.

Genetic effects on bone geometry are only one part of an exceedingly complex system of genetic regulation of bone strength. Rodent studies consistently reveal that various measures of bone quality are subject to independent genetic effects and also to genetic effects that act pleiotropically on the trait in question and on other bone strength-related traits [15–16; 19–20; 22]. Some of these genetic effects are in common with those that affect BMD, while many others are independent [13; 15–16; 19–21]. Furthermore, it is apparent that genes not only influence the individual bone traits, but also influence the functional relationships between and among traits [24]. Bone geometry components of bone strength are an essential part of a complex suite of traits that result from complex interactions among a number of genetic factors.

Dissecting and characterizing the genetic architecture that ultimately underlies variation in bone strength and its myriad of contributing bone density and quality traits will require an animal model, such as the baboon, in which a comprehensive set of traits can be measured and for which the results can confidently be translated to humans. The baboon model affords the opportunity to assess multiple traits (e.g. BMD [35], material and mechanical properties [54], cortical bone microstructure [55], bone geometry [56], and matrix and mineral properties [57]) for both trabecular and cortical bone in the same animals to capture maximum information on variation in bone density and quality in the study animals. This will, for the first time, allow for thorough investigation of the genetic architecture underlying bone strength in a manner that identifies, then incorporates, pleoitropic genetic effects on networks of bone strength-related traits in an outbred population.

Although limited by practical issues surrounding sample acquisition and complicated by environmental heterogeneity, human studies are yielding results that are consistent with those of the animal studies. In sum, the human studies detect genetic effects on bone shape [28–30, 58–59] that result from multiple genes and that are, to a large degree, independent of genetic effects of BMD [29, 58]. The human studies underscore that genetic influences on bone strength are quite complex, with both independent and pleiotropic genetic effects on all aspects of bone strength, including, but probably not limited to, aspects of geometry and density.

This study establishes the potential of the baboon model for the identification of genes that regulate bone geometry in primates. The baboon model is particularly valuable in that it allows for the testing of hypotheses generated in inbred rodent models and in other animal models more distantly related to humans. It also allows for experimental designs, availability of tissues, and comprehensive assessments of multiple integrated bone phenotypes that are not logistically or ethically possible in human populations. Additionally, the use of a captive population provides an environmental consistency across the sample that is not possible in humans. Finally, this model is of particular importance in genetic studies because it provides results that are likely highly relevant to the human condition due to the phylogenetic proximity of baboons to humans.

Fig. 2.

I_MIN vs. age for males (r²=0.32) and females (r²=0.10).

I_MIN=Minimum Principal Moment of Inertia

Fig. 3.

J vs. age for males (r²=0.31) and females (r²=0.08).

J=Polar Moment of Inertia