Agreement between the Heidelberg Retina Tomograph (HRT) Stereometric Parameters Estimated Using HRT-I and HRT-II

Abstract

Purpose

To assess agreement between HRT-I and HRT-II stereometric parameters and to determine whether parabolic error correction (PEC) to the topographies improves agreement.

Methods

UCSD Diagnostic Innovations in Glaucoma Study (DIGS) participants with 2 HRT-II exams (n=380) or 1 HRT-I and 1 HRT-II exams (n=344) acquired on the same day were included. From the group of 380 eyes, 200 eyes were randomly selected to estimate the repeatability coefficients of HRT-II rim area and volume, cup area and volume and mean RNFL thickness parameters (HRT-II control group) and the remaining 180 eyes were used to assess agreement between 2 HRT-II exams (HRT-II study group). Agreement between stereometric parameters of HRT-I and HRT-II exams (HRT-1vs2 study group) were assessed with: 1) no parabolic error correction, 2) HRT PEC, and 3) modified PEC. Bland-Altman plots were used to assess agreement using estimates of bias and clinical limits of agreement (CLA) based on repeatability coefficients.

Results

In the HRT-II study group, agreement between stereometric measurements was good, with no statistically significant biases. For all parameters, differences were within the CLA in 94% of participants. In the HRT-1vs2 study group, there was a small statistically significant bias between the stereometric parameters, but all differences were within CLA for ≥95% of participants. In both study groups, parabolic error correction did not improve agreement.

Conclusions

Agreement between HRT-I and HRT-II stereometric parameters was good and parabolic error correction did not improve agreement. These results suggest that HRT- I and HRT-II examinations can be used interchangeably to detect changes in stereometric parameters over time.

The Heidelberg Retina Tomograph (HRT) is a confocal scanning laser ophthalmoscope commonly used for glaucoma detection and management that includes software to calculate quantitative measurements of the optic nerve head topography, known as stereometric parameters. After manually defining the optic disk margin in HRT topographies, stereometric parameters such as neuroretinal rim area and volume, are automatically estimated. HRT stereometric parameters are in good agreement with clinician assessment,¹ are predictive of the onset of primary open angle glaucoma (POAG) in ocular-hypertensive eyes,² and can discriminate ocular-hypertensive from POAG and normal eyes .^3-5

Historically, HRT scans can be divided into two types, HRT-I and HRT-II, which differ in significant ways but are theoretically compatible. The transverse resolution of HRT-I scans range from 11μm at 10° field of imaging to 23μm at 20° field of imaging with a constant digital imaging area of 256×256 pixels. HRT-II acquires scans at 15° field of imaging with a transverse resolution of 11μm that corresponds to a digital imaging area of 384×384 pixels. HRT-I scans at 10° field of imaging are theoretically comparable with the topographic measurements in the central 10° imaging area of HRT-II scans at 15° field of imaging. Therefore, HRT software allows converting 10° HRT-I scans into HRT-II format (HRTImport module ver. 1.2 or higher) and both scan types can be combined for automated analysis of change over time.

In a recent study, we observed that when an HRT-I baseline exam (reformatted to HRT-II format) was combined with HRT-II follow-up exams in a single longitudinal series, HRT Topographic Change Analysis (TCA) detected significantly more locations with retinal height decrease than when HRT-II exams alone were used (the same baseline date and follow-up dates were used for both series with either HRT-I or HRT–II as the baseline exam).⁶ HRT software (HRTS glaucoma module, ver. 3.1.2.5) applies a data normalization procedure known as parabolic error correction to longitudinal series containing only HRT-II exams. It does not apply the parabolic error correction when HRT-I exams are included in the series with HRT-II exams. Application of the parabolic error correction procedure to longitudinal series containing both HRT-I and HRT-II exams improved the agreement of TCA parameters with that of longitudinal series from the same eyes with same exam dates containing only HRT-II exams.⁶ In addition, a modified parabolic error correction procedure was proposed to remove any influence of measurements within the optic disk margin on the parabolic error estimates.⁶

In this study, we estimate the agreement between HRT-I and HRT-II stereometric parameters. In addition, we evaluate whether agreement between HRT-I and HRT-II stereometric measurements improves with parabolic error correction.

METHODS

Study Participants

All participants in the University of California San Diego (UCSD) Diagnostic Innovations in Glaucoma Study (DIGS) with 2 HRT-II exams acquired on the same day or 1 HRT-I exam and 1 HRT-II exam acquired on the same day were selected. HRT exams with mean pixel height standard deviation (MPHSD) < 50μm, good centering, and even image exposure were considered to be of acceptable quality for analysis after quality review by the UCSD Imaging Data Evaluation and Assessment (IDEA) Center according to standard protocols.⁷ One eye was randomly chosen when both the eyes of a participant were eligible. A total of 724 eyes from 724 participants were included in the study. All eligible participants were divided into 3 study groups described below and the demographics of the 3 study groups are presented in Table 1.

Table 1.

Demographics of participants classified into 3 study groups.

	HRT-II control group (with 2 HRT-II repeat exams)	HRT-II study group (with 2 HRT-II repeat exams)	HRT-1vs2 study group (with 1 HRT-I and 1 HRT-II exam on the same day)
No of eyes (participants)	200 (200)	180 (180)	344 (344)
Median age (range) in years	65.92 (23.65, 89.47)	68.92 (23.43, 93.76)	70.11 (28.98, 93.98)
Glaucomatous optic neuropathy only*	33 eyes (16.5%)	18 eyes (10%)	78 eyes (22.7%)
Glaucomatous visual field damage only†	39 eyes (19.5%)	47 eyes (26.1%)	38 eyes (11.1%)
Glaucomatous optic neuropathy* and glaucomatous visual field damage†	20 eyes (10%)	31 eyes (17.2%)	90 eyes (26.2%)

^*Optic disk with evidence of excavation, neuroretinal rim thinning or notching, localized or diffuse retinal nerve fiber defects indicative of glaucoma or a between-eye asymmetry of the vertical cup-disk ratio more than 0.2 by review of simultaneous stereophotographs by two experienced graders

^†Visual field pattern standard deviation (PSD) with p≤0.05 and/or Glaucoma Hemifield Test outside normal limits by StatPac analysis.

Out of the 724 eyes, 129 eyes had glaucomatous optic neuropathy only, 124 eyes had glaucomatous visual field damage only, and 141 eyes had both glaucomatous optic neuropathy and visual field damage at the time of their respective HRT exams included in this study. Glaucomatous optic neuropathy was defined based on the appearance of the optic disk with evidence of optic disk excavation, neuroretinal rim thinning or notching, localized or diffuse retinal nerve fiber layer defects indicative of glaucoma or a between-eye asymmetry of the vertical cup-disk ratio more than 0.2 by review of simultaneous stereophotographs (TRC-SS, Topcon Instruments Corp. of America, Paramus, NJ) by two experienced graders. Glaucomatous visual field damage was defined as standard automated perimetry (SAP; Humphrey HFA-II, Carl Zeiss Meditec, Dublin, CA) pattern standard deviation (PSD) with p≤0.05 and/or Glaucoma Hemifield Test outside normal limits by StatPac analysis (Carl Zeiss Meditec). The optic disk and visual field status of the eyes in the 3 study groups during their respective HRT examinations are presented in Table 1. The UCSD Institutional Review Board approved the study methodologies and all methods adhered to the Declaration of Helsinki guidelines for research in human subjects and the Health Insurance Portability and Accountability Act (HIPAA).

Group 1: HRT-II control group to estimate the repeatability of HRT-II stereometric parameters

Three hundred and eighty eyes from 380 participants had at least 2 good quality HRT-II exams on same day. Out of the 380 eligible eyes, a set of 200 eyes (HRT-II control group) were randomly selected as control group to estimate the repeatability of HRT-II stereometric parameters under various parabolic error correction settings.

Group 2: HRT-II study group to assess agreement between 2 HRT-II exams

The remaining180 eyes (out of 380) with 2 HRT-II exams on the same day were used to assess the agreement between the stereometric parameters estimated using the current HRT parabolic error correction and the modified parabolic error correction procedure.

Group 3: HRT-1vs2 study group to assess agreement between HRT-I and HRT-II exams

Three hundred and forty four eyes from 344 participants with 1 HRT-I exam and 1 HRT-II exam acquired on the same day with MPHSD < 50μm were selected to assess the agreement between the stereometric parameters estimated using the 3 parabolic correction settings.

HRT Data Preparation

Two HRT exams from each participant (2 HRT-II repeat exams or 1 HRT-I and 1 HRT-II exam) used for analysis from each participant were included in a single HRT progression analysis tab to utilize the same optic disk contour margin coordinates in both HRT exams for stereometric parameter estimation. For each participant, an optic disk contour margin was manually drawn on the first of the 2 exams and was automatically transferred to the second exam by the HRT software (HeyEx software ver. 1.6.1.0) after HRT topograph alignment and data normalization. The second HRT exam was aligned with the first HRT exam for each participant by correcting for horizontal and vertical shifts, rotational misalignment, and any tilt misalignment between the two HRT exams. HRT-I topographies at 10° field of imaging in the HRT-1vs2 study group were converted to HRT-II format using the HRT software (HRTImport module, ver. 1.3). HRT topographies in relative-tilted coordinates of both exams from all participants were exported from the HRT software (as .RAW files).⁸

Parabolic Error Correction

Details of the sources of parabolic error in HRT exams and the parabolic error correction procedure currently available in the HRT software are presented elsewhere.⁶ In brief, when the eye being imaged is at an optimal distance of 10mm from the HRT, the focal plane of the HRT lies parallel to the retinal surface and therefore, the HRT images are optimal without any distortion. When the optimal imaging distance of 10mm is not maintained between the eye and the HRT, the focal plane becomes parabolically distorted. The parabolic distortion is prominent in the periphery compared to the central imaging region. Therefore, in addition to correcting for horizontal and vertical shifts, and rotational and tilt misalignment, the HRT software also corrects for any difference in the parabolic distortion of retinal measurements between baseline and follow-up topographies. Because the parabolic distortion is prominent only in the periphery compared to the central imaging region, currently the HRT software applies parabolic correction only to the 15° HRT-II topographies. Therefore, the current HRT software does not correct for differences in parabolic distortion between exams when there is at least one 10° HRT-I exam in a longitudinal series of topographies. Longitudinal study of HRT topographies with an HRT-I exam at baseline using HRT topographic change analysis (TCA) has shown that differences in parabolic distortion between HRT-I and HRT-II exams of each participant need to be corrected to provide good agreement between the TCA change parameters estimated from a longitudinal series with both HRT-I and HRT-II exams.⁶ In addition, a modified parabolic error correction procedure was proposed to improve the accuracy of the parabolic error correction for both between 2 HRT-II exams and between an HRT-I exam and an HRT-II exam to minimize the influence of deeper optic disk measurements on the parabolic error estimate and to adjust the parabolic error correction based on the imaging area.

In this study, agreement between the stereometric parameter estimates of an HRT-I exam and an HRT-II exam of each study participant, acquired on the same day, were assessed using the following 3 parabolic error correction settings: 1) without HRT parabolic error correction, 2) using the HRT parabolic error correction procedure (HRTS glaucoma module ver. 3.1.2.4), and 3) using the modified parabolic error correction procedure. The algorithmic details of the parabolic error correction procedures are described in detail elsewhere.⁶ In addition, to determine whether the agreement between stereometric parameters of 2 HRT-II exams with the modified parabolic error correction was similar to agreement between 2 HRT-II exams with the current HRT parabolic error correction, we assessed agreement between the stereometric parameter estimates of 2 repeated HRT-II exams using: 1) the current HRT parabolic error correction procedure (HRTS glaucoma module ver. 3.1.2.5), and 2) the modified parabolic error correction procedure.⁶

Stereometric Parameter Estimation

HRT topographies in relative-tilted coordinates without correcting for differences in parabolic distortion were exported using the HRT software (i.e. the second HRT exam aligned with the first HRT exam by correcting for horizontal and vertical shift, and rotational and tilt misalignment exported as .RAW files). The 3 parabolic error correction procedures were implemented in MATLAB (The Mathworks, Inc., Natick, MA) and were separately applied to the HRT topographies. Five HRT stereometric parameters (global rim area and volume above reference plane, global cup area and volume below reference plane, and mean RNFL thickness) were calculated from the mean HRT topographies using MATLAB programs developed to investigate the agreement in stereometric parameter estimates under various parabolic error correction settings. All stereometric parameters were estimated using the standard reference plane (reference plane height calculated as 50μm below the mean topographic height along the contour line between 350° and 356°). The MATLAB routines for stereometric parameter estimation were tested and refined using several test HRT topographies to match with the HRT software estimates to a high accuracy (up to 4 decimal places in mm scale).

Assessing Stereometric Parameter Agreement between HRT Exams

Bland-Altman plots

For all 5 stereometric parameters, mean and difference between the stereometric parameter estimates of 2 HRT exams (i.e., Exam1 and Exam2) were estimated and Bland-Altman mean vs. difference plots were generated.⁹

Stereometric parameter mean of the ith participant m_i=(E x a m_i−1 E x a m_i)2/2

Stereometric parameter difference of the ith participant d_i=(Exam_i1−Exam_i2_i)

Bias between 2 HRT exams and the 95% limits of agreement for the Bland-Altman plots were estimated as described in Appendix A (available online at [LWW insert link]).

Clinical Limits of Agreement

Repeatability coefficients, coefficient of variation, and intraclass correlation coefficients of the 5 HRT-II stereometric parameters were estimated using the stereometric parameter estimates of 2 HRT-II exams acquired on the same day from each of the study participants in the HRT-II control group (n = 200). The repeatability coefficient was calculated as

$$\mathit{Repeatability}\mathit{coefficient}\left({\mathit{RC}}_{\mathrm{HRT}-\mathrm{II}}\right)=1.96\sqrt{2}\times {\mathit{SD}}_W$$

where, SD_w is the within-subject standard deviation (i.e. standard deviation of the repeated measurements) estimated from the 2 HRT-II exam pair of each participant in the HRT-II control group.¹⁰ The within-subject standard deviation (SD_w) represents the size of the measurement error in the HRT-II stereometric parameter estimates due to any inherent measurement imprecision of the HRT-II instrument. Therefore, differences in the stereometric parameter estimates of 2 HRT-II exam pairs of 95% of the participants in the HRT-II study group are expected to be within the repeatability coefficient value of the respective stereometric parameter (i.e. $<1.96\sqrt{2}\times {\mathit{SD}}_W$).¹⁰

Using repeatability coefficients of the HRT-II stereometric parameters (i.e. estimates of inherent measurement error), clinical limits of agreement of each parameter were estimated for inclusion in the Bland-Altman plots to assess agreement between 2 repeated HRT-II exams of each participant in the HRT-II control group. Differences in stereometric parameter estimates between the HRT-II exam pairs are statistically significant only when any differences observed within the 95% limits of agreement in the Bland-Altman plots are outside the clinical limits of agreement. The clinical limits of agreement (CLA) were estimated using the repeatability coefficients of the respective HRT-II parameters (RC_HRT-II) as follows.

$$\mathrm{CLA}=0\pm {\mathit{RC}}_{\mathrm{HRT}-\mathrm{II}}$$

We assumed that the repeatability coefficients of HRT-I stereometric parameters were the same as those of HRT-II stereometric parameters.¹¹ The combined estimate of measurement error in the observed difference between the stereometric parameters of an HRT-I and an HRT-II exam pair was estimated as ^{12, 13}

$${\mathit{RC}}_{\text{combined}}=\sqrt{2{\mathit{RC}}_{\mathrm{HRT}-\mathrm{II}}^2}$$

and the clinical limits of agreement for the Bland-Altman plots were estimated as

$$\mathrm{CLA}=0\pm {\mathit{RC}}_{\mathit{combined}}$$

Definition of a Good Agreement between 2 HRT Exams

The clinical limits of agreement for each of the stereometric parameters were included in the respective Bland-Altman plots of the study eyes in the HRT-II study group and the HRT-1vs2 study group. The agreement between the stereometric parameter estimates of 2 HRT exams was defined using the Bland-Altman plots as follows.

1. Any observed bias between the stereometric parameters of 2 HRT exams was statistically significant only when the 95% confidence interval of the bias estimate does not include the line of equality.

2. Differences observed are statistically significant only when differences of fewer than 95% of participants in the study group are within the clinical limits of agreement (i.e. the observed differences between 2 repeated exam pairs are significantly greater than the instrument measurement error).

For quantitative analysis, 1) bias estimates, 2) percentage of eyes with stereometric parameter differences within the clinical limits of agreement, and 3) number of eyes with observed parameter differences outside the clinical limits of agreement but within the 95% limits of agreement (called outliers) were compared across the 3 parabolic error correction settings.

RESULTS

Repeatability coefficients, coefficient of variation, and intraclass correlation coefficients of the HRT-II stereometric parameters calculated from the HRT-II control group using the 3 parabolic correction settings are presented in Table 2. There was no statistically significant difference among the repeatability coefficients of the HRT-II stereometric parameters estimated using the 3 parabolic error correction settings (95% confidence intervals of the repeatability coefficients overlap).

Table 2.

Repeatability coefficient, coefficient of variation, and intraclass correlation coefficient of stereometric parameters estimated using the HRT-II control group (n = 200).

	Without parabolic error correction			Using the HRT parabolic error correction			Using the modified parabolic error correction procedure
Parameter	RC (95% CI)	COV	ICC	RC (95% CI)	COV	ICC	RC (95% CI)	COV	ICC
Global rim area	0.16 (0.15, 0.18)	0.0432	0.9577	0.16 (0.14, 0.17)	0.0426	0.9587	0.16 (0.15, 0.18)	0.0432	0.9571
Global rim volume	0.11 (0.10, 0.12)	0.1125	0.9068	0.11 (0.10, 0.12)	0.1111	0.9097	0.11 (0.10, 0.12)	0.1138	0.9052
Global cup area	0.16 (0.15, 0.18)	0.1793	0.9828	0.16 (0.14, 0.17)	0.1785	0.9832	0.16 (0.15, 0.18)	0.1796	0.9826
Global cup volume	0.07 (0.06, 0.08)	0.2787	0.9818	0.07 (0.06, 0.08)	0.2767	0.9822	0.07 (0.07, 0.08)	0.2807	0.9816
Mean RNFL thickness	0.06 (0.06, 0.07)	0.1115	0.8951	0.06 (0.06, 0.07)	0.1109	0.8977	0.07 (0.06, 0.07)	0.113	0.893

RC: Repeatability coefficient; COV: Coefficient of variation; ICC: Intraclass correlation coefficient (Parameters with low RC and COV values have high repeatability and parameters with high ICC values have high reliability)

HRT-II Study Group

Figure 1 shows the Bland-Altman stereometric parameter mean vs. difference plots for the participants in the HRT-II study group (n = 180). Estimates of bias between the stereometric parameters of 2 HRT-II exam pairs of the participants in the HRT-II study group are presented in Table 3. For all parameters, except the global cup volume parameter, there was no statistically significant bias between the stereometric parameters of the repeated exams (line of equality is within the 95% CI limits of the bias estimate). Global cup volume differences were not normally distributed and therefore the bias was estimated using a regression fit (p-value of slope < 0.05) as shown in Figure 1d. The global cup volume bias estimate was statistically significant in the higher measurement range (i.e., 95% CI limits of the bias did not include the line of equality at mean global cup volume = 1mm³ in Figure 1d), but the bias estimate is relatively small (bias = -0.036 mm³), and therefore may not be clinically significant. Moreover, stereometric parameter differences were within the clinical limits of agreement in ≥94% of eyes in the HRT-II study group (Table 3).

Figure 1.

Bland-Altman plots to assess agreement between stereometric parameters of 2 HRT-II exams (HRT-II study group) using the current HRT parabolic error correction and the modified parabolic error correction procedure. For all parameters, except global cup volume, there was no statistically significant bias between 2 HRT-II exam pairs of participants in the HRT-II study group. Bias present in the global cup volume parameter is relatively small and may not be clinically significant. Difference in global cup area and volume parameters for at most 3 eyes within the 95% limits of agreement (LOA) were outside the clinical limits of agreement (CLA). For all parameters, parameter differences of ≥95% eyes were within the CLA. Also, there was no statistically significant difference in the agreement using the current HRT parabolic error correction and the modified parabolic error correction procedure indicating good agreement using both methods.

Table 3.

Inferences from the Bland-Altman plots (Figure 1) to assess agreement between the stereometric parameter estimates of 2 HRT-II exams of participants in the HRT-II study group (n = 180).

	Using the HRT parabolic error correction			Using the modified parabolic error correction
Parameter	Bias (95% CI)	% eyes with differences within the clinical limits of agreement	Outliers*	Bias (95% CI)	% eyes with differences within the clinical limits of agreement	Outliers*
Global rim area (mm2)	0.0103 (−0.0002, 0.0209)	95.56% (172 eyes)	0% (0 eyes)	0.0104 (−0.0004, 0.0211)	95.56% (172 eyes)	0% (0 eyes)
Global rim volume (mm3)	0.0024 (−0.0045, 0.0093)	97.22% (175 eyes)	0% (0 eyes)	0.0023 (−0.0047, 0.0094)	96.67% (174 eyes)	0% (0 eyes)
Global cup area (mm2)	−0.0103 (−0.0209, 0.0002)	95.56% (172 eyes)	1.11% (2 eyes)	−0.0104 (−0.0211, 0.0004)	95.56% (172 eyes)	1.11% (2 eyes)
Global cup volume (mm3)	(−0.0003 − 0.0365×mean)†	93.89% (169 eyes)	1.67% (3 eyes)	(−0.0001 − 0.0387×mean)†	93.89% (169 eyes)	1.67% (3 eyes)
Mean RNFL thickness (mm)	0.0004 (−0.0043, 0.0050)	97.22% (175 eyes)	0% (0 eyes)	0.0002 (−0.0046, 0.0050)	97.78% (176 eyes)	0% (0 eyes)

^*Outliers: % eyes with stereometric parameter differences within the 95% limits of agreement, but were outside the corresponding clinical limits of agreement

^†Regression based bias estimate

In the Bland-Altman plots of global cup area and volume parameters in Figures 1c and 1d, stereometric parameter differences in the higher measurement range in a maximum of 3 eyes within the 95% limits of agreement were outside the clinical limits of agreement. The 95% limits of agreement in the Bland-Altman plots for all other parameters were within the clinical limits of agreement (Figures 1a, 1b, and 1e).

Bland-Altman plots for the stereometric parameters estimated using the current HRT parabolic error correction and the modified parabolic error correction procedure were very similar. Therefore, for all stereometric parameters, there was a good agreement (i.e. repeatable parameter estimates) and there was no statistically significant bias between the stereometric parameters of 2 HRT-II exam pairs using the HRT parabolic error correction and the modified parabolic error correction procedures.

HRT-1vs2 Study Group

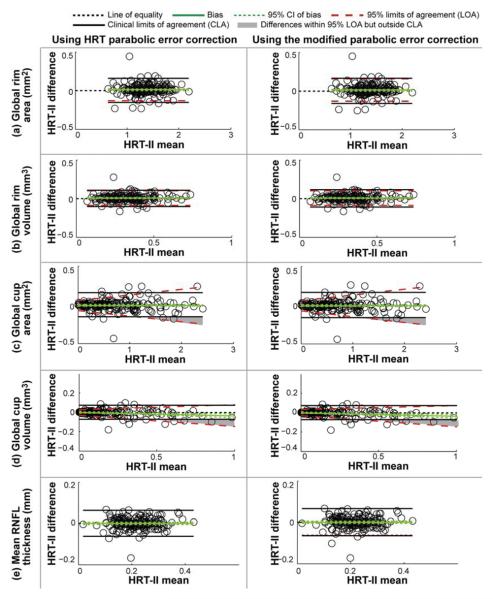
Figure 2 shows the Bland-Altman mean vs. difference plots of the stereometric parameters estimated from the HRT-I and HRT-II exams of the study participants in the HRT-1vs2 study group (n = 344). Stereometric parameter bias observed with the 3 parabolic error correction settings are presented in table 4. For all parameters, there was a statistically significant bias between the stereometric parameters estimated from the HRT-I and HRT-II exam pairs (in all Bland-Altman plots in Figure 2, the line of equality was not within the 95% CI limits of the bias estimate; also see table 4); however, for all parameters, bias was relatively small (≤5% of average parameter values in healthy normals and advanced glaucoma patients). Global rim area and volume, and mean RNFL thickness estimates were somewhat higher for HRT-I exams compared to the corresponding HRT-II exams (positive bias estimates) and the global cup area and volume estimates were slightly lower for HRT-I exams compared to the corresponding HRT-II exams (negative bias estimates). When compared to the stereometric parameter estimates without parabolic error correction, bias between HRT-I and HRT-II stereometric parameters were lower when using the current HRT parabolic error correction and the modified parabolic error correction procedure; however, the differences among the 3 parabolic correction settings were not statistically significant. Also, there was no statistically significant difference in the stereometric parameter bias with the current HRT parabolic correction and the modified parabolic error correction procedure.

Figure 2.

Bland-Altman plots of the stereometric parameters estimated from the HRT-I and HRT-II exam pairs in the HRT-1vs2 study group. For all parameters, there was statistically significant bias between the stereometric parameters estimated from the HRT-I and HRT-II exam pairs. However, the bias is small and may not be clinically significant. Number of eyes with stereometric parameter differences within the 95% limits of agreement (LOA) but outside the clinical limits of agreement (CLA) were relatively small (≤ 4 eyes without using parabolic error correction and ≤ 2 eyes using the HRT parabolic error correction and the modified parabolic error correction) indicating good agreement between the stereometric parameters of HRT-I and HRT-II exam pairs. For all parameters, parameter differences of ≥95% eyes in the HRT-1vs2 study group were within the CLA indicating good agreement between the stereometric parameters of HRT-I and HRT-II exams. In general, application of parabolic error correction to HRT-I and HRT-II exam pairs reduced the bias between HRT-I and HRT-II exam pairs with only a few outliers, however the differences among the 3 parabolic correction settings were not statistically significant.

Table 4.

Inferences from the Bland-Altman plots (Figure 2) to assess agreement between HRT-I and HRT-II exam pair acquired on the same day in the HRT-1vs2 study group (n = 344).

	Without parabolic error correction			Using the HRT parabolic error correction			Using the modified parabolic error correction
Parameter	Bias (95% CI)	% eyes with differences within the clinical limits of agreement	Outliers*	Bias (95% CI)	% eyes with differences within the clinical limits of agreement	Outliers*	Bias (95% CI)	% eyes with differences within the clinical limits of agreement	Outliers*
Global rim area (mm2)	0.0643 (0.0537, 0.0750)	95.06% (327 eyes)	0.87% (3 eyes)	0.0466 (0.0369, 0.0563)	95.06% (327 eyes)	0% (0 eyes)	0.0483 (0.0385, 0.0581)	96.8% (333 eyes)	0% (0 eyes)
Global rim volume (mm3)	0.0202 (0.0141, 0.0264)	97.09% (334 eyes)	0.58% (2 eyes)	0.0134 (0.0081, 0.0188)	97.67% (336 eyes)	0.29% (1 eyes)	0.0132 (0.0077, 0.0187)	97.67% (336 eyes)	0% (0 eyes)
Global cup area (mm2)	(−0.0447 − 0.0290×mean)†	95.06% (327 eyes)	1.16% (4 eyes)	−0.0466 (−0.0563, −0.0369)	95.06% (327 eyes)	0.29% (1 eyes)	(−0.0483 − 0.0581 ×mean)†	96.8% (333 eyes)	0% (0 eyes)
Global cup volume (mm3)	(−0.0083 − 0.0524×mean)†	96.51% (332 eyes)	1.16% (4 eyes)	−0.0089 (−0.0128, −0.0050)	96.22% (331 eyes)	0.58% (2 eyes)	(−0.0061 − 0.0283×mean)†	95.93% (330 eyes)	0.87% (3 eyes)
Mean RNFL thickness (mm)	0.0072 (0.0035, 0.0110)	97.67% (336 eyes)	0% (0 eyes)	0.0047 (0.0014, 0.0081)	97.97% (337 eyes)	0% (0 eyes)	0.0045 (0.0011, 0.0080)	98.26% (338 eyes)	0% (0 eyes)

^*Outliers: % eyes with stereometric parameter differences within the 95% limits of agreement, but were outside the corresponding clinical limits of agreement

^†Regression based bias estimate

For all parameters, stereometric parameter differences were within the clinical limits of agreement indicating good agreement between the stereometric parameters of HRT-I and HRT-II exams (Table 4) in ≥95% of eyes in the HRT-1vs2 study group. In the Bland-Altman plots without parabolic error correction in Figures 2a and 2b, global rim area and volume differences (i.e. HRT-I minus HRT-II) of 2 of the 344 (0.58%) eyes within the 95% limits of agreement were outside the upper clinical limit of agreement. When using parabolic error correction to normalize HRT-I and HRT-II exams, all of the rim area and volume differences between HRT-I and HRT-II exams within the 95% limits of agreement also were within the clinical limits of agreement.

Similarly, in the Bland-Altman plots of cup area and volume parameters in Figures 2c and 2d constructed without the parabolic error correction, the cup area and volume differences (i.e., HRT-I minus HRT-II) of 4 of the 344 (1.2%) eyes within the lower 95% limits of agreement were outside the lower clinical limit of agreement. Application of the parabolic error correction procedure reduced the outliers to 2 eyes.

The 95% limits of agreement for the mean RNFL thickness differences between HRT-I and HRT-II exams were within the clinical limits of agreement using all of the 3 parabolic error correction settings.

For the HRT-II study group, the mean parabolic error at a radius of 500μm from the center of the topography was −0.44 (−0.95, 0.06) μm using the current HRT parabolic error correction and was −2.23 (−3.36, −1.09) μm using the modified parabolic error correction. For the HRT-1vs2 study group, the mean parabolic error at a radius of 500μm was 16.92 (13.84, 20.00) μm using the current HRT parabolic error correction and 12.96 (9.81, 16.12) μm using the modified parabolic error correction procedure.

DISCUSSION

A high repeatability of HRT stereometric parameters is essential for both cross-sectional classification of patients as normal and glaucomatous and for sensitive and specific detection of glaucomatous change over time. In another study, we observed that a parabolic error correction improved the agreement of TCA results between series using both HRT-I and HRT-II exams and series using only HRT-II exams.⁶ In the current study, we found that the agreement between the stereometric parameter estimates of an HRT-I measurement and an HRT-II measurement was good, even without parabolic error correction. Moreover, we found that the agreement between the stereometric parameter estimates of 2 HRT-II repeated measurements was good using the parabolic error correction procedure utilized in the HRT software. Specifically, there was no statistically significant bias between the stereometric parameter estimates between the 2 HRT-II exam pairs.

In the HRT-1vs2 study group, there were statistically significant biases between the stereometric parameters of HRT-I and HRT-II exams of the study participants. However, the values of the bias estimates were relatively small and likely reached statistical significance at least in part because of the large sample size (n=344). For all parameters, stereometric parameter differences in the HRT-1vs2 study group were within the clinical limits of agreement for ≥95% of eyes, indicating good agreement between the stereometric parameters of HRT-I and HRT-II exams.

One of the limitations of this study is that we assumed that the measurement error in the stereometric parameter estimates from HRT-I are the same as those from HRT-II. This assumption is supported by the evidence from a previous study indicating that the repeatability coefficient of HRT-I rim area (in HRT-II format) is similar to the repeatability coefficient of HRT-II rim area (intra-observer/intra-visit repeatability coefficient = 0.28).¹¹ In addition, the repeatability coefficient (0.28) and coefficient of variation (9%) of rim area in the previous study were higher (worse) than the estimates from the current study using the HRT-II control group (global rim area repeatability coefficient = 0.16 and coefficient of variation =4%, see Table 2). Therefore, our narrower estimates of the clinical limits of agreement may be considered as conservative estimates. Another possible limitation is that differences in the stereometric parameter estimates of 2 HRT exams can be influenced by the variability in the coordinates of the contour lines drawn on the HRT exams.¹⁴ However, in this study the 2 HRT exams used for analysis (2 HRT-II exams in the HRT-II control group and 1 HRT-I exam and 1 HRT-II exam in the HRT-1vs2 study group) were included in the same HRT progression tab that allows utilizing the same contour line coordinates in both exams.

Clinical limits of agreement were defined in the Bland-Altman plots to assist in visual assessment of whether differences of ≥95% of the participants in the study group (represented by the 95% limits of agreement) are within the limits of instrument measurement error. It should be noted that other studies have demonstrated the use of repeatability coefficient, coefficient of variation and total error to define the allowable limits of variation in the Bland-Altman plots which we formally called in this study as the clinical limits of agreement.^{12, 13, 15} To our knowledge, there are no predefined clinically allowable limits of bias and measurement errors for HRT stereometric parameters. Therefore, we utilized the repeatability coefficients of HRT stereometric parameters estimated from the HRT-II control group with 2 HRT-II repeated exams to define the clinical limits of agreement. As suggested by Bland and Altman, acceptability of agreement between two methods or instruments should be a clinical decision by considering the domain knowledge rather than applying a statistical criteria.^{16, 17} In this study, the clinical limits of agreement and the 95% limits of agreement were very close, and would likely overlap completely if 95% confidence limits were estimated around these limits. We did not calculate 95% confidence limits around these limits of agreement because in some cases the 95% limits of agreement estimates were based on a mixture of two regression models (see Appendix A - available online at [LWW insert link]). In these cases estimating the standard error for the mixture of regression terms is not straight forward and may require other non-parametric approaches.

As mentioned previously, we assumed that the measurement error is constant over the entire range of measurement to estimate the clinical limits of agreement from the repeatability coefficient. For instance, although this might not be the case for all parameters, the difference and the range of measurement (mean) for global cup area and volume are likely related (see Figures 2c and 2d), possibly due to any relationship between the stereometric parameter estimate and the disease stage,¹⁸ or between the stereometric parameter estimate and the quality of HRT topographies.^19-21 Therefore, the estimated clinical limits of agreement for these parameters (estimated using the repeatability coefficients) may be too wide in the smaller measurement range and too narrow in the higher measurement range (see Figure 2c).

While constructing the Bland-Altman plots, if the difference estimates do not follow normal distribution or when the variance of differences is not constant over the measurement range, a logarithmic transformation,⁹ a ratio ²² or a relative difference of measurements ²³ may provide a normal distribution of differences. Two limitations in using the data transformation are: 1) the Bland-Altman plots will not be in the original measurement units and therefore, may not be easily accessible for clinical inference, and 2) the theoretical difficulty in estimating the clinical limits of agreement for the transformed measurements. In this study, the stereometric parameter differences of some parameters (global rim volume, global cup area and volume) were not normal and/or the variance of differences was not constant over the data measurement range (mean). Therefore, for those parameters, we used regression based Bland-Altman plots to estimate bias and its 95% confidence interval, 95% limits of agreement, and clinical limits of agreement in the original units of the parameters that can also be easier for clinical inference (Figures 1c, 1d, and 2b–2d).

In a previous report, HRT TCA detected poor agreement in detecting glaucomatous changes between longitudinal series containing both HRT-I and HRT-II exams and longitudinal series containing only HRT-II exams of the same participants.⁶ Further, it was observed that it is essential to apply parabolic correction to longitudinal series containing both HRT-I and HRT-II exams to improve the agreement with longitudinal series containing only HRT-II exams. In the current study, stereometric parameters of HRT-I and HRT-II exams estimated without parabolic correction showed good agreement. Even though the parabolic error observed between an HRT-I exam and an HRT-II exam was larger (16.92μm) than between 2 HRT-II exams (-0.44μm), application of parabolic error correction procedures did not improve the agreement between the stereometric parameters of HRT-I and HRT-II or between 2 HRT-II exams. Our results suggest that regional summary measures such as stereometric measures based on mean topographies are less influenced by differences in parabolic distortion between HRT exams than TCA measures calculated from localized retinal height differences between topographies.

The optical design of HRT-I and HRT-II instruments are similar and the transverse resolution of the 10° HRT-I scans are comparable to the 15° HRT-II scans.⁶ Therefore, the HRT-3 software allows combining HRT-I and HRT-II exams in a single longitudinal series after converting 10° HRT-I exams to the HRT-II format.⁶ There are several differences between HRT-I and HRT-II exams: 1) in HRT-I, 3 optic disk scans are manually acquired in succession that constitutes an optic disk exam whereas 3 optic disk scans are automatically acquired in succession in HRT-II. 2) HRT-I has a variable axial resolution from 62 to 128 μm, whereas, HRT-II maintains a constant axial resolution of 62.5 μm between optical sections independent of the scan depth. Despite these differences, in this study, it was observed that the stereometric parameters of HRT-I and HRT-II topographies are comparable.

In summary, there is good agreement between the stereometric parameters of HRT-I and HRT-II exams of same participants without parabolic error correction. These results suggest that HRT- I and HRT-II examinations can be used interchangeably to detect changes in stereometric measurements over time.

APPENDIX A

Estimating Bias between 2 HRT Exams and their 95% Limits of Agreement

For all 5 stereometric parameters, mean and difference between the stereometric parameter estimates of 2 HRT exams (i.e., Exam1 and Exam2) were estimated and Bland-Altman mean vs. difference plots were generated.⁹

Stereometric parameter mean of the ith participant m_i=(Exam1_i+ Exam-2_i)/2

Stereometric parameter difference of the ith participant d_i=(Exam1_i−Exam2_i)

Normal distribution of the parameter difference estimates were tested using Kolmogorov-Smirnov test (p<0.05 indicates that differences in stereometric parameter values do not follow normal distribution). Any relationship between variability in the stereometric parameter difference (i.e. standard deviation of differences) and the measurement range (i.e. stereometric parameter mean) were tested using Kendall's Tau measure (p<0.05 indicates variability in the observed differences is not uniform through out the entire range of the stereometric parameter mean). When the measurement differences follow normal distribution and when the variability in the measurement differences is uniform over the entire range of measurement (p-value of the Kendall's Tau > 0.05), a constant bias and 95% limits of agreement between the stereometric parameters estimates of 2 HRT exams were computed as the mean of the observed differences in stereometric parameter estimates and the standard deviation of the stereometric parameter differences respectively as follows.

$$\mathrm{Bias}\left(\text{constant}\right)\stackrel{-}{d}=\frac{{\displaystyle \underset{i=1}{\overset{N}{\Sigma }}}{d}_i}{N},$$

where, d_i is the stereometric parameter difference of the ith study participant and N is the number of study participants.

$$95\%\text{limits of agreement}=\stackrel{-}{d}\pm t_{\alpha =0.05,\mathit{df}=N-1}\times \text{Standard error}\left(\stackrel{-}{d}\right),$$

where, d̄ is the constant bias estimate.

When the bias and variability of the parameter differences are not uniform through out the entire range of measurement, a variable bias and 95%limits of agreement were estimated using a regression approach ⁹ as follows. A variable bias is estimated by fitting a linear regression line for the parameter differences d_i versus the mean m_i of the two HRT exams as follows.

$$\mathrm{Bias}\left(\text{variable}\right)\widehat{D_i}=b_0+b_1\times m_i,$$

where, m_i is the parameter mean of the ith study participant and b₀ and b₁ are the regression coefficients. The Working-Hotelling 95% confidence band for the bias $\widehat{D_i}$ (regression line) was estimated as

$$95\%\text{Confidence interval of the bias}=\widehat{D_i}\pm W\times \text{Standard error}\left(\widehat{D_i}\right)$$

where, $\widehat{D_i}$ is the variable bias estimate and $W=\sqrt{2F_{(0.95;2,N-2)}}$, and

$$\text{Standard error}\left(\widehat{D_i}\right)=\mathit{MSE}\times \left(\frac{1}{N}+\frac{{(d_i-\stackrel{-}{d})}^2}{{\displaystyle \underset{i=1}{\overset{N}{\Sigma }}}{(d_i-\stackrel{-}{d})}^2}\right)$$

The bias is considered to be significant only when the 95% confidence interval of the bias includes 0.

When the variability of the parameter differences is not uniform through out the entire range of measurement, the 95% limits of agreement were estimated as

$$95\%\text{limits of agreement}=\widehat{D_i}\pm 2.46\times (c_0+c_1{m}_i),$$

where, (c₀ + c₁m_i) is the regression fitted for the absolute value of the residual difference between bias estimate $\widehat{D_i}$ and the observed parameter difference d_i (i.e. $\widehat{D_i}-d_i$ vs. m_i).⁹