Mind the Gap: Bridging economic and naturalistic risk-taking with cognitive neuroscience

Abstract

Economists define risk in terms of variability of possible outcomes whereas clinicians and laypeople generally view risk as exposure to possible loss or harm. Neuroeconomic studies using relatively simple behavioral tasks have identified a network of brain regions that respond to economic risk, but these studies have had limited success predicting naturalistic risk-taking. In contrast, more complex behavioral tasks developed by clinicians (e.g., Balloon Analogue Risk Task and Iowa Gambling Task) correlate with naturalistic risk-taking but resist decomposition into distinct cognitive constructs. We propose that to bridge this gap and better understand neural substrates of naturalistic risk-taking, new tasks are needed that: (1) are decomposable into basic cognitive/economic constructs; (2) predict naturalistic risk-taking; and (3) engender dynamic, affective engagement.

Defining Risk

When economists and clinical psychologists characterize behavior as “risky”, they use the same word but mean different things. Risk in the economics and finance literatures (e.g. [1]) is usually defined in terms of variance of possible monetary outcomes, and risk-seeking is defined as a preference for a higher-variance payoff, holding expected value (EV) constant. In contrast, when clinicians and laypeople identify behaviors as risky—for example, drug use, unprotected-sex, or mountain-climbing—they invoke a broader meaning of the term. Clinicians typically define risky behavior as behavior that can harm oneself or others [2]. Interviews with experienced managers suggest that they also tend to see risk in terms of possible negative outcomes, rather than conceiving it in terms of chance probabilities or some quantifiable construct [3]. Psychometric studies have found that that the lay conception of riskiness encompasses a “dread” dimension that is characterized by lack of control and/or potential catastrophic consequences, and an “unknown” dimension that is characterized by unobservable, unfamiliar, and/or delayed consequences [4].

This gap in definitions is reflected in distinct approaches to studying risk. Neuroeconomics is a field aimed at understanding the neural basis of economic/decision making theories using neuroimaging techniques [5]. The bulk of the neuroeconomics literature has focused (with substantial success) on disentangling the role of specific brain regions in coding economic variables implicated in traditional expectation-based models of risk-taking (see Box 1), or mean-variance models of risk-taking used in financial decision theories (see Box 2). However, economic paradigms have had limited success in predicting individual differences in naturalistic risk-taking, even in the monetary domain. Meanwhile, clinical psychologists and clinical neuroscientists have advanced behavioral paradigms that better predict real-world risk-taking behaviors and resonate more closely with the lay conception of risk. However, they cannot readily be decomposed to identify separate underlying cognitive and neural mechanisms involved in naturalistic risk-taking. In this review, we propose a research approach that combines the conceptual rigor of neuroeconomics with the predictive validity of clinical neuroscience, thus bridging these disciplines. We believe that such an approach will eventually yield a better understanding of the neural mechanisms involved in risky decision-making in both healthy and clinical populations.

BOX 1: Expectation-Based Models of Risk-Taking

Expectation-based models posit that preferences are a function of the magnitudes probabilities of possible outcomes. Consider a prospect (x, p) that offers $x with probability p (and nothing otherwise). A basic decision rule is to choose the outcome maximizes expected value (EV):

$$\mathit{\text{EV}}=px.$$ (1)

Expected value maximization implies risk-neutrality (e.g., indifference between receiving: (a) $50 for sure, or (b) a .5 chance to win $100). To accommodate risk-aversion, expected utility theory [66] allows subjective value of money to decrease wealth increases. This gives rise to a concave utility function, u(․) over states of wealth, W. Decision makers choose the option that maximizes expected utility (EU):

$$\mathit{\text{EU}}=pu(x),$$ (2)

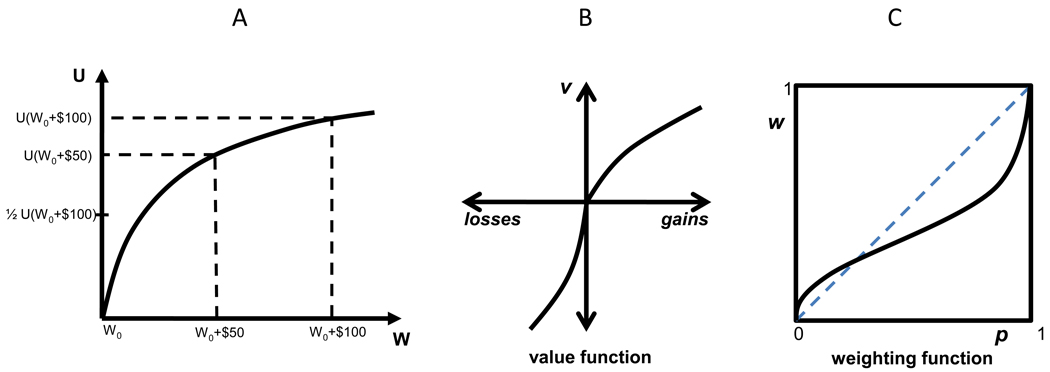
where u(x) represents the utility of outcome x. For example, a concave utility function (u″(x) < 0) implies that gaining $50 (in addition to one’s current state of wealth) adds more than half the utility of gaining $100 (see Figure I, Panel A). Therefore, such utility function implies that a sure $50 is preferred to a .5 chance of $100.

A utility function over states of wealth cannot readily accommodate pronounced risk aversion for gambles involving possible losses [67], nor can it accommodate the commonly observed fourfold pattern of risk preferences: risk-aversion for high probability gains and low probability losses, coupled with risk-seeking for low-probability gains and high probability losses. Prospect theory [68,69] accommodates these patterns by proposing that decision makers maximize the value V of a prospect:

$$V(x,p)=w(p)v(x),$$ (3)

where v(․) measures the subjective value of the consequence x, and w(․) measures the impact of probability p on the attractiveness of the prospect.

A typical value function v(․), displayed in Figure I, Panel B, is characterized by: (1) reference dependence—it is a function of changes in wealth relative to a reference point such as the status quo; (2) diminishing sensitivity—it is concave for gains but convex for losses; and (3) loss aversion—the loss limb is much steeper than the gain limb. Loss aversion accommodates pronounced risk aversion for mixed (gain-loss) gambles, e.g., rejection of a gamble that offers a 50% chance of winning $150 and a 50% chance of losing $100. Tom et al. [70] and De Martino et al. [71] identified neural correlates of loss-aversion in humans. Diminishing sensitivity explains a general tendency toward risk-seeking for gains (as in expected utility theory) but risk-aversion for losses. Reference-dependence allows risk preferences to differ depending on whether prospects are described (framed) in terms of gains or losses relative to different reference points. De Martino et al. [72] studied framing susceptibility in humans using fMRI.

The weighting function w(․), depicted in Figure I, Panel C, captures diminishing sensitivity to probabilities away from natural boundaries of impossibility (p=0) and certainty (p=1). A weighting function is characterized by: (1) overweighting of probabilities near zero; (2) underweighting of probabilities otherwise, especially near 1; and (3) reduced sensitivity to differences between intermediate probabilities. Overweighting low-probability events can supersede the impact of nonlinearities of the value function, leading to risk-seeking for low-probability gains (e.g., the attraction of lottery tickets) and risk-aversion for low-probability losses (e.g., the attraction of insurance). Underweighting moderate to high probabilities reinforces the impact of nonlinearities of the value function, leading to risk-aversion for high-probability gains and risk-seeking for high-probability losses. The weighting function was recently studied using fMRI by Hsu et al. [73], Paulus and Frank [74] and Berns et al. [75].

BOX 2: Risk-Value Models of Risk-Taking

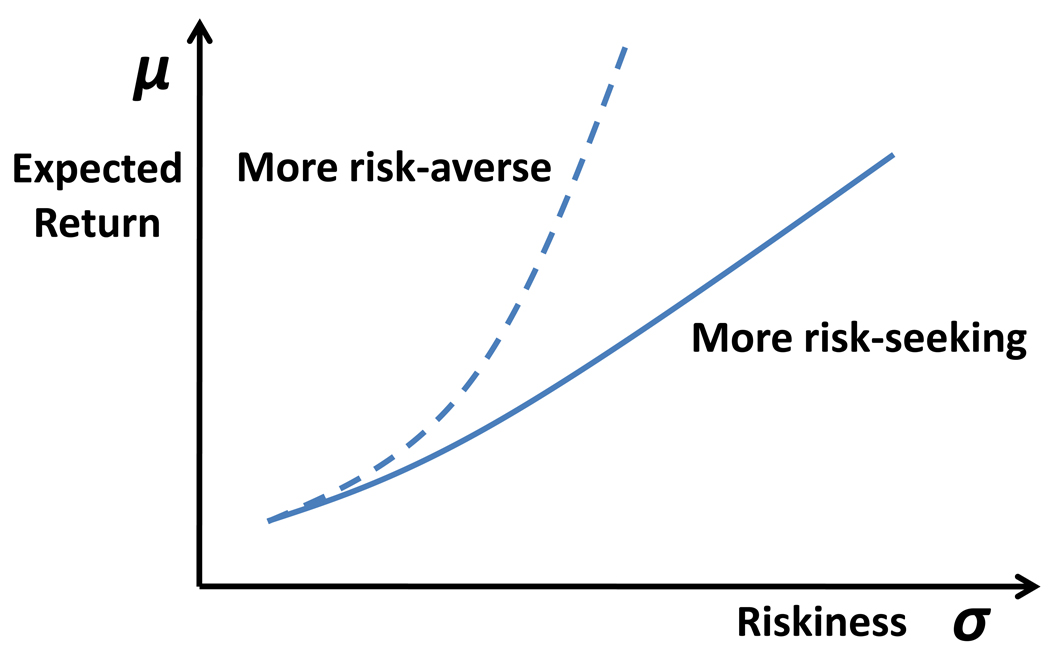
The risk-value approach to risk-taking, advanced in financial decision theory [1] assumes that preferences are a function of two parameters—risk, operationalized as variance (or standard deviation) in the probability distribution over possible outcomes, σ, and expected value, the mean of that distribution, μ. Functions of these two variables define indifference curves reflecting portfolios that a person considers equally attractive (see Figure I). A steeper indifference curve represents greater risk-seeking because it suggests that a given increase in risk of a portfolio must be accompanied by a greater increase in expected value to maintain its attractiveness.

The risk-value approach is appealing from a modeling standpoint because it segregates an objective measure of riskiness from expected reward. Unfortunately, behavioral studies show that perceived riskiness is a function of more than merely variance. For instance, holding variance constant, perceived riskiness can vary with: (a) the absolute magnitude of payoffs, (b) whether they are perceived as gains or losses, and (c) skewness of the probability distribution over outcomes. An alternative approach that can accommodate such behavioral tendencies includes a measure of perceived riskiness that can diverge from objective measures (e.g. [76–78]).

Neuroeconomics of risk perception and risk-taking

Since Knight [6] economists have distinguished decision under risk, in which the decision maker knows the objective probability distribution over possible outcomes, from decision under uncertainty, in which this information is assessed with some degree of vagueness (see Box 3).

BOX 3: From Risk to Uncertainty

Most naturalistic decisions, other than simple games of chance, must be made with incomplete knowledge of the probability distribution over possible outcomes. Subjective expected utility theory (SEU) [79] accommodates uncertainty by simply replacing objective probabilities with subjective probabilities, inferred from choices, which are assumed to accord with standard axioms of probability theory. However, empirical studies of decision under uncertainty raise challenges to this model that can be accommodated by an extension of prospect theory from risk to uncertainty [69]. In particular:

1. Subjective probabilities are not additive. If we ask a bettor how much she is willing to pay to bet on each of several horses entered in a race, her prices would typically sum to more than the total prize paid for picking the winning horse. Under SEU with concave utility this implies subjective probabilities that sum to more than one. This is because the tendency to overweight unlikely events and underweight likely events (captured by the inverse S-shaped weighting function under risk, see Box 1), is amplified by similar bias in the subjective assessment of probabilities [80–82].

2. People generally find uncertainty aversive. Ellsberg [83] devised a problem involving an urn with 50 red balls and 50 black balls, and an urn with 100 red and black balls in unknown proportion. He asserted that most people would rather bet that they would blindly draw a red (black) ball from the urn with known probabilities than a red (black) ball from the urn with unknown probabilities. This aversion to betting on events with vague probabilities (“ambiguity aversion”) has since been validated and modeled in numerous studies (for a review, see [84]). It appears to be driven by an aversion to betting in situations in which one feels relatively ignorant or incompetent [85–87].

Neuroimaging studies of ambiguity aversion have aimed to identify brain mechanisms that code risk and ambiguity. Hsu et al. [88] and Levy et al. [89] conclude that the same regions code both, only to a different degree. However, Huettel et al. [90] and Bach et al. 91] conclude that distinct regions code risk and ambiguity. This disagreement may be due to differences in empirical paradigms, and further studies are needed to sort this out.

Early neuroimaging studies of risk largely relied on task paradigms (see Tables 1 and 2) that manipulate variance in the probability distribution of reward, allowing the identification of neural responses associated with objective risk defined in economic terms. This work has identified risk-related responses in a number of regions, mainly the anterior cingulate cortex (ACC), lateral orbitofrontal cortex (OFC), and insula, all of which are also responsive to monetary gains and/or losses. The lateral OFC and ACC were implicated in a positron emission tomography (PET) study coding risk in terms of increased variance due to differences in probabilities of points lost or gained [7]. These regions, as well as the insula, also responded to different levels of risk in a gambling task, as measured using functional magnetic resonance imaging (fMRI) [8]. The posterior parietal cortex, dorsolateral prefrontal cortex (DLPFC) and anterior insula were found to be more active during choice of risky versus safe options [9]; in addition, fMRI activity levels in the right insula following a negative outcome were negatively correlated with subsequent risky choices. Similarly, in a study using a financial decision-making paradigm (involving uncertainty and learning), increased activity in anterior insula was associated with subsequent switching by participants from a risky to a safe option [10]. Preuschoff et al. [11] segregated risk (defined as variance of possible outcomes) from expected reward in modeling a similar paradigm to [8]. They found that risk was coded in the ventral striatum, but on a more delayed time scale than the phasic response to the reward prediction error signal that is usually observed in this region. This fMRI signal resembled sustained activity of dopamine neurons from electrophysiological recordings in non-human primates [12] (though see [13]), suggesting that dopamine neurons may encode both reward and its variance at different time scales. The authors further used a model-driven approach to study the concepts of risk prediction and risk-prediction errors [14], suggesting that both are encoded by the anterior insula, again at different time scales.

Table 1.

Risk tasks used in the studies cited in the main text

Task Name (Original author)	Study with task cited in main text	Brief task description	Used by other Studies cited in main text
Cambridge Gambling Task [7]	[7]	A token is hidden under one of six boxes that are each one of two colors. Different trials have different ratios between box colors (3:3, 4:2, 5:1). On each trial participants choose a color on which to bet. The color with the higher probability (more boxes) is associated with lower potential gains and lower potential losses of points than the color with lower probability.	[22,23]
Probabilistic gambling [8]	[8]	Two cards are drawn without replacement from a deck containing cards numbered from one to ten (one of each). After the first card is presented, participants bet whether the next card will be higher or lower than the first card. Thus, there is maximal risk when the first card is 5 and 6, zero risk when it is 10 or 1.	[11,14] use a similar task described below
	[9]	On each trial participants must respond quickly to receive a small sure gain of 20 points. A longer wait involves potential higher gain or loss of either 40 points (longer wait) or 80 points (longest wait). All choices have the same expected value.
Behavioral Investment Allocation strategy (BIAS) [10]	[10]	On each trial participants choose between two stocks (gain/loss gambles, one stochastically dominating the other) and one bond (a sure gain of $1). They must learn through trial-and-error the characteristics of the stocks, which change over blocks of trials. Feedback on payoffs of the forgone options are presented on each trial.
[11]	[11,14]	Similar to [8] but participants bet on whether the second card will be higher or lower prior to seeing the first card.
	[15]	Each of 12 stimuli (circles of different colors, numbers, and sizes) is associated with a different reward magnitude and probability. These include all combinations of (100, 200) point rewards with (0, 0.25, 0.5, 0.75, 1) probabilities, plus 300 and 400 rewards with .5 probability. Participants are first trained to learn the probabilities and outcomes associated with each stimulus. Next, on each trial a stimulus appears in one of four quadrants of the screen, and participants indicate which quadrant using a button press.	[16]
	[18]	Experiment 1: On each trial participants choose between a risky and safe option. The risky option is a lottery that offers a 50-50 chance of different outcomes (10£,90£ or 40£,60£) and the safe option offers the participants’ own certainty equivalent for the corresponding risky lottery, as determined in a previous phase of the experiment.	[16]
		Experiment 2: As in Experiment 1, on each trial participants choose between a risky and safe option. This time possible outcomes of the risky option include (10£,50£), (15£,45£), (40£,80£), and (30£,90£), and the safe options offer a range of semi-random values.
The Cups Task [92]	[17]	On each trial participants choose between a risky and safe option. Each trial involves either gains or losses. The options are presented as a choice of cups. The risky option involves 2 to 5 cups—one containing a gain (loss) of $2, $3, or $5 and the others containing $0. If this option is selected the payoff from one cup is selected at random. The safe cup offers a sure gain (loss) $1.
Iowa Gambling Task [38]	[38]	On each trial, participants select a card from one of four decks; two “bad” decks offer a higher reward on most trials but also higher possible loss and lower overall expected value, whereas two “good” decks offer a lower reward on most trials but lower possible loss and higher expected value. Participants learn the nature of the decks through trial-and error. In some versions of the task, the probabilities are not stationary.	[39]
Balloon Analogue Risk Task [44]	[44]	On each trial, participants pump a simulated balloon without knowing when it will explode. Each pump increases the potential reward to be gained but also the probability of explosion, which wipes out all potential gains for that trial. In most studies balloon explosion probabilities are drawn from a uniform distribution, and participants must learn explosion probabilities through trial-and-error.	[52,53]
Devil’s Task [55]	[54]	This task is a forerunner to the BART: On each trial, participants decide how many of seven treasure chests to open. They are informed that six boxes contain a prize and one box contains a “devil” that will cause them to lose all their potential gains on that trial. Similar to the BART, participants make sequential choices and after opening each chest, decide whether to continue to the next chest or cash-out their earnings to that point.

Table 2.

Decomposition of specific constructs that are isolated by tasks listed in Table 1

Studies with task cited in main text	Contrast used in study	Uncertainty	Variance of outcomes	Probability of gain	Probability of loss	Expected value	Magnitude of gain	Magnitude of loss
[7,22,23]	Risk conditions versus a control task		+	+	+	+	+	+
[8]	Different risk levels during anticipation of second card		+	+	+	+
[9]	Risky options vs. Safe option		+	+	+		+	+
[10]	Compared to a rational choice determined by a computational learning model	+	+	+	+	+	+	+
[11,14]	Contrast 1 - Variance of outcomes		+	+	+
	Contrast 2- EV			+	+	+
[15]	Contrast 1 – Variance of outcomes	?	+	+			+
	Contrast 2- EV	?		+		+	+
[18]	Contrast 1 – Risky option vs. Safe		+				+
	Contrast 2 – EV					+	+
[17]	Risky cups vs. Safe cup		+	+	+	+*	+	+
[38]	Low EV Decks vs. High EV Decks	+	+	+	+	+	+	+
[44,52,53]	Pumping the balloon	+	+	+	+	+	+	+
[54]	Average number of chests open		+	+	+	+	+	+

Although tasks are often described as identifying a single cognitive or economic construct of interest, many tasks also engage additional potentially confounding processes. This Table presents a decomposition of the specific constructs that are engaged by the tasks listed in Table 1. For each task, the contrast of interest that was used to measure risk (or expected value) is analyzed to identify the cognitive or economic constructs it also manipulated (listed in the top row of the Table).

Note: Some of the studies listed below accounted for these confounds using parametric statistical modeling.

+ Indicates that the relevant construct (column) is engaged by that contrast (row)

? Indicates unclear involvement of the relevant construct in the task

^*In one condition the expected value is equal.

In sum, neuroeconomic studies of risk have implicated many of the same regions involved in processing of monetary gains and/or losses, putatively related to the midbrain dopamine system and its targets, though potentially using different coding schemes and time scales within those same systems.

Individual risk attitudes

A first step towards linking economic models to naturalistic risk-taking is to identify neural systems in which activity is correlated with individual differences in economic risk attitudes. Recent work has shown that many (but not all) of the areas that exhibit sensitivity to economic risk (i.e., variance in the probability distribution over possible outcomes) also reveal individual differences that covary with risk preferences. Tobler et al. [15] found positive associations between risk-aversion and fMRI signals coding variance of outcomes in lateral OFC, and positive associations with risk-seeking in more medial OFC regions. The same authors [16] also found an EV-related fMRI signal in lateral OFC that was positively correlated with risk-aversion and negatively correlated with risk-seeking. Another study found risk-seeking to be negatively correlated with the fMRI signal in dorsomedial prefrontal cortex (DMPFC), whereas positive correlations were found with reward magnitude signals in ventromedial PFC [17]. A fourth study reported that the fMRI signal in inferior frontal gyrus (IFG) increased during low-risk gambles and this increase was positively correlated with individual risk-aversion [18]. Collectively, these studies suggest that individual economic risk preferences modulate brain activity in the regions implicated in risk processing: risk-aversion was correlated with lateral PFC regions in OFC, DMPFC and IFG (adjacent to DLPFC) whereas risk-seeking was positively correlated with activity in more medial PFC regions. Interestingly, the insula was not found to code individual risk attitudes (for more on insula involvement in risk-taking see [19]). The correlation of risk-attitudes with areas in inferior prefrontal cortex accords with previous studies implicating this region in cognitive control and inhibition (see [20]). The dorsolateral prefrontal cortex (DLPFC), a region previously implicated in self-control during decision-making (e.g. [21]), has also been implicated in modulation of risk attitudes. Knoch et al. [22] used repetitive Transcranial Magnetic Stimulation (rTMS) to suppress activity in the DLPFC, which led to increased risk-seeking on the Cambridge Gambling Task [7]. Conversely, when excitability of the same regions was increased using transcranial Direct Current Stimulation (tDCS), subjects exhibited increased risk-aversion [23]. Thus, the DLPFC may play a key role inmodulation of risk attitudes, even though it has not been implicated in representation of risk per se.

Despite this success in mapping neural building blocks of economic risk-taking, such studies have seldom, if ever, attempted to examine the association between individual differences in neural response to economic risk and naturalistic risk-taking behavior. In fact, laboratory measures of economic risk attitudes have rarely been used to predict naturalistic risk-taking (or perhaps they have just rarely succeeded). A small number of studies have had modest success predicting naturalistic financial risk-taking from laboratory measures (e.g., hog farmers who were more risk-averse for lotteries were also more likely to hedge on the hog futures market [24]). In other studies, researchers have predicted naturalistic risk-taking behaviors from psychometric measures of risk-tolerance (e.g., citizens who said they were more risk tolerant were more likely to move from one part of Germany to another [25]) or the association between distinct real-world manifestations of risk-taking (e.g., choice of labor contracts with different levels of income risk could be predicted from other naturalistic behaviors such as expenditures on gambling and insurance [26]).

It bears mentioning that there may be inherent limits to the proportion of variance in naturalistic risk-taking behavior that can be explained using any measure of risk preference. First, there is substantial variation in individual risk preferences across life domains, though these likely reflect differences in perceived risks and/or benefits of such activities [27,28]. Second, a number of situational variables can influence risk perception and risk preferences. These range from the way in which prospects are framed (e.g., interms of gains and losses [29]), depicted (e.g., as a bar graph or density function [30]) or labeled (e.g., Republicans reminded of their political affiliation were subsequently more attracted to options labeled “conservative” [31]) to the way in which preferences are elicited (e.g., by pricing risky prospects versus choosing between them, [32,33]). Third, economic risk-preferences covary with state variables including specific emotions (e.g., people are apparently more risk-seeking when angry than fearful [34]) and motivational state (e.g., whether one is in an aspirational or protective mode [35]).

Characterizing the components of naturalistic risk-taking behavior

The neuroeconomic perspective on risk-taking has begun to lay a foundation for understanding how the brain responds to risky monetary payoffs, but the question remains how to bridge the gap with risk-taking in situ. To do so we first need to characterize risk-taking in naturalistic environments. A popular inventory of such behaviors, the Domain-specific Risk-attitude scale (DOSPERT; [28]) identifies five domains of risk-taking (recreational, financial, health, social and ethical) that differ across individuals according to their self-reports. Such behaviors (e.g., extreme sports, investing in stocks, smoking, taking the unpopular stand in a social discussion, cheating in a tax return) all entail a potential negative outcome and variance of possible outcomes. However, we argue that willingness to accept variance in outcomes or negative outcomes does not fully capture what drives participation in such “risky” behaviors.

In fact, several factors distinct from the economic conception of risk preference may contribute to what has been called “risky” behavior in the field. Consider, for example, the choice to engage in unprotected sex. This decision could stem from: (1) underestimating the likelihood of negative consequences; (2) discounting possible negative consequences because they are in the future; (3) bowing to social pressure or perceived norms. Only after we control for such factors, and also related constructs such as sensation-seeking and impulsivity, can we distill what might be properly deemed individual “risk preference” and identify economic factors contributing to naturalistic risk-taking behavior.

Even if we are successful in mapping distilled measures of naturalistic risk-taking onto economic variables, these “cold” cognitive constructs still fail to fully capture what are largely emotional decisions. In an influential survey, Loewenstein et al. [36] observe that risky decisions are driven not just by anticipated emotions that a decision maker associates with possible consequences, but also “anticipatory” emotions experienced at the time of the decision. While these researchers emphasized negative emotions such as fear and anxiety, we suggest that positive emotions may also play an important role in risk-taking behavior: e.g., the exhilaration of waiting for a roulette ball to land in its slot or driving a car beyond the speed limit (see also [37] on “need-for-arousal”).

Decomposing current naturalistic risk-taking tasks

Well-designed neuroeconomic tasks have been relatively decomposable (see Table 2), but as discussed above they often lack external validity. Two prominent behavioral paradigms have had unique success predicting naturalistic risk-taking behaviors. The first is the Iowa Gambling Task (IGT), described in Table 1. The original study employing this task showed that patients with vmPFC lesions who exhibited “real-life” risky behaviors were impaired on the task [38] (for a recent fMRI study with healthy subjects showing differences in this region see [39]). Patients with lesions in the amygdala, DLPFC, OFC or DMPFC, and other clinical populations such as drug abusers, alcoholics and pathological gamblers were also found to be impaired on the IGT (for a critical review see [40]). While the “bad” decks are indeed “riskier” in an economic sense, increased variance in this case is confounded with lower expected value. Moreover, risk preferences are confounded with the need to learn the long term EV of the decks (for critiques, see [41,42]). Thus, it is almost impossible to determine the degree to which individual differences in behavior in the IGT reflect differences in learning, risk attitudes, and/or sensitivity to gain/loss magnitude (however, a computational model of distinct components of the task is presented in [43]).

A second task that has successfully predicted naturalistic risk-taking is the Balloon-Analogue-Risk-taking task (the “BART”) [44], described in Table 1. The average number of pumps a person tolerates in the task was found to correlate with self-reported drinking, smoking, stealing and substance use in healthy adults and adolescents [44–50], but interestingly, not with performance on the IGT [44] (but see [51]).

Recent neural research on the BART implicates the DLPFC in risk-taking. Using fMRI, Rao et al. [52] compared active risk-taking/pumping versus passive pumping on the task, and found that DLPFC activity was higher during active risk-taking. Further evidence for the role of the lateral PFC in risk-taking in the BART was provided in a study [53] that used bilateral tDCS to putatively enhance excitability in DLPFC, resulting in decreased risk-taking/pumping behavior in the BART. Gianotti et al. [54] used the similar Devil’s task [55], which requires no learning (see Table 1). They reported that greater risk-taking was positively correlated with lower tonic EEG activity (delta and theta bands) in right lateral PFC, consistent with a negative association between lateral PFC engagement and risk-taking. Jentsch et al. developed a version of the BART for rodents [56] and found that temporary inactivation of a region homologous to the human DLPFC resulted in increased variability in behavior and sub-optimal performance, whereas inactivation of the OFC homologue resulted in overall decreased risk-taking. Together, these results suggest a convergence in the neural basis of risky choice between neuroeconomic paradigms and more naturalistic tasks: increased activity in the DLPFC (primarily in the right hemisphere) underlies risk-avoidance and self-control, whereas increased activity in the OFC underlies risk-taking.

Although the BART is attractive due to its predictive validity, it does not lend itself well to decomposition. In particular, a task analysis reveals that every pump increases the probability of explosion and the variance of possible outcomes, but (like the IGT) this increased risk is confounded with varying expected value. Moreover, because the probability distribution of explosions is unknown to subjects, this task also involves learning under uncertainty (see [57] for a computational model of behavior in the BART and [51] for comparison of models of BART and IGT). A modified version of this task in which “explosion” probabilities are transparent remains correlated with self-reported naturalistic risk-taking [58], suggesting that these associations do not necessarily reflect the learning component, but decomposition of this task remains challenging.

Exhilaration and Tension in naturalistic risk-taking

Despite the BART’s limitations, it has appealing features. First, as discussed above it predicts self-reported measures of naturalistic risk-taking reasonably well and distinguishes clinical populations. Second, the BART employs a familiar naturalistic metaphor that engenders a strong affective response—a sense of escalating tension and exhilaration—that mimics the affective phenomenological experience of risk-taking in naturalistic environments, which may partially explain its capacity to predict naturalistic risk-taking behaviors.

Another task that appears to tap directly into the affective dimension of risk-taking is a variation of the “near-miss” paradigm (see [59]) developed by Clark et al. [60]. The task imitates a slot machine with two reels, each with six icons—the icon on the first reel is fixed either by the participant or a computer, and the second reel spins on each trial. Participants rated “near-miss” losses in which the second reel stopped one position away from a “match” as more unpleasant than “far-miss” losses in which the second reel was farther from matching. Interestingly, they also rated near misses as more motivating for continued play than far miss losses. This was only the case for trials on which participants had personal control by fixing the position of the first reel themselves. Areas in both anterior insula and ventral striatum were found to be more active during near misses versus full misses (although both reflect the same objective loss, they entail varying degrees of subjective regret for one’s choice, cf. [61]). Moreover, Chase and Clark [62] found that among gamblers, fMRI activity in dopaminergic midbrain regions during near miss events correlated positively with gambling severity. These results suggest that individual differences in risk attitudes (at least in the case of gambling) may be driven by individual differences in dopaminergic response (see [63]), in this case to events coding loss but which might simultaneously be experienced as exhilarating and motivating for further action. It is worth noting that reward prediction error signals in the striatum reach their peak during adolescence [64], a time of heightened risk-taking, consistent with a role for dopamine in risk-taking.

Bridging the gap

To bridge the gap between economic models and naturalistic risk-taking behaviors, we suggest that the former models must incorporate both the positive and negative affective dimensions of risk-taking, through empirical paradigms that can capture them in more compelling ways. We thus propose three criteria for such new laboratory paradigms:

1. Decomposable: The tasks must allow for decomposition and analysis in terms of cognitive and economic primitives (e.g., magnitude of gains and losses, probabilities), both for the sake of conceptual clarity and as a prerequisite for identifying neural mechanisms using functional imaging and other tools of behavioral neuroscience.

2. Externally valid: The tasks must exhibit empirical associations with naturalistic risk-taking behaviors in healthy or clinical populations and/or allow us to distinguish between them. Naturally, a requirement for validity is reliability of such measures (on reliability of fMRI see [65]).

3. Emotionally engaging: The tasks must capture not only static and cognitive dimensions of risk-taking (e.g., an evaluation of the probability distribution over possible outcomes) but also engage dynamic and affective dimensions (e.g., the hope, exhilaration, tension, and/or fear that may accompany risky behaviors).

To our reading, no single task yet conforms to all three criteria. We argue that new tasks that do conform will offer greater promise in helping identify behavioral and neural factors that predict naturalistic risk-taking. For instance, the recently developed Columbia Card Task (CCT) [37] is dynamic and affective, and appears to be decomposable. It remains to be seen whether cognitive primitives of the CCT can be isolated using current modeling techniques in a neuroimaging study, and its predictive validity is yet to be formally established.

As noted above, behavior in any task may vary systematically with state variables, such as arousal or motivation of participants at the time of elicitation, just as naturalistic risk-taking does. This presents both a challenge to establishing predictive validity and an opportunity to determine moderators of emotional engagement.

Concluding remarks

We still have a great distance to cover in bridging the gap between economic and naturalistic risk-taking, which we suggest will require development of new empirical paradigms. Many existing paradigms exhibit one or two of the three criteria suggested above. For instance, most tasks in the neuroeconomics literature are decomposable but are not especially predictively valid or emotionally engaging. On the other hand, tasks in the naturalistic side of the divide, such as the BART and IGT tend to be emotionally engaging and predictively valid, but not particularly decomposable. The “near-miss” paradigm [60,62] provides another example of an emotionally engaging and externally valid task that is decomposable; however, it does not entail a risky decision and thus is not designed to decompose performance into economic variables related to risk-taking. We propose that progress in understanding the neural systems underlying naturalistic (including clinical and abnormal) risk-taking awaits development of tasks that fulfill all of these criteria (see also Box 3).

Box 3. Questions for future research

• How to do neural representations of risk differ between static or description-based tasks and dynamic or experience-based tasks (see [93])?

• What are the neural correlates of alternative, noncompensatory strategies for risky choice, such as choosing the option that minimizes overall probability of losing (for an early attempt see [94])?

• To what extent do neural representations of risk differ across different domains of real-world naturalistic risk taking, and to what extent is there a “common pathway” or set of regions for risk processing in the brain?

• To what degree are representations of risk coded by patterns of activity across relevant regions (on this method see [95]) rather than their overall activation?

Figure_Box1.

(A) An Illustration of How Expected Utility Theory Explains Risk-Aversion: Utility (U) as a function of increasing Wealth (W), starting at an initial level (W0). The utility of gaining $50, U(W0+$50), is more than half the utility of gaining $100, ½ U(W0+$100). Thus, according to this function, the individual would rather receive $50 for sure than face a ½ chance of gaining $100 (and nothing otherwise). (B) A Representative Prospect Theory Value Function depicts subjective value (v) of losing or gaining a particular amount of money relative to the reference point; (C) A Representative Prospect Theory Probability Weighting Function depicts the decision weight (w) as a function of objective probability (p).

Figure_Box2. Indifference Curves for a Relatively Risk-Averse Individual and a Risk-Seeking Individual in a Mean-Variance Model.

Lines are indifference curves that depict the mean (μ) and standard deviation (σ) of portfolio returns that an individual finds equally attractive. The dashed line represents a relatively risk-averse individual and the solid line a relatively riskseeking individual.