Conditional Differences in Mean Reaction Time Explain Effects of Response Congruency, but not Accuracy, on Posterior Medial Frontal Cortex Activity

Abstract

According to the conflict-monitoring model of cognitive control, the posterior medial frontal cortex (pMFC) plays an important role in detecting conflict between competing motor responses. Consistent with this view, pMFC activity is greater in high-conflict trials (e.g., incongruent trials and errors) than in low-conflict trials (e.g., congruent trials and correct responses) of distractor interference tasks. However, in both low- and high-conflict trials, pMFC activity increases linearly with reaction time (RT). Thus, heightened pMFC activity in high-conflict trials may simply reflect the fact that mean RT is longer in high-conflict than in low-conflict trials. To investigate this hypothesis, we reanalyzed data from a previously published fMRI study in which participants performed an event-related version of the multi-source interference task. Critically, after controlling for conditional differences in mean RT, effects of response congruency on pMFC activity were eliminated; in contrast, effects of response accuracy on pMFC activity remained robust. These findings indicate that effects of response congruency on pMFC activity may index any of several processes whose recruitment increases with time on task (e.g., sustained attention). However, effects of response accuracy reflect processes unique to error trials. We conclude that effects of response accuracy on pMFC activity provide stronger support for the conflict-monitoring model than effects of response congruency.

Introduction

Response conflict is a ubiquitous challenge in human cognition that is linked to increased reaction time (RT) and reduced accuracy. Thus, a major goal of cognitive neuroscience has been to determine how the brain detects and resolves such conflict during the performance of cognitive tasks (Banich et al., 2000; MacDonald et al., 2000; Weissman et al., 2003; van Veen and Carter, 2005). According to the conflict-monitoring model of cognitive control, the posterior medial frontal cortex (pMFC) signals the presence of response conflict to the dorsolateral prefrontal cortex, which, in turn, increases the recruitment of cognitive control in subsequent trials (Botvinick et al., 2001; Yeung et al., 2004). Consistent with this model, pMFC activity is greater in high-conflict trials (e.g., incongruent trials and errors) than in low-conflict trials (e.g., congruent trials and correct responses) of distractor interference tasks (Botvinick et al., 1999). Moreover, functional connectivity between the pMFC and the dorsolateral prefrontal cortex is greater in incongruent than in congruent trials (Fan et al., 2008).

Nonetheless, recent findings present a potential challenge for the conflict-monitoring model. Specifically, in both low- and high-conflict trials, activity in a widespread network of frontal and parietal regions that includes the pMFC increases linearly with RT (Weissman et al., 2006; Hahn et al., 2007; Yarkoni et al., 2009). Given that mean RT is slower in high-conflict than in low-conflict trials, these findings suggest that effects of response conflict on pMFC activity might be explained, either fully or in part, by conditional differences in mean RT. For example, activity in congruent trials with relatively slow RTs might equal activity in incongruent trials with relatively fast RTs. Consistent with this possibility, effects of various experimental manipulations on brain activity are sometimes eliminated, or even reversed, after controlling for conditional differences in mean RT (Christoff et al., 2001; Epstein et al., 2007). However, no previously published study has investigated whether effects of response conflict on pMFC activity can be explained by conditional differences in mean RT (but for data supporting this hypothesis, see Grinband et al., in press).

Such a result would complicate the interpretation of conflict-related activity in the pMFC. Indeed, if conflict-related activity in the pMFC could be explained by conditional differences in mean RT, then such activity could reflect any of several processes whose recruitment increases with RT. For example, Yarkoni et al. (2009) proposed that participants must sustain attention on a given trial until a response is made. Thus, effects of response conflict on pMFC activity might index greater attentional demands in high-conflict than in low-conflict trials, rather than conflict detection or resolution per se. Analogously, such effects might reflect greater demands on other processes that are likely recruited until a response is made, such as arousal or effort. For instance, task performance evokes increased autonomic arousal relative to the inter-trial interval (Kobayashi et al., 2007), and such task-related arousal may persist longer on trials with slow RTs. Similarly, slow RTs may recruit effortful performance-monitoring processes to compensate for prior lapses of attention (Weissman et al., 2006). Consistent with these alternative views, pMFC activity increases with demands on attention (Orr and Weissman, 2009), autonomic arousal (Critchley et al., 2003), and cognitive effort (Mulert et al., 2005).

In the present study, we therefore investigated whether effects of response conflict on pMFC activity could be explained by differences in mean RT between high-conflict and low-conflict trials. To this end, we reanalyzed data from a recently published functional MRI study of conflict effects in the pMFC (Fitzgerald et al., 2010). This experiment used the multi-source interference task (MSIT; Bush et al., 2003), a paradigm known to produce robust neural and behavioral effects of response conflict. To determine whether effects of response conflict on pMFC activity could be explained by conditional differences in mean RT, we estimated effects of response congruency (i.e., incongruent versus congruent trials) and response accuracy (i.e., errors versus correct responses) on pMFC activity both before and after statistically correcting for such differences.

Materials and Methods

Participants

Twenty-one healthy adults participated in the experiment (mean age = 39.8 years; six female). Participants were screened for neurological or psychiatric illness, head trauma, and mental retardation. Analyses of these data unrelated to the present investigation were described in previous reports (Stern et al., 2009; Fitzgerald et al., 2010).

Task

Participants performed an event-related version of the MSIT, which is known to activate a network of brain regions involved in cognitive control (Bush et al., 2003). The task is described briefly here; a more detailed description can be found in a previous report of these data that did not analyze trial-by-trial variations of RT (Fitzgerald et al., 2010). In each trial, participants identified the unique digit (1, 2, or 3) among a set of three alphanumeric characters. The digits 1, 2, and 3, respectively, were mapped to the thumb, index finger, and middle finger of the right hand. In incongruent trials, the unique digit appeared among digits (e.g., “311”), and its position (e.g., left) was incompatible with its associated response (e.g., middle finger). In congruent trials, the unique digit appeared among letters (e.g., “x2x”), and its position (e.g., center) was compatible with its associated response (e.g., index finger).

Participants completed five runs of the MSIT, each of which contained 24 incongruent trials and 24 congruent trials. In each trial, the stimuli were presented for 500 ms, followed by a 2500 ms fixation cross. Twelve 3000 ms fixation trials were randomly interspersed among MSIT trials in each run.

Data acquisition

Neuroimaging data were collected using a 3T GE Signa MRI scanner. Functional images were acquired using a reverse spiral sequence (repetition time, TR = 2000 ms; echo time, TE = 30 ms; flip angle, FA = 90°; field of view, FOV = 20 cm). Each functional volume included 40 slices of thickness 3 mm with an in-plane resolution of 3.44 by 3.44 mm. During each functional run, 94 volumes were acquired; the first four volumes were discarded to allow for the equilibration of the BOLD signal. High-resolution T1-weighted images were collected for subsequent spatial normalization (3D SPGR, slice thickness 1.5 mm, 0 skip).

Data analysis

Pre-processing

Functional images were slice-time corrected, realigned to the first volume, spatially normalized to the MNI brain atlas, and spatially smoothed using a Gaussian kernel (FWHM = 6 mm) as described by Fitzgerald et al. (2010).

Model estimation

Functional data were analyzed using the general linear model (GLM) as implemented in SPM5 (Wellcome Department of Cognitive Neurology, London, UK¹). BOLD responses evoked by correct congruent, correct incongruent, and error trials were modeled separately. We also included parametric regressors to code for trial-specific RT in correct congruent and correct incongruent trials (Weissman et al., 2006). Because mean error rates were low (2.68%), we did not include RT regressors for incorrect trials. Parametric RT regressors were mean-centered, rendering the RT regressor for each condition orthogonal to the corresponding activity regressor. Trials in which no response was made and trials with RTs greater than three SD from the conditional mean were modeled separately and discarded from subsequent analyses; 1.48% of all trials were discarded in this way.

Whole-brain analyses used a height threshold of p < 0.005 and an extent threshold of k ≥ 30 voxels. Monte Carlo simulations implemented in the resting-state fMRI data analysis toolkit (REST, Song Xiao-Wei et al.²) showed that these thresholds yielded a corrected cluster-wise false positive rate of p < 0.01. This empirical threshold derivation procedure maintains precise control of the cluster-wise alpha level and increases sensitivity up to fivefold relative to methods that focus solely on voxel-level thresholds (Forman et al., 1995).

We also performed a conjunction analysis to identify common activations evoked by incongruent (versus congruent) trials and by the parametric effect of increasing RT. To do so, we identified the voxels that showed significant activation for both contrasts independently. Peak activations for this analysis were defined as local maxima of the products of the whole-brain t-maps for the congruency and RT contrasts (Weissman et al., 2006).

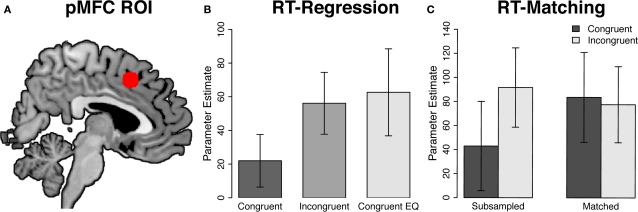
Whole-brain analysis requires the use of conservative statistical thresholds to correct for multiple comparisons and may not reveal small but significant effects. In contrast, region of interest (ROI) analyses do not require the use of such thresholds and are therefore more sensitive to small differences between conditions (Saxe et al., 2006). Thus, we also conducted ROI analyses of pMFC activity. Coordinates for the pMFC ROI (x = 2, y = 16, z = 46; Figure 2A) were derived from a recent meta-analysis of neuroimaging studies of interference resolution (Nee et al., 2007). We also conducted ROI analyses in regions that showed maximal effects of response congruency in the present data. Each ROI analysis averaged activity across a sphere of voxels (radius, 8 mm) centered on the ROI's coordinates.

Figure 2.

Region of interest analyses in the posterior medial frontal cortex. (A) Posterior medial frontal cortex region of interest (pMFC; x = 2, y = 16, z = 46), overlaid on the Ch2bet template in MNI space. (B) RT-regression analysis. Activity in the pMFC ROI was significantly greater in incongruent than in congruent trials [t(20) = 5.06, p < 0.001] but did not differ between incongruent and RT-equated congruent trials [t(20) = −0.39, p = 0.7]. (C) RT-matching analysis. Activity in the pMFC ROI was significantly greater in incongruent than in congruent trials in the RT-subsampled data [t(20) = 3.17, p = 0.005] but not in the RT-matched data [t(20) = −0.44, p = 0.67]. Furthermore, the congruency effect in the pMFC ROI was significantly greater in the RT-subsampled data than in the RT-matched data [F(1, 20) = 9.33, p = 0.006]. Error bars denote ± 1 SE of the mean.

RT-regression analysis: response congruency

To determine whether congruency effects in the pMFC could be explained by conditional differences in mean RT, we used a within-participant RT-regression analysis to correct for RT differences between correct congruent and correct incongruent trials. First, we estimated the relationship between trial-by-trial changes in RT and trial-by-trial changes in the amplitude of the BOLD response in correct congruent trials (in which response conflict is thought to be minimal), yielding an RT-BOLD slope (β_RT) for each voxel. Second, we estimated how much activity would have been present in correct congruent trials whose RT equaled the mean RT in correct incongruent trials (RT-equated congruent trials, CongruentEQ). To do so, we multiplied each voxel's RT-BOLD slope above, β_RT, by the difference in mean RT between correct incongruent and correct congruent trials $({\overline{\text{RT}}}_{\text{Incongruent}}-{\overline{\text{RT}}}_{\text{Congruent}})$ and added this quantity to the regression-derived estimate of mean activity for correct congruent trials (Congruent). Thus, the RT-equated congruent-trial activation for each voxel was calculated according to the following formula:

$$\text{CongruentEQ}=\text{Congruent}+{\beta }_{\text{RT}}\ast \left({\overline{\text{RT}}}_{\text{Incongruent}}-{\overline{\text{RT}}}_{\text{Congruent}}\right)$$ (1)

This analysis derived the RT-BOLD slope solely from low-conflict trials. In high-conflict conditions, variations of RT may reflect trial-to-trial variations of response conflict. In other words, response conflict and RT are likely confounded in incongruent trials. In contrast, RT variability in low-conflict trials is unlikely to reflect variations of response conflict. Thus, estimating the RT-BOLD relationship using only congruent trials yields a relatively pure effect of RT on activity, which is uncontaminated by trial-by-trial variations of response conflict.

As mentioned above, CongruentEQ was an estimate of BOLD amplitude that would have been present on correct congruent trials whose RT equaled the mean RT in correct incongruent trials. Thus, we reasoned that if correct incongruent trials evoked greater activation than CongruentEQ trials, then effects of response congruency on pMFC activity could not be explained by conditional differences in mean RT between correct incongruent and correct congruent trials.

We also tested an important assumption of the RT-regression analysis, which is that the association between RT and brain activity is predominantly linear and therefore does not include significant higher–order relationships. To evaluate this assumption, we conducted a separate polynomial regression analysis that measured linear, quadratic, cubic, and quartic effects of RT on brain activation (Chee et al., 2008; Prado et al., 2010).

RT-regression analysis: response accuracy

We used a comparable analysis to determine whether effects of response accuracy on pMFC activity could be explained by differences in mean RT between correct and incorrect responses. Specifically, we conducted separate analyses to control for RT differences between (a) correct incongruent trials and error trials and (b) correct congruent trials and error trials (because participants committed relatively few errors on congruent trials, the present data did not permit separate analysis of incongruent and congruent errors). These analyses estimated activity in RT-equated correct incongruent trials and RT-equated correct congruent trials using the following formulae:

$$\begin{array}{c}\text{CorrectIncongruentEQ}=\text{CorrectIncongruent }\\ \text{+ }{\beta }_{\text{RT}}\ast ({\overline{\text{RT}}}_{\text{Error}}-{\overline{\text{RT}}}_{\text{CorrectIncongruent}})\end{array}$$ (2)

$$\begin{array}{c}\text{CorrectCongruentEQ = CorrectCongruent }\\ \text{+ }{\beta }_{\text{RT}}\ast ({\overline{\text{RT}}}_{\text{Error}}-{\overline{\text{RT}}}_{\text{CorrectCongruent}})\end{array}$$ (3)

Previous research has empirically demonstrated that robust estimation of error-related brain activation requires at least three error trials (Stern et al., 2009). Thus, six participants who committed less than three errors were excluded from this analysis, leaving 15 participants.

RT-matching analysis

The RT-regression analysis described above assumes that the trial-by-trial relationship between RT and BOLD amplitude is predominantly linear. Consistent with this assumption, prior work has demonstrated that this relationship is indeed linear (Chee et al., 2008; Prado et al., 2010). Nevertheless, we wished to confirm the results of the RT-regression analysis using an analysis that makes no assumptions about the nature of the RT–BOLD relationship.

To do so, we compared activation in correct incongruent and correct congruent trials that were closely matched in terms of RT. Specifically, for each participant, we selected all pairs of incongruent and congruent trials with RTs that differed by less than 10 ms. Trials that could not be matched were modeled separately in the GLM and discarded from subsequent analyses. This resulted in the exclusion of an average of 59.84% of trials.

In short, the RT-matching procedure selected a subset of correct incongruent and correct congruent trials that were essentially equated in terms of RT. Thus, we reasoned that if RT-matched incongruent trials evoked greater activation than RT-matched congruent trials, then effects of response congruency in the pMFC could not be explained by conditional differences in mean RT. Because mean error rates were low (2.68%), we did not use the RT-matching approach to analyze accuracy effects.

Excluding trials in the RT-matching analysis likely resulted in a loss of statistical power, making a direct comparison between the RT-matched data and the original data inappropriate. Thus, we constructed a second subset of trials in which behavioral congruency effects were preserved, but the number of trials was equated to that in the RT-matched data. We refer to this second subset of trials as the RT-subsampled data. These trials were selected as follows. For each participant, we sorted correct congruent and correct incongruent trials separately by RT. Next, we selected trials from each condition at uniform intervals, such that the number of trials selected was the same as that used in the RT-matching analysis. For example, if a hypothetical subject had 120 correct incongruent and 120 correct congruent trials in total, and had 40 incongruent and 40 congruent trials in the RT-matched subset, then this procedure selected every third trial from the RT-sorted incongruent and congruent trials. We reasoned that if effects of response congruency on pMFC activity were absent in the RT-matched data but present in the RT-subsampled data, then the absence of such effects in the RT-matched data would not simply reflect a reduction in the number of trials being analyzed.

Results

Replicating previous studies using the MSIT (Bush et al., 2003), we observed poorer performance in incongruent than in congruent trials. Mean RTs were slower in incongruent [M = 1035.2 ms, SEM = 41.5 ms] than in congruent trials [M = 794.8 ms; SEM = 42.7 ms; t(20) = 16.35, p < 0.001]. Participants also committed more errors in incongruent [M = 4.7%, SEM = 1.3%] than in congruent trials [M = 0.69%, SEM = 0.23%; t(20) = 3.21, p = 0.0044].

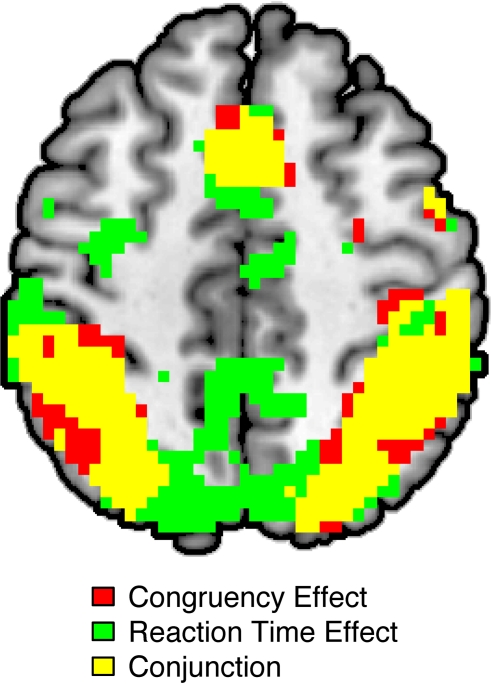
Consistent with prior studies (for a review, see Nee et al., 2007) and a prior report of these data (Fitzgerald et al., 2010), activity in a network of frontal, parietal, and sensory regions was significantly greater in incongruent than in congruent trials (Figure 1; Table 1). As expected, this network included a large cluster in the pMFC with peak coordinates close to those reported in a meta-analysis of neuroimaging studies of interference resolution (Nee et al., 2007). Also echoing recent studies, trial-by-trial variations of RT were positively (and linearly) related to trial-by-trial variations of BOLD amplitude in a widespread fronto-parietal network, which included the pMFC as well as lateral frontal and parietal regions (Figure 1; Table 1). Specifically, in these regions, relatively slow responses were associated with increased activity while relatively fast responses were associated with decreased activity. Critically, a conjunction analysis revealed striking similarity in the spatial distributions of the congruency and RT effects, showing substantial overlap in prefrontal and parietal regions (Figure 1; Table 1).

Figure 1.

Overlap between effects of congruency and effects of reaction time (RT) on BOLD amplitude as revealed by whole-brain analyses. Significant congruency effects (incongruent > congruent) are highlighted in red; significant RT effects (slow RT > fast RT) are indicated in green. The conjunction of these contrasts is highlighted in yellow. All activations are overlaid on the Ch2bet template in MNI space. Activations are displayed using a height threshold of p ≤ 0.005 and an extent threshold of k ≥ 30 voxels.

Table 1.

Effects of congruency and RT on brain activity.

Region	Number of voxels	MNI coordinates			Peak t-value
		X	Y	Z
(A) BRAIN REGIONS SHOWING HIGHER ACTIVATION FOR INCONGRUENT THAN CONGRUENT TRIALS
Medial frontal gyrus	349	−3	18	51	5.70
Medial frontal gyrus	349	0	−3	60	4.90
L. inferior frontal gyrus	157	−33	27	−6	4.10
R. inferior frontal gyrus	3218	36	24	0	5.52
L. middle frontal gyrus	131	−39	0	60	4.85
R. middle frontal gyrus	3218	33	−6	63	6.82
L. inferior parietal lobule	3218	−42	−51	51	6.35
R. inferior parietal lobule	3218	36	−51	45	8.41
L. thalamus	2609	−12	−6	9	4.26
R. thalamus	2609	9	−9	6	6.16
L. middle occipital gyrus	2609	−51	−60	−9	4.97
R. middle occipital gyrus	2609	45	−69	0	5.75
(B) BRAIN REGIONS SHOWING HIGHER ACTIVATION FOR SLOW THAN FAST RTs, REGARDLESS OF RESPONSE CONGRUENCY
Medial frontal gyrus	849	−3	27	39	4.72
L. superior temporal gyrus	168	−51	18	−9	4.16
R. insula	79	36	24	3	4.65
L. middle frontal gyrus	60	−54	12	39	4.12
R. inferior frontal gyrus	6034	48	3	33	5.11
Cingulate gyrus	849	3	−30	30	4.14
Precuneus	6034	3	−60	66	4.39
L. superior parietal lobule	6034	−30	−63	45	4.98
R. superior parietal lobule	6034	27	−63	54	6.36
L. lingual gyrus	6034	−12	−69	3	5.62
R. lingual gyrus	6034	18	−66	0	5.13
CONJUNCTION OF (A) REGIONS SHOWING HIGHER ACTIVATION FOR INCONGRUENT THAN CONGRUENT TRIALS AND (B) HIGHER ACTIVATION FOR SLOW THAN FAST RTs
Medial frontal gyrus	282	0	18	51	–
Medial frontal gyrus	282	3	−3	60	–
L. middle frontal gyrus	78	−27	0	69	–
R. middle frontal gyrus	2097	54	6	42	–
L. superior temporal gyrus	61	−51	18	−9	–
R. inferior frontal gyrus	39	36	24	0	–
L. inferior parietal lobule	2097	−36	−54	54	–
R. inferior parietal lobule	2097	39	−51	45	–
L. fusiform gyrus	200	−45	−66	−18	–
R. inferior temporal gyrus	127	45	−69	−6	–

RT-regression analysis

Next, we asked whether the neural congruency effects described above could be explained by differences in mean RT between correct incongruent and correct congruent trials. To test this hypothesis, we compared activity in incongruent trials to activity in RT-equated congruent trials (CongruentEQ). In contrast to the analysis of the raw data described above, a whole-brain analysis revealed no significant effects of congruency. Thus, using the RT-regression analysis to control for conditional differences in mean RT eliminated congruency effects at the whole-brain level.

Next, we conducted an ROI analysis on pMFC activity. This region showed a significant effect of congruency in the raw data [t(20) = 5.06, p < 0.001; Figure 2B, center bar versus left bar]. Critically, however, this effect was eliminated, and even non-significantly reversed, after controlling for conditional differences in mean RT [t(20) = −0.39, p = 0.7; Figure 2B, center bar versus right bar].

These results show that controlling for RT differences between conditions eliminates congruency effects in an independently defined region of interest. However, they do not rule out the possibility that congruency effects remained significant in neighboring regions of the pMFC. To investigate this possibility, we conducted an additional ROI analysis focusing on the pMFC region that showed the most significant congruency effect before controlling for RT (x = −3, y = 18, z = 51). We reasoned that this would be the region most likely to show a congruency effect, even after controlling for RT. However, consistent with the previous analysis, we found that correcting for conditional differences in mean RT all but eliminated the congruency effect in this pMFC region. Before controlling for RT, this region showed greater activity in incongruent than in congruent trials [t(20) = 5.24, p < 0.001]. In contrast, after controlling for RT, the congruency effect in this region failed to approach significance [t(20) = 0.34, p = 0.74].

Although ROI analyses may be more sensitive than whole-brain tests, they do not rule out the possibility that subthreshold congruency effects were present elsewhere in the pMFC. To investigate this possibility, we repeated the voxel-wise analysis of neural congruency effects with a more lenient height threshold of p < 0.05 (we retained the cluster-size threshold of k ≥ 30 voxels). Even using this sensitive criterion, however, we observed no congruency effects in the pMFC.

As noted earlier, the RT-regression analysis assumes that the relationship between RT and brain activity is predominantly linear. Consistent with this assumption, previous studies have documented robust linear effects of RT on fronto-parietal activation; in contrast, higher-order RT effects have been weak or non-significant. Our data replicated this pattern: as described earlier, a voxel-wise analysis revealed significant linear effects of RT throughout the fronto-parietal network (Figure 1; Table 1). In contrast, additional voxel-wise analyses revealed that second-, third-, and fourth-order effects of RT did not reach significance in any brain region.

RT-matching analysis

The RT-regression analysis above suggests that effects of response congruency on pMFC activity were entirely accounted for by differences in mean RT between incongruent and congruent trials. As stated earlier, however, this analysis assumes a predominantly linear relationship between trial-by-trial variations of RT and trial-by-trial variations of BOLD amplitude. Although our data supported this assumption, our whole-brain analysis may have failed to detect small but significant non-linear relationships between RT and BOLD amplitude. Therefore, we next examined the results of the RT-matching analysis, which made no assumptions about the nature of the RT-BOLD relationship and was therefore robust to non-linear associations between RT and BOLD amplitude.

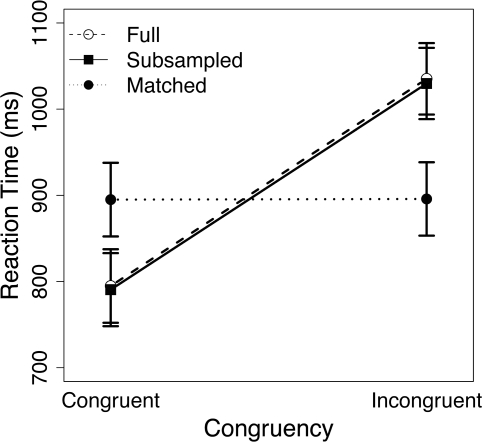
The RT-matching procedure removed the bulk of the congruency effect from the behavioral data (Figure 3): while incongruent trials were 240.4 ms slower than congruent trials in the full data set [t(20) = 16.35, p < 0.001], this difference was reduced to 0.8 ms in RT-matched trials [t(20) = 2.64, p = 0.02]. Thus, although the congruency effect remained significant in the RT-matched data, the matching procedure reduced this effect by 99.7%. In contrast, the RT-subsampling procedure successfully preserved the congruency effect in the behavioral data (Figure 3), yielding a congruency effect of 239.2 ms [t(20) = 16.13, p < 0.001].

Figure 3.

Mean reaction time (RT) for congruent and incongruent trials in the full data set (open circles), the RT-subsampled data set (filled squares), and the RT-matched data set (filled circles). Errors bars denote ± 1 SE of the mean.

As in the RT-regression analysis, voxel-wise analysis of the RT-matched data revealed no congruency effects in the pMFC. Critically, the reduced number of trials in the RT-matching analysis could not explain these null results: significant congruency effects in the pMFC were observed in the RT-subsampled data, which included the same number of trials as the RT-matched data. In contrast, congruency effects in bilateral posterior parietal cortex (left PPC: −36, 51, 48; right PPC: 39, 54, 48) remained significant even in the RT-matched data, indicating that congruency effects in these regions could not be fully explained by conditional differences in mean RT.

Next, we investigated the effects of RT-matching on pMFC activity using a more sensitive ROI analysis. As in the RT-regression analysis, coordinates for this pMFC ROI (x = 2, y = 16, z = 46) were derived from a recent meta-analysis of interference-processing studies (Nee et al., 2007). Consistent with the whole-brain analysis described above, we did not observe a congruency effect in this pMFC ROI [t(20) = −0.44, p = 0.67; Figure 2C]. In fact, activity was non-significantly greater in RT-matched congruent trials than in RT-matched incongruent trials. Importantly, echoing the whole-brain analysis of the full data set, the RT-subsampled data showed a robust congruency effect in this ROI [t(20) = 3.17, p = 0.005]. Thus, the absence of a neural congruency effect in the RT-matched data was not due to the reduced number of trials in this analysis. Finally, the congruency effect in this pMFC ROI was significantly smaller in the RT-matched data than in the RT-subsampled data [F(1, 20) = 9.33, p = 0.006]. This result provides direct evidence that controlling for differences in mean RT between incongruent and congruent trials reduces the size of congruency effects in the pMFC.

To provide a more stringent test of the hypothesis that controlling for RT eliminates congruency effects in the pMFC, we repeated this analysis in the region of pMFC that showed the strongest congruency effect in the full data set. Consistent with the foregoing voxel-wise and ROI analyses, this region did not exhibit a significant congruency effect in the RT-matched data [t(20) = 0.12, p = 0.9], but did show a robust congruency effect in the RT-subsampled data [t(20) = 4.08, p < 0.001]. Furthermore, the congruency effect in this pMFC ROI was significantly smaller in the RT-matched data than in the RT-subsampled data [F(1, 20) = 12.27, p = 0.002].

Finally, to test for congruency effects in regions of the pMFC outside these ROIs, we conducted a voxel-wise analysis using a lenient height threshold of p < 0.05 (this analysis retained the cluster-size threshold of k ≥ 30 voxels). Even using this lenient criterion, however, the RT-matching analysis did not reveal congruency effects in the pMFC.

In sum, while congruency effects in pMFC were robust in the original data, RT-regression and RT-matching analyses revealed that these effects were wholly eliminated after controlling for differences in mean RT between incongruent and congruent trials. Thus, congruency effects in the pMFC were fully explained by the fact that mean RT was slower in incongruent than in congruent trials.

Accuracy analysis

According to the conflict-monitoring model, errors are associated with greater response conflict than correct responses (Yeung et al., 2004). Consistent with this view, previous studies using EEG (van Veen and Carter, 2002) and fMRI (Carter et al., 1998) have revealed increased pMFC activity for errors relative to correct responses. Therefore, we next investigated whether effects of response accuracy on pMFC activity could also be explained by conditional differences in mean RT.

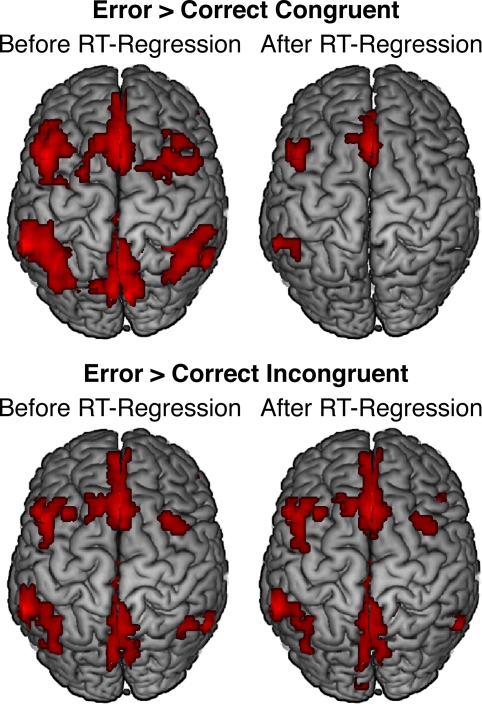
Mean RT was non-significantly faster in error trials than in correct incongruent trials [t(20) = −1.16, p = 0.26] but significantly slower in error trials than in correct congruent trials [t(20) = 3.53, p = 0.002]. Moreover, consistent with previous studies, errors evoked significantly greater pMFC activation than both correct congruent trials (Figure 4, top left; Table 2) and correct incongruent trials (Figure 4, bottom left; Table 3). Thus, we reasoned that differences in pMFC activity between error trials and correct congruent trials might be explained by conditional differences in mean RT.

Figure 4.

Effects of response accuracy on brain activity before (left panels) and after (right panels) statistically correcting for conditional differences in mean RT. For both contrasts, error-related pMFC activity remained robust after controlling for RT differences between conditions. All activations are overlaid on the Ch2bet template in MNI space. Activations are displayed using a height threshold of p ≤ 0.005 and an extent threshold of k ≥ 30 voxels.

Table 2.

Differences in brain activity between errors and correct congruent trials before and after controlling for conditional differences in mean RT.

Region	Number of voxels	MNI coordinates			Peak t-value
		X	Y	Z
BRAIN REGIONS SHOWING HIGHER ACTIVATION FOR ERRORS THAN FOR CORRECT CONGRUENT TRIALS
Anterior cingulate cortex	734	0	27	24	5.14
Superior frontal gyrus	734	0	18	57	5.46
Superior frontal gyrus	734	−3	51	36	4.31
L. middle frontal gyrus	154	−48	15	42	5.12
R. superior frontal gyrus	56	33	15	54	4.30
L. inferior frontal gyrus	43	−48	30	−12	4.60
R. inferior frontal gyrus	251	45	27	0	5.36
Posterior cingulate cortex	104	−9	−66	9	4.33
Precuneus	468	−3	−72	48	4.55
L. supramarginal gyrus	248	−63	−45	36	6.46
R. inferior parietal lobule	34	45	−57	42	3.83
R. supramarginal gyrus	73	57	−54	27	4.55
BRAIN REGIONS SHOWING HIGHER ACTIVATION FOR ERRORS THAN FOR RT-EQUATED CORRECT CONGRUENT TRIALS
Anterior cingulate cortex	745	0	27	24	5.15
Superior frontal gyrus	745	0	18	57	5.44
Superior frontal gyrus	745	−3	51	36	4.06
L. inferior frontal gyrus	66	−45	30	6	3.83
R. inferior frontal gyrus	220	42	24	3	4.96
L. middle frontal gyrus	166	−48	15	45	4.51
R. superior frontal gyrus	45	33	15	54	3.33
Precuneus	492	−3	−72	48	4.01
Posterior cingulate cortex	161	−9	−66	9	4.44
L. supramarginal gyrus	181	−63	−45	36	5.52
R. supramarginal gyrus	46	57	−54	27	4.14

Table 3.

Differences in brain activity between errors and correct incongruent trials before and after controlling for conditional differences in mean RT.

Region	Number of voxels	MNI coordinates			Peak t-value
		X	Y	Z
BRAIN REGIONS SHOWING HIGHER ACTIVATION FOR ERRORS THAN FOR CORRECT INCONGRUENT TRIALS
Anterior cingulate cortex	918	0	27	24	5.63
Medial frontal gyrus	918	0	15	51	5.33
Superior frontal gyrus	918	−3	51	36	3.74
L. inferior parietal lobule	1157	−51	−45	51	4.84
R. inferior parietal lobule	449	48	−48	51	4.97
Precuneus	1157	3	−57	63	4.97
L. extrastriate cortex	141	−9	−72	12	4.46
L. thalamus	205	−9	−9	6	5.52
R. thalamus	205	12	−12	0	4.74
L. middle temporal gyrus	101	−54	−39	−3	3.97
L. precentral gyrus	263	−42	24	42	4.74
R. precentral gyrus	36	39	21	42	3.81
BRAIN REGIONS SHOWING HIGHER ACTIVATION FOR ERRORS THAN FOR RT-EQUATED CORRECT INCONGRUENT TRIALS
Anterior cingulate cortex	301	6	24	27	4.42
Superior frontal gyrus	301	0	21	57	5.52
L. inferior frontal gyrus	55	−36	27	0	3.42
R. inferior frontal gyrus	107	42	24	3	3.88
L. middle frontal gyrus	69	−48	15	45	4.87
L. inferior parietal lobule	52	−54	−45	48	3.48

To investigate whether error-related pMFC activity might be explained by conditional differences in RT, we used the RT-regression analysis described earlier. Specifically, we estimated the level of activity that would have been observed in correct congruent and correct incongruent trials if each condition's mean RT had been equal to the mean RT in error trials. As noted in the “Materials and Methods” Section since most participants made relatively few errors, we could not supplement this approach with the RT-matching strategy described earlier.

Whole-brain analyses using the RT-regression analysis revealed that effects of response accuracy on pMFC activity remained robust in many regions after controlling for conditional differences in mean RT. Specifically, after RT-regression, we continued to observe significantly greater pMFC activity for errors than for (a) correct congruent responses (Figure 4, top right; Table 2) and (b) correct incongruent responses (Figure 4, bottom right; Table 3). Thus, effects of response accuracy on pMFC activation could not be explained by differences in mean RT between errors and correct responses.

Discussion

The conflict-monitoring model of cognitive control posits that the pMFC detects the presence of conflict between incompatible motor responses (Botvinick et al., 2001; Yeung et al., 2004). Consistent with this view, pMFC activity is greater in high-conflict trials (e.g., incongruent trials and incorrect responses) than in low-conflict trials (e.g., congruent trials and correct responses) of distractor interference tasks (Botvinick et al., 1999; MacDonald et al., 2000; Orr and Weissman, 2009). However, pMFC activity increases linearly with RT in both low- and high-conflict trials (Weissman et al., 2006; Yarkoni et al., 2009). Thus, effects of response conflict on pMFC activity may simply reflect the fact that mean RT is greater in high-conflict than low-conflict trials. The present results provided partial support for this hypothesis: congruency effects in the pMFC were wholly eliminated after controlling for differences in mean RT between incongruent and congruent trials. However, not all effects of response conflict on pMFC activity could be explained by conditional differences in mean RT. Specifically, we observed greater pMFC activity for errors than for correct responses, even after controlling for conditional differences in mean RT.

We used two independent strategies to control for conditional differences in mean RT. First, we used an RT-regression method to estimate activity that would have been observed in congruent trials whose RT equaled the mean RT in incongruent trials. This strategy considers all of the available data, thereby maximizing statistical power. However, this analysis assumes that the RT-BOLD relationship is predominantly linear. Our data supported this assumption. Nevertheless, we sought to confirm the results of this analysis using a method that makes no assumptions about the form of the RT-BOLD relationship. Specifically, we selected RT-matched pairs of incongruent and congruent trials, while excluding trials that could not be matched across conditions. Importantly, the results of the RT-regression and RT-matching analyses showed remarkable agreement with regard to pMFC activity: in both cases, controlling for conditional differences in mean RT wholly eliminated congruency effects in the pMFC (Figure 2). Thus, both approaches supported the conclusion that congruency effects in the pMFC could be explained by conditional differences in mean RT.

In contrast, results from the two methods diverged with regard to parietal activity. Correcting for RT differences using RT-regression eliminated congruency effects in the posterior parietal cortex; however, correcting for these differences using RT-matching did not. This difference may reflect the fact that the RT-regression analysis assumes a linear RT-BOLD relationship, while the RT-matching method does not. The two methods also may have differed because the RT-regression method considered all correct trials, while the RT-matching method discarded trials that could not be matched. In sum, our results do not rule out a role for the posterior parietal cortex in detecting response conflict independent of time on task.

Our finding that congruency effects in the pMFC could be explained by conditional differences in mean RT presents an interpretive difficulty for the conflict-monitoring model. On the one hand, it could be consistent with the model if heightened demands on conflict detection in incongruent (relative to congruent) trials lead to both greater RT and greater pMFC activity. On the other hand, it could be inconsistent with the model if heightened demands on some other cognitive process whose recruitment increases with RT lead to greater pMFC activity in incongruent trials. Along these lines, Yarkoni et al. (2009) argued that greater pMFC activity in trials with slow RTs reflects heightened demands on processes that sustain attention until a response is made. Consistent with this view, the pMFC has been implicated in sustained attention (Murtha et al., 1996; Dosenbach et al., 2006) and various other processes whose recruitment likely also increases with RT, such as autonomic arousal (Critchley et al., 2003) and cognitive effort (Mulert et al., 2005). For these reasons, the present findings indicate that congruency effects in the pMFC may be explained equally well by heightened demands on conflict detection or a variety of other processes whose recruitment increases with RT. These findings do not rule out the conflict-monitoring model. However, they indicate that effects of response congruency on pMFC activity do not provide direct support for the model.

In contrast, effects of response accuracy on pMFC activity were more consistent with processes that detect response conflict than with other processes whose recruitment varies with RT. Specifically, such effects persisted in the pMFC after controlling for RT differences between errors and correct responses (Figure 4). Thus, in the present study, effects of response accuracy on pMFC activity provided stronger support for the view that the pMFC plays a role in detecting response conflict than effects of response congruency. Nevertheless, our data do not rule out the possibility that error-related pMFC activity reflects other processes that are uniquely recruited in error trials, such as emotional reactions (Kiehl et al., 2000) or heightened attention (Posner and Petersen, 1990; Orr and Weissman, 2009) following suboptimal performance. Future studies could explore this issue with tasks that include a larger number of errors. Such tasks would not only maximize statistical power for comparing errors to correct responses, but also allow researchers to test focused hypotheses regarding error-related activity.

Although the present research focuses on the role of the pMFC in detecting response conflict, the issue raised here is germane to a wide range of studies in cognitive neuroscience. Indeed, conditional differences in mean RT are a ubiquitous confound in brain imaging studies of human cognition. For example, this confound is present in work investigating differential brain activity for high versus low memory load (Cohen et al., 1997), task-switch versus task-repeat trials (Dove et al., 2000), and difficult versus easy moral judgments (Greene et al., 2004). In such studies, conditional differences in brain activity are often attributed to a specific cognitive process but might, in fact, reflect any of several processes whose recruitment varies with RT. Nonetheless, a recent survey of neuroimaging studies revealed that only 9% modeled trial-by-trial variations in RT (Grinband et al., 2008). Some of these studies reported that conditional differences in brain activity could be explained by conditional differences in mean RT (Christoff et al., 2001; Epstein et al., 2007) while others reported that this was not the case (Dobbins and Han, 2006; Simons et al., 2006). The fact that so few studies have explicitly tested this important hypothesis underscores the need for future research in this area.

In summary, we found that conditional differences in mean RT explained effects of response congruency, but not response accuracy, on pMFC activity in an event-related version of the MSIT. These findings indicate that effects of response accuracy on pMFC activity provide stronger support for the conflict-monitoring model than effects of response congruency. More broadly, they emphasize the importance of controlling for conditional differences in mean RT in all functional neuroimaging studies of cognition.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.