The Effect of Small Changes in Hematocrit on Nitric Oxide Transport in Arterioles

Abstract

We report the development of a mathematical model that quantifies the effects of small changes in systemic hematocrit (Hct) on the transport of nitric oxide (NO) in the microcirculation. The model consists of coupled transport equations for NO and oxygen (O2) and accounts for both shear-induced NO production by the endothelium and the effect of changing systemic Hct on the rate of NO production and the rate of NO scavenging by red blood cells. To incorporate the dependence of the plasma layer width on changes in Hct, the model couples the hemodynamics of blood in arterioles with NO and O2 transport in the plasma layer. A sensitivity analysis was conducted to determine the effects of uncertain model parameters (the thicknesses of endothelial surface layers and diffusion coefficients of NO and O2 in muscle tissues and vascular walls) on the model's predictions. Our analysis reveals that small increases in Hct may raise NO availability in the vascular wall. This finding sheds new light on the experimental data that show that the blood circulation responds to systematic increases of Hct in a manner that is consistent with increasing NO production followed by a plateau. Antioxid. Redox Signal. 14, 175–185.

Introduction

Nitric oxide (NO) is a secretory product of mammalian cells that is thought to act as a key messenger in various physiological processes in central and peripheral nervous systems, the cardiovascular system, immune and inflammatory systems, and the like. (21). The physiologic importance of NO generated a large number of experimental and modeling studies (3) that vary in complexity and fidelity. In what is often considered to be the first mathematical model of NO endothelium production and hemoglobin scavenging, Lancaster (14) accounted for the intracellular and intercellular diffusion and reaction of free NO with oxygen (O2) and hemoglobin (Hb). This model was subsequently modified by Butler et al. (4) to account for the presence of a plasma layer (Fig. 1)—a region in the immediate vicinity of the endothelium in which blood contains no red blood cells (RBCs)—and to incorporate the scavenging effect of hemoglobin. A mathematical model (26) of interactions between hemoglobin O2 carriers and NO demonstrated the dependence of NO scavenging rates on hematocrit (Hct). Lamkin- Kennard et al. (13) further generalized these models by incorporating two mechanisms by which NO influences O2 transport to tissue: “O2 is required for NO production,” and “tissue O2 consumption is reversibly inhibited by NO.”

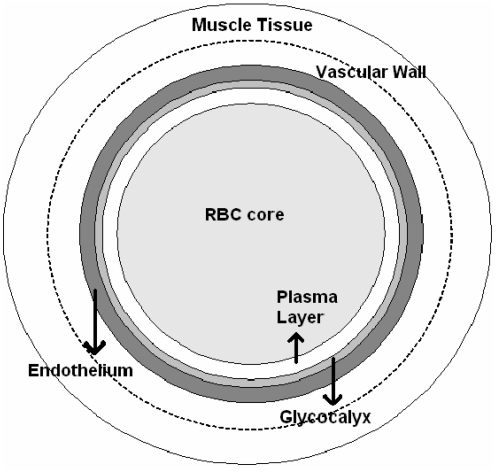
FIG. 1.

Cross section of an arteriole. A version of the Krogh tissue cylinder model used in our analysis consists of RBC-rich core, RBC-free plasma layer, glycocalyx, endothelium, vascular wall, and smooth muscle tissue. RBC, red blood cell.

This study aims to elucidate the third mechanism in this complex phenomenon identified in refs. (3, 13): “interactions between NO and Hb influence blood flow and O2 delivery.” Specifically, we investigate quantitatively how changes in Hct affect both NO production and scavenging and O2 transport. Physicochemical processes affecting this process are well understood. As Hct increases so does apparent blood viscosity (23) and shear stress at the vessel wall (26). This, in turn, leads to changes in the rate of NO production by the endothelium (1, 11, 19, 20, 24). Additionally, simulation results and experimental data show that the rate of NO scavenging increases with rising Htc (29).

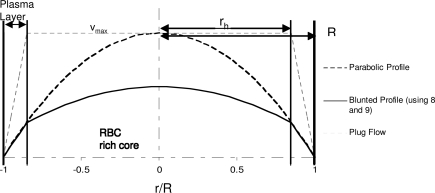
While recognizing the importance of shear-stress-dependent NO production, two of the most recent and complete models of coupled NO/O2 transport (5, 9) do not account for this effect. Moreover, these models rely on assumed rather than rigorously derived velocity profiles. The parabolic velocity profile adopted in ref. (5) implies Poiseuille flow of a single-phase Newtonian fluid, which neglects the presence of a plasma layer. The plug-flow velocity profile used by both Chen et al. (5) and Gundersen et al. (9) assumes blood velocity to be constant across the RBC-rich core and to vary linearly in the plasma layer. This leads to inaccurate predictions of shear stress at the wall, as can be seen from Figure 2.

FIG. 2.

Blood velocity profiles corresponding to the two-phase flow model and their parabolic and plug-flow counterparts used in the previous analyses (5, 9).

The model of coupled NO/O2 transport we present below generalizes its current state-of-the-art counterparts (5, 9, 13) in the following ways. First, it employs a blood velocity profile that is rigorously derived from a representation of arteriolar hemodynamics as two-phase flow with the RBC-rich core and the RBC-free plasma layer (26). Second, it incorporates the experimentally observed dependence of NO endothelium production on shear stress. Third, it accounts for the theoretically derived [refs. (2, 27) and references therein] and experimentally observed (8, 15) differences between values of diffusion coefficients in free fluids (e.g., plasma layer) and porous media (e.g., glycocalyx and muscle tissue). Finally, experimental data (12, 33) are used to characterize the dependence of the plasma layer thickness on Hct, thus relating the blood hemodynamics to NO availability in smooth muscle tissue and vascular walls.

Our analysis is motivated in part by the experimental observations of Martini et al. (17, 18, 25), who found that small Hct increases in hamsters can lead simultaneously to lowered blood pressure and increased cardiac output. Gundersen et al. (9) postulated that this effect might be caused by vessel dilation due to increased shear-stress-induced NO production rather than due to increased O2 transport across the blood vessel wall. Our mathematical model supports this hypothesis.

Methods

Mathematical model

Model geometry

Following Lamkin-Kennard et al. (13), Chen et al. (5), and Gundersen et al. (9), among many others, we adopt a modified Krogh tissue cylinder model of an arteriole. This model idealizes an arteriole by a series of concentric cylinders representing (from the center outward): (a) RBC-rich core, (b) RBC-free plasma layer, (c) glycocalyx, (d) endothelium, (e) vascular wall, and (f ) smooth muscle tissue (Fig. 1). Other versions of the Krogh tissue cylinder model can be used in the analysis below as well.

A cylindrical coordinate system (r, z) is used to describe coupled transport of NO and O2 in an arteriole. The two-phase blood flow is in the z direction, along the arteriole's length. To facilitate the comparison with the analyses in refs. (4, 9, 13, 14), that is, to elucidate the effects of shear-stress-dependent NO endothelium production on coupled NO and Hb transport and on resulting O2 delivery, we take the endothelium NO production to be uniform along the arteriole's length and set the concentrations of NO and O2 in the arteriole's inlet and outlet to be the same. This physiological setting is justified by both modeling results and experimental evidence. Specifically, numerical results of Chen et al. (5), whose model accounts for advective transport in an arteriole, demonstrates that the axial variability of these concentrations is negligibly small as long as NO production is uniform along the length of an arteriole. Experimental investigations of Intaglietta et al. (10) found the longitudinal (axial) O2 gradient measured in blood micro-vessels to be very small (on the order of 8 mmHg/cm).

Under these conditions, both NO concentration C_NO and O2 partial pressure P_O2 vary in the radial (r) direction only, so that u · ∇C_NO ≡ 0 and u · ∇P_O2 ≡ 0, where u is the blood velocity vector whose only nonzero component u is in the z direction. This leaves diffusion and reactions in the radial direction as the only transport mechanisms. These are described by a system of coupled steady-state reaction–diffusion equations (5, 9, 13) presented below.

Transport equations

RBC-rich core (0 < r < r_h)

In this region, O2 partial pressure P_O2 is constant and NO concentration C_NO satisfies a steady-state reaction–diffusion equation,

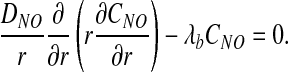[1]

Here D_NO is the diffusion coefficient of NO in the RBC-rich core, and λ_b is the reaction rate constant of NO scavenging by RBCs. The latter varies linearly with Hct (5, 9, 29), λ_b = λ₀Hct, where λ₀ is the value of λ_b at the reference value of Hct (45%).

Plasma layer (r_h < r < R) and glycocalyx (R < r < r_g)

Owing to the absence of RBCs in plasma layer, no biochemical reactions occur in either plasma layer or glycocalyx. Hence, NO concentration C_NO and O2 partial pressure P_O2 satisfy steady-state diffusion equations

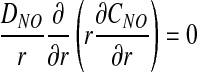[2]

and

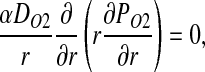[3]

respectively. Here α denotes the O2 solubility, and the diffusion coefficients of NO (D_NO) and O2 (D_O2) in plasma layer are larger than their counterparts in glycocalyx (8, 15).

Endothelium (r_g < r < r_e)

Assuming that the rate of O2 consumption is twice the rate of NO production (5), C_NO and P_O2 satisfy a coupled system of steady-state reaction–diffusion equations

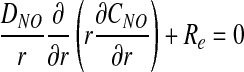[4]

and

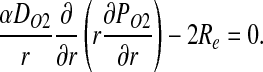[5]

The reaction rate R_e is assumed to follow Michaelis–Menten kinetics (3),

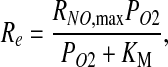[6]

where K_M is the Michaelis–Menten constant. We allow the maximum reaction rate R_NO,_max to vary with shear stress at the vessel wall, as discussed later. This dependence enables our model to account for the effect of shear stress on NO production.

Vascular wall (r_e < r < r_w) and smooth muscle tissue (r_w < r < r_m)

Following (3), we assume that NO undergoes a pseudo first-order reaction with reaction rate constant λ_t, and that O2 consumption is inhibited by NO and follows Michaelis–Menten kinetics. The corresponding transport equations take the form

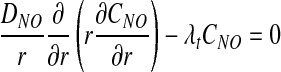[7]

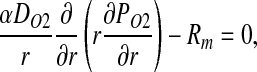[8]

where peak O2 consumption rate R_O2,max is lower in the vascular wall than in the muscle tissue, and (3)

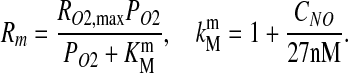Boundary conditions

Transport equations [1]–[8] are subject to the following boundary conditions. NO concentration C_NO is symmetric about the arteriole center r = 0,

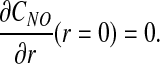[9]

We assume that both C_NO and P_O2 reach their respective asymptotic in the vicinity of the outer boundary of the muscle tissue r = r_m, so that (13)

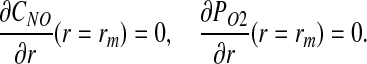[10]

Mass conservation across the interfaces between adjacent layers requires that

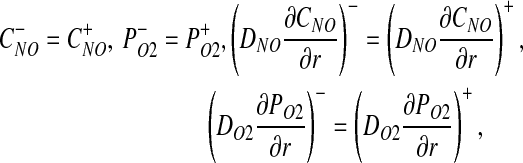[11]

where the superscripts minus and plus indicate that the corresponding quantities are computed, respectively, inside and outside of each interface shown in Figure 1.

It is worthwhile emphasizing that, if and when physiologically appropriate, this model can readily be generalized to account for axial variability of the concentrations of NO and O2 by adding the advective terms u · ∇C_NO ≡ 0 and u · ∇P_O2 ≡ 0 to equations [1]–[2] and [3], respectively. Such a generalization of the transport model 1–11 is important for tackling spatially variable NO production, for example, NO production from neuronal NOS, but lies outside the scope of the present analysis and is left for follow-up studies.

Blood flow velocity and shear stress

All previously described models of coupled NO and O2 transport implicitly employ a two-phase model of blood flow in a cylinder of constant diameter (26). The first fluid (phase) is the RBC-rich core and has viscosity μ_c; the second phase is plasma that has viscosity μ_p. These two phases are assumed to be immiscible. Assuming steady-state fully developed flow in the inertial regime, Stokes equations yield velocities of the core, u_c, and plasma, u_p (26),

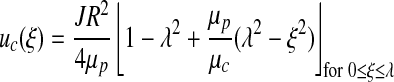[12]

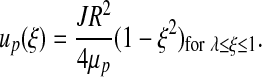[13]

Velocity profiles [12] and [13] are written in the dimensionless coordinate system ξ = r/R with λ = r_h / R; and J =(P_i − P_o)/L is the pressure gradient along the arteriole of length L with entry and exit pressures P_i and P_o, respectively. Figure 2 presents the velocity profiles [12] and [13] and compares them with the parabolic and plug-flow velocity profiles used in the previous analyses (5) and (9). The parameter values used are presented in Table 1.

Table 1.

Values of Parameters Used in Simulations

Parameter	Symbol used	Value	Reference
Solubility of O2	α	1.34 Mm/torr	13
Diffusivity of O2 in fluid layers	DO2	2800 μm2/s	13
Diffusivity of NO in fluid layers	DNO	3300 μm2/s	14
Diffusivity of O2 in solid layers	DO2	2800 or 1400 μm2/s	8, 15
Diffusivity of NO in solid layers	DNO	3300 or 1650 μm2/s
Maximum O2 consumption rate in tissue	RO2,max	20 μM/s	5
Maximum NO production rate in endothelium	RNO,max	150 μM/s	5
Scavenging rate of NO in blood at 45% hematocrit	λb	382.5 s−1	2, 27
Rate of consumption of NO in tissue	λt	1 s−1	13
Michaelis–Menten constant for NO in endothelium	KM	4.7	3
Ratio of diffusivities in solid andliquid phases	Dr	1, 1/2
Arteriole diameter (i.e., fluid domain)	R	20 μm	13
Glycocalyx		0.25–1 μm	31
Endothelium		1 μm
Smooth muscle tissue		80 μm	5

O2, oxygen; NO, nitric oxide.

Flow rate Q is obtained by integrating the velocity profile given by expressions 12 and 13 over the cross section of the arteriole with dimensionless radius ξ = 1,

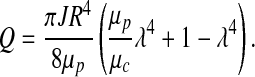[14]

It follows from expression [13] that shear stress τ at the wall, ξ = 1, is given by

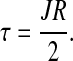[15]

Combining expressions [13] and [14] yields

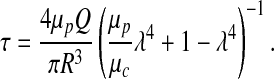[16]

Equation [16] expresses shear stress τ in terms of blood viscosity μ_p and the width of plasma layer δ = (1 − λ)R.

Shear-stress-dependent NO production

In our model, changes in Hct affect the shear stress τ in equation [16] via the dependence on Hct of both blood viscosity, μ_c = μ_c (Hct), and the width of plasma layer, δ = δ(Hct). The model is capable of accommodating any phenomenological relations (constitutive laws). To be concrete, we employ:

1. a linear relationship μ_c = μ_c(Hct) suggested by the experimental data reported in ref. (17); and

2. a linear relationship between δ and systemic Hct H_d suggested by the experimental data presented in the Appendix.

Specifically, the Martini et al. (17) viscometry data suggest that in the physiological range of Hct

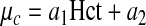[17]

where a₁ =0.1678 and a₂=−4.348 cp. The experimental data presented in the Appendix lead to

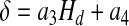[18]

with a₃=−7.55μm and a₄ = 6.91μm. The core (Hct) and systemic (H_d) Hcts are related through mass conservation of RBCs (13),

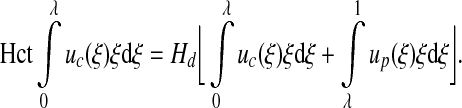[19]

For the velocity profile given by expressions [12] and [13], this gives

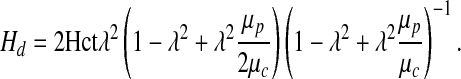[20]

Equation [20] is nonlinear, since λ(H_d) = 1 − δ(H_d)/R where δ(H_d) given by the linear relation [18]. This equation can be approximated by a linear relation

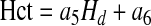[21]

with a₅ = 0.9608 and a₆ = 0.1012 for the arteriole radius R = 20 μm. This linear fit is very accurate within the physiological range of Hct being studied (from around 35 to 55) with R² = 0.998.

Recalling that λ = 1 − δ/R, and substituting relations [17], [18], and [21] into expression [16], we obtain a closed-form relation between shear stress τ and systemic Hct H_d,

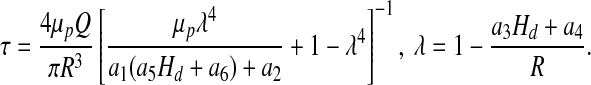[22]

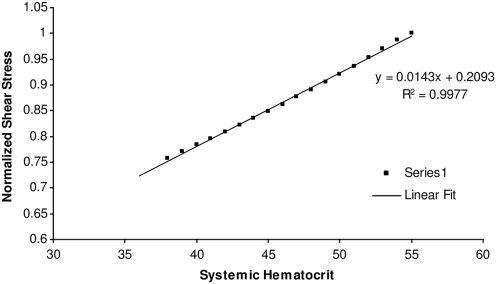
The variation of shear stress with systemic Hct given by equation [22] is plotted in Figure 3, in the range of Hct considered in this study (and for a vessel diameter of 40 μm); the relationship is well described with a straight line (Fig. 3). We consider a range of systemic Hct values from 35% to 55%, and normalize the shear stress with the shear stress calculated at 55% Hct.

FIG. 3.

Relationship between shear stress and systemic Hct for a vessel diameter of 40 μm (calculated using equation [22]). Hct, hematocrit.

Experimental data (1, 11, 19, 20, 24) suggest that the rate of NO production by the endothelium increases with shear stress. We model this effect by allowing the maximum NO production rate R_NO,_max in the Michaelis–Menten kinetics law [6] to vary with shear stress τ according to

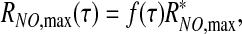[23]

where f(τ) ≤1 is a positive monotonically increasing function, and 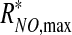is the maximum NO production rate reached at τ = τ*, such that f(τ*) = 1 and R_NO,_max remains constant (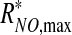) for τ ≥ τ*.

To be specific, we employ a logistic (S-shaped) curve suggested by experimental data in ref. (6),

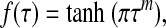[24]

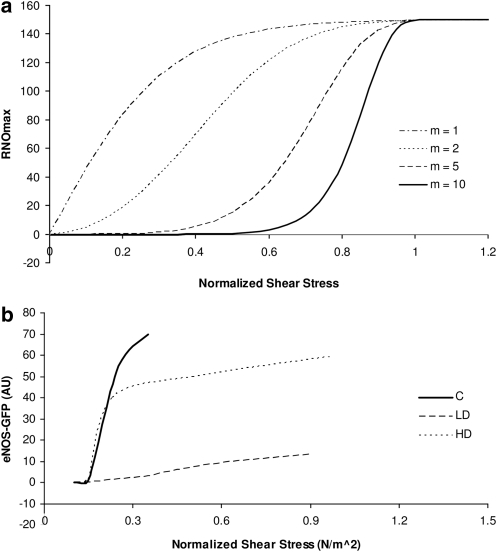
where the exponent m is a real number that determines how fast the curve approaches its asymptote f(τ*) = 1. Another possibility, which we do not pursue here because it has a kink at τ = τ*, is to choose f (τ) to be linear (20). Figure 4 exhibits the maximum NO production rate predicted with relations [23] and [24] (Fig. 4a) and observed experimentally in ref. (6) (Fig. 4b). Shear stress is normalized with respect to its counterpart at the 55% systemic Hct.

FIG. 4.

Dependence of (a) R_NO,_max on shear stress for different values of the exponent m, and (b) eNOS activation on shear stress, for different dosages of rampmycin in mice. C, control; LD, low dosage; HD, high dosage. Experimental data from ref. (6). AU signifies arbitrary units used by the authors of ref. (6) to quantify eNOS activation. NO, nitric oxide.

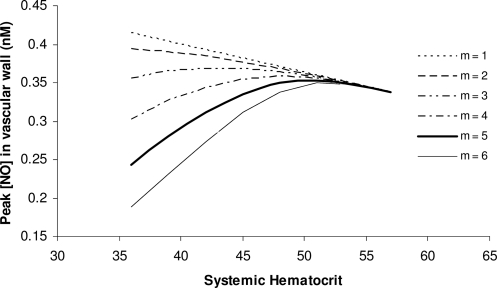
The exponent m in relation [24] determines the width of the transitional zone between the minimum and maximum NO production by the endothelium. The experimental data (6) on the dependence of the activation of endothelial NO synthase on shear stress suggest that the width of this zone, and hence the value of m, can be highly variable and requires further experimental attention. Unless otherwise noted, the simulations reported below correspond to m = 5. We also explore the effect of choosing other values of m.

The proposed model of shear-stress-dependent NO production and coupled NO/O2 transport can be represented with the following algorithm. First, expression [19] is used to compute shear stress on the arteriole wall for a given level of Hct. Second, relations [23] and [24] are used to obtain the corresponding maximum NO production rate. Third, equations [1]–[11] are solved numerically to simulate the coupled NO/O2 transport in the arteriole.

Model parameterization

The vast majority of the existing analyses of coupled NO/O2 transport employ the same values of diffusion coefficients D_NO and D_O2 in all layers of the Krogh tissue cylinder model of arterioles. In a typical example (14), diffusion data for an aqueous solution (16) are used to select the values D_NO =  3300 μm²/s and D_O2 =  2800 μm²/s for both fluid (RBC-rich core and plasma layer) and solid (glycocalyx, endothelium, vascular wall, and smooth muscle tissue) layers of the computational domain. Chen et al. (5) assumed D_NO and D_O2 in the glycocalyx to be 10 times smaller than their counterparts in all other layers. The data reported in refs. (8, 15) put the diffusion coefficient of O2 in muscle tissue at D_O2 =  1400 μm²/s, that is, half the value of its counterpart in a free solution. Therefore, we take D_NO and D_O2 in the solid layers to be half of those in the fluid layers. We also compare this with the assumption used in the previous studies, according to which D_NO and D_O2 are constant throughout the computational domain. The values of these and other parameters used in our simulations are presented in Table 1.

Summary of modeling assumptions

• Blood flow is treated as a two-phase flow, with the phases being immiscible and Newtonian.

• Flow rate in the arteriole is constant.

• Linear relationship for blood viscosity versus Hct.

• The rate of scavenging of NO by RBCs increases linearly with Hct.

• Each individual layer is homogeneous.

• The simulation is carried out in steady state.

• Linear relationship between plasma layer thickness and systemic Hct.

• The blood vessel has constant diameter.

• Linear relationship between NO scavenging rate and Hct.

Numerical solution

We used a finite difference method to solve the system of coupled reaction–diffusion equations [1]–[11]. A method of discontinuous coefficients (30) is used at all interfaces between the adjacent layers (Fig. 1) to obtain suitable finite difference formulae. The equations were discretized using a second-order central difference scheme, and the resulting finite difference matrix equations were solved with the Thomas algorithm (22).

The system of coupled ordinary differential equations was solved iteratively as follows. First, the simulation is initialized with zero NO concentration everywhere, and O2 partial pressure constant across the RBC core and zero everywhere else. Second, the transport equations for O2 are solved, to obtain an initial O2 partial pressure profile. Third, the transport equations for NO are solved. Fourth, the O2 profile is recalculated, and the procedure is repeated until convergence criteria are met. As a convergence criterion, we chose the relative error in calculated NO profiles (i.e., the maximum relative error of calculated NO concentration between successive iterations) to be less than 10⁻⁶. Due to the relatively weak coupling between the systems of transport equations for NO and O2, the convergence was obtained after a relatively small number of iterations. The numerical code is written in MATLAB.

Simulation Results

The simulation results presented below aim to elucidate the importance of (a) variable Hct, (b) spatially varying diffusion coefficients of NO and O2 in the tissue and the blood stream, and (c) shear-induced NO production. These three effects are explored below in the order of the complexity of the underlying model.

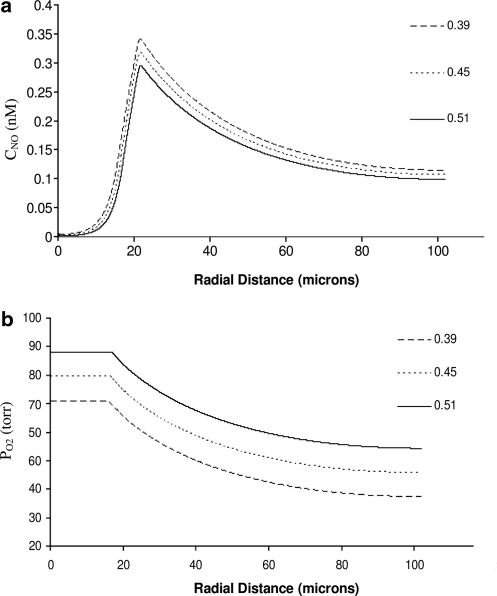
We begin by isolating the effects that different levels of Hct have on NO production. This is done by keeping R_NO,_max constant (i.e., by assuming that NO production is independent of shear stress) and assuming that diffusion coefficients in all layers shown in Figure 1 are the same. These assumptions correspond to the current state of the art in NO transport modeling (5, 9, 13). Figure 5 shows the resulting distributions of NO concentration C_NO and O2 partial pressure P_O2 for three levels of systemic Hct. Increasing Hct causes an appreciable rise in P_O2 (Fig. 5b), while its effects on C_NO are much less pronounced (Fig. 5a). Regardless of the Hct level, C_NO near the centerline of the vessel, r ≅ 0, is close to 0 because NO is scavenged by RBCs; the level of NO drops steadily across the smooth muscle where NO is consumed according to the kinetics described by equation [7]. The levels of O2 gradually decrease, as it is consumed by the endothelium, vascular wall, and the smooth muscle tissue. O2 consumption in the tissue is impeded by high NO concentrations, in accordance with equation [7]. This general behavior of both C_NO and P_O2 is in accordance with previous findings, for example, refs. (5, 9, 13).

FIG. 5.

Profiles of (a) NO concentration and (b) O2 partial pressure for several systemic Hct with the diffusion coefficients of NO and O2 same in all layers. O2, oxygen.

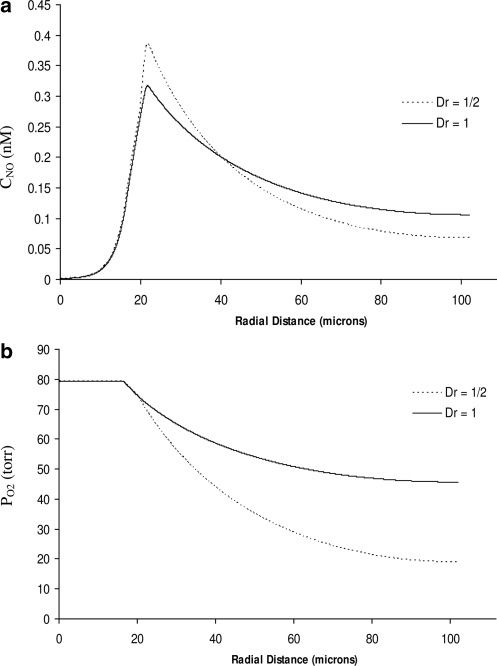
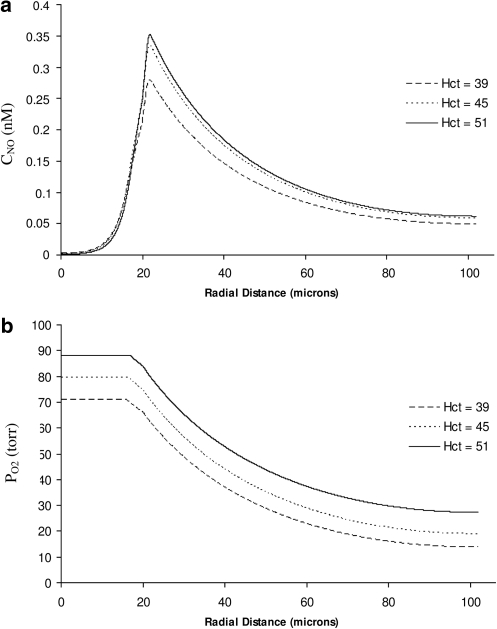
Next, we incorporate the effects of variability of the diffusion coefficients D_NO and D_O2 between the fluid (the RBC core and plasma layer) and solid (the endothelial surface layer, endothelium, and tissue) layers of the modified Krogh tissue cylinder model of an arteriole (Fig. 1). To be concrete, we set the ratio between the solid and fluid diffusion coefficients to D_r = 0.5. The resulting distributions of C_NO and P_O2 are shown in Figure 6. The qualitative behavior of the two concentrations remains unchanged, but their profiles become steeper. Comparison of Figures 5 and 6 reveals that accounting for reduced diffusion coefficients in the tissue leads to higher peak NO concentrations in the vascular wall and to sharper decreases of availability of both NO and O2 with the distance from the blood vessel. Figure 7 facilitates this comparison by plotting the C_NO and P_O2 profiles at 45% Hct, computed with the model that accounts for the spatial variability of the diffusion coefficients (the dotted lines) and with the model that ignores their variability (solid lines).

FIG. 6.

Profiles of (a) NO concentration and (b) O2 partial pressure for several systemic Hct. The model with fixed R_NO,max and the variable diffusion coefficients (D_r = 0.5).

FIG. 7.

Profiles of (a) NO concentration and (b) O2 partial pressure for 45% systemic Hct, with the model that accounts for the spatial variability of the diffusion coefficients (D_r = 0.5, dotted lines) and with model that ignores their variability (solid lines).

According to Figures 5a and 6a, the coupled NO/O2 model with the fixed value of R_NO,max predicts that the peak NO concentration in the vascular wall declines as systemic Hct increases. While not shown here, we found this decrease to be monotonic and nearly linear. This behavior is due to the nonlinear interplay of the following three phenomena. First, increasing Hct causes the rate of NO consumption by the RBC core to rise. Second, increasing Hct reduces the plasma layer thickness, thereby reducing the distance NO must diffuse before being consumed by the RBCs in the core. Third, increasing Hct raises O2 availability, thus increasing NO production rates in accordance with equation [7]. The first two mechanisms contribute to the reduction of NO availability, and their combined effect on NO availability is only slightly offset by the third factor.

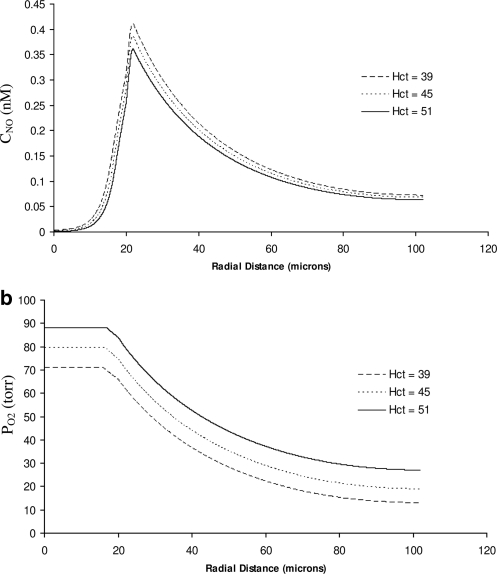
Finally, we consider the general version of our model, which also incorporates a shear dependence of NO production. Figure 8 exhibits the spatial distributions of C_NO and P_O2 computed with this model for several values of systemic Hct and the diffusion coefficients ratio D_r = 0.5. Figure 8a suggests that the shear-dependent NO production exhibits a qualitatively different relationship between peak NO concentration and systemic Hct: NO availability in the vascular wall appears to increase with Hct.

FIG. 8.

Profiles of (a) NO concentration and (b) O2 partial pressure for several systemic Hct. The model with shear-dependent R_NO,_max (equation [24] with m = 5) and the variable diffusion coefficients (D_r = 0.5).

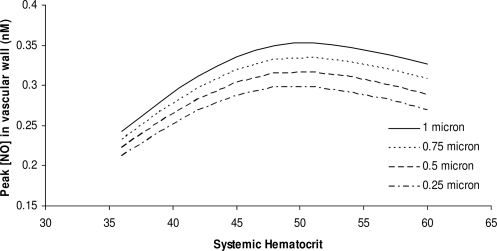
Figures 9 and 10 explore this behavior in detail. Figure 9 shows the relationship between peak C_NO and systemic Hct for several values of the exponent m in the constitutive equation [24]. For m = 5 used in the simulations presented in Figure 8 (and other values of m as small as 2), the C_NO-Hct relationship exhibits an inflection point, at which C_NO reaches its maximum and then starts to decrease. This is due to the asymptotic behavior of R_NO,_max (see the constitutive equation [24] and/or Figure 3a). In this limit, further increases in shear stress (and Hct) do not affect NO production and the increased consumption of NO by RBCs is no longer compensated by increasing shear-induced NO production, thus causing NO availability to decrease beyond the inflection point. The exponent m in the constitutive equation [24] determines its steepness and, hence, the rate at which NO production varies with shear stress. Larger values of the parameter m correspond to a steeper increase in NO production with shear stress and, hence, to a sharper increase in NO availability with rising Hct. Figure 10 confirms that this behavior remains essentially the same for different values of the glycocalyx thickness (in these simulations we set m = 5).

FIG. 9.

The dependence of peak NO concentration on systemic Hct predicted by the shear-dependent NO production model with the constitutive equation [24] and several values of the exponent m.

FIG. 10.

The dependence of peak NO concentration on systemic Hct for several values of glycocalyx thickness.

The following mechanisms combine to produce the nonlinear relationship between C_NO and Hct.

1. The rate of NO consumption by the RBC core increases with Hct.

2. Blood viscosity and shear stress at the vessel wall increase with Hct.

3. O2 availability and NO production rates increase with Hct (equation [7]).

4. The thickness of the plasma layer decreases and shear stress increases with Hct (equation [16]).

5. The distance NO must diffuse before being consumed by RBCs in the core decreases with Hct.

Effects 2, 3, and 4 cause NO availability to increase, whereas effects 1 and 5 have the opposite effect. Interaction of these competing effects results in the behavior shown in Figures 9 and 10. It is worthwhile emphasizing that changes in the relative strengths of any of these phenomena may have quantitative and qualitative effects on the final relationship between NO availability in the vascular wall and systemic Hct.

Summary and Discussion

The principal result of our analysis is to elucidate and quantify mechanisms by which changes in Hct affect the NO availability in the vascular wall of arterioles. Using the two-phase blood flow model (26), we have shown how the relationship between NO production and shear stress affects the overall behavior of the system for different levels of Hct.

Theoretical reasoning and experimental evidence suggest that diffusion coefficients for solutes undergoing diffusion in porous media must be smaller than their counterparts in free fluids. We explored the effects different diffusion coefficients for NO and O2 in the fluid (the RBC core and plasma layer) and solid (the endothelial surface layer, endothelium, and tissue) layers of the modified Krogh tissue cylinder model of an arteriole have on coupled NO/O2 transport. Reduced diffusion coefficients in the tissue cause NO concentration (C_NO) in the vascular wall to increase. This suggests that NO produced by the endothelium may be even more important than previously thought in controlling vascular tone.

Examination of the O2 partial pressure (P_O2) distributions reveals that the resulting profiles for the cases, where shear-induced NO production is (a) ignored, and (b) taken into account are very similar, due to the weak coupling of NO and O2 transport. The strength of this coupling is determined by the parameters describing the Michaelis–Menten kinetics of NO production in the endothelium and O2 consumption in the vascular wall and tissue. Hence, the transport of O2 in the microcirculation can be evaluated without considering influences such as shear-induced NO production to a good first approximation.

The relationship between NO production and shear stress has been documented in previous studies (5, 6, 19, 20). However, there is as yet no definitive conclusion on the functional relationship between these quantities, especially in vivo, at physiological levels of shear stress. We used a constitutive relation (a logistic or S-shaped curve) to describe a relation between the maximum NO production by the endothelium and fluid shear stress at the vessel wall. Figure 9 demonstrates that this relationship has a significant effect on the resulting behavior of the system for different levels of systemic Hct. This suggests the need for additional investigations, both theoretical and experimental, either to better parameterize this constitutive law or to replace it with a physicochemical model based on the first principles, or both.

We demonstrated that relatively small changes in systemic Hct may significantly raise C_NO in the vascular wall. This has implications for NO production by the endothelium on vascular tone. Martini et al. (17, 18) found that the increase in Hct can result in decreased blood pressure. Our study suggests that changing Hct can potentially cause C_NO in the vascular wall to increase, thereby causing vasodilation. This may result in a net reduction in blood pressure even as Hct rises, as the resulting vasodilation compensates for increases in blood viscosity as Hct increases.

It has been suggested that the glycocalyx is crucial in mechanotransduction of shear stress from the blood flow in the lumen to the endothelium (32). Therefore, the current approach of relating NO production to shear stress at the wall may be an oversimplification of a more complex bio-mechanical system. This is particularly important considering the variety of glycocalyx thicknesses reported in the literature. Our study indicates that greater glycocalyx thicknesses result in higher C_NO in the vascular wall, a result consistent with Chen et al. (5). The resulting higher C_NO is because the glycocalyx acts as a barrier for NO diffusion from the endothelium to the blood stream, thereby reducing scavenging rates. This is offset slightly by the impedance of O2 diffusion from bloodstream to the tissue, which slightly alters NO production rates by the endothelium.

The rheological model (26) used in our study is a simplification of hemodynamics in small blood vessels. Blood flow in vessels of small diameter is generally non-Newtonian and shear-rate-dependent (7). Hence, while our present model highlights the methodology for correlating blood rheology with shear stress, future work will focus on the development of more realistic rheological models and their application to the shear-dependent coupled NO/O2 transport model presented in this paper.

Following the standard practice in the field (5, 9, 13), we did not model vasodilation, assuming that the vessel wall does not respond to changes in C_NO.This is a major simplification since smooth muscle in the arteriolar wall responds to changes in both C_NO and P_O2 due to varied O2 carrying capacity induced by changes in Hct. An additional simplification is that blood flow is constant, and is not affected by the change of blood viscosity caused by varying Hct. Experimental data from awake hamsters subjected to small changes in Hct illustrates the complex behavior of the vascular compartment when Hct varies (25). These results, obtained with Hct variations implemented with O2 carrying and noncarrying RBCs, show that the circulation appears to behave according to conditions where increasing Hct produces a maximum NO concentration at a specific Hct. At this C_NO peripheral vascular resistance and peripheral vascular hindrance (vascular resistance independent of the effects of blood viscosity) reach their minima, which should be indicative of maximal dilatation. Finally, our model only deals with the endothelium as an NO source; however, the circulation presents additional potential sources of NO (28) such as those derived from cellular or acellular hemoglobin, which must eventually be accounted for in this type of analysis.

In conclusion, this model shows that comparatively small variations of Hct can affect NO concentration in the vascular wall of arterioles due to changes in the competition between NO production by shear stress and NO consumption by Hb in RBCs. The resulting balance of NO concentration in the vascular wall is strongly dependant on the relationship between NO production by the endothelium and shear stress. Exploration of the functional dependence of NO on shear stress and comparison with results from studies where Hct was systematically varied within a comparatively small range supports the suggestion that the circulation as a whole appears to behave as if NO bioavailability increases as Hct is increased before reaching a point of inflection.

Characterization of Plasma Layer Thickness as a Function of Variations in Hct

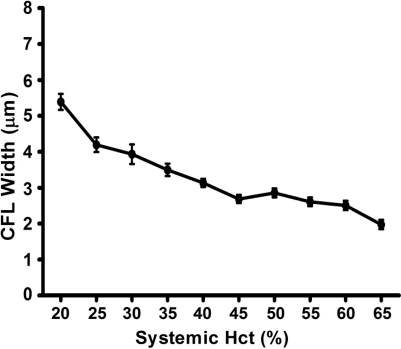
The plasma layer thickness was measured in the rat cremaster muscle preparation (33) according to the technique of Kim et al. (12). Hct was varied using either plasma or packed RBCs, from blood donors, for isovolemic hemodilution or hemoconcentration, respectively. Figure 11 shows the data used in our simulation.

FIG. 11.

Plasma layer (cell-free layer or CFL) width as a function of systemic Hct in rat cremaster muscles arterioles of 20–30 μm diameter.

Abbreviations Used

CFL

cell-free layer

D

diffusion coefficient

Hb

hemoglobin

Hct

hematocrit

NO

nitric oxide

O2

oxygen

RBC

red blood cell

Acknowledgments

This study was supported in part by the USPHS Bioengineering Research Partnership grant R24-HL 064395 (M.I.), R01-HL 062354 (M.I.), and R01-HL 076182 (P.C.J.).

Author Disclosure Statement

No competing financial interests exist.