Effects of Time between Trials on Rats' and Pigeons' Choices with Probabilistic Delayed Reinforcers

Abstract

Parallel experiments with rats and pigeons examined reasons for previous findings that in choices with probabilistic delayed reinforcers, rats' choices were affected by the time between trials whereas pigeons' choices were not. In both experiments, the animals chose between a standard alternative and an adjusting alternative. A choice of the standard alternative led to a short delay (1 s or 3 s), and then food might or might not be delivered. If food was not delivered, there was an “interlink interval,” and then the animal was forced to continue to select the standard alternative until food was delivered. A choice of the adjusting alternative always led to food after a delay that was systematically increased and decreased over trials to estimate an indifference point—a delay at which the two alternatives were chosen about equally often. Under these conditions, the indifference points for both rats and pigeons increased as the interlink interval increased from 0 s to 20 s, indicating decreased preference for the probabilistic reinforcer with longer time between trials. The indifference points from both rats and pigeons were well described by the hyperbolic-decay model. In the last phase of each experiment, the animals were not forced to continue selecting the standard alternative if food was not delivered. Under these conditions, rats' choices were affected by the time between trials whereas pigeons' choices were not, replicating results of previous studies. The differences between the behavior of rats and pigeons appears to be the result of procedural details, not a fundamental difference in how these two species make choices with probabilistic delayed reinforcers.

The relation between delay of reinforcement and probability of reinforcement has been of considerable interest to researchers who study choice (e.g., Green & Myerson, 2004; Kirby & Marakovic, 1996; Rachlin, Raineri, & Cross, 1991; Wilhelm & Mitchell, 2008; Yi, Mitchell, & Bickel, 2010). In an influential article, Rachlin, Logue, Gibbon and Frankel (1986) proposed that a reinforcer that is delivered with a probability of less than 1 is analogous to a delayed reinforcer. Their reasoning can be explained using a simple example. Suppose an animal can choose, as one option, a food delivery that occurs with a probability of .2 after a 5-s delay. If food is not delivered, there is an intertrial interval (ITI) of 10 s, and then the animal again faces a .2 probability of food after another 5-s delay. Because the probability of reinforcement is .2, it will take an average of five trials to obtain the food, so the total time from the animal's first choice to a food delivery will average 65 s (five 5-s delays, plus four 10-s ITIs). Therefore, the theory of Rachlin et al. suggests that the probabilistic reinforcer in this example would be equivalent to food delivered with certainty after a delay of 65 s. Another implication of the theory is that preference for a probabilistic reinforcer, compared to one delivered with certainty, should decrease as the ITI increases because increasing the ITI lengthens the average time between the first choice response and the eventual delivery of the reinforcer. Rachlin et al. found support for this prediction in a study with college students choosing between guaranteed and probabilistic money reinforcers.

In testing this approach with pigeons, Mazur (1989) concluded that a few modifications of the Rachlin et al. (1986) theory were needed. First, Mazur proposed that probabilistic reinforcers were analogous to reinforcers delivered after variable delays, not fixed delays as Rachlin et al. had suggested. This is because the number of trials needed to obtain food is variable and unpredictable with a probabilistic reinforcer. For the above example, the probabilistic option will deliver food once every five trials on average, but sometimes food will be delivered after just one trial, sometimes after two trials, and so on. Therefore, Mazur proposed using a version of the hyperbolic-decay equation that had been successfully applied to variable delays:

where V is the value of a reinforcer delivered after any one of n possible delays, A is a measure of the amount of reinforcement, and P_i is the probability that a delay of D_i seconds will occur on any particular trial. K is a decay parameter that determines how quickly V decreases with increases in D_i.

The second modification proposed by Mazur (1989) concerned the role of the ITI. In two experiments with pigeons, he found that varying ITI duration had no discernable effect on pigeons' choice responses. Mazur therefore proposed that the time spent in the ITI should not be included as part of D_i in Equation 1 when calculating the value of a probabilistic reinforcer. More specifically, Mazur proposed that only time spent in the presence of the distinctive stimuli that preceded food presentations should be included in D_i. For instance, in Mazur's experiments, the two choice alternatives were represented by green and red response keys, and green and red houselights were present during the delays between each choice response and a potential food delivery. Mazur proposed that the red and green keylights and houselights served as conditioned reinforcers because they preceded and predicted food presentations, whereas the white houselights that were lit during the ITIs were not conditioned reinforcers because they were never paired with food. He proposed that D_i should only include the time spent in the presence of these putative conditioned reinforcers, not the time spent in the presence of the white houselights of the ITIs.

To explain exactly how D_i was calculated, the sequence of trials in Mazur's (1989) experiments needs to be examined in detail. Each daily session was divided into blocks of four trials that included two forced trials followed by two choice trials. On a forced trial, only one key was lit, and the animal had to choose that alternative. The two forced trials of each block featured one presentation of each alternative, with the order of presentation varying randomly across blocks. On a choice trial, both the red and green keys were lit, and the pigeon chose between the two by making a single key peck on either one. A peck on the red key (called the standard alternative) led to a fixed delay with red houselights, and then food was presented on a probabilistic basis. A peck on the green key (the adjusting alternative) led to an adjusting delay with green houselights, and then food was delivered with a probability of 1. The duration of the adjusting delay was increased and decreased over trials so as to estimate an indifference point, or a delay at which the standard and adjusting alternatives were chosen about equally often.

For the adjusting alternative, which delivered food on every trial, measuring D_i was straightforward—it was simply the delay between the choice response and the food delivery. However, measuring D_i for the standard alternative was more complex, because several trials (some forced trials and some choice trials, some with one alternative and some with the other) might occur between the pigeon's first choice and the eventual delivery of a reinforcer. For example, a pigeon might experience the following sequence: a forced trial with the red key and no food; an ITI; a forced trial with the green key and food; an ITI; a choice trial with the red key and no food; an ITI; a choice trial with the red key and food.

As a specific example, in one condition of Mazur's (1989) experiment, a choice of a red (standard) key led to a 5-s delay with red houselights, and then food was presented with a probability of .2. The pigeons took about 1 s to peck the red key on a typical trial. Therefore, there was a .2 probability that food would be delivered after the first choice of the red key, and if so, D_i would equal 6 s (1 s of the red keylight plus 5 s of the red houselights). There was a .16 probability that food would be delivered only after two trials with the red key, and if so, D_i would equal 12 s (two trials with a red keylight for 1 s and red houselights for 5 s). Similar calculations of P_i and D_i were made for cases in which food was delivered after three or more trials with the red key. (In all cases, some of these trials could be forced standard trials and some could be choice trials; no differentiation was made between the two in calculating P_i and D_i .) These different values of D_i were used in Equation 1 to obtain an overall value for the standard alternative, V_s. It should be emphasized that in these calculations, D_i was defined as the cumulative time spent in the presence of the red keylights and red houselights from the initial choice response on the red key until the eventual delivery of food by this alternative, which often did not occur until several trials later.

Mazur (1989) assumed that at the indifference point, the value of the adjusting alternative, V_a, should equal V_s. He used Equation 1 to predict the indifference points for a set of conditions in which the probability of reinforcement for the standard alternative was varied. In this experiment and in several other studies with pigeons, the predictions of Equation 1 proved to be fairly accurate when D_i was calculated in this way (Mazur, 1989, 1991, 1998; Mazur & Romano, 1992).

In later research with rats, however, the results were different in two respects. First, in choice situations involving probabilistic delayed reinforcers, Mazur (2005) found that the presence or absence of distinctive stimuli (the putative conditioned reinforcers) during the delays that followed each response had no effect on the choice behavior of the rats, whereas the presence or absence of such distinctive stimuli had major effects on the pigeons' choices (Mazur, 1989, 1991). Second, when the rats chose between certain and probabilistic delayed reinforcers, there was a small but statistically significant effect of ITI duration—preference for the probabilistic alternative decreased as ITI duration increased. Mazur (2005, 2007) found that the results from rats could be described quite well if D_i included all the time between a rat's choice response and the eventual delivery of food, including time spent in the ITI. This was obviously different from the results obtained with pigeons, and Mazur suggested that this might represent a difference in how these two species are affected by stimuli that occur in the time between a response and reinforcer delivery.

Making comparisons across species is always difficult, because it is possible that an apparent difference in behavior is actually the result of some procedural details. One possibility worth exploring is that the complexity of the choice procedure itself was somehow responsible for the apparent species differences in these experiments. The purpose of the present pair of parallel experiments (Experiment 1 with rats and Experiment 2 with pigeons) was to determine whether the performance of these two species might appear more similar if the choice procedure was modified to avoid the complexity of having many trials of different types (forced and choice trials, standard and adjusting trials) separate an animal's first choice of the standard alternative from the eventual delivery of food by this alternative. As in the previous experiments, the procedure included four-trial blocks with two forced trials followed by two choice trials. Also as in the previous experiments, a choice of the adjusting alternative led to an adjusting delay that was always followed by a food delivery, and then the ITI. The main difference in the present procedure from the previous experiments was that once an animal made a choice response on the standard alternative (which delivered food on a probabilistic basis), the animal was forced to continue to respond on the standard alternative until food was delivered. That is, each trial with the standard alternative consisted of one or more “links” in which a response on the standard key (or lever) was followed by a delay and then a possible food delivery, and these links continued until there was a food delivery. For instance, in one condition of Experiment 1, a rat's first response on the standard lever led to a 3-s delay, and if food was delivered, this was followed by the ITI and then a new trial. However, if no food was delivered, there was a 10-s interlink interval (ILI), and then the standard lever was again presented and the rat needed to respond on this lever again. A response on the standard lever led to another 3-s delay that was followed either by food or by another 10-s ILI. This cycle of links and ILIs continued until food was delivered, which marked the end of one standard trial. (To avoid excessively long standard trials, the maximum number of links before a food delivery was limited to four. That is, a food delivery was scheduled to occur after the first, second, third, or fourth link of a standard trial.)

In different conditions, the duration of the ILI was varied from 0 s to 20 s to determine whether ILI duration had any effect on the indifference points for rats and for pigeons. Based on the results of previous experiments, one might expect that ILI duration would affect the indifference points for rats but not for pigeons, because the distinctive stimuli that occurred during the delays (the putative conditioned reinforcers—lever lights for the rats; colored houselights for the pigeons) were not present during the ILIs. However, another possibility is that, by changing the procedure so that each choice of the standard alternative led to an uninterrupted series of links and ILIs until food was delivered, it might help the animals to learn the consequences of a choice of the standard alternative. To be more explicit, our working hypothesis was that when each trial of the standard alternative consisted of a continuous sequence of links and ILIs that eventually ended with a food delivery, the pigeons would be sensitive to the entire time between the first choice response and food (not just the times when the delay lights were lit), and therefore their choices would be affected by ILI duration. Of course, we also expected that the rats' choices would also be affected by ILI duration, since they were affected by ITI duration in previous experiments (Mazur, 2005).

EXPERIMENT 1

Method

Subjects

The subjects were 4 male Long Evans rats approximately 17 months old at the start of the experiment. All rats were maintained at 80% of their free feeding weights, and all had previous experience on a variety of different experimental procedures.

Apparatus

The experimental chamber was a modular test chamber for rats, 30.5 cm long, 24 cm wide, and 21 cm high. The side walls and top of the chamber were Plexiglas, and the front and back walls were aluminum. The floor consisted of steel rods, 0.48 cm in diameter and 1.6 cm apart, center to center. The front wall had two retractable response levers, 11 cm apart, 6 cm above the floor, 4.8 cm long, and extending 1.9 cm into the chamber. Centered in the front wall was a nonretractable lever with the same dimensions, 11.5 cm above the floor. A force of approximately 0.20 N was required to operate each lever, and when a lever was active, each effective response produced a feedback click. Above each lever was a 2-W white stimulus light, 2.5 cm in diameter. A pellet dispenser delivered 45-mg food pellets (Bio-Serv Rodent Dustless Precision Pellets) into a receptacle through a square 5.1-cm opening in the center of the front wall, below the center lever and 1.5 cm above the floor. A 2-W white houselight was mounted at the top center of the rear wall.

The chamber was enclosed in a sound-attenuating box containing a ventilation fan. All stimuli were controlled and responses recorded by an IBM-compatible personal computer using the Medstate programming language.

Procedure

The experiment consisted of 18 conditions that used an adjusting-delay procedure. The conditions were divided into four phases. Experimental sessions were usually conducted 6 days a week.

Phase I (Conditions 1–5)

Each session lasted for 64 trials or 60 min, whichever came first. Each block of four trials consisted of two forced trials followed by two choice trials. At the start of each trial the light above the center lever was illuminated, and the houselight was off. A single lever press on the center lever initiated the start of the trial. On choice trials, after a response on the center lever, the light above this lever was turned off, the two front levers were extended into the chamber, and the lights above the two side levers were turned on. A single response on the left lever constituted a choice of the standard alternative, and a single response on the right lever constituted a choice of the adjusting alternative.

The procedure in a representative condition (Condition 2) will be described in detail, and then the procedures for the other conditions can be explained more briefly. If the adjusting (right) lever was pressed during the choice period, the two side levers were retracted, only the light above the right lever remained on, and there was a delay of adjusting duration. At the end of the adjusting delay, the light above the right lever was turned off, a food pellet was delivered, and the chamber was dark for 1 s. Then the houselight was turned on, and a 10-s ITI began.

If the standard (left) lever was pressed during the choice period, the two side levers were retracted, the light over the right lever was turned off, and the light over the left lever remained lit. There were then four possible outcomes, each of which occurred on 25% of the trials. A standard trial might include one, two, three, or four links. Each link consisted of a left lever press followed by a 3-s delay during which the light above the left lever was lit. At the end of the standard delay, the light above the left lever was turned off, and a food pellet might or might not be delivered. If a food pellet was delivered, the chamber remained dark for 1 s, and that concluded the trial. Then the houselight was lit and a 10-s ITI began, followed by the next trial. If the 3-s delay was not followed by a food pellet, there was a 10-s ILI during which only the houselight was lit. After the ILI, the houselight was turned off, the left lever was extended into the chamber, the light above the left lever was lit, and another link began. In summary, each standard trial consisted of between one and four links that consisted of a lever press and a 3-s delay, and only the last link of the trial ended with the delivery of a food pellet.

The procedure on forced trials was the same as on choice trials, except that after a response on the center lever, only one side lever was extended, the light above that lever was lit, and a press on that lever was followed by the same sequence of events as on a choice trial. Of every two forced trials, there was one for the standard lever and one for the adjusting lever, and the temporal order of the two types of trials varied randomly. As with choice trials, a standard trial might include one, two, three, or four links, separated by ILIs, and only the last link of the trial ended with the delivery of a food pellet.

After every two choice trials, the duration of the adjusting delay might be changed. If the rat chose the standard lever on both trials, the adjusting delay was decreased by 1 s. If the rat chose the adjusting lever on both choice trials, the adjusting delay was increased by 1 s (up to a maximum of 45 s). If the rat chose each lever on one trial, no change was made. In all three cases, this adjusting delay remained in effect for the next block of four trials. At the start of the first session of a condition, the adjusting delay was 0 s. At the start of later sessions of the same condition, the adjusting delay was determined by the above rules as if it were a continuation of the preceding session.

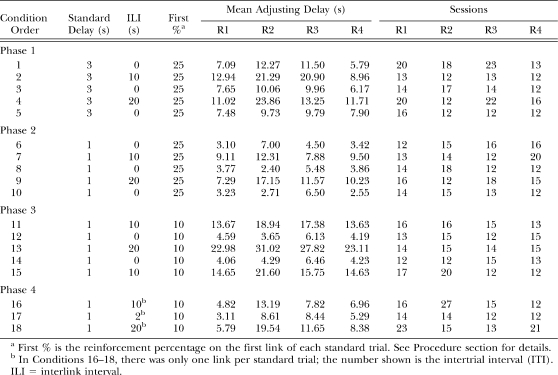
The other four conditions of Phase 1 were identical to Condition 2 in all ways except the duration of the ILI was varied, as shown in Table 1. The ILI was 20 s in Condition 4, and 0 s in Conditions 1, 3, and 5. However, the ITI was kept at 10 s in all conditions. The main purpose of Phase 1 was to determine if the rats' choices were affected by variations in the duration of the ILI.

Table 1.

Order of conditions, mean adjusting delays, and number of sessions per condition for each rat in Experiment 1.

Phase 2 (Conditions 6–10)

These five conditions were identical to the five conditions of Phase 1, except that the standard delay for each link was reduced from 3 s to 1 s. This was done because calculations based on Equation 1 suggested that the effects of ILI on the rats' indifference points should be greater (on a percentage basis) with shorter delays. As shown in Table 1, the five conditions included ILIs of 0 s, 10 s, and 20 s, presented in the same order as in Condition 1.

Phase 3 (Conditions 11–15)

In most respects, these conditions were identical to those of Phase 2, with standard delays of 1 s and ILIs of 0 s, 10 s, or 20 s. The only difference was that the percentage of standard trials on which food was delivered after the first link was reduced from 25% to 10%. For the other 90% of the standard trials, a food delivery occurred equally often after the second, third, or fourth link (30% each). This reduction in the probability of food after the first link was made because calculations based on Equation 1 predicted that this would increase the effects of ILI duration on the rats' indifference points.

Phase 4 (Conditions 16–18)

The procedure in these three conditions was more similar to the procedures used in Mazur's (1989, 2005, 2007) experiments on probability, delay, and ITI. The main difference from the previous three phases was that each standard trial ended after just one link, whether a food pellet was delivered or not. There was therefore no ILI, but the duration of the ITI was varied (10 s, 2 s, and 20 s in the three conditions, respectively). In each condition, the same ITI duration was in effect after both standard and adjusting trials. The standard delay was always 1 s. The scheduling of the food deliveries was similar to that of Phase 3, except that the percentages applied across trials rather than across links. That is, there was a 10% chance that the first trial with the standard alternative would end with a food delivery. If not, food was delivered after the second, third, or fourth standard trial (each with a probability of 30%). Once a standard trial ended with a food delivery, this same sequence of probabilities began again for subsequent standard trials (i.e., after a standard trial with food, another food delivery would occur on one of the next four standard trials, with probabilities of 10%, 30%, 30%, and 30%, respectively). A probability generator determined which trials ended with food by using a pseudorandom sequence to ensure that the actual percentages were close to the nominal percentages.

The purpose of this phase (and the corresponding phase in Experiment 2 with pigeons) was to try to replicate Mazur's (1989, 2005) findings of a species difference between rats and pigeons regarding the effects of ITI duration when standard trials could end with or without food.

Criteria for changing conditions

All conditions lasted for a minimum of 12 sessions. After 12 sessions, a condition was terminated for each rat individually when several stability criteria were met. To assess stability, each session was divided into two 32-trial blocks, and for each block the mean adjusting delay was calculated. The results from the first two sessions of a condition were not used, and the condition was terminated when the following criteria were met, using the data from all subsequent sessions: (a) Neither the highest nor the lowest single-block mean of a condition could occur in the last six blocks of a condition. (b) The mean adjusting delay across the last six blocks could not be the highest or the lowest six-block mean of the condition. (c) The mean delay of the last six blocks could not differ from the mean of the preceding six blocks by more than 10% or by more than 1 s (whichever was larger).

Results and Discussion

The right side of Table 1 shows the number of sessions needed for each rat to meet the stability criteria in each condition. For every condition, the mean adjusting delay from the six half-session blocks that met the stability criteria was used as an estimate of a rat's indifference point. These indifference points are also shown for each rat in Table 1.

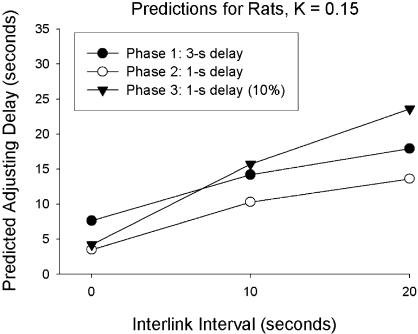
It is useful to compare the indifference points of the rats to predictions generated with Equation 1. Because the amount of reinforcement was the same for standard and adjusting alternatives, the value of A in Equation 1 does not affect the predictions, but a value for the discounting rate parameter K needs to be chosen. To derive these predictions, K was set equal to 0.15, because this value is typical of estimates of K obtained from previous studies with rats (Calvert, Green, & Myerson, 2010; Green, Myerson, Holt, Slevin, & Estle, 2004; Mazur & Biondi, 2009; Richards, Mitchell, de Wit, & Seiden, 1997). Besides the durations of the delays and ILIs used in each condition, all measures of D_i included an additional 1 s for each response on the choice lever to approximate response latencies in this procedure. For each condition in Phases 1–3, a predicted indifference point was obtained by (1) using Equation 1 to calculate the value of the standard alternative, V_s, and then (2) solving the equation with P_i  =  1.0 to determine the delay duration that would make V_a  =  V_s, based on the assumption that the values of the two alternatives were equal at the indifference point. Figure 1 shows these predictions for the different conditions. According to these predictions, the mean adjusting delays should (1) increase with longer ILIs in all three phases, (2) be greater with the 3-s delays used in Phase 1 than with the 1-s delays used in Phase 2, and (3) increase more sharply in Phase 3, with its 10% probability of food on the first link of each standard trial. (Calculations based on response latencies other than 1 s led to slight changes in the predictions compared to those shown in Figure 1. The predicted indifference points increased if longer latencies were used and decreased with shorter latencies, but the same overall pattern of changes across conditions and phases was predicted.)

Fig 1.

Predictions from Equation 1 with K  =  0.15 are shown for each condition in Phases 1–3 of Experiment 1. See text for details.

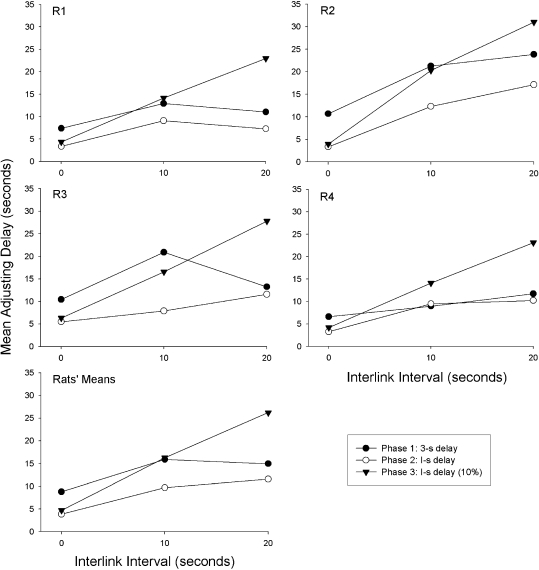
Figure 2 uses the same format as Figure 1 to plot the indifference points for each rat from the first three phases of the experiment. The group means are plotted in the bottom panel. For conditions that were conducted more than once, the data points in Figure 2 are the means of all replications. For all rats in all phases, the mean adjusting delays were shorter with 0-s ILIs than with 10-s or 20-s ILIs. The differences between ILIs of 10 s and 20 s were smaller and less consistent: The indifference points were shorter with the 10-s ILIs in 9 of 12 cases. As predicted by Equation 1, the effects of ILI duration were greatest in Phase 3, where the probability of food in the first link was 10%. A two-way repeated-measures ANOVA found a significant effect of ILI duration, F(2, 6)  =  32.34, p < .001, and a significant difference among phases, F(2, 6)  =  25.47, p < .001. There was also a significant interaction between ILI duration and phase, F(4, 12)  =  22.66, p < .001, which reflects the greater changes with increasing ILI duration in Phase 3 than in the other two phases.

Fig 2.

Mean adjusting delays are shown for each rat and for the group from each condition in Phases 1–3 of Experiment 1. For conditions that were conducted more than once, the data points are the means of all replications.

A comparison of the predictions in Figure 1 and the group means in Figure 2 shows that the group's performance closely resembled the predictions of the hyperbolic-decay model. Because the value of K used for the predictions (0.15) was based on previous experiments with rats, and because estimates of K vary for different experiments and different individual animals, there is no reason to expect that these predictions should be accurate at a quantitative level. However, the relative sizes of the indifference points across conditions should be similar in the predictions and in the actual data. A comparison of the predictions in Figure 1 and the group means found a correlation of r  =  .97, (df  =  7, p < .01), indicating a close correspondence between the predictions and the group data.

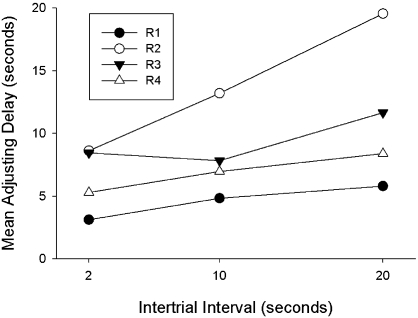
Figure 3 shows the results from Phase 4, in which each standard trial included just one link consisting of a 1-s delay that might or might not end with food. With one exception (Rat 3 with an ITI of 10 s), mean adjusting delays increased with longer ITIs. An ANOVA found a significant effect of ITI duration, F(2, 6)  =  5.74, p < .05. This finding is consistent with the results obtained by Mazur (2005), who used a similar procedure with rats and found a significant increase in the mean adjusting delays as the ITI was increased from 40 s to 90 s. The increase in indifference points with longer ITIs was quite small for 3 of the 4 rats, however. The size of this effect will be discussed in more detail in the General Discussion.

Fig 3.

Mean adjusting delays are shown as a function of ITI duration for each rat in Phase 4 of Experiment 1.

In summary, the results of this experiment showed that for rats, indifference points were longer when the time between trials was increased, regardless of whether this was done by varying the ILIs in Phases 1–3 or the ITIs in Phase 4. The pattern of results in Phases 1–3 was well predicted by the hyperbolic-decay model by calculating D_i for the standard alternative as the total time (including the ILIs) from the first choice response to a food delivery, as a comparison of Figures 1 and 2 shows. These results are consistent with those of Mazur (2005), who found longer indifference points with rats as ITI duration was increased. However, the main question of this pair of experiments is whether or not pigeons' indifference points would also be affected by the ILI if the procedure required continued choices of the probabilistic alternative until there is a food delivery. This question was addressed in Experiment 2.

EXPERIMENT 2

Method

Subjects

The subjects were 4 male white Carneau pigeons maintained at about 80% of their free-feeding weights. All the subjects had previous experience with a variety of experimental procedures.

Apparatus

The experimental chamber was 30 cm long, 25 cm wide and 28.5 cm high. The chamber had three response keys, each 2 cm in diameter, mounted on the front wall of the chamber, 24 cm above the floor and 8 cm apart. A force of approximately 0.15 N was required to operate each key. Each key could be transilluminated with lights of different colors. A hopper below the center key provided controlled access to grain (whole-grain red winter wheat), and when the grain was available, the hopper was illuminated with a 2-W white light. Six 2-W houselights (two white, two green, and two red) were mounted in a row above the Plexiglas ceiling toward the rear of the chamber. The chamber was enclosed in a sound-attenuating box with a ventilation fan. All stimuli were controlled and responses were recorded using an IBM-compatible computer using the Medstate programming language.

Procedure

The four phases (18 conditions) of this experiment were designed to be as similar as possible to those used with the rats in Experiment 1. The same adjusting-delay procedure was used, as well as the same criteria for changing conditions. As shown in Table 2, the sequence of conditions, standard delays, reinforcement probabilities, ILI durations, and ITI durations were all the same as in the corresponding 18 conditions of Experiment 1. The main differences from Experiment 1 were in the operanda, stimuli, and reinforcers used, as explained below.

Table 2.

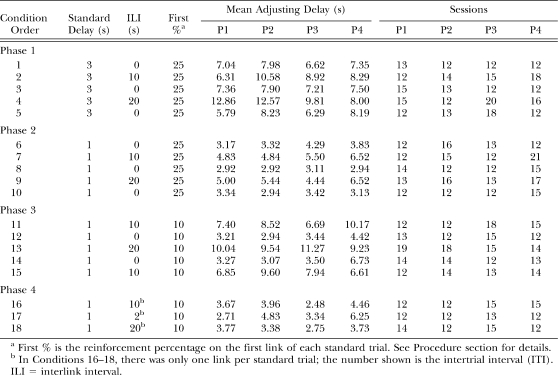
Order of conditions, mean adjusting delays, and number of sessions per condition for each pigeon in Experiment 2.

Phase 1 (Conditions 1–5)

Each session lasted for 64 trials or 60 min, whichever came first. Each block of four trials consisted of two forced trials followed by two choice trials. At the start of each trial the center key was transilluminated with white light, and the houselight was off. A single peck on the center key initiated the start of the trial. On choice trials, after a response on the center key, the keylight was turned off, and the left and right keylights were lit green and red, respectively. A single peck on the left key constituted a choice of the standard alternative, and a single peck on the right key constituted a choice of the adjusting alternative.

The following description applied to Condition 2; the other conditions were identical except for the duration of the ITI. If the adjusting (right) key was pecked during the choice period, the two side keylights were turned off, the red houselights were lit, and there was a delay of adjusting duration. At the end of the adjusting delay, the red houselights were turned off, the white hopper light was turned on, and grain was presented for 3 s. Then the white houselight was turned on, and a 10-s ITI began.

If the standard (left) key was pecked during the choice period, the two side keylights were turned off, and the green houselights were lit during a 3-s delay. Then, just as on the standard trials in Experiment 1, there were four possible outcomes, each of which occurred on 25% of the trials. A standard trial might include one, two, three, or four links. Each link consisted of a peck on the green key followed by a 3-s delay with green houselights on. At the end of the standard delay, the green houselights were turned off, and a 3-s presentation of grain might or might not occur. If grain was presented, that concluded the trial. Then there was a 10-s ITI with white houselights, followed by the next trial. If the 3-s delay was not followed by food, there was a 10-s ILI during which only the white houselights were lit. After the ILI, the white houselights were turned off, the left green keylight was again lit, and another link began. In summary, each standard trial consisted of between one and four links that consisted of a peck on the left green key and a 3-s delay with green houselights, and only the last link of the trial ended with a food delivery.

The procedure on forced trials was the same as on choice trials, except that after a peck on the center key, only one side key was lit, and a peck on that key was followed by the same sequence of events as on a choice trial. The other four conditions of Phase 1 were identical to Condition 2 in all ways except that the duration of the ILI was varied, as shown in Table 2. The ITI was 10 s in all conditions.

Phases 2, 3, and 4

As shown in Table 2, these phases used the same variations in procedures as in the corresponding phases in Experiment 1. The five conditions of Phase 2 (Conditions 6–10) were identical to the five conditions of Phase 1, except that the standard delay for each link was reduced from 3 s to 1 s. In Phase 3 (Conditions 11–15), the percentage of standard trials on which food was delivered after the first link was reduced from 25% to 10%. For the other 90% of the standard trials, a food delivery occurred equally often after the second, third, or fourth link (30% each). Finally, in Phase 4 (Conditions 16–18), the main difference was that each standard trial ended after just one link, whether food was delivered or not, just as in Phase 4 of Experiment 1. There was therefore no ILI, but the duration of the ITI was varied (10 s, 2 s, and 20 s in the three conditions, respectively). In each condition, the same ITI duration was in effect after both standard and adjusting trials. The standard delay was always 1 s. There was a 10% chance that the first trial with the standard alternative would end with a food delivery. If not, food was delivered after the second, third, or fourth standard trial (each with a probability of 30%).

Results and Discussion

The right side of Table 2 shows the number of sessions needed for each pigeon to meet the stability criteria in each condition. For every condition, the mean adjusting delay from the six half-session blocks that met the stability criteria was used as an estimate of a pigeon's indifference point. These indifference points are also shown for each pigeon in Table 2.

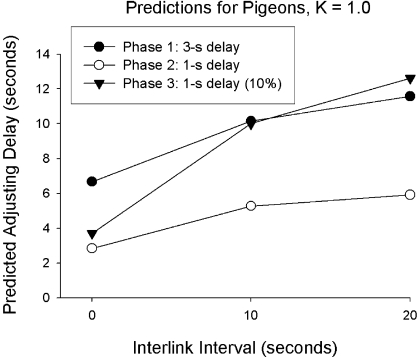
Figure 4 shows predictions from Equation 1 that were obtained by setting K equal to 1.0, because this value is typical of estimates of K obtained from previous studies with pigeons (e.g., Mazur, 1984, 1989). This larger value of K implies greater delay discounting for pigeons than for rats—reinforcer value declines more rapidly with increasing delay. Except for the different value of K, the predictions were made in the same way as for Figure 1. That is, D_i included all the time between the first choice response on the standard key and the delivery of food, and a 1-s response latency was included for each response on the standard lever. Comparing Figures 1 and 4, one main difference is that with the larger value of K used for the pigeons, the predicted indifference points are shorter, especially when the ILIs are greater than 0. (Note the different scales on the y-axes of these two figures.) In other words, the hyperbolic-decay model predicts that with steeper delay discounting, preference for the standard alternative over the adjusting alternative should increase, resulting in shorter mean adjusting delays. This is because the standard alternative offers the possibility of food after a relatively short delay (1 s or 3 s). Notice also that as ILI increases, the predicted increases in adjusting delays are quite small in the first two phases. In Phase 3, where the probability of food after the first link of the standard alternative was 10%, the predicted increases in adjusting delays are greater as ILI increases.

Fig 4.

Predictions from Equation 1 with K  =  1.0 are shown for each condition in Phases 1–3 of Experiment 2. See text for details.

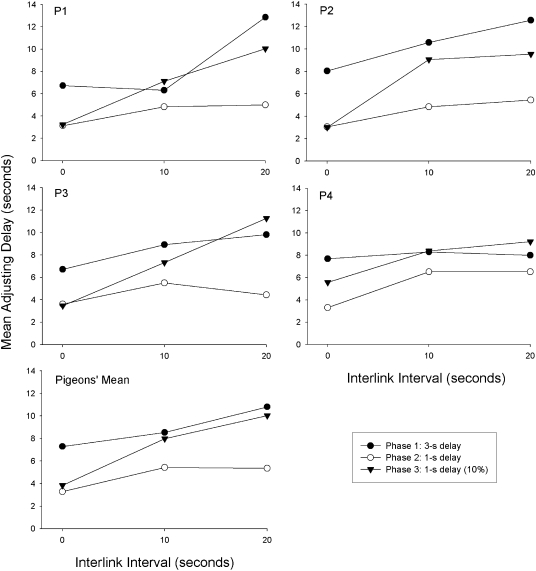
Figure 5 shows the indifference points for each pigeon from the first three phases of the experiment. The group means are plotted in the bottom panel. For conditions that were conducted more than once, the data points in Figure 5 are the means of all replications. Although the differences were small and there were some exceptions, mean adjusting delays tended to increase as ILI increased. In 23 of the 24 cases shown in Figure 5, the mean adjusting delays were shorter with a 0-s ILI than with an ILI of 10 s or 20 s. As predicted by Equation 1, the sharpest increases in mean adjusting delays occurred in Phase 3. A two-way repeated-measures ANOVA found a significant effect of ILI duration, F(2, 6)  =  27.99, p < .001, and a significant difference among phases, F(2, 6)  =  30.07, p < .001. There was also a significant interaction between ILI duration and phase, F(4, 12)  =  4.00, p < .05, which reflects the greater changes with increasing ILI duration in Phase 3 than in the other two phases.

Fig 5.

Mean adjusting delays are shown for each pigeon and for the group from each condition in Phases 1–3 of Experiment 2. For conditions that were conducted more than once, the data points are the means of all replications.

A comparison of the predictions in Figure 4 and the group means in Figure 5 shows that the group's performance was similar to the predictions at a qualitative level, but at a quantitative level the actual indifference points were, on average, slightly smaller than predicted. The value of K used for the predictions (1.0) was based on previous experiments with pigeons, and this value may not be optimal for the animals in this experiment. Nevertheless, there was a significant correlation between the predicted and obtained indifference points, r  =  .97, df  =  7, p < .01.

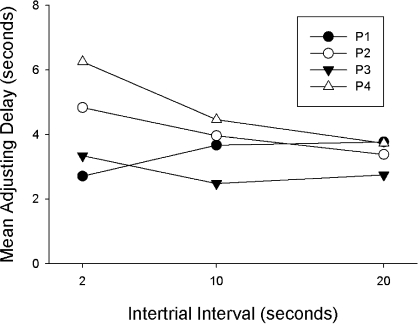
Figure 6 shows the results from Phase 4, in which each standard trial included just one link consisting of a 1-s delay that might or might not end with food. There were no systematic effects of ITI duration on the mean adjusting delays. With ITIs of 2 s, 10 s, and 20 s, the mean adjusting delays for the group were 4.3 s, 3.6 s, and 3.4 s, respectively. An ANOVA found no significant effect of ITI duration, F(2, 6)  =  1.28, and the nonsignificant downward trend is the opposite of what would be predicted if ITI duration was included in the calculation of D_i in Equation 1. This result is consistent with previous studies with pigeons that used a similar adjusting-delay procedure and standard trials that might or might not end with reinforcement, in which indifference points did not increase with longer ITIs (Mazur, 1989). It should be noted that the delays and probabilities used in Phase 4 (a standard delay of 1 s, and a 10% probability of food on the first choice of the standard alternative) were the same as those used in Phase 3, where the greatest effects of ILI duration were found in the previous phases of the experiment. These values were chosen to maximize the chances of finding an effect of ITI on the indifference points in Phase 4, yet no such effect was found.

Fig 6.

Mean adjusting delays are shown as a function of ITI duration for each pigeon in Phase 4 of Experiment 2.

In summary, there were significant increases in the mean adjusting delays with increasing ILI duration in Phases 1–3, in which the pigeons had to continue to choose the standard alternative until there was a food delivery. The patterns of variation in the mean adjusting delays in these three phases were consistent with the predictions of Equation 1. However, there was no effect of ITI duration on the mean adjusting delays in Phase 4, in which standard trials consisted of a single 1-s delay that might or might not be followed by a food delivery.

GENERAL DISCUSSION

In previous experiments that used an adjusting-delay procedure and probabilistic reinforcers, varying the duration of the ITI had different effects on the choice behavior of rats compared to pigeons. For rats, increasing the ITI led to small but reliable increases in the indifference points, which indicated a decrease in preference for the probabilistic reinforcer as the time between trials grew longer (Mazur, 2005). This effect of ITI was consistent with results found with human subjects (Rachlin et al., 1986). However, a similar procedure with pigeons found no effect of ITI on their indifference points (Mazur, 1989). Because of this discrepancy between the results from rats and pigeons, Mazur (2005) suggested that there could be a difference in how these two species make choices involving probabilistic delayed reinforcers.

However, the two experiments reported here suggest that there is no fundamental difference in how rats and pigeons choose between certain and probabilistic delayed reinforcers. These experiments found that the difference between rats and pigeons disappeared when the trials with the probabilistic reinforcer were arranged in a slightly different way. In the earlier studies (Mazur, 1989, 2005), each choice of the standard (probabilistic) alternative might or might not end with food, and then there was an ITI followed by the next trial. In contrast, in the present experiments (Phases 1–3), once the standard alternative was chosen on one trial, the animal was forced to keep selecting the standard alternative until there was a food delivery. For ease of description, we have called each repeated presentation of the standard key or lever a “link,” and we have called the sequence of links that finally ended with food a “trial.” Also for ease of description, we have distinguished between the “ILIs” that separated the links and the “ITIs” that separated trials. However, semantics aside, these links can be considered a series of forced trials, separated by ITIs during which only the white houselights were lit. Under this procedure, indifference points for both pigeons and rats increased as the time between the links increased.

To attempt to replicate the species difference found in previous studies (Mazur, 1989, 2005), Phase 4 of both experiments reverted to the procedure used in those studies, in which each trial with the standard alternative included just one delay that might or might not be followed by food. Then, in the three conditions, there was an ITI of 2, 10, or 20 s, followed by a new trial. Under these conditions, the species difference seen in the earlier studies was found: the indifference points increased with increasing ITI for the rats, but not for the pigeons.

Taken as a whole, these results seem to imply that some feature of the discrete-trials procedure used in Phase 4 and in the experiments of Mazur (1989) was responsible for the failure to find an effect of ITI with pigeons. One likely candidate is the way trials were arranged in blocks of two forced trials followed by two choice trials. Because of this arrangement, after each trial with the standard alternative (whether or not food was delivered), the next trial might be (1) a forced trial with the standard alternative, (2) a forced trial with the adjusting alternative, or (3) a choice trial on which either alternative could be chosen. Compared to Phases 1–3 of the present experiments, this can be considered a more complex choice procedure, at least in terms of the possible events that could occur between the first choice of the standard alternative and the eventual delivery of food by that alternative.

It is possible that the pigeons' lack of sensitivity to ITI duration in Phase 4 was due to the complexity of the procedure. This, of course, does not explain why the pigeons showed no effect of ITI duration whereas the rats did. However, it should be noted that although there was a statistically significant effect of ITI duration for the rats in Phase 4, it was a small effect—much smaller than predicted by Equation 1. With K set at 0.15, a value that provided good predictions for the rats in Phases 1–3, Equation 1 predicts indifference points of 7.1 s, 16.2 s, and 24.6 s for the conditions in Phase 4 with ITIs of 2 s, 10 s, and 20 s, respectively. The actual indifference points for all the rats except R2 were much shorter than this, and the group means were 6.4 s, 8.2 s, and 11.3 s, respectively. Therefore, the results from the rats and pigeons in Phase 4 were similar in at least one respect—neither species showed as much change in indifference points as was predicted by Equation 1.

Further studies manipulating different features of the procedure used in Phase 4 could help to determine why the rats showed less effect of ITI duration than predicted and why pigeons showed no systematic effect at all. From our perspective, however, the most important contribution of the present experiments is not the analysis of procedural details but rather the finding that in Phases 1–3, both pigeons and rats exhibited a decrease in preference for the probabilistic alternative as the time between trials increased. Furthermore, for these three phases, Equation 1 provided a good description of the results for both species when D_i was calculated as the total time between the first response on the standard alternative and the eventual delivery of food after one or more links. This correspondence between predictions and results can be seen by comparing the predicted indifference points in Figures 1 and 4 with the group means in Figures 2 and 5.

As already explained, we used different values of K for rats and pigeons, based on previous results suggesting different rates of temporal discounting for these two species. As a further test of the adequacy of hyperbolic-decay model, an additional analysis was conducted in which K was treated as a free parameter, and Equation 1 was fitted to the group means from the rats and the pigeons. For the rats, it turned out that the best-fitting value of K was 0.15 (which was the value used for the predictions shown in Figure 1), and Equation 1 accounted for 93.4% of the variance in the group data. For the pigeons, the best-fitting value of K was 2.25, and Equation 1 accounted for 92.8% of the variance in the group data. The predictions with K  =  2.25 are very similar to those shown in Figure 4 for K  =  1, except that the predicted indifference points are slightly shorter (by an average of less than 1 s), thereby bringing them closer to the group means shown in Figure 5.

It therefore appears that with the procedures used in Phases 1–3, the main difference between the performance of the rats and the pigeons was a quantitative one—the best-fitting value of K was much smaller for the rats. This finding is consistent with the results of previous studies that suggested that the rate of temporal discounting is substantially slower for rats than for pigeons (e.g., Green et al., 2004; Green, Myerson, Shah, Estle, & Holt, 2007; Mazur, 1984; Mazur & Biondi, 2009; Richards et al., 1997). The quantity 1/K can be called a reinforcer's “half-life,” because it represents the delay at which a reinforcer's value decreases by half in Equation 1 (cf. Yoon & Higgins, 2008). The values of K obtained in these different studies suggest that the typical half-life is about 1 or 2 s for pigeons, but about 5 or 10 s for rats. By way of comparison, Helms, Reeves, and Mitchell (2006) obtained values of K indicating half-lives of about 2.5 s and 8 s for two different strains of mice, and the difference between strains was statistically significant. With rhesus monkeys, the data of Freeman, Green, Myerson, and Woolverton (2009) implied an average half-life of about 10 s with saccharine as a reinforcer, but when cocaine was used as a reinforcer, the data suggested a half-life of about 120 s (Woolverton, Myerson, & Green, 2007). With humans, estimated half-lives can range from mere seconds with reinforcers such as juice (Forzano & Logue, 1992, 1994) or video games (Millar & Navarick, 1984) to months or years when the choices involve hypothetical amounts of money (e.g., Beck & Triplett, 2009; Green, Fry, & Myerson, 1994). It appears that the rate of delay discounting can vary substantially for different species, for different individuals of the same species, and for different types of reinforcers.

In conclusion, these two experiments showed that when choosing between certain and probabilistic delayed reinforcers, the choices of both rats and pigeons were affected by the time between trials. With increasing time between trials (which we called the ILIs in these experiments), preference for the probabilistic option decreased, as reflected in longer adjusting delays. There is still considerable debate about the relation between reinforcer probability and delay, and some studies have found potentially important differences in how these two variables can affect behavior in choice situations (e.g., Green & Myerson, 2010; McKerchar, Green, & Myerson, 2010; Shead & Hodgins, 2009). However, the results from the present experiments were well described by including reinforcer delay and probability in a single conceptual framework. The results were generally consistent with both the hyperbolic-decay model and the more general proposal of Rachlin et al. (1986) that probabilistic reinforcers are functionally equivalent to delayed reinforcers.