A Model of Resurgence Based on Behavioral Momentum Theory

Abstract

Resurgence is the reappearance of an extinguished behavior when an alternative behavior reinforced during extinction is subsequently placed on extinction. Resurgence is of particular interest because it may be a source of relapse to problem behavior following treatments involving alternative reinforcement. In this article we develop a quantitative model of resurgence based on the augmented model of extinction provided by behavioral momentum theory. The model suggests that alternative reinforcement during extinction of a target response acts as both an additional source of disruption during extinction and as a source of reinforcement in the context that increases the future strength of the target response. The model does a good job accounting for existing data in the resurgence literature and makes novel and testable predictions. Thus, the model appears to provide a framework for understanding resurgence and serves to integrate the phenomenon into the existing theoretical account of persistence provided by behavioral momentum theory. In addition, we discuss some potential implications of the model for further development of behavioral momentum theory.

Resurgence is generally defined as the reappearance of an extinguished target behavior when an alternative behavior reinforced during extinction is also subsequently placed on extinction (e.g., Cleland, Foster, & Temple, 2000). In the laboratory, experiments examining resurgence typically include three phases. During Phase 1, a target behavior is reinforced on a baseline schedule. In Phase 2, the target behavior is placed on extinction and an alternative behavior is reinforced. In Phase 3, the alternative behavior is also placed on extinction and the target behavior increases (i.e., resurgence occurs). For example, Leitenberg, Rawson, and Bath (1970) reinforced lever pressing of rats on a variable-interval (VI) 30-s schedule of food delivery in Phase 1. In Phase 2, pressing the original lever was no longer reinforced, and pressing an alternative lever was reinforced on a fixed-ratio (FR) 10 schedule. In Phase 3, pressing the alternative lever was also placed on extinction, and responding on the original lever then increased. Such resurgence effects have been noted repeatedly in a number of situations and with a range of different species (see Doughty & Oken, 2008; Epstein, 1985; Lattal & St. Peter Pipkin, 2009, for reviews).

The phenomenon of resurgence is of particular interest because it could be a major source of relapse following behavioral interventions for a variety of applied problems. For example, the treatment of problem behavior in persons with developmental disabilities often involves simultaneous extinction of the problem behavior and reinforcement of appropriate behavior (e.g., Carr & Durand, 1985). Resurgence of problem behavior can occur with such treatments when reinforcement for the alternative behavior is later reduced or eliminated (e.g., Volkert, Lerman, Call, & Trosclair-Lasserre, 2009; see also Lieving, Hagopian, Long, & O'Connor, 2004). In addition, resurgence effects have been suggested as a possible source of relapse to drug abuse with a decrease in the availability of alternative nondrug reinforcers (Podlesnik, Jimenez-Gomez, & Shahan, 2006; Winterbauer & Bouton, 2010).

Although resurgence is increasingly recognized as an important behavioral phenomenon, there has been little attempt to systematize the existing literature or to provide a formal account of the processes governing resurgence. In what follows, we develop a quantitative model of resurgence. The model suggests that resurgence can be understood as an extension of the process of extinction as characterized by behavioral momentum theory.

A Model of Relapse and the Problem of Resurgence

Resurgence is just one of a number of relapse phenomena characterized by the reappearance of previously extinguished behavior. Other examples of such phenomena include reinstatement and renewal. Reinstatement refers to the reappearance of extinguished responding when a response-independent reinforcer is delivered (e.g., Reid, 1958). Renewal refers to the recurrence of a behavior that was trained in one stimulus context, extinguished in a different context, and then reappears when the original training context is presented again (i.e., ABA renewal; Nakajima, Tanaka, Urushihara, & Imada, 2000). Bouton (e.g., 2004) has suggested that such relapse phenomena are consistent with accounts of extinction that are based on the assumption that extinction does not produce unlearning. Furthermore, Bouton suggests that the effects of extinction are context specific and that relapse occurs when stimulus conditions different from those present during extinction are subsequently encountered.

Bouton's approach to extinction shares some important properties with behavioral momentum theory. Behavioral momentum theory (e.g., Nevin & Grace, 2000) also suggests that the decreases in behavior associated with extinction are not a result of unlearning, and that resistance to extinction depends upon the value of the Pavlovian stimulus–reinforcer relation between a discriminative stimulus context and all reinforcers obtained in that context. Based on these considerations, Podlesnik and Shahan (2009, 2010) suggested that an extension of the augmented model of behavioral momentum (Nevin & Grace, 2000; Nevin, McLean, & Grace, 2001) could provide a quantitative model of relapse of extinguished operant behavior.

The augmented model of behavioral momentum suggests that decreases in responding during extinction result from the disruptive effects of terminating the contingency between a response and a reinforcer and the generalization decrement associated with removal of reinforcers from the situation. Furthermore, the disruptive impact of extinction varies inversely with the rate of reinforcement previously experienced in the discriminative-stimulus context. Quantitatively, that is,

where B_t is response rate at a particular time t in extinction, B₀ is the preextinction baseline response rate, c is the disruption produced by terminating the contingency between the response and reinforcer, d scales disruption from the elimination of reinforcers (i.e., generalization decrement), r is the rate of reinforcement in the presence of the discriminative stimulus context in baseline, and b is sensitivity to reinforcement rate. Thus, as time in extinction progresses, the disruption characterized by the numerator increases, but the impact of this disruption is lessened for responding previously occurring in a context associated with a higher rate of reinforcement. Importantly, the rate of reinforcement (i.e., r) experienced in the preextinction discriminative context includes all sources of reinforcement occurring in that context, regardless of whether they are contingent upon the target response, independent of the target response, or even contingent on an alternative response. The prediction that resistance to extinction (or other disruptors) in the presence of a discriminative stimulus depends upon all sources of reinforcement obtained in the presence of that stimulus has been confirmed in numerous experiments with a variety of species, responses, and reinforcer types (e.g., Ahearn, Clark, Gardenier, Chung, & Dube, 2003; Cohen, 1996; Grimes & Shull, 2001; Harper, 1999; Igaki & Sakagami, 2004; Mace et al., 1990; Nevin, Tota, Torquato, & Shull, 1990; Shahan & Burke, 2004).

To extend the augmented model of extinction to relapse of extinguished behavior, Podlesnik and Shahan (2009, 2010) suggested that relapse occurs when some change in contextual circumstances produces a decrease in the disruption associated with extinction. As a result of the decrease in disruption, responding increases. Specifically,

where the added parameter m scales a reduction in the disruptive effects of contingency suspension (i.e., c) and n scales a reduction in the generalization decrement (i.e., dr) associated with the occurrence of the relapse-producing event, and other terms are as in Equation 1. During extinction, m and n are equal to 1, and Equation 2 is the same as Equation 1. With the occurrence of a relapse-producing event, m and n may assume values of less than 1 and responding increases because of a reduction in extinction-associated disruption in the numerator. In addition, as is true with resistance to extinction, Equation 2 predicts that response rates as a proportion of baseline during relapse should be greater in the presence of a stimulus associated with a higher rate of reinforcement prior to extinction (i.e., higher r). This prediction is consistent with the data from a number of experiments by Podlesnik and Shahan (2009, 2010) examining relapse in reinstatement, renewal, and resurgence preparations.

Despite the fact that Equation 2 has provided good fits to data from some resurgence experiments (Podlesnik & Shahan, 2010), further consideration suggests that the model fails as a theory of resurgence. The problem is that when Equation 2 is used to describe data from resurgence experiments, the value of the c parameter required for the fits has been considerably larger than for the value (i.e., ≈ 1) in typical applications of Equation 1 to extinction data (Nevin et al. 2001) and applications of Equation 2 to other relapse phenomena (e.g., reinstatement). The reason is that in a resurgence preparation, reinforcement for an alternative response is introduced during Phase 2 extinction and tends to produce faster elimination of responding than standard extinction (e.g., Leitenberg et al., 1970). But, the c parameter should only be capturing the disruptive effect of eliminating the contingency between the target response and its reinforcer, not the added disruptive effects of having an alternative source of reinforcement present during extinction. In short, c is serving as an inappropriate catchall disruptor term when Equation 2 is applied to resurgence.

A second and related problem with Equation 2 as an account of resurgence is that the equation cannot predict an important finding in the resurgence literature. Leitenberg, Rawson, Mulick (1975, Experiment 3) showed that higher rates of alternative reinforcement during Phase 2 extinction produce faster elimination of the target response, but a larger increase in responding (i.e., resurgence) when the alternative reinforcer is removed in Phase 3. The difficulty for Equation 2 is that even with an inflated value of the c parameter to accommodate the added disruptive effects of alternative reinforcement and the associated faster response elimination, the equation cannot capture the larger increase in responding when a higher rate of alternative reinforcement is removed. The reason is that the value of the c parameter remains constant during the alternative reinforcement phase and during the resurgence phase when the alternative reinforcer is removed. Simply reducing disruptive impact by decreasing m and/or n when alternative reinforcement is removed cannot predict the opposite effects of a higher rate of reinforcement during response elimination and during resurgence. Thus, a more specific model is required to provide an acceptable theory of resurgence.

A Model of Resurgence

The model of resurgence we develop here is based on the augmented model of extinction (i.e., Equation 1) with two additions. First, the presence of an alternative source of reinforcement during extinction is assumed to have a disruptive effect of its own. Second, the additional source of reinforcement in the context during extinction is also assumed to contribute to the future strength of the initially trained target behavior. Specifically,

where all terms are as in Equation 1. Like the augmented model upon which it is based, Equation 3 has parameters for suspending the contingency between the target behavior and reinforcement (i.e., c), scaling the generalization decrement associated with removal of reinforcers for the target behavior from the situation (i.e., d), and sensitivity to reinforcement (i.e., b). The added variable R_a is the rate of alternative reinforcement introduced during extinction, and the added parameter k scales the disruptive impact of that alternative reinforcement on the target behavior. Thus, the addition of alternative reinforcement during extinction increases the disruptive impact in the numerator by kR_a, and higher rates of alternative reinforcement produce larger decrements in the target behavior as a result. When alternative reinforcement is removed, R_a in the numerator goes to zero, and the suppressive effect of the alternative reinforcement on the target behavior is removed—thus resulting in increased responding (i.e., resurgence). In addition, the inclusion of R_a in the denominator suggests that, like reinforcement experienced in the preextinction baseline (i.e., r), alternative reinforcement experienced within the discriminative context during extinction of the target behavior also strengthens the target behavior. It is important to note that in both the standard augmented model of extinction (Equation 1) and in Equation 3, the rate of reinforcement experienced during baseline (r) is carried forward to extinction, and thus represents the effects of a history of reinforcement in the stimulus context on resistance to extinction. Similarly, in addition to r, the added R_a in the denominator of Equation 3 is carried forward to the resurgence condition and represents the strengthening effects of the history of alternative reinforcement during extinction of the target behavior.

As suggested for the previous relapse model of Podlesnik and Shahan (2010), we use the exponentiated version of the resurgence model because doing so does not require log- transformed data and permits the inclusion of zero values common in research examining postextinction relapse. Accordingly, the exponentiated version1 is:

where all terms are as in Equation 3. Although Equations 3 and 4 have four parameters, in practice, sensitivity to reinforcement (i.e., b) is typically near 0.5 (Nevin, 2002) and we have fixed it as a constant at that value for all fits and simulations reported here. In addition, the value of d has been near 0.001 in previous fits of Equation 1 to extinction data (e.g., Nevin & Grace, 2000) and fits of Equation 2 to relapse data (Podlesnik & Shahan, 2010). Thus, we have fixed d as a constant at that value for the fits and simulations reported here. As a result, fits of Equation 4 below include the use of two free parameters (i.e., k and c) and two fairly well established constants (i.e., b and d).

It should be noted that, like Equation 1 and behavioral momentum theory more generally, Equations 3 and 4 use responding relative to baseline as the primary dependent measure. A version of the model predicting absolute response rates during extinction and resurgence is easily obtainable by multiplying both sides of Equation 4 by baseline response rates (i.e., B₀) such that,

where all terms are as in Equation 4. Even though Equation 5 predicts absolute response rates, it nonetheless suggests that preextinction baseline response rates must be considered when accounting for extinction and the response rate increases associated with resurgence. Fits of Equation 4 and Equation 5 to data produce the same parameter values and account for the same percentages of variance. Regardless, from the perspective of behavioral momentum theory responding relative to baseline is the appropriate measure of resistance to change (i.e., response strength), and thus we will use Equation 4 in the analyses below.

As we will describe in detail below, Equation 4 appears to provide a fairly comprehensive account of findings in the resurgence literature. Where possible, we provide fits of the model to existing datasets using the Frontline Systems Solver for Mac Excel 2008. Typically, tabled data were not available in the original publications. Thus, where possible, data were electronically extracted from figures using GraphClick 3.0. Unfortunately, the data from most reports in the literature are not amenable to formal fits because some of the relevant data required for fitting the model are not presented. Often, rates of alternative reinforcement during extinction of the target response are not reported or recoverable from other measures, and/or behavioral data are not presented with sufficient detail. Nonetheless, even though formal fits are not possible for many findings in the literature, we will discuss how existing data appear to be consistent with the predictions of the model. We begin by examining the core assumption of the model that the rate of the alternative source of reinforcement during response elimination in Phase 2 and its removal during Phase 3 play a critical role in resurgence.

The Source of Alternative Reinforcement and Resurgence

Equation 3 suggests that it is the dual effects of alternative reinforcement as an added disruptor during Phase 2 (i.e., kR_a in the numerator) and as an added source of reinforcement in the discriminative stimulus context (i.e., R_a in the denominator) that determine resurgence in Phase 3. Furthermore, because resurgence occurs as a result of the decrease in disruption associated with the change in frequency of alternative reinforcement, resurgence should only occur when the rate of alternative reinforcement in the situation is decreased. Importantly, resurgence should occur in Phase 3 when alternative reinforcement is reduced relative to Phase 2, regardless of the details of the source of alternative reinforcement. For example, although higher rates of alternative reinforcement should produce greater disruption during Phase 2 and greater resurgence in Phase 3, the details of the type of schedule should not matter. In what follows, we discuss the existing data with respect to these predictions.

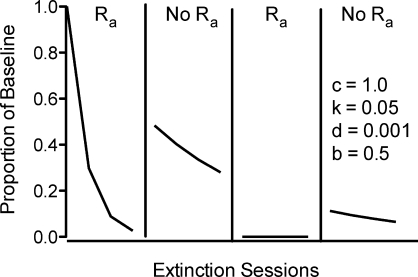
As noted above, Leitenberg et al. (1975) examined the effects of frequency of alternative reinforcement during extinction on subsequent resurgence when that alternative reinforcement was removed. Specifically, three groups of pigeons responded on a VI 120-s schedule of food delivery during the Phase 1 baseline. In Phase 2, one group received standard extinction with no alternative source of reinforcement, a second group received a low rate of reinforcement (i.e., VI 240 s) for pecks to a second key, and a third group received a high rate of reinforcement (i.e., VI 30 s) for pecks to the second key. During this phase, the group with the high rate of reinforcement for the alternative response showed faster elimination of the target response than the low-rate and no-alternative-reinforcement groups. Nonetheless, in Phase 3 when all reinforcement was withheld, the group with the high rate of alternative reinforcement during the previous extinction condition showed more resurgence than the group with the lower rate of reinforcement. The group with no alternative reinforcement during extinction did not show resurgence.

Figure 1 shows the fit of Equation 4 to the data from the high and low rate alternative reinforcement groups from Leitenberg et al. (1975, Experiment 3) expressed as a proportion of baseline rates. The model provides a good description of the data, accounting for 95% of the variance. The obtained value of c (i.e., 0.89) is comparable to previous fits of Equation 1 to standard extinction data. The fact that Leitenberg et al. included a control group with no alternative reinforcement during extinction provides a useful opportunity to evaluate the c parameter in Equation 4. If Equation 4 has remedied the concern with the previous model that c was serving as an inappropriate disruptor term, then fitting Equation 1 to the data from the control group that did not show resurgence should yield a value of c that is similar to the value obtained by fitting Equation 4 to the groups with alternative reinforcement during extinction. Accordingly, Equation 1 accounts for 90% of the variance in the data from the control group with c as a free parameter and a  =  0.5 and d  =  0.001, as in the fit above. The obtained value of c is 0.93, and fixing it as a constant at the 0.89 value obtained above changes the percentage of variance accounted for by less than 1%. Furthermore, including the data from the control group in the fits of Equation 4 reported in Figure 1 results in similar values of c (i.e., 0.91) and k (i.e., 0.05) and percentage of variance accounted for (i.e., 93%) as the fits to data for just the two groups with alternative reinforcement during extinction. Thus, Equation 4 appears to provide a reasonable account of the effects of alternative reinforcement on the speed of response elimination and subsequent resurgence when the alternative reinforcement is removed.

Fig 1.

Reanalysis of data from Leitenberg et al. (1975) in which alternative reinforcement (i.e., R_a) during extinction of a target behavior occurred at either a high rate (VI 30) or a low rate (VI 120) and then also was placed on extinction (i.e., No R_a). The lines and reported parameter values were generated with least-squares regression of Equation 4 to the data.

Lieving and Lattal (2003) provide support for the prediction of Equation 4 that it is a reduction in the rate of an alternative source of reinforcement that produces resurgence. In their Experiment 3, pigeons' key pecking was reinforced on a VI 30-s schedule of food delivery during the Phase 1 baseline. During Phase 2 extinction, alternative reinforcement was arranged for pressing a treadle on a VI 30 s. When the VI 30 s of treadle-press reinforcement was changed to response-independent reinforcement on a variable-time (VT) 30-s schedule, resurgence of key pecking did not occur. However, when the VT 30-s reinforcement was removed in the next phase, resurgence of key pecking did occur. Thus, the occurrence of resurgence required that the alternative reinforcement be removed. Lieving and Lattal obtained a similar result when VI 120-s schedules were used for the Phase 1 baseline, Phase 2 extinction, and the switch to VT reinforcement. Also consistent with Equation 4, the amount of resurgence was smaller when the rate of alternative reinforcement being removed was lower as arranged by the VI 120 s than the VI 30 s. In addition, in Experiment 4, Lieving and Lattal showed that a reduction of alternative reinforcement to a nonzero level can also result in resurgence of an extinguished target behavior. A reduction in the rate of alternative reinforcement from a VI 30-s schedule to a VI 360-s schedule resulted in a small amount of resurgence. This outcome is consistent with Equation 4 because even reductions of alternative reinforcement to nonzero levels in the numerator (i.e., kR_a) result in some reduction of disruption, and thus increases in the target response. When alternative reinforcement was completely removed in a subsequent condition, a larger amount of resurgence occurred than with the decrease to a VI 360-s schedule.

As noted above, Equation 4 suggests that it is rate of alternative reinforcement that plays a critical role in resurgence rather than the schedule type. Leitenberg et al. (1975, Experiment 2) examined resurgence with groups of rats exposed to either FR or yoked VI schedules providing the same rates of alternative reinforcement during extinction of the target behavior. The groups exposed to alternative reinforcement provided by both FR and VI schedules showed faster response elimination than a control group receiving no alternative reinforcement. Most important for present purposes, the FR and VI groups showed similar amounts of resurgence when the alternative reinforcement was removed. Winterbauer and Bouton (2010) recently obtained similar results. They exposed different groups of rats to FR, random-interval (RI), and response-independent random-time (RT) schedules of alternative reinforcement during Phase 2 extinction of a target behavior (i.e., lever pressing). The different schedules arranged the same rate of alternative reinforcement and, as suggested by Equation 4, produced similar amounts of resurgence when they were removed. Furthermore, consistent with findings from the RT alternative reinforcement group in Winterbauer and Bouton, the presence of even a freely available cup of food during extinction speeds response elimination and produces recurrence of extinguished responding when it is removed (Enkema, Slavin, Spaeth, & Neuringer, 1972).

Finally, another way of arranging alternative reinforcement during response elimination is to reinforce the absence of the target behavior with a differential-reinforcement-of-other-behavior schedule (DRO). It should be noted that Equation 4 models the disruptive impact of extinction in the numerator, and is not an explicit model of DRO. Regardless, for present purposes it is sufficient to note that within the general framework provided by Equation 4, removal of alternative reinforcement provided by a DRO should also produce resurgence. Consistent with this suggestion, Uhl and Garcia (1969) found that rats receiving alternative reinforcement on a DRO schedule showed a recurrence of responding when that reinforcement was removed (see also da Silva, Maxwell, & Lattal, 2008). A subsequent study with squirrel monkeys by Mulick, Leitenberg, and Rawson (1976) showed that removal of DRO reinforcement did not produce resurgence when it was suspended in Phase 3. However, because the DRO was relatively ineffective at eliminating responding in Phase 2, little DRO reinforcement was actually obtained. Thus, when the DRO was suspended, little reinforcement was removed, and consistent with Equation 4 little resurgence occurred (cf. Pacitti & Smith, 1977).

One experiment by Doughty, da Silva, and Lattal (2007) with pigeons at first appears to suggest that the use of a DRO to schedule alternative reinforcement during response elimination could produce different effects than reinforcement of an alternative response. In their Experiment 1, rates of alternative reinforcement provided by an alternative key peck response or by a DRO were equated during Phase 2 response elimination. Despite the equal reinforcement rates, greater resurgence occurred in Phase 3 following the DRO than following reinforcement of the alternative key peck during extinction. Unfortunately, this effect is difficult to interpret given that it was not replicated in their Experiment 4 when treadle pressing was used as the alternative response. This lack of replication occurred despite the fact that a direct comparison of resurgence using key pecking versus treadle pressing as the alternative response failed to produce any compelling difference in resurgence in their Experiment 5. Other research has also shown that the topography of the alternative response during extinction does not affect resurgence (cf. Leitenberg et al., 1975). As a result, the reason for the initial finding in Doughty et al. and its failure to replicate remain unclear. Thus, at present it remains unclear if removing equal rates of DRO reinforcement versus reinforcement produced by an alternative response produces any systematic differences in resurgence. The general approach suggested by Equation 4 would predict that no such differences should be expected. Should removal of equal rates of reinforcement delivered by a DRO and an alternative response ultimately turn out to produce reliable differences in resurgence, the disruptor terms in the numerator of Equation 4 would likely need to be modified to capture the added complexities of DRO. Regardless, what is clear from the available data is that when reinforcement obtained for the nonoccurrence of a target behavior on a DRO schedule is subsequently removed, resurgence occurs.

Together, the results of the studies reviewed above suggest that, consistent with Equation 4, resurgence results from the removal of alternative reinforcement, regardless of the source. As suggested by the equation, higher rates of alternative reinforcement accelerate response elimination but increase the magnitude of resurgence when they are removed. Resurgence requires that at least some of the alternative reinforcement be removed, and the amount of resurgence that occurs appears to increase with the magnitude of decrease in alternative reinforcement rate. Finally, at this point, the details of the schedule of alternative reinforcement during response elimination appear not to matter, as long as similar rates of reinforcement are arranged.

Time in Extinction and Exposure to Alternative Reinforcement

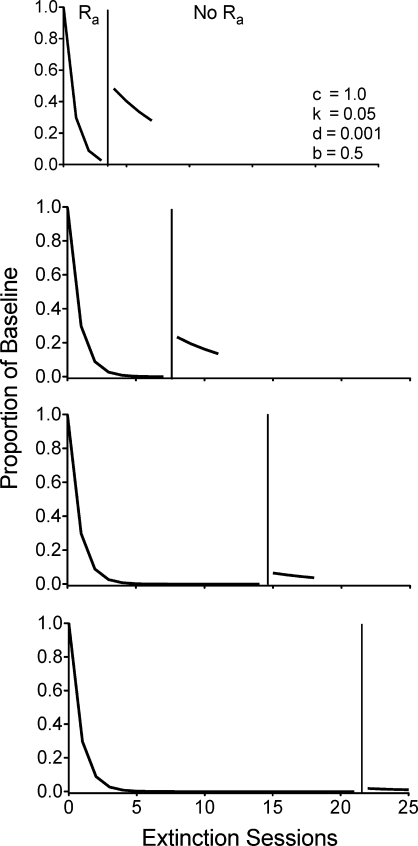
In Equation 4, time plays a critical role in the reduction of responding produced by exposure to extinction plus alternative reinforcement. The overall magnitude of the disruptive impact of extinction and exposure to alternative reinforcement in the numerator grows continuously with time (i.e., t). Thus, longer durations of exposure to extinction and alternative reinforcement during Phase 2 would be expected to reduce the magnitude of resurgence. Figure 2 shows a simulation of how different durations of exposure to extinction plus alternative reinforcement in Phase 2 affect resurgence in Phase 3. As the duration of exposure to extinction plus alternative reinforcement increases, the expected amount of resurgence decreases. Data reported in Leitenberg et al. (1975, Experiment 4) are consistent with this prediction. In their experiment, different groups of rats were exposed to either 3, 9, or 27 days of extinction plus alternative reinforcement in Phase 2 before the alternative reinforcer was removed in Phase 3. Although the authors do not describe the schedule of alternative reinforcement used, the data appear to be generally consistent with the model. The rats exposed to 27 days of extinction plus alternative reinforcement showed no significant resurgence, but those exposed to 3 and 9 days did. Although the difference between the amount of resurgence for the 3-day and 9-day groups was not statistically significant, the data are visually ordered such that 3 days > 9 days > 27 days.

Fig 2.

Simulation of the effects of increasing durations of extinction plus alternative reinforcement (i.e., R_a) on resurgence (i.e., No R_a) as generated by Equation 4. The simulations are based on a VI 60-s schedule of reinforcement during the baseline and a VI 30-s schedule of alternative reinforcement during extinction using the parameter values listed in the figure.

The continuous growth of disruption in the numerator of Equation 4 as a function of time in extinction also suggests that repeated resurgence tests should produce less responding as extinction progresses. Specifically, when alternative reinforcement is successively added and removed during continued exposure to extinction, resurgence should occur repeatedly, but with decreasing magnitudes across exposures. Figure 3 shows a simulation of two successive exposures to Phases 2 and 3 during which alternative reinforcement is present during extinction and then removed. Initial removal of the alternative reinforcement during extinction produces a robust increase in responding, but when alternative reinforcement is returned, responding quickly decreases. Finally, when alternative reinforcement is again removed, responding increases, but the increase is smaller than when alternative reinforcement was initially removed. Examination of the simulation in Figure 3 reveals an important aspect of the model of resurgence suggested by Equation 4. When alternative reinforcement is present, Equation 4 generates one extinction function with a larger disruptor term, and thus, less overall responding. When alternative reinforcement is absent, Equation 4 generates another extinction function associated with a smaller disruptor term and overall more responding. When alternative reinforcement is repeatedly presented and removed, as in Figure 3, the predictions of the model result from switching between these two extinction functions across time. In addition, because time in extinction (i.e., t) continues to increase regardless of the presence or absence of alternative reinforcement, lower overall levels of responding are predicted with successive removals of alternative reinforcement occurring at later time points in extinction.

Fig 3.

Simulation of the effect of repeated addition (i.e., R_a) and removal (i.e., No R_a) of alternative reinforcement during extinction as generated by Equation 4. Simulations are based on a VI 60-s schedule of reinforcement during the baseline and a VI 30-s schedule of alternative reinforcement during extinction using the parameter values listed in the figure.

The predictions in Figure 3 could represent an interesting test of the model. However, experiments in which resurgence has been repeatedly examined have included a return to the Phase 1 baseline condition before the successive exposures to Phases 2 and 3 (Lieving & Lattal, 2003; da Silva et al., 2008). When baseline conditions are reestablished between subsequent Phase 2 and 3 tests, time in extinction (i.e., t) is reset to zero prior to each test. Thus, under these conditions, Equation 4 predicts the each reexposure to Phases 2 and 3 should produce the same amount of resurgence. The data from the two experiments appear to be consistent with this prediction. We know of only one relevant report examining the effects of successive conditions in which alternative reinforcement was present or removed (Nevin & Wacker, in press). Nevin and Wacker provide summary data from a number of cases in which alternative reinforcement associated with functional communication training alternated with more typical extinction of problem behavior of children in naturalistic environments. Consistent with the predictions of Equation 4, their summary suggests that resurgence of problem behavior decreased with successive presentations and removals of alternative reinforcement provided by functional communication training. Nonetheless, a more thorough assessment of the prediction of Equation 4 that resurgence results from switching between two extinction functions with differential disruption terms will require additional experimental investigation.

Reinforcement Rates Prior to Response Elimination

Like the relapse model of Podlesnik and Shahan (2009, 2010), the model of resurgence suggested by Equation 4 is based on behavioral momentum theory. Thus, Equation 4 predicts that higher baseline reinforcement rates should produce relatively greater resistance to extinction and greater resurgence. However, as we demonstrate below, the addition of alternative reinforcement (i.e., R_a) in Equation 4 reduces the expected impact of differential baseline reinforcement rates compared to that predicted by the standard augmented model (Equation 1).

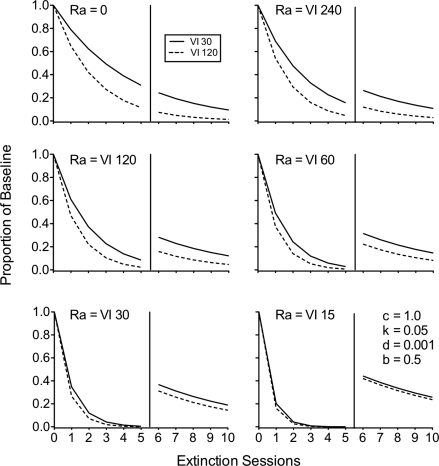
Figure 4 shows a simulation of the effects of a four-fold difference in baseline reinforcement rates (i.e., VI 30 s vs. VI 120 s) and a range of alternative reinforcement rates on resistance to extinction and resurgence. The top-left panel shows extinction in the absence of alternative reinforcement (i.e. R_a  =  0), where responding previously maintained by the higher rate of reinforcement arranged by a VI 30 s (i.e., Rich) is clearly more resistant to extinction than that previously maintained by a VI 120 s (i.e., Lean). In the absence of alternative reinforcement, Equation 4 reduces to the standard augmented model of extinction (i.e., Equation 1), and no resurgence occurs. In the top right panel, low-rate alternative reinforcement is arranged during extinction and then removed on the sixth session. Comparison with the top-left panel shows that, as discussed above, response elimination is faster with the added reinforcement than without it. Most importantly, the difference between the Rich and Lean components is reduced with the addition of alternative reinforcement, and removal of that alternative reinforcement produces resurgence. The other panels show the effects of increases in the rate of alternative reinforcement. As the rate of alternative reinforcement increases (i.e., the duration of the VI schedule of R_a is shortened), response elimination is faster, and the difference between the Rich and Lean components decreases. The decreasing difference for the Rich and Lean components with higher rates of alternative reinforcement occurs despite the fact that the overall magnitude of the resurgence effect increases when those higher rates of alternative reinforcement are removed. Thus, although the model predicts that differential baseline reinforcement rates affect both resistance to extinction and resurgence, the effects of differential reinforcement during baseline are relatively small in most cases because of an interaction with the rate of alternative reinforcement.

Fig 4.

Simulations of the effects of baseline reinforcement rate (i.e., VI 30 or VI 120) and rate of alternative reinforcement during extinction (i.e., R_a) on resurgence as generated by Equation 4.

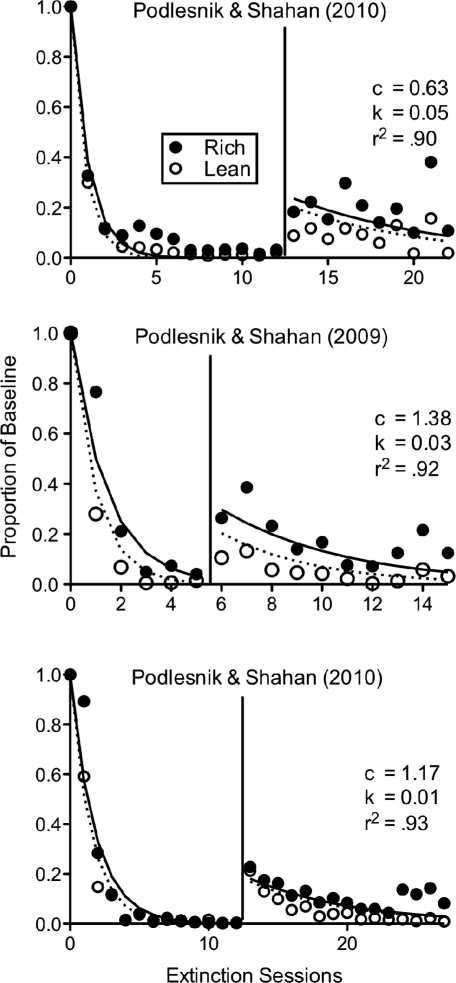
Although a parametric examination of the effects of baseline reinforcement rate on resurgence has not been published, our laboratory has examined such effects in a few experiments. Figure 5 shows the data from three experiments in which the effects of different baseline reinforcement rates on resurgence were examined using multiple schedules of reinforcement. The top panel shows data from 5 pigeons that received Phase 1 baseline training on a multiple schedule with a VI 30 s in a Rich component and a VI 120 s in a Lean component (Podlesnik & Shahan, 2010). A VI 30-s schedule arranged reinforcement for pecking an alternative key during Phase 2 extinction of the target behavior. The middle panel shows data for 7 pigeons trained on a multiple schedule with a VI 120-s + VT 20-s schedule in a Rich component and a VI 120-s schedule alone in a Lean component during Phase 1 baseline training (Podlesnik & Shahan, 2009). Although the higher rate of baseline reinforcement was accomplished by including response-independent reinforcers during the baseline, behavioral momentum theory (e.g., Nevin et al., 1990) and Equation 4 both predict that the overall stimulus reinforcer relation arranged by a multiple-schedule component stimulus is the relevant determinant of resistance to extinction and resurgence. During Phase 2 extinction of the target behavior (and removal of the VT reinforcers), a VI 30-s schedule arranged reinforcement for pecking an alternative key. Finally, the bottom panel shows data from 4 rats trained on a Phase 1 multiple schedule with a VI 45-s + VT 15-s schedule in the Rich component and a VI 45 s alone in a Lean component (Podlesnik & Shahan, 2010). Alternative reinforcement during Phase 2 extinction was arranged for pulling a chain on a VI 10-s schedule. In all three experiments, resistance to extinction in Phase 2 and resurgence in Phase 3 were somewhat greater in the Rich component than in the Lean component. Nonetheless, as expected, the effects of arranging differential reinforcement rates in the baseline tended to be relatively small as a result of the high rates of alternative reinforcement arranged during extinction. These effects were well described by Equation 4, which accounted for > 90% of the variance for each dataset with reasonable parameter values.

Fig 5.

Least-squares regressions of Equation 4 to existing datasets in which different baseline reinforcement rates were arranged in the baseline condition. See text for details.

Additional support for the suggestion that resurgence depends upon the overall rate of reinforcement experienced during the preextinction baseline comes from da Silva et al. (2008), who examined resurgence of pigeons' key pecking following training on concurrent schedules of reinforcement. In three experiments, they arranged concurrent schedules in Phase 1 such that: (1) one response occurred at a higher rate and produced higher reinforcement rates, (2) one response occurred at a higher rate, but the two responses produced equal reinforcement rates, and (3) the responses occurred at similar rates, but produced different reinforcement rates. In Phase 2, responding was eliminated with either extinction plus alternative reinforcement for pecking a third key or DRO imposed on both of the target responses. In Phase 3, all alternative reinforcement was removed. In all three experiments, absolute response rates during Phase 3 resurgence were higher for the response that previously had the highest response rate during baseline. Differential reinforcement rates for the two concurrent responses during Phase 1 had no impact on resurgence. However, from the perspective of behavioral momentum theory and Equation 4, the overall rate of reinforcement in the stimulus context is the critical variable, not the rate of reinforcement produced by a particular response. With concurrent schedules of reinforcement, the two responses occur in the same stimulus context, and thus share the same overall stimulus–reinforcer relation (e.g., Nevin et al., 1990). Accordingly, differential resurgence would not be expected for concurrent operants differing in the reinforcement rates they produce. da Silva et al. also showed response rates expressed as a proportion of baseline and demonstrated that, consistent with Equation 4, resurgence relative to baseline did not differ for the concurrent responses, despite the differences in baseline absolute response rates. Thus, the overall reinforcement rate experienced in the baseline condition appears to govern subsequent resurgence of all responses in that context, regardless of their baseline frequency of occurrence.

Contrary to the conclusion above, Reed and Morgan (2007) have suggested that resurgence is governed by baseline response rates rather than baseline reinforcement rates. In two experiments with rats, Reed and Morgan arranged a multiple schedule in Phase 1 such that reinforcement rates were similar in two components, but response rates were higher in one component than the other (Experiment 1  =  RR vs. RI; Experiment 2  =  differential reinforcement of high rates vs. differential reinforcement of low rates). However, in Phase 2, rather than reinforcing an alternative response or using a DRO to eliminate responding, Reed and Morgan exposed their rats to a multiple fixed-interval (FI) schedule for the same target response used in Phase 1. Although subsequent removal of the FI reinforcement in a third phase produced an increase in responding in some cases, this unusual procedure introduces numerous complexities. First, in both experiments, the rate of the previously low-rate behavior tended to increase during the FI-reinforcement condition, an outcome that is clearly inconsistent with viewing that phase as a form of response elimination. As a result of this procedure, when FI reinforcement was removed in Phase 3, the high-rate behavior was starting at a rate lower than baseline and the low-rate behavior at a rate higher than baseline. This difference makes it difficult to interpret responding during extinction in Phase 3 relative to the Phase 1 baseline. Second, the fact that the target response continued to produce the reinforcer during Phase 2 argues against characterizing such reinforcers as alternative reinforcers at all. Together, these differences from the usual resurgence preparation make it difficult to interpret Reed and Morgan's findings. Given that in some cases baseline response rates have been shown to impact resistance to change independent of reinforcement rates using procedures similar to Reed and Morgan (e.g., Lattal, 1989; Nevin, Grace, Holland, & McLean, 2001), it is certainly possible such effects could also occur with resurgence. Additional experiments using typical resurgence procedures will be required to examine whether baseline response rates impact resurgence independent of reinforcement rates, and how such effects should be interpreted if they occur.

Extinguishing the Target Behavior Prior to Alternative Reinforcement

In all of the resurgence experiments discussed above, alternative reinforcement was introduced at that same time that extinction started for the target behavior. A small subset of experiments have also shown that resurgence occurs if the target response is extinguished prior to introduction of alternative reinforcement (Cleland et al., 2000; Epstein, 1983; Lieving & Lattal, 2003, Experiment 1). For example, Epstein (1983) initially reinforced and then extinguished key pecking of pigeons. Once key pecking had ceased, some other response (e.g., wing raising) was reinforced 20 times on a FR 1 schedule. Following the 20 reinforcers for the alternative behavior, all reinforcement was withheld and key pecking increased. Thus, even when the target response is eliminated beforehand, extinction of a subsequently reinforced alternative behavior appears to produce resurgence. For convenience, we will refer to this type of resurgence as Epstein-type resurgence.

Before we begin a discussion of the applicability of Equation 4 to Epstein-type resurgence, it is worth noting that few data generated by this procedure are available. In addition, with the exception of the Lieving and Lattal (2003) experiment, the data are not presented with sufficient detail to allow assessment of the size of the increase in responding relative to baseline training levels. Regardless, in trying to understand this type of resurgence from the perspective of Equation 4, initial extinction of the target behavior in the absence of alternative reinforcement would mean that R_a  =  0, and thus, Equation 4 reduces to the standard augmented model of extinction (i.e., Equation 1). When the alternative reinforcer is introduced, R_a would then appear in the numerator as an added source of disruption and in the denominator as a source of reinforcement in the situation. Given the low levels of responding prior to the addition of alternative reinforcement, the added source of disruption in the numerator would have little measureable effect on behavior. Subsequent release from the added disruption when the alternative source of reinforcement is removed would also have a small effect, and Equation 4 predicts a small increase in responding due the presence of R_a in the denominator. Given that Cleland et al. (2000) and Epstein (1983) provide no information about the rate of the target behavior prior to extinction, it is possible that the small increase in responding predicted by Equation 4 could account for the increases observed in those experiments.

The Epstein-type resurgence experiment reported by Lieving and Lattal (2003) obtained larger increases in responding with removal of the alternative reinforcer (to about 25–50% of baseline rates), and Equation 4 does not predict such large increases in responding in its current form. However, one aspect of the Epstein-type resurgence procedure overlooked by Equation 4 is the possibility that the reintroduction of reinforcement to the situation after extinction of the target behavior might have a reinstatement-like effect. As noted above, reinstatement refers to the reappearance of extinguished responding following the delivery of response-independent reinforcement (e.g., Reid, 1958). If one assumes that reinforcers delivered contingent upon an alternative response following extinction of a target behavior might also have a reinstatement-like effect, then inclusion of this effect in the model of resurgence provided by Equation 4 would be required in order to account for resurgence in Epstein-type preparations. One approach to including a reinstatement-like effect of alternative reinforcement in Equation 4 would be to combine that equation with the model of reinstatement (i.e., Equation 2 above) suggested by Podlesnik and Shahan (2009, 2010). Thus, the combined model would simply be Equation 4 with the m and n parameters from Equation 2. With appropriate parameter values, such a combined model can predict an Epstein-type resurgence effect comparable in magnitude to that obtained by Lieving and Lattal. Regardless, given the paucity of data on Epstein-type resurgence, further speculation about how such a model might capture this phenomenon would seem unjustified at present. Suffice it to say that such a model might provide a reasonable starting point to approach the phenomenon once additional data are available.

Relationship to Existing Accounts of Resurgence

The model of resurgence proposed here suggests that resurgence can be understood within the larger theoretical framework of behavioral momentum theory. When an alternative source of reinforcement is added during extinction of the target behavior, the availability of that alternative reinforcement serves as an additional source of disruption. In addition, the alternative source of reinforcement in the situation increases the future strength of the target behavior by contributing to the Pavlovian stimulus–reinforcer relation associated with the context. When the alternative reinforcement is removed, disruption of the target behavior is reduced and responding increases (i.e., resurgence occurs).

A common previous account of resurgence was that the phenomenon results from an interaction between the target behavior and the alternative behavior reinforced during extinction. This response-prevention hypothesis (e.g., Rawson, Leitenberg, Mulick, & LeFebvre, 1977) suggests that when an alternative behavior is introduced during extinction of the target behavior, the occurrence of the alternative behavior competes with the target behavior and prevents it from completely extinguishing. When the alternative behavior is no longer reinforced, the competition between the two behaviors is eliminated and the incompletely extinguished target behavior is free to occur again. Thus, unlike the present account, which suggests that it is the occurrence of alternative reinforcement that disrupts the target behavior, the response prevention hypothesis suggests that it is the occurrence of behavior maintained by the alternative reinforcer that disrupts the target behavior. It is worth noting that similar dueling interpretations about interactions between two concurrently available operant responses were addressed in the 1960s and 1970s. The question was whether decreases in one behavior with increases in reinforcement for the other behavior occurred because of a competition between the two responses or because of the direct interaction between reinforcement sources (i.e., relative reinforcement rate). The data clearly supported an interpretation based on direct interaction between the sources of reinforcement rather than an indirect interaction mediated through response competition (e.g., Catania, 1963; Rachlin & Baum, 1972). In fact, such direct reinforcement interaction provides the foundation for all of matching theory (i.e., Herrnstein, 1961, 1970) and behavioral momentum theory (e.g, Nevin & Grace, 2000). Thus, the previous failures of response interactions to provide an account for the relative allocation of current responses seem to argue against such interactions playing a major role in the effects of alternative reinforcement during extinction.

In addition to the concern noted above, the most problematic aspect of the response-prevention hypothesis is that it suggests occurrence of the target behavior during Phase 2 response elimination and during Phase 3 resurgence should be inversely related. The reason is that when the target behavior occurs more during response elimination, it should be more completely extinguished, and thus occur less when the alternative reinforcement is removed during Phase 3. Although some data could be interpreted as being consistent with this expectation (e.g., the Leitenberg et al., 1975 data modeled in Figure 1), the response-prevention hypothesis nonetheless appears to be false. For example, in a series of experiments, Winterbauer and Bouton (2010) have shown that the frequency of occurrence of the target behavior during response elimination is not related to the amount of resurgence obtained. This outcome led Winterbauer and Bouton to conclude that response prevention plays little role in resurgence. Further evidence that the response-prevention hypothesis is false comes from Epstein-type resurgence, which demonstrates that resurgence occurs even if the target behavior is extinguished prior to introduction of the alternative reinforcement. Thus, the above considerations suggest that the response-prevention hypothesis does not provide a viable account of resurgence.

The model of resurgence proposed here also shares some features with the only other previous formal attempt to model resurgence. Cleland, Guerin, Foster, and Temple (2001) proposed an account of resurgence based on the matching law such that:

where B_1E is the rate of the target behavior during extinction plus alternative reinforcement for a second behavior in Phase 2, and B_1R is the rate of the target behavior during Phase 3 resurgence when the alternative reinforcer is removed. The reinforcement term r₁ is the rate of reinforcement for the target behavior in the Phase 1 baseline prior to response elimination and the term r_2E is the rate of alternative reinforcement for the second behavior during Phase 2 response elimination.

Like the model proposed above, Equation 7 suggests that occurrence of the target behavior during extinction is directly related to the baseline rate of reinforcement and inversely related to the rate of reinforcement for the alternative behavior. Despite these similarities to the present approach, Equation 7 has two problems as an account of resurgence. First, it predicts that although responding during extinction is positively related to the baseline reinforcement rate, resurgence (i.e., B_1R) is inversely related to baseline reinforcement rate. The data in Figure 5 clearly show that responding during extinction and during resurgence are positively related (see also Podlesnik & Shahan, 2010). Second, and most importantly, the left-hand side of Equation 7 is a formal statement of the response prevention hypothesis. The model suggests that target responding during Phase 2 response elimination and Phase 3 resurgence is allocated to one or the other of those phases, and thus, resurgence results from the prevention of extinction of the target behavior. As discussed above, the response-prevention hypothesis is likely false. Given these considerations, Equation 7 does not appear to provide a viable account of resurgence.

Finally, Bouton and Swartzentruber (1991) have suggested that resurgence might be understood as resulting from a contextual renewal effect. As noted above, renewal involves an increase in extinguished responding with a change in context from that in which extinction took place. For example, in ABA renewal, training occurs in Context A, extinction in Context B, and then responding increases when the subject is returned to Context A. Bouton and Swartzentruber suggested that resurgence might occur because training in which an operant response is reinforced represents Context A, and extinction in the presence of an alternative source of reinforcement serves as Context B. When the alternative source of reinforcement is removed, the context may be more similar to Context A than Context B, and responding increases. However, more recently, Winterbauer and Bouton (2010) have suggested that resurgence would be more appropriately characterized as ABC renewal because the absence of reinforcement in Phase 3 resurgence is more like a new context (i.e., Context C) than the original training context (i.e., Context A). Although this account seems plausible, ABC renewal of operant behavior has not been reliably observed, and the increase in responding appears to be rather small when it does occur (Bouton, Todd, Vurbic, & Winterbauer, in press; Zironi, Burattini, Aicardi, & Janak, 2006). As a result, it is not clear that ABC renewal can account for the robust increases in responding often observed in resurgence experiments. In addition, it is not clear how a renewal-based approach to resurgence can account for the variety of effects reviewed above. Thus, at present, it is not clear that an ABC renewal effect will provide a viable account of operant resurgence. Generating and testing differential predictions based on the model of resurgence proposed here and based on an ABC-renewal account could be a promising area for future research. Nonetheless, the concept of context might prove sufficiently flexible to make a renewal-based account difficult to test and/or falsify.

Potential Implications for Behavioral Momentum Theory

Although the model of resurgence presented here (i.e., Equation 4) is a relatively straightforward extension of behavioral momentum theory, it does raise some interesting issues about the augmented model of extinction (i.e., Equation 1) upon which it is based. For convenience we again present the augmented model of extinction here:

where all terms are as in Equation 1. In previous applications of the augmented model to extinction data, a baseline is established and then Equation 8 is applied to account for the decrease in responding associated with exposure to extinction (e.g., Nevin et al., 2001). As noted above, such applications of the augmented model carry the reinforcement rate experienced in baseline (i.e., r in the denominator) into the extinction condition. In essence, the r term serves as a sort of perfect memory of the reinforcement history in the baseline condition. All decreases in responding are driven by the growth of the disruption in the numerator of the equation. This approach has proven fairly successful in terms of accounting for the effects of baseline reinforcement rate on resistance to extinction.

In extending Equation 8 to account for resurgence, we have followed the same basic approach by carrying forward the reinforcement rate experienced in baseline into the extinction plus alternative reinforcement phase (i.e., Phase 2). With the transition to Phase 2, a question that immediately arises is how to incorporate the rate of reinforcement provided by the alternative response. As is clear from Equations 3 and 4, we have assumed that the effects of the baseline reinforcement rate (r) and the alternative reinforcement rate (R_a) are additive. With the transition to Phase 3 when all reinforcement is removed from the situation, we have carried forward both r and R_a in order to be consistent with the initial transition from baseline to Phase 1. As demonstrated by the success of the current model, this approach seems to work well in accounting for existing data from resurgence experiments.

One interesting implication of the approach above is that it assumes that the target response from baseline can be further strengthened while it is undergoing extinction if an alternative source of reinforcement is introduced into the discriminative stimulus context. Given that behavioral momentum theory suggests that resistance to extinction is driven by the discriminative stimulus–reinforcer relation, this implication may not seem particularly controversial. As noted above, it is well established that the inclusion of additional response-independent reinforcement or reinforcement contingent upon a concurrent response increases resistance to change of a target behavior via the stimulus–reinforcer relation (e.g., Nevin et al., 1990). However, because the current model assumes that reinforcement from previous conditions is carried forward to the next temporal epoch and added to the prevailing reinforcement conditions, it is not difficult to imagine scenarios in which the underlying logic of this approach becomes strained. For example, consider a sequence of conditions like those simulated above in Figure 3 in which alternative reinforcement is repeatedly added and removed from the situation. For the simulation in Figure 3 the alternative reinforcement rate was included in the denominator of Equation 4 for the initial extinction plus alternative reinforcement condition only. The subsequent increases and decreases in responding occurred as a result of the addition and removal of the disruptive effects of alternative reinforcement (R_a) in the numerator of Equation 4. One could reasonably argue that for the sake of consistency another R_a term should be added to the denominator with the reintroduction of alternative reinforcement in the final condition. It turns out that doing so produces only a modest increase in the amount of resurgence predicted in the final condition.

The simulation of alternations between different conditions of alternative reinforcement presented in Figure 3 only includes a series of four conditions. But, what of longer sequences involving transitions between multiple rates of alternative reinforcement? Should the reinforcer rates from a long series of experienced reinforcement rates across temporal epochs similarly be included in the denominator additively (e.g., r+R_a1+R_a2+…R_an)? Clearly, such perfect memory for experienced reinforcement rates and their additive strengthening across many temporal epochs becomes absurd over the long run. In order to account for changing reinforcement rates across conditions, behavioral momentum theory will need to deal with how reinforcement rates across conditions and temporal epochs should be integrated.

In developing of the present model of resurgence, we have pursued the path that seemed the simplest and most consistent with previous applications of the augmented model of extinction. As we hope is clear from the success of the model, this approach appears adequate for the time being and provides a reasonable starting point as a theory of resurgence based on behavioral momentum theory. Nonetheless, a number of alternative approaches could be used to account for resurgence, but these approaches would need to inform behavioral momentum theory more generally in order to maintain conceptual consistency. For example, rather than assuming that reinforcement rates experienced across conditions are additive, one could assume that reinforcement rates are averaged. It turns out that using average rather than additive reinforcement rates changes parameter values and the quality of fits of the present model very little. If such an approach were to be pursued, it would suggest that fits of the augmented model to standard extinction data (i.e., without alternative reinforcement) should also use the average of reinforcement rates during baseline and during extinction. This, of course, would amount to nothing more than using 0.5r (i.e., [r+0]/2) in the denominator of applications of the augmented model to standard extinction, thus requiring a standard sensitivity value slightly greater than the usual 0.5. One can also imagine more complex approaches to calculating the integration of reinforcement rates across conditions such as decaying effects of previously experienced reinforcement rates with time, or a variety of other more complex algorithms. At present, the available data do not appear to justify such additional complexity or to adequately constrain the choice of one approach over the other. Nonetheless, the generation of additional data based on sequences of changing reinforcement conditions for a target behavior and alternative reinforcement might suggest more appropriate ways to proceed with the future development of behavioral momentum theory in general. Such development could lead to a fairly broad quantitative theory of how behavioral history is mediated through the integration of experienced reinforcement conditions as amassed in the Pavlovian stimulus–reinforcer relation.

Conclusions

The model of resurgence developed here suggests that resurgence can be understood within the framework of behavioral momentum theory as expressed in an extension of the augmented model of extinction. The model suggests that resurgence occurs as a result of the dual effects of alternative reinforcement during extinction of a target response. First, alternative reinforcement suppresses the target behavior by acting as an additional source of disruption. Second, alternative reinforcement strengthens the Pavlovian stimulus–reinforcer relation, thus increasing the future strength of the target behavior when the countervailing disruptive effects are removed. The model does a good job of providing a coherent approach for systematizing the existing resurgence literature and it makes novel and testable predictions about effects that have not yet been observed. Thus, we suggest that the model as formalized in Equation 4 provides a good framework within which to pursue the study of resurgence and to integrate the phenomenon into the larger existing theoretical account of operant response persistence provided by behavioral momentum theory. In addition, consideration of the present model suggests that future development of behavior momentum theory should focus on how the effects of reinforcement conditions experienced across temporal epochs might be integrated.