Effects of Signal Level and Background Noise on Spectral Representations in the Auditory Nerve of the Domestic Cat

Abstract

Background noise poses a significant obstacle for auditory perception, especially among individuals with hearing loss. To better understand the physiological basis of this perceptual impediment, the present study evaluated the effects of background noise on the auditory nerve representation of head-related transfer functions (HRTFs). These complex spectral shapes describe the directional filtering effects of the head and torso. When a broadband sound passes through the outer ear en route to the tympanic membrane, the HRTF alters its spectrum in a manner that establishes the perceived location of the sound source. HRTF-shaped noise shares many of the acoustic features of human speech, while communicating biologically relevant localization cues that are generalized across mammalian species. Previous studies have used parametric manipulations of random spectral shapes to elucidate HRTF coding principles at various stages of the cat’s auditory system. This study extended that body of work by examining the effects of sound level and background noise on the quality of spectral coding in the auditory nerve. When fibers were classified by their spontaneous rates, the coding properties of the more numerous low-threshold, high-spontaneous rate fibers were found to degrade at high presentation levels and in low signal-to-noise ratios. Because cats are known to maintain accurate directional hearing under these challenging listening conditions, behavioral performance may be disproportionally based on the enhanced dynamic range of the less common high-threshold, low-spontaneous rate fibers.

Introduction

Individuals with normal hearing adapt remarkably well to complex acoustic environments, but hearing-impaired listeners may experience a profound communication breakdown. To understand the physiological mechanisms that preserve sound coding in challenging listening conditions, and how they may be affected by communication disorders, the present study investigated the coding limitations of auditory nerve fibers at high sound levels and in continuous background noise.

Many elemental speech sounds are identified by their formant structure, which in the case of steady-state vowels is defined by the frequency location of energy peaks in a broad bandwidth spectrum (Peterson and Barney 1952). The coding of vowel formant structure has been previously described in the auditory nerve of domestic cats with normal hearing and experimentally induced hearing loss (Miller et al. 1997; Sachs et al. 2002). These studies have shown that the frequency of vowel formants can be derived by comparing average discharge rates across a population of auditory nerve fibers. In normal-hearing cats, each fiber responds best to spectral energy at its most sensitive “best frequency” (BF). Consequently, formant frequencies are revealed by the BFs of fibers displaying relatively high discharge rates (Le Prell et al. 1996; Sachs and Young 1979). The quality of this distributed representation depends on fiber type, sound level, and the presence of background noise (Delgutte and Kiang 1984; May et al. 1998; Sachs et al. 1983).

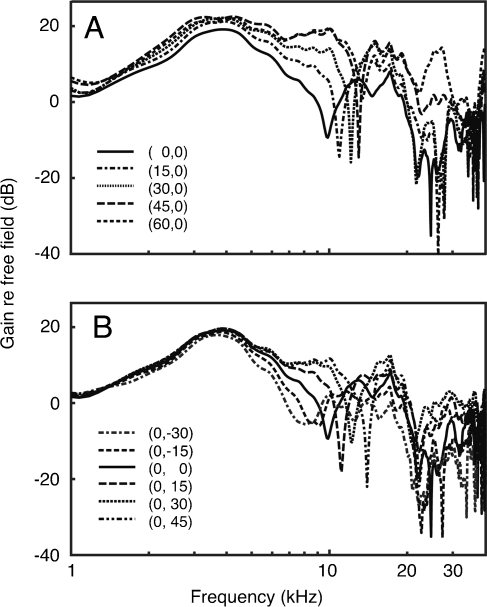
Recent studies have used random spectral shapes to describe how spectral energy is integrated across the frequencies surrounding a neuron’s BF (Young et al. 2005; Yu and Young 2000). The derived integration patterns have been used to predict responses to complex natural sounds such as the sound localization cues that are associated with the directionality of the cat’s head and external ear. These acoustic properties are specified as head-related transfer functions (HRTFs), which plot the change in energy reaching the tympanic membrane relative to its free-field source. In cats, HRTFs display a sharp mid-frequency notch that shifts in frequency when the sound source moves in azimuth or elevation (Fig. 1) (Musicant et al. 1990; Rice et al. 1992). Cats rely on these mid-frequency cues for accurate sound localization (Huang and May 1996; Tollin and Yin 2003). In addition to sharing the acoustic features that define speech sounds, HRTFs are ideal stimuli for electrophysiological studies because they convey informative spectral features across the full range of auditory nerve frequency tuning.

FIG. 1.

Spectra for broadband noise that has been shaped by the cat’s HRTF at different sound source azimuths (A) and elevations (B). The frequency location of the prominent mid-frequency notch (7–15 kHz) is directionally dependent.

When responses to random spectral shapes are used to predict the neural coding of HRTFs, a sharp dichotomy is noted between auditory nerve fibers and central auditory neurons (Young et al. 2005). Whereas central neurons tend to be non-linear and sensitive to off-BF excitatory/inhibitory interactions, the transformation of spectral energy into discharge rates by auditory nerve fibers is nearly linear, narrowly tuned, and largely driven by on-BF excitatory influences (Yu and Young 2000). The integration patterns of auditory nerve fibers suggest that their responses to changes in sound level and background noise can be modeled by computing the simple linear relationship between sound-evoked discharge rates and on-BF spectrum level. Under the assumption of linearity, the quality of coding is implicit in the slope of the rate-level relationship, with steeper slopes (larger rate changes) indicating more detailed representations of HRTF-based spectral features. This linear model has been previously applied to vowel representations in the auditory nerve (Le Prell et al. 1996) and cochlear nucleus (May et al. 1998).

The present study used linear modeling to estimate the dynamic range of HRTF coding in the auditory nerve of barbiturate-anesthetized cats. Single fiber discharge rates were sampled with a library of HRTF shapes that were previously recorded in the cat’s ear canal during free-field presentations in the frontal sound field (Rice et al. 1992). Therefore, closed-field presentations to the experimental ear recreated generic monaural localization cues that are conveyed by spectral features of the HRTF. Variations in the shapes of the HRTFs across sound source locations produced a unique range of on-BF levels for each fiber depending on the fiber’s frequency tuning characteristics.

The quality of the neural representation of HRTF shapes was derived from rate-level functions relating single fiber discharge rates to on-BF spectrum level. The dynamic range of the representation was determined by repeating the measures at different presentation levels. The effects of background noise were evaluated by applying a signal detection analysis to discharge rates that were obtained under quiet conditions and in different signal-to-noise ratios (S/Ns). High-spontaneous rate fibers produced faithful representations of HRTF spectra at low signal levels and in quiet backgrounds, but were limited by rate saturation at higher presentation levels and in background noise. Low-spontaneous rate fibers were constrained by threshold effects at low presentation levels, but showed enhanced coding at high levels and in noise.

Methods

Subjects and surgical procedures

All protocols were approved by the Johns Hopkins Animal Care and Use Committee. Unilateral auditory nerve recordings were conducted on 18 adult male cats (3–4 kg) with infection-free ears and clear tympanic membranes. The cats were anesthetized for initial surgical preparations with xylazine and ketamine (0.5:40 mg/kg, i.m.). Atropine (0.03 mg/kg, i.m.) was given to control mucous secretions. Core body temperature was maintained at 38.5°C using a regulated heating pad. A catheter was inserted into the cephalic vein and subsequent anesthesia was maintained with periodic intravenous injections of pentobarbital, as needed to prevent withdrawal reflexes (≈3 mg/kg/h). The bulla was vented with small bore polyethylene tubing to prevent the buildup of static pressure in the middle ear. A tracheal tube was inserted to facilitate quiet breathing.

After initial surgical preparations, the cat was moved to a warm, acoustically isolated recording chamber. The experimental ear was dissected and the ear canal opened 2–3 mm from the tympanic membrane. Hollow ear bars were inserted into the ear canals. The cat was secured in a stereotaxic apparatus using the ear bars and a plate that held the head in a 45° downward orientation. An electrostatic speaker was coupled to the ear bar in the test ear and calibrated in situ using a probe tube microphone. The microphone was inserted into a calibration bore in the ear bar to a location 2–3 mm from the tympanic membrane. Calibrations deviated by less than 10 dB across frequencies from 0.5 to 30 kHz.

The scalp and temporalis muscles were reflected to expose the parietal bone. A 1.5-cm fenestration was made in the posterior fossa to gain access to the cerebellum. The lateral cerebellum was retracted medially to uncover the auditory nerve at its point of exit from the temporal bone. Wet cotton balls were placed along the margins of the exposure to stabilize the retraction.

Recording protocol

A glass micropipette (3 M NaCl, 10–30 MΩ) was visually positioned over the nerve using a surgical microscope and then advanced into the nerve with a hydraulic micromanipulator. As the electrode passed through the nerve, individual fibers were revealed by their sound-driven responses to search stimuli (50-ms tone or noise bursts). When a fiber with well isolated action potentials was encountered, its BF and threshold were determined using an automated tuning curve algorithm. Discharge rates were sampled in the absence of acoustic stimulation over 10-s intervals for classification as high (HSR; ≥18/s) or low spontaneous rate fibers (LSR; ≤1/s) (Liberman 1978). The present analysis excludes the responses of the minority of medium spontaneous rate fibers (1 < SR <18/s) to contrast the dichotomous coding properties that distinguish the more numerous LSR and HSR fibers. In general, MSR fibers displayed intermediate coding properties that were largely determined by their sensitivity to acoustic stimulation.

After classification, the quality of HRTF coding was characterized at multiple presentation levels under quiet conditions and in background noise. At each presentation level and noise condition, average discharge rates were measured in response to ten different HRTF-shaped noise bursts. The bursts were generated by passing 400 ms of “frozen” Gaussian noise through digital filters that simulated ten generic HRTFs at various azimuths and elevations in the median plane (Rice et al. 1992). The spectral shapes are shown in Figure 1.

Each HRTF-shaped noise burst was presented five times (one burst/s) to allow a statistical analysis of the mean and standard deviation of the rate responses. Natural variations in the shape of the HRTFs produced a unique relationship between on-BF spectrum levels and the mean discharge rates of each fiber. The resulting rate-level functions were fit with linear models to characterize the fiber’s dynamic range properties. The analysis was repeated at multiple presentation levels and noise conditions to establish the limits of spectral coding.

Noise effects were determined by repeating dynamic range measures in a continuous white noise background. The noise spectrum was not shaped by HRTF-filter functions; therefore, the paradigm simulated a directional signal in omnidirectional noise, or in noise from an overhead location where the HRTF is relatively featureless (Rice et al. 1992).

Global S/Ns were specified as the ratio of the HRTF spectrum level at a gain of 0 dB and the noise spectrum level at 2 kHz (Rice et al. 1995). With this metric, global S/Ns ranged from −30 to 10 dB. Because spectral peaks and notches of the cat’s HRTF tend to distribute evenly above and below a gain of 0 dB in the biologically significant region of mid-frequency directional cues (Fig. 1), the global S/N approximates the statistical average of on-BF S/Ns. The signal level for each stimulus presentation varied around the global S/N, depending on the actual gain of individual HRTFs at the fiber’s BF. As in quiet, these variations were used to derive linear models that characterize the correlations between HRTF-driven rates and on-BF spectrum levels.

Linear model of dynamic range adjustment

A linear model was used to estimate rate-level functions relating the discharge rates of individual auditory nerve fibers to the on-BF spectrum levels of the ten HRTFs in Figure 1. On-BF spectrum levels indicate the gain of each HRTF at a fiber’s BF relative to the spectrum level of white noise at the same presentation level. The range of on-BF spectrum levels varied across fibers and was determined by the frequency location of spectral notches and peaks within the stimulus set. For example, when the frequency of a spectral notch matched a fiber’s BF, the HRTF produced a low spectrum level.

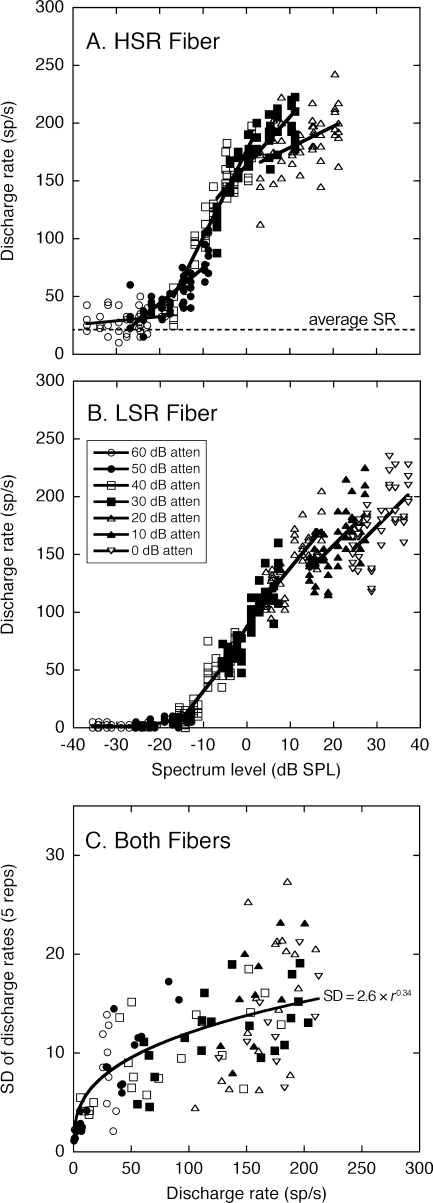
Representative rate-level functions are plotted in Figure 2. The range of on-BF levels shown in this figure has been expanded by repeating the stimulus set at presentation levels from 60 to 0 dB attenuation (on-BF spectrum levels ranging from approximately ±40 dB SPL). Each data set has been fit with a first-order polynomial (line) to quantify level-dependent changes in the acuity of spectral coding.

FIG. 2.

HRTF-driven rates for representative auditory nerve fibers with high (A) and low spontaneous rates (B). Rates are plotted relative to the on-BF spectrum level of the ten HRTFs in Figure 1. Each HRTF was presented five times at presentation levels that are indicated by symbol type. Data from the same presentation level have been fit with first-order polynomials (lines). Standard deviations (SDs) of the discharge rates (C) were based on repetitions of the same HRTF and presentation level. These data are plotted relative to the average discharge rate of the five repetitions. The relationship between rate and variance replicates the previous results of May and Huang (1997), which are indicated by the power function and equation.

Because the rate-level relationships illustrated in Figure 2 were independent of BF, linear dynamic range models were based on the average slope calculations for the discharge rates of all fibers within the same SR class and stimulus condition. The linear fits produced by the representative HSR and LSR fibers are indicated by the line segments in Figure 2A and B.

The general physiological characteristics that separated the two response classes are apparent in the representative data. The HSR fiber had a more sensitive threshold but showed saturation effects at high presentation levels. The LSR fiber exhibited a high threshold but maintained steeply sloped rate-level functions at high levels. Similar dynamic range constraints have been noted for the representation of vowels by auditory nerve fibers (Le Prell et al. 1996).

Signal detection analysis

A signal detection analysis was performed on the linear fits to estimate the quality of HRTF representations. This process involved the linear transformation of two HRTF spectral shapes into pseudo-population rate profiles using the appropriate linear model and then calculating the magnitude and variation of rate differences between the spectra (Conley and Keilson 1995). Each model was defined by SR class, presentation level, and noise condition.

The d′ statistic was used to normalize the magnitude of the rate differences between HRTFs in relation to the standard deviation of rate responses to the same HRTF (Green and Swets 1966). This unbiased statistical index of rate discrimination was calculated using Eq. 1:

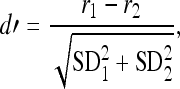1

where the numerator is the difference between simulated discharge rates at matching frequency components in HRTF₁ and HRTF₂ and the denominator is the estimated joint standard deviation (SD) for the rates.

The SD of each fiber’s rate responses was calculated from the five repetitions of the same stimulus condition. This measure is plotted relative to the average HRTF-driven rates of the five repetitions in Figure 2C. The data for the representative HSR and LSR fibers have been combined because fibers with matching discharge rates display similar SDs regardless of BF or SR class (May and Huang 1997). For both fibers, SDs increased and displayed greater variation at higher discharge rates.

An exponential of the form

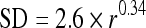2

has been superimposed on the data, where r is discharge rate. This exponential was derived in a previous analysis of auditory nerve variance (May and Huang 1997) and corresponds well with the population data of the present study.

The linear model was combined with Eqs. 1 and 2 to estimate d’ population profiles for pairwise comparisons of the HRTFs. Firstly, simulated rates were determined for all frequency components of the HRTFs using the linear model. Next, the simulated rates were input to Eq. 2 to calculate their corresponding SDs. Finally, the rates and SDs were transformed to d′ values using Eq. 1. The overall discriminability of the two HRTFs was specified in terms of the maximum d′ value at frequencies between 5 and 30 kHz. This frequency range is emphasized because it contains spectral cues that are critical for accurate directional hearing in cats (Huang and May 1996).

Results

A total of 78 LSR and 175 HSR fibers were recorded from 18 animals. Only units with BFs between 7 and 15.7 kHz were included in the analysis. These BFs correspond to the frequency range where the ten HRTFs were distinguished by the frequency location of a single, directionally dependent spectral notch. Although spectral peaks and notches exist at higher frequencies, the shape of the HRTF tends to fluctuate widely over a narrow frequency range making it difficult to relate discharge rates to on-BF spectrum levels. Previous behavioral studies suggest that cats rely most heavily on mid-frequency spectral cues when orienting to free-field sound locations (Huang and May 1996). No significant difference in BF distributions was seen between the populations of LSR and HSR fibers recorded in this study (P = 0.67, Wilcoxon rank-sum test).

Dynamic range of auditory nerve representations in quiet

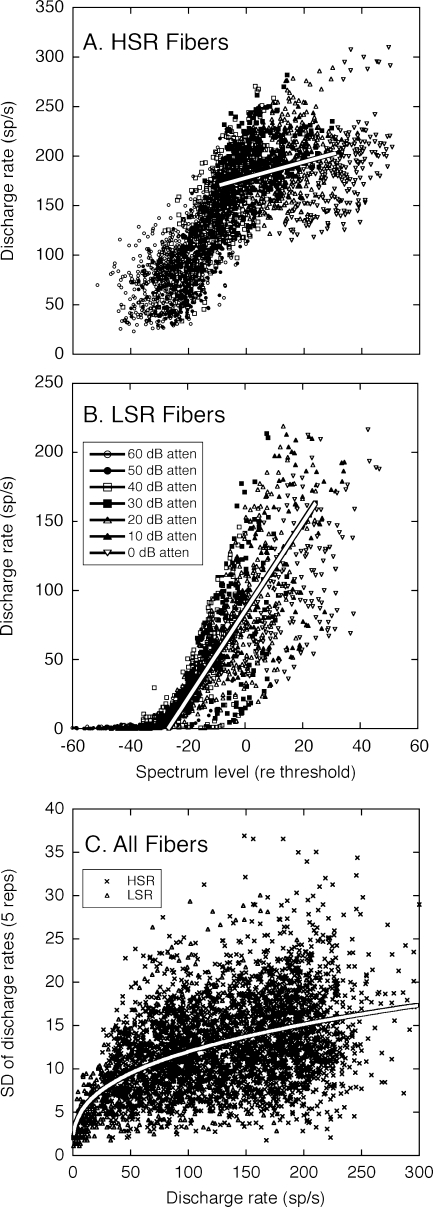
The dynamic range of auditory nerve representations in quiet was determined by performing the analysis summarized in Figure 2 with up to 89 HSR fibers and 40 LSR fibers for a given stimulus condition. The complete sets of population data are shown in Figure 3. In general, the HRTF-driven rates of auditory nerve fibers were relatively homogeneous and followed the basic trends summarized in Figure 2.

FIG. 3.

The complete population of HRTF-driven rates for high (A) and low spontaneous rate fibers (B), and the standard deviations (SDs) of those rates (C). Plotting conventions are described in Figure 2 except that spectrum level is specified relative to each fiber’s threshold to compensate for differences in sensitivity. Linear fits have been performed on rate-level data from both groups of fibers at a presentation level of 20 dB attenuation. The power function relating SD to average discharge rate was originally derived by May and Huang (1997).

The HSR fibers (Fig. 3A) had steep slopes in their rate-level functions and a large dynamic range for level coding at low sound levels, but exhibited saturation effects at high sound levels. The optimal representations of these fibers, therefore, were limited to near-threshold spectral features. The LSR fibers (Fig. 3B) attained slopes that approached the steepness of their more sensitive HSR counterparts at moderate sound levels but showed less saturation at high sound levels.

The linear fits in Figure 3A and B compare the dynamic range properties of all HSR and LSR fibers that were sampled at 20 dB attenuation. Within the population of HSR fibers, the attenuation produced on-BF spectrum levels that ranged from −15 to 35 dB relative to the threshold for a BF tone. Because LSR fibers tended to show higher and more variable thresholds, the same 20 dB attenuation produced spectrum levels ranging from −35 to 25 dB. The steep slope of the LSR rate-level functions relative to the HSR data set indicates that LSR fibers responded to changes in on-BF spectrum levels with more robust changes in discharge rate. From the perspective of directional coding, the modulated discharge rates of LSR fibers are expected to produce a better representation of HRTF-dependent spectral peaks and notches at higher sound levels.

The SDs of the discharge rates are summarized in Figure 3C. These results conform well to previous estimates of response variability in the auditory nerve, which are indicated by the exponential fit (May and Huang 1997). Although driven rates are highly variable between auditory nerve fibers, estimated SDs produced a good fit to the central tendencies of actual data from both response classes (R² = 0.334, p < 0.001).

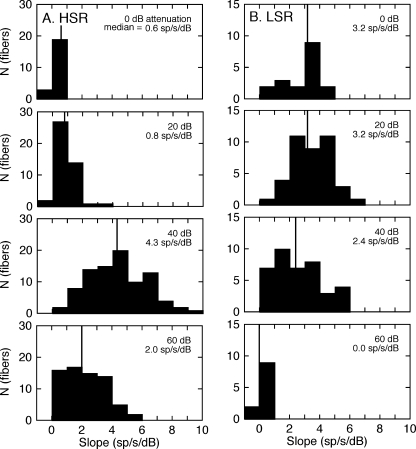
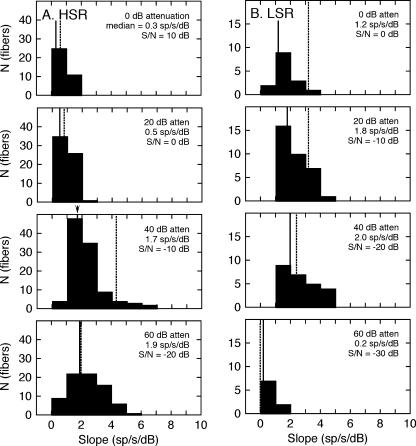
The slopes of the linear rate-level fits were computed for individual auditory nerve fibers and grouped by spontaneous rate and presentation level to evaluate the dynamic range of spectral coding for the two response classes. The resulting distributions are shown for the HSR fibers in Figure 4A and for the LSR fibers in Figure 4B. Presentation levels increase from the bottom to top of each column in 20-dB steps. The median slope for the response class and presentation level is displayed in each panel. The consistent difference in absolute counts (N) is observed between response classes because HSR fibers are more numerous than LSR fibers (Liberman 1978).

FIG. 4.

Dynamic range properties of the rate-level data in Figure 3. The histograms show the distribution of slopes for linear fits to the responses of all high (A) and low spontaneous rate fibers (B) at presentation levels between 60 and 0 dB attenuation. Vertical lines indicate the median slope for each test condition. A steeper slope suggests more precise spectral coding.

As in the examples that were shown in Figure 2, the population of HSR fibers produced median slopes that surpassed the LSR fibers at the lowest presentation levels (60–40 dB attenuation) but were limited by strong saturation effects at high levels. Most of the LSR fibers failed to respond to HRTF stimuli at 60 dB attenuation, yielding a mean slope of 0 sp/s/dB. The count for this condition is relatively small because fibers were not sampled at this low sound level if they had failed to respond at higher presentation levels. With increasing presentation levels (40–0 dB attenuation), the population of LSR fibers produced relatively constant median slopes that ranged from 2.4 to 3.2 sp/s/dB.

A close inspection of the representative rate-level functions in Figure 2B suggests a mechanism for the preservation of spectral representations by LSR fibers at high signal levels. The parallel shift of the linear fits at 10 and 0 dB attenuation indicates the fibers’ discharge rates were dictated by the relative on-BF level of the HRTFs and not their absolute level. That is, HRTFs with low on-BF levels produced the same low rates at both presentation levels because the response was suppressed by higher levels of energy in surrounding features (Sachs and Kiang 1968). Consequently, rate profiles saturated at high levels but preserved high discharge rates for spectral peaks and low rates for spectral notches. It has been shown that similar suppression effects dictate the enhanced vowel coding properties of LSR fibers (May et al. 1998).

Neural discrimination of HRTF shapes in quiet

Spatial localization of complex acoustic stimuli requires the perceptual separation of directionally dependent HRTF features. A prerequisite for this biological process is a peripheral representation that produces a discrete pattern of discharge rates for individual HRTF shapes. Although the complete neural representation of an HRTF spectrum is distributed across a population of auditory nerve fibers, the most significant rate changes occur among select fibers that are tuned to directional features such as the mid-frequency spectral notches of the cat’s HRTF (May and Huang 1997; Rice et al. 1995).

The quality of HRTF representations was estimated by computing the expected population rate profile for a given stimulus level and spontaneous rate classification. This process involved the linear transformation of spectrum level to simulated discharge rates using the mean rate-level slopes in Figure 4. The statistical averages for this calculation were derived from fibers that were tuned to mid-frequency spectral features. The BFs of model fibers were linearly spaced in increments of 100 Hz, reflecting the original sampling of HRTF spectrum levels (Rice et al. 1992).

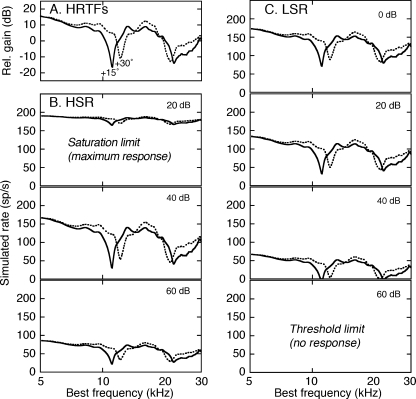
Examples of simulated rate profiles are shown for two HRTFs in Figure 5. The stimuli (Fig. 5A) were recorded in the median plane at elevations (ELs) of 15° and 30° (Rice et al. 1992). The change in elevation shifted the frequency location of the mid-frequency notch from 11.1 to 12.2 kHz. Behavioral studies of domestic cats suggest that cats rely on this spectral cue when orienting to free-field sounds (Huang and May 1996).

FIG. 5.

Effects of presentation level on HRTF coding. A Representative HRTF stimuli for two elevations in the median vertical plane (+15° and +30° EL). B Simulated rate profiles for the responses of HSR fibers to the two stimuli. Results are compared at three presentation levels. C Simulated responses for LSR fibers at four levels.

The effects of presentation level on simulated rate profiles are summarized for the HSR and LSR fibers in Figure 5B and C, respectively. As was the case for actual data, the predicted HRTF-driven rates of HSR fibers provided a sensitive representation of the mid-frequency spectral notches at low levels (60–40 dB attenuation), but saturated at moderate levels (20 dB attenuation). By contrast, the LSR fibers were limited by threshold at low levels (60 dB attenuation), but produced an accurate representation of the spectral features at moderate and high levels (40–0 dB attenuation).

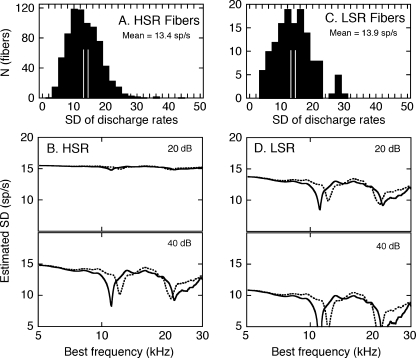
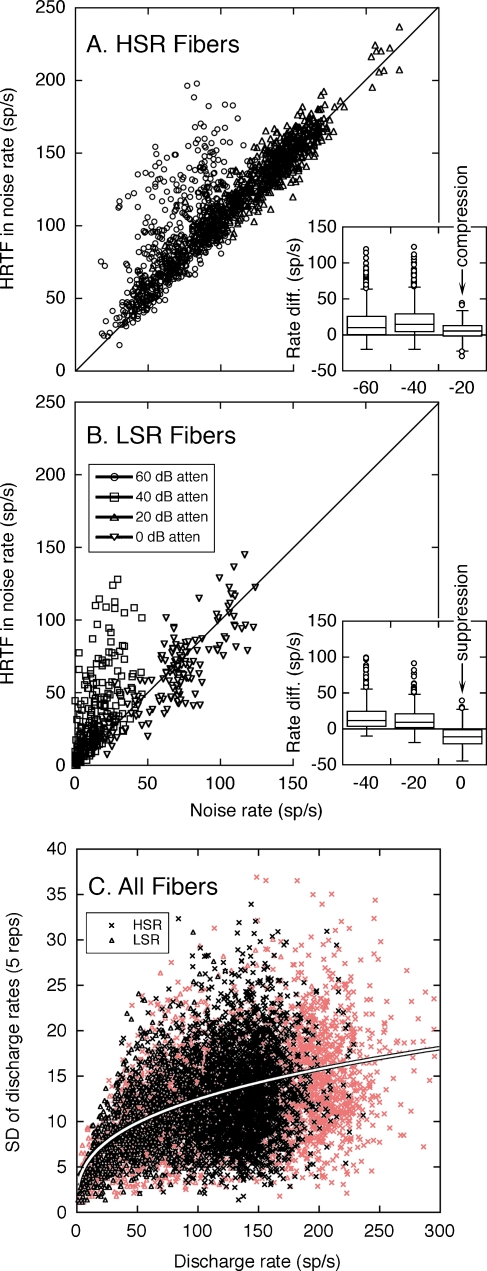
Statistical estimates of rate variability were derived by applying Eq. 2 to the simulated rate profiles in Figure 5. These results are summarized for the HSR and LSR fibers in Figure 6B and D. Prior to this analysis, the reliability of the calculation was evaluated by comparing SD estimates with the actual SDs for all of the HRTF-driven rates that fell between 125 and 175 sp/s in Figure 3. These distributions are shown in Figure 6A and C. The average SDs for the LSR and HSR fibers were 13.9 and 13.4, respectively, confirming the similarity of the metric across the two spontaneous rate classifications. The separation between the parallel vertical lines in each histogram indicates the range of SDs predicted by Eq. 2 for HRTF-driven rates (r) between 125 and 175 sp/s. In both cases, the predicted range fell near the median value of the distribution of actual SDs.

FIG. 6.

Estimates of the variability of auditory nerve responses to HRTF stimuli. Distributions of actual SDs for all HSR (A) and LSR fibers (C). Results are limited to discharge rates between 125 and 175 sp/s, which were plotted in Figure 3A and B. The separation between the parallel vertical lines indicates the SD range that is predicted by Eq. 2 for the same discharge rates. The variability of HRTF-driven rates among HSR (B) and LSR fibers (D) was estimated by applying Eq. 2 to the simulated rate profiles in Fig. 5.

The estimated SD profiles in Figure 6 suggest that the quality of the HSR representation was compromised at higher presentation levels not only by rate saturation but also by increased variability. At lower levels, spectral notches elicited reduced, and therefore less variable, discharge rates. The LSR response was lower in magnitude, well modulated by changes in spectrum level, and less variable.

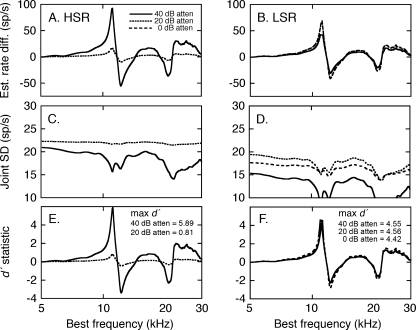
Simulated HRTF-driven rates and their corresponding SDs were combined to quantify the neural discrimination of the two HRTFs in terms of d′ statistics. For this calculation, the numerator of Eq. 1 was derived by subtracting the estimated rate profile for the +15° HRTF from the profile for the +30° HRTF (Fig. 5). The resulting rate difference profiles are presented at two presentation levels in Figure 7A and B. The denominator of Eq. 1 was computed from the predicted SD profiles (Fig. 6). These estimates of the joint SD are shown in Figure 7C and D.

FIG. 7.

Signal detection analysis of the quality of HRTF representations under quiet conditions. HRTF-dependent rate differences were calculated for HSR (A) and LSR fibers (B) by subtracting the simulated rates for the EL +15° HRTF from the rates for the EL +30° HRTF (Fig. 5). The joint SDs for HSR (C) and LSR fiber (D) were derived from the estimated SD profiles for the two stimuli (Fig. 6). The d′ index of discrimination (E and F) reflects the ratio of the rate difference and joint SD, as specified by Eq. 1.

The d′ statistics for HSR and LSR simulations are shown for two presentation levels in Figure 7E and F. When the magnitude of rate differences and variance were taken into account, the HSR and LSR fibers provided an accurate representation of HRTF-based spectral features that fell within their dynamic range. The essential difference between the two neural populations was the physiological constraint that imposed an upper (saturation) or lower bound (sensitivity) on the representations. With the exception of very low stimulus levels, the LSR fibers matched or exceeded the coding capabilities of the HSR fibers.

Dynamic range properties of neural representations in noise

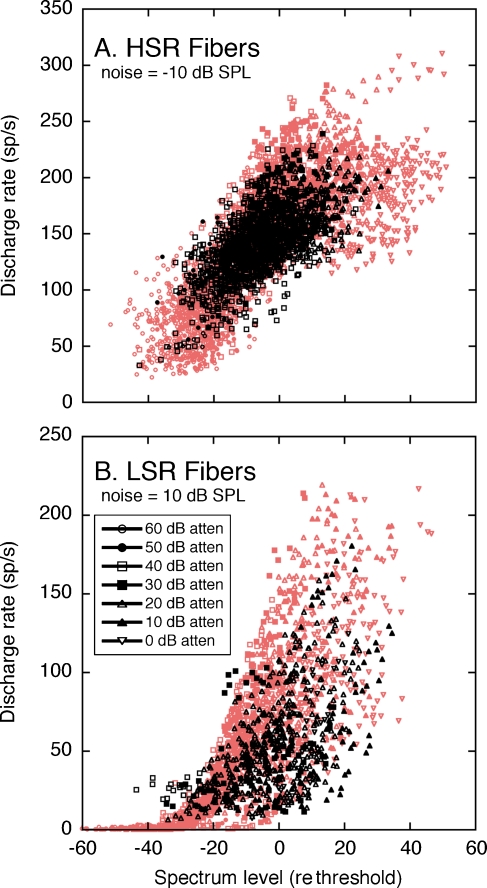
Two sampling paradigms were used to characterize effects of background noise on HRTF coding. In the first, continuous noise was held at a constant level while HRTF signals were pulsed across a range of presentation levels. This is the same method that was used to sample the dynamic range of HRTF representations under quiet conditions (Fig. 3). The HRTF-driven rates of the HSR and LSR fibers were recorded in noise spectrum levels of −10 and 10 dB SPL, which match the respective mid points of the dynamic range for the two response classes. The more sensitive HSR fibers were most extensively tested at HRTF signal levels of 60–20 dB attenuation, while the less sensitive LSR fibers were mainly tested at 40–0 dB attenuation. Consequently, noise effects were characterized at equivalent locations within the dynamic range of the two response classes and at similar global S/Ns.

The results of the first noise analysis are presented in Figure 8. As in Figure 3, HRTF-driven rates are plotted relative to on-BF spectrum level (black symbols). Noise levels were not included in the calculation of spectrum level for the purpose of comparison with equivalent rate-level functions in quiet (data from Fig. 3 overlaid as red symbols). Relative to their responses in quiet, both groups of fibers displayed higher minimum rates at low signal levels and lower maximum rates at high signal levels. This compression of the rate-level function was induced by sustained responses to the continuous background noise. Minimum HRTF-driven rates increased at sub-threshold signal levels because spontaneous activity was replaced by noise-driven activity. Maximum rates decreased at saturation levels because responses were adapted by noise-driven activity (Costalupes et al. 1984). The HSR fibers (Fig. 8A) tended to exhibit more compression than the LSR fibers (Fig. 8B).

FIG. 8.

Effects of a constant noise level on HRTF coding by HSR (A) and LSR fibers (B). Responses were obtained at multiple HRTF presentation levels in noise spectrum levels that were fixed at −10 and 10 dB SPL for HSR and LSR fibers, respectively. Plotting conventions are the same as those in Figure 3. Results are superimposed on discharge rates that were recorded in quiet, as previously shown in Figure 3 (red symbols).

The rate-level data of the LSR fibers showed a general rightward shift relative to responses in quiet. The effect is less apparent for HSR fibers, which were tested at a lower noise level. Previous studies of the auditory nerve representation of tones in noise have attributed this shift to two-tone suppression, where cochlear mechanical responses at one frequency are diminished by higher levels of energy in surrounding frequencies (Costalupes et al. 1984; Sachs and Kiang 1968). In this context, suppression effects may be bi-directional. Energy in the background noise may suppress a fiber’s response to energy in an HRTF notch, or noise-driven activity may be suppressed by energy in an HRTF peak.

Representations of signals in noise are not inherently degraded by suppression (Winslow and Sachs 1988). A linear translation of the rate-level function to a higher dynamic range preserves rate coding for spectral components that are not masked by noise energy. By contrast, compression of the HSR rate-level data in background noise indicates that the spectral shape of the HRTFs must be encoded by a more constrained range of discharge rates. The LSR fibers are expected to provide a more robust representation of directionally dependent changes in HRTF features than the HSR fibers because they exhibit stronger suppression.

The dynamic range properties of the HSR and LSR fibers are summarized by the statistical distribution of HRTF rate-level slopes in Figure 9. At very low presentation levels (60 dB attenuation), there was little difference between median slopes in background noise and quiet because dynamic range was determined by the threshold properties of the neural populations. As level increased (40-dB attenuation), the HSR fibers reached their maximum slope under quiet conditions but showed substantial rate compression in noise. Beyond this point (20–0 dB attenuation), the dynamic range of the HSR representation was lost to saturation and could not be further degraded by noise. Although the slopes of the LSR fibers declined across the same range of presentation levels, the effects of noise were less pronounced.

FIG. 9.

Dynamic range properties of HRTF coding in a constant noise level. Slope distributions are taken from rate-level data in Figure 8. Because noise levels were fixed during these recordings, S/Ns changed with presentation level. Vertical lines indicate changes in median slopes for noise conditions (solid lines) relative to results that were obtained under quiet conditions (dashed lines), as previously shown in Figure 4.

Interpretations of our first sample of noise effects are made difficult by coincident changes in presentation level and global S/Ns. Such confounds were avoided by our second sampling method, which manipulated signal and noise levels in unison to maintain a constant S/N of −10 dB. Experiments with the first sampling paradigm (Fig. 9) confirmed that this S/N evoked robust dynamic range adjustments among both groups of fibers.

The rate-level relationships for this S/N at signal levels ranging from 60 to 0 dB attenuation are shown in Figure 10. As in Figure 8, the discharge rates are plotted relative to HRTF on-BF spectrum level as black symbols, and the results from quiet are shown as red symbols (Fig. 3). Relative to responses obtained in quiet, the most obvious change in the HRTF coding properties of HSR fibers (Fig. 10A) was a loss of rate representation that was due to the compression of maximum driven rates at higher presentation levels, and therefore, higher noise levels. Although the LSR fibers (Fig. 10B) also showed a decrease in maximum HRTF-driven rates at high presentation levels, they preserved their relatively steep slopes in background noise.

FIG. 10.

Effects of a constant S/N ratio on HRTF coding by HSR (A) and LSR fibers (B). Responses were obtained at multiple HRTF presentation levels with covarying changes in noise levels to maintain constant S/Ns of –10 dB. Plotting conventions are the same as those in Figure 8.

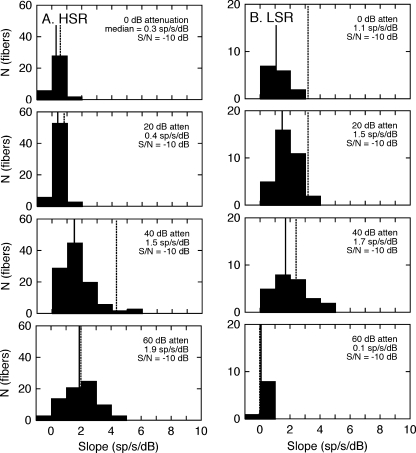
The statistical distributions of the rate-level slopes are presented in Figure 11. These results followed the same general trends that were shown in Figure 9. The dynamic range of HSR fibers (Fig. 11A) was largely constrained by signal levels; consequently, there was little difference between slopes that were obtained at the same signal level in quiet or with either noise sampling paradigm. An exception was observed at a presentation level of 40 dB attenuation, where the fibers showed exceptional dynamic range in quiet but much lower slopes in noise. The population of LSR fibers (Fig. 11B) also showed consistent slope decreases in noise, but maintained slopes greater than 1 sp/s/dB at signal levels as high as 0 dB attenuation.

FIG. 11.

Dynamic range properties of HRTF coding in a constant S/N of −10 dB. Slope distributions of HSR (A) and LSR fibers (B) are taken from the rate-level data in Figure 10. Plotting details are the same as those described in Figure 9.

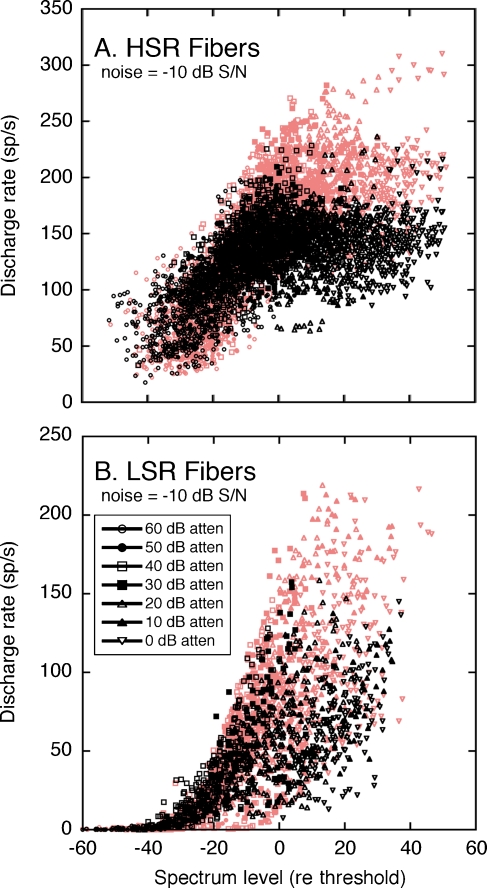
The underlying mechanisms of dynamic range adjustments in the −10 dB S/N can be revealed by contrasting the discharge rates that were elicited by the combination of HRTFs with noise and by noise alone. The analysis is illustrated in Figure 12. At lower presentation levels, the HSR (Fig. 12A) and LSR fibers (Fig. 12B) displayed large positive departures from the unity line in each figure. The magnitude of these deviations indicates the full range of rate coding for HRTF spectral features. At higher presentation levels, the responses of HSR fibers fall close to the unity line, suggesting only small rate differences between each fiber’s response to HRTFs with noise and noise alone. The population of LSR fibers also exhibited smaller positive rate differences, but these effects were offset by a greater prevalence of negative rate differences.

FIG. 12.

Dynamic range adjustments of HSR (A) and LSR fibers (B) in a fixed S/N ratio of −10 dB. Responses to HRTFs in noise are compared with responses of the same fibers to noise alone. Rate differences between the two stimulus conditions are indicated by deviations of individual data points from the unity line. Statistical distributions of rate differences are summarized by box plots (insets). As in quiet (red symbols), the SDs of HRTF-driven rates in noise (C) cluster around the power function derived from Eq. 2.

The opposing dynamic range adjustments of the HSR and LSR fibers are highlighted by the “box and whisker” plots in the insets of Figure 12A and B. Each box summarizes the statistical distribution of rate differences at the same signal level. The upper and lower limits of the box indicate the interquartile range (lower 25% to upper 75%) of each sample. The box is bisected at the median of the distribution. Whiskers (error bars) encompass all data points within 1.5× the interquartile distance. Outliers beyond this distance are plotted as individual data points.

The range of HRTF-driven rates for the middle 50% of HSR fibers is indicated by the vertical height of the box plots in Figure 12A. At increasing signal levels, the box plots compress because maximum rate differences lessened while minimum rate differences remained anchored to 0 sp/s. Constraints in the dynamic range properties of HSR fibers, therefore, were primarily dictated by rate compression.

An additional noise effect is suggested by the responses of LSR fibers at high signal levels. Although maximum rate differences fell toward zero, minimum rate differences fell below zero. At the highest presentation level (0 dB attenuation), the interquartile range of the distribution maintained its relative height but was entirely comprised of negative rate differences. A negative rate difference indicates that the fibers exhibited lower driven rates for HRTFs in noise than for noise alone. The most likely explanation for this effect is that noise-driven responses at low-energy HRTF components were suppressed by nearby high-energy components.

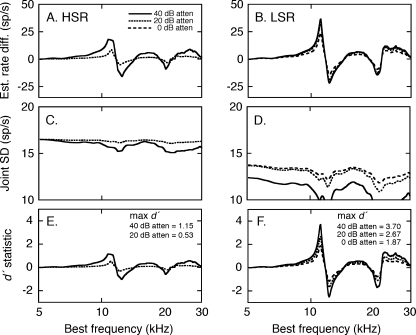
The interactions of compression and suppression on HRTF coding were evaluated by applying a signal detection analysis to simulated discharge rates at the −10 dB S/N. Rate profiles for the EL +15° and EL +30° HRTFs were computed using the median linear fits in Figure 11. As for Figure 7, rate difference profiles were calculated by subtracting one rate profile from another. The resulting rate difference profiles are shown in Figure 13. Due to saturation effects, the analysis of HSR fibers (Fig. 13A) was limited to presentation levels of 40 and 20 dB attenuation. The LSR fibers (Fig. 13B) were also modeled at 0 dB attenuation. The rate differences for spectral notches appear truncated for the HSR fibers because the energy minima are effectively filled by background noise. The LSR fibers conveyed a sharper representation of the notches because these responses were suppressed below noise-driven rates. Whereas, HSR responses showed strong rate compression at a presentation level of 20 dB attenuation, LSR representations were only modestly affected.

FIG. 13.

Signal detection analysis of the quality of HRTF representations in background noise. A, B Differences in the discharge rates elicited by the EL +15° and EL +30° HRTFs were estimated by applying the linear rate-level relationships in Figure 11 to the two spectral shapes (see Fig. 6). C, D Joint SDs were derived by inserting the rate profiles into Eq. 2. E, F The d′ index of discrimination for the two HRTFs is computed from the ratio of rate differences and joint SDs.

The predictive relationship between HRTF-driven rates and SD (Fig. 3C) were not altered by background noise (Fig. 12C). On average, the SDs estimated by applying Eq. 2 to discharge rates that were evoked by HRTFs in noise differed from the predicted values of actual fits by 0.3 sp/s. Consequently, the joint SDs for rate difference profiles in noise were derived with Eq. 2, using the same procedures as responses in quiet. These values are shown in Figures 13C and D. Not only did the LSR fibers yield larger rate differences than the HSR fibers, they also displayed smaller SDs.

The simulated rate difference profiles and joint SDs for the −10 dB S/N were combined to produce the d′ profiles in Figures 13E and F. Maximum d′ scores for the discrimination of the two HRTF shapes suggest that background noise degraded spectral coding relative to representations in quiet (Fig. 7), but the effects were more pronounced among HSR fibers.

Discussion

As suggested by previous studies (May and Huang 1997; Yu and Young 2000), our results support the practicality of linear modeling for the quantitative analysis of spectral coding in the auditory nerve. When this statistical approach was used to evaluate the effects of sound level and background noise on the coding of HRTF spectra, the less common LSR fibers played a singularly important role in representations that were based on average discharge rates.

Differences in HRTF coding among fiber types

The major finding of this study was that HRTF spectral shapes were well represented by the discharge rates of auditory nerve fibers across a wide range of signal levels and in the presence of background noise. Just as no single fiber encoded the multiple frequency components of a complex sound, no fiber encoded the full range of audible hearing levels. Instead, both dimensions of sound were communicated by the orchestrated response of a population of neurons with complementary frequency tuning and dynamic range. It is curious that the former characteristic has been considered a refinement of auditory processing, while the latter has been maligned as “the dynamic range problem” (Evans 1981; Viemeister 1988). Results presented here, and elsewhere (Le Prell et al. 1996; May et al. 1998; Sachs and Young 1979), indicate that the perceived limitation of rate coding vanishes when the neural representation of frequency and level is defined in terms of a distributed population response.

The effective coding of spectral features by the more sensitive HSR fibers was limited to signal levels near neural thresholds that fall closely around the threshold of hearing in domestic cats. Saturation effects degraded their representations of HRTF shapes at higher sound levels and in background noise. Conversely, decreased sensitivity constrained the ability of LSR fibers to encode HRTF features at low sound levels. Nevertheless, the quality of coding across most of the dynamic range of hearing, and in background noise, was established by the responses of the LSR fibers.

The coding differences that distinguish the HSR and LSR fibers were not eliminated when rate-level functions were constructed in relation to each fiber’s threshold (e.g., Fig. 3). This observation suggests that the enhanced dynamic range of the LSR fibers was dictated by the absolute levels to which the neurons were most sensitive. Because the LSR fibers operated at higher sound levels, they were most directly influenced by compressive nonlinearities of the basilar membrane and two-tone suppression (Le Prell et al. 1996; Sachs and Young 1979).

Previous investigations of the auditory nerve representation of human vowel sounds (Sachs and Young 1979; Sachs and Young 1979; Le Prell et al. 1996) have established the critical role of LSR fibers in the rate representation of complex sounds under quiet conditions. Our present analysis extends those observations to the more generalized spectral cues that communicate directional information over most of the upper frequency limits of mammalian hearing. Unlike previous interpretations that suggested a detrimental effect of two-tone suppression on population coding (Sachs and Young 1979), our results suggest that the nonlinearity is an essential mechanism for preserving spectral contrast at high sound levels.

The potentially disruptive influence of background noise on HRTF representations also appears to be ameliorated by suppression effects that are largely directed toward LSR fibers. An intriguing result in the present study was the observation that fibers responding to the combined energy of the HRTF spectrum and background noise may show lower driven rates than when responding to noise alone (Fig. 12). Previous studies of vowel representations in background noise suggest that the noise response is suppressed by the HRTF signal (Sachs et al. 1983). The effect is exacerbated when a fiber is tuned to a spectral notch in the HRTF because the sharp spectral contrast minimizes energy at BF and maximizes energy in surrounding suppressive regions. The resulting rate decrease shifts the dynamic range of the rate-level relationship to higher sound levels. Although the HSR fibers tend to show slightly larger shifts than the LSR fibers in the same noise levels (Costalupes et al. 1984), suppression effects are most prominent for LSR fibers because their dynamic range extends to higher sound levels (Sachs et al. 1989).

Other studies have characterized the auditory nerve coding of HRTF spectra under quiet conditions (May and Huang 1997; Poon and Brugge 1993; Rice et al. 1995). At stimulus conditions that were limited to low sound levels, HSR fibers provided the best representations of HRTF spectra (May and Huang 1997; Rice et al. 1995). Although this initial evaluation was constrained by the inherent difficulty in relating traditional population measures to the sharp spectral modulations of HRTF stimuli, subsequent analyses have confirmed that observation by applying a more quantifiable modeling approach to the same data set (May and Huang 1997). In studies that simulated HRTF features by manipulating the frequency of a spectral notch in broadband noise, the most informative notch-driven responses shifted from HSR to LSR fibers with increasing sound level (Poon and Brugge 1993). In both instances, the results were consistent with our current characterizations of HRTF coding in quiet.

The extended dynamic range of LSR fibers is less apparent when suppression effects are reduced by constraining the natural spectral variation of HRTF shapes. For example, the psychophysical discrimination of rectangular spectral notches in flat-spectrum noise suggests a non-monotonic relationship between the just-detectable notch depth and overall sound pressure level (Alves-Pinto and Lopez-Poveda 2005). A transition from HSR to LSR coding is suggested by a threshold maximum that is seen at 70–80 dB. When suppression effects are enhanced by the deep notches of actual HRTF shapes, LSR fibers appear to dictate the quality of coding at much lower sound levels.

Despite the dynamic range changes that were exhibited by auditory nerve fibers at high signal levels and in background noise, the maximum d′ values of LSR fibers are sufficient to support the accurate behavioral discrimination of HRTF shapes. Although direct psychophysical descriptions of HRTF discrimination have not been obtained in domestic cats, the quality of HRTF representations in the auditory nerve are likely to contribute to directional acuity in the median vertical plane. Previous behavioral studies in a variety of mammalian species, which includes the domestic cat (Martin and Webster 1987; May and Huang 1997), have confirmed that the minimum detectable change in sound source elevation approaches its optimal value as signal level increases to approximately 30 dB above threshold. Beyond this transition, directional thresholds are relatively unaffected by changes in signal level.

Domestic cats also display only small changes in spatial acuity when auditory signals are embedded in moderate levels of continuous background noise (May et al. 2004). Although data are not presently available to link perceptual performance to the coding properties of auditory nerve fibers in a quantitative manner, these general relationships suggest that the quality of the peripheral representation of spectral cues for sound localization is preserved by the response patterns of LSR fibers under a variety of adverse listening conditions.

Spectral coding in the central auditory system

The critical role of LSR fibers in spectral coding appears counter-intuitive in light of their small numbers. In cats, only 16% of auditory nerve fibers meet the criterion for this classification (Liberman 1978). This sparse representation is offset by the distribution of auditory nerve terminations within the ventral cochlear nucleus (Liberman 1991). Although LSR fibers are few in number, they contact a greater number of second-order neurons than HSR fibers. The proliferation of LSR inputs is especially evident for contacts with multipolar cells. With the exception of the most posterior regions of the ventral cochlear nucleus, auditory nerve inputs to multipolar cells are almost exclusively made by LSR and MSR fibers, with individual LSR fibers contacting an average of three to five neurons.

Multipolar cells are identified by their “chopper” type peristimulus time histograms (PSTHs) in electrophysiological studies of the ventral cochlear nucleus (Rhode et al. 1983). Because the neurons integrate a large number of axodendritic inputs from the auditory nerve, they exhibit superior spectral coding properties (Young et al. 1988). Although their ability to encode HRTF features has not been described, chopper units provide the most sensitive representation of vowel formant structure in the cochlear nucleus (Blackburn and Sachs 1990; May et al. 1998). Like LSR fibers, the superiority of vowel coding by chopper units is most obvious at high sound levels and in background noise. A key difference between ascending LSR inputs and their post-synaptic target is the added ability of chopper units to encode spectral shapes at low sound levels.

The extended dynamic range of chopper units may be created by the convergence of both HSR and LSR inputs upon multipolar cells, and the spatial organization of those dichotomous inputs. A switching circuit has been proposed in which HSR inputs are located on distal dendrites and LSR inputs near the cell body of multipolar cells (Lai et al. 1994). At high sound levels, the activation of local inhibitory inputs shunts the saturated HSR inputs before they reach the cell body. Glycinergic radiate neurons found in the ventral cochlear nucleus are a potential source for this inhibition (Doucet and Ryugo 2006). A reciprocal low-level switch is not needed to silence LSR inputs because their action is limited by threshold. This “selective listening” circuit endows chopper units with the coding properties of HSR fibers at low sound levels and LSR fibers at high sound levels.

A better understanding of the respective roles of HSR and LSR fibers may be important clinically for extending the dynamic range of patients with cochlear implants. It is known that the effective dynamic range provided by cochlear implants is limited (Shannon 1983), and this could potentially be due to electrical stimulation preferentially activating only one SR group of fibers.

Efferent control and noise cancellation

The medial olivocochlear (MOC) pathways represent an additional mechanism for the preservation of rate coding in the presence of background noise (Warr and Guinan 1979). By attenuating the gain of cochlear amplification, MOC neurons reduce noise-driven activity. The resulting decrease in rate compression can “unmask” auditory nerve responses to signals in noise (Winslow and Sachs 1987).

The importance of MOC feedback in the perception of auditory signals was first established by the animal behavior studies of Dewson (1967). Dewson measured the effects of background noise on vowel discrimination in macaque monkeys before and after cutting the crossed olivocochlear bundle, which contains MOC axons en route to the contralateral cochlea. Lesioned monkeys were unable to maintain performance unless the noise was significantly reduced relative to pre-lesion levels. Performance in quiet was not affected. This potentiation of noise masking is relevant to the present study because spectral processing is a common prerequisite for vowel discrimination and the localization of complex sounds.

The MOC pathways exert a strong modulatory influence on the auditory nerve responses of domestic cats (Guinan and Gifford 1988; Wiederhold and Kiang 1970). Descending control is particularly powerful at mid frequencies where the cochlea receives dense efferent innervation (Liberman et al. 1990). The bias toward the frequencies that convey HRTF-based directional cues (Huang and May 1996) suggests that MOC feedback has been shaped by the evolutionary advantage for accurate sound localization. Consequently, the lower frequencies of human vowel sounds may not be an optimal stimulus for assessing the full functional consequences of this feedback system in cats.

The contributions of the MOC pathways to sound localization have been explored by measuring the effects of olivocochlear lesions on the spatial acuity of domestic cats (May et al. 2004). The specificity of the resulting impairment was striking. The minimum detectable change in elevation increased without altering the discrimination of azimuth. This outcome is further evidence for the enhanced processing of spectral information because the perception of elevation is dictated by monaural spectral cues. Moreover, as previous noted by Dewson, the deficits were only observed in background noise.

The strength of olivocochlear feedback in intact animals may be compromised by the use of barbiturate anesthesia (Boyev et al. 2002; Samara and Tonndorf 1981). Consequently, future studies that maintain normal olivocochlear function might be expected to demonstrate even greater noise cancellation effects than our current descriptions of HRTF coding. Nevertheless, because efferent-induced changes in cochlea sensitivity are known to affect all spontaneous rate classifications (Kawase et al. 1993), these unexplored aspects of dynamic range adjustment are not likely to alter the relative coding capabilities of HSR and LSR fibers that are emphasized in the present study.