Using the Cochlear Microphonic as a Tool to Evaluate Cochlear Function in Mouse Models of Hearing

Abstract

The cochlear microphonic (CM) can be a useful analytical tool, but many investigators may not be fully familiar with its unique properties to interpret it accurately in mouse models of hearing. The purpose of this report is to develop a model for generation of the CM in wild-type (WT) and prestin knockout mice. Data and modeling results indicate that in the majority of cases, the CM is a passive response, and in the absence of outer hair cell (OHC) damage, mice lacking amplification are expected to generate WT levels of CM for inputs less than ~30 kHz. Hence, this cochlear potential is not a useful metric to estimate changes in amplifier gain. This modeling analysis may explain much of the paradoxical data in the literature. For example, various manipulations, including the application of salicylate and activation of the crossed olivocochlear bundle, reduce the compound action potential but increase or do not change the CM. Based on this current evaluation, CM measurements are consistent with early descriptions where this AC cochlear potential is dominated by basal OHCs, when recorded at the round window.

Introduction

Although cochlear microphonic (CM) potentials have been measured for about 80 years (Adrian 1931; Wever and Bray 1931), these compound graded responses are perhaps the least understood and least utilized indices of cochlear performance. Because the CM is principally produced by outer hair cells (OHC; Dallos and Cheatham 1976a), these potentials are important for characterizing OHC function since their removal results in a loss of sensitivity and frequency selectivity (Dallos and Wang 1974; Dallos and Harris 1978; Liberman and Dodds 1984; Ryan and Dallos 1975). This phenotype is similar to what is observed in mice lacking prestin (Cheatham et al. 2004; Liberman et al. 2002) and presumably cochlear amplification (Dallos et al. 2008). Because recording from individual OHCs may never become routine (Dallos et al. 1982; Russell and Sellick 1983), it is still important to understand how the CM is generated so that these compound responses are not misinterpreted. Hence, the purpose of this paper is to provide a framework to assist interpretation of the CM and its use as an analytical tool

The CM is a field potential that can be recorded from fluids and tissues within, around and remote from the cochlea. However, there is value in recording the CM near its source to maximize signal-to-noise ratio, i.e., the remote recording of CM still presents technical challenges and difficulties with interpretation. The prevailing notion is that mechanical stimulation of cochlear hair cells results in the modulation of their transducer currents (Davis et al. 1958; Hudspeth and Corey 1977). Since the cells are embedded in the electrical network of the organ of Corti and surrounding fluid spaces, alterations of transducer currents produce changes in extracellular current flow. The latter are detectable as a remote reflection of voltage changes measured across any available electrical impedance. Because any acoustic stimulus activates groups of hair cells, the recording electrode integrates receptor currents produced by large numbers of individual generators. This integration is key to understanding the CM because depending on the physical relationship between electrode(s) and active hair cell groups, the spectrum and level of stimulation, and the electroanatomy (von Békésy 1960) of intervening tissues and fluid spaces, the recorded CM can have radically different properties. For example, due to rapid phase changes around the peak of the traveling wave, responses from hair cells with characteristic frequencies (CF) near the stimulus frequency are largely canceled (Dallos 1973b; Whitfield and Ross 1965). The CM is, therefore, dominated by hair cell receptor currents produced on the more linear tails of mechanical excitation patterns. In contrast, the compound action potential (CAP) elicited at low levels reflects responses from spatially localized single units innervating frequency-specific regions along the cochlear partition (Özdamar and Dallos 1976; Teas et al. 1962). Hence, neurons contributing to the CAP have CFs approximately equal to the stimulus frequency.

Because cochlear potentials are frequently used to characterize peripheral performance in transgenic animals, we developed a model of CM generation in mice. Simulations of response patterns in wild-type (WT) and prestin knockout (KO) mice assist our understanding of the complicated behaviors of summed hair cell receptor currents (CM) and neural (CAP) responses, especially when the cochlear amplifier is inactivated. In previous experiments, it was demonstrated (Cheatham et al. 2004; Liberman et al. 2002) that neural thresholds in KOs are raised by ~50 dB. We now show that, for a low-magnitude criterion voltage, corresponding CM isoresponse functions are near normal in young prestin KO mice when compared with WT littermates. This disparity between the CM and CAP is supported by model simulations and assists explanation of several anomalous findings in the literature that report increase in CM in spite of the decrease in neural sensitivity.

Methods

All recordings were made from surgically anesthetized (sodium pentobarbital, 80 mg/kg IP) mice, of both sexes and on a mixed genetic background (129/C57BL6), between postnatal days P22 and P47. The animals were bred on site and genotyped by DNA analysis of tail snips. Mice lacking prestin included both the original KO designated prestin^Jnz and initially characterized by Liberman et al. (2002) and a second one designated prestin^Hsk (Cheatham et al. 2007). Although both lack prestin protein, prestin^Hsk but not prestin^Jnz shows low levels of prestin mRNA. Both models display a similar phenotype. Methods were approved by the National Institutes of Health and by Northwestern University’s Institutional Review Committee.

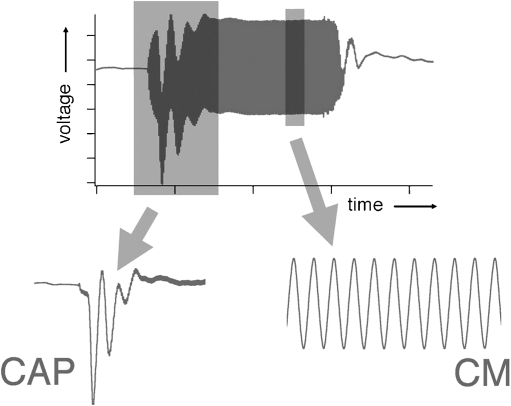
Because basic properties and recording techniques were detailed decades ago (Dallos 1973b) and since these descriptions are mostly valid today, we provide only a brief précis in this report. Signals were generated using the Card Deluxe 24-bit sound card with a sample rate of 96 kHz and attenuated by decreasing the output voltage produced by the sound card. A single radio Shack #40 Super Tweeter was placed in the external auditory meatus that had been shortened to allow the speculum to be placed close to the tympanic membrane forming a closed system. Sound calibration was performed using a tubing coupler with a volume approximating that of the experimental cavity between the end of the speculum and the terminating tympanic membrane, which was replaced by an 1/8″ B&K microphone. A round-window (RW) electrode was used to record all responses including CAP pseudo-thresholds, measured as the sound pressure level required to generate a small, 10-μV N1/P1 response. Following amplification (gain = 100) and A/D conversion, the responses were low-pass filtered (200–2,000 Hz) and values obtained after fast-Fourier transformation. In addition, an analogous “threshold” was provided for the CM by measuring isoresponse functions for a 0.1-μV rms criterion voltage. In this case, the CM responses were band-pass filtered around the stimulus frequency. These two potentials reflect different aspects of the stimulus-related response. For example, the CAP is a response to stimulus onset, while the CM is measured during the steady-state part of the response, as shown in Figure 1. A continuous tone can, therefore, be used to elicit the CM, which increases the signal-to-noise ratio by approximately two orders of magnitude. This change in stimulus parameters allows one to resolve the CM at 0.1 μV and to obtain a pseudo-threshold measurement.

FIG. 1.

This schematic shows the responses to a tone-burst stimulus, which is generally used to elicit potentials recorded at the round window. As shown below, the CAP is generated at stimulus onset, while the CM is measured during the steady-state portion of the response. The latter also follows the waveform of the acoustic input. In contrast, the CAP reflects unit responses produced by the ensemble activity of a small group of auditory nerve fibers with CFs near stimulus frequency. Since the dominant spectral component of the CAP is ~1 kHz, this neural response is obtained by filtering between 0.3 and 2.0 kHz. Although not shown here, the CM as recorded in these experiments is produced in response to a continuous tone in order to enhance signal-to-noise ratio, making it possible to observe the CM at very low levels.

CAP tuning curves were also collected using the simultaneous tone-on-tone masking paradigm (Dallos and Cheatham 1976b). In this procedure, the probe alone produces a 25-μV N1/P1, which is then decreased by 3 dB by adjusting masker frequency and level, thereby defining a masking pattern. Similar functions are acquired for the CM but again using continuous tones rather than tone bursts. Probe level is set so that a CM response of 0.3 μV rms is observed. Masker frequency and level are then adjusted to decrease this response by 0.1 μV rms. Because of the possibility of electrical pickup, only CM measurements that are at least 6 dB above the monitored background are deemed biological, and only these are included in the data presented here.

Results

Physiological measurements

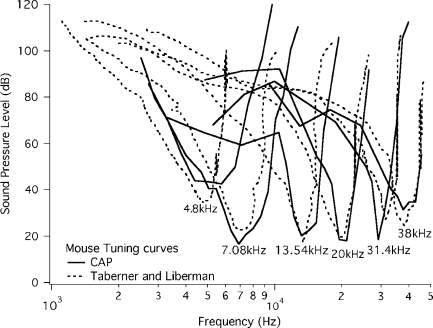
We introduce our results by showing CAP tuning curves obtained using the simultaneous tone-on-tone masking paradigm in WT mice. In Figure 2, CAP data are compared with single-unit responses derived from Taberner and Liberman (2005). Dotted lines show average single-unit isoresponse functions ranging in CF from 4.8 to 38 kHz; the solid lines are the representative simultaneous masking functions for the CAP recorded using a round-window electrode. These comparisons indicate that CAP tuning curves provide a fair representation of single-unit threshold responses. The fact that only maskers around the probe reduce the CAP when the probe is introduced at low levels implies that the stimulus activates a small number of auditory nerve fibers and that they innervate a relatively specific and narrow region along the cochlear partition. In prestin KO mice, however, the tip segments are lost probably due to the elimination of cochlear amplification and the loss of prestin from the OHC’s lateral wall (Cheatham et al. 2004).

FIG. 2.

Tuning functions for single units (dotted lines) and for the CAP (solid lines) obtained using simultaneous masking. The isoresponse functions for individual auditory nerve fibers are taken from Taberner and Liberman’s (2005) Figure 2. Using their data, we traced an average tuning curve at the CFs indicated using GraphClick (Arizona Software, Neuchâtel, Switzerland) and matched these by using a probe of the same frequency to obtain the compound CAP tuning functions.

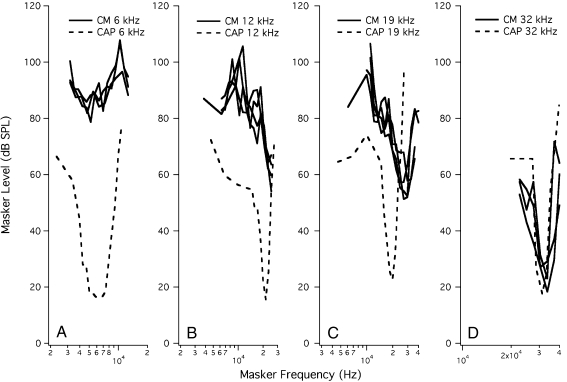
A similar approach was also applied to the CM recorded from the round window. This effort to extract frequency-specific information from the CM was originally performed by Legouix et al. (1973) and was referred to as CM interference. However, because the approach is similar for both CAP and CM and involves the use of a simultaneous two-tone masking paradigm, the results are referred to here as CM masking functions rather than CM interference functions. Representative CM simultaneous masking functions are plotted for probe tones at 6, 12, 19, and 32 kHz in Figure 3. The probe tones generate alone (no masker) responses of 0.3 μV. Maskers are then introduced to achieve a reduction of 0.1 μV. Only for the 32-kHz probe (Fig. 3D) do masker frequencies near the probe decrease the CM in a frequency-specific manner (solid lines) when presented at low levels. For 6 and 12 kHz, the near-probe masker levels are high and no tip region is discernible. However, CM functions for 19 kHz show a tip, but it is located around ~32 kHz, meaning that it is shifted to frequencies higher than the probe. This CM behavior contrasts with the CAP tuning curves (dashed lines) where CF-specific activity is the norm, irrespective of probe frequency. In fact, all of the CAP tuning curves in Figure 3 show sharp tip segments. Because the CM is thought to be dominated by generators at the base of the cochlea, generally responding to inputs well below CF (Patuzzi et al. 1989a), they do not reflect the active, amplified status of the normal cochlea, except at high frequencies above ~30 kHz.

FIG. 3.

In A, we provide several examples of individual CM masking functions (solid lines) at 6 kHz. A representative CAP tuning curve (dashed lines) also at 6 kHz is appended for comparison. B–D Functions for probes at 12, 19, and 32 kHz, respectively. Only for 32 kHz is a tip observed in the CM data at the probe frequency similar to that observed for the CAP.

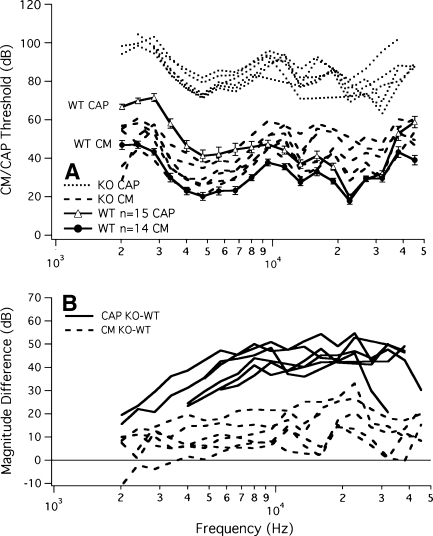
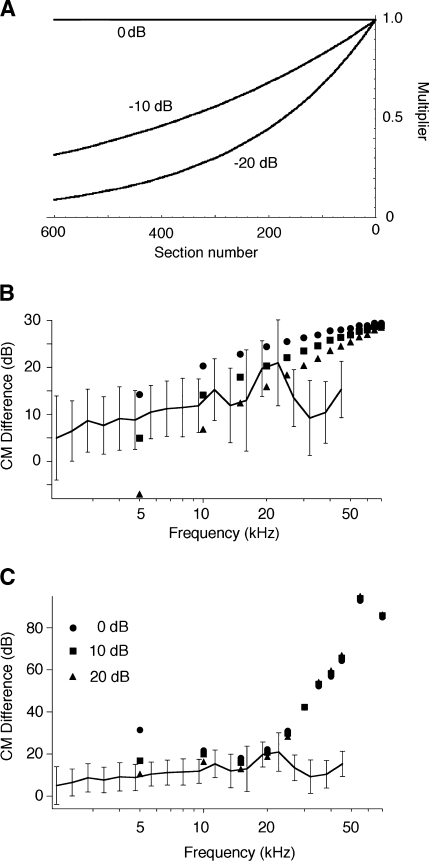
Results suggest that the CM recorded at relatively low frequencies is a passive (non-amplified) response generated by hair cells at the base of the cochlea, which in this configuration is near the recording electrode. Because these cells are responding to inputs well below CF, they produce more linear responses that are minimally influenced by cochlear amplification. If this were true, then one would predict that CM responses at lower frequencies in prestin KO mice would be similar to CM responses in WT controls. In other words, without prestin-based amplification only “tail” segments are expected to exist (Cheatham et al. 2004), and consequently, no differences should be seen between the two genotypes, except at the highest frequencies. This possibility was evaluated by recording CM isoresponse functions for a criterion amplitude of 0.1 μV rms, as shown in Figure 4A. Average CM responses and standard deviations from WT controls (solid circles, solid lines) are provided for comparison, along with average CAP thresholds (open triangles, solid lines). Even though the CM functions for KO mice (dashed lines) are only slightly elevated, the CAP thresholds (dotted lines) indicate a shift in sensitivity, attesting to the lack of amplification. Panel B provides CAP (solid lines) and CM (dashed lines) magnitude differences between mice lacking amplification and the respective mean WT responses. CM magnitude differences measured relative to WT tend to be ~12 dB at 10 kHz. If the CM were primarily reflecting quasi-linear contributions from basal hair cells responding on their tails, one would a priori expect that prestin KO and WT mice would produce similar CM responses, assuming they both had comparable numbers of functional OHCs at the base of the cochlea. This prediction has been difficult to demonstrate because KO mice suffer progressive, basal OHC loss due to some unknown mechanism (Wu et al. 2004). Hence, it is possible that the modest, relatively flat CM loss is due to the reduced number of OHC current sources in the KO. In contrast to the CM, differences in CAP thresholds are ~45 dB at 10 kHz, consistent with a loss of amplification. The modeling work presented below using suitable parameter selection predicts such a loss even with a full complement of OHCs.

FIG. 4.

A Average WT CAP thresholds (solid lines, open triangles) and WT CM isoresponse functions (0.1 μV; solid lines, closed circles). CAP thresholds from KO mice are plotted with dotted lines; KO CM with dashed lines. B The magnitude difference between average WT and KO for the CM (dashed lines) and the CAP (solid lines). Magnitude differences between WT and KO are much larger for the CAP responses.

Modeling of cochlear microphonics: spatial patterns and CM calculation

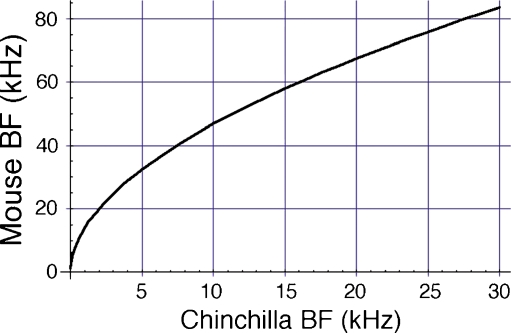
The nature of the CM response is supported by a model of CM generation specifically designed for comparing responses obtained from WT and prestin KO mice. Our purpose is to demonstrate how longitudinal interactions from contributing current sources influence the round-window-recorded CM. The excitation of individual sources is assumed to be proportional to basilar membrane (BM) displacement (He et al. 2004). Consequently, the first step is to construct spatial patterns of BM motion. One approach is to model this traveling wave motion on the basis of first principles. This, in various forms, constitutes much of the relevant modeling literature. However, a simpler method is chosen such that spatial functions are constructed from BM displacement vs. frequency data, with the usual assumption that frequencies map onto distance with a logarithmic transformation. As the basis for the simulations, we use a complete basilar membrane data set obtained by Ruggero et al. (2000) from the chinchilla cochlea (animal L208). These data need to be appropriately scaled for mice and converted from gain (millimeters per second per Pascal) to displacement (nanometers). The chinchilla-to-mouse conversion is based on the direct comparison between their respective maps as provided by the Müller et al. (2005, 2010). This relation is shown in Figure 5, in which mouse CF is plotted against chinchilla CF, assuming that corresponding CFs are located at equal percentage distances along the basilar membrane. Accordingly, the chinchilla data that were obtained at the CF = 9.5 kHz site, scale to ~46 kHz in the mouse. The equations representing the two maps and their relationship are (distance, d, is expressed in percent of basilar membrane length):

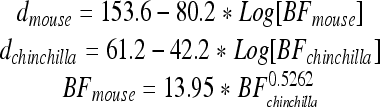1a, b, c

FIG. 5.

Conversion plot between chinchilla and mouse CFs. The plot is based on the assumption that equal percentage distances along the basilar membrane map to corresponding CFs. The data are derived from Müller et al. (2005, 2010).

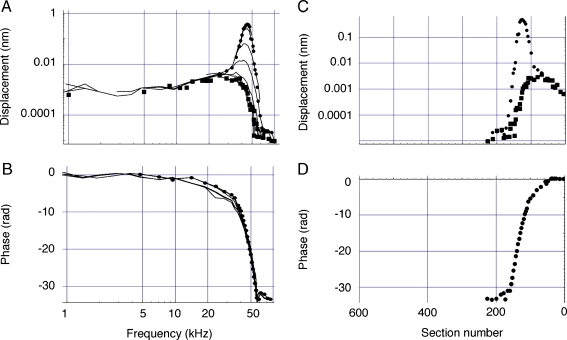
In Figure 6A, B the data upon which all modeling is based are shown as displacement and phase with thin continuous lines. These data have been converted to “equivalent” mouse measures from the results of Ruggero and colleagues. Several plots are shown that were recorded at different sound levels, from 0 to 100 dB SPL from top to bottom. The functions at all levels are plotted as if they were obtained at 0 dB SPL. This quasi-normalization permits the extraction from the data of an overall low-level response pattern (at 0 dB SPL), which is shown with closed circles. The process was necessitated by the incomplete low-level data set, which was confined to the tip region. It is our assumption that the pattern obtained at very high sound levels, 100 dB, appropriately represents the passive, non-amplified, response of the basilar membrane, in as much as these high-level responses approximate postmortem response patterns (Robles and Ruggero 2001). Accordingly, this pattern (solid squares) is taken as representing the knockout mouse response. Each symbol corresponds to an actual data point in the Ruggero data set. While there are significant differences between high- and low-level response magnitudes, the phase functions show only modest changes around CF (Robles and Ruggero 2001), which are ignored in the calculations. Hence, only one set of symbols is shown in Figure 6B; they represent both low-level (WT) and high-level (KO) phase as a function of stimulus frequency.

FIG. 6.

A, B Chinchilla basilar membrane amplitude and phase as a function of stimulus frequency and level from Ruggero et al. (2000). The original data at CF = 9.5 kHz were expressed as gain: millimeters per second per Pascal and in cycles for the phase. The plots were first converted to the mouse frequency scale with the aid of Figure 5, giving a CF = 46 kHz. The velocity plots were then converted to displacement and expressed in nanometers and radians. The best approximation of the low-level (0 dB SPL) response is shown with circles. These data points serve as the basis for all computations pertaining to wild-type mice. The 100-dB SPL plot is approximated by the squares, and these are used to represent the low-level mechanical response in knockout mice. Wild-type and knockout phase are assumed to be identical. In C and D, the frequency plots (A and B) are translated into spatial plots. Distance along the mouse basilar membrane (length ~6 mm) is represented on the abscissa as 600 sections with the round window at zero.

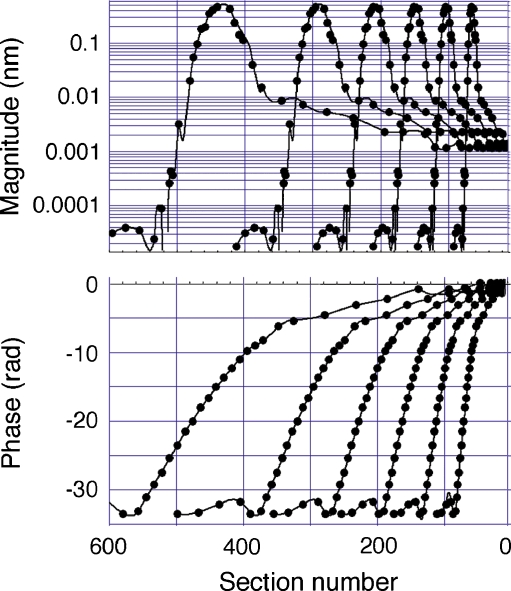
Computing the CM requires spatial magnitude and phase patterns. These are represented in our computations by 600 sections. Because the mouse basilar membrane is ~6 mm long, each section is 10 μm in length, or approximately one hair cell width. As stated previously, the prototype displacement and phase functions are based on mechanical data obtained in the chinchilla cochlea at a location corresponding to CF = ~9.5 kHz. These patterns are translated according to the Müller mouse map to peak at ~46 kHz (Fig. 6A, B), which corresponds to the x-coordinate at section 116 (Fig. 6C, D). This spatial displacement-phase pattern is generalized to any CF using a two-step process. First, the frequencies in the mouse data set that are represented by the circles in Figure 6A, B are normalized to the CF. Subsequently, the Müller function (Eq. 1a, b, c) is mapped onto this data set in Mathematica™, for other desired CFs. Results are shown in Figure 7 with circles. It is noted that this transformation naturally expands the spatial extent of the plots, which are representations of the traveling wave envelope, as CF is reduced. The spatial plots are used to compute locally generated electrical responses (see below) and to vectorially sum them in order to produce a facsimile of the CM. Since the actual data points are few, a summing of the responses for each CF would be based on a coarse raster, producing jagged results. To eliminate this problem, each spatial function, represented by a series of data points, is rerepresented using an interpolating function available in Mathematica. Such interpolating functions can be treated as any continuous analytic function. Consequently, vectorially summing responses for any CF can be done with any desired precision over the number of sections covered by a given spatial plot. The interpolated functions so obtained are also shown in Figure 7 with continuous thin lines, and these are used in all subsequent computations. It is emphasized that there is no artificial modeling involved in these computations, except for the assumptions outlined above. The original chinchilla data, expressed as gain and phase frequency plots, are simply converted to mouse displacement in the spatial domain.

FIG. 7.

Generalization of spatial plots (Fig. 6C, D) to other stimulus frequencies: 10, 20, 30, 40, 50, and 60 kHz, moving from right to left. The black circles represent the actual translation of data from Figure 6. The continuous thin lines are interpolated functions that are used as continuous, analytic functions in subsequent computations.

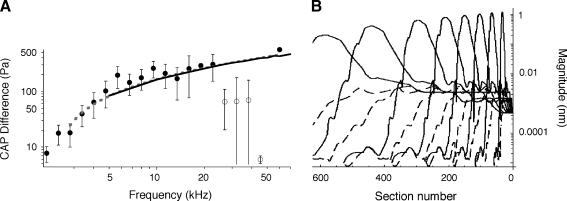
Inasmuch as the tip segments of the plots arise from the cochlear amplifier, their height (corresponding to the gain of the amplifier) is location dependent. That the gain of the cochlear amplifier is not constant can be derived from numerous sources. For example, mechanical data have been summarized by Robles and Ruggero (2001). Results obtained from prestin knockout and knockin (KI) mice (Cheatham et al. 2004; Dallos et al. 2008; Liberman et al. 2002) also demonstrate a variable loss of gain that increases with increasing frequency. Inasmuch as the actual patterns and degree of change with CF have not been established with certainty, we use our own CAP data to gauge the amount of gain provided by the cochlear amplifier at different CFs. In Figure 8A, the mean and standard deviation of the CAP threshold difference between WT and KO animals is replotted as the ratio of absolute units in Pascals. The mean data are fit with a power function, shown with dashed line. This function (Eq. 2) is used to adjust the tip segments of the WT displacement functions. The resultant spatial patterns are given in Figure 8B. The KO patterns (dashed lines) lack tip segments and are, therefore, not adjusted for longitudinal variations in gain.

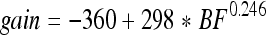2

FIG. 8.

A CAP average magnitude ratio (and ±SD) between WT and KO mice (filled circles with error bars). Four data points that are suspected as contaminated by other factors, probably hair cell dysfunction in all mice at the very base of the cochlea, are shown with open circles. These points are not used in curve fitting. The point at 60 kHz is added to the data set, inasmuch as a great deal of information suggests that at high frequencies the amplification is ~55 dB. The result of curve fitting of the data points is given by the interrupted line (Eq. 2). The heavy continuous line gives the result of model computation. B Interpolating functions at stimulus frequencies of 5, 10, 20, 30, 40, 50, 60, and 70 kHz for both WT (continuous lines) and KO (dashed lines). The plots reflect the spatial gradient of cochlear amplifier gain (as represented by the height of the tip segment above the tail) that was derived in the curve-fitting procedure in A. However, KO patterns (dashed lines) do not show any gradation because they lack tip segments.

Our assumption is that the round-window CM reflects vectorially summed hair cell contributions according to the magnitude (phase) patterns shown in Figure 8B (Fig. 7), meaning that the CM is related to the mechanical excitation pattern at a given location and input level. While this relationship occurs via the displacement versus transducer conductance function, represented by the asymmetrical Boltzmann pattern of Figure 10B, initial CM computations are performed for 0 dB SPL responses (Figs. 6, 7, and 9) without including the nonlinearity. At 0 dB SPL, all cochlear processes are linear (Robles and Ruggero 2001) with a maximum displacement amplitude of ~0.7 nm at the 9.5 kHz CF in chinchilla, which corresponds to ~46 kHz CF in mouse. Because the small-input approximation of the Boltzmann transducer function is also linear, the computation of differences between WT and KO CM responses is legitimately linear.

FIG. 10.

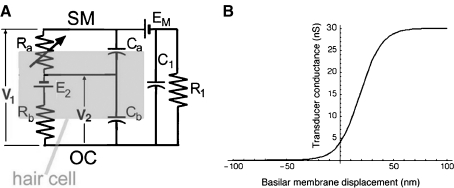
A The electrical circuit representation of a single OHC within its organ of Corti environment. The parameter values are as follows: R_a (no-stimulus value) = 256 MΩ, R_b = variable, E₂ = 80 mV, E_M = 80 mV, R₁ = 0.1 MΩ, C_a = 2 pF, C_b = 20 pF, C₁ = 0. While the capacitance associated with the extracellular space is set to zero, C₁ is included in the circuit diagram for the sake of completeness. The hair cell transducer function in B was used in the model calculations.

FIG. 9.

A The electrical attenuation patterns of signals generated at a given section, as seen at the round window (section 0). The three plots correspond to 0, 10, and 20 dB maximal attenuation. B Computational results as well as mean and standard deviation of CM data expressing decibel differences between WT and KO mice. Simulations represent computations with a full complement of hair cells contributing to the response. Different symbols are used to represent the three electrical attenuation patterns: triangles 20 dB total attenuation, squares 10 dB, and circles 0 dB. The plot in C provides computational results when summation of elementary CM components is made only between segments 200 and 600 for KO mice to simulate basal OHC loss. For reference, the mean and standard deviation of the CM data are appended. It is likely that the discrepancy between model prediction and CM difference in panels B and C is exacerbated by electrical pickup for the 4 highest frequencies due to the higher level required to elicit criterion CM in KOs and the fragility of high-frequency hearing even in WT mice.

The computed response is also modified by a spatial weighting function that reflects two contributions. The first adjustment is for electrical attenuation, whereby sources more distant from the measuring location contribute less than more localized ones (von Békésy 1960). The second adjustment reflects the recent observations that outer hair cells produce transducer currents that increase in size from apex to base (He et al. 2004; Housley and Ashmore 1992; Ricci et al. 2003). These factors are combined in an ad hoc spatial attenuation function that arbitrarily produces an exponential gradient, with maximum attenuation of a signal produced at section 600, as shown in Figure 9A. Since the electrical attenuation along the mouse cochlea is unknown, we present responses with total attenuations of 20, 10, and 0 dB in order to examine the effects of different spatial weighting values on the round-window CM recorded at section 0. It should also be stated that any electrical filtering effect due to the interconnected RC network used to represent the organ of Corti (Strelioff 1973; Mistrik et al. 2009) will influence both WT and KO responses equally and is, therefore, immaterial for the purposes of the present work.

The computational strategy is as follows: At a given stimulus frequency and level, the appropriate spatial amplitude and phase patterns, represented by the interpolation functions, are computed as above (Fig. 8B). The local CM contribution for any section is proportional to the local amplitude and is affected by the local phase. For computational purposes, it is represented by:

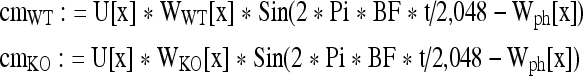3a, b

In the equations, cm_WT and cm_KO are the local CM responses in time (t), W_WT[x] and W_KO[x] are the amplitudes along the spatial pattern, and W_ph[x] is the phase, all at section x. The local contribution is weighted by the attenuation factor (U[x]), and all individual contributions are vectorially summed in Mathematica™. The result is a sine wave, the fundamental Fourier component of which is computed over five cycles. The computation provides one CM data point for WT and one for KO.

Model computations are presented over a range of stimulus frequencies (5 kHz steps between 5 and 70 kHz) for the difference between normal (WT) and no-amplification (KO) cases. Different symbols are used to show the effect of the three different attenuation schemes (Fig. 9B). For reference, the means and standard deviations of the CM data from Figure 4B are also included. While measurements were taken at frequencies down to ~2 kHz, computations are made down to only 5 kHz, approximately the lowest discernible CF in the mouse. Computations extend up to the highest mouse frequency, ~80 kHz, which is beyond the highest-tested frequency. We note several interesting outcomes. Using the function (Fig. 8A) derived from the CAP data shows good agreement with the experimental data below 30 kHz (circles). In addition, attenuation has the greatest effect at the low frequencies, while all symbols converge at the highest frequencies. High (20 dB total, triangles) attenuation produces computational results that can be “better” than the data, i.e., producing significantly smaller WT–KO differences. However, the 10-dB attenuation (squares) yields computational results that are indistinguishable from the data below 30 kHz. The modeling procedure can also be used to check its validity by predicting CAP WT–KO differences. To this end, the raw interpolation functions were summed over the tip-segment alone, with no phase shifts used. This summation is legitimate, inasmuch as threshold-level CAP responses are mediated by neurons emerging from the spatial extent of the tip (Dallos and Cheatham 1976b; Özdamar and Dallos 1976). The resulting function is included in Figure 8A as a heavy black line. The agreement validates our computational approach.

We also modeled the KO response in the presence of basal outer hair cell loss, which is prevalent in KO mice at the base of the cochlea (Liberman et al. 2002; Wu et al. 2004) and shown in Figure 9C. This was accomplished, as an example, by only summing the KO CM contributions between sections 200 and 600, as if basal OHCs did not contribute to the response. Results were again obtained for three spatial attenuation values. There are interesting interactions among hair cell loss, attenuation and gradient of amplification. We also note that the predicted threshold increase is very large at high frequencies. This is fully expected as there is no contribution from the high-frequency, 0–200 segments in KOs.

Circuit considerations

As a result of some experimental manipulations, the round-window CM is reported to increase while the cochlear output, i.e., CAP or single-unit responses decrease. A popular explanation for these divergent responses can be found in the suggestion (Fex 1959) that the basolateral resistance of hair cell membranes is reduced due to experimental manipulation. For example, during stimulation of the crossed olivocochlear bundle, the CM increases because the extracellular current is assumed to increase. We examine this proposal in light of recent data on hair cell characteristics. The discussion pertains to OHCs as they are considered to be the dominant source of extracellular current and thus of the CM (Dallos and Cheatham 1976a). The electrical equivalent circuit of an OHC is shown in Figure 10A. The cell is represented by the variable transducer resistance (R_a) and the parallel capacitance (C_a) of the apical cell membrane, the resistance (R_b) and capacitance (C_b) of the basolateral membrane, and the electrochemical driving force (E₂). The entire external circuit in which the cell is embedded is symbolized by a parallel resistance (R₁) and capacitance (C₁), along with the scala media driving voltage (E_M). V₂ is the receptor potential of the cell, while V₁ represents the CM component produced by the cell. Simple circuits of this sort have been analyzed by numerous investigators, for example, Dallos in 1984 (Dallos 1984).

In the computations that follow, the input to the circuit is sinusoidal modulation of R_a about a no-stimulus resting value. Transducer conductance (G_a = 1/R_a) is assumed to vary as a first-order Boltzmann function, which is represented in Figure 10B as transducer current. Appropriate numerical values are chosen to represent basal (high-frequency) OHCs. Transducer conductance is derived from whole-cell recordings in the hemicochlea (He et al. 2004; Jia et al. 2006). The maximum transducer conductance is 30 nS, and in low external calcium, the no-stimulus conductance is ~13% of maximum. Thus, the resting value of R_a is 256 MΩ. Other parameters, obtained from Housley and Ashmore (1992) and Dallos (1983, 1984), are provided in the figure caption. Kirchoff node equations for the circuit are solved in Mathematica™.

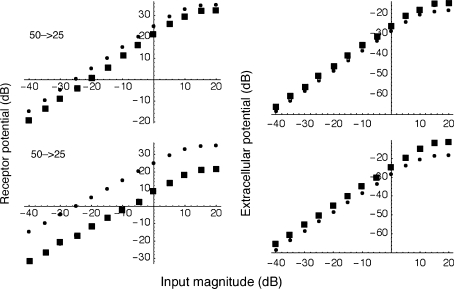
In Figure 11, two example computations are shown for low-frequency (100-Hz) inputs where the effects to be examined are the largest. The plots show input–output functions for both receptor potentials (V₂; left column) and extracellular potentials (V₁; right column) when the basolateral membrane resistance is shifted from 50 to 25 MΩ or from 50 to 5 MΩ. We note that receptor potential and extracellular potential (CM) both change, but in opposite directions. Thus, the receptor potential shows a large decrease, while the CM increases by a few decibels. This single-cell example can be generalized by building the circuit into each model section. The result is as expected, showing modest increases in the simulated CM. In vivo, the decreased receptor potential would yield lower amplification and a consequent decrease in CAP, consistent with experimental observations.

FIG. 11.

The left panel shows simulated receptor potentials at 100 Hz plotted versus input magnitude for two cases: when the basolateral membrane resistance is reduced from 50 to 25 MΩ (top) and when it is reduced from 50 to 5 MΩ (bottom). Companion plots for the corresponding extracellular potential are shown on the right. Notice that the AC receptor potential (left; the presumed driving force for amplification) decreases as basolateral resistance decreases (squares), while the extracellular potential (right), the CM, increases (squares). In all panels, the small circles are associated with the original, resting condition (50 MΩ); the larger squares with the altered condition, either 25 or 5 MΩ.

Discussion

Use of the CM in assessing the state of the cochlea

Although the CM response has been difficult to interpret, its judicial use can assist analysis of cochlear function in mouse models of hearing. For example, CM responses to single and two-tone inputs indicate that prestin KO mice produce nonlinear responses including harmonics, combination tones, and two-tone suppression (Cheatham et al. 2006, 2004; Liberman et al. 2004). The relative degree of nonlinearity is comparable to that in controls. CM pseudo-transducer functions and CM isoresponse functions (Fig. 4A) are also WT like, implying that mechanoelectrical transduction is operating normally in mice lacking prestin. This prediction was later confirmed by measuring transducer currents produced by individual OHCs in both prestin KO and KI mice (Dallos et al. 2008; Jia et al. 2006). That the low-frequency round-window CM can be used to assess OHC mechanoelectric transduction is consistent with the work of Patuzzi and Moleirinho (1998) and Patuzzi et al. (1989b). A nonlinear system identification procedure has even been used to model cochlear responses in humans with potential clinical applications for monitoring changes in the peripheral auditory system (Krishnan and Chertoff 1999). All of these reports support using the CM as an analytical tool.

Modeling the spatial summation of extracellular currents shows that the resultant voltage recorded at the round window (CM) is dominated by nearby sources. In fact, Patuzzi et al. (1989a) showed that amputation of the apical two turns of the guinea pig cochlea did not change the CM response to a 1-kHz tone burst recorded at the round window. Additional results in mouse (Fig. 3) indicate that it is only for high frequencies, above ~30 kHz in the mouse, that CM interference functions show a tip at 32 kHz, the probe frequency. This is also the stimulus frequency at which CM input–output functions show saturation (Cheatham et al. 2005). At lower frequencies, the functions continue to grow with increasing level, as more hair cells begin to contribute to the CM response. According to the arguments of Özdamar and Dallos (1976), the recorded responses in most extant experiments are produced by cells operating on the tails of their respective tuning curves. As a result, the CM does not generally reflect the influence of the cochlear amplifier, inasmuch as tail responses are not amplified. Even when the amplifier is shut down, as in the case of a prestin KO with relatively good OHC preservation, the CM appears near normal in magnitude, as shown in Figure 4. The large amplified peaks around CF, even if they are >40 dB above the tails, do not usually dominate the round-window CM due to the rapidly changing phase, which produces cancelation. Hence, the remaining contributions from the tail regions are commensurate for the two genotypes.

It is useful to compare these results with earlier publications (Cheatham and Dallos 1982; Dallos et al. 1974) in which first-turn differential electrodes were used to obtain CM simultaneous masking functions in guinea pig. The use of an electrode pair was introduced in an attempt to restrict the number of hair cells contributing to the gross cochlear potentials (Dallos 1969; Tasaki and Fernandez 1952; Tasaki et al. 1952). These earlier data reveal that the tips of the CM masking functions were always above probe frequency even when the latter was thought to be at the best frequency of the recording location. This differs from the data in Figure 3 for 32-kHz probes. Because the guinea pig data were recorded at some distance from the round window and because placement of the two electrodes was never perfect, hair cells basal to the recording location were probably not prevented from contributing to the response. As a result, all probe tones were probably lower than the CFs of the OHCs dominating the CM. It is also acknowledged that using the CM to determine the best frequency of the recording location will vastly underestimate this metric (Dallos 1973a).

Implications of modeling results for the RW-recorded CM

Since circuit models of the cochlear electrical network have been analyzed by several investigators (Dallos 1973b; Johnstone et al. 1966; Mistrik et al. 2009; Strelioff 1973) and models of cochlear mechanics abound, it was not our purpose to construct a marriage of such models in order to analyze RW-recorded CM. Instead, we used extensive chinchilla basilar membrane data (Ruggero et al. 2000) to represent the frequency-dependent excitation of cochlear hair cells. This approach is legitimate, inasmuch as low-level basilar membrane displacement and auditory nerve response patterns are virtually indistinguishable around the CF (Narayan et al. 1998).

The principal results of the modeling study are summarized in Figure 9. The main finding is that at the round window (section 0), differences between simulated WT and KO CM responses are small for low stimulus frequencies. If 10-dB attenuation is used (Fig. 9B, squares), computational and experimental results overlap up to ~30 kHz. This finding supports and explains the results of physiological studies (Cheatham et al. 2004; Dallos et al. 2008; Liberman et al. 2002). It also reaffirms that low-frequency CM is not a useful measure of cochlear amplification. The model suggests, however, that if it were possible to measure CM at frequencies that peak near the base of the cochlea and if hair cell loss were not a factor, the KO CM would be somewhat smaller than the amplified response and, in the case of basal OHC loss, the predicted decibel difference would approach high values.

An interpretation of some paradoxical results in the literature

Differences in generation and summation of the round-window CM and the CAP may assist interpretation of some seemingly anomalous results in the literature. The CAP, measured anywhere in or around the cochlea, is a frequency-specific response at low sound levels (Dallos and Cheatham 1976b; Özdamar and Dallos 1976; Teas et al. 1962). It reflects largely synchronized firings of a small group of nerve fibers arising from the spatial region tuned to the stimulus frequency. In other words, at low levels, it is intimately associated with the tip region of basilar membrane response and, consequently, with the cochlear amplifier. In contrast, the CM recorded from the RW reflects the spatial summation of hair cell receptor currents. Inasmuch as these currents vary in amplitude and phase according to the spatial properties of the traveling wave, their summation can produce peculiar behaviors with the result that the CM generally reflects contributions from the non-amplified tail portion of mechanical excitation of hair cells.

Differential effects of manipulating the state of the cochlea upon intracellular receptor potentials (that affect amplification) and extracellular currents (that sum as the CM) can also produce unexpected results. For example, activation of the crossed olivocochlear bundle by electric shocks or perfusion of the perilymphatic space with acetylcholine has similar consequences, and application of salicylate to some extent mimics these effects. Single-unit and compound action potential thresholds are increased by ~20 dB, while high-level responses remain unchanged. These changes principally affect the sharply tuned tip region of neural tuning curves, such that the low-frequency tail is not significantly altered (reviewed in Guinan 1996). Later measurements show that these behaviors are recapitulated in BM responses (Murugasu and Russell 1996; Russell and Murugasu 1997). This is not surprising in light of the similarity between neural and BM response patterns (Narayan et al. 1998). Intracellular responses from inner hair cells (IHCs) behave similarly, but their resting potentials are not affected (Brown and Nuttall 1984).

The efferent-mediated decrease in BM and neural responses around CF is explained by a reduction in efficacy of cochlear amplification (Murugasu and Russell 1996). The assumed mechanism is a hyperpolarization of OHCs (Art et al. 1984; Flock and Russell 1976; Housley and Ashmore 1992) and a consequent unfavorable shift in the operating point of OHC motility (Hallworth et al. 1993; Santos-Sacchi 1991; Santos-Sacchi and Dilger 1988), which results in reduced amplification. In contrast to BM, neural, or IHC responses, the CM is not decreased. In fact, with stimulation of the crossed olivocochlear bundle, the CM can increase (Fex 1959, 1962; Klinke and Galley 1974; Patuzzi and Rajan 1990; Wiederhold and Kiang 1970). Application of salicylate also results in contrasting behavior between neural and CM responses (Fitzgerald et al. 1993), i.e., large reductions in the CAP are accompanied by relatively small changes in the CM. In fact, CM changes due to efferent activation or salicylate application are highly variable (e.g., Klinke and Galley (1974), +3–4 dB at 8 kHz; Fitzgerald et al. (1993), +10 dB at 1 kHz; Murugasu and Russell (1996), highly variable; Kujawa et al. (1992), no significant change). The increase in CM was first explained by efferent-mediated hyperpolarization and increase in the conductance of the OHC basolateral membrane with consequent increase in current flux into the extracellular space (Fex 1959). This suggestion was widely adopted (Guinan 1996). Salicylates also increase OHC basolateral membrane conductance (Shehata et al. 1991) and can produce CM increase by mechanisms similar to those due to efferent stimulation (Fitzgerald et al. 1993). In addition, salicylates can reduce amplification by directly interfering with prestin’s function (Kakehata and Santos-Sacchi 1996; Oliver et al. 2001).

By keeping in mind the distinction between the CM and the CAP, it is possible to avoid inappropriate conclusions (Peleg et al. 2007) that question the original and still valid premise that the round-window-recorded CM primarily represents summed OHC receptor currents. Because the latter are dominated by basal generators responding more linearly on the tails of mechanical excitation patterns, these responses do not usually reflect changes in cochlear amplification. Hence, the implications of this work include constraints on the use of the CM, explanation of some of its peculiar behavior, and use of a relatively simple, physiology-based model of computation.