Variables associated with odds of finishing and finish time in a 161-km ultramarathon

Abstract

We sought to determine the degree to which age, sex, calendar year, previous event experience and ambient race day temperature were associated with finishing a 100-mile (161-km) trail running race and with finish time in that race. We computed separate generalized linear mixed-effects regression models for (1) odds of finishing and (2) finish times of finishers. Every starter from 1986 to 2007 was used in computing the models for odds of finishing (8,282 starts by 3,956 individuals) and every finisher in the same period was included in the models for finish time (5,276 finishes). Factors associated with improved odds of finishing included being a first-time starter and advancing calendar year. Factors associated with reduced odds of finishing included advancing age above 38 years and warmer weather. Beyond 38 years of age, women had worse odds of finishing than men. Warmer weather had a similar effect on finish rates for men and women. Finish times were slower with advancing age, slower for women than men, and less affected by warm weather for women than for men. Calendar year was not associated with finish time after adjustment for other variables.

Introduction

The Western States Endurance Run (WSER) is the premier 161-km trail running competition in the world. Although no longer the largest running event of this distance, it remains among the largest with nearly 400 runners participating each year. It is also one of the most challenging 161-km runs with 5,500 m of climb, 7,000 m of descent, altitude reaching 2,667 m, the possibility of encountering snow in the early sections of the course, and the likelihood of high temperatures later in the run.

The seemingly accidental origin of the WSER dates back to 1974 when a horse race over a course similar to the present-day WSER was completed on foot by a man who would have participated on horseback had it not been for his horse going lame (Ainsleigh 2004; Klein 1998). By 1979, the run had become an international event and it had grown to its present limit of nearly 400 runners by 1984. Since 1986, the course has been essentially unchanged and complete data on starters and finishers have been maintained.

In preceding papers, we detailed some characteristics of WSER participants (Hoffman 2008; Hoffman and Wegelin 2009) and the trends in participation and performance over the history of the event (Hoffman and Wegelin 2009). We have also analyzed the participation and performance trends of all 161-km ultramarathons in North America (Hoffman 2010; Hoffman et al. 2010b). From this work, age (Hoffman 2010; Hoffman and Wegelin 2009), sex (Hoffman 2010; Hoffman and Wegelin 2009), and body composition (Hoffman 2008) have been shown to be associated with performance in 161-km ultramarathons. Ambient temperature is a factor that has been shown to affect marathon performance (Ely et al. 2007a, b, 2008; Trapasso and Cooper 1989; Zhang et al. 1992), but it has not been examined for ultramarathons. Furthermore, a large-scale and focused analysis to define other factors associated with finishing and how fast one completes an ultramarathon has not been performed. Such an analysis is of interest in delineating factors affecting physiological capacity in extreme endurance activities under conditions that could not be replicated in a non-competitive laboratory environment. And in an annual event continuing across a time span of over two decades, the possibility of a historical trend must be acknowledged and its effect sifted out, if possible, from the other variables.

Thus, in this paper, we assess the relationship of variables publicly available at the start of each year’s WSER (age, sex, previous WSER experience and performance, and calendar year), along with race day ambient temperature, with the odds of finishing the run. And, among those who finished in any year, we assess the relationship between these variables and finish time.

Methods

Data source

Race results posted on the WSER website were used to compile a spreadsheet covering the races between 1986 and 2007 inclusive. Variables included the year of the event, name, sex, and age of each starter, whether the starter finished or dropped out, and finish time for those who finished. In addition, the number of WSER races finished by each starter from 1974 to 1985 was compiled. Information about who had started the race but not finished was not available for this time period. Discrepancies in name, age, and sex were reconciled to the extent possible as described earlier (Hoffman and Wegelin 2009).

Statistical analyses

A linear spline was computed for age with knots at the 25th and 75th percentiles to permit the computation of piecewise linear relationships between outcomes (i.e., log odds of finishing and finish time) and age, and thereby to accommodate differing effects of age during youth, middle and advanced age (Gould 1993).

Ambient temperature data for Auburn, CA (the location of the finish) from the start date of each yearly event were obtained from the National Climatic Data Center. Ambient temperature data were not available at other course locations, and although minimum and maximum temperatures were known to be more extreme at other locations on the course, it was felt that the temperatures at the finish would reflect the overall temperature trends. Minimum, maximum, and mean temperatures were tabulated, but regression models included only one of these variables at a time because of the likelihood that they were highly correlated with each other. The measure of temperature that yielded greatest statistical significance was included in reported models.

Each starter was coded as a first-timer at his or her first start after 1985. For those who started more than once after 1985, at the second and subsequent starts the individual’s past finish rate (proportion of starts finished from 1986 to the previous year inclusive) was computed. For finishers who were not first-timers, if the finisher had failed to finish his or her previous WSER start, the finisher was coded as “previous drop” for that year.

For those who finished after 1985, for each year when they finished, a measure of performance relative to his or her gender was computed from finish time (t) as

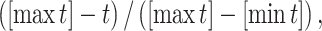where the maximum (max t) and minimum (min t) finish times were computed separately each year for men and women. Thus, the first finisher for each gender and each year obtained a score of 1, the last finisher a score of 0, and all other finishers obtained scores between 0 and 1 that reflected their performance relative to their peers. Subsequently for each finisher, his or her “first-time” status, “previous drop” status, or previous relative finish performance was recorded.

Generalized linear mixed-effects (GLME) regression models were computed to assess the effects of individual variables on the odds of a starter completing the race and on the predicted finish time of a finisher. Regression models were computed rather than statistics that include only two variables at a time so that assessments of the effects of variables would simultaneously take into account and adjust for all other available variables. Models with logit link were employed for odds of finishing and with identity link for finish time (McCullagh and Nelder 1989). Random effects for starter and year were included to account for correlation that might be caused by the same individual starting the WSER on more than one year or by similarities within year not accounted for by available covariates (Diggle et al. 2002).

In models for the odds of finishing, the following were considered as possible predictors: sex and age of the starter, whether or not the starter had finished a WSER event before 1986, starter’s “first-time” status or finish rate since 1986, ambient temperature on the day of the run, and calendar year. All starts between 1986 and 2007 inclusive were used for computing these models. In models for finish time, in addition to the above variables, the finisher’s “previous drop” status or relative performance for the previous race in which the finisher had participated was considered. Thus, in models for finish time, at each year, and for each finisher, either the relative performance at the previous WSER was defined or the finisher had “first-timer” or “previous drop” status. All finishes between 1986 and 2007 inclusive were used for computing these models.

Statistical significance of fixed effects was assessed by the Wald test, and of random effects by the likelihood ratio test. Main effects were included in regression models if p < 0.05. The interaction of two variables was considered only if both the main effects individually satisfied p < 0.05. If an interaction between two main effects satisfied p < 0.05, it was included in the model. Subsequently, those main effects were retained even if inclusion of their interaction caused a main effect to no longer satisfy p < 0.05. An indicator (yes/no) variable for each starter’s “first-time” status was included in all models regardless of its p value and similarly an indicator variable for each finisher’s “previous drop” status was included in all models for finish time.

Coefficients, standard errors, Wald statistics, and p values from the final regression models are reported in tabular format. From these models, average probabilities of finishing and average finish times were computed (Diggle et al. 2002). Subsequently, graphical displays were constructed to illustrate the relationships between explanatory variables and outcomes for typical levels of the explanatory variables.

Results

From 1986 to 2007, there were 8,282 starts by 3,956 different individuals (3,253 men, 703 women) and 5,276 finishes by 2,933 different individuals (2,437 men, 496 women). Complete data were available for all starters and finishers. Minimum temperatures ranged from 11.1 to 22.0°C, mean from 13.8 to 30.0°C, maximum from 15.5 to 37.8°C. Minimum, maximum, and mean temperatures were highly correlated (minimum with mean, r = 0.89; minimum with maximum, r = 0.65; mean with maximum, r = 0.90). Both the mean and maximum were exceptionally low in 1991, which skewed the distributions of these variables. Minimum temperature, on the other hand, had no outliers and yielded the smallest p values in regression models. Consequently, the minimum temperature was used in reported models.

For 13.3% of starts and 7.8% of starters, the starter had finished the WSER before 1986; in 52.3% of starts, the runner had started a previous WSER since 1985 and thus possessed a past finish rate. 48.1% of finishes corresponded to the finisher’s first start since 1985. In 12.6% of finishes, the finisher had started the WSER since 1985, but had dropped out of his or her most recent WSER event. Thus, the remaining 39.3% of finishes had a previous finish time for the same runner. For these, the relative performance at previous WSER start was computed and employed in the regression model.

Between the years 1986 and 2007, the youngest starter was 18 years and the oldest was 75 years. The quartiles of age were 38, 44, and 50 years. Accordingly, relationships with age were modeled as piecewise curves with different coefficients for age intervals 18–38, 38–50, and 50–75 years.

The coefficients of the regression model for odds of finishing are presented in Table 1. Coefficients for first starts after 1985 and for starters with a WSER history since 1985 represent differences from the constant term. Because men constituted the majority of starters, main effects represent the effects for men, whereas the coefficients for women represent differences from men.

Table 1.

Coefficients of the regression model for odds of finishing

Effect	Coefficient	Standard error	Coef/SE	p
Calendar year	0.052	0.011	4.823	<0.001
First time since 1985	0.116	0.055	2.087	0.037
Proportion of previous starts finished since 1986	0.877	0.096	9.169	<0.001
Female	−0.118	0.106	−1.109	0.267a
One year greater age within 38–50-year interval	−0.039	0.007	−5.546	<0.001
One year greater age above 50 years	−0.088	0.010	−9.056	<0.001
Minimum ambient temperature (°C)	−0.080	0.018	−4.347	<0.001
One year greater age within 38–50-year interval × female	−0.036	0.016	−2.293	0.022
Proportion of previous starts finished since 1986 × calendar year	0.069	0.015	4.473	<0.001
One year greater age within 38–50-year interval × calendar year	−0.002	0.001	−2.097	0.036

Positive coefficients increase and negative coefficients decrease the odds of finishing. Specifically, the coefficient for a dichotomous variable (first-timer or female) is added directly to the log odds of finishing. The coefficient for a quantitative variable is multiplied by a difference in the variable’s value (e.g., a difference in years for an age variable or a difference between zero and one for proportion of previous starts finished since 1986) and this product is added to the log odds of finishing. The log odds are related to the probability by log odds = log(p/(1 − p))

^aThe main effect for female gender remains in the model because it was statistically significant before the addition of its interaction with age, as explained in the “Methods”

Factors that improved the odds of finishing included being a first-time starter at the WSER, having a higher finish rate if one had previously started the WSER, and starting in a later calendar year. Factors that adversely affected the odds of finishing included being a woman, advanced age above 38 years, and warmer weather.

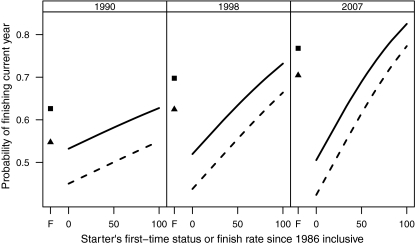
The effects, on the predicted probability of finishing, of calendar year, gender, and the starter’s first-time status or proportion of past WSERs finished, are shown in Fig. 1. The three panels provide snapshots of representative years, indicating the effect of the starter’s sex and past finish rate or first-time status at a point in WSER history. The differences between the panels indicate the way these effects changed across the history of the WSER. The point symbols on the left of each panel indicate the finish probability of a first-time starter (with no WSER experience since 1985), whereas the smooth curves in each panel demonstrate the effect of an experienced starter’s past finish rate on his or her predicted probability of finishing. Year 1990 is the first year displayed, because not until 1990 could finishers possess a diverse range of finish records since 1986. Year 1998 is displayed because it lies approximately halfway between 1990 and the latest year under study.

Fig. 1.

Predicted probability of finishing as a function of calendar year, sex, and a starter’s first-time status (“F”) or past finish rate. Squares and solid curves indicate men; triangles and dashed curves represent women. Probabilities are for an average male starter aged 44 years at 16.3°C minimum ambient temperature

The most marked effect in Fig. 1 is that, within each panel, the smooth curves slope upward from left to right. This reflects the fact that, as expected, the greater the starter’s personal past WSER finish rate the more likely he or she is to finish the current race. A comparison between panels, however, illustrates a historical difference: a first-time starter’s probability of finishing increased between 1990 and 2007, but the finish probability of a starter with a 100% past finish record increased more rapidly. In 1990, a first-timer’s probability of finishing was roughly equal to that of a starter with a 100% finish record whereas by 2007, those with a 100% finish record were substantially more likely to finish than a first-timer. The change across panels at the leftmost end of the smooth curve indicates that the finish probability of a starter with a history of starting and never finishing (zero on the horizontal axis) decreased across the years. But for past finish rates above approximately 33%, the level of the curve increases across the years, indicating that the finish probability of a starter with a history of finishing the WSER at least one-third of the time increased over the history of the WSER. The better the starter’s past finish history, the more rapid the historical increase in probability of finishing. Thus, the finish probability of starters with a history of finishing at least three-fourth of the time increased more rapidly across the years than did the finish probability of a first-timer. By 2007, first-timers’ finish probabilities were no longer roughly equal to that of starters with a perfect finish record, but rather to those who had finished 76% of WSER events since 1985. The effect of starter’s WSER history on the starter’s predicted probability of finishing did not differ between men and women.

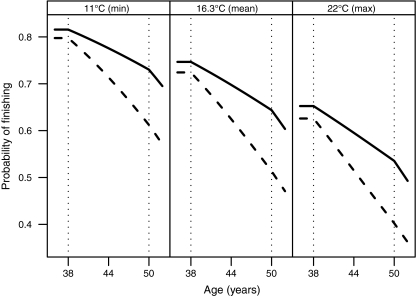
The effects of age, temperature, and sex on a starter’s predicted probability of finishing are shown in Fig. 2. While warmer weather was associated with a reduced probability of finishing, there was no evidence that heat affected women differently from men. No effect of age was found during the first quartile (18–38 years) and the difference in probability of finishing between men and women in that quartile, although visible in the figure, was not statistically significant. Between ages 38 and 50, however, an increase in age was associated with a decreased probability of finishing, and women’s probability of finishing dropped more quickly over this interval. Probabilities of finishing dropped more quickly after age 50, but across this age range, men and women experienced the same decrease with advancing age.

Fig. 2.

Predicted probability of finishing as a function of age, sex, and ambient temperature. Solid curves represent men and dashed curves represent women. Vertical dotted lines mark the first and third quartiles of age, where the model allowed the slope to change as described in “Methods”. Probabilities are for an average starter who had not started since 1985 (a “first-timer”). The three panels correspond to the least, average, and greatest values of minimum air temperature that occurred among the 22 yearly WSER events under consideration. Probabilities are adjusted to 1996 rates; for other years the pattern is adjusted up or down as shown in Fig. 1. The display has been truncated after 60 years because extrapolation of results to the small population of WSER starters above that age would likely be inaccurate. Probabilities for starters who had previously started since 1985 were similar, but adjusted up or down as shown in Fig. 1

A very small and barely statistically significant interaction was found between the calendar year and the effect of age during the 38–50-year interval. This relationship is not displayed herewith, as we do not deem it practically significant. In addition, we note that finishing or not finishing a WSER event before 1986 was not associated with finishing an event from 1986 to 2007.

The coefficients of the regression model for finish time are presented in Table 2. Factors related to a shorter finish time included a better relative performance at the previous WSER, having a WSER finish prior to 1986 and having finished more of one’s previous WSER starts. Factors associated with a longer finish time included being a woman, advanced age, and warmer weather. Unlike the odds of finishing, we found no relationship between calendar year and finish time after adjustment for other variables, and no difference between the sexes in the relationship between age and finish time.

Table 2.

Coefficients of the regression model for finish time

Effect	Coefficient	Standard error	Coef/SE	p
First time since 1985 (constant)	24.060	0.545	44.131	<0.001
Previous drop (constant)	18.490	1.399	13.216	<0.001
Finished previous start (constant)	24.160	0.561	43.030	<0.001
Relative performance at previous start (for those who finished the previous start)	−1.725	0.310	−5.566	<0.001
Female	1.347	0.123	10.968	<0.001
One year greater age up to 38 years	0.043	0.015	2.840	0.005
One year greater age within 38–50-year interval	0.167	0.010	16.375	<0.001
One year greater age above 50 years	0.122	0.018	6.857	<0.001
Minimum ambient temperature (°C)	0.081	0.039	2.089	0.037
Finished WSER before 1986	−4.302	1.509	−2.851	0.004
Proportion of previous starts finished since 1986	−1.821	0.317	−5.750	<0.001
Finished WSER before 1986 × first time since 1985	−0.533	0.219	−2.436	0.0148
One year greater age up to 38 years × previous drop	0.139	0.036	3.836	<0.001
Relative performance at previous start × minimum ambient temperature (°C)	0.070	0.031	2.263	0.0236
Relative performance at previous start × proportion of previous starts finished since 1986	−2.198	0.894	−2.459	0.0139
Female × minimum ambient temperature (°C)	−0.047	0.023	−2.047	0.0407
One year greater age up to 38 years × finished WSER before 1986	0.083	0.040	2.088	0.0368
One year greater age within 38–50-year interval × proportion of previous starts finished since 1986	0.099	0.028	3.522	<0.001
One year greater age above 50 years × finished WSER before 1986	0.080	0.033	2.408	0.016

The constants apply to the three categories into which all finishes are sorted each year. Subsequent coefficients apply equally to all finishes except where noted explicitly. Positive coefficients increase and negative coefficients decrease the average finish time. Specifically, the coefficient for a dichotomous variable (female or finished WSER before 1986) is added directly to the average finish time. On the other hand, the coefficient for a quantitative variable is multiplied by a difference in the variable’s value and this product is added to the average finish time

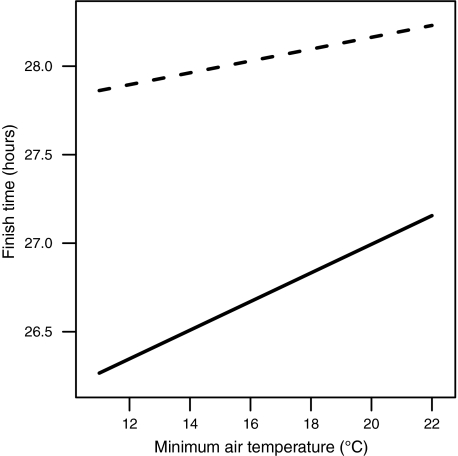
Although women finished slower than men on the average, the size of the difference varied with air temperature, in that women were less affected by hot weather than men. Average finish times by gender and air temperature are shown in Fig. 3.

Fig. 3.

Average finish time as a function of ambient temperature and sex, for individuals finishing the first WSER event that they started after 1985. Solid curves represent men and dashed curves represent women. Estimates are adjusted to represent average men and women aged 44 with no WSER finish before 1986

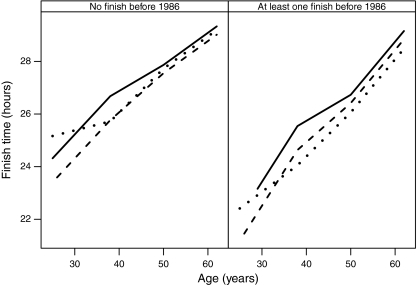
Increased age was associated with longer finish times, but the relationship between age and finish time differed according to two other variables: whether the finisher had finished a WSER before 1986 and, for those who had previously started the WSER since 1985, the proportion of past WSERs that the finisher had finished. The complex interaction of these variables with respect to finish time is shown in Fig. 4.

Fig. 4.

Average finish time as a function of age, for finishers for whom previous relative performance was not defined. Dotted curves represent “first-timers,” dashed curves represent those who had finished 50% of their starts since 1986, but not their most recent start, and solid curves represent finishers who had started at least once, but failed to finish each start since 1986. Estimates are adjusted to represent an average man, subject to 16.3°C minimum air temperature

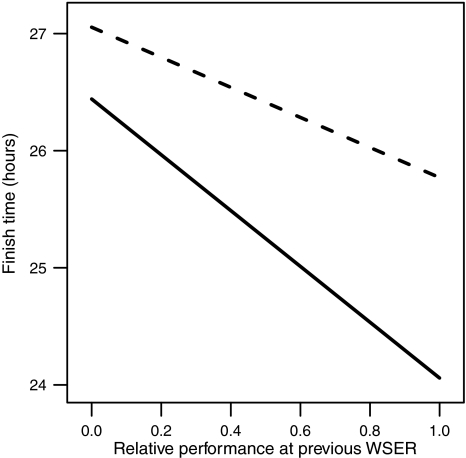
For current finishers who had also finished their previous WSER start, better performance at the previous finish was associated with a shorter finish time at the current finish, as expected. But this relationship was stronger for those who had finished a greater percentage of their previous starts. This relationship is shown in Fig. 5.

Fig. 5.

Average finish time as a function of relative performance at previous WSER start and percent previous starts finished since 1986, for finishers for whom previous relative performance was defined. The solid line represents those who had finished 100% of previous starts, the dashed line those who had finished 50% of previous starts. Finishers who finished 0% of their previous WSER starts since 1985 are represented in Fig. 4. Estimates are adjusted to represent an average man aged 44 with no WSER finish before 1986, subject to 16.3°C minimum air temperature

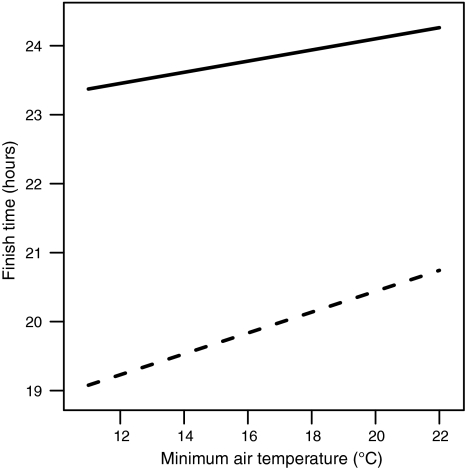
Although warmer weather was associated with slower finish times, the effect was more marked in faster runners. This is illustrated in Fig. 6. For current finishers who finished last at their previous WSER, one additional degree was associated with an approximately 0.34% longer finish time, whereas for those who had finished first at their previous WSER, the difference was approximately 0.77%.

Fig. 6.

Interaction between previous relative performance and minimum air temperature in the prediction of finish time. The solid line represents current finishers who finished last at their previous WSER, and the dashed line represents current finishers who previously finished first. Estimates are adjusted to represent an average man aged 44 who had finished all of his previous WSER starts

Discussion

The present study made use of publicly available information to model the odds of finishing and finish time in the WSER. Every starter and finisher from 1986 to 2007 was used in computing these models. While WSER is no longer the largest running event of this distance, it is the premier 161-km ultramarathon and accounted for around 20% of all 161-km ultramarathon finishes in North America through 2008 (Hoffman et al. 2010b; Hoffman and Wegelin 2009). Furthermore, around 35% of those who had finished a 161-km ultramarathon in North America prior to 2009 had completed the WSER (Hoffman et al. 2010b; Hoffman and Wegelin 2009). Therefore, a focused analysis of this event captures a sizable proportion of those participating in running events of this distance.

Average annual finish rates at the WSER have ranged from 51 to 80% since 1986 (Hoffman and Wegelin 2009). Factors found to be associated with an enhanced likelihood of finishing the WSER included being a first-time starter, and advancing calendar years for first-timers and those who had finished at least 75% of their previous starts. Factors that were associated with a lower likelihood of finishing the WSER included advancing age above 38 years and increasing ambient temperature. Women and men under 38 years were equally likely to finish, but beyond 38 years women had a lower likelihood of finishing than men. Furthermore, advancing age between 38 and 50 years decreased the odds of finishing at a more rapid rate among women compared with men. While higher ambient temperature was associated with a reduced probability of finishing, there was no evidence that the higher temperatures affected the likelihood of finishing differently for men and women.

With regard to finish times at the WSER, it was demonstrated that women finished slower than men on the average, and women’s finish times were less affected by increasing air temperature than men. There was no change in finish time across calendar years after adjustment for other variables. Increased age was associated with slower finish times, but this effect was affected by two other variables. Having finished a WSER before 1986 and having a higher WSER finish rate for those who had previously started the WSER since 1985 were associated with faster times. For runners who had finished their previous WSER start, performance at the previous finish was strongly associated with their current finish time, and this relationship was stronger for finishers who had finished a greater percentage of their previous starts.

Aging is known to adversely affect finish times in running competitions of the marathon distance (42 km) (Jokl et al. 2004) and in long distance triathlons (Lepers and Maffiuletti 2010; Lepers et al. 2010), so it is not surprising to observe the same effect for 161-km runs. In fact, we have previously demonstrated this finding from the same WSER dataset (Hoffman and Wegelin 2009) as well as from the results of participants in all 161-km ultramarathons in North America (Hoffman 2010) when considering all finishers. Of course, the situation is different when focusing on the fastest runners where we have shown that it is the 30–39 and 40–49-year brackets that produce the fastest finish times at the 161-km distance (Hoffman 2010; Hoffman and Wegelin 2009).

The effect of aging on the likelihood of finishing an extreme endurance event has received little attention. A small analysis of the 1989 Leadville Trail 100 (161-km) ultramarathon offered some suggestion that increasing age was associated with a lower likelihood of finishing (Siguaw 1990). The present study provides solid support that increasing age beyond 38 years adversely affects the likelihood of finishing the WSER, and that this effect is greater for women than for men. We hypothesize that these findings are due to an increasing difficulty at meeting check point cutoff times with aging, and that this issue is more important for women given that they are slower than men on the average.

The typical temperature conditions at the WSER would be considered by most runners to include some relatively hot sections given that only once between 1986 and 2007 did the maximum recorded temperature at the location of the finish remain below 25°C. Yet, even with the WSER typically including relatively hot temperatures, we were able to demonstrate that increasing ambient temperatures were associated with slower finish times and lower finish rates. Several studies have shown finish times in the marathon to be negatively impacted by warm environmental temperatures (Ely et al. 2007a, b, 2008; Trapasso and Cooper 1989; Zhang et al. 1992). Interestingly, the negative effect on marathon finish times from increases in temperature has been shown to be similar for men and women (Ely et al. 2007a, b). In contrast, we found that increases in temperature had less effect on 161-km finish times for women than for men. On the other hand, the effect of hot weather on finish rates did not differ between men and women.

In the present study, we also found that increasing ambient temperatures adversely affected the finish times of the faster runners slightly more than the slower runners. This is in contrast to the situation in the marathon where it has been demonstrated that the finish times of slower runners are most affected by increases in temperature (Ely et al. 2007b, 2008). The present finding of a greater effect of temperature on faster runners is partially accounted for by slower runners dropping out under hotter conditions, so that their finish time did not enter into the model. In a shorter run or a run without cutoff times, the slower runners might have recorded a slower time, rather than dropped out, because of the increased heat. In contrast, perhaps the faster finishers were more likely to simply be slowed down by the increased temperature rather than drop out. Since women were generally slower than men, the same rationale might explain why finish times for women were found to be less affected by increasing temperatures than for men.

Although there was no effect of calendar year on finish time, finish rates were shown to improve across time. Examination of interaction effects revealed that the improvement in finish rate with advancing calendar year was for first-time WSER runners and for those who had finished at least 75% of their previous starts. It should not be surprising that previous success at finishing the WSER would be associated with a greater likelihood of finishing again. However, an explanation for the improved finish rate across calendar years among first-time WSER runners may not seem so obvious. This effect is likely reflective of these runners being more experienced from other races now than in the past, given that the number of such events has been rising exponentially (Hoffman et al. 2010b).

Several variables are known to have associations with performance in 161-km ultramarathons, such as age (Hoffman 2010; Hoffman and Wegelin 2009), sex (Hoffman 2010; Hoffman and Wegelin 2009), and body composition (Hoffman 2008; Hoffman et al. 2010a). Others are presumed to be related to performance, such as maximal oxygen uptake, anaerobic threshold, heat acclimatization, and training regimen. In light of these known and presumed associations, one limitation in the current study is apparent. Because we used only those variables that were publicly available, we were unable to account for body composition, anaerobic threshold, heat acclimatization, or training regimen. Most notably, we did not account for maximal oxygen uptake. Thus, the current study does not in any way report a true quantitative analysis of performance.

Another limitation is related to our choice of analytic method. Since the model for finish time was based only on finishers, starters who ran so slowly that they were unable to finish within the time limit were not accounted for in that model. It would have been possible to treat the odds of finishing and the finish time in a single analysis using techniques of survival analysis (Therneau 2000). However, we chose to analyze finish time based only on finishers because that is more consistent with the reality of these events in that one does not get credit for finishing if it is not done within the time limits of the event. It is also recognized that runners drop out of an event of this nature for reasons besides being unable to finish within the allocated time limit. For instance, some of the top performers may drop out if they are having a poor day, hoping that they can perform better in an upcoming event if they do not continue in the race just to finish. It was not possible to identify such situations in this analysis.

Conclusion

The current study investigated human capacity to perform a particular kind of extreme endurance exercise: a 161-km ultramarathon on mountain trails. Through the use of variables publicly available on all starters, phenomena were assessed that could not have been reproduced in a laboratory setting. Among those attempting the WSER for the first time, finish rates improved between 1986 and 2007. This may have been because the population of individuals represented by WSER starters had become more experienced through participation in other races. Advancing age and hot weather adversely affected the ability to finish as well as how fast one could finish. Women were typically less likely to finish and slower than men, but their finish rates were no more affected by hot weather than men’s finish rates. Finally, hot weather adversely affected the finish times of faster runners more than those of slower runners. This stands in contrast to previous findings related to the marathon, where increases in ambient temperature had a greater effect on the slower runners.

Research reported in this article was performed in compliance with the current laws of the United States and of the states of California and Virginia. This study was approved by our institutional review board with the requirement for informed consent being waived, since all data analyzed or reported were publicly available.