Solid-State Forms of β-Resorcylic Acid: How Exhaustive Should a Polymorph Screen Be?

Abstract

A combined experimental and computational study was undertaken to establish the solid-state forms of β-resorcylic acid (2,4-dihydroxybenzoic acid). The experimental search resulted in nine crystalline forms: two concomitantly crystallizing polymorphs, five novel solvates (with acetic acid, dimethyl sulfoxide, 1,4-dioxane, and two with N,N-dimethyl formamide), in addition to the known hemihydrate and a new monohydrate. Form II°, the thermodynamically stable polymorph at room temperature, was found to be the dominant crystallization product. A new, enantiotropically related polymorph (form I) was obtained by desolvation of certain solvates, sublimation experiments, and via a thermally induced solid−solid transformation of form II° above 150 °C. To establish their structural features, interconversions, and relative stability, all solid-state forms were characterized with thermal, spectroscopic, X-ray crystallographic methods, and moisture-sorption analysis. The hemihydrate is very stable, while the five solvates and the monohydrate are rather unstable phases that occur as crystallization intermediates. Complementary computational work confirmed that the two experimentally observed β-resorcylic acid forms I and II° are the most probable polymorphs and supported the experimental evidence for form I being disordered in the p-OH proton position. These consistent outcomes suggest that the most practically important features of β-resorcylic acid crystallization under ambient conditions have been established; however, it appears impractical to guarantee that no additional metastable solid-state form could be found.

Short abstract

An extensive experimental screen, coupled with a computational study, revealed seven new solid-state forms of β-resorcylic acid. The known, stable polymorph II° shows a reversible phase transformation to the new, kinetically stable, probably disordered high temperature form I. The study provides a consistent picture of the solid-state of β-resorcylic acid.

1. Introduction

The existence of different crystalline forms (polymorphs, hydrates, and solvates) represents one of the most challenging phenomena in solid-state chemistry and related sciences, since we are still not able to predict the number of practically relevant forms and the conditions under which these can be grown or exist. The existence of different solid-state forms of a compound is important as these usually show different physical properties,^1,2 for example, solubility, density, hardness, melting point, etc. Polymorphism and solvate formation is important for both fundamental research and industrial practice. This is true for pharmaceuticals (the majority of the active ingredients are used in a crystalline form(2)), because the solid-state form can profoundly influence the manufacturing process, the long-term stability, and the performance of drug products,^3,4 and for many other materials used in the chemical industry (plant protection substances, dyes, explosives, etc.).

The present study deals with the solid-state of β-resorcylic acid (2,4-dihydroxybenzoic acid, βRA, Figure 1), a small organic molecule exhibiting molecular flexibility and the ability to form different hydrogen bonding motifs. The compound is used as a starting material for the production of dyestuffs, pharmaceuticals, cosmetic preparations, and fine organic chemicals. The Cambridge Structural Database (CSD)(5) contains entries for three βRA solid-state forms, namely two anhydrates (ZZZEEU:(6)P1̅, Z′ = 2 and ZZZEEU01 to ZZZEEU04:(7)P2₁/n, Z′ = 1, measured at 90, 100, 110, and 150 K), and a hemihydrate (QIVTUK:(8)P1̅, Z′ = 1). For the triclinic anhydrate, only the lattice dimensions have been reported, and the volume of ZZZEEU corresponds to a monohydrate rather than an anhydrous form(9) but not to the new monohydrate described in this work. For the monoclinic polymorph (form II° hereafter), the temperature range has been extended very recently down to 20 K.(10) Furthermore, different hydrate stoichiometries, ranging from 0.5 to 3 mol water per mol of acid can be found in literature reports,^8,11 but only the crystal structure of the hemihydrate has been determined. A recent study comparing six isomeric dihydroxybenzoic acids failed to crystallize new polymorphs by melt crystallization and sublimation experiments.(12) Joint experimental and computational studies have shown that there is no cooperative hydrogen atom disorder in the COOH and o-OH groups in form II° at temperatures up to 150 K.^7,10 However, βRA was neither subjected to a systematic solution crystallization screen nor to a comprehensive solid-state characterization program, and also theoretical predictions of possible crystal structures have not been reported so far.

Figure 1.

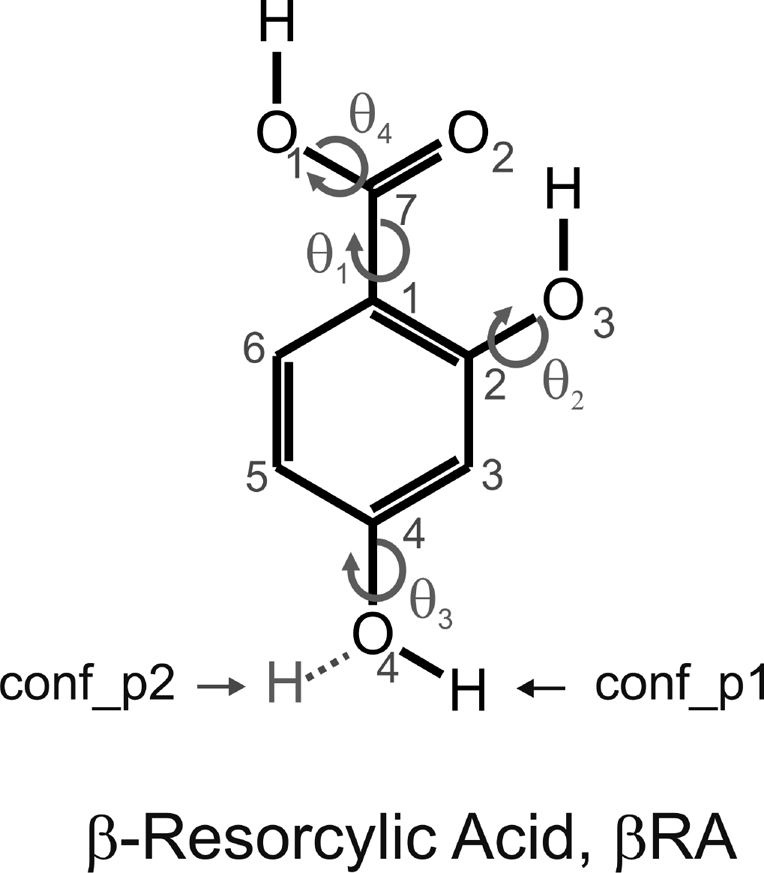
Global (conf_p1) and second lowest conformational minima (conf_p2) of β-resorcylic acid (βRA). The intramolecular degrees of freedom (dihedral angles) that were optimized within the crystal energy minimizations are indicated with arrows: θ₁: C6−C1−C7−O2, θ₂: C3−C2−O3−H, θ₃: C5−C4−O4−H and θ₄: C1−C7−O1−H.

Therefore, our investigation aimed at an efficient screening program, using an experimental¹³⁻¹⁵ and computational(16) approach to complement and validate the results and comprehensively characterize all βRA solid-state forms at ambient conditions. The experimental screen was based on manual solution crystallizations of the compound in a variety of solvents and crystallization conditions, sublimation and moisture sorption experiments. The thermodynamic and kinetic stability of the solid-state forms were ascertained by hot-stage microscopy, differential scanning calorimetry, thermogravimetic analysis, and solvent-mediated transformation studies. Vibrational spectroscopy (mid infrared and Raman) and X-ray diffractometry (powder and single crystal) were employed to determine the structural features of the phases. However, as neither high-throughput methodologies^17,18 or other widely applied screening strategies(19) guarantee all possible forms will be found, we supported and complemented our manual screen with computational crystal structure prediction (CSP). By contrasting the thermodynamically feasible crystal structures with the experimentally observed ones, we discuss the factors that control crystallization and polymorphism^20,21 of βRA.

2. Experimental Section

2.1. Manual Crystallization Screen and Preparation of the Individual Forms

βRA was purchased from Fluka (form II°). For the solvent screens, a set of 25 solvents was chosen (Supporting Information, section 1.1), which were all of analytical quality. Crystallization conditions included solvent evaporation, fast and slow cooling crystallization, precipitation with a miscible antisolvent, vapor diffusion, and solvent-mediated transformation. In total, more than 150 manual crystallization experiments were performed (conditions and crystallization outcomes are provided in the Supporting Information, Tables S1−S5).

We have named the polymorphs according to the Kofler notation using Roman numerals in the order of the melting points (i.e., the highest melting is named form I) and flagged the thermodynamically stable form at room temperature with the symbol °. Form II° was either prepared by slow crystallization from numerous solvents, including n-butanol, n-propanol, i-propanol, acetonitrile, ethyl methyl ketone, ethyl acetate, or by solvent-mediated transformation of any βRA form, using water-free solvents that did not form a solvate. Form I could be obtained from solvent crystallization, but it predominantly grew concomitantly with form II°. The easiest way to produce form I was heating any βRA form above the transition temperature of the polymorphic transition II° → I (150−170 °C). However, decomposition, although slow compared to the polymorphic transformation, starts at ca. 160 °C. Other methods included sublimation experiments in the same temperature range or the desolvation of the hemihydrate (HH), dimethyl formamide hemisolvate (S_DMF-I), dimethyl sulfoxide hemisolvate (S_DMSO), or dioxane hemisolvate (S_DX) at temperatures above 60 °C.

The two hydrates could be prepared by crystallization from a hot, saturated water solution, with the resulting solid form depending on the cooling rate. Fast crystallization to the final temperature of 0 °C (in ice) led to the monohydrate (MH), whereas slow cooling (test tube wrapped in aluminum foil) produced the hemihydrate (HH). The MH samples obtained in this way were often contaminated with HH. The dioxane hemisolvate (S_DX), dimethyl formamide 0.75-solvate (S_DMF-II), and the dimethylsulfoxide hemisolvate (S_DMSO) were prepared from II° by solvent-mediated transformation experiments in the respective solvent, the acetic acid monosolvate (S_AA) by fast crystallization (cooling a hot saturated solution in acetic acid to ca. 8 °C). Finally, the dimethyl formamide hemisolvate (S_DMF-I) was obtained as an intermediate desolvation product of the S_DMF-II solvate. Every crystallization or solvent-assisted grinding experiment with pyridine resulted in the formation of the pyridinium salt.(22)

2.2. Thermal Analysis

For hot-stage thermomicroscopic (HTM) investigations a Reichert Thermovar polarization microscope equipped with a Kofler hot stage (Reichert, A) was used. Photographs were taken with a digital camera (Olympus ColorView IIIu digital camera, D).

Differential Scanning Calorimetry (DSC)

DSC was performed with a DSC 7 (Perkin-Elmer, Norwalk, CT, USA) using the Pyris 2.0 software. Approximately 1−3 ± 0.0005 mg sample (UM3 ultramicrobalance, Mettler, CH) was weighed into Al-pans (25 μL). Dry nitrogen was used as the purge gas (purge: 20 mL min⁻¹). A heating rate of 10 K min⁻¹ was used. The instrument was calibrated for temperature with pure benzophenone (mp 48.0 °C) and caffeine (mp 236.2 °C), and the energy calibration was performed with pure indium (purity 99.999%, mp 156.6 °C, heat of fusion 28.45 J g⁻¹).

Thermogravimetric Analysis (TGA)

TGA was carried out with a TGA7 system (Perkin-Elmer, USA) using the Pyris 2.0 software. Approximately 3 mg of sample was weighed into a platinum pan. Two-point calibration of the temperature was performed with ferromagnetic materials (Alumel and Ni, Curie-point standards, Perkin-Elmer). Heating rates ranging from 10 to 20 K min⁻¹ were applied, and dry nitrogen was used as a purge gas (sample purge: 20 mL min⁻¹, balance purge: 40 mL min⁻¹).

The stated error limits of thermochemical data are calculated as confidence intervals at a 95% level.

2.3. Gravimetric Moisture Sorption

Isothermal (25 ± 0.1 °C) moisture sorption isotherms were acquired using a SPS-11 moisture sorption analyzer (Projekt Messtechnik, D). The samples were gently ground prior to measurement to exclude the influence of particle size and surface area. The measurement cycles were started at 40% relative humidity (RH). Sorption and desorption cycles covered the 10−90% RH range in 10% steps and the 0−10% range in 5% steps. The equilibrium condition for each step was set to a mass constancy of ±0.001% over 35 min.

2.4. Spectroscopy

Fourier Transform Infrared (FT-IR) Spectra

Spectra were recorded with a Bruker (Bruker Optic GmbH, D) IFS 25 spectrometer connected to a Bruker IR microscope I (15×-Cassegrain-objective, spectral range 4000 to 600 cm⁻¹, resolution 4 cm⁻¹, 64 scans per spectrum). The samples (rolled on a ZnSe disk or fused between two ZnSe windows) were measured in transmission mode. For elevated temperature measurements, a Bruker heatable accessory holder was used.

Fourier Transform Raman (FT-Raman) Spectra

Spectra were recorded with a Bruker RFS 100 Raman-spectrometer (Bruker Analytische Messtechnik GmbH, D), equipped with a Nd:YAG Laser (1064 nm) as the excitation source and a liquid-nitrogen-cooled, high sensitivity Ge-detector. The spectra (128 scans per spectrum) were recorded in aluminum sample holders with a laser power of 200 mW and a resolution of 2 cm⁻¹.

2.5. X-ray Diffractometry

Single Crystal X-ray Experiments

Experiments were performed on an Oxford Diffraction Gemini R Ultra (4-circle kappa-goniometer, 135 mm Ruby CCD detector, MoKα radiation, monocapillary collimator) with an Oxford Cryosystems 700 series Cryostream Plus low temperature attachment. The single crystal structures of HH, S_DMSO, and the pyridinium salt were solved by direct methods using the program package WinGX(23) (SIR2004(24) and SHELXL97(25)). All hydrogen atoms bonded to carbon atoms were generated by a riding model on idealized geometries with U_iso(H) = 1.2 U_eq(C). The polar hydrogens were identified from the difference map and refined isotropically, with the exception of H9 in S_DMSO, where the position was refined with a constrained O−H bond distance. For further details, see Table 1.

Table 1. Summary of Experimental Conditions and Structure Analysis of βRA Forms.

phase designator	form I	HHa	SDMSO	pyridinium salt
empirical formula	C7H6O4	C7H6O4·0.5(H2O)	C7H6O4·0.5(C2H6OS)	C7H5O4·C5H6N
formula weight	154.12	163.13	193.18	233.22
temperature/K	298(2)	173(2)	173(2)	173(2)
sample formulation	powder	single crystal	single crystal	single crystal
wavelength/Å	1.54056	0.71073	0.71073	0.71073
crystal size, specimen shape/mm	12 × 1.0 × 0.7	0.40 × 0.24 × 0.24	0.40 × 0.32 × 0.30	0.48 × 0.24 × 0.24
crystal system	monoclinic	triclinic	orthorhombic	monoclinic
space group	P21/a	P-1	P212121	P21/n
a/ Å	23.1978(4)	7.0270 (4)	6.39832 (12)	11.7363 (4)
b/ Å	5.5469(1)	9.5449 (4)	11.7099 (3)	8.5691 (2)
c/ Å	5.1980(1)	11.1763 (5)	23.2362 (5)	11.8310 (4)
α/ °		96.684 (4)
β/ °	92.215(1)	104.319 (5)		115.973 (5)
γ/ °		98.903 (4)
volume/ Å3	668.36(2)	708.15 (6)	1740.94(7)	1069.67 (7)
Z	4	2	4	4
density (calculated)/ g cm−3	1.532	1.530	1.474	1.448
absorption		μ = 0.131 mm−1 (calculated)	μ = 0.230 mm−1 (calculated)	μ = 0.110 mm−1 (calculated)
theta range for data collection/ °	3−70	3.04−25.35	3.15−25.99	3.05−25.34
background treatment	Chebyshev polynomial
index ranges		−8 ≤ h ≤ 8	−7 ≤ h ≤ 7	−14 ≤ h ≤ 12
		−10 ≤ k ≤ 11	−12 ≤ k ≤ 14	−10 ≤ k ≤ 10
		−13 ≤ l ≤ 10	−28 ≤ l ≤ 23	−13 ≤ l ≤ 14
no. of measured, independent and observed [I > 2σ(I)] reflections	284	4832/2604/2081	11590/3400/3014	7775/1953/1639
refinement method	Rietveld	full-matrix least-squares on F2	full-matrix least-squares on F2	full-matrix least-squares on F2
data/parameters/restraints	284/61/0	2604/239/0	3400/261/1	19536/166/0
goodness-of-fit	2.88 (on yobs)	0.97 (on F2)	1.02 (on F2)	1.03 (on F2)
final R indices [I > 2σ(I)]		R1 = 0.0382, wR2 = 0.0941	R1 = 0.0367, wR2 = 0.0863	R1 = 0.0337, wR2 = 0.0839
R indices (all data)	Rwp = 0.055, Rexp = 0.019, Rp = 0.046	R1 = 0.0527, wR2 = 0.0966	R1 = 0.0431, wR2 = 0.0887	R1 = 0.0436, wR2 = 0.0874
largest diff. peak and hole		0.40 and −0.20 e·Å−3	0.62 and −0.24 e·Å−3	0.19 and −0.20 e·Å−3

^aLow temperature redetermination.

Powder X-ray Diffraction (PXRD) Data

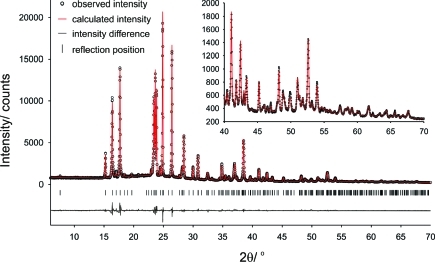
PXRD was used to determine the structure of form I. The sample was loaded in a rotating 1.0 mm borosilicate glass capillary and mounted on a Bruker AXS D8 powder X-ray diffractometer equipped with primary monochromator (CuKα₁, l = 1.54056 Å) and Lynxeye position sensitive detector. Data was collected at room temperature using a variable count time scheme (Supporting Information, Table S6). The diffraction pattern indexed to a monoclinic unit cell (omitting an impurity peak at 20.8° 2θ arising from a suspected decomposition product) and the space group was determined to be P2₁/a based on a statistical assessment of systematic absences,(26) as implemented in the DASH structure solution package.(27) The data were background subtracted and truncated to 50.5° 2θ for Pawley fitting(28) (Pawley χ² = 15.91). Simulated annealing was used to optimize the form I model against the diffraction data set (115 reflections) in direct space. The internal coordinate (Z-matrix) description was derived from the HF/6-31G(d,p) gas phase global conformational minimum (conf_p1), with O−H distances normalized to 0.9 Å and C−H distances to 0.95 Å. The structure was solved using 200 simulated annealing runs of 2.5 × 10⁷ moves per run as implemented in DASH, allowing 7 degrees of freedom (6 external and 1 internal). The best solutions returned a χ² ratio of ca. 4.66 (profile χ²/ pawley χ²) and was used as the starting point for a rigid body Rietveld refinement(29) in TOPAS V4.1.(30) The rigid body description was derived from the z-matrix used in the simulated annealing runs and the final refinement included a total of 61 parameters (40 profile, 4 cell, 1 scale, 1 U_iso, 9 preferred orientation, 3 position, and 3 rotation) yielding a final R_wp = 5.53 (Figure 2).

Figure 2.

Powder X-ray diffraction pattern and Rietveld fit (rigid body) of βRA form I at 25 °C.

2.6. Computational Generation of the Crystal Energy Landscape (CSP)

We considered all eight planar HF/6-31G(d,p) conformational minima produced by varying the torsion angles θ₁ − θ₃ (Figure 1) in the CSP searches for anhydrate crystal structures, using a three-stage methodology.(31) First, Z′ = 1 and Z′ = 2 crystal structures were generated using CrystalPredictor(32) in 25 common space groups for organic molecules. The molecules were held rigid and the lattice energy was evaluated by an exp-6 potential with atomic charges derived using the CHELPG scheme(33) and minimized. All crystallographically distinct low energy crystal structures were used as starting points for optimizing the intermolecular lattice energy (U_inter), with an improved model for the intermolecular forces. This was calculated using the FIT³⁴⁻³⁶exp-6 potential parameters and the distributed multipoles(37) derived from the PBE0/aug-cc-pVTZ charge density using GDMA2.(38) Finally the 28 most stable structures were refined with CrystalOptimizer(39) to allow small changes in conformation (torsion angles θ₁ − θ₄ in Figure 1) by minimizing the lattice energy, E_latt = U_inter + ΔE_intra, where ΔE_intra is the conformational energy penalty (with respect to the global conformational minimum) paid to improve the intermolecular interactions. The conformational energy penalty was computed at the PBE0/6-31G(d,p) level. All isolated-molecule wave function calculations were performed using GAUSSIAN03(40) and intermolecular lattice energies by DMACRYS.(41) More details of the conformational analysis, model testing, and search procedure and results are given in Supporting Information.

3. Results

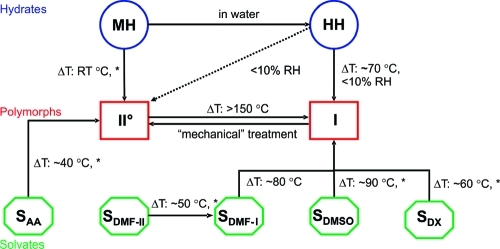
The solvent screening program resulted in a new βRA polymorph (form I), a new monohydrate (MH), and five new solvates, namely acetic acid (S_AA), dioxane (S_DX), DMSO (S_DMSO), and two DMF solvates (S_DMF-I and S_DMF-II). The previously described anhydrous form (form II°)(7) and the hemihydrate (HH)(8) could be reproduced. The relationships between the βRA solid state forms (Figure 3) and their structures are described in Experimental Section 3.1, and their relationship to the computed possible structures are described in section 3.2.

Figure 3.

Transition pathways of the βRA forms at different temperatures and relative humidities (RH); MH: monohydrate, HH: hemihydrate, I: form I, II°: form II°, S_AA: acetic acid monosolvate, S_DMF-II (0.75) and S_DMF-I (hemi): dimethyl formamide solvates, S_DMSO: dimethyl sulfoxide hemisolvate and S_DX: dioxane hemisolvate, ΔT: heating, *: removing from the mother liquor, “mechanical” treatment, for example, grinding.

3.1. Experimental Search for Solid-State Forms and Their Characterization

3.1.2. Thermal Analysis, Thermodynamic and Kinetic Stability

Anhydrates

The two βRA polymorphs can be easily distinguished by their distinct morphologies. Form II° occurs in solvent crystallization/evaporation experiments as long needles, whereas form I occurs as a polycrystalline powder comprising multilayered plates.

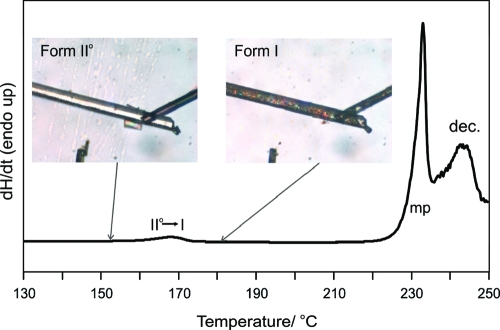
HTM and DSC experiments revealed that form II° transforms to form I upon heating at temperatures above 150 °C. Optically this transformation can be recognized by a darkening of the form II° needles due to cleavage and the formation of small aggregates of form I (Figure 4). TGA experiments and further thermomicroscopic investigations (silicon oil embedding) showed that no desolvation process is involved in this process, confirming that the reaction is a single component (polymorphic) transition. The weak endotherm in the DSC curve (Figure 4) at an experimental transition temperature (T_trs,exp) of 159.8 ± 0.5 °C corresponds to the solid−solid transformation II° → I with a transition enthalpy of Δ_trsH = 2.1 ± 0.1 kJ mol⁻¹. From the fact that the transition is endothermic, it can be concluded that the two polymorphs are enantiotropically related (heat of transition rule^42,43). This implies that the melting point of form II° is lower than that of form I, which melts at 231 °C with decomposition (second endotherm in DSC curve of Figure 4, overlapping with a broader endotherm, indicating the decomposition process). Form II° is thus the thermodynamically stable polymorph at room temperature (RT) and form I represents the high temperature form, which nevertheless shows a high kinetic stability at RT. A reversible transformation I → II° was only observed if the sample was mechanically treated (e.g., grinding at room temperature). No transformation occurred under storage at ambient conditions within 18 months. The fact that form II° is thermodynamically stable at 20 °C was also confirmed with solvent-mediated transformation experiments. The energy-temperature diagram of the two polymorphs derived from the thermoanalytical data is provided in Supporting Information (Figure S2).

Figure 4.

Hot-stage microscopy photographs of the βRA form II° to form I transformation, along with the DSC curve that shows the transformation (II° → I), melting (mp), and decomposition (dec.) of form I (heating rate: 10 K min⁻¹).

Hydrates and Solvates

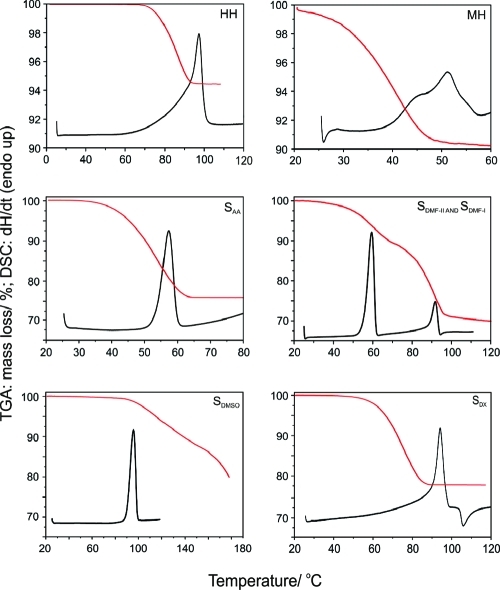
The HH forms transparent blocklike crystals (Figure 5), which are stable when removed from the aqueous mother liquor. Single crystals of HH turn opaque when heated above 70 °C, while the original shape of the crystals is more or less maintained (pseudomorphosis). In silicon oil preparations, the release of bubbles accompanies the darkening of the crystals and confirms the desolvation process (see Figure S1, Supporting Information). The mass loss of 5.55% (TGA, Figure 6) is consistent with the theoretical water content of a hemihydrate (5.52%). The second hydrate (monohydrate, MH) crystallizes as needles and was found to be very unstable at ambient conditions. TGA shows (Figure 6) that the dehydration of MH occurs below 60 °C resulting in form II°. A transformation of MH to HH can only be observed in a water slurry. The measured mass loss (Figure 6) of ca. 9.5% corresponds to 0.9 mol water per acid molecule, which is slightly lower than expected for a monohydrate (theory: 10.47%) due to some loss of water during the preparation of the unstable MH.

Figure 5.

Photomicrographs (dry preparation) showing the dehydration process of βRA HH to form I in a HTM experiment (heating rate ca. 5 K min⁻¹).

Figure 6.

DSC (black) and TGA (red) curves of βRA hydrates and solvates (pin-holed DSC capsules and a heating rate of 10 K min⁻¹ was used for all thermograms).

All five solvates form transparent, thin, needle- or plate-like crystals losing their transparency within hours when removed from the mother liquor. Upon heating (Figure 6), desolvation of S_AA occurs in one step between about 40 and 60 °C resulting in needle-shaped form II° crystals. S_DMF-II shows two desolvation steps under heating. The first desolvation process (Figure 6, mass loss ca. 0.25 mol DMF/mol acid) occurs between ca. 50 and 70 °C and corresponds to the transformation of the 0.75-solvate (S_DMF-II) to the hemisolvate (S_DMF-I), which then desolvates at ca. 90 °C to form I. S_DMSO shows a peritectic melting/decomposition at ∼90 °C. Upon further holding the temperature, long plates (form I) slowly crystallize from the melt (observed in HTM, not visible in shown DSC curve). It was not possible to clearly determine the stoichiometric solvent content from TGA experiments, as the desolvation and decomposition process overlaps. However, the course of the first step of the curve shows that the desolvation process decelerates before the fast decomposition process starts at about 150 °C, indicating that the majority of the solvent is released. We can extrapolate the end of the first step to about 80%, suggesting that S_DMSO is a hemisolvate (theoretical mass loss: 20.2%). S_DX shows an inhomogeneous melting process consisting of the following events: peritectic melting/decomposition, evaporation of the solvent (DSC: endotherm at ca. 85 °C), and the crystallization of form I (exotherm above 110 °C).

3.1.3. Moisture Dependent Stability

Forms I, II°, and HH were subjected to a gravimetric moisture sorption study at 25 °C (Figure 7). The anhydrous phases absorb water and transform only to HH even at the highest RH value (90%). The moisture sorption cycle of form I was completed within 48 h, whereas only ca. 25% of form II° transformed to HH within the same time period. HH dehydrates only under rather dry conditions (5% RH and below) demonstrating its high stability. Under these conditions, HH transforms to a mixture of the two anhydrous forms. The complete dehydration process took ca. five days, although after one day 95% of the water was already released. The profile of the moisture sorption−desorption isotherm (sharp steps, strong hysteresis between sorption and desorption) is a very clear indication that HH is a “stoichiometric” hydrate.(44) From the huge hysteresis, we can deduce that the anhydrates and HH can be handled and stored as stable phases provided extremely low or high moisture conditions are avoided.

Figure 7.

Moisture sorption isotherm of βRA performed at 25 °C showing a moisture sorption cycle of anhydrous βRA to HH and a desorption cycle of HH to a polymorphic mixture of forms I and II^o.

3.1.4. Vibrational Spectroscopy

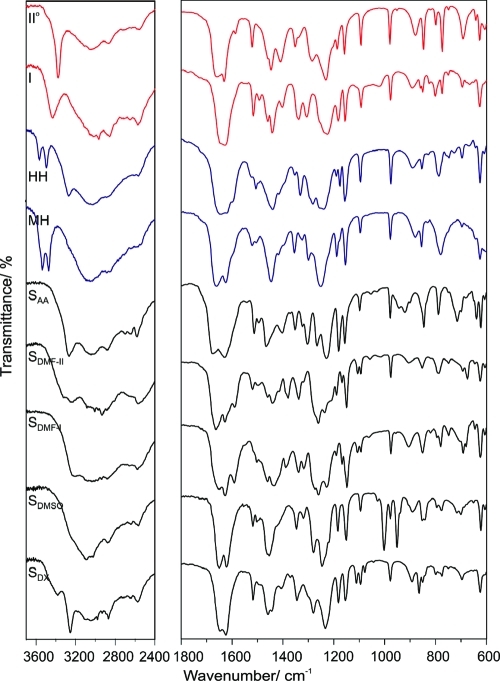
The FT-IR spectra (Figure 8) allow an unambiguous identification of all forms, as variations were found in numerous regions, for example, ν(O−H), ν(C_ar−H), ν(C=O), and δ(C−O−H) vibrations. The most striking difference in the IR spectra of the two polymorphs concerns the ν(O−H) vibration of the p-OH group. In form II° a sharp band occurs at 3373 cm⁻¹, whereas in form I the band is broader and shifted to higher wavenumber (3432 cm⁻¹) implying weaker and more complex hydrogen bonding. The presence of two ν(O−H) bands is characteristic of the two hydrates. S_AA exhibits additional bands in the range of 970−880 cm⁻¹ due to the out of plane O−H···O hydrogen deformations(45) (most intensive band: 920 cm⁻¹). The two DMF solvates showed two distinct vibrations at 1107 and 1094−1095 cm⁻¹, whereas all other phases exhibit only one or three bands in this region. On the basis of the ν(C=O) vibrations, the DMF solvates can be discriminated, with S_DMF-II at 1666 cm⁻¹ and S_DMF-I at 1652 cm⁻¹. The ν(S=O) vibrations(46) in S_DMSO occur at 1002 cm⁻¹ (strong band). Finally, the symmetric stretch vibrations of the ether group in S_DX can be found at 865 cm⁻¹.

Figure 8.

FT-IR spectra of βRA polymorphs (I, II^o), hydrates (HH, MH), and solvates (S_AA, S_DMF-II, S_DMF-I, S_DMSO, and S_DX).

FT-Raman spectroscopy (Figure 9) also allows the identification of the different βRA solid-state forms. The presence of the solvent molecules (acetic acid, DMF, DMSO, and dioxane) can be clearly seen in the spectral range around 2900 cm⁻¹ (stretching vibrations of the aliphatic CH₃ and CH₂ groups, only present in the solvent molecules). Moreover, the lattice phonon vibrations below 150 cm⁻¹ differ markedly, indicating that the crystal structures of the βRA solid-state forms are different and also that the solvates are not obviously isostructural as frequently observed if compounds form a series of such adducts.^47,48

Figure 9.

FT-Raman spectra of βRA polymorphs (I, II^o), hydrates (HH, MH), and solvates (S_AA, S_DMF-II, S_DMF-I, S_DMSO, and S_DX).

3.1.5. X-ray Diffractometry

Powder X-ray Diffractometry

The clear differences in PXRD patterns from each phase studied are consistent with the very distinct structures for all βRA solid-state forms (Supporting Information, Figure S3 and Table S6). Temperature- and humidity-controlled powder X-ray diffraction studies of the dehydration process (Supporting Information, Figures S4 and S5) confirmed the results presented in sections 3.1.2 and 3.1.5.

Structural Features (Crystal Structures). Anhydrates (Form I and II^o7)

Form I crystallizes in the monoclinic space group P2₁/a (Z′ = 1) and form II° in P2₁/n (Z′ = 1), both adopting a conformation similar to conf_p1 (Figure 1). The two polymorphs form inversion related R₂²(8) dimers and furthermore share the same 1D arrangement (supramolecular construct(49)) of inversion related dimeric units (Figure 10a,c). However, they differ in the way the 1D constructs are linked to neighboring units, the O4−H···O3 hydrogen bonds, and consequently in the packing. In form II°, the O4−H···O3 interaction exhibits n glide symmetry (Figure 10b), leading to puckered hydrogen-bonded sheets (Figure 10a) and to a dihedral angle between the 1D constructs (benzene rings) of 31°. In form I, where 2₁ symmetry is present a dihedral angle between the benzene rings of 82° is observed.

Figure 10.

Crystal packing of form II°⁷ (a, b) and form I (c, d) viewed along the a-axis (a), [101] direction (b), c-axis (c), and b-axis (d). Black dotted lines indicate the hydrogen bonds. For clarity only selected symmetry symbols are shown. Hirshfeld surfaces^50,51 for forms II° (e) and I (f) were generated using the program Crystal Explorer v. 2.1,(52) with C−H and O−H distances normalized to neutron values, d_norm is mapped on the surfaces over the range −0.48 to 0.78 Å. This function highlights contact distances relative to the sum of van der Waals radii, with closest contracts shown in red. The circles in (e, f) highlight the p-OH group and Hirshfeld surface around it, arrows mark the H-bonds involving the p-OH proton.

Hirshfeld d_norm surface(50) plots (Figure 10e,f) clearly indicate that the p-OH proton forms only one H-bond in form II°, but that the assumed p-OH conformation in form I corresponds to two hydrogen bonds. The p-OH proton can form a hydrogen bond to either the o- or p-OH oxygen, without otherwise changing the structure. The difference in shape and larger volume of the surface around the p-OH in form I in contrast to form II° is consistent with possible disorder of the p-OH proton between the two positions, which due to the weak scattering contribution of hydrogen could not be verified based on the fit to the PXRD data alone but would be consistent with the broad IR band. It appears that there is an unusual freedom in the position of the p-OH proton in the form I structure and so there will be ambiguities in the proton position.

Hemihydrate

HH crystallizes in the triclinic space group P1̅ with two molecules of βRA (similar to conf_p1 and conf_p2) and one water molecule in the asymmetric unit, in agreement with the stoichiometry determined by TGA. The structure comprises columns of R₂²(8) dimers, formed by symmetrically equivalent, inversion related βRA molecules (homodimers). Each dimeric unit is directly linked to the adjacent alternate dimers with an O4−H···O4′ hydrogen bond and indirectly via a water molecule bridge, that forms two hydrogen bonds (O4′−H···O_water and O_water−H···O4), leading to sheets. Hence, water plays a major role forming and stabilizing the structure. In addition to connecting the acid dimers, water forms the only strong hydrogen bond between the parallel stacked sheets, leading to a 3D network structure (Figure 11). The dehydration of HH involves a structural collapse, as despite the water interactions the O4−H···O4′ hydrogen bonds also break due to the conformational change, which is around 180° in the torsion angle for the p-OH proton in every second molecule. As seen in the polymorphs HH exhibits inversion related dimeric units within the sheets. The units differ from the 1D construct present in the polymorphs in the location of the inversion center (Figure 11a).

Figure 11.

Crystal packing of HH: (a) (046) plane shown, (b) viewed along the a-axis showing the parallel sheets. Hydrogen bonds are denoted with dotted lines, and for clarity the water protons were omitted.

DMSO Solvate

Two acid molecules and one DMSO molecule are present in the asymmetric unit of S_DMSO, which crystallizes in the orthorhombic space group P2₁2₁2₁. The two symmetry inequivalent molecules adopt a conformation similar to conf_p1 and form R₂²(8) heterodimers. The acid dimers stack along a, forming columns. Each heterodimer is interlinked via the DMSO to adjacent heterodimers, forming corrugated bands. The stacking of parallel bands leads to layers parallel to (001). Strong hydrogen bonds are only present within the alternating heterodimer - DMSO bands (Figure 12) and not in between the layers or stacking of the bands, which implies that the solvent could escape easily compared with HH and could explain why S_DMSO is not a long-living solvate. The solvate and the desolvation product, form I, both contain similar 1D stacks of acids, along a in S_DMSO (perpendicular distance: 3.024 Å, centroid distance: 6.398 Å) and c in form I (perpendicular distance: 3.489 Å, centroid distance: 5.198 Å). This implies that on losing the solvent a rearrangement of the acid stacks with respect to adjacent stacks is necessary. On the other hand, no major change of the conformation is required for the transformation.

Figure 12.

Crystal packing of S_DMSO: (a) corrugated heterodimer − DMSO bands, view along the b-axis, (b) viewed along a-axis. Hydrogen bonds are denoted with dotted lines.

Pyridinium Salt (P2₁/n, Z′ = 1)

The pyridinium cation interacts with βRA carboxylate via an ionic N⁺−H···O hydrogen bond (Supporting Information, Figure S5).

3.2. Theoretical Predictions of Anhydrates

The crystal energy landscape showed that only the two most stable conformations, differing in the position of the p-OH proton, could generate crystal structures within the likely energy range of polymorphism. The lowest energy crystal structures had the lowest energy conformation (conf_p1, Figure 1), there were a few with the alternative p-OH conformation (conf_p2), but the majority of hypothetical structures contained both conformations, conf_p1 and conf_p2, in a 1:1 ratio producing Z′ = 2 structures. The lack of any crystal structures varying the conformation of the intramolecular H-bond, involving the o-OH proton and C=O oxygen, is consistent with the experimental cocrystals,⁵³⁻⁵⁵ solvates, including hydrates and modifications.(7) Experimentally, only conformations closely related to conf_p1 and conf_p2, or a mix of the two, were observed, with the largest deviation of up to 10° in the position of the p-OH proton from planarity.

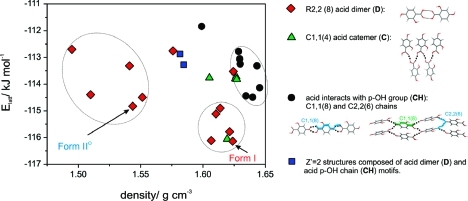
All low-energy structures (Figure 13) form one intra- and two intermolecular hydrogen bonds. The majority of computed crystal structures exhibit the experimentally observed R₂²(8) acid dimer (D), but there are also acid catemer (C), COOH···OH chain (CH), and the combination of D and CH structures. The two experimental anhydrates were found to correspond to the lowest-energy structures within the two lowest energy groups of structures, with form I being the global minimum. However, there is a low energy catemeric structure that is very competitive in energy with the known forms, and various other high density structures which also appear thermodynamically feasible.

Figure 13.

Lattice energy landscape for the βRA anhydrates (E_latt = U_inter + ΔE_intra) after relaxation of the conformation within the crystal structure, classified by the hydrogen-bonding motif. All structures with the same hydrogen bonding motif (symbol) within an ellipse are closely related.

The reproduction of form II° was excellent, given the neglect of thermal effects in our model, with an optimal root-mean square overlay of all non-hydrogen atoms in a 15 molecule coordination cluster (rmsd₁₅)(56) of 0.16 Å. In contrast, the reproduction of form I was poor with an rmsd₁₅ of ca. 1 Å, and it was wrongly predicted to be denser and more stable than form II°. The estimated Helmholtz free energies(57) derived from the elastic constants(58) and k = 0 phonons(59) calculated in rigid-body harmonic approximation (Table S11, Supporting Information) for the two polymorphs bring forms I and II° to within 0.2 kJ mol⁻¹ in energy. Hence, the static lattice energy model (Figure 13) is certainly overestimating the energy differences between the two polymorphs.

Since proton disorder is suggested by the IR spectrum and the Hirshfeld d_norm plot (section 3.1.3 and 3.1.4), we computationally generated three alternative ordered versions of form I differing only in the proton conformations which were kept fixed (Supporting Information, section 2.3). This resulted in structures that were slightly less dense, and in similar or better agreement with the experimental structure than the global minimum on the crystal energy landscape. Hence, proton disorder in form I would result in a less dense structure, and some of the destabilization(60) may be counteracted by configurational entropy. The calculations also showed that there was no barrier in this crystal structure to the proton moving by ±30° from the lowest energy planar conformation.

4. Discussion

The extensive screen for solid-state forms revealed nine crystalline βRA phases. Unfortunately, we were not able to grow single crystals suitable for structure determination for all solid-state forms. From the IR and Raman spectra, it could be assumed that in all phases the βRA molecules are dimerized, as the symmetric ν(C=O) band appeared in the region 1675−1625 cm⁻¹.^61,45,46 Furthermore, information about the hydrogen bonding of the p-OH group in the two anhydrates could be derived from the IR spectra. The shift of ν(OH) in form II° to lower wavenumbers indicates a stronger intermolecular O−H···O hydrogen bond compared to form I. The broadening in the form I spectrum was attributed to the undetermined p-OH proton position between adjacent o- and p-OH groups (see section 3.1.4). On the basis of the experimental as well as theoretical results, we could not rule out the p-OH proton showing static or dynamic disorder. Static proton disorder has been shown to be possible by lattice energy minimization calculations which also show that there is no barrier to changing the proton position within the form I crystal structure, so it could also be dynamically disordered. Further insight into the disorder could be obtained from periodic ab initio calculations,(62) but the possibilities of experimental verification are very limited without neutron diffraction data.

The βRA solid-state forms differ considerably in their relative stability. At ambient conditions only the two anhydrates and HH are stable. MH and all five solvates survive only for a short time after harvesting from the mother liquor. The formation of such unstable solvent adducts is common in organic molecules; however, these are easily overlooked, especially when the product is dried prior to analysis or when the analysis is not performed immediately after the removal from the mother liquor.(44) In contrast to the metastable solvates, HH, in which water plays a structural role, is a very stable phase, as dehydration occurs only at temperatures higher than 60 °C or under the driest conditions (below 10% RH, 25 °C). The extreme hysteresis between the sorption and desorption process of HH attests to the high kinetic barrier of the hydration and dehydration processes with respect to vapor pressure. It is interesting that all hemisolvates (incl. HH) exhibit a desolvation temperature above 60 °C in the DSC/TGA experiments and revert to the metastable form I. The monosolvates (S_AA and MH) desolvate below 60 °C to the thermodynamically most stable form II°. Therefore, it is obvious that the desolvation temperature is critical for the formation of a specific polymorph.

Even though a large number of experiments were performed, we cannot guarantee that all possible βRA forms were found, as the range of variables in crystallization experiments that could influence the outcome is very large. The anhydrate crystal energy landscape showed that the two known forms are the most likely polymorphs. The alternative dimer−based structures (Figure 13) are sufficiently similar to the known polymorphs suggesting that they could readily transform to form I or II° in the unlikely event that they were distinct at the nucleation stage. However, the lattice energy landscape suggests that other polymorphs could exist, which do not have the carboxylic acid dimer motif, but form exclusively COOH catemers or chains. A CSD(5) analysis of o-OH benzoic acid derivatives(63) showed that the R₂²(8) carboxylic acid dimer motif is the predominant hydrogen bonding motif, as seen in all four structurally characterized βRA phases. The relative stability of the catemeric structures on the crystal energy landscape may be overestimated by the computational model. We cannot exclude the possibility that the formation of the dimer motif is kinetically favored in all the crystallization conditions we have explored, hence ruling out the formation of catemers during our screening experiments.

5. Conclusions

β-Resorcylic acid represents another organic molecule exhibiting a complex solid-state behavior, that is, polymorphism, salt, and solvate (hydrate) formation. The experimental search has resulted in seven new solid-state forms (anhydrate, monohydrate, and five solvates), in addition to the previously known, and structurally characterized anhydrate II°⁷ and hemihydrate HH.(8) We found no evidence for a triclinic polymorph (ZZZEEU(6)) or a hydrate showing a water/acid stoichiometry greater than 1:1.(64)

Before we can answer the question “how exhaustive should a polymorph screen be?”, perhaps we must add a supplementary question, namely, “how exhaustive does your knowledge of physical form diversity need to be?”; that is, do we need to confirm that the most thermodynamically favorable form at 25 °C is already known or do we want to identify all accessible solid forms, perhaps to select a metastable form that has superior properties? It is worth considering these alongside any limitations in terms of available material, stability, time, etc. when designing a comprehensive screening strategy. However, recognizing that it is impractical to sample all possible nucleation and growth conditions for a given molecule, we can conclude that as a minimum, a polymorph screen should include sufficient diversity to at least find the thermodynamically most stable polymorph (non solvated) and hydrate form(s) as well as those thermodynamically unstable forms that show sufficient kinetic stability at ambient conditions (termed metastable forms) to enable them to be isolated and identified. Furthermore, a polymorph screen should identify all crystallization products, including intermediates in the crystallization process, for example, solvates, amorphous form, etc. and characterize transformation pathways in order to find alternative, or perhaps only,^65,66 routes to obtain a specific form. Therefore, a robust screening approach requires the combination of a variety of experimental approaches(67) including crystallization from solution (evaporation, cooling, slurry conversions), sublimation, crystallization from the melt, thermal and moisture dependent studies and desolvation methods. The statement by Maria Kuhnert-Brandstaetter,(68) “Probably every substance is potentially polymorphous. The only question is, whether it is possible to adjust the external conditions in such a way that polymorphism can be realized or not”, reflects the problem that there are numerous additional strategies, at ambient and nonambient conditions, which might be adequate for the nucleation and growth of further solid-state forms. It is practically not feasible to cover the whole range of techniques that have been shown to produce new polymorphs for certain systems,(21) particularly using all kinds of templates, additives, seeds, or impurities that might generate new forms or stabilize metastable phases.⁶⁹⁻⁷¹ The instability of many solvates of β-resorcylic acid, the possibility of considerable variation in the p-OH position in form I, and the computed thermodynamically feasible anhydrates mean that we cannot exclude the discovery of other solid-state forms. Therefore, our results for β-resorcylic acid emphasize the problems of determining the complete set of solid-state forms when there is evidence of disorder or short-lived intermediate crystallization products whose lifetime is very dependent on conditions. Thus, the consistency between the experimental and computational techniques used in this study adds confidence that the practically most important β-resorcylic acid solid-state forms at ambient conditions have been characterized, showing the value of calculating the crystal energy landscape as part of the screening process.

Supporting Information Available

Conditions and outcomes of the manual solvent crystallization screen, photomicrographs showing the dehydration of the βRA HH embedded in silicon oil, semi/schematic energy-temperature diagram, PXRD patterns and characteristic peak positions for each βRA phase and the pyridinium salt, dehydration of the hydrates monitored with PXRD, crystallographic information (.cif files), hydrogen bonding motif for the pyridinium salt, potential energy surface (PES) scans, testing of the repulsion-dispersion model and basis set, computational modeling for form I, list of hypothetical βRA low-energy structures. This information is available free of charge via the Internet at http://pubs.acs.org.