Detecting disease-specific patterns of brain structure using cortical pattern matching and a population-based probabilistic brain atlas

Abstract

The rapid creation of comprehensive brain image databases mandates the development of mathematical algorithms to uncover disease specific patterns of brain structure and function in human populations. We describe our construction of probabilistic atlases that store detailed information on how the brain varies across age and gender, across time, in health and disease, and in large human populations. Specifically, we introduce a mathematical framework based on covariant partial differential equations (PDEs), pull-backs of mappings under harmonic flows, and high-dimensional random tensor fields to encode variations in cortical patterning, asymmetry and tissue distribution in a population-based brain image database (N =94 scans). We use this information to detect disease-specific abnormalities in Alzheimer's disease and schizophrenia, including dynamic changes over time. Illustrative examples are chosen to show how group patterns of cortical organization, asymmetry, and disease-specific trends can be resolved that are not apparent in individual brain images. Finally, we create four-dimensional (4D) maps that store probabilistic information on the dynamics of brain change in development and disease. Digital atlases that generate these maps show considerable promise in identifying general patterns of structural and functional variation in diseased populations, and revealing how these features depend on demographic, genetic, clinical and therapeutic parameters.

1 Introduction

The widespread and rapidly accelerating collection of normal and diseased brain images in vivo and ex vivo has led to a tremendous increase in the number of investigations focusing on the structural and functional organization of the brain [1]. The complexity and variability of human brain structure across subjects is so great that mathematical algorithms are essential to effectively analyze and interpret brain data. Digital brain atlases, for example, represent anatomy in a 3-dimensional coordinate system. New data can be aligned with the atlas coordinate system using linear or nonlinear registration techniques [2], making it easier to pool and compare brain data from multiple subjects. Nonetheless, design of population-based brain atlases presents considerable challenges, since these systems must capture how anatomy and function vary across age and gender, in different disease states, and across imaging modalities. They must also represent these variations in such a way that systematic patterns can be identified. Beyond Individual Atlases. Recent developments in computational anatomy have expanded the atlas concept to store information on anatomical variation in a population [3-5]. Deformable brain atlases [6-8] are digital brain templates that can be elastically deformed to match the anatomy of a new subject. These atlases have powerful applications in automated image labeling [9], automated morphometry [10] and multimodality correlation [11]. They can also transfer metabolic, functional, and cytoarchitectural maps into the coordinate system of a new patient for surgical planning [12] or to relate in vivo functional and post mortem molecular hallmarks of disease [13]. Probabilistic atlases [3,14,15] store information on structural and functional variability in a population. Depending on the attribute whose statistical distribution is modeled, the information they encode can support pathology detection in an individual or group [14], or provide Bayesian prior information for tissue classification [16], image matching [8] or functional image analysis [17]. Probabilistic atlases have enormous promise in revealing the anatomical distribution and timing of clinical abnormalities in disease [18,5]. Although many diseases affect the anatomy of the cortex, there have been major difficulties in developing average and statistical representations of cortical anatomy, in view of the extreme variations in cortical patterning across subjects. Systematic differences or dynamic changes in cortical organization, gray matter distribution or asymmetry have been difficult to distinguish from normal variations, which also complicate the direct averaging of imaging data in stereotaxic space. Goals of the Paper. In this paper, we introduce a mathematical framework based on covariant partial differential equations (PDEs) and multivariate random tensor fields to encode variations in cortical patterning, tissue distribution and asymmetry. We build on earlier work by applying new algorithms to brain image databases from diseased populations with Alzheimer's disease and schizophrenia, including longitudinal data. We present three illustrative examples of algorithms detecting underlying patterns of disease-specific tissue loss, cortical asymmetry and dynamic brain change that are not easily identifiable in individual subjects' images. These applications suggest the potential of the approach in biomedical and clinical research settings.

2 Methods

Imaging and Subject Populations

94 high-resolution (256²×124) T1-weighted fast SPGR (spoiled GRASS) MRI volumes were acquired from four distinct subject populations: patients with Alzheimer's Disease, adolescents with schizophrenia, and their corresponding matched healthy control populations. 26 subjects with mild to moderate Alzheimer's Disease (AD; NINCDS-ARDRA criteria) were imaged on GE Signa 1.5T clinical scanner (TR/TE 14.3/3.2 msec, flip angle 35°, NEX=1, 25cm FOV, contiguous 1.2 mm thick slices). Patients were matched for disease severity(Mini-Mental State Exam score: 20.0±0.9), and were matched for age (75.8±1.7 yrs.; 14 females/12 males), educational level (15.2±0.4 yrs.), and handedness (all right-handed) with 20 identically-imaged elderly control subjects (age: 72.4±1.3 yrs.; 8 females/12 males; education: 15.4±0.5 yrs.). A separate group of 24 subjects, recruited as part of an ongoing NIMH study of childhood-onset schizophrenia [19], were imaged longitudinally a t baseline and after a 5-year interval. The 12 healthy controls (aged 13.5±0.7 years at initial scan, 18.0±0.8 years at follow-up) were age- and gender-matched with the 12 schizophrenic patients and scanned identically at exactly the same ages and intervals (patients' ages: 13.9±0.8 and 18.6±1.0 years; interval between scans: 4.6±0.3 years). Image data were initially transformed into a Talairach-based coordinate system [20] which (1) places the anterior commissure (AC) at the origin; (2) vertically orients the midsagittal plane; and (3) horizontally orients the AC-PC line. Aligned MR volumes were corrected for non-uniformity of MR signal intensity[16], and high-resolution surface models of the cerebral cortex were extracted, as described previously [14,21].

Mapping Cortical Patterns

To begin encoding patterns of cortical variability, parametric curves representing 36 major external fissures and sulci in the brain were manually out lined on highly magnified surface-rendered images of each cortical surface. Detailed anatomic criteria were applied as set out in [14] and the Ono sulcal atlas [22] to define sulci with consistent incidence and topology across subjects. In both brain hemispheres, 3D curves were traced to represent superior and inferior frontal, precentral, central, postcentral, intraparietal, superior and inferior temporal, primary and secondary intermediate, collateral, olfactory and occipito-temporal sulci, as well as the Sylvian fissures. Additional 3D curves represented gyral limits at the interhemispheric margin [14]. Stereotaxic locations of contour points derived from the data volumes were redigitized to produce 36 uniformly parameterized cortical contours per brain, representing each subject's primary gyral pattern.

Measuring Gyral Pattern Differences

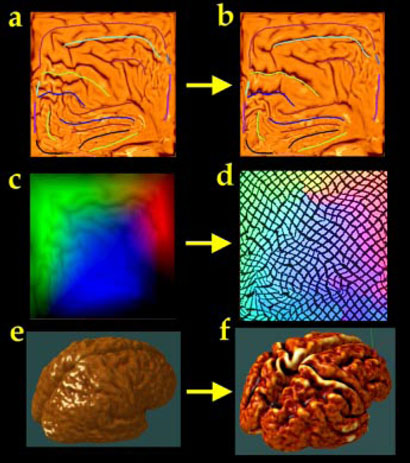
Due to variations in gyral patterning, cortical variability is severely underestimated unless elements of the gyral pattern are matched from one subject to another (cf. [9,14]). This matching is also required for cortical averaging; otherwise, corresponding gyral features will not be averaged together. To find good matches among cortical regions we performed the matching process in the cortical surface's parametric space, which permits more tractable mathematics (Fig. 1; [14,23,24]). This vector flow field in the parametric space indirectly specifies a correspondence field in 3D, which drives one cortical surface into the shape of another. This mapping not only matches overall cortical geometry, but matches the entire network of the 36 landmark curves with their counterparts in the target brain, and thus is a valid encoding of cortical variation. Maps of the Cortical Parameter Space. Cortical models were created by driving a tiled, spherical mesh into the configuration of each subject's cortex [25,21,26], so any point on the cortical surface must map to exactly one point on the sphere and vice versa. Each cortical surface is parameterized with an invertible mapping D_p,D_q: (r,s) → (x,y,z), so sulcal curves and landmarks in the folded brain surface can be re identified in a spherical map (cf. [24]). To retain relevant 3D information, cortical surface point position vectors (x,y,z) in 3D stereotaxic space were color-coded using a unique RGB color triplet, to form an image of the parameter space in color image format (Fig. 1). These spherical locations, indexed byt wo parameters, can also be mapped to a plane (Fig. 1; [14]). Cortical differences between any pair of subjects were calculated as follows. A flow field was first calculated that elastically warps one flat map onto another from the other subject (Fig. 1; or equivalently, one spherical map onto the other). On the sphere, the parameter shift function u(r):Ω → Ω, is given by the solution F_pq:r → r-u(r) to a curve-driven warp in the spherical parametric space Ω =[0,2π) × [0, π) of the cortex (Fig. 1; [14]). For points r=(r,s) in the parameter space, a system of simultaneous partial differential equations can be written for the flow fieldu(r):

$$L^{\text{\#}}\text{(u(r))}\text{+}\text{F(r-u(r))}\text{=}\text{0,}\forall \text{r}\in \Omega \text{,\hspace{0.25em}with}\text{u(r)}\text{=}{\text{u}}_{\text{0}}\text{(r),}\forall \text{r}\in {\text{M}}_{\text{0}}\cup {\text{M}}_{\text{1}}\text{.}$$ 1

Here M₀, M₁ are sets of points and (sulcal or gyral) curves where displacement vectors u(r)=u₀ (r) matching corresponding anatomy across subjects are known. The flow behavior is modeled using equations derived from continuum mechanics, and these equations are governed by the Cauchy-Navier differential operator L = μ∇²+(λ+μ)∇(∇^T●) with body force F [14,27,4]. The only difference is that L^# is the covariant form of the differential operator L (for reasons explained below¹). This approach not only guarantees precise matching of cortical landmarks across subjects, but creates mappings that are independent of the surface metrics, and therefore independent of the surface parameterizations. Cortical Averaging using Pull-backs and Flows in Parameter Space. The inter subject variability of the cortex is computed by first creating an average cortex for each subject group and measuring individual differences from the deformation mappings that drive the average model onto each individual. By defining probability distributions on the space of deformation transformations applied to the average template [4], statistical parameters of these distributions are estimated from the data based anatomic data to determine the magnitude and directional biases of anatomic variation. To do this, all 36 gyral curves for all subjects are first transferred to the parameter space. Next, each curve is uniformly re-parameterized to produce a regular curve of 100 points whose corresponding 3D locations are uniformly spaced. A set of 36 average gyral curves for the group is created by vector averaging all point locations on each curve. This average curve template (curves in Fig. 1(a)) serves as the target for alignment of individual cortical patterns [24]. Each individual cortical pattern is transformed into the average curve configuration using a flow field in the parameter space (Fig. 1(b); cf. [33]). By carrying a color code (that indexes 3D locations; Fig. 1(c)) along with the vector flow that aligns each individual with the average folding pattern, information can be recovered at a particular location in the average folding pattern (Fig. 1(d)) specifying the 3D cortical points mapping each subject to the average. In the language of Lie algebras, corresponding 3D cortical points across the subject database are defined as the pull-back Dp*(r) [28] of the parameterization mappings Dp: (r,s)→(x,y,z) under the covariant vector flow u(r) that maps each subject to the average curve template. [For any smooth function Dp*: Ω→Rⁿ and any diffeomorphic map u(r): Ω→N, there is a function on N, D_p*: N→Rⁿ called the pull-back of D_p by u(r), and defined by Dp ○ u [28]. This produces a new coordinate grid [the pull-back D_p*(r); Fig. 1(d)] on a given subject's cortex in which particular grid-points appear in the same location across subjects relative to the mean gyral pattern. By averaging these 3D positions across subjects, an average 3D cortical model can be constructed for the group. An example of this type of cortical average, based on 9 subjects with Alzheimer's disease, is shown in Fig. 1(f). The resulting mapping is guaranteed to average together all points falling on the same cortical locations across the set of brains, and ensures that corresponding features are averaged together.

Fig. 1. Averaging Cortical Models.

A well-resolved average cortical model (f) for a group of subjects can be created by first flattening each subject's cortical model to a 2D square (a). A color coded map (c) stores a unique color triplet (RGB) at each location in the 2D parameter space encoding the (x,y,z) coordinate of the 3D cortical point mapped to that 2D location. However, a well-resolved average model (f) is produced, with cortical features in their group mean location, if each subject's color map is first flowed (d) so that sulcal features are driven into the configuration of a 2D average sulcal template (b). Codes indexing similar 3D anatomical features are placed at corresponding locations in the parameter space, and are thus reinforced in the group average (f).

Affine Shape Adjustment

Prior to generating an average cortex, an average image template is generated with the average affine shape for the subjects in the group, and individual scans are globally aligned to this template. This is done so that (1) differences in global brain scale and affine position are factored out before computation of variability, and (2) measurements are made and maps generated at the mean spatial scale for the group. To produce a template with the mean image intensity and geometry for the group, a subset of brains was selected for which a comprehensive set of anatomic surface models had been created (84 per brain), including models of deep brain structures [34]. An initial image template for the group was constructed by (1) using automated linear transformations [35] to align the MRI data with a randomly selected image, (2) intensity-averaging the aligned scans, and then (3) recursively re-registering the scans to the resulting average affine image. The resulting average image was adjusted to have the mean affine shape for the group, using matrix logarithms for transformation averaging and exponentiation [35]. Images and surface models were then linearly aligned to this template, and an average surface set was created for the group [34]. Displacement maps (Fig. 2(e)) driving the surface anatomy of each subject into correspondence with the average surface set were then extended to the full volume with a 3D warping algorithm based on surfacedriven elasticity[14,25,27]. These warping fields reconfigured each subject's 3D image into the average anatomic configuration for the group. By averaging the reconfigured images (after intensity normalization), a crisp image template was created to represent the group (Fig. 2(c)). Note the better-resolved cortical features in the average images after high-dimensional cortical registration (Fig. 2(c)). If desired, this AD-specific atlas can retain the coordinate matrix of the Talairach system (with the anterior commissure at (0,0,0)) while refining the gyral map of the Talairach atlas to encode the unique anatomy of the AD population. By explicitly computing matching fields that relate gyral patterns across subjects, a well-resolved and spatially consistent set of probabilistic anatomical models and average images can be generated to represent the average anatomy and its variation in a subpopulation.

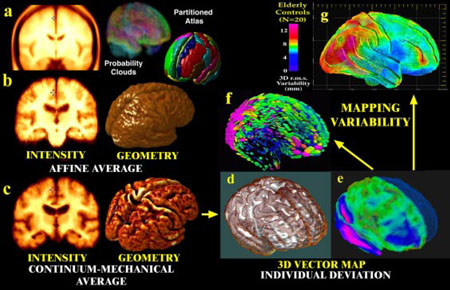
Fig. 2. Probabilistic Modeling of Brain Anatomy.

Direct averaging of imaging data after a simple affine transform into stereotaxic space washes cortical features away((a); Evans et al., 1994; N=305 normals); (b) a similar approach with N=9 Alzheimer's patients). By first averaging a set of vector-based 3D geometric models, and warping each subject's scan into the average configuration, a well-resolved average brain template is produced (c). Deformation vector maps (e) store individual deviations (brown mesh) from a group average (white surface, (d)), and their covariance fields (f) store information on the preferred directions and magnitude (g) of anatomic variability(pink colors, large variation; blue colors, less).

3 Results

Tensor Maps of 3D Cortical Variation

By using cortical pattern matching to identify corresponding cortical locations in 3D space, rather than simple image averaging (Fig. 2(a),(b)), deformation maps can be recovered mapping each patient into gyrus-by-gyrus correspondence with the average cortex (Fig. 2(e)). Anatomic variability can thus be defined at each point on the average cortical mesh as the root mean square magnitude of the 3D displacement vectors, assigned to each point, in the surface maps from individual to average. This variability pattern is visualized as a color-coded map (Fig. 2(g)). This map shows the anatomic differences, due to gyral pattern variation, that remain after affine alignment of MR data into a brain template with the mean shape and intensity for the group. After these affine components of the deformation fields are factored out, the deformation vector required to match the structure at position x in the average cortex with its counterpart in subject i can be modeled as:

$${\mathbf{\text{W}}}_i(\text{x})=\mu (\text{x})+\Sigma {(\text{x})}^{1/2}{\in }_i(\text{x}).$$ 4

Here μ(x) is the mean deformation vector for the population (which approaches the zero vector for large N), Σ(x) is a non-stationary, anisotropic covariance tensor field estimated from the mappings, Σ(x)^½ is the upper triangular Cholesky factor tensor field, and ϵ_i(x) can be modeled as a trivariate random vector field whose components are independent zero-mean, unit variance, stationary random fields. This 3D probability distribution makes it possible to visualize the principal directions (eigenvectors) as well as the magnitude of gyral pattern variability, and these characteristics are highly heterogeneous across the cortex. For any desired confidence threshold α, 100(1-α)% confidence regions for possible locations of points corresponding to x on the average cortex are given by nested ellipsoids Eλ(α)(x) in displacement space (Fig. 2(f)).

$${\text{E}}_{\text{λ}}(\text{x})=\{\mu (\text{x})+\text{λ}{[\Sigma (\text{x})]}^{-1/2}\text{p}|\forall \text{p}\in \text{B}(\text{0};\text{1})\},$$ 5

where B(0; 1) is the unit ball in R³, and

$$\text{λ}(\alpha )={[{[N(N-3)/3(N^2-1)]}^{-1}{F}_{\alpha ,3,N-3}]}^{1/2},$$ 6

where F_{α,3, N−3} is the critical value of the F distribution such that Pr{F_3,N−3 ≥ F_α,3,N−3} = α and N is the number of subjects. Mean Asymmetry. By analysis of variance in 3D deformation fields that match different subjects' anatomies, it is also possible to differentiate intra-subject (between hemisphere), inter-subject, and inter-group contributions to brain variation in human populations, and detect significant differences using null distributions for features in Hotelling's T² random fields [14,36,37]. Mapping the pattern of brain asymmetry in a group is an interesting application. Although the set of mappings computed so far specifies the set of cortical points that correspond across subjects, the mean asymmetry cannot yet be computed without an additional set of mappings to define the points that correspond across hemispheres. To do this, all left hemisphere sulcal curves are projected into the cortical parameter space, reflected in the vertical axis, and averaged with their flattened counterparts in the right hemisphere, to produce a second average curve template. Color maps (Fig. 1(c)) representing point locations in the left and right hemispheres are then subjected to a second covariant flow that transforms corresponding features in each hemisphere to the same location in parameter space. 3D deformation fields can then be recovered matching each brain hemisphere with a reflected version of the opposite hemisphere (cf. [36]). The parameter flows are advantageous in that the asymmetry fields are also registered; in other words asymmetry measures can be averaged across corresponding anatomy at the cortex. This is not necessarily the case if warping fields are averaged at the same coordinate locations in stereotaxic space (cf. Fig. 1(a)). The pattern of mean brain asymmetry for a group of 20 subjects is shown in Fig. 3. The resulting asymmetry fields ai(r) (at parameter space location r in subject i) were treated as observations from a spatially-parameterized random vector field [14,36], with mean μ_a(r) and a nonstationary co variance tensor Σ_a(r) (Fig. 3(c)). The significance α of deviations from symmetry can be assessed using a T² or F statistic that indicates evidence of significant asymmetry in cortical patterns between hemispheres:

$$\begin{array}{l}\alpha (\text{r})=F_{3,N-3}^{-1}([(N\text{-}3)/3(N\text{-}1)]{\text{T}}^2(\text{r}))\\ {\text{where\hspace{0.25em}T}}^2(\text{r})=N[{\mu }_{\text{a}}{\text{(r)}}^T{\Sigma }_{\text{a}}{}^{-1}(\text{r}){\mu }_{\text{a}}\text{(r)}].\end{array}$$ 7

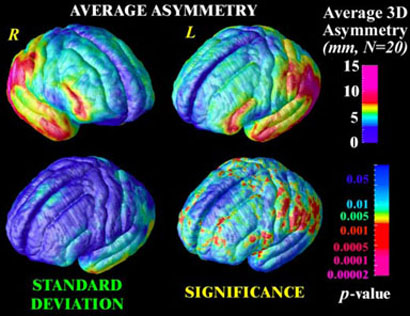
Fig. 3. Mapping Brain Asymmetry in a Population.

The average magnitude of brain asymmetry in a group (N=20, elderly normals) can be assessed based on warping fields that map the cortical pattern of one hemisphere onto the other, and then flow the observations again so that corresponding measures can be averaged across subjects. Variations in asymmetry are also non-stationary across the cortex (lower left), and a Hotelling's T² statistical field can be computed to map the significance of the asymmetry (lower right) relative to normal anatomic variations.

Multiple Comparisons Correction

By calculating these statistics, and their corresponding significance values (p -values), at each lattice location across a parameterized 3D anatomical surface, a statistic image is formed (Fig. 3(d)). To assess the significance of the effect, analytical null distributions have been derived for the number and extent of signal components that are likely to occur by accident above a given threshold in a statistic image, such as a T²-distributed random field on a manifold. Because these formulae require the residuals of the statistical model to be stationary an disotropic [38,39], we adopted a non-parametric approach. A null distribution for the area of the T2 statistic image above a fixed high threshold on the average cortical surface was computed empirically by permutation of the covariate vector (here a binary vector coding for hemisphere) and conducting 1,000,000 randomizations. By reference to this null distribution, the significance of the asymmetry was found to be p < 0.01.

Gray Matter Loss in a Diseased Population

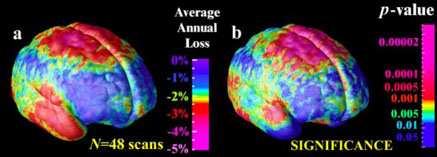
A second application was to reveal the average profile of gray matter loss across the cortex in Alzheimer's disease, based on a large number of subjects at a specific stage in the disease. Gyral pattern variation makes it difficult to make inferences if gray matter maps are directly averaged together in stereotaxic space (e.g.,Fig. 1(a)), and the ability to localize results to specific cortical regions is also lost. To address this, we used covariant flows to assist in computing group averages and statistics. First, we segmented all images in the database with a previously validated Gaussian mixture classifier. Maps of gray matter, white matter, CSF and a background class were created for each subject (Fig. 4.). The proportion of gray matter lying within 15 mm of each cortical point was then plotted as an attribute on each cortex, and aligned across subjects by projecting it into flat space (Fig. 1(c)) and warping the resulting attribute field with the elastic matching technique (as inFig. 1(d)). (Again, the gray matter proportion can be thought of as a scalar attribute G(r) defined in the cortical parameter space, which can be subjected to a pull-back with the flow field u(r) to compensate for gyral pattern differences). By averaging the aligned maps, and texturing them back onto a group average model of the cortex, the average magnitude of gray matter loss was computed for the Alzheimer's disease population (Fig. 4.). Regions with up to 30% reduction in the measure were sharply demarcated from adjacent regions with little or no loss. The group effect size was measured by attaching a field of t statistics, t (r), to the cortical parameter space, and computing the area of the t field on the group average cortex above a fixed threshold (p < 0.01, uncorrected). In a multiple comparisons correction, the significance of the overall effect was confirmed to be p < 0.01, by permuting the assignment of subjects to groups 1,000,000 times. (The resulting 46×65536×10⁶≅3.0×10¹² linear regressions for 46 subjects, 65,536 cortical points, and 10⁶ permutations - were run in parallel on an SGI RealityMonster with 32 R10000 180MHz internal CPUs, requiring 33 CPU hours in total). Dynamic Brain Change. In a third application, the same procedure was applied to longitudinal MRI data from 12 schizophrenic patients and 12 adolescent controls scanned at both the beginning and end of a 5-year interval. The goal was to estimate the average rate of gray matter loss at the cortex, by matching cortical patterns and comparing changes in disease with normal changes in controls. Cortical models and gray matter measures were elastically matched first within each subject across time, to compute individual rates of loss, and then flowed into an average configuration using flat space warping (Fig. 1(d)). The resulting maps (Fig. 5) suggested dynamic loss of gray matter in superior parietal, motor and frontal brain regions (up to 5% annually), and the group differences were highly significant (p < 0.01, permutation test; Fig. 5(b)). Conclusion. Atlasing of brain data from large human populations presents major challenges because of the need to compare or integrate imaging data from subjects whose anatomy is different. Although direct averaging of data in stereotaxic space may be ideal for many applications, group patterns in brain structure or function may go unnoticed because cortical regions are not well-aligned across subjects. We presented an approach that allows the generation of well-resolved average brain maps that accommodate the wide variations in cortical patterning. By capturing variations in cortical attributes and cortical geometry using separate statistical fields, general features of cortical organization also emerged, such as the consistent pattern of brain asymmetry in perisylvian cortices (Fig. 3). Finally, by mapping gray matter differences or dynamic changes in diseased populations with Alzheimer's disease and schizophrenia, we resolved general features of the disease process that may be hard to identify in individual scans. The resulting atlasing techniques show promise in elucidating the dynamics of disease in human populations, and their relationship to genetic, cognitive, or therapeutic factors.

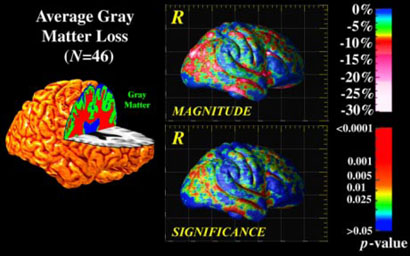
Fig. 4. Mapping Gray Matter Loss in a Population.

Scalar fields that represent the distribution of gray matter across the cortex can be aligned using elastic matching of cortical patterns. A localized and highly significant loss of gray matter is revealed in temporo-parietal cortices of Alzheimer's patients relative to matched elderly controls, in a similar pattern to the metabolic and perfusion deficits seen early in the disease.

Fig. 5. Dynamic Rates of Gray Matter Loss in a Population.

Scalar fields representing the rates of gray matter loss in individuals with schizophrenia can be aligned and compared with age-matched controls. Adolescents with schizophrenia experience statistically higher rates of loss in motor, frontal and temporal regions.