Abstract
Background:
The complex motions of the wrist are described in terms of four anatomical directions that are accomplished through the multiple articulations of the carpus. With minimal tendinous insertions, the carpus is primarily a passive structure. This emphasizes the importance of its mechanical properties, which few studies have examined to date. The purpose of the present study was to determine the mechanical properties of the wrist in twenty-four different directions of wrist motion.
Methods:
The moment-rotation mechanical behavior of six fresh-frozen cadaver wrists was determined in four directions: flexion, extension, ulnar deviation, and radial deviation. Twenty other directions that were a combination of these anatomical directions were also studied. A custom-designed jig was interfaced with a standard materials testing system to apply unconstrained moments. Moments of ±2 Nm were applied, and the moment-rotation data were recorded and analyzed to determine the neutral zone, range of motion, and stiffness values as well as the orientation of the envelope of these values.
Results:
The envelope of wrist range-of-motion values was ellipsoidal in shape and was oriented obliquely (p < 0.001) to the direction of pure flexion-extension by a mean (and standard deviation) of 26.6° ± 4.4°. The largest wrist range of motion was a mean of 111.5° ± 10.2°, in the direction of ulnar flexion, 30° from pure flexion. The largest stiffness (mean, 0.4 Nm/deg) was in the direction of radial flexion, while the smallest stiffness (mean, 0.15 Nm/deg) was in the direction of ulnar flexion.
Conclusions:
The mechanical axes of the wrist are oriented obliquely to the anatomical axes. The primary mechanical direction is one of radial extension and ulnar flexion, a direction along a path of the dart thrower's wrist motion.
Clinical Relevance:
Understanding the mechanical function of the wrist can aid clinical treatment decisions, arthroplasty, and implant designs. The findings of this study provide new evidence that the mechanical axes of the wrist are not collinear with the anatomical axes.
The movements of the wrist are described with use of the four orthogonal and anatomically defined directions of flexion and extension in the sagittal plane and radial and ulnar deviation in the coronal plane1. More complex movements of the wrist are required for daily living activities, and these motions are described with use of combinations of these motions2,3. For example, circumduction is the “circular” motion that traces an envelope about these four motions. The so-called dart thrower's motion, a functionally important wrist motion4-6, describes a direction of wrist motion that is oblique to these orthogonal anatomical planes. Specifically, the dart thrower's motion is used to define a direction of wrist movement that is from a position of combined extension and radial deviation to a position of combined flexion and ulnar deviation.
All wrist movements are accomplished through the complex motions of the eight carpal bones7-13. With no tendon attachments, the static and dynamic stability of the carpus, particularly the proximal row of carpal bones (scaphoid, lunate, and triquetrum), is dependent solely on the shape of the carpal articulations and on the mechanical properties of the attached capsule and ligaments. Accordingly, numerous studies have focused on carpal bone shape14-17, carpal bone kinematics11-13, ligament properties18,19, and cartilage properties20. While these studies have focused on the elements of the wrist, few studies have examined the mechanical properties of the wrist itself, defined herein as the compound joint from the distal end of the radius to the proximal part of the metacarpals.
To date, the determination of the mechanical properties of the wrist has focused on distractive loading21,22 with the aim of understanding the effects of traction in the reduction of intra-articular distal radial fractures23 and in arthroscopic surgery24,25. Determining the mechanical properties of the wrist along the directions of the various wrist movements can aid in understanding the function of the normal wrist and wrists with a pathological condition, improving treatments for wrist disorders26, constructing and validating mathematical models27-30, and developing design specifications for wrist implants31. Given that radial deviation has the smallest range of motion of the four primary anatomical directions26, we anticipated that radial deviation would have the largest stiffness values, but we were unable to find support for this in the literature. Moreover, recent studies of the dart thrower's motion and the carpal kinematics associated with this motion5,13,32,33 have suggested that the mechanical behavior of the wrist may be more complex than previously appreciated and led us to hypothesize that the mechanical axes of the wrist are not aligned with the anatomical axes.
The purpose of this study was to determine the mechanical properties of the wrist in the four anatomical directions of wrist motion and in twenty additional directions that are combinations of these motions. We quantified the mechanical properties by measuring the moment-rotation behavior of the cadaver wrist.
Materials and Methods
We studied the wrist motion of six upper-extremity cadaver specimens (three pairs from one female and two male donors, with an age of fifty-nine, sixty-two, and sixty-five years, respectively, at the time of death). Each fresh-frozen specimen was a complete upper extremity, extending from the humerus to the distal phalanges, and was confirmed to be free of gross anatomical abnormalities by visual inspection and fluoroscopic imaging. The specimens were maintained in a freezer at –20°C until thawing, approximately twenty-four hours prior to mechanical testing. In each thawed specimen, two Kirschner wires pinned the proximal part of the radius to the proximal part of the ulna in neutral forearm rotation. Neutral forearm rotation (defined clinically when the radially abducted thumb is aligned with the long axis of the humerus and the elbow is flexed at 90°) was obtained in each cadaver specimen by placing the humerus and forearm flat on the dissecting table, flexing the elbow to 90°, and then rotating the forearm so that the palm lay down flat on the dissecting table in the same plane as the forearm and humerus. Neutral forearm rotation was then further standardized under fluoroscopic examination by carefully supinating or pronating the forearm to maximize the distance between the radial and ulnar styloids on the anteroposterior view (Fig. 1). No more than 10° of correction was necessary in any specimen to achieve this standardized position. After pinning, the radius and ulna were transected between the Kirschner wire and the elbow. Distally, the digits were disarticulated at the metacarpophalangeal joints. Screws were inserted into the metacarpal heads, and soft tissues were removed to allow secure fixation in the potting material. The proximal parts of the radius and ulna and the metacarpal heads were potted in a urethane compound (Smooth-On, Easton, Pennsylvania) in cylindrically shaped molds. The finger flexors and extensors were removed. The extensor carpi radialis longus and brevis, extensor carpi ulnaris, flexor carpi radialis, and flexor carpi ulnaris were isolated, and each of these four tendon groups was whip-stitched for later attachment to constant force springs on the specimen jig. Throughout preparation and testing, the specimens were kept moist with a wrapping of saline solution-soaked gauze. Care was taken to preserve all ligamentous attachments and specimen integrity.
Fig. 1.
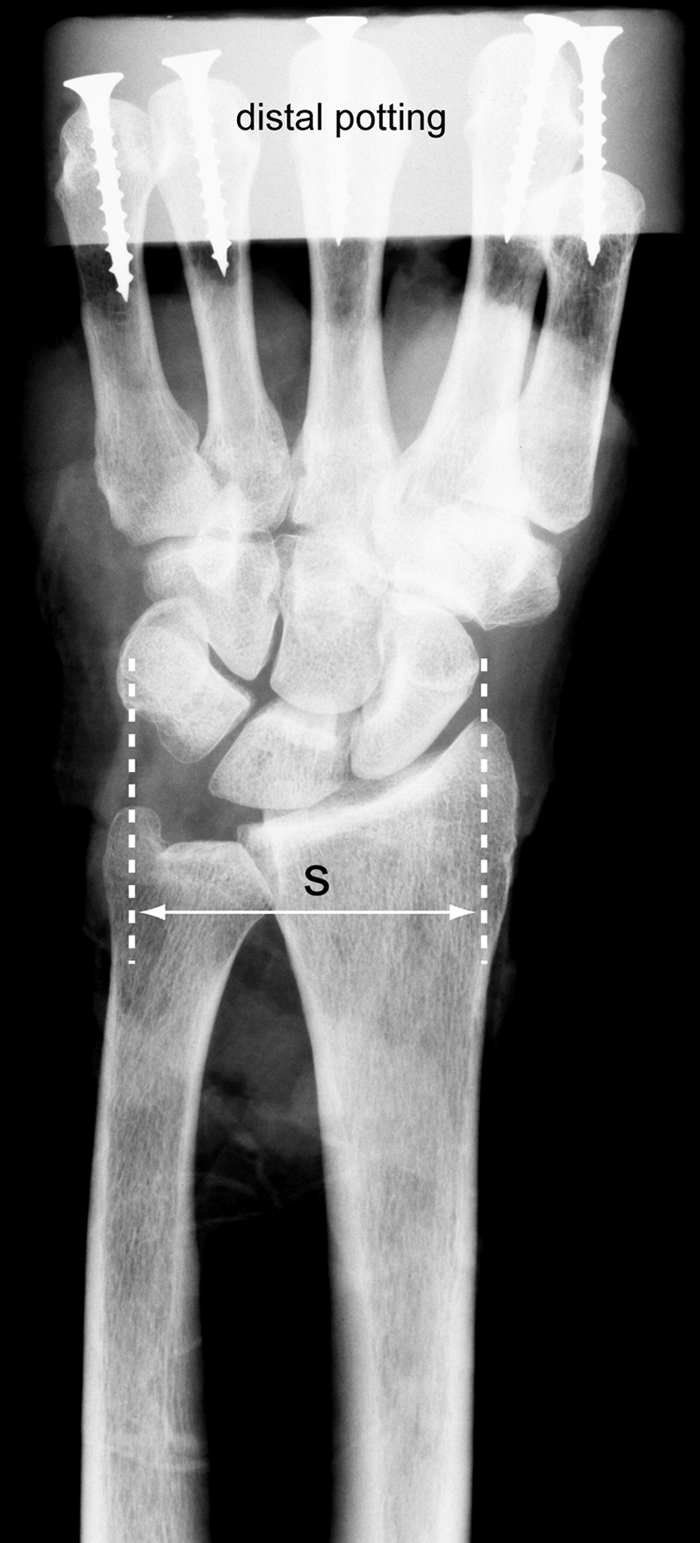
An anteroposterior radiograph of the hand and wrist of a cadaveric specimen during the potting process. The forearm of each specimen was fixed in a neutral pronation-supination posture, which was then further standardized by maximizing the distance (S) between the radial and the ulnar styloid. The proximal potting fixture and the Kirschner wires used to fix the forearm in this neutral posture are not shown.
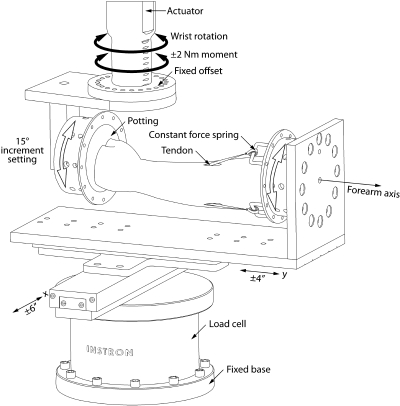
In order to apply an unconstrained moment to the wrist in each of twenty-four directions of wrist motion, a novel specimen jig was designed and fabricated to interface with a materials testing system (model 8521S; Instron, Norwood, Massachusetts) (Fig. 2). The design of the jig was based on previous studies that applied pure unconstrained moments to determine the mechanical properties of the cadaver spine, permitting the joint to rotate about its physiological axes throughout its entire range of motion34,35. In our jig design, the forearm specimen was oriented horizontally. The potting fixture for the distal part of the metacarpals was directly mounted to the torsion actuator of the materials testing device. The potting fixture for the forearm was mounted to a vertical plate. The vertical plate was attached to low-friction (0.003 coefficient of friction) x-y linear bearing slides (RS3-12 ± 6 in and RS3-8 ± 4 in; Del-Tron Precision, Bethel, Connecticut) that were directly mounted to the base of the materials testing device such that the axis of wrist rotation was not constrained. Both mountings allowed the specimen to be rotated about the long axis of the forearm and fixed at 15° increments. Fixing the specimen at 15° increments about its forearm axis permitted the testing to occur in twenty-four different directions of wrist motion. Four constant force springs (4.45 N each; McMaster-Carr, Robbinsville, New Jersey), whose force value was consistent with the loads applied to study tendon excursion and gliding in cadaver studies36, were attached to each of the isolated tendons.
Fig. 2.
Moments were applied in twenty-four different directions of wrist motion with use of a specifically designed specimen jig that interfaced to a standard materials testing system. The forearm, pinned in neutral rotation, was mounted to the jig horizontally. Moments of ±2.0 Nm were applied sinusoidally in each direction of wrist motion. The application of moments in twenty-four different directions of wrist motion was achieved by rotating the specimen about the forearm axis and then locking the potting fixtures to the jig in 15° increments. Two orthogonal linear slides (x and y) permitted the specimen to travel freely in the horizontal plane, providing an unconstrained application of the moments and allowing the wrist to rotate about its physiological axes. Four constant force springs (each 4.45 N) attached the flexors and extensors to the potting fixture.
The moment-rotation behavior was determined from 0 to 2 Nm in twenty-four directions of wrist motion. Moment was applied as a sinusoidal wave in angular displacement control to a load limit of 2 Nm at a test frequency of 0.1 Hz. To mechanically precondition the specimens in each direction, they were cyclically loaded for a total of nine cycles. Throughout testing, the vertical movement of the actuator was held at a constant position that was set to the neutral position of the wrist at the beginning of each directional test. Neutral wrist position was defined visually when the dorsal surfaces of the hand and forearm were flush and the long axes of the third metacarpal and the forearm were aligned. The vertical load, consisting of the weight of the distal potting fixture and wrist, was zeroed at the beginning of each directional test with the wrist in neutral position. Data were collected digitally at a rate of 25 Hz, with use of the test frame control system (FastTrack 8800; Instron). Only the loading portion of the last cycle was used in the data analysis. The moment-rotation behaviors were determined in the anatomically defined directions of flexion, extension, and radioulnar deviation, oriented 90° relative to each other. The remaining twenty directions of wrist motion were defined at 15° increments within these anatomical directions. For example, a direction of 45° from the flexion-extension axis would be a direction of coupled wrist motion that was equally composed of flexion-extension and radioulnar deviation.
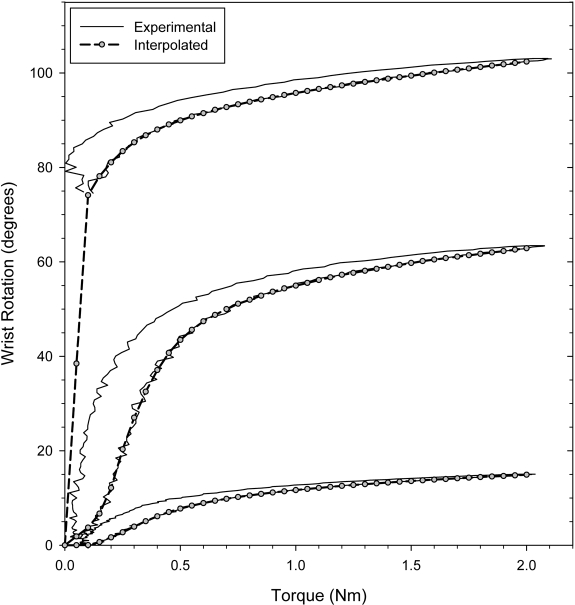
The moment-rotation curves in all directions of wrist motion were analyzed to determine the neutral zone, range of motion (ROM), and stiffness (KROM) (Fig. 3). The neutral zone is a measure of joint motion for which there is negligible stiffness. In this study, the neutral zone was defined as the wrist rotation at a moment of 0.2 Nm during the loading portion of the test. The range of motion was defined as the wrist rotation at a moment of 2.0 Nm during the loading portion of the test. All wrist rotations were calculated with respect to the neutral wrist position. To calculate stiffness, the loading portion of the moment-rotation curve was first fit with a fifth order polynomial with use of a commercially available algorithm (MATLAB; The MathWorks, Natick, Massachusetts). The final (KROM) tangential stiffness was calculated as the slope of the curve of the interpolated values between 1.5 and 2.0 Nm. The envelopes for range of motion, neutral zone, and stiffness were constructed with the set of values from all directions of testing, ordered about wrist circumduction.
Fig. 3.
Typical moment-rotation curves for three different directions of wrist motion. Range of motion was defined as the rotation at 2.0 Nm, and the neutral zone was defined as the rotation at 0.2 Nm. A fifth order polynomial was fit to the loading portion of the moment-rotation curve, and the interpolated data were used to calculate the stiffness in the region of the range of motion (KROM).
The mean and standard deviation of the neutral zone, range of motion, and KROM for all specimens, with each specimen treated as an independent observation, were calculated for each direction of wrist loading. A repeated-measures one-way analysis of variance with the Holm-Sidak method for post hoc analysis (SigmaPlot, version 11; Systat Software, San Jose, California) was used to determine if the mean range of motion and neutral zone in the directions of pure flexion, pure extension, pure ulnar deviation, and pure radial deviation were significantly different from the range of motion and neutral zone in the direction of wrist motion with the largest mean values. A p value of 0.05 was defined as significant a priori and adjusted for multiple comparisons. To examine the orientation of the range of motion, neutral zone, and stiffness envelopes, the principal axes of these envelopes were calculated for each specimen37. A one-sample t test (SigmaPlot) was then used to determine if the orientation of the principal axes of the envelopes differed significantly from the orientation of the anatomical axes with use of an a priori p value of 0.05.
Sources of Funding
This work was supported by the National Institutes of Health (NIH) HD052127 and by Extremity Medical, LLC. Funding from NIH supported the efforts of two authors (J.J.C. and S.W.W.). Funding from Extremity Medical supported the efforts of two authors (R.R.R. and D.J.P.), purchase of the cadaver specimens, and fabrication of the specimen jig.
Results
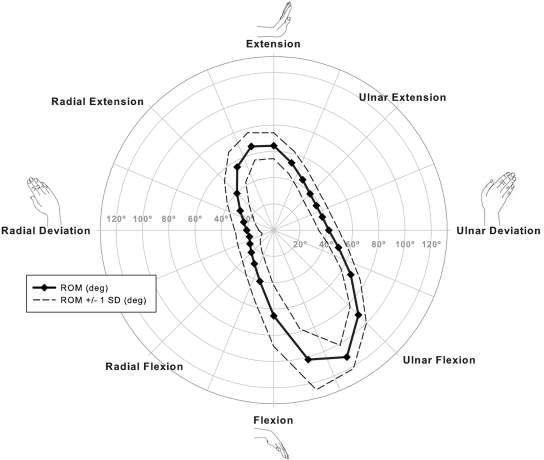
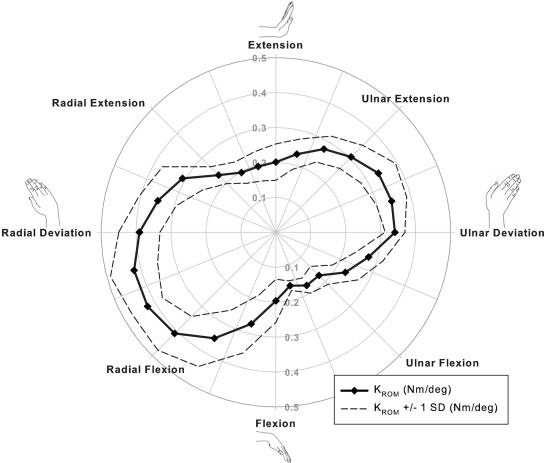
The envelope of the average values for wrist range of motion was generally elliptical in shape, but was not oriented along the orthogonal axes of pure extension and pure flexion. Instead, it was found to be oriented in a radial extension to ulnar flexion direction (Fig. 4). The orientation of the major axis of the range-of-motion envelope was significantly (p < 0.001) oblique to the anatomical direction of flexion-extension by a mean (and standard deviation) of 26.6° ± 4.4°.
Fig. 4.
The mean values (±1 standard deviation [SD]) for wrist range of motion (ROM) differed with the direction of wrist motion and were maximal in ulnar flexion, 30° from pure flexion. The envelope of range-of-motion values was oriented in a radial extension to ulnar flexion direction of wrist motion.
The largest wrist range-of-motion value was 111.5° ± 10.2° in the direction of ulnar flexion, 30° from pure flexion (Fig. 4). This value was significantly (p < 0.001) larger than the range of motion value in each of the four directions of pure wrist motion. Wrist range of motion in pure extension and pure flexion were considerably less at 64.2° ± 9.8° and 65.2° ± 23.2°, respectively. The largest wrist range of motion with an extension component was in the direction of radial extension, 15° from pure extension, with a range of motion value of 65.9° ± 10.8°. This value was not significantly different (p = 0.536) than the range of motion in pure extension. Thus, the largest total range of motion was approximately 178° ± 10.5° and was oriented in the oblique direction of wrist radial extension and ulnar flexion. Wrist range of motion in pure ulnar deviation and pure radial deviation were 42.3° ± 7.2° and 20.5° ± 9.0°, respectively.
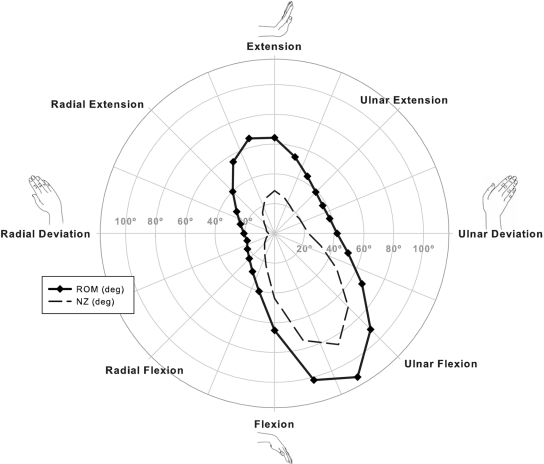
The neutral zone envelope and values in general paralleled those of the range of motion (Fig. 5). The orientation of the major axis of the neutral zone envelope was significantly (p < 0.001) oblique to the anatomical direction of flexion-extension by 30.2° ± 8.6°. The largest wrist neutral zone of 86.1° ± 10.4° was in the direction of ulnar flexion, 30° from pure flexion. This neutral zone value was significantly (p < 0.001) larger than the neutral zone value of 43.7° ± 18.4° in the direction of pure flexion and also significantly (p < 0.001) larger than the neutral zone in each of the other three anatomical directions of wrist motion. The neutral zone values in pure extension (28.6° ± 10.9°) and pure ulnar deviation (22.8° ± 10.8°) were found to be similar. The neutral zone value of 5.2° ± 4.3° in pure radial deviation was significantly (p = 0.002) less than the neutral zone values in each of the other directions of pure wrist motion.
Fig. 5.
The mean neutral zone (NZ) values had a similar general relation with the direction of wrist as did the mean range-of-motion (ROM) values.
The envelope of KROM values for the wrist was oriented orthogonally to the range of motion and neutral zone envelopes (Fig. 6). The major axis of the KROM envelope was significantly (p < 0.001) oriented an average of –69.3° ± 8.4° from the pure axes of flexion-extension. The largest stiffness value of approximately 0.4 Nm/deg was in the direction of radial flexion, while the smallest stiffness value of approximately 0.15 Nm/deg was in the direction of ulnar flexion.
Fig. 6.
The mean values (±1 standard deviation [SD]) for wrist stiffness (KROM) ranged from approximately 0.15 to 0.45 Nm, with the smallest stiffness value in the direction of ulnar flexion and the largest stiffness value in the direction of radial flexion. The resulting stiffness envelope was essentially orthogonal to the range of motion and neutral zone envelopes (Fig. 5).
Discussion
The aim of this study was to determine the mechanica properties of the human wrist by measuring its moment-rotationl behavior. To do so, we used a cadaver model and a specially designed specimen jig that allowed us to apply unconstrained moments in twenty-four directions of wrist motion. In each of these twenty-four directions, we recorded the moment-rotation behavior and reduced these data by calculating a neutral zone, range of motion, and stiffness. Grouping these values in the order of wrist circumduction permitted us to construct and analyze an envelope of mechanical behavior. An important finding was that the primary axis of the motion envelopes was oriented obliquely to the anatomical planes, in a direction of wrist radial extension to ulnar flexion. This direction is consistent with the description of the dart thrower's motion. The dart thrower's motion is a highly functional motion of the wrist5, used during a wide variety of occupational, household, and sporting activities, including hammering, pouring, and overhand throwing. Interestingly, the dart thrower's motion may be unique to the human species4. Young proposed that this unique wrist motion, which enables high-velocity trajectories of the upper extremity, may have lent a survival advantage to early human ancestors by facilitating hunting, use of weaponry, and defense38. These theories and our findings suggest that a correlation may exist between neuromuscular capabilities and the mechanical properties of some joints; the highly functional, useful, and most repetitive joint motions may be aligned with the direction of joint motion with the largest range of motion and the least stiffness.
We determined the mechanical properties of the wrist by the application of unconstrained moments. This experimental approach allows the specimen to rotate about its physiological axes, even if the location and orientation of rotational axes changes during the resulting motion. While this approach has not been previously reported for the wrist, it is well established for studying the mechanical properties of the spine34,35,39. To achieve unconstrained moments in this study, we mounted the specimen jig onto two horizontal, linear bearing slides to allow the specimen to translate freely. Our moment application was not fully unconstrained as previously defined in the biomechanical testing of the cadaver spine34,35. We eliminated the two additional rotational degrees of freedom not aligned with the direction of the applied moment because we sought to limit the measurement of the mechanical properties of the wrist solely to the direction of testing. In addition, the actuator was held at a constant vertical position that was defined by the neutral position of the wrist and forearm. In holding this position, we recorded axial loads in some directions that varied within ±20 N, suggesting the possibility of complex motions at the extreme positions. The extent of these motions cannot be determined with the current design of the specimen jig. The large neutral zone and range of motion of the wrist, compared with the spine, necessitated these simplifications in the application of the moments, primarily because of the challenges to the control system of the materials testing device.
Several limitations of our study should be considered when interpreting the findings. We measured the motion of the wrist as defined by the metacarpals with respect to the forearm; therefore, the mechanical properties we calculated are those of the wrist and we were not able to differentiate the contribution of the midcarpal joints from those of the radiocarpal joints. We hypothesized that the contributions of the midcarpal and radiocarpal joints to the overall mechanical properties vary with the direction of wrist motion, since most kinematic studies of the carpus have demonstrated that the kinematic patterns of carpal motion vary with the direction of wrist motion12,13,33. We limited our measurements to twenty-four different directions of wrist motion. It is possible that we may have missed a change in mechanical properties within one of the 15° increments. We believe this is unlikely, given the smooth envelope of motion reported by others40,41. Measuring the mechanical properties in pure translation is needed to characterize the mechanical properties of the wrist completely. Similarly, we did not measure the supination-pronation motion of the wrist relative to the forearm, which has been reported in a two-dimensional in vivo study42 to be approximately 17°. Furthermore, our measurements were only obtained in neutral forearm rotation, so it is unclear if forearm rotation would influence our findings. Another limitation of this study is the fact that we used three paired cadaver upper extremities and statistically analyzed them as six independent samples. We do not believe that this limitation influences our findings because we examined the normal physiological properties of the wrist and did not examine the effects of treatments or interventions. Finally, since our aim was to measure the mechanical properties of the wrist during passive motion, the loads we applied to the wrist through both flexor and extensor tendons were based on previous studies to approximate resting muscle tone36.
To our knowledge, the mechanical properties of the wrist have not been previously reported, precluding a direct comparison of our results. There is, however, extensive data on the active range of motion of the wrist to which we can compare our passive range-of-motion data. Considering the four anatomical directions, our findings that the range of motion was greatest in flexion, followed by extension and then ulnar deviation, and least in radial deviation are consistent with previous studies that have measured the active range of motion in human subjects1-3,26,43-45. Across these studies, the average total flexion-extension range of motion of approximately 142° is greater than the total range of motion of 129° that we measured in flexion-extension. We also found that the greatest total range of motion was in the direction of wrist radial extension to ulnar flexion, with an average value of 178°. While this value is substantially larger than those previously reported, we note that it is in an oblique direction that previous studies had not examined. These discrepancies may be attributed to the differences in protocols used to measure range of motion. Those previous studies used goniometers or motion tracking systems to measure active motion in healthy subjects, whereas we measured range of motion in cadavers with the application of a 2-Nm moment. However, given the low magnitude of this moment, the high stiffness of the wrist at the extremes of motion, and the findings that our range of motion values were less in flexion-extension but greater in an oblique direction than those previously reported, it is more likely, in our opinion, that the discrepancies in these range-of-motion values are due to the challenges of the use of a goniometer or a surface-based measurement system to accurately differentiate a wrist position of pure flexion or pure extension from a position along an oblique axis46. Our finding of 42° of ulnar deviation and 21° of radial deviation in the range of motion are in general agreement with the averages of 36° and 21°, respectively, in previous reports1,2,26. This agreement is consistent with our opinion because of the relative ease with which the motions of ulnar and radial deviation can be measured with use of a goniometer.
Recent studies of wrist circumduction have most often described an elliptically shaped envelope of motion with the principal direction aligned with wrist flexion-extension3,45,47,48, despite the observations by Fick49, Bunnell50, Capener51, and others summarized by Moritomo et al.5 on the importance of an oblique wrist motion. The active range-of-motion envelope reported by Palmer et al.3 had a slight radial extension to ulnar flexion orientation, but this observation was not discussed in their work. Most recently, Gehrmann et al.40 measured active wrist circumduction in healthy male subjects, using surface markers on the hand and forearm, and found that the greatest range of motion was achieved with the least constraints on finger posture and task. They recorded an average wrist range of motion of 151° and 80° for flexion-extension and radioulnar deviation, respectively. Their envelope of motion was more egg-shaped than elliptical with full flexion having a greater range of radioulnar positions than full extension. In agreement with our findings, the orientation of this envelope for a representative subject was obliquely oriented to the anatomical axes. While the specific orientation of the envelope was not reported40, their findings support our observations that simple measurements of what appear to be pure flexion-extension and pure radioulnar deviation may not be accurate representations of the actual range of motion. Some measurement methods may also not be able to accurately account for forearm rotation, confounding the definition of the anatomical planes relative to the wrist. In our study, a difference in the direction of wrist movement of 30°, between pure flexion and ulnar flexion, resulted in an increase of 46° in the range-of-motion value. A previous cadaver study found a kidney-shaped envelope of motion, with radial deviation as the minimum52. This kidney-shaped envelope is not consistent with the elliptically shaped envelope we measured, and neither is the substantial motion in wrist extension and radial flexion that the previous study described52. The imposition of displacements to the hand of the cadaver rather than the application of unconstrained moments may be the cause of this inconsistency with our results.
This study provides new insight into the mechanical behavior of the wrist and its function. The findings may improve our understanding of the functional limitations of wrist injury and expectations following reconstructive wrist surgery. These data may also help therapists to modify rehabilitation protocols to expedite functional recovery. These data may also help to explain why objective measurements of range of motion in traditional planes of measurement may not directly correlate with functional outcomes and may be less predictive of differences in subjective outcome between different surgical procedures. Finally, wrist implant and wrist arthroplasty designs should take into account not only the anatomical axes of wrist motion but also the mechanical axes.
Footnotes
Disclosure: In support of their research for or preparation of this work, one or more of the authors received, in any one year, outside funding or grants in excess of $10,000 from the National Institutes of Health (HD052127) and Extremity Medical, LLC. In addition, one or more of the authors or a member of his or her immediate family received, in any one year, payments or other benefits in excess of $10,000 or a commitment or agreement to provide such benefits from a commercial entity (Extremity Medical, LLC).
References
- 1.Boone DC, Azen SP. Normal range of motion of joints in male subjects. J Bone Joint Surg Am. 1979;61:756-9 [PubMed] [Google Scholar]
- 2.Ryu JY, Cooney WP, 3rd, Askew LJ, An KN, Chao EY. Functional ranges of motion of the wrist joint. J Hand Surg Am. 1991;16:409-19 [DOI] [PubMed] [Google Scholar]
- 3.Palmer AK, Werner FW, Murphy D, Glisson R. Functional wrist motion: a biomechanical study. J Hand Surg Am. 1985;10:39-46 [DOI] [PubMed] [Google Scholar]
- 4.Wolfe SW, Crisco JJ, Orr CM, Marzke MW. The dart-throwing motion of the wrist: is it unique to humans? J Hand Surg Am. 2006;31:1429-37 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Moritomo H, Apergis EP, Herzberg G, Werner FW, Wolfe SW, Garcia-Elias M. 2007 IFSSH committee report of Wrist Biomechanics Committee: biomechanics of the so-called dart-throwing motion of the wrist. J Hand Surg Am. 2007;32:1447-53 [DOI] [PubMed] [Google Scholar]
- 6.Li ZM, Kuxhaus L, Fisk JA, Christophel TH. Coupling between wrist flexion-extension and radial-ulnar deviation. Clin Biomech (Bristol, Avon). 2005;20:177-83 [DOI] [PubMed] [Google Scholar]
- 7.Kobayashi M, Berger RA, Nagy L, Linscheid RL, Uchiyama S, Ritt M, An KN. Normal kinematics of carpal bones: a three-dimensional analysis of carpal bone motion relative to the radius. J Biomech. 1997;30:787-93 [DOI] [PubMed] [Google Scholar]
- 8.de Lange A, Kauer JM, Huiskes R. Kinematic behavior of the human wrist joint: a roentgen-stereophotogrammetric analysis. J Orthop Res. 1985;3:56-64 [DOI] [PubMed] [Google Scholar]
- 9.Ruby LK, Cooney WP, 3rd, An KN, Linscheid RL, Chao EY. Relative motion of selected carpal bones: a kinematic analysis of the normal wrist. J Hand Surg Am. 1988;13:1-10 [DOI] [PubMed] [Google Scholar]
- 10.Snel JG, Venema HW, Moojen TM, Ritt JP, Grimbergen CA, den Heeten GJ. Quantitative in vivo analysis of the kinematics of carpal bones from three-dimensional CT images using a deformable surface model and a three-dimensional matching technique. Med Phys. 2000;27:2037-47 [DOI] [PubMed] [Google Scholar]
- 11.Moojen TM, Snel JG, Ritt MJ, Kauer JM, Venema HW, Bos KE. Three-dimensional carpal kinematics in vivo. Clin Biomech (Bristol, Avon). 2002;17:506-14 [DOI] [PubMed] [Google Scholar]
- 12.Moritomo H, Murase T, Goto A, Oka K, Sugamoto K, Yoshikawa H. In vivo three-dimensional kinematics of the midcarpal joint of the wrist. J Bone Joint Surg Am. 2006;88:611-21 [DOI] [PubMed] [Google Scholar]
- 13.Crisco JJ, Coburn JC, Moore DC, Akelman E, Weiss AP, Wolfe SW. In vivo radiocarpal kinematics and the dart thrower's motion. J Bone Joint Surg Am. 2005;87:2729-40 [DOI] [PubMed] [Google Scholar]
- 14.Crisco JJ, Coburn JC, Moore DC, Upal MA. Carpal bone size and scaling in men versus in women. J Hand Surg Am. 2005;30:35-42 [DOI] [PubMed] [Google Scholar]
- 15.Belsole RJ, Hilbelink DR, Llewellyn JA, Dale M, Ogden JA. Carpal orientation from computed reference axes. J Hand Surg Am. 1991;16:82-90 [DOI] [PubMed] [Google Scholar]
- 16.Keir PJ. Magnetic resonance imaging as a research tool for biomechanical studies of the wrist. Semin Musculoskeletal Radiol. 2001;5:241-50 [DOI] [PubMed] [Google Scholar]
- 17.Moore DC, Crisco JJ, Trafton TG, Leventhal EL. A digital database of wrist bone anatomy and carpal kinematics. J Biomech. 2007;40:2537-42 [DOI] [PubMed] [Google Scholar]
- 18.Nowalk MD, Logan SE. Distinguishing biomechanical properties of intrinsic and extrinsic human wrist ligaments. J Biomech Eng. 1991;113:85-93 [DOI] [PubMed] [Google Scholar]
- 19.Savelberg HH, Kooloos JG, Huiskes R, Kauer JM. Stiffness of the ligaments of the human wrist joint. J Biomech. 1992;25:369-76 [DOI] [PubMed] [Google Scholar]
- 20.Xu L, Strauch RJ, Ateshian GA, Pawluk RJ, Mow VC, Rosenwasser MP. Topography of the osteoarthritic thumb carpometacarpal joint and its variations with regard to gender, age, site, and osteoarthritic stage. J Hand Surg Am. 1998;23:454-64 [DOI] [PubMed] [Google Scholar]
- 21.Loebig TG, Badia A, Anderson DD, Baratz ME. Correlation of wrist ligamentotaxis with carpal distraction: implications for external fixation. J Hand Surg Am. 1997;22:1052-6 [DOI] [PubMed] [Google Scholar]
- 22.Ishikawa J, Cooney WP, 3rd, Niebur G, An KN, Minami A, Kaneda K. The effects of wrist distraction on carpal kinematics. J Hand Surg Am. 1999;24:113-20 [DOI] [PubMed] [Google Scholar]
- 23.Agee JM. Distal radius fractures. Multiplanar ligamentotaxis. Hand Clin. 1993;9:577-85 [PubMed] [Google Scholar]
- 24.Grechenig W, Peicha G, Fellinger M, Seibert FJ, Weiglein AH. Anatomical and safety considerations in establishing portals used for wrist arthroscopy. Clin Anat. 1999;12:179-85 [DOI] [PubMed] [Google Scholar]
- 25.Abrams RA, Petersen M, Botte MJ. Arthroscopic portals of the wrist: an anatomic study. J Hand Surg Am. 1994;19:940-4 [DOI] [PubMed] [Google Scholar]
- 26.Greene WB, Heckman JD. The clinical measurement of joint motion. Rosemont, IL: American Academy of Orthopaedic Surgeons; 1994 [Google Scholar]
- 27.Schuind F, Cooney WP, Linscheid RL, An KN, Chao EY. Force and pressure transmission through the normal wrist. A theoretical two-dimensional study in the posteroanterior plane. J Biomech. 1995;28:587-601 [DOI] [PubMed] [Google Scholar]
- 28.Iwasaki N, Genda E, Barrance PJ, Minami A, Kaneda K, Chao EY. Biomechanical analysis of limited intercarpal fusion for the treatment of Kienböck's disease: a three-dimensional theoretical study. J Orthop Res. 1998;16:256-63 [DOI] [PubMed] [Google Scholar]
- 29.Fischli S, Sellens RW, Beek M, Pichora DR. Simulation of extension, radial and ulnar deviation of the wrist with a rigid body spring model. J Biomech. 2009;42:1363-6 [DOI] [PubMed] [Google Scholar]
- 30.Carrigan SD, Whiteside RA, Pichora DR, Small CF. Development of a three-dimensional finite element model for carpal load transmission in a static neutral posture. Ann Biomed Eng. 2003;31:718-25 [DOI] [PubMed] [Google Scholar]
- 31.Grosland NM, Rogge RD, Adams BD. Influence of articular geometry on prosthetic wrist stability. Clin Orthop Relat Res. 2004;421:134-42 [DOI] [PubMed] [Google Scholar]
- 32.Goto A, Moritomo H, Murase T, Oka K, Sugamoto K, Arimura T, Masumoto J, Tamura S, Yoshikawa H, Ochi T. In vivo three-dimensional wrist motion analysis using magnetic resonance imaging and volume-based registration. J Orthop Res. 2005;23:750-6 [DOI] [PubMed] [Google Scholar]
- 33.Werner FW, Green JK, Short WH, Masaoka S. Scaphoid and lunate motion during a wrist dart throw motion. J Hand Surg Am. 2004;29:418-22 [DOI] [PubMed] [Google Scholar]
- 34.Crisco JJ. The biomechanical stability of the human lumbar spine: experimental and theoretical investigations [doctoral dissertation]. New Haven: Yale University; 1989 [Google Scholar]
- 35.Panjabi MM, Oxland TR, Yamamoto I, Crisco JJ. Mechanical behavior of the human lumbar and lumbosacral spine as shown by three-dimensional load-displacement curves. J Bone Joint Surg Am. 1994;76:413-24 [DOI] [PubMed] [Google Scholar]
- 36.An KN. Tendon excursion and gliding: clinical impacts from humble concepts. J Biomech. 2007;40:713-8 [DOI] [PubMed] [Google Scholar]
- 37.Crisco JJ., 3rd The volume of motion: introduction, derivation, and an application comparing various spinal fixation devices. J Biomech Eng. 1993;115:43-6 [DOI] [PubMed] [Google Scholar]
- 38.Young RW. Evolution of the human hand: the role of throwing and clubbing. J Anat. 2003;202:165-74 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Crawford NR, Brantley AG, Dickman CA, Koeneman EJ. An apparatus for applying pure nonconstraining moments to spine segments in vitro. Spine (Phila Pa 1976). 1995;20:2097-100 [DOI] [PubMed] [Google Scholar]
- 40.Gehrmann SV, Kaufmann RA, Li ZM. Wrist circumduction reduced by finger constraints. J Hand Surg Am. 2008;33:1287-92 [DOI] [PubMed] [Google Scholar]
- 41.Werner FW, Short WH, Green JK. Changes in patterns of scaphoid and lunate motion during functional arcs of wrist motion induced by ligament division. J Hand Surg Am. 2005;30:1156-60 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gupta A, Moosawi NA. How much can carpus rotate axially? An in vivo study. Clin Biomech (Bristol, Avon). 2005;20:172-6 [DOI] [PubMed] [Google Scholar]
- 43.Volz RG, Lieb M, Benjamin J. Biomechanics of the wrist. Clin Orthop Relat Res. 1980;149:112-7 [PubMed] [Google Scholar]
- 44.Brumfield RH, Champoux JA. A biomechanical study of normal functional wrist motion. Clin Orthop Relat Res. 1984;187:23-5 [PubMed] [Google Scholar]
- 45.Salvia P, Woestyn L, David JH, Feipel V, Van S, Jan S, Klein P, Rooze M. Analysis of helical axes, pivot and envelope in active wrist circumduction. Clin Biomech (Bristol, Avon). 2000;15:103-11 [DOI] [PubMed] [Google Scholar]
- 46.Carter TI, Pansy B, Wolff AL, Hillstrom HJ, Backus SI, Lenhoff M, Wolfe SW. Accuracy and reliability of three different techniques for manual goniometry for wrist motion: a cadaveric study. J Hand Surg Am. 2009;34:1422-8 [DOI] [PubMed] [Google Scholar]
- 47.Ojima H, Miyake S, Kumashiro M, Togami H, Suzuki K. Ranges of dynamic motion of the wrist in healthy young and middle-aged men. Ergonomics. 1992;35:1467-77 [DOI] [PubMed] [Google Scholar]
- 48.Leonard L, Sirkett D, Mullineux G, Giddins GE, Miles AW. Development of an in-vivo method of wrist joint motion analysis. Clin Biomech (Bristol, Avon). 2005;20:166-71 [DOI] [PubMed] [Google Scholar]
- 49.Fick R. Ergebnisse einer Untersuchung der Handbewegungen mit X-strahlen. Anat Gessel Vehr. 1901;15:175-84 [Google Scholar]
- 50.Bunnell S. Surgery of the hand. Philadelphia: JB Lippincott; 1944 [Google Scholar]
- 51.Capener N. The hand in surgery. J Bone Joint Surg Br. 1956;38:128-51 [DOI] [PubMed] [Google Scholar]
- 52.Savelberg HH, Otten JD, Kooloos JG, Huiskes R, Kauer JM. Carpal bone kinematics and ligament lengthening studied for the full range of joint movement. J Biomech. 1993;26:1389-402 [DOI] [PubMed] [Google Scholar]