Analysis of Mechanical Failure of Polymer Microneedles by Axial Force

Abstract

A polymeric microneedle has been developed for drug delivery applications. The ultimate goal of the polymeric microneedle is insertion into the specified region without failure for effective transdermal drug delivery. Mechanical failure of various geometries of microneedles by axial load was modeled using the Euler formula and the Johnson formula to predict the failure force of tapered-column microneedles. These formulas were compared with measured data to identify the mechanical behavior of microneedles by determining the critical factors including the actual length and end-fixed factor. The comparison of the two formulas with the data showed good agreement at the end-fixity (K) of 0.7. This value means that a microneedle column has one fixed end and one pinned end, and that part of the microneedle was overloaded by axial load. When the aspect ratio of length to equivalent diameter is 12:1 at 3 GPa of Young’s modulus, there is a transition from the Euler region to the Johnson region by the decreased length and increased base diameter of the microneedle. A polymer having less than 3 GPa of stiffness would follow the Euler formula. A 12:1 aspect ratio of length to equivalent diameter of the microneedle was the mechanical indicator determining the failure mode between elastic buckling and inelastic buckling at less than 3 GPa of Young’s modulus of polymer. Microneedles with below a 12:1 aspect ratio of length-to-equivalent diameter and more than 3 GPa of Young’s were recommended for reducing sudden failure by buckling and for successfully inserting the microneedle into the skin.

I. INTRODUCTION

Tapered micro-columns are generating increasing interest for drug delivery applications. These structures are usually called microneedles, which are used to pierce the outer layer of skin and thereby provide a minimally invasive method to drug delivery that avoids the complications and safety concerns associated with hypodermic needles.

Arrays of microneedles have been created to act as a bridge between conventional injections and transdermal patches [1–3]. Microneedles have been fabricated from polymer, which offers safety, versatility, and cost-effectiveness [4–7]. Replicate microneedle arrays have been made out of various kinds of polymer, including non-biodegradable polymers and biodegradable polymers, for example, by filling a micro-mold with a polymer melt and solidifying it [2, 8]. Microneedles made in this way can be intentionally or unintentionally broken off in the skin.

Microneedles require proper design to be inserted into the skin without breaking. Insertion is achieved largely by using needles with sharp tips and with sufficient length to overcome the deflection of the skin’s compliant surface that occurs before insertion. Needle integrity during insertion has been achieved primarily by minimizing the required insertion force by using sharp-tipped needles and by maximizing the mechanical strength through increasing Young’s modulus and needle diameter [2]. These studies have quantitatively measured the force required to fracture microneedles pressed against a rigid surface and the force required to insert microneedles into the skin of human subjects. The goal of these studies was to assure the robust design of a microneedle that could be inserted without breaking.

Previous studies have provided analysis of the expected failure force using an elastic buckling model for the specified geometries based on the Euler formula [9–11]. However, the ideal elastic buckling mode, which assumes that the structures are “long,” cannot explain the failure of microneedle column that are intermediate-length or short columns, and other approaches are needed [12].

To increase successful insertion of microneedles, a comprehensive analytical model of failure is needed to estimate the mechanical behavior of various geometries of tapered columns of solid microneedles made of various kinds of polymer. Inelastic stability of intermediate-length and short columns should also be considered as the critical failure mode of tapered microneedles, given that they tend to be short. The ratio of length-to-equivalent diameter should be considered as the critical factor determining the mechanical failure mode because it can vary with application, such as in transdermal drug delivery and ocular drug delivery [4, 13].

II. EXPERIMENTS AND DISCUSSION

Various geometries of microneedles were designed and fabricated for mechanical analysis using the lens technique and the inclined rotation method, as described previously [2]. Briefly, UV incidence with a fixed longitudinal angle was applied to an SU-8 (SU-100, MicroChem, Newton, MA) slab through a clear glass window in a dark field photomask as shown in Figure 1(a)[14]. Poly-di-methyl-siloxane (PDMS, Sylgard 184, Dow Conring) was poured into an SU-8 mold, and the PDMS structure was prepared from the mold. Next, the PDMS mold was obtained by micromolding a PDMS master structure made by the inclined rotation method. Using this micromolding method, various geometries of microneedles were made out of polymers including poly-lactic-co-glycolic acid (PLGA, 50–60 kDa), poly-L-lactic acid (PLLA, 70–80 kDa) poly-DL-lactic acid (PLA, 50–60 kDa) and poly-glycolic acid (PGA, 100 kDa) (Lakeshore Biomaterials, Birmingham, AL) with different mechanical properties. To measure the failure force of a microneedle under an axial load, a displacement-force test station (Model 921A, Tricor System, Elgin, IL) was used, as described previously [2]. Stress-versus-strain curves were generated by measuring force and displacement while the test station pressed an array of microneedles against a hard surface at a rate of 1.1 mm/s. Upon needle failure, the force suddenly dropped, and the maximum force applied immediately before dropping was interpreted as the force of needle failure.

Fig 1.

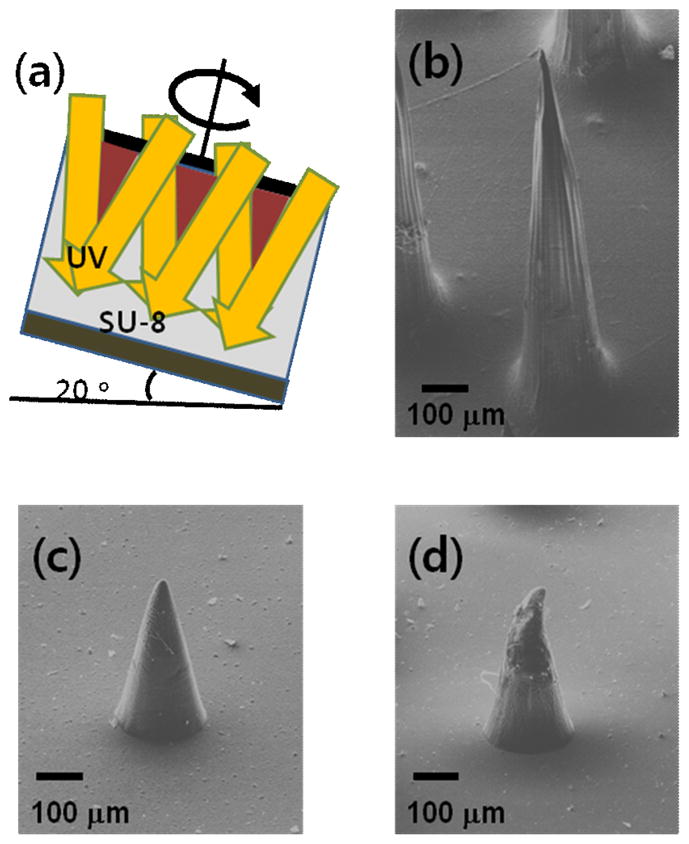
(a) Schematic representation of the microneedle fabrication process using rotational and inclined exposure of UV. (b) Scanning electron micrograph of a microneedle made of poly-lactic-co-glycolic-acid with 1000-μm length, 200-μm base diameter, and 25-μm tip diameter (c) poly-lactic-co-glycolic-acid with 500-μm length, 200-μm base diameter, and 25-μm tip diameter, and (d) failed microneedle by 0.4N of axial force.

We first prepared a set of microneedles in order to measure their failure force as a function of microneedle geometry (L) and material properties (E). Figure 1(b) and 1(c) show representative fabricated microneedle structures with a height of 1000 μm and a base diameter of 200 μm and a height of 500 μm and a base diameter of 200 μm respectively, resulting from inclined UV incidence through a 200 μm-diameter clear window in a dark field photomask. UV (i-line, 365 nm) exposure was carried out at an angle of 20° while the sample was rotated for 900 min, which resulted in a conical shape of non-crosslinked SU-8. Using this approach, various geometries of microneedles were prepared by the inclined rotation and lens technique, and mechanical failure forces were measured. To predict the failure force of tapered-column microneedles, we first consider theoretical approaches to predicting failure of straight columns and then adapt the solutions to tapered columns. We assume that the applied force is acting parallel to the microneedle axis. In the case of an axial load on the column structure, an analytical solution based on failure due to buckling caused by inelastic or elastic instability of the structure is developed. To predict the force required for needle failure due to buckling, the transition slenderness ratio (column constant, C_c), defined by equation 1, should be determined.

$$C_c=\sqrt{\frac{2{\pi }^{2}E}{S_y}}$$ (1)

where E is Young’s modulus of the material and S_y is yield strength of the material. The slenderness ratio of a column is computed from equation 2:

$$SR=\frac{L_e}{r_g}=\frac{KL}{r_g}$$ (2)

where the effective length, L_e, and radius of gyration, r_g, for a solid circular sectional column are defined as L_e = K·L and r_g = D/4, respectively [12], where L is an actual length, K is the end-fixity factor, and D is a diameter of a circular section.

The end-fixity factor is a measure of the degree to which each end column is restrained against movement. The value of K is 1.0, 0.7, and 0.5 for a pinned-pinned column, a fixed-pinned column, and a fixed-fixed column, respectively [12]. A fixed column is one where the end and angle of the column at the end does not move. A pinned column is one where the end does not move, but the angle is free to rotate. For microneedle mechanical analysis, the end-fixity factors from K = 0.5 to K = 1.0 are scanned because the needle bases are fixed to a support and the tips of the needles are not allowed to rotate in any direction about any axis due to friction with the contacting surface.

If the actual slenderness ratio, SR, is greater than the column constant, C_c, then the column is considered “long,” and the Euler formula, defined in equation 3, should be used to predict the critical load, P_cr, at which the column would be expected to buckle:

$$P_{cr}=\frac{{\pi }^{2}EI}{{L_e}^2}=\frac{{\pi }_{2}EA}{{(L_e/r_g)}^2}$$ (3)

where I is the moment of inertia for a circular section, defined as I = πD⁴/64 (D is the diameter of a circular section), and A is the area of a circular section [12].

As the column gets shorter, it exhibits a tendency to fail at loads less than are predicted using the Euler formula, and this has led to the development of a companion expression to properly account for failure in the intermediate region. This parabolic equation was first suggested by J. B. Johnson, and the point at which the Euler formula is shifted to the Johnson formula is governed by the column constant, C_c. If the slenderness ratio, KL/r_g, is less than the column constant, C_c, then the column is considered “short,” and the Johnson formula, as shown in equation 4, should be used [15].

$$P_{cr}={AS}_y\left[1-\frac{S_y{(L_e/r_g)}^2}{4{\pi }^{2}E}\right]$$ (4)

For a tapered column, the surface area, A, varies depending on the height of the column. To evaluate the mechanical failure of the tapered microstructure, the general buckling formula for a straight column needs to be adapted to the tapered column by introducing an equivalent diameter. The equivalent diameter of a linearly tapered column can be calculated from equation 5 to analyze a tapered member [16]. This equivalent value is used for computing the slenderness ratio and the critical load from the Euler formula and the Johnson formula.

$$D_{\mathit{equivalent}}=D_{\mathit{tip}}+\frac{(D_{\mathit{base}}-D_{\mathit{tip}})}{3}$$ (5)

Microneedles can fail by different modes. In some cases (e.g., Figure 1b), microneedles failed by elastic buckling, consistent with the Euler formulation (Equation 3) used in previous models [10, 17]. However, in other cases (e.g., Figure 1(c)), failure of the microneedle occurred at the tapered section, which cannot be explained by the elastic buckling model. The Johnson formula (Equation 4) should be used to evaluate the inelastic stability of this tapered column. The calculated failure force of a PLGA microneedle with 25 μm of tip diameter, 200 μm of base diameter and 500 μm of height is 0.57 N from Euler equation (Equation 3) and 0.24 N from Johnson equation (Equation 4). When 0.4 N of force was applied a microneedle shown in Figure 1(c), the failure of a microneedle occurred at the lower force than calculated value by Euler equation as shown in Figure 1(d). Because the Johnson formula was developed for straight columns, Equation 5 is needed to determine the equivalent diameter, which should be utilized to correct the formula to account for the tapered column of the microneedle.

In order to know when the transition occurs from “long” columns analyzed by the Euler formula to “short” columns analyzed by the Johnson formula, we need to determine the end-fixity factor, K, which is a measure of the degree of the restraint against movement at the ends of the microneedle. Considering the range of values K = 0.5 to K = 1.0 (see above), we can find the value of K that best fits the data by comparing the predicted loads to the experimental data.

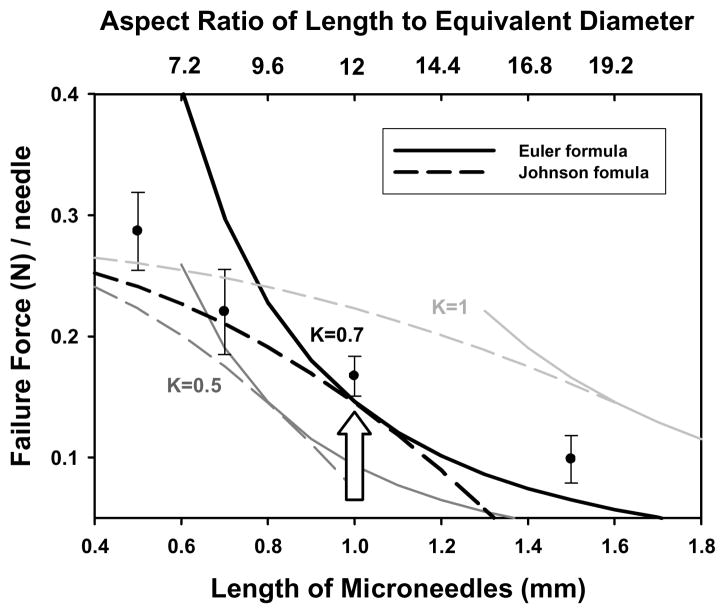
As shown in Figure 2, experimental data are placed between K = 0.5 and K = 1.0 and they are well fitted to the line calculated at K = 0.7. The end-fixity factor of 0.7 is the combination of one fixed end and one pinned end, and the buckled shape approaches the fixed end with a zero slope while the pinned end rotates freely [18]. Using a value of K = 0.7 in Equations 3 and 4 leads to good agreement between theory and experimental data. The value K = 0.7 means that part of the microneedle was overloaded by axial load. The increase of K value increases the effective length and the slenderness ratio and moves the transition point to the intersection of the solid line from the Euler formula and the dashed line from the Johnson formula.

Fig 2.

Experimental and predicted failure force of a microneedle with D_tip = 25 μm and D_base = 200 μm, as a function of microneedle length and end-fixity (K = 0.5, 0.7, and 1).

It is evident from Figure 2 that over the range of microneedle geometries considered, the failure mode is best calculated using the Johnson formula for shorter needles and the Euler formula for longer ones. To find the transition point, we use Equation 1 to calculate the column constant equal to 34.4 for a column made of PLGA with E = 3 GPa and S_y = 50 MPa. Setting this equal to the slenderness ratio, KL/r_g for a column with fixed-pinned ends (K = 0.7) and D_tip = 25 μm and D_base = 200 μm yields a microneedle length of 1000 μm. Thus, because most microneedles of interest for drug delivery applications are shorter than 1000 μm, the failure force in most cases is best predicted using the Johnson formula. Use of the Euler formula would significantly overpredict the failure force (Figure 2).

Further inspection of Figure 2 shows that adaptation of the Euler formula and the Johnson formula, which were developed for straight columns, by using the equivalent diameter calculated in Equation 5 yielded good agreement between predictions and the measured data. We conclude that the defined equivalent diameter works for calculating the critical load of failure.

The transition from “long” microneedles to “short” microneedles identified by comparing the slenderness ratio to the column constant can alternatively be expressed as a transitional aspect ratio of length-to-equivalent diameter for a microneedle made of a given material. For the tapered PLGA microneedles considered in the study with E = 3 GPa, the transition from the Euler region to the Johnson region occurs at an aspect ratio of 12:1.

Having varied microneedle length/aspect ratio, we next examined the effect of microneedle base diameter with D_tip = 25 μm, L = 0.7 mm, and E = 3 GPa on the failure force. Figure 3 compares experimental measurements to predictions by the Euler formula and the Johnson formula using K=0.7. The Euler region changes to the Johnson region by an increase in the base diameter. The transition point, where SR = C_c, occurs at a base diameter D_base = 120 μm. This transition again occurred at about the aspect ratio of length-to-equivalent diameter of 12:1, which is close to the transition point obtained by the change of length.

Fig 3.

Experimental and predicted force at microneedle failure as a function of microneedle base diameter for a needle with D_tip = 25 μm, L = 0.7 mm, and E = 3 GPa at K = 0.7.

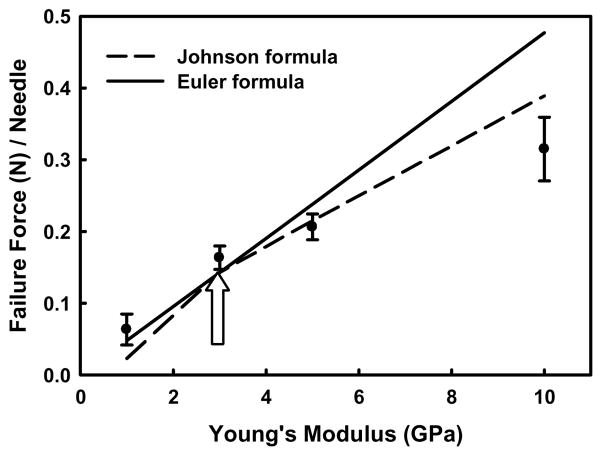
Finally, we studied the effect of Young’s modulus, E, on the failure force of a needle with D_tip = 25 μm, D_base = 200 μm, and L = 1 mm. Figure 4 shows experimental data compared to prediction by the Euler formula and the Johnson formula using K = 0.7. The Euler region transitions to the Johnson region by the increase of Young’s modulus, and the transition point, where SR = C_c, occurs at E = 3 GPa. As expected, the Johnson formula fits the data better than the Euler formula at higher values of Young’s modulus, which effectively makes needles “short.”

Fig 4.

Experimental and predicted force at microneedle failure as a function of Young’s modulus of the polymer microneedle material at K = 0.7, L = 1000 μm, D_base = 200 μm, and D_tip = 25 μm.

III. CONCLUSION

The calculations from the Euler formula and the Johnson formula with K = 0.7 showed good agreement with the measured data. The value of K = 0.7 means the column has fixed-pinned ends and that part of the microneedle was overloaded. Microneedle failure depended on the aspect ratio of length-to-equivalent diameter, and the failure mode changed from the Euler formula to the Johnson formula at an aspect ratio of 12:1 by the increase of base diameter and the decrease of length. Most microneedle geometries of interest for drug delivery applications (i.e., short and strong needles) were best predicted by the Johnson formula.

Overall, this study provided a simple mathematical model to anticipate the mechanical behavior of a polymeric microneedle. Various kinds of microneedles for various applications can be designed based on this model. To avoid sudden failure of a microneedle by buckling, and to insert the microneedle into the skin successfully, we recommend geometries below a 12:1 aspect ratio of length-to-equivalent diameter and a polymer with more than 3 GPa of Young’s modulus.