Abstract
Gamma band synchronization has drawn increasing interest with respect to its potential role in neuronal encoding strategy and behavior in awake, behaving animals. However, contamination of these recordings by power line noise can confound the analysis and interpretation of cortical local field potential (LFP). Existing denoising methods are plagued by inadequate noise reduction, inaccuracies, and even introduction of new noise components. To carefully and more completely remove such contamination, we propose an automatic method based on the concept of adaptive noise cancellation that utilizes the correlative features of common noise sources, and implement with AutoRegressive model with eXogenous Input (ARX). We apply this technique to both simulated data and LFPs recorded in the primary visual cortex of awake macaque monkeys. The analyses here demonstrate a greater degree of accurate noise removal than conventional notch filters. Our method leaves desired signal intact and does not introduce artificial noise components. Application of this method to awake monkey V1 recordings reveals a significant power increase in the gamma range evoked by visual stimulation. Our findings suggest that the ARX denoising procedure will be an important preprocessing step in the analysis of large volumes of cortical LFP data as well as high frequency (gamma-band related) electroencephalography/magnetoencephalography (EEG/MEG) applications, one which will help to convincingly dissociate this notorious artifact from gamma-band activity.
Keywords: awake macaque, local field potential, gamma band, autoregression model with exogenous input (ARX), adaptive noise cancellation (ANC), wavelet transform
1. Introduction
Recording of intracortical extracellular local field potentials (LFP) with microelectrodes date back at least to the 1930s (Haberly and Shepherd, 1973; Mitzdorf, 1985). The cortical LFPs are believed to reflect an aggregate measure of local input (intrinsic afferent) activity and local intracortical processing mediated by the sub-threshold signals of interneurons (Logothetis, 2003; Niessing et al., 2005). Numerous studies have underscored the functional importance of gamma-band (>30hz) frequency signals from cortical recordings in awake, behaving animals (Berens et al., 2008; Engel et al., 2001; Fries et al., 2007; Gail et al., 2004; Gregoriou et al., 2009; Liu and Newsome, 2006; Pesaran et al., 2002; Schnitzler and Gross, 2005; Singer, 1999; Womelsdorf et al., 2007). The technical demands of recording in awake animals include managing various surgical, electronic and mechanical conditions imposed by the animal performance on the trained task (Baker et al., 1999; Gray et al., 2007; Lemon, 1984). One of the significant problems in awake LFP recordings is that of 50/60 Hz line noise, which is difficult to eliminate even in anesthetized preparations (Belitski et al., 2008; Henrie and Shapley, 2005; Mitra and Pesaran, 1999; Niessing et al., 2005). And it is becoming more prominent with regard to the recent debates on possible artifactual components of gamma-band response (Melloni et al., 2009; Yuval-Greenberg et al., 2008).
One approach to reduce this noise has been to make use of an extra auxiliary or reference channel to provide information about the interference noise component that is corrupting the signal. An estimation of the noise component can be made from this “side information”, and subtracted from the primary input to “cancel out” the additive noise component. This so called adaptive noise cancellation (ANC) was first described by Widrow and his colleagues (Widrow et al., 1975) and, although not commonly used, has been shown to be safe and reliable method with minimal risk of distorting the signal (Liu and Newsome, 2006). Since extracellular recording in behaving animals suffers serious decrease in the signal-to-noise ratio (SNR) due to the presence of various kinds of noise sources (e.g., motion-related), one has to repeat the same stimulus task for hundreds, even thousands, of trials to get reliable results. Thus it is very desirable if the algorithm of mitigating the power line interference can be run with no or minimal adjustments of the input parameters from trial to trial.
In this study, we present a different perspective to ANC within the context of the system identification based on the idea of signal modeling and related parameters estimation (Friedlander, 1982; Johnson, 1995). In order to reliably detect the gamma-band LFP responses of awake primates in single trials, we develop an automatic trial-by-trial procedure of the 60 Hz cancellation by using an AutoRegressive model with eXogenous Input (ARX). This treatment takes advantage of identification algorithms that has been fully developed for several decades, which require lower computational complexity and minimal human supervision. In fact, knowledge of the signal model parameters has been widely and successfully applied in processing of neurophysiological signal for various purposes such as signal extraction of evoked potentials (Liberati et al., 1992), monitoring the depth of anesthesia (Jensen and Litvan, 2000; Litvan et al., 2002) and deconvolution (Mirsattari et al., 2006). In this paper we apply the ARX model to remove mains noise in simulated data and assess its effectiveness on experimental data recorded from awake primates. The approach in this paper is also applicable to electroencephalography/magnetoencephalography (EEG/MEG) measurements.
2. Materials and methods
2.1. ARX model for adaptive noise cancellation (ANC)
The essentials of an ARX model for adaptive noise cancellation are generally equivalent to applying the classic least-mean-square (LMS) algorithm in the ANC (Widrow et al., 1975, see Haykin, 1996 for more details of adaptive filter theory). The adaptive cancellation of interference requires the use of a primary input (e.g., cortical LFP), that contains the signal contaminated by the interference, and another reference input (e.g., power line noise), that contains a signal highly correlated with the noise contained in the primary input but uncorrelated with the signal under study. With this method, the reference signal is adaptively filtered and removed from the primary input to obtain an estimation of the studied signal. In the present study, the ANC problem is cast as a system identification problem (Friedlander, 1982; Johnson, 1995) so that this preprocessing procedure can be readily implemented without manually adjusting the input parameters trial by trial. A linear model with ARX kernel structure that is similarly used in a previous study (Mirsattari et al., 2006) is adopted here.
The ANC process
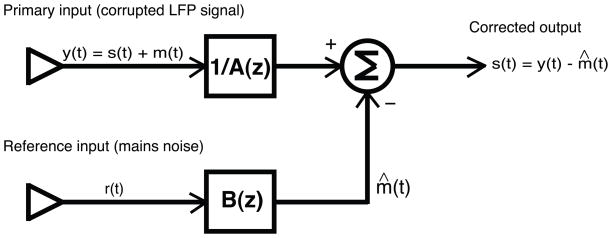
The conceptual steps are plotted schematically in Fig. 1. We model the corrupted signal from a single trial (the raw LFP traces): y(t), contains an interference component, m(t), with the additive superposition of an information-bearing signal component, s(t).
Fig. 1.
Schematic plot of ARX model for adaptive noise cancellation (ANC). y(t) and r(t) represent the primary input and reference input to the ARX model, respectively. And the primary input y(t) is modeled by the addition of interference component m(t) and information-bearing signal component s(t). The output of the model is given by subtracting the estimated noise component m̂ (t) from the primary input. See the corresponding text for a detailed explanation.
| (1) |
The interference sources recorded by an auxiliary channel are used as reference input r(t) to the black-box. The objective is to find a method for estimating a certain component (i.e., m(t)) of the primary input y(t) as quickly and accurately as possible with the use of the reference input. Such a method should not be sensitive to the noise and potential time variations of the input signal. Subsequently, the estimated m̂ (t) of the noise process is subtracted from the primary input y(t) to obtain the interference-free signal component:
| (2) |
The ARX model
The raw signal is then modeled by the above sum in the general ARX form: the recorded interference component r(t) (times a coefficient) and a white noise component e(t) (times a coefficient) (this is equation 3). If r(t) and m(t) are related by a linear model and s(t) is an ARX process, then the generic signal model has the form of a linear regression in the z-transform domain (Friedlander, 1982):
| (3) |
| (4) |
| (5) |
where e(t) is a white noise process. Since two time series r(t) and y(t) are measured in the experiment, it is possible to identify the coefficients ai (i= 1...na) and bj (j= nk....nb + nk + 1) in the transfer functions B(z) A(z) and 1 A(z) once the orders of the ARX model (na,nb,nk) are determined.
Minimizing the error through iteration
We describe how the coefficients are derived by an iterative standard least-mean-square (LMS) algorithm. The aim is to iteratively minimize a quadratic function of the prediction error y(t)− ŷ (t), where ŷ (t) is the output of the ARX model. The reference input r(t) is iteratively processed by the model which automatically adjusts the coefficients of the transfer function, depending on the above prediction error. Then the output signal ŷ (t) is generated, and reduces the interference m(t) from the primary signal y(t). In principle, the LMS algorithm can be applied to each value of na,nb,nk, independently. The selection of a specific value for each of them is required to minimize their sum but also use coefficients (na + nb) large enough to maximize the correlation between the processes y(t) and r(t). Our procedure implements an a posteriori evaluation of the optimal order for the data acquired in each trial, using the Akaike’s Information Criterion (AIC) (Akaike, 1974) over defined ranges for na,nb,nk.
| (6) |
where N is the number of data points in a trial and σ2 is the variance of the prediction error. After s(t) (actually the estimated value) is computed from the selected order of ARX model, its power spectrum is calculated to visualize the outcome of ARX filtering interference.
Performance measures
The computer simulations of mains noise with various kinds of SNR levels are designed to quantitatively compare the performance of our ARX method to that of the commonly used band-stop filters such as second-order infinite impulse response (IIR) notch filter. The IIR filter used here was a standard configuration using the built-in routine in MATLAB (iirnotch.m in Filter Design Toolbox) with Q-factor 60 at a level of −40dB considering the SNR levels in the simulated case. Two different bandwidths (1 and 2 Hz, also called narrower-band and wider-band IIR filters below) were chosen to demonstrate frequency mismatches between the simulated signal and predetermined filters. Simulated data are generated by the following equation:
| (7) |
where se (t) is a Gaussian-modulated sinusoidal pulse train which represents the signal component. The sinusoidal wave with an arbitrary initial phase is used to represent the power line noise. The nominal sampling rate is 1 kHz and f0 is set to 58, 60 and 62 Hz, se (t) is set to 40 Hz. The SNR is defined as the ratio of variances of signal and noise components, and values of −20dB, −40dB, −46dB, −60dB and −66dB are used here. The residual signal entropy is introduced here to evaluate relative performance of the ARX and IIR filters (Hamilton, 1996). If se (t) is accurately estimated, the residual signal will contain a lower level of noise contaminating the signal. As the noise is reduced, the entropy of the residual signal should decrease as well. The entropy, S, of the residual signal is calculated as:
| (8) |
A Student t-test of the entropy of all SNR conditions is used as statistical analysis of relative performance of these two filters. The entire procedure (including the ARX model from the System Identification Toolbox, signal simulation with various SNR and statistical test) was implemented in the MATLAB environment with the use of its Filter Design Toolbox (Mathworks, Natick, MA).
2.2. Experimental methods
All experimental procedures were conducted in compliance with the guidelines of the National Institute of Health and were approved by the Vanderbilt Animal Care and Use Committee. The electrophysiological data in this study was acquired from V1 of two healthy adult rhesus macaque monkeys (Macaca mulatta). The specifics of the surgical procedure have been previously described (Chen et al., 2002) and is briefly summarized. The awake electrophysiology procedures including training and recording are reported here in detail.
2.2.1. Surgical Procedures
Preparation of subjects for intracortical recording including two chronic implants (recording chamber and restraining head post) was performed using aseptic technique, under general anesthesia. Anesthesia was induced initially with an injection of ketamine (10 mg/kg i.m.) followed by atropine sulfate (1.0 mg/kg i.m.). The animals were maintained under isoflurane inhalation anesthesia (0.5–2% in O2 and CO2) while body temperature was maintained with a heated blanket and continuously monitored. Heart rate, respiratory rate, CO2 and O2 saturation were also monitored closely for the duration of the surgery. To provide access to the cortex, a craniotomy and durotomy was performed and a recording chamber implanted (cf. Chen et al., 2002).
2.2.2. Training Procedures
Chamber implanted monkeys were trained to sit in an upright primate chair with head secured by a headpost and to fixate on a small, centrally placed dot (0.15° × 0.15°, fixation window radius < 0.75°) on a LCD projector placed at a distance of 120 cm. Eye position during the training and recording session was continuously monitored with an infrared eye tracker (500 Hz, Eyelink II, SR Research, Toronto, ON, Canada). To enforce the performance of training, monkeys were maintained on a water regulation regimen. During the training and recording sessions water reward was applied by using a commercial liquid reward system. The water was delivered via a tube and a plastic sipper attached to the upper board of the monkey chair and could be conveniently reached by the animal’s mouth. Fluid reward after the completion of successful trials was given only during interstimulus intervals, thereby minimizing face and body movements related to licking during data acquisition.
The present study did not aim to determine the tuning of individual neurons through the use of stimuli to which they were optimally sensitive, but rather, to examine the visual responses of neural populations via LFP recordings. Four natural color movie clips extending to 24° × 18° were binocularly presented to the monkey. The monkey typically performed 100 ~ 200 trials of the task. Each 4500 ms trial consisted of a 500 ms baseline, followed by a 3000 ms stimulus presentation and followed a 1000 ms poststimulus period. The onset of visual stimulus in each trial was chosen at irregular interstimulus intervals and controlled by a custom-written software on the NI LabVIEW platform (National Instruments, Austin, TX).
2.2.3. Electrophysiological Recording
Cortical electrical activity was recorded extracellularly with commercially available tungsten microelectrodes (FHC Inst., Bowdoinham, ME). Electrodes were Epoxylite-coated tungsten with exposed rounded tip (< 1 μm) of ~1 MΩ impedance (measured at 1 kHz). Recording was conducted through the chamber implanted over V1. A computerized micromanipulator (NAN-S4, Nan Instruments, Israel) was mounted on the chamber to advance the recording electrode very slowly (to minimize dimpling effect, < 1.5 mm/s) through the gray matter 0.5–1.0 mm deep. Voltages were measured against a local reference electrode that was close to the recording electrode inside the chamber. The neural signal and power line-frequency noise reference signal were passed through a headstage (unit gain). The field potential signal was further amplified with PBX2 preamplifier (0.7 Hz–300 Hz, 1000× gain) (Plexon Inc., Dallas, TX) and digitized at 2000 Hz. The recorded data was stored in MATLAB compatible format for further time-frequency analysis. Trials in which the subject’s eye position deviated more than 0.75° from the fixation spot were excluded from analysis. The synchronization setup between eye tracking, stimulus presentation, date acquisition, and liquid reward system was controlled by custom designed software on a NI LabVIEW platform.
2.2.4. Time-frequency Wavelet Decomposition
In order to estimate the temporal structure in the frequency content of the LFP signal, the time-frequency analysis usually was performed after low-pass filtering the recorded signals, i.e., the short-time Fourier transform (STFT), by repeatedly calculating sliding-window fast Fourier transforms across the duration of the trial. This allowed tracking of the temporal evolution of spectral values. However, a problem with the conventional STFT is that signals with different spectral components are treated with the same frequency resolution (since a constant window length is chosen throughout the analysis). To overcome this weakness, we chose the wavelet transform that decomposes a signal on the basis of the scaled and shifted versions of a mother wavelet with finite duration. The idea of the wavelet transform is to convolve the signal to be analyzed with several oscillatory filter kernels representing different frequency bands. At low scales the mother wavelet is contracted to match the high frequency components, while at high scales it is expanded to match low frequency components. Although it is mathematically equivalent to other decomposition methods such as multi-taper (Bruns, 2004; Kiebel et al., 2005; Le Van Quyen et al., 2001), for any particular parameter set, these methods partition the time-frequency domain in a different manner. In particular, the wavelet transform uses a variable length data window from coarser (i.e., low-frequency) to finer (i.e., high frequency) signal structures and acts like a ‘mathematical microscope’, enabling a diversified trade-off between time and frequency resolution. It dissects the instantaneous frequency content of signal, which gives good time resolution for high-frequency events and good frequency resolution for low-frequency events. To study visually-evoked neural response in awake subjects, specifically for high-frequency signal (e.g., gamma-band), it is desirable to have a good time resolution to visualize the fast stimulus-related power changes in the time-frequency domain. The details of this method have been described extensively elsewhere (Tallon-Baudry et al., 1997).
One of the most commonly used wavelets in practice is the Morlet wavelet (or Gabor function), which is known as a complex sine wave within a Gaussian envelope and defined at central frequency and time t:
| (9) |
where standard deviation in time domain σt= 1/(2πσf). The time-frequency representation of the signal in a frequency band around f0 is simply the result of the convolution of the complex conjugate of the Morlet wavelet with of the recorded neural signal x(u):
| (10) |
The time-varying energy of the signal (or spectrogram) is the square norm of the above product. To better visualize the spectral structure, the computed spectrograms were normalized by the baseline mean and averaged across trials within one recording session (Henrie and Shapley, 2005).
3. Results
3.1. Simulation Results
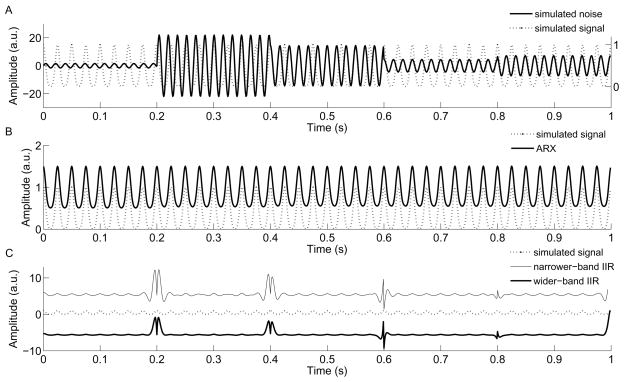
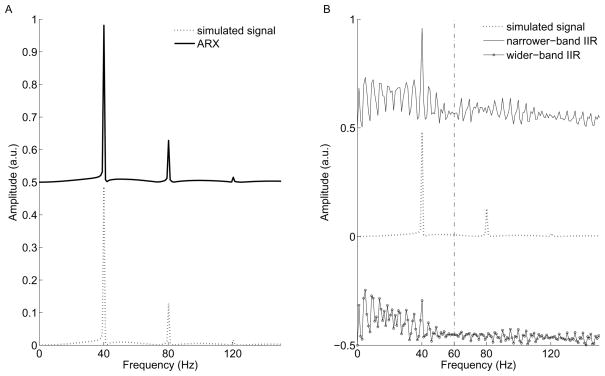
Fig. 2A illustrates five segments of the synthetic data (generated as described in Methods) with different SNR levels (−20dB, −66dB, −60dB, −40dB, −46dB, respectively): each segment plotted is 200 ms and contains 200 data points. In order to mimic the drifting effect of the power line, the frequencies of the simulated noise in the first two segments were set at 58 and 62 Hz, respectively. The other three were set at 60 Hz. The simulated signal component was maintained unchanged (dashed line). With the use of our ARX technique, the estimated signal component was almost perfectly matched with the simulated signal. This is demonstrated both in time and frequency domains (Fig. 2B and Fig. 3A). Since in both figures the data points of the plot highly overlap and appear indistinguishable, the results of ARX filtered are shifted deliberately for visual comparison (see the figure legends for shift details). The subtracted residuals between the estimated and original signals that are used to assess the performance of the adaptive filters are reduced to ~0.1% order of the magnitude of the simulated signal. The IIR filters with two different bandwidths, in contrast, both failed to recover the original signal, especially at the starting and ending points of each segment (Fig. 2C). The narrower-band IIR filter in fact introduced more ringing artifact than the wider-band IIR filter did (shown in Fig. 3B). With the use of frequency analysis, Figure 3 further illustrates the difference in performance between the ARX and the IIR filter methods (the filtered results are shifted by an arbitrary unit along y-axis for better visual comparison). Although the IIR filters removed a large portion of energy at 60 Hz in this example (seen from the time domain in Fig. 2C, also seen in Fig. 3B), it could not capture the temporal variations of the targeted frequency and furthermore introduced artificial fluctuations (ringing) into the original signal (see Fig. 3B). Again, the wider-band IIR filter which caused less ringing artifact removed both 58 and 62 Hz noise, both of which actually were contained only in the first two segments of simulated data.
Fig. 2.
Simulation example. (A) Five segments of synthetic data are generated with different SNR levels. In order to mimic the drifting effect of the power line, the frequencies in the first two segments were set at 58 and 62 Hz, respectively. The other three were set at 60 Hz. The dashed curve is the simulated signal component embedded in the sinusoid noises (see right y-axis for its amplitude scale). (B) Comparison of the simulated signal and the estimated signal by ARX model. For visual comparison purpose, the ARX plot was deliberately shifted up by an arbitrary unit 0.5 along y-axis. (C) Comparison of the simulated signal and the results obtained by the IIR filters with 1 Hz (narrower-band) and 2 Hz (wider-band) design. For visual comparison, the narrower-band IIR filtered curve was shifted up by an arbitrary unit 6 along y-axis and the wider-band curve was shifted to the opposite direction. It shows the IIR filter with narrower bandwidth causes more ringing artifact than the wider bandwidth.
Fig. 3.
Comparisons of the simulated signal and filtered results in frequency domain. (A), (B) Plots of single-sided amplitude spectra of the simulated signal, ARX modeled and IIR filtered signals. In (A), since the spectra of the ARX filtered and simulated signal are barely distinguishable, the spectrum of the ARX filtered is arbitrarily shifted up by a unit 0.5 for comparison. In (B), the narrower- and wider-band IIR filtered spectra were shifted up and down by a unit 0.5, respectively. The narrower-band IIR filter recovers larger signal at 40 Hz but introduces more ringing effect compared to the wider-band IIR filter.
To quantitatively assess the performance of these two methods on the simulated signals, we calculated the entropy of the residuals between the simulated and filtered signals by ARX and IIR methods, respectively (see Table 1). Under all different levels of SNR, the residual signal entropies of the ARX method were significantly smaller than those of the narrower- and wider-band IIR filter methods (Table 1p< 2.08×10−6; p< 1.28× 10−5). The decrease of the signal entropies indicated that the signal filtered by the ARX contained much lower level of noise, clearly demonstrating the ARX performance is better than the conventional IIR notch filter in this simulated case.
Table I.
Residual signal entropy of ARX and IIR filters (narrower- and wider-bands) as a function of SNR.
The results obtained by the ARX model are significantly smaller than those of IIR filters (p< 2.08× 10−6, p< 1.28× 10−5 for narrower-band and wider-band IIR filters, respectively), which indicates the performance of ARX model is better than the predetermined IIR filters in this simulated case.
| SNR (dB) | ARX | Narrower-band IIR | Wider-band IIR |
|---|---|---|---|
| −20 | 0 | 3.9037 | 3.4040 |
| −40 | 0 | 3.2102 | 3.0692 |
| −46 | 0 | 3.3879 | 3.1261 |
| −60 | 0.5032 | 3.1766 | 2.6725 |
| −66 | 0.9896 | 4.0606 | 4.1467 |
3.2. Experimental results
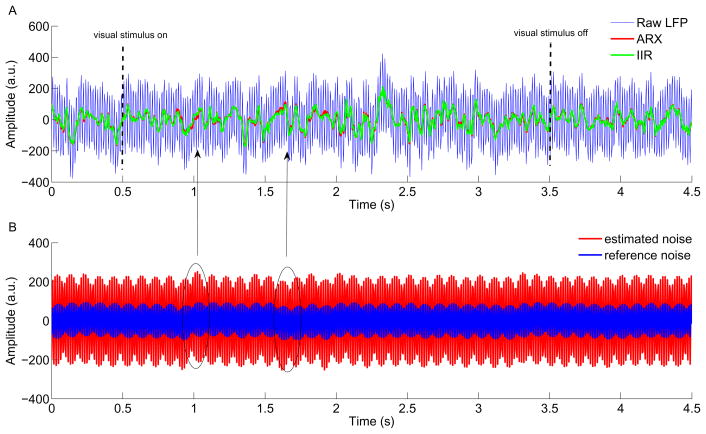
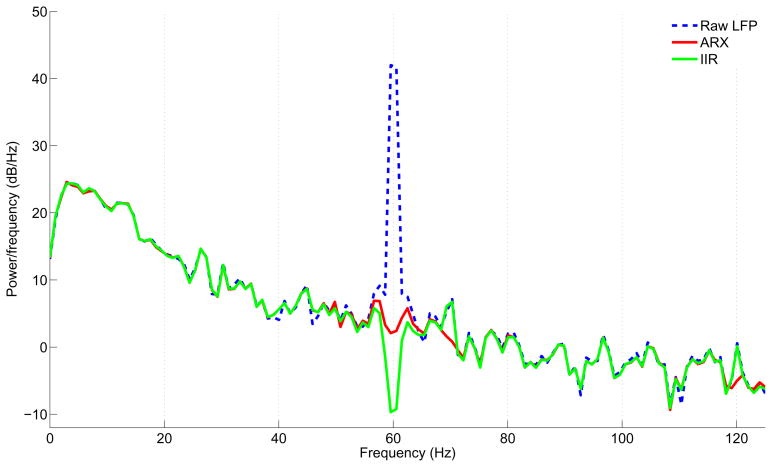
Fig. 4A depicts the raw LFP trace in an example trial with severe power line contamination recorded in the primary visual cortex of awake behaving monkeys. The vertical dashed lines mark the visual stimulus on/off (3,000 ms duration of stimulus). The resultant LFPs filtered by ARX (red) and IIR filter (green) methods are also presented. The corresponding reference input for ARX model is shown in Fig. 4B together with the estimated 60 Hz noise component embedded in the raw LFP signal. During this trial, the reference input that recorded the actual line noise exhibited some very slow variations of unknown origin (for example, indicated by the circles in the Fig. 4B), as reflected in the estimated noise. The corresponding power spectra of these three signals of Fig. 4A (shown in Fig. 5) demonstrates that the ARX filtering procedure eliminated 60 Hz noise without causing a significant signal loss. In contrast, the IIR filter removes excessive energy at 60 Hz, thereby producing a notch in the power spectrum curve.
Fig. 4.
Example trial of real electrophysiological data. (A) Raw LFP trace (blue) was severely contaminated by the power line artifact. The red and blue curves are the LFP signals recovered by the ARX model and conventional notch filter. The vertical dash lines indicate the visual stimulus interval. (B) The reference noise (blue) that was recorded by an extra channel entered into the ARX model to estimate the line artifact contained in the raw LFP recordings. The clean LFP signal was obtained by subtracting the estimated noise from the raw LFP recording. The circles point to where some unknown slow variations of reference input occurred. The corresponding arrows point to small mismatches between ARX and notch filtered LFPs.
Fig. 5.
Power spectrum density of the data presented in Fig. 4A. The difference in performance of two filtering procedure is evident.
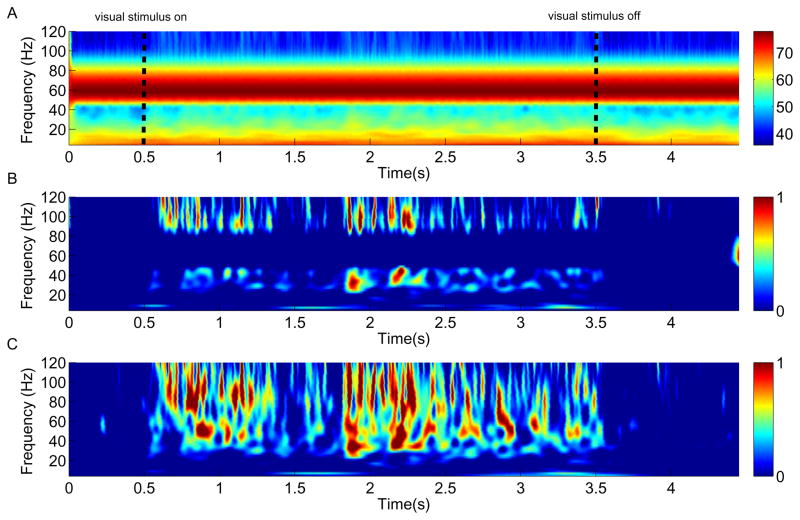
In order to visualize the temporal structure of the LFP signal, we computed the spectrogram of each individual LFP trace recorded within one entire block of trials and averaged all of these spectrograms in this recording session (Fig. 6A-C). The wavelet transform was applied here for time-frequency decomposition (specifically the complex Gaussian Morlet’s wavelets with a ratio f/σf of 7 in the frequency ranging from 5 to 120 Hz in 2 Hz steps). This resulted at 30 Hz in a wavelet with a σt of 37.2 ms and a σf of 4.28 Hz. In Fig. 6A, it is evident that the raw LFP signal was severely contaminated by the mains noise which masked the power changes related to the stimulation. To visualize stimulus-induced activity patterns, a normalized spectrogram is computed whereby the power of each frequency is divided by the mean of its prestimulus 500 ms baseline period. The spectrograms obtained from the IIR filter (Fig. 6B) and ARX (Fig. 6C) methods both exhibited remarkably enhanced power in the gamma band, except for the power around 60 Hz frequency bins in Fig. 6B due to the signal loss caused by the IIR filter (also see Fig. 5). After the stimulus onset the power of the LFP signal disperses into the gamma band and higher frequency ranges, and retreats back to the pre-stimulus level when the stimulus turns off. The structure of this normalized spectrogram is markedly changing during the stimulus presentation. Note that the strongest increase of power is predominantly located in the frequency bands greater than 40 Hz, consistent with some recent studies (Belitski et al., 2008).
Fig. 6.
(A) Averaged spectrogram from 28 trials in one recording session. Stimulus presentation starts at 0.5 and lasts 3.0 s. The vertical dashed lines indicate the visual stimulus onset and offset. Color scale shows the logarithm of power. (B) Normalized spectrogram obtained with the IIR notch filter. Although the activation evoked by the visual stmulus can be discerned, the signal loss around 60 Hz frequency bins caused by the IIR filter is evident along the time course. Color scale indicates relative modulation elicited by the stimulus when compared to the mean of preceding baseline. (C) Normalized spectrogram obtained with the ARX model.
4. Discussion
Recording neuronal activity in the awake, behaving primate brain has become established as one of the major tools available to study the neuronal encoding of specific sensorimotor behaviors. It is vital in this type of experiment as well as EEG/MEG recordings, to be able to reliably eliminate ambiguous noise sources in event-related neural responses (Melloni et al., 2009; Tallon-Baudry et al., 1997; Yuval-Greenberg et al., 2008). To deal with trial-to-trial noise fluctuation in awake preparation, the present study sets this issue within the context of the ANC and initiates it as a system identification problem by using the ARX model, as can be conveniently implemented in MATLAB since many algorithms in this field are included in the System Identification Toolbox of MATLAB (some built-in routines such as arx.m and arxstruc.m). Although it looks similar to many previous reports, the approach is from the other side of the coin. We applied this treatment in a straightforward simulation and experimental data, and conducted a comparative evaluation of the adaptively-designed and predetermined filters, qualitatively and quantitatively, so as to provide more practical solutions for denoising issue in awake recording.
Often, a proper recording environment with carefully designed shielding is not sufficient to get rid of the electrical interference in awake preparations (Gregoriou et al., 2009; Liu and Newsome, 2006; Pesaran et al., 2002). As the simulation demonstrated in this study (Fig. 2 and 3), the predetermined notch filter has difficulty in tracking any time-varying changes in signals, something that is frequently encountered in the neural recording. For example, unpredictable body movements in individual trials, can cause some artifacts resulting from the fluid leakage inside the chamber (saline solution can in some cases effectively suppress noise (Courtemanche et al., 2003)). But a low-profile recording chamber popularly used in many studies (Baker et al., 1999; Gray et al., 2007) cannot contain a sufficient amount of fluid to maintain a stable reference recording; this results in a varying degree of power line contamination. Consequently, large variations in the magnitude of the line noise that contaminate the collected data are expected on the trial-to-trial basis. Usually, the suppression band of the notch filter is designed to be as narrow as possible. Whenever the power line frequency is not stable or not accurately known a priori (Mitra and Pesaran, 1999), it gives rise to problems such as a mismatch between the suppression band and the power line frequency, leading to inadequate interference rejection or disruption of relevant signals (Fig. 3 and Fig. 5). These filters can cause distortion of the signal since they cannot distinguish line noise from the useful 50-/60-Hz components in the gamma range of the targeted LFP signal (Fig. 5). In contrast, the performance of the method proposed in this study was robust to this frequency mismatch, shown in Fig. 2B.
On the other hand, in event-related behavior paradigms, one usually needs to take into account information derived from numerous repetitions of the stimulus- or task-related event (hundreds or thousands of trials) for purposes of improving sensitivity. Throughout the recording period, the quality of the recorded signals depends on the performance of the behaving subjects, performance that often introduces unexpected variations. It is impractical to apply predetermined parameters of a static filter on trial-by-trial basis as tedious human supervision would be required for thousands of these trials. In fact there are other data-driven methods such as independent component analysis (ICA) that has been used to remove the power line interference in EEG applications (Ren et al., 2006). However, with ICA decomposition, identification of the components that contain the mains noise is always challenging because the noise interference often spreads into more than one independent component. Moreover, some useful signal may still be embedded in these noise components (Ren et al., 2006). In addition, depending on the number of components, ICA decomposition generally requires a minimal data length of each trial in term of the number of components, which would impose extra constraint on designing the experimental paradigm for awake primate training. In the ARX model proposed here, the monitored noise information is used to automatically estimate the trial-by-trial level of line noise contamination in the recorded signals. Under such circumstances, the method in the current study demonstrates better performance than the conventionally-predesigned IIR filters and is more appropriate for noise reduction in awake preparation.
The ringing artifacts (Fig. 3B) can be better minimized if one switches to a finite impulse response (FIR) notch filter. But, considering the limited data points of one trial collected from behaving animals (low sampling rate and short sampling window), there would implementation limits, as an IIR filter typically requires a much lower filter order to meet a given set of specifications than a corresponding FIR filter. Furthermore, one of its disadvantages is that it can introduce a nonlinear phase distortion. The LMS algorithm implemented in ARX model has an all-zero (moving average) or FIR configuration, which maintains the constant phase relationships of its spectral components between the two inputs (Titchener, 1982). Note that using complex wavelets, it is possible to retrieve the time-varying phases of an oscillatory signal in the complex two-dimensional plane. In this case, the wavelet decomposition provides both the amplitude (real part) and phase (imaginary part) information of the oscillation and performs the phase coherence analysis (Tallon-Baudry et al., 1997). It is an invaluable benefit since phase coupling is both necessary and sufficient to yield non-zero coherence (Bruns, 2004).
In summary, we have shown that the ARX model is optimally designed to automatically estimate the noise components of synthetic data and can be used to effectively and accurately remove ongoing trial-specific noise from neurophysiological recordings in awake animals. As shown by estimating sinusoid amplitude and power in test signals, this simple procedure is a considerable improvement over the conventional IIR notch filter, and provides a reliable means of eliminating the notorious power line artifact from LFP data. Our ARX implementation of ANC process will be an important pre-processing step in analyzing thousands of trials of cortical LFP data. An additional important future application of this procedure is to examine microsaccade-related activity in cortical LFP recordings. As well, it may prove to be useful for high frequency EEG/MEG applications.
Research Highlights.
An adaptive noise cancellation (ANC) method which is implemented with AutoRegressive model with eXogenous Input (ARX) is described to remove power line noise in cortical local field potential (LFP) recordings in primary visual cortex of awake, behaving animals. In light of the recent flurry of publications on the behavioral significance of surrounding gamma band (30–90hz) frequencies, the ability to remove 50/60 hz line noise from within this significant signal-laden frequency range has become a pressing issue.
We compare the accuracy and efficiency of such trial-by-trial noise cancellation method to the conventional notch filter. The ARX implementation has great computation efficiency and simplified algorithm, and is automated across thousands of trials dataset.
We demonstrate that this procedure, combined with wavelet time-frequency analysis, effectively removes the mains noise from synthetic data as well as real experimental data acquired from awake monkey.
Acknowledgments
This work was funded by NIH EY11744 (AWR), DA023002 (AWR), Vanderbilt Vision Research Center, and Vanderbilt University Center for Integrative & Cognitive Neuroscience. We thank Robert Friedman for providing the NI LabVIEW support, Roger Williams and Bruce Williams for excellent mechanic support, and Lisa Chu for awake primate training. We acknowledge two anonymous reviewers for their invaluable criticism and comments that improved the manuscript.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akaike H. A new look at the statistical model identification. IEEE Trans Automat Contr. 1974;19:716–23. [Google Scholar]
- Baker SN, Philbin N, Spinks R, Pinches EM, Wolpert DM, MacManus DG, Pauluis Q, Lemon RN. Multiple single unit recording in the cortex of monkeys using independently moveable microelectrodes. J Neurosci Methods. 1999;94:5–17. doi: 10.1016/s0165-0270(99)00121-1. [DOI] [PubMed] [Google Scholar]
- Belitski A, Gretton A, Magri C, Murayama Y, Montemurro MA, Logothetis NK, Panzeri S. Low-frequency local field potentials and spikes in primary visual cortex convey independent visual information. J Neurosci. 2008;28:5696–709. doi: 10.1523/JNEUROSCI.0009-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berens P, Keliris GA, Ecker AS, Logothetis NK, Tolias AS. Comparing the feature selectivity of the gamma-band of the local field potential and the underlying spiking activity in primate visual cortex. Front Syst Neurosci. 2008;2:2. doi: 10.3389/neuro.06.002.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bruns A. Fourier-, Hilbert- and wavelet-based signal analysis: are they really different approaches? J Neurosci Methods. 2004;137:321–32. doi: 10.1016/j.jneumeth.2004.03.002. [DOI] [PubMed] [Google Scholar]
- Chen LM, Heider B, Williams GV, Healy FL, Ramsden BM, Roe AW. A chamber and artificial dura method for long-term optical imaging in the monkey. J Neurosci Methods. 2002;113:41–9. doi: 10.1016/s0165-0270(01)00475-7. [DOI] [PubMed] [Google Scholar]
- Courtemanche R, Fujii N, Graybiel AM. Synchronous, focally modulated beta-band oscillations characterize local field potential activity in the striatum of awake behaving monkeys. J Neurosci. 2003;23:11741–52. doi: 10.1523/JNEUROSCI.23-37-11741.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engel AK, Fries P, Singer W. Dynamic predictions: oscillations and synchrony in top-down processing. Nat Rev Neurosci. 2001;2:704–16. doi: 10.1038/35094565. [DOI] [PubMed] [Google Scholar]
- Friedlander B. System identification techniques for adaptive signal processing. Circuits Systems Signal Process. 1982;1:3–41. [Google Scholar]
- Fries P, Nikolic D, Singer W. The gamma cycle. Trends Neurosci. 2007;30:309–16. doi: 10.1016/j.tins.2007.05.005. [DOI] [PubMed] [Google Scholar]
- Gail A, Brinksmeyer HJ, Eckhorn R. Perception-related modulations of local field potential power and coherence in primary visual cortex of awake monkey during binocular rivalry. Cereb Cortex. 2004;14:300–13. doi: 10.1093/cercor/bhg129. [DOI] [PubMed] [Google Scholar]
- Gray CM, Goodell B, Lear A. Multichannel micromanipulator and chamber system for recording multineuronal activity in alert, non-human primates. J Neurophysiol. 2007;98:527–36. doi: 10.1152/jn.00259.2007. [DOI] [PubMed] [Google Scholar]
- Gregoriou GG, Gotts SJ, Zhou H, Desimone R. High-frequency, long-range coupling between prefrontal and visual cortex during attention. Science. 2009;324:1207–10. doi: 10.1126/science.1171402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haberly LB, Shepherd GM. Current-density analysis of summed evoked potentials in opossum prepyriform cortex. J Neurophysiol. 1973;36:789–802. doi: 10.1152/jn.1973.36.4.789. [DOI] [PubMed] [Google Scholar]
- Hamilton PS. A comparison of adaptive and nonadaptive filters for reduction of power line interference in the ECG. IEEE Trans Biomed Eng. 1996;43:105–9. doi: 10.1109/10.477707. [DOI] [PubMed] [Google Scholar]
- Haykin S. Adaptive filter theory. Prentice Hall; Upper Saddle River, New Jersey: 1996. [Google Scholar]
- Henrie JA, Shapley R. LFP power spectra in V1 cortex: the graded effect of stimulus contrast. J Neurophysiol. 2005;94:479–90. doi: 10.1152/jn.00919.2004. [DOI] [PubMed] [Google Scholar]
- Jensen EW, Litvan H. Detection of level of consciousness during propofol anaesthesia by rapidly extracted auditory evoked potentials. In: Jordan C, Vaughan DJA, Newton DEF, editors. Memory and Awareness in Anaesthesia. Imperial College Press; London: 2000. pp. 88–96. [Google Scholar]
- Johnson CR., Jr On the interaction of adaptive filtering, identification and control. IEEE Signal Processing Mag. 1995;12:22–37. [Google Scholar]
- Kiebel SJ, Tallon-Baudry C, Friston KJ. Parametric analysis of oscillatory activity as measured with EEG/MEG. Hum Brain Mapp. 2005;26:170–7. doi: 10.1002/hbm.20153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Van Quyen M, Foucher J, Lachaux J, Rodriguez E, Lutz A, Martinerie J, Varela FJ. Comparison of Hilbert transform and wavelet methods for the analysis of neuronal synchrony. J Neurosci Methods. 2001;111:83–98. doi: 10.1016/s0165-0270(01)00372-7. [DOI] [PubMed] [Google Scholar]
- Lemon R. Methods for neuronal recording in conscious animals. John Wiley & Sons; New York: 1984. [Google Scholar]
- Liberati D, DiCorrado S, Mandelli S. Topographic mapping of single sweep evoked potentials in the brain. IEEE Trans Biomed Eng. 1992;39:943–51. doi: 10.1109/10.256428. [DOI] [PubMed] [Google Scholar]
- Litvan H, Jensen EW, Galan J, Lund J, Rodriguez BE, Henneberg SW, Caminal P, Villar Landeira JM. Comparison of conventional averaged and rapid averaged, autoregressive-based extracted auditory evoked potentials for monitoring the hypnotic level during propofol induction. Anesthesiology. 2002;97:351–8. doi: 10.1097/00000542-200208000-00011. [DOI] [PubMed] [Google Scholar]
- Liu J, Newsome WT. Local field potential in cortical area MT: stimulus tuning and behavioral correlations. J Neurosci. 2006;26:7779–90. doi: 10.1523/JNEUROSCI.5052-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Logothetis NK. The underpinnings of the BOLD functional magnetic resonance imaging signal. J Neurosci. 2003;23:3963–71. doi: 10.1523/JNEUROSCI.23-10-03963.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melloni L, Schwiedrzik CM, Wibral M, Rodriguez E, Singer W. Response to: Yuval-Greenberg et al., “Transient Induced Gamma-Band Response in EEG as a Manifestation of Miniature Saccades”. Neuron. 58:429–441. doi: 10.1016/j.neuron.2008.03.027. [DOI] [PubMed] [Google Scholar]; Neuron. 2009;62:8–10. author reply -2. [Google Scholar]
- Mirsattari SM, Wang Z, Ives JR, Bihari F, Leung LS, Bartha R, Menon RS. Linear aspects of transformation from interictal epileptic discharges to BOLD fMRI signals in an animal model of occipital epilepsy. Neuroimage. 2006;30:1133–48. doi: 10.1016/j.neuroimage.2005.11.006. [DOI] [PubMed] [Google Scholar]
- Mitra PP, Pesaran B. Analysis of dynamic brain imaging data. Biophys J. 1999;76:691–708. doi: 10.1016/S0006-3495(99)77236-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitzdorf U. Current source-density method and application in cat cerebral cortex: investigation of evoked potentials and EEG phenomena. Physiol Rev. 1985;65:37–100. doi: 10.1152/physrev.1985.65.1.37. [DOI] [PubMed] [Google Scholar]
- Niessing J, Ebisch B, Schmidt KE, Niessing M, Singer W, Galuske RA. Hemodynamic signals correlate tightly with synchronized gamma oscillations. Science. 2005;309:948–51. doi: 10.1126/science.1110948. [DOI] [PubMed] [Google Scholar]
- Pesaran B, Pezaris JS, Sahani M, Mitra PP, Andersen RA. Temporal structure in neuronal activity during working memory in macaque parietal cortex. Nat Neurosci. 2002;5:805–11. doi: 10.1038/nn890. [DOI] [PubMed] [Google Scholar]
- Ren X, Yan Z, Wang Z, Hu X. Noise reduction based on ICA decomposition and wavelet transform for the extraction of motor unit action potentials. J Neurosci Methods. 2006;158:313–22. doi: 10.1016/j.jneumeth.2006.06.005. [DOI] [PubMed] [Google Scholar]
- Schnitzler A, Gross J. Normal and pathological oscillatory communication in the brain. Nat Rev Neurosci. 2005;6:285–96. doi: 10.1038/nrn1650. [DOI] [PubMed] [Google Scholar]
- Singer W. Neuronal synchrony: a versatile code for the definition of relations? Neuron. 1999;24:49–65. 111–25. doi: 10.1016/s0896-6273(00)80821-1. [DOI] [PubMed] [Google Scholar]
- Tallon-Baudry C, Bertrand O, Delpuech C, Permier J. Oscillatory gamma-band (30–70 Hz) activity induced by a visual search task in humans. J Neurosci. 1997;17:722–34. doi: 10.1523/JNEUROSCI.17-02-00722.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Titchener PF, Gooch RP, Widrow B. A linear phase adaptive filter. Record of the Sixteenth Asilomar Conference on Circuits, Systems and Computers; 1982. pp. 40–4. [Google Scholar]
- Widrow B, Glover JR, McCool JM, Kaunitz J, Williams CS, Hearn RH, Zeidler JR, Dong EJ, Goodlin RC. Adaptive noise cancelling: principles and applications. Proc IEEE. 1975;63:1692–716. [Google Scholar]
- Womelsdorf T, Schoffelen JM, Oostenveld R, Singer W, Desimone R, Engel AK, Fries P. Modulation of neuronal interactions through neuronal synchronization. Science. 2007;316:1609–12. doi: 10.1126/science.1139597. [DOI] [PubMed] [Google Scholar]
- Yuval-Greenberg S, Tomer O, Keren AS, Nelken I, Deouell LY. Transient induced gamma-band response in EEG as a manifestation of miniature saccades. Neuron. 2008;58:429–41. doi: 10.1016/j.neuron.2008.03.027. [DOI] [PubMed] [Google Scholar]