A comparative analysis of OTF, NPS, and DQE in energy integrating and photon counting digital x-ray detectors

Abstract

Purpose: One of the benefits of photon counting (PC) detectors over energy integrating (EI) detectors is the absence of many additive noise sources, such as electronic noise and secondary quantum noise. The purpose of this work is to demonstrate that thresholding voltage gains to detect individual x rays actually generates an unexpected source of white noise in photon counters.

Methods: To distinguish the two detector types, their point spread function (PSF) is interpreted differently. The PSF of the energy integrating detector is treated as a weighting function for counting x rays, while the PSF of the photon counting detector is interpreted as a probability. Although this model ignores some subtleties of real imaging systems, such as scatter and the energy-dependent amplification of secondary quanta in indirect-converting detectors, it is useful for demonstrating fundamental differences between the two detector types. From first principles, the optical transfer function (OTF) is calculated as the continuous Fourier transform of the PSF, the noise power spectra (NPS) is determined by the discrete space Fourier transform (DSFT) of the autocovariance of signal intensity, and the detective quantum efficiency (DQE) is found from combined knowledge of the OTF and NPS. To illustrate the calculation of the transfer functions, the PSF is modeled as the convolution of a Gaussian with the product of rect functions. The Gaussian reflects the blurring of the x-ray converter, while the rect functions model the sampling of the detector.

Results: The transfer functions are first calculated assuming outside noise sources such as electronic noise and secondary quantum noise are negligible. It is demonstrated that while OTF is the same for two detector types possessing an equivalent PSF, a frequency-independent (i.e., “white”) difference in their NPS exists such that NPS_PC≥NPS_EI and hence DQE_PC≤DQE_EI. The necessary and sufficient condition for equality is that the PSF is a binary function given as zero or unity everywhere. In analyzing the model detector with Gaussian blurring, the difference in NPS and DQE between the two detector types is found to increase with the blurring of the x-ray converter. Ultimately, the expression for the additive white noise of the photon counter is compared against the expression for electronic noise and secondary quantum noise in an energy integrator. Thus, a method is provided to determine the average secondary quanta that the energy integrator must produce for each x ray to have superior DQE to a photon counter with the same PSF.

Conclusions: This article develops analytical models of OTF, NPS, and DQE for energy integrating and photon counting digital x-ray detectors. While many subtleties of real imaging systems have not been modeled, this work is illustrative in demonstrating an additive source of white noise in photon counting detectors which has not yet been described in the literature. One benefit of this analysis is a framework for determining the average secondary quanta that an energy integrating detector must produce for each x ray to have superior DQE to competing photon counting technology.

INTRODUCTION

At a broad level, digital x-ray detectors can be divided into two main types: Energy integrating (EI) and photon counting (PC). An energy integrator detects the total energy deposition of the incident x rays, while a photon counter detects the presence of individual x-ray quanta as discrete events. In this work, we propose the existence of a fundamental difference in the noise properties of the two detector types. As a prerequisite to that analysis, it is helpful to review the physics of the two detector types.

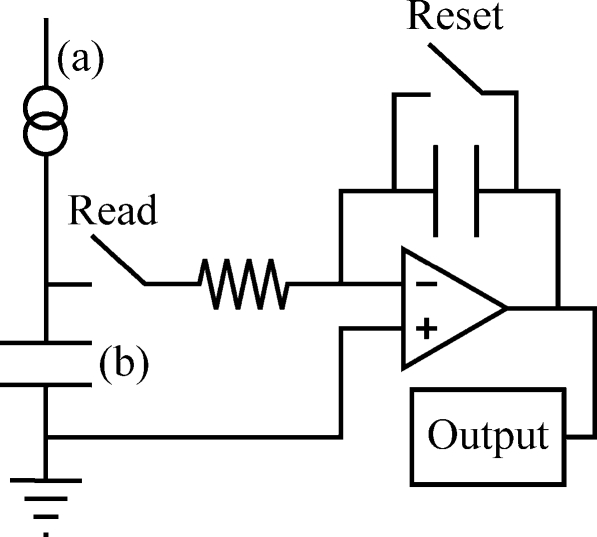
A typical energy integrating detector is an indirect converter consisting of a scintillator placed in optical contact with a large area plate of amorphous silicon (a-Si). The x rays excite electrons in the scintillator from the valence band to the conduction band. In returning to the valence band, some electrons transition through an intermediate state created by activator impurities and optical photons are emitted in proportion to the incident x-ray energy.¹ Common scintillators include gadolinium oxysulfide doped with terbium (Gd₂O₂S:Tb); a turbid granular phosphor in which visible light spreads by optical scatter; and cesium iodide doped with thallium (CsI:Tl), a structured phosphor in which needlelike crystals approximately 10 μm in diameter channel the light down to the a-Si plate by total internal reflection. Although structured phosphors have the drawback of being more expensive to produce, they have the advantage of improved spatial resolution, as they minimize the lateral spread of visible light.^{1, 2} Ultimately, the visible light produced by the scintillator is absorbed by light-sensitive photodiodes arranged in a rectangular array within a-Si and is re-emitted as electrons via the photoelectric effect.^{3, 4, 5} The current established by the flow of photoelectrons in the photodiode of each pixel provides the input for an integrating circuit such as the one illustrated schematically in Fig. 1. The circuit sums the current produced by each x ray [Fig. 2a] and integrates the net current over time to increase the charge and hence voltage on a storage capacitor [Fig. 2b]. The output signal is then determined by the maximum potential difference (V_max) across the capacitor. Although Figs. 12 are simplified by not taking into account the complex cascade of Compton x-ray interactions within the detector or the different energies of photoelectrons produced by K, L, and M fluorescence,^{6, 7, 8, 9} they illustrate the concept that the readout voltage per pixel is essentially proportional to the sum of the energies of the incident x rays.

Figure 1.

A schematic diagram of the electrical circuit for processing current in the photodiode of an energy integrating detector is shown.

Figure 2.

(a) The energy integrating circuit of Fig. 1 sums the current from each individual x ray and (b) integrates the net current over time to increase the charge and hence voltage across a storage capacitor. The output voltage per pixel is determined by the maximum potential difference (V_max) across the capacitor. The two subplots (a) and (b) are matched to their respective points in the circuit of Fig. 1.

Outside of phosphor-based detectors, an additional example of an energy integrating detector is an amorphous selenium (a-Se) photoconductor operated in drift mode. This energy integrating detector is said to be a direct converter, as the x-ray signal generates an image without intermediate conversion of x rays to visible light. In such a detector, an absorbed x ray ionizes a Se atom located within the thickness of the a-Se semiconductor and creates an electron-hole pair. As a result of an electric field applied normal to the photoconductor surface, the electron and hole migrate in a nearly perfect orthogonal path to the two different ends of the detector and an image is formed.¹ A defining characteristic of drift mode is that the electric field is small enough so that the electron moving along the field lines does not have sufficient kinetic energy between collisions to ionize additional Se atoms and hence to create an avalanche formation of electrons and holes. Photoconducting detectors operated in drift mode have superior spatial resolution to phosphor-based detectors. In fact, to a first approximation, the modulation transfer function (MTF) of a-Se operated in drift mode is essentially unity for all spatial frequencies.¹⁰ Although photoconductors and phosphor-based detectors differ in terms of their spatial resolution, they are similar in that they both present the advantage of a large sensitive area and that they both possess the drawbacks of limited dynamic range and sensitivity to dark current and electronic read-out noise.¹¹

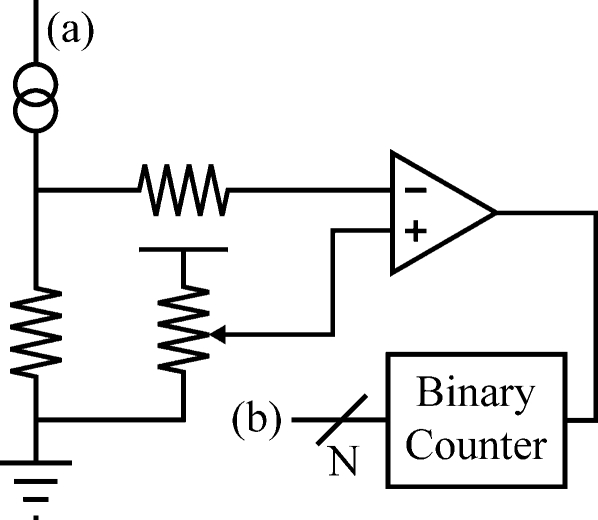
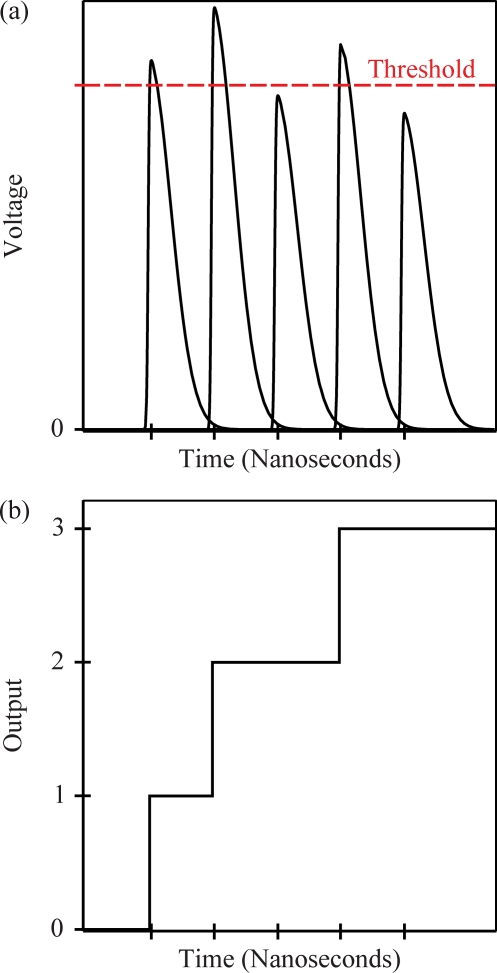
To overcome the drawbacks associated with energy integrating detectors, photon counting detectors have been developed. One common photon counter used in mammography, for example, consists of many thin silicon strip detectors with their long axis parallel to the x-ray beam. This orientation increases the path length of absorption and hence quantum efficiency, which often exceeds 90%.^{12, 13, 14} X-ray photons incident on the detector interact with silicon atoms via the photoelectric or Compton effect. Since 3.6 eV is required to generate a single electron-hole pair, thousands of electron-hole pairs are created per x ray. A bias voltage applied across the detector generates an electric field which causes the electron-hole pairs to migrate toward opposite ends of the detector. Signal is then transferred from an aluminum strip to a preamplifier and shaper through wire bonds and the voltage gain is compared against the threshold established by the potentiometer of a circuit such as the one shown in Fig. 3. Voltage gains exceeding the threshold are counted as representative of a single x-ray photon [Fig. 4a] and the total signal per pixel is found by summing these counts [Fig. 4b]. Since each x ray generates approximately 5000 electrons and since the RMS noise is approximately 200 electrons, the threshold might typically be set to 2000 electrons.¹⁴ A key advantage of counting individual x-ray quanta over accumulating total charge is that the background noise can be completely removed from the image. In addition, because the height of the voltage gain before thresholding is proportional to the energy of the incident x ray, another advantage of photon counting is that thresholds can be adjusted to achieve energy discrimination in a polyenergetic beam.^{15, 16, 17, 18} This information can be used to remove anatomical noise, quantify contrast uptake over a set of voxels, or perform material decomposition. Additional benefits of photon counting detectors include high absorption efficiency, virtually no electronic noise power or dark current rate, unlimited dynamic range, fast readout, and a slit geometry that efficiently eliminates scatter.¹⁹

Figure 3.

A schematic diagram of the electrical circuit for processing current in the photodiode of a photon counting detector is shown.

Figure 4.

In the photon counting circuit of Fig. 3, (a) the voltage gains exceeding the threshold established by the potentiometer are counted as representative of one x ray and (b) the total signal per pixel is found by summing these counts. The two subplots (a) and (b) are matched to their respective points in the circuit of Fig. 3.

In addition to silicon strip detectors, there has been considerable interest in gaseous detectors as alternative forms of photon counters. In these detectors, each x ray generates a cascade of ionizations of gas atoms and voltage gains exceeding a threshold are counted as representative of one x ray. Since x rays in the medical imaging energy range interact with the gas primarily by the photoelectric effect, which increases in prevalence with the atomic number Z of the gas, high Z inert gases such as krypton (Kr) and xenon (Xe) are commonly used in these detectors. To increase absorption efficiency further, the gases are typically placed under high pressure. Finally, to smooth avalanche amplification, which is exponential with the applied electric field, a quencher gas such as carbon dioxide (CO₂) is added to the mixture.²⁰

One important area of distinction between energy integrating and photon counting detectors, regardless of the specific form of either detector type, is in the weighting of the information carried by individual x rays in a polyenergetic beam. Energy integrating detectors give the output signal of high-energy photons more weight than low-energy photons, while photon counting detectors give the output signals equal contribution. As a direct result of this distinction, Tapiovaara and Wagner²¹ have shown that a difference in detective quantum efficiency (DQE) arises between the two detector types when they are exposed to polyenergetic x-ray beams. Assuming screen film imaging systems, DQE is calculated for both detector types from the expression

$$\text{DQE}=A\frac{{\left[\int \left(\overline{N_1\left(E\right)}-\overline{N_2\left(E\right)}\right)\eta \left(E\right)\psi \left(E\right)dE\right]}^2}{\int \left(\overline{N_1\left(E\right)}+\overline{N_2\left(E\right)}\right)\eta \left(E\right){\psi }^2\left(E\right)dE}.$$ (1)

Following the notation of the authors, N_i(E) is the photon fluence spectra for energy E either in the absence of signal (i=1) or presence of signal (i=2), η(E) is the fraction of absorbed x-ray quanta, ψ(E) is the output response of the detector for each incident x ray, and A is the detector area which is taken to be large compared against the width of the point spread function (PSF). Equation 1 assumes that the incident photons of energy E are Poisson-distributed random variables with mean $A\overline{N_i\left(E\right)}$ and are detected by a binomial process whose resultant distribution is Poisson with mean $A\overline{N_i\left(E\right)}\eta \left(E\right)$. The calculation of DQE is different for the two detector types in that the energy integrator has the output response ψ(E)=E, while the photon counter exhibits the output response ψ(E)=constant. Using these two substitutions in Eq. 1, Tapiovaara and Wagner investigated the degradation in DQE as a function of the x-ray tube kilovoltage (kV), assuming the presence of an ideal antiscatter grid, a noiseless detector, and complete x-ray absorption. Raising the kV served the purpose of increasing the width of the polyenergetic x-ray spectra. The authors demonstrated that while both detector types have DQE degradation with increasing kV, the degradation is more considerable as a function of kV for the energy integrating detector than for the photon counting detector. Furthermore, for any fixed kV, the DQE difference between the two detector types is much more pronounced in imaging bone and iodine than in imaging soft tissue.²¹

Tapiovaara and Wagner do not predict a DQE difference between the two detector types when they are both exposed to monoenergetic x rays. However, since their work is limited to screen film systems, it is an open question whether a DQE difference exists in the monoenergetic case if the two detector types are digital. For this reason, the purpose of this work is to propose analytical models of the optical transfer function (OTF), noise power spectra (NPS), and DQE for digital energy integrating and photon counting detectors in the case of monoenergetic x rays. The proposed models demonstrate an intrinsic difference in imaging performance between the two detector types which has not yet been explored in the literature.

This work begins by deriving analytical expressions for the signal intensity autocovariance of the two detector types from first principles and shows that these expressions are different for energy integrating and photon counting digital x-ray detectors. The autocovariance analysis facilitates the development of a key theorem regarding the NPS difference between the two detector types. An important corollary of this theorem is then derived as it relates to OTF and DQE. To illustrate OTF, NPS, and DQE calculations for the two detector types, a PSF modeling the blurring of the x-ray converter as a Gaussian is analyzed.

ENERGY INTEGRATING AUTOCOVARIANCE

Suppose that a two-dimensional (2D) rectangular energy integrating digital x-ray detector of dimensions L_x×L_y is centered on the origin and evenly partitioned into rectangular pixels of dimensions l_x×l_y placed side-by-side. The center of each pixel may be defined as position X_n, where n is a doublet with integer components n_x and n_y used for unique labeling of the pixels in the lattice. For the purpose of this work, we will assume that each x ray landing on the detector at position x is counted by each pixel centered at X_n with a weight w(x−X_n) ranging from zero to unity. The weighting function for counting x rays is taken to be dependent only on the displacement of each x ray from the pixel center, that is, it exhibits invariance under translations across pixels. Under these assumptions, the total signal intensity I_n recorded by each pixel centered at X_n is found by simply summing the weights for counting each incident x ray

$$I_{\mathbf{n}}=\sum _{m=1}^{N}w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right),$$ (2)

where x_m is the position at which the mth x-ray photon is incident on the detector and where N is the total number of x rays landing on the detector.

In stipulating that the detector’s response to each x ray is a weighting function determined only by the position of the photon relative to the pixel centers, our model neglects a few factors which we point out here for completeness. For example, the model neglects detector lag and ghosting,^{22, 23, 24} which alter the effective number of x rays incident on the detector from N in Eq. 2 to a different value. In addition, the model does not incorporate the possibility for scatter within the detector.^{25, 26, 27, 28, 29} Because scatter is a stochastic process, a more complete description of the weighting function would include probabilities of x-ray interactions within the detector using Monte Carlo simulations.^{30, 31} Finally, the model does not take into account the energy-dependent amplification of secondary quanta in an indirect-converting detector¹ or the energy-dependent response of photodiodes in converting optical photons to electrons. Although our model neglects to consider all the properties of real imaging systems, it will be sufficient to describe a fundamental difference between energy integrating and photon counting digital x-ray detectors.

In an ideal energy integrating detector, the weighting function w(x−X_n) should be exactly unity if the x ray lands within the pixel area and zero if the x ray lands elsewhere, so that there is no cross-talk between pixels. In a blurring detector, however, an x ray landing outside of the nth pixel may indeed cause that pixel to record a count. Assuming that the noise is stationary, the spatial correlation of pixels can be expressed in terms of the signal intensity autocovariance function

$$K_{\mathbf{n}{\mathbf{n}}^{\prime }}=⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}\right)\left(I_{{\mathbf{n}}^{\prime }}-{\overline{I}}_{{\mathbf{n}}^{\prime }}\right)⟩$$ (3)

$$=⟨I_{\mathbf{n}}{I}_{{\mathbf{n}}^{\prime }}⟩-{\overline{I}}_{\mathbf{n}}{\overline{I}}_{{\mathbf{n}}^{\prime }}.$$ (4)

In the case of nonstationary noise, a more general formulation of pixel correlation would make reference to a covariance function. However, a study of nonstationary noise would merit a separate investigation, as it is less readily adapted to Fourier theory.³² Defining the x-ray fluence as

$$\Phi =\frac{N}{L_x{L}_y}$$ (5)

and defining the intensity transfer characteristic of the nth pixel as

$$G_{\mathbf{n}}={\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}w\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)dxdy,$$ (6)

it follows from Eqs. 2, 3, 4, 5, 6 that the signal intensity autocovariance is

$${⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}\right)\left(I_{{\mathbf{n}}^{\prime }}-{\overline{I}}_{{\mathbf{n}}^{\prime }}\right)⟩}_N=⟨\left(\sum _{m=1}^{N}w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right)\right)\left(\sum _{m^{\prime }=1}^{N}w\left({\mathbf{x}}_{m^{\prime }}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)\right)⟩-{\Phi }^2{G}_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }}$$ (7)

$$=\sum _{m=1}^N\sum _{m^{\prime }=1}^N⟨w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right)w\left({\mathbf{x}}_{m^{\prime }}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)⟩-{\Phi }^2{G}_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }},$$ (8)

where the linearity of the expectation operation permits the transition from Eq. 7 to Eq. 8. On the left-hand side of Eq. 7, the subscript N is applied to emphasize that the number of x rays landing on the detector is precisely known. This condition will be removed shortly. In the double sum of Eq. 8, the N terms for which m=m^′ and the N²−N terms for which m≠m^′ can now be evaluated separately, giving

$${⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}\right)\left(I_{{\mathbf{n}}^{\prime }}-{\overline{I}}_{{\mathbf{n}}^{\prime }}\right)⟩}_N=N⟨w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right)w\left({\mathbf{x}}_m-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)⟩+\left(N^2-N\right)⟨w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right)⟩⟨w\left({\mathbf{x}}_{m^{\prime }}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)⟩-{\Phi }^2{G}_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }}.$$ (9)

The second term of the expansion in Eq. 9 incorporates the fact that the quantities w(x_m−X_n) and w(_xm^′−X_n^′) are independent provided m≠m^′. Noting that

$$⟨w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right)⟩⟨w\left({\mathbf{x}}_{m^{\prime }}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)⟩={\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{dxdy}{L_x{L}_y}w\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right){\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{d{x}^{\prime }d{y}^{\prime }}{L_x{L}_y}w\left({\mathbf{x}}^{\prime }-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)=\frac{G_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }}}{L_x^2{L}_y^2},$$ (10)

one finds

$${⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}\right)\left(I_{{\mathbf{n}}^{\prime }}-{\overline{I}}_{{\mathbf{n}}^{\prime }}\right)⟩}_N=N⟨w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right)w\left({\mathbf{x}}_m-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)⟩-\frac{\Phi G_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }}}{L_x{L}_y}.$$ (11)

The second term in Eq. 11 is negligible in the limit of an infinitely large detector (L_x,L_y→∞).

In order to generalize Eq. 11 to incorporate the possibility that the number of x rays landing on the entire detector is not uniform from one experiment to the next but instead exhibits temporal variation, one may assume that N is a Poisson-distributed random variable. To compute the signal intensity autocovariance in this case, begin by noting that

$$⟨I_{\mathbf{n}}{I}_{{\mathbf{n}}^{\prime }}⟩-{\overline{I}}_{\mathbf{n}}{\overline{I}}_{{\mathbf{n}}^{\prime }}=⟨{⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}+{\overline{I}}_{\mathbf{n}}\right)\left(I_{{\mathbf{n}}^{\prime }}-{\overline{I}}_{{\mathbf{n}}^{\prime }}+{\overline{I}}_{{\mathbf{n}}^{\prime }}\right)⟩}_N⟩-{\overline{I}}_{\mathbf{n}}{\overline{I}}_{{\mathbf{n}}^{\prime }}.$$ (12)

The nested brackets emphasize that one can first average for fixed values of N and then average over the varying numbers of incident x-ray quanta. Expanding the terms gives

$$⟨I_{\mathbf{n}}{I}_{{\mathbf{n}}^{\prime }}⟩-{\overline{I}}_{\mathbf{n}}{\overline{I}}_{{\mathbf{n}}^{\prime }}=⟨{⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}\right)\left(I_{{\mathbf{n}}^{\prime }}-{\overline{I}}_{{\mathbf{n}}^{\prime }}\right)⟩}_N⟩+⟨{⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}\right){\overline{I}}_{{\mathbf{n}}^{\prime }}⟩}_N⟩+⟨{⟨{\overline{I}}_{\mathbf{n}}{I}_{{\mathbf{n}}^{\prime }}⟩}_N⟩-{\overline{I}}_{\mathbf{n}}{\overline{I}}_{{\mathbf{n}}^{\prime }}.$$ (13)

Since

$${⟨I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}⟩}_N=0,$$ (14)

one sees that the second term of the expansion in Eq. 13 vanishes. The third and fourth terms combine as

$$⟨{⟨{\overline{I}}_{\mathbf{n}}{I}_{{\mathbf{n}}^{\prime }}⟩}_N⟩-{\overline{I}}_{\mathbf{n}}{\overline{I}}_{{\mathbf{n}}^{\prime }}=\frac{G_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }}}{L_x^2{L}_y^2}\left[⟨N^2⟩-{⟨N⟩}^2\right].$$ (15)

The assumption that the variance in the number of x rays is equal to the mean number of x rays, as would be the case for Poisson statistics,³³ can be introduced into Eq. 15 so that Eq. 13 can be simplified as

$$⟨I_{\mathbf{n}}{I}_{{\mathbf{n}}^{\prime }}⟩-{\overline{I}}_{\mathbf{n}}{\overline{I}}_{{\mathbf{n}}^{\prime }}=⟨{⟨\left(I_{\mathbf{n}}-{\overline{I}}_{\mathbf{n}}\right)\left(I_{{\mathbf{n}}^{\prime }}-{\overline{I}}_{{\mathbf{n}}^{\prime }}\right)⟩}_N⟩+\frac{\overline{\Phi }{G}_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }}}{L_x{L}_y}.$$ (16)

Combining Eq. 16 with Eq. 11 yields the final expression for the signal intensity autocovariance of an energy integrating detector

$$K_{\mathbf{n}{\mathbf{n}}^{\prime }}=\overline{N}⟨w\left({\mathbf{x}}_m-{\mathbf{X}}_{\mathbf{n}}\right)w\left({\mathbf{x}}_m-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)⟩$$ (17)

$$=\overline{\Phi }{\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}w\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)w\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)dxdy,$$ (18)

where $\overline{\Phi }$ is given by Eq. 5 with the exchange of N for $\overline{N}$.

PHOTON COUNTING AUTOCOVARIANCE

Suppose now that the output of each pixel in detecting an x ray landing at position x is binary (i.e., either zero or unity), as would be the case for a photon counter. Consequently, instead of being detected by the nth pixel based on a weight ranging from zero to unity, each x ray is either counted as unity with probability p(x−X_n) or counted as zero with probability 1−p(x−X_n). For the purpose of this work, we will assume that p(x−X_n) is mathematically equivalent to w(x−X_n), although its interpretation is different. Denoting C_n as the total counts of the nth pixel, similar logic up to Eq. 11 holds so that the signal intensity autocovariance can be calculated as

$${⟨\left(C_{\mathbf{n}}-{\overline{C}}_{\mathbf{n}}\right)\left(C_{{\mathbf{n}}^{\prime }}-{\overline{C}}_{{\mathbf{n}}^{\prime }}\right)⟩}_N=N⟨Q_{\mathbf{n}}\left({\mathbf{x}}_m\right)Q_{{\mathbf{n}}^{\prime }}\left({\mathbf{x}}_m\right)⟩-\frac{\Phi G_{\mathbf{n}}{G}_{{\mathbf{n}}^{\prime }}}{L_x{L}_y},$$ (19)

where G_n is the intensity transfer characteristic given by Eq. 6 with the exchange of w(x−X_n) for p(x−X_n) and where the quantity Q_n(x_m) is defined to be unity if the mth x ray is counted by the nth pixel and zero otherwise. Unlike the energy integrating detector, one must separately consider the cases n≠n^′ and n=n^′ in order to calculate the signal intensity autocovariance of Eq. 19. Beginning with n≠n^′, one observes that

$$⟨Q_{\mathbf{n}}\left({\mathbf{x}}_m\right)Q_{{\mathbf{n}}^{\prime }}\left({\mathbf{x}}_m\right)⟩={\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{dxdy}{L_x{L}_y}p\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)p\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)\left(1\right)\left(1\right)+{\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{dxdy}{L_x{L}_y}p\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)\left[1-p\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)\right]\left(1\right)\left(0\right)+{\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{dxdy}{L_x{L}_y}\left[1-p\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)\right]p\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)\left(0\right)\left(1\right)+{\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{dxdy}{L_x{L}_y}\left[1-p\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)\right]\left[1-p\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)\right]\left(0\right)\left(0\right),$$ (20)

where the four terms represent the four possible outcomes of the x ray being counted by two distinct pixels. Conveniently, the final three terms vanish. However, the case n=n^′ is different,

$$⟨Q_{\mathbf{n}}^2\left({\mathbf{x}}_m\right)⟩={\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{dxdy}{L_x{L}_y}p\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)\left(1^2\right)+{\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\frac{dxdy}{L_x{L}_y}\left[1-p\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)\right]\left(0^2\right),$$ (21)

for there are only two possible outcomes of the x ray being counted by a single pixel. Again, only the first term is nonzero. Combining Eqs. 19, 20, 21 with Eq. 16 to incorporate the assumption that N is a Poisson-distributed random variable, one can write in summary that the signal intensity autocovariance of the photon counting detector is

$$K_{\mathbf{n}{\mathbf{n}}^{\prime }}=\{\begin{array}{ll}\overline{\Phi }{G}_{\mathbf{n}}\hfill & \mathbf{n}={\mathbf{n}}^{\prime }\hfill \\ \overline{\Phi }{\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}p\left(\mathbf{x}-{\mathbf{X}}_{\mathbf{n}}\right)p\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)dxdy\hfill & \mathbf{n}\ne {\mathbf{n}}^{\prime }\hfill \end{array}\phantom{\}}.$$ (22)

One sees that covariance has the same form for both detector types, but variance does not.

COMPARATIVE ANALYSIS OF THE TWO DETECTOR TYPES

With expressions for the signal intensity autocovariance of the two detector types established, local NPS or Wiener spectra W(ν) for pixel n^′ can now be calculated as the discrete space Fourier transform (DSFT) of the signal intensity autocovariance^{34, 35}

$$W\left(\mathbf{\nu }\right)=l_x{l}_y\sum _{n_y}\sum _{n_x}{K}_{\mathbf{n}{\mathbf{n}}^{\prime }}{e}^{-2\pi i\left[\left(n_x-n_x^{\prime }\right)l_x{\nu }_x+\left(n_y-n_y^{\prime }\right)l_y{\nu }_y\right]},$$ (23)

where i denotes the imaginary unit $\sqrt{-1}$ and where ν_x and ν_y denote spatial frequency in the x and y directions, respectively. This formulation of NPS implicitly makes the assumption that x rays are converted to photoelectrons in the detector elements in a single step. As a result, it ignores noise due to stochastic variation in the number of optical photons produced for each incident x ray in an indirect-converting energy integrating detector. Stochastic amplification adds white noise³⁶ to the baseline NPS established by Eq. 23 and will be addressed separately in Sec. 7.

Assuming that the two detector types have the same point spread function P(x−X_n), which is equivalent to w(x−X_n) and p(x−X_n), a frequency-independent difference in their NPS may arise from the differing variance

$$W_{\text{PC}}-W_{\text{EI}}=l_x{l}_y\left(K_{{\mathbf{n}}^{\prime }{\mathbf{n}}^{\prime }}^{\text{PC}}-K_{{\mathbf{n}}^{\prime }{\mathbf{n}}^{\prime }}^{\text{EI}}\right)$$ (24)

$$=\overline{\Phi }{l}_x{l}_y{\int }_{-L_y∕2}^{L_y∕2}{\int }_{-L_x∕2}^{L_x∕2}\left[P\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)-P^2\left(\mathbf{x}-{\mathbf{X}}_{{\mathbf{n}}^{\prime }}\right)\right]dxdy,$$ (25)

where K_n^′n^′ denotes the variance of either the photon counting detector or energy integrating detector based on the superscripts. A key theorem can be written about the NPS difference established by Eq. 25. Namely, the difference vanishes if and only if P(x−X_n^′)=P²(x−X_n^′). This property is uniquely satisfied by a binary PSF that is either zero or unity everywhere along the detector. Otherwise, a frequency-independent difference in NPS exists such that NPS_PC>NPS_EI. This result assumes a piecewise continuous PSF appropriately bounded between zero and unity.

Unlike NPS, the optical transfer function T(ν) is equivalent for the two detector types provided that they possess the same PSF and is calculated as the Fourier transform of the PSF. This property arises immediately from linear response theory for digital detectors,³⁷ since the expected output D_n at X_n in response to an input x-ray flux f is given for either detector type as

$$D_{\mathbf{n}}={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }P\left({\mathbf{x}}^{\prime }-{\mathbf{X}}_{\mathbf{n}}\right)f\left({\mathbf{x}}^{\prime }\right)d{x}^{\prime }d{y}^{\prime }.$$ (26)

To verify that the expected output in response to a single x ray landing at position x is P(x−X_n), as we have assumed repeatedly throughout this work for both detector types, one simply inserts the Dirac delta function δ(x^′−x) as the input flux f in Eq. 26. Now, with local DQE calculated for both detector types as

$$\text{DQE}\left(\mathbf{\nu }\right)=\frac{\overline{\Phi }{\left|T\left(\mathbf{\nu }\right)\right|}^2}{W\left(\mathbf{\nu }\right)},$$ (27)

it follows that one important corollary of the comparative NPS theorem and the observation that the two detector types possess the same OTF is that DQE may differ between the two detector types in the case where NPS_PC>NPS_EI, so that DQE_PC<DQE_EI. Unlike the NPS difference between the two detector types, the DQE difference is indeed spatial frequency dependent.

IDENTITIES FOR CALCULATING AUTOCOVARIANCE AND NPS IN LARGE DETECTORS

In the special case of an infinitely large detector (L_x,L_y→∞), one can show that NPS_EI may be computed directly from knowledge of the OTF. To prove this claim, consider a pixel centered at the origin to be surrounded by infinitely many neighbors on all sides. In a physical application, this geometry would be approximately applicable to a pixel positioned at or near the center of a large detector, whose pixel dimensions are small relative to the overall size of the detector. From Eq. 18, the energy integrating signal intensity autocovariance in multiples of pixel spacingn_xl_x×n_yl_y is given by the expression

$$K_{\mathbf{n},\mathbf{0}}^{\text{EI}}=\overline{\Phi }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }w\left(x,y\right)w\left(x-n_x{l}_x,y-n_y{l}_y\right)dxdy,$$ (28)

where 0 denotes the doublet (0, 0), corresponding to the location of the central pixel. From Parseval’s theorem,³⁸ Eq. 28 can be rewritten as

$$K_{\mathbf{n},\mathbf{0}}^{\text{EI}}=\overline{\Phi }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|T\left({\xi }_x,{\xi }_y\right)\right|}^2{e}^{-2\pi i\left(n_x{l}_x{\xi }_x+n_y{l}_y{\xi }_y\right)}d{\xi }_{x}d{\xi }_y,$$ (29)

so that NPS_EI is

$$W_{\text{EI}}\left(\mathbf{\nu }\right)=l_x{l}_y\sum _{n_y=-\infty }^{\infty }\sum _{n_x=-\infty }^{\infty }{K}_{\mathbf{n},\mathbf{0}}^{\text{EI}}{e}^{-2\pi i\left(n_x{l}_x{\nu }_x+n_y{l}_y{\nu }_y\right)}$$ (30)

$$=\overline{\Phi }{l}_x{l}_y{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|T\left({\xi }_x,{\xi }_y\right)\right|}^2\sum _{n_y=-\infty }^{\infty }\sum _{n_x=-\infty }^{\infty }{e}^{-2\pi i\left[n_x\left({\xi }_x+{\nu }_x\right)l_x+n_y\left({\xi }_y+{\nu }_y\right)l_y\right]}d{\xi }_{x}d{\xi }_y.$$ (31)

Using standard properties concerning comb functions to simplify the double summation in Eq. 31, one finds

$$W_{\text{EI}}\left(\mathbf{\nu }\right)=\overline{\Phi }\sum _{k_y=-\infty }^{\infty }\sum _{k_x=-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{\left|T\left({\xi }_x,{\xi }_y\right)\right|}^2\delta \left({\xi }_x+{\nu }_x+k_x{l}_x^{-1}\right)\delta \left({\xi }_y+{\nu }_y+k_y{l}_y^{-1}\right)d{\xi }_{x}d{\xi }_y$$ (32)

$$=\overline{\Phi }\sum _{k_y=-\infty }^{\infty }\sum _{k_x=-\infty }^{\infty }{\left|T\left({\nu }_x+k_x{l}_x^{-1},{\nu }_y+k_y{l}_y^{-1}\right)\right|}^2.$$ (33)

Equation 33 provides a method for determining NPS_EI directly from the OTF. This technique is useful in circumstances in which the OTF is known but in which it is difficult to determine autocovariance directly. To calculate NPS_PC, one simply adds to Eq. 33 the frequency-independent NPS difference given by Eq. 24 or Eq. 25.

RESULTS FOR MODEL DETECTORS

The OTF, NPS, and DQE calculations for the two detector types are now illustrated for a PSF given as the convolution of a Gaussian with the product of rect functions for a pixel centered on the origin of an infinitely large detector. The Gaussian models the blurring of the x-ray converter, while the product of rect functions models the sampling of the detector.

$$P\left(x,y\right)=\frac{1}{2\pi {\sigma }^2}{e}^{-\left(x^2+y^2\right)∕2{\sigma }^2}\ast \text{rect}\left(\frac{x}{al}\right)\text{rect}\left(\frac{y}{al}\right)$$ (34)

$$=\frac{1}{4}\left[\text{erf}\left(\frac{\sqrt{2}\left(2x+al\right)}{4\sigma }\right)-\text{erf}\left(\frac{\sqrt{2}\left(2x-al\right)}{4\sigma }\right)\right]\left[\text{erf}\left(\frac{\sqrt{2}\left(2y+al\right)}{4\sigma }\right)-\text{erf}\left(\frac{\sqrt{2}\left(2y-al\right)}{4\sigma }\right)\right].$$ (35)

Following convention, the Gaussian has been normalized by area and its standard deviation has been denoted σ. In Eq. 34, the rect function is defined by the relation

$$\text{rect}\left(z\right)\equiv \{\begin{array}{cc}1& ,\left|z\right|\le 1∕2\\ 0& ,\left|z\right|>1∕2\end{array}\phantom{\}}$$ (36)

and in Eq. 35, the error function is defined by the integral

$$\text{erf}\left(z\right)\equiv \frac{2}{\sqrt{\pi }}{\int }_0^z{e}^{-t^2}dt.$$ (37)

Recent work by Freed et al.³⁹ has verified that a Gaussian provides a valid approximation for the blurring function of a thick CsI:Tl scintillator irradiated at normal incidence. While most photon counting detectors do not use a scintillator, the choice of a Gaussian as the approximate blurring function of the x-ray converter is expected to be relatively independent of technology.

The PSF convolution of Eq. 34 assumes a square pixel with sides of length l_x=l_y=l and a photosensitive areaal×al that is symmetric about the pixel center. The effect of a translational shift in the sensitivity area on OTF, NPS, and DQE is explored in Appendix A. It is straightforward to show that the PSF of Eq. 34 is bounded above by unity, as required for application of the comparative NPS theorem, since

$$P\left(x,y\right)={\int }_{y-al∕2}^{y+al∕2}{\int }_{x-al∕2}^{x+al∕2}\frac{1}{2\pi {\sigma }^2}{e}^{-\left(x^{\prime 2}+y^{\prime 2}\right)∕2{\sigma }^2}d{x}^{\prime }d{y}^{\prime }$$ (38)

$$\le {\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }\frac{1}{2\pi {\sigma }^2}{e}^{-\left(x^{\prime 2}+y^{\prime 2}\right)∕2{\sigma }^2}d{x}^{\prime }d{y}^{\prime }=1.$$ (39)

Because the Gaussian itself is nonnegative, it follows from Eq. 38 that the PSF is nonnegative, which is also necessary for application of the comparative NPS theorem.

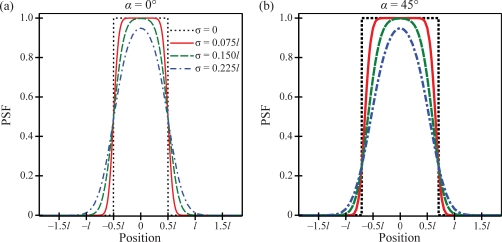
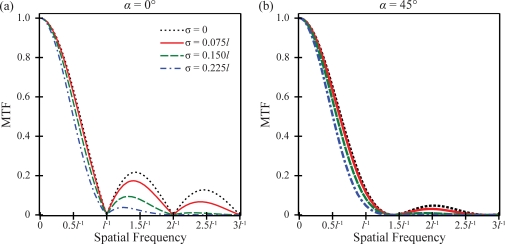
In Fig. 5, cross sections of the PSF surface are plotted versus position for two polar angles of the position vector (α=0° and 45°), assuming that the entire pixel area is sensitive to x rays. Unless otherwise indicated, all figures also make the assumption that a=1. Following convention, the polar angle is defined as the angle of the position vector relative to the x axis, so that the two cross sections are taken along the x axis and the diagonal of the detector lattice, respectively. Before smoothing by the Gaussian, each cross section is a rect function which is unity over the length l sec α and is zero elsewhere. Increasing the polar angle from 0° to 45° thus increases the width of the plateau before smoothing from l to 1.414l. Increasing the blurring parameter σ increases the spread of the tails of the PSF and hence increases the cross-talk between pixels.

Figure 5.

Cross sections of the PSF surface are plotted versus position for two polar angles of the position vector (α=0° and 45°) and four blurring parameters (σ), assuming that the pixel is square with sides of length l and that the entire pixel is sensitive to the detection of x rays. The PSF is interpreted as a weighting function for detecting x rays in an energy integrator and as a probability function for detecting x rays in a photon counter.

In order to calculate the OTF associated with the PSF of Eq. 34, one may apply the convolution theorem³⁸ to obtain

$$T\left(\mathbf{\nu }\right)=G{e}^{-2{\pi }^2{\sigma }^2\left({\nu }_x^2+{\nu }_y^2\right)}\text{\hspace{0.17em}sinc}\left(al{\nu }_x\right)\text{sinc}\left(al{\nu }_y\right),$$ (40)

where

$$\text{sinc}\left(z\right)\equiv \frac{\text{sin}\left(\pi z\right)}{\pi z}$$ (41)

and where G, the intensity transfer characteristic, is the sensitive area of the pixel

$$G=a^2{l}^2.$$ (42)

Normalizing the OTF to unity at ν=0 and taking its modulus gives the MTF

$$\text{MTF}\left(\mathbf{\nu }\right)=e^{-2{\pi }^2{\sigma }^2\left({\nu }_x^2+{\nu }_y^2\right)}\left|\text{sinc}\left(al{\nu }_x\right)\text{sinc}\left(al{\nu }_y\right)\right|.$$ (43)

In Fig. 6, MTF is plotted versus frequency for two polar angles of the frequency vector (α=0° and 45°). Figure 6 shows that increasing σ decreases MTF, thereby worsening spatial resolution. In addition, Fig. 6 indicates that altering the directionality of the frequency vector shifts the zeros of the MTF. The zeros of the first subfigure, in which frequency is measured along the x direction, occur at integer multiples of l⁻¹. By contrast, the zeros of the second subfigure, in which frequency is measured along the diagonal of the detector lattice, occur at integer multiples of 1.414l⁻¹. Altering the blurring of the x-ray converter has no effect on the zeros of the MTF.

Figure 6.

The MTF is plotted versus frequency at two polar angles of the frequency vector (α=0° and 45°), assuming that the entire pixel is sensitive to the detection of x rays.

A comparative NPS analysis for the two detector types can now be made. From Eqs. 33, 40, NPS_EI is

$$W_{\text{EI}}\left(\mathbf{\nu }\right)=\overline{\Phi }{G}^2\sum _{k_y=-\infty }^{\infty }\sum _{k_x=-\infty }^{\infty }{e}^{-4{\pi }^2{\sigma }^2\left[{\left({\nu }_x+k_x{l}^{-1}\right)}^2+{\left({\nu }_y+k_y{l}^{-1}\right)}^2\right]}{\text{sinc}}^2\left[a\left(l{\nu }_x+k_x\right)\right]{\text{sinc}}^2\left[a\left(l{\nu }_y+k_y\right)\right].$$ (44)

To determine NPS_PC, one adds to Eq. 44 the NPS difference $l^2\left(K_{\mathbf{00}}^{\mathrm{PC}}-K_{\mathbf{00}}^{\mathrm{EI}}\right)$ given from Eq. 24, where $K_{\mathbf{00}}^{\mathrm{PC}}$ is $\overline{\Phi }G$ and where $K_{\mathbf{00}}^{\mathrm{EI}}$ is calculated from Eq. 29 as

$$K_{\mathbf{00}}^{\text{EI}}=\overline{\Phi }{G}^2{\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{e}^{-4{\pi }^2{\sigma }^2\left({\xi }_x^2+{\xi }_y^2\right)}{\text{sinc}}^2\left(al{\xi }_x\right){\text{sinc}}^2\left(al{\xi }_y\right)d{\xi }_{x}d{\xi }_y$$ (45)

$$=\frac{\overline{\Phi }}{\pi }{\left[2\sigma \left(1-e^{-a^2{l}^2∕4{\sigma }^2}\right)-al\sqrt{\pi }\text{\hspace{0.17em}erf}\left(\frac{al}{2\sigma }\right)\right]}^2.$$ (46)

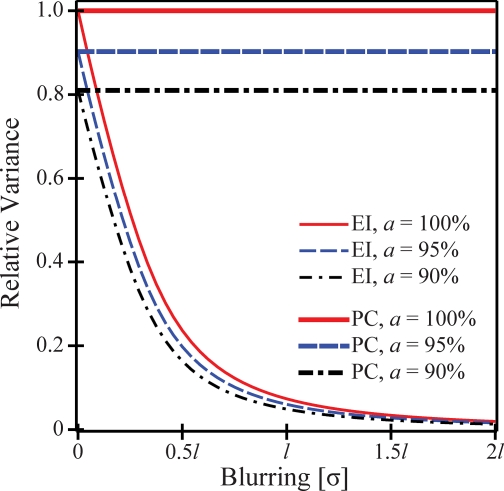
In Fig. 7, the variances of the two detector types are plotted versus the blurring of the x-ray converter for multiple pixel sensitivity areas. The three values of a investigated in the figure (100%, 95%, and 90%) correspond to 100%, 90.25%, and 81% sensitive areas, respectively. Figure 7 shows that the variance of the photon counter is independent of the blurring of the x-ray converter, while the variance of the energy integrator is reduced with increased blurring, tending to zero in the limit of infinite blurring. Figure 7 also indicates that lowering the pixel sensitivity area reduces the variance. In the limit of a perfectly resolving x-ray converter (σ=0), the variances of the two detector types match.

Figure 7.

The variance of the two detector types is plotted versus the blurring of the x-ray converter for three pixel sensitivity areas.

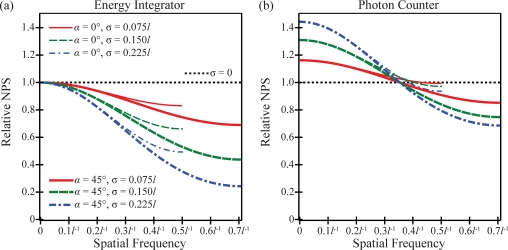
In Fig. 8, plots of NPS versus frequency are shown for the two detector types. The plots are terminated at the alias frequency or the frequency beyond which the plots would begin to slope upward and replicate. The alias frequency is 0.5l⁻¹ with frequency measured along the x direction and is 0.707l⁻¹ with frequency measured along the diagonal of the detector lattice. At a fixed spatial frequency, Fig. 8 shows that for both detector types, aliasing generates more noise along the x direction than along the diagonal of the detector lattice. Importantly, Fig. 8 also demonstrates that a photon counter is noisier than an energy integrator with the same blurring (σ), except in the limit of a perfectly resolving x-ray converter. In taking this limit, the two detector types possess the same white NPS

$$\underset{\sigma \to 0}{\text{lim}}W\left(\mathbf{\nu }\right)=\overline{\Phi }{G}^2\sum _{k_y=-\infty }^{\infty }\sum _{k_x=-\infty }^{\infty }{\text{sinc}}^2\left[a\left(l{\nu }_x+k_x\right)\right]{\text{sinc}}^2\left[a\left(l{\nu }_y+k_y\right)\right]$$ (47)

$$=a^2\overline{\Phi }{l}^4.$$ (48)

A mathematical justification for the transition from Eq. 47 to Eq. 48 is provided in Appendix B.

Figure 8.

The NPS is plotted versus the frequency, assuming that the entire pixel is sensitive to the detection of x rays for (a) an energy integrator and (b) a photon counter.

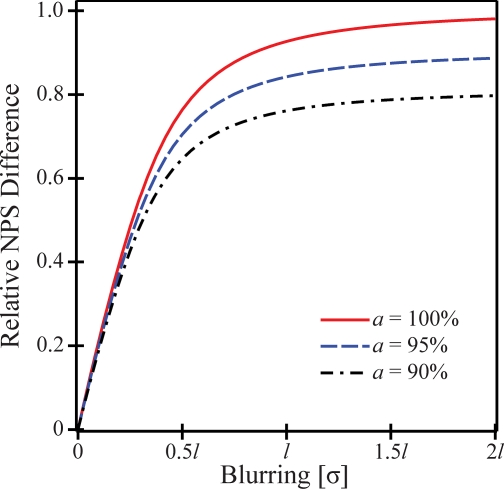
To illustrate that the NPS difference between the two detector types increases with the blurring of the x-ray converter, the NPS difference is plotted versus σ in Fig. 9. The NPS difference plateaus to its maximum $a^2\overline{\Phi }{l}^4$ in the limit of infinite blurring within the x-ray converter, as would be found in a nonimaging system which simply detects the number of incident x-ray quanta without distinguishing their position along the detector. An additional property seen in Fig. 9 is that decreasing the pixel sensitivity area reduces the NPS difference.

Figure 9.

The NPS difference between the two detector types is shown to increase with the blurring of the x-ray converter for three pixel sensitivity areas.

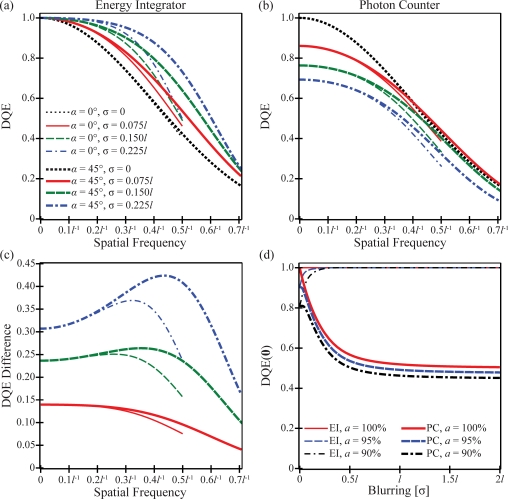
Using Eq. 27 and the preceding NPS results, DQE is plotted versus frequency in subplots a and b of Fig. 10. The two subplots show that at a fixed spatial frequency in either detector type, aliasing generates lower DQE along the x direction than along the diagonal of the detector lattice. In addition, subplots a and b demonstrate that DQE_PC is inferior to DQE_EI, except in the limiting case of a perfectly resolving x-ray converter. The DQEs of both detector types match in taking this limit

$$\underset{\sigma \to 0}{\text{lim}}\text{\hspace{0.17em}DQE}\left(\mathbf{\nu }\right)=a^2\cdot {\text{sinc}}^2\left(al{\nu }_x\right){\text{sinc}}^2\left(al{\nu }_y\right).$$ (49)

Figure 10 also illustrates that the DQEs of the two detector types have different dependence on the blurring of the x-ray converter. While DQE_EI increases with blurring, DQE_PC for the most part decreases with blurring; the exceptional case for DQE_PC is comparing σ=0 and σ=0.075l at high frequencies measured along the diagonal of the detector lattice.

Figure 10.

The DQE is plotted versus the frequency, assuming that the entire pixel is sensitive to the detection of x rays for (a) an energy integrator and (b) a photon counter. In (c), the DQE difference between the two detector types is shown to be frequency dependent and to increase with the blurring of the x-ray converter. Subplots (a)–(c) implicitly share a common legend. In (d), DQE(0) is plotted versus the blurring of the x-ray converter for three pixel sensitivity areas.

Unlike the difference in NPS between the two detector types, the difference in DQE is indeed spatial frequency dependent, as shown in Fig. 10c. Like the NPS difference, the DQE difference increases with the blurring of the x-ray converter. At all frequencies, there is a smaller DQE difference along the x direction than along the diagonal of the detector lattice due to aliasing.

In Fig. 10d, the dependence of DQE on the blurring of the x-ray converter is studied in the special case ν=0. Figure 10d shows that DQE(0) is the same for the two detector types in the limit of a perfectly resolving x-ray converter and is equivalent to the percentage of the pixel area that is sensitive to x rays. However, once the blurring of the x-ray converter begins to increase from zero, the behavior of DQE(0) is quite different for the two detector types. DQE_EI(0) is unity for all blurring profiles of the x-ray converter if the entire pixel is sensitive to x rays and increases with blurring from a² to unity in the limit of a nonimaging detector if only a portion of the pixel is sensitive to x rays. By contrast, DQE_PC(0) decreases with blurring for all sensitive areas and in the limit of a nonimaging detector attains a different horizontal asymptote.

$$\underset{\sigma \to \infty }{\text{lim}}{\text{DQE}}_{\text{PC}}\left(\mathbf{0}\right)=\frac{a^2}{1+a^2}.$$ (50)

With a=100%, 95%, and 90% in Fig. 10d, the horizontal asymptotes from Eq. 50 are 0.500, 0.474, and 0.448, respectively.

REVISITING THE ENERGY INTEGRATING DETECTOR MODEL

To incorporate additional realism into the detector modeling, one can investigate outside noise sources which are commonly found in phosphor-based energy integrating detectors but which are not present in direct converting photon counting detectors to a first approximation. These additional noise sources include (1) stochastic variation in the number of secondary quanta produced for each incident x ray (i.e., secondary quantum noise)³⁶ and (2) electronic noise. Based on the work of Albert and Maidment,³⁷ the two noise sources add frequency-independent terms to the baseline NPS_EI determined from Eq. 33

$$W_{\text{EI}}\left(\mathbf{\nu }\right)=\overline{\Phi }\sum _{k_y=-\infty }^{\infty }\sum _{k_x=-\infty }^{\infty }{\left|T\left({\nu }_x+k_x{l}^{-1},{\nu }_y+k_y{l}^{-1}\right)\right|}^2+\frac{\overline{\Phi }{G}^2}{m}+W_{\text{E}},$$ (51)

where m is the average number of secondary quanta produced for each incident x ray and W_E is the electronic noise power. In Eq. 51, the number of secondary quanta produced for each incident x ray is taken to be a Poisson-distributed random variable. The previous NPS results for the energy integrating detector can be viewed as limiting cases of Eq. 51 with infinitely many secondary quanta produced for each incident x ray and with the electronic noise power set to zero.

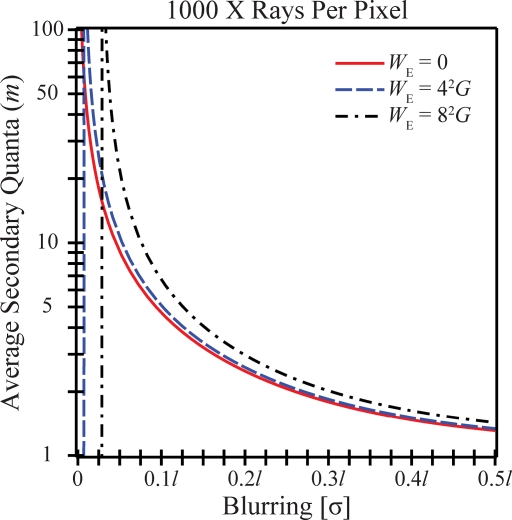
According to the comparative NPS theorem, a photon counter has white noise added to baseline NPS_EI as given by Eq. 25, just as a phosphor-based energy integrator has white noise added to baseline NPS_EI as specified by Eq. 51. It is natural then to ask how the additive white noise sources of the two detector types compare. Equating the NPS of the two detector types, we generate Fig. 11 showing the average secondary quanta that must be produced for each incident x ray in the energy integrating detector in order to generate equivalent NPS and thus DQE with a photon counting detector having the same PSF. The figure assumes 1000 x rays per pixel and electronic noise levels of W_E=0, 4²G, and 8²G, corresponding to zero, four, and eight x rays per pixel. The plot possesses vertical asymptotes at the blurring parameters σ=0, σ=0.007 12l, and σ=0.0288l, corresponding to electronic noise levels of zero, four, and eight x rays per pixel, respectively. If the blurring parameter is less than the value specified by the vertical asymptote, the electronic noise power exceeds the NPS difference given by Eq. 25 and the energy integrator has inferior DQE to a photon counter with the same PSF regardless of the average secondary quanta produced for each incident x ray. However, if the blurring parameter exceeds the value specified by the vertical asymptote, the energy integrator has superior DQE to a photon counter with the same PSF, provided that the average secondary quanta produced for each x ray exceeds the values specified by the curves in Fig. 11. For blurring parameters (σ) exceeding 0.05l, as would be typical for many phosphor-based imaging systems, approximately 10–20 visible quanta must be produced on average for each incident x ray in order to generate superior DQE to a photon counter with the same PSF.

Figure 11.

For equivalent NPS and DQE between the two detector types, the average number of secondary quanta (m) that must be produced for each incident x ray in the energy integrating detector is plotted versus the blurring of the x-ray converter. The figure assumes 1000 x rays per pixel and electronic noise power (W_E) of zero, four, and eight x rays per pixel.

Since optical photons have an energy of approximately 2–3 eV, which is small compared against the energy of the incident x rays, most energy integrating detectors can produce on average between 400 and 1000 optical photons per keV of an x-ray photon.¹ As a result, Fig. 11 would seem to imply that over many typical values of the blurring of the x-ray converter, energy integrating detectors produce more than enough average secondary quanta to achieve superior DQE to a photon counting detector with the same PSF. However, since so many factors characteristic of real imaging systems were not modeled in generating Fig. 11, ranging from polyenergetic x rays to scatter within the detector, the reader should take caution against concluding that an energy integrating detector has superior DQE to a photon counter over these blurring parameters. A more thorough description of the limitations of this work and directions for future modeling are given in Sec. 8.

DISCUSSION

This work develops analytical models of OTF, NPS, and DQE for two types of digital x-ray detectors: Energy integrating and photon counting. To distinguish the two detector types, the PSF of the energy integrating detector is treated as a weighting function for counting x rays, while the PSF of the photon counting detector is interpreted as a probability. Under these assumptions, this paper demonstrates that while OTF is equivalent for two detector types possessing the same PSF, NPS and DQE are not. More specifically, it is shown that as a result of differing variance between the two detector types, a frequency-independent difference in NPS exists such that NPS_PC≥NPS_EI. The necessary and sufficient condition for equality is that the PSF is a binary function given as zero or unity everywhere along the detector. The implication of this finding is that thresholding output voltage gains in a photon counter, in order to detect individual x rays, generates additive white noise to baseline NPS. From the NPS inequality and the observation that two detector types with the same PSF possess the same OTF, it immediately follows that DQE_PC≤DQE_EI.

The OTF, NPS, and DQE calculations for the two detector types have been illustrated for a model detector whose PSF is the convolution of a Gaussian with the product of rect functions. The Gaussian models the blurring of the x-ray converter, while the product of rect functions models the sampling of the detector. Using this model detector, we have shown that the NPS and DQE difference between the two detector types increases with the blurring of the x-ray converter. In addition, if secondary quantum noise and electronic noise are present in the energy integrator, we determine the average secondary quanta that the energy integrator must produce for each x ray to have superior DQE to a photon counter with the same PSF.

Many of the assumptions required for deriving the results in this paper have been noted throughout this work. These assumptions include a monoenergetic x-ray beam and the absence of detector lag, ghosting, and scatter. Since these factors will have considerable variation between imaging systems, it is appropriate to omit an analysis of each one from this work. In experimental practice, they should be modeled on a case-by-case basis for each detector under consideration.

A few additional assumptions and points for future investigation are now noted. One difficulty encountered in photon counting detectors is charge sharing at the border of two detector elements due to an x-ray photon landing at the border. As a consequence, one photon may be counted as two photons of low energy or may be not counted at all if the energies in the two detector elements do not exceed the threshold. A technique designed to suppress charge sharing between detector elements is anticoincidence (AC) logic. If two detector elements simultaneously fire, some imaging systems record the signal as representative of a single high-energy x ray in the detector element with the greater voltage gain.¹⁷ Other systems use fitting techniques to determine the most likely position of the x ray. Although AC logic has not been modeled in this work, it merits a future investigation in conjunction with the concepts of this paper.

In diagnostic applications with a high count rate, it is possible for the detector to be too slow to distinguish consecutive x-ray photons and a pileup of charge within a detector element may occur. As a result, multiple photons are counted as a single photon and the absorption efficiency is reduced. In silicon strip units with dead times of 200 ns, for example, an efficiency loss of approximately 2.5% is typical.¹⁸ Such an absorption loss was not modeled in the current study.

In a phosphor-based energy integrating detector, DQE_EI is reduced if less than 100% of the incident x rays generate visible light and less than 100% of the visible light is converted to photoelectrons in the a-Si pixel layer.⁴⁰ The absorption efficiency of both detector types was taken to be 100% in this paper, but in future work, it should be expressed as a parameter that is typically smaller for energy integrating detectors than photon counting detectors. In addition, the OTF, NPS, and DQE calculations can be affected by the possibility of differing x-ray interactions at various depths of the phosphor. In Sec. 6 of this work, we have observed that if the entire pixel is sensitive to x rays, DQE_EI(0) is unity regardless of the blurring of the x-ray converter [Fig. 10d]. However, based on classic observations by Swank and Lubberts, the presence of different x-ray interactions at each depth of a phosphor may lower DQE_EI(0) from unity.^{41, 42, 43} In modeling the PSF of the detector, we have also not investigated the effect of the x-ray focal spot size⁴⁴ or non-normal x-ray incidence.^{39, 45, 46, 47, 48, 49}

One final limitation of Sec. 6 of this work is the stipulation that each pixel is homogeneously sensitive to the detection of x rays over the area al×al. Under this assumption, we have neglected to consider the lateral diffusion of photoelectrons to neighboring wells within the a-Si pixel layer. If one were to incorporate this effect rigorously into the analysis, the rect functions of the PSF convolution in Eq. 34 should be replaced with trapezoids based on the research of Schumann and Lomheim.⁵⁰ Schumann and Lomheim have shown that lateral diffusion of photoelectrons is considerable when dealing with long wavelengths (>800 nm) of infrared light incident on the a-Si pixel layer. However, they have demonstrated that lateral diffusion is negligible when shorter wavelengths of visible light land on the pixel layer, such as the wavelengths generated by CsI:Tl in typical imaging systems. It is for this reason that we have omitted Schumann and Lomheim’s correction in Sec. 6 of this work. The wavelength dependence of their correction arises from the fact that silicon is a poor absorber of long wavelengths and a strong absorber of short wavelengths; significant lateral diffusion can only occur in the presence of weak absorption.⁵¹

CONCLUSION

This work establishes fundamental techniques for calculating OTF, NPS, and DQE for energy integrating and photon counting digital x-ray detectors. The central novelty of this paper is a demonstration that photon counting detectors have a white noise source analogous to electronic noise and secondary quantum noise in energy integrating detectors. As noted in Sec. 8, several aspects of real imaging systems were not modeled to simplify the mathematics in deriving this result. However, this general finding should continue to apply when other subtleties of the detector are modeled.

One of the benefits of this work is that it generates a platform for determining the average secondary quanta that an energy integrating detector must produce for each incident x ray to have superior DQE to a photon counter with the same PSF. In order to investigate how polyenergetic spectra alter the average secondary quanta that the energy integrating detector must produce to have superior DQE to competing photon counting technology, this work should ultimately be integrated with the prior research of Tapiovaara and Wagner. Since Tapiovaara and Wagner have shown that increasing the broadness of the polyenergetic x-ray spectra generates DQE benefits in photon counting detectors over energy integrating detectors, we anticipate that the average secondary quanta necessary for superior DQE in the energy integrator should be greater than the values found in this paper for monoenergetic x rays.

APPENDIX A: THE EFFECT OF A SHIFT IN THE PIXEL SENSITIVITY AREA

It is now shown that shifting the sensitivity area off the pixel center does not affect MTF, NPS, or DQE calculations in an infinitely large detector. To derive this result, suppose that the pixel sensitivity area is centered on (b_xl_x,b_yl_y), so that

$$P\left(x,y\right)=\frac{1}{2\pi {\sigma }^2}{e}^{-\left(x^2+y^2\right)∕2{\sigma }^2}\ast \text{rect}\left(\frac{x-b_x{l}_x}{a_x{l}_x}\right)\text{rect}\left(\frac{y-b_y{l}_y}{a_y{l}_y}\right).$$ (A1)

The pixel sensitivity lengths in the x and y directions are kept as general as possible (a_xl_x and a_yl_y, respectively). From the Fourier shift theorem,³⁸ the OTF is

$$T\left(\mathbf{\nu }\right)=e^{-2\pi i\left(b_x{l}_x{\nu }_x+b_y{l}_y{\nu }_y\right)}G{e}^{-2{\pi }^2{\sigma }^2\left({\nu }_x^2+{\nu }_y^2\right)}\text{\hspace{0.17em}sinc}\left(a_x{l}_x{\nu }_x\right)\text{sinc}\left(a_y{l}_y{\nu }_y\right),$$ (A2)

where G is the pixel sensitivity area (a_xl_x×a_yl_y). Since this OTF differs from Eq. 40 only by the phase term, it is immediately evident that the MTF, or the normalized modulus of the OTF, is unaltered. Furthermore, because Eq. 33 for calculating NPS_EI is dependent only on the modulus of the OTF and not on its phase, NPS_EI is unaffected. Assuming that the detector is infinitely large, the integral of Eq. 25 giving the NPS difference is unchanged. With |T(ν)| and W(ν) unaffected for either detector type, DQE is unaltered as well by Eq. 27.

Shifting the pixel sensitivity area is indeed expected to have an effect on NPS and DQE in certain applications involving the presence of a detector edge, but this topic is reserved for study in future work.

APPENDIX B: A PARSEVAL IDENTITY

We now provide a justification for the transition from Eq. 47 to Eq. 48 by proving the following general identity:

$$\sum _{k=-\infty }^{\infty }{\text{sinc}}^2\left[a\left(l\nu +k\right)\right]=\frac{1}{a}.$$ (B1)

Equation 47 can be viewed as the product of two cases of this identity. To prove Eq. B1, begin by defining the piecewise function h(x) as

$$h\left(x\right)=\{\begin{array}{ll}\frac{1}{al}{e}^{-2\pi i\nu x},\hfill & \left|x\right|\le al∕2\hfill \\ 0,\hfill & \left|x\right|>al∕2\hfill \end{array}\phantom{\}}.$$ (B2)

The Fourier series³⁸ of h(x) on the interval [−l∕2,l∕2], with l≥al, is

$$h\left(x\right)=\sum _{k=-\infty }^{\infty }{c}_k{e}^{2\pi ikx∕l},$$ (B3)

where

$$c_k=\frac{1}{l}{\int }_{-l∕2}^{l∕2}h\left(x\right)e^{-2\pi ikx∕l}dx$$ (B4)

$$=\frac{1}{l}\text{sinc}\left[a\left(l\nu +k\right)\right].$$ (B5)

From Parseval’s theorem

$$\frac{1}{l}{\int }_{-l∕2}^{l∕2}{\left|h\left(x\right)\right|}^{2}dx=\sum _{k=-\infty }^{\infty }{\left|c_k\right|}^2,$$ (B6)

it follows that

$$\frac{1}{a{l}^2}=\frac{1}{l^2}\sum _{k=-\infty }^{\infty }{\text{sinc}}^2\left[a\left(l\nu +k\right)\right],$$ (B7)

which yields Eq. B1.

APPENDIX C: GLOSSARY

⟨ ⟩N	Expectation operator assuming exactly N x rays incident on the detector
⟨ ⟩	Expectation operator incorporating the possibility for Poisson variation in N
*	Convolution operator
α	Polar angle of either the 2D position vector or the 2D spatial frequency vector
δ	Dirac delta function
η(E)	Fraction of x rays absorbed by the detector at each energy E using the notation of Tapiovaara and Wagner21
ν	Two-dimensional spatial frequency vector with components νx and νy
ξx,ξy	Dummy variables with units of spatial frequency used in intermediate integral calculations
σ	Standard deviation of a 2D Gaussian used for the example blurring function of the x-ray converter
Φ	Fluence for exactly N x rays incident on the detector
$\overline{\Phi }$	Mean fluence incorporating the possibility for Poisson variation in N
ψ(E)	Output of a detector in response to a photon of energy E using the notation of Tapiovaara and Wagner.21 It is equivalent to E in an energy integrating detector and to a constant in a photon counting detector.
A	Detector area under the notation of Tapiovaara and Wagner21
AC	Anticoincidence
a	Percentage of pixel length in the x or y direction that is sensitive to x-ray detection (with subscripts, ax and ay denote differing sensitivities in the x and y directions)
(bxlx,byly)	Coordinate of the center of the sensitivity area of a pixel centered on the origin (Appendix A)

Cn	Total counts recorded by the nth pixel in a photon counting detector
${\overline{C}}_{\mathbf{n}}$	Mean counts recorded by the nth pixel in a photon counting detector
Dn	Expected output of the nth pixel in response to an x-ray flux f
DQE	Detective quantum efficiency
DSFT	Discrete space Fourier transform
E	X-ray energy
EI	Energy integrator
Gn	Intensity transfer characteristic of the nth pixel
In	Total signal intensity recorded by the nth pixel in an energy integrating detector
${\overline{I}}_{\mathbf{n}}$	Mean signal intensity recorded by the nth pixel in an energy integrating detector
Knn′	Signal intensity autocovariance of pixel n against pixel n′
kV	X-ray tube kilovoltage
lx,ly	Dimensions of each rectangular pixel in the x and y directions. If the x and y subscripts are removed, it is assumed that the pixel is square (lx=ly=l).
Lx,Ly	Dimensions of the 2D rectangular detector in the x and y directions
m	Average number of secondary quanta produced for each incident x ray in a phosphor-based energy integrating detector
MTF	Modulation transfer function
n	A doublet with coordinates (nx,ny) used for labeling pixels in a rectangular array
N	Total number of x rays landing on the detector, used in intermediate calculations before Poisson variations are considered
$\overline{N}$	Mean number of x rays landing on the detector after accounting for Poisson variation
Ni(E)	Photon fluence spectra at energy E in the absence of signal (i=1) or presence of signal (i=2) under the notation of Tapiovaara and Wagner21
NPS	Noise power spectra
OTF	Optical transfer function
p(x−Xn)	Point spread function of the photon counting detector, specifying the probability that an x ray landing at position x is counted by the pixel centered at Xn
P(x−Xn)	Point spread function of the nth pixel of either detector type.
PC	Photon counter
PSF	Point spread function
Qn(x)	A quantity defined to be unity if an x ray landing at position x is counted by the nth pixel and zero otherwise in a photon counting detector
T(ν)	Optical transfer function of either detector type, given as the Fourier transform of the point spread function
W(ν)	Noise power or Wiener spectra of either detector type, given as the discrete space Fourier transform of the autocovariance of signal intensity
WE	Electronic noise power
w(x−Xn)	Point spread function of the energy integrating detector, specifying the weight by which an x ray landing at position x is counted by the pixel centered at Xn
x	Generalized position vector with components (x,y) specifying the coordinates of each x ray landing on the detector
Xn	Position vector of the center of the nth pixel in a 2D rectangular detector lattice
Z	Atomic number