Photoinduced electron transfer from semiconductor quantum dots to metal oxide nanoparticles

Abstract

Quantum dot-metal oxide junctions are an integral part of next-generation solar cells, light emitting diodes, and nanostructured electronic arrays. Here we present a comprehensive examination of electron transfer at these junctions, using a series of CdSe quantum dot donors (sizes 2.8, 3.3, 4.0, and 4.2 nm in diameter) and metal oxide nanoparticle acceptors (SnO₂, TiO₂, and ZnO). Apparent electron transfer rate constants showed strong dependence on change in system free energy, exhibiting a sharp rise at small driving forces followed by a modest rise further away from the characteristic reorganization energy. The observed trend mimics the predicted behavior of electron transfer from a single quantum state to a continuum of electron accepting states, such as those present in the conduction band of a metal oxide nanoparticle. In contrast with dye-sensitized metal oxide electron transfer studies, our systems did not exhibit unthermalized hot-electron injection due to relatively large ratios of electron cooling rate to electron transfer rate. To investigate the implications of these findings in photovoltaic cells, quantum dot-metal oxide working electrodes were constructed in an identical fashion to the films used for the electron transfer portion of the study. Interestingly, the films which exhibited the fastest electron transfer rates (SnO₂) were not the same as those which showed the highest photocurrent (TiO₂). These findings suggest that, in addition to electron transfer at the quantum dot-metal oxide interface, other electron transfer reactions play key roles in the determination of overall device efficiency.

Semiconducting quantum dots (QDs) are a widely studied material with many interdisciplinary applications (1, 2). Perhaps the most appealing attribute of these materials, from both an academic and industrial perspective, is their size-dependent electronic structure—the ability to design systems and devices with tailor-made electronic properties simply by altering the size of one of the constituent materials (3). As less expensive and less complex routes are continually developed to synthesize a variety of QD materials, further implementation of QDs into next-generation devices and procedures is inevitable.

The properties of QDs are often exploited in a system or device through their complexation with other materials of interest: functionalizing QDs with biomolecules for imaging (4); linking many QDs together with short-chain molecules to create nanostructured electronic arrays (5); creating highly emissive core-shell QD particles for sensors and optoelectronic displays (6); or sensitizing semiconducting systems with other semiconductors to create inexpensive, next-generation photovoltaic devices (7, 8). In each of the aforementioned applications, QDs are utilized because of their size-dependent electronic structure.

Although electronic interactions between QDs and organic molecules have been well established (9, 10), often times QDs are coupled to other inorganic species, a pairing which has been elucidated to a lesser extent. Such interactions are fundamentally different from those in QD-molecular systems because inorganic materials possess a continuum of electronic states, as opposed to discrete states inherent to molecular acceptors. When coupled with other inorganic materials, the role of the QD can be either to donate (photovoltaic devices) or both accept and donate (light emitting diodes) electrons. In each instance where QDs are implemented into a practical device, electron transfer reactions are intimately involved with their proper function. As a consequence, understanding the factors which drive electron transfer in these systems is critical to better understand and further exploit the unique properties of QDs. We have now elucidated interactions between multiple sizes of CdSe QDs and three unique nanostructured semiconducting metal oxides (MOs): SnO₂, TiO₂, and ZnO, with a primary focus on donor (QD) to acceptor (MO) electron transfer rates, the nature of that electron transfer, and the implications of such findings for a device which utilizes QDs—quantum dot sensitized solar cells (QDSSCs).

Modeling Electron Transfer in QD–MO Nanoparticulate Systems

In a landmark paper, Rudolph Marcus described electron transfer between two states, a model which was the basis for his 1992 Nobel Prize in Chemistry (11). Later, this model was extended to describe electron transfer from a single donating state to a continuum of accepting states, such as those present in the conduction band of a semiconductor (12). This model, which has been used to successfully describe the dependence of electron transfer rate on free energy driving force for systems of organic dyes coupled to various metal oxides (13–18), has yet to be applied to a quantized semiconducting nanocrystal donor and nanoparticulate metal oxide acceptor (QD–MO) system. The functional form of this many-state Marcus model is as follows:

[1]

Where k_ET is the electron transfer rate, ℏ is the reduced Planck’s constant, k_B is Boltzmann’s constant, λ is the system reorganizational energy, and 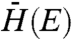, ρ(E), and ΔG are the overlap matrix element, density of accepting states, and change in system free energy, all described in detail below. Generally, plots of Eq. 1 depict a steep rise at energies ΔG ∼ λ, and a gradual increase at energies ΔG > λ, the region where transfer dynamics are dominated by the density of electron accepting states. A plot of k_ET vs. ΔG for various reorganizational energies is shown in Fig. S1.

Fitting experimental data with Eq. 1 necessitates the modeling of three terms. The first, 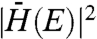, is a quantification of the physical overlap between the transferred electron in its initial and final states. Accurate computational modeling of this parameter in to-scale CdSe–MO systems has yet to be achieved due to the innate complexity of these systems. Therefore, in an attempt to simplify this analysis, we take 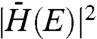to be independent of energy. Although this assumption is likely a simplification of an inherently complex system, it is required to make a comparison between our experimental data and Eq. 1. Further, this same assumption has been employed previously by Lian and coworkers in an investigation of electron transfer rate constants between organic dyes and metal oxide nanoparticles, which reported good agreement between the many-state Marcus formula and experimental findings (13).

Second, ρ(E) is the density of unoccupied states in the MO acceptor, which includes both bulk and defect (trap, surface, etc.) states. In a perfect semiconducting crystal of known volume V₀ and electron effective mass 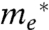, the density of states is expressed as (12)

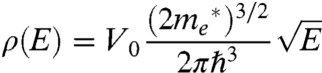[2]

Experimentally, we are not utilizing perfect MO crystals, but rather MO nanoparticles with high surface to volume ratios. Such defect states have been modeled previously as a Gaussian distribution of width Δ (19, 20). The density of states in a MO crystal with defect states is modeled as

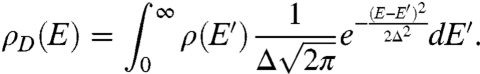[3]

Substitution of Eq. 3 as the density of states term in Eq. 1 accounts for the contribution of both bulk and defect states toward electron transfer.

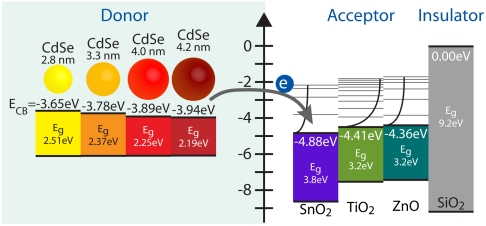
Third, ΔG is the free energy change associated with moving the electron from the donating species to the accepting species. Multiple factors can contribute to the overall change in free energy, the sum of which constitute ΔG. In our specific system—CdSe QDs coupled to MO nanoparticles under vacuum—three major contributions to ΔG need to be taken into consideration. First, the free energy of charging, ΔG_charging, accounts for the energy difference associated with having nonneutral donating and accepting species following the electron transfer. Second, the free energy of coulombic interactions, ΔG_coulomb, accounts for the energy needed to spatially separate the electron and the hole. Finally, the change in electronic energy ΔG_electronic, accounts for the difference in energy between the initial and final electronic states. Of these three terms, only ΔG_electronic can be measured experimentally, where electron affinities for bulk semiconductors are established (21) and those of quantized CdSe nanoparticles can be estimated using the effective mass approximation (22). A depiction of ΔG_electronic for the CdSe QD donor and MO acceptor pairs under investigation is shown in Fig. 1. The summation of models for ΔG_charging and ΔG_coulomb along with measured values for ΔG_electronic = E_MO - E_1Se yields the overall change in free energy for the electron transfer reaction

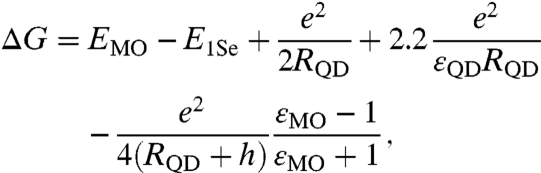[4]

where E_MO and E_1Se are the energies of the electron at the conduction band edges of the MO particle and QD, respectively, e is the elementary charge, R_QD and ε_QD are the radius and dielectric permittivity of the QD, h is the QD–MO separation distance, and ε_MO is the dielectric permittivity of the MO particle. A full derivation of Eq. 4 is provided in the SI Text and a numerical summary of relevant parameters for this study is provided in Table S1.

Fig. 1.

Diagram of the relative electronic energy differences between CdSe donating species and MO accepting species for all CdSe–MO combinations used in this study.

Results and Discussion

CdSe–MO Electron Transfer Rates.

Transparent MO films of SiO₂, SnO₂, TiO₂, and ZnO were sensitized with four unique sizes of CdSe QDs: 2.8, 3.3, 4.0, and 4.2 nm in diameter (Fig. S2). Quantum dots were attached to MO films utilizing direct absorption, which (as opposed to linker assisted) provides adequate QD uptake to achieve reasonable signal in optical measurements while maintaining, however, the less than monolayer coverage necessary to prevent overcrowding (agglomeration) of QDs on single MO particles.

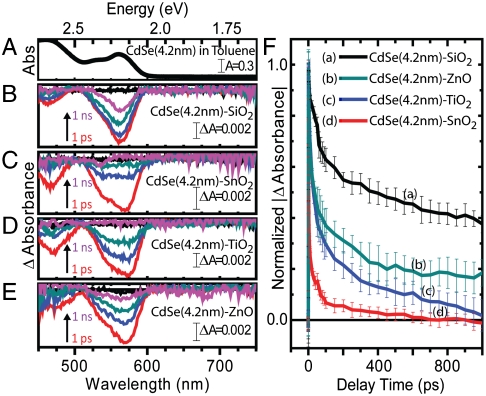
Transient absorption spectra were collected utilizing pump energies adjusted to maintain average carrier densities of 〈N₀〉 = 0.1 excitation per QD to prevent contribution from Auger decay pathways (23). Ground-state absorption spectra of CdSe QDs (d = 4.2 nm) in toluene are shown in Fig. 2A, and time-resolved transient absorption spectra recorded following 387 nm excitation of CdSe QDs (d = 4.2 nm) attached to SiO₂, SnO₂, TiO₂, and ZnO are shown in Fig. 2 B–E, respectively. The characteristic QD 1S_3/2-1S_e transition is present both in solution and on each MO film at the same wavelength, suggesting that ground-state electronic transitions inherent to the QD sample remain unchanged despite their attachment to various MO species. The spectral transient traces on all four MO species show similar features, however, decay at different rates. This phenomenon is highlighted in the transient absorption kinetic decay traces of the 1S_3/2-1S_e transition, as shown in Fig. 2F.

Fig. 2.

UV-visible (A) and transient absorption spectral (B–E) traces of 4.2-nm-diameter CdSe quantum dots in toluene (A) and attached to SiO₂ (B), SnO₂ (C), TiO₂ (D), and ZnO (E). Transient spectra shown at pump-probe delay times of 0 (black), 1 (red), 10 (blue), 100 (cyan), and 1,000 ps (pink). Also, transient absorption kinetic traces (F) of 4.2-nm-diameter CdSe quantum dots attached to each MO substrate at the 1S_3/2-1S_e transition. Error bars are representative of standard deviation of eight measurements collected at four unique spots on each CdSe-Mo film.

The amplitude of the transient signal obtained from an ensemble QD–MO sample is proportional to the number of QDs in the excited state. This signal then decays when the QD undergoes electron-hole recombination or charge transfer to an accepting species. Transient absorption kinetic decay spectra were normalized and fit to a biexponential decay function, where each fit yielded both a short (τ_s) and long (τ_l) lifetime. The long lifetime was attributed to a combination of electron-hole radiative recombination and back electron transfer from the MO to the QD, whereas the short lifetimes were attributed to either trapping (in the case of QDs coupled to SiO₂) or a convolution of trapping and electron transfer (in the case of QDs coupled to SnO₂, TiO₂, and ZnO). This electron transfer, which is expected to take place in timescales of picoseconds (24), is thus suited to be studied with ultrafast transient absorption, which has a subpicosecond (FWHM = 150 fs) time resolution and a kinetic window of 0–1000 ps. To deconvolute electron transfer from trapping, we make the assumption that the only difference between the kinetic behavior of an electron-hole pair in a QD coupled to SiO₂ and one coupled to one of the electron acceptors (SnO₂, TiO₂, or ZnO) is the added pathway of electron transfer. Under this assumption, we can then write the apparent electron transfer rate as follows (25):

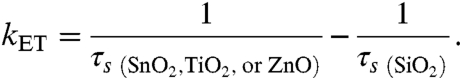[5]

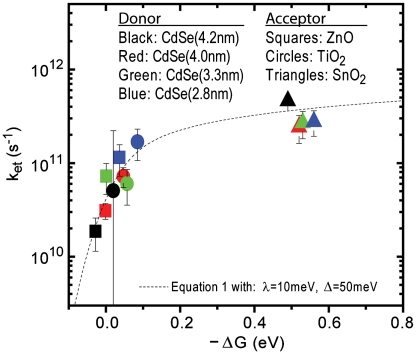
Using Eqs. 5 and 4, we were able to globally plot k_ET vs. ΔG_ET,total for all 12 CdSe–MO combinations under investigation (Fig. 3), where MOs coupled with CdSe QDs with diameters of 4.2, 4.0, 3.3, and 2.8 nm are depicted in black, red, green, and blue, respectively, and QDs anchored to SnO₂, TiO₂, and ZnO are depicted as squares, circles, and triangles, respectively. A numerical summary of these findings is given in Table 1. As predicted by Eqs. 4 and 1, because both TiO₂ and ZnO are in the reorganizational energy dominated region (ΔG_ET,total ≈ λ), k_ET exhibits strong dependence on ΔG_ET,total. Conversely, SnO₂ lies within the density of states dominated region (ΔG_ET,total > λ) whereby k_ET is mostly independent of ΔG_ET,total.

Fig. 3.

Global plot of all CdSe (donor) to MO (acceptor) electron transfer data and trace of Eq. 1 with λ = 10 meV and Δ = 50 meV.

Table 1.

Numerical summary of electron transfer data

	Metal oxide species (acceptor)
CdSe diam., nm (donor)	SnO2		TiO2		ZnO
	-ΔG, eV	kET, s-1	-ΔG, eV	kET, s-1	-ΔG, eV	kET, s-1
2.8	0.56	2.77 × 1011	0.085	1.68 × 1011	0.037	1.15 × 1011
3.3	0.53	2.69 × 1011	0.057	6.02 × 1010	0.0092	7.26 × 1010
4.0	0.52	2.42 × 1011	0.047	7.18 × 1010	−0.00091	3.10 × 1010
4.2	0.49	4.62 × 1011	0.020	5.07 × 1010	−0.028	1.86 × 1010

Values for -ΔG and k_ET were computed from Eqs. 4 and 5, respectively.

Previously, electron transfer rates between QDs and MOs have been studied in solution (24, 26), with QDs grown by chemical bath deposition (27, 28), using single particle microscopy (29), and in nanocrystaline thin films utilizing a single size of QD (30, 31). This work, however, provides a comprehensive examination of electron transfer rates between QDs and MOs which varies both the size of the QD and the species of MO systematically. A body of work exists which focuses on electron transfer reactions between organic dyes and semiconducting metal oxide nanoparticles (16, 17). Generally, these studies involve the anchoring of an organic dye (donor) with known oxidation potential to a nanoparticulate metal oxide (acceptor) thin film and collecting transient absorption data at the picosecond or nanosecond scale. Electron transfer rates are typically compared with predictions made by Eq. 1. In the following paragraphs, we discuss the agreement of the experimental data points in Fig. 3 with Eq. 1 within the context of previous studies of electron transfer from organic dyes to MO nanoparticles.

Overlapped in Fig. 3 is a trace of Eq. 1 with reorganizational energy λ = 10 meV and defect width Δ = 50 meV. The implications of these values, along with potential values for 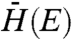and 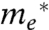, are discussed below. Generally, reorganizational energy increases when a donor–acceptor system comprises, or is surrounded by, a large number nuclear coordinates that need to be rearranged following the transfer of an electron. Previous reports of reorganizational energies in dye–MO systems indicated an increase of λ from ∼100 to ∼500 meV when films were surrounded by a buffer layer, as opposed to air, which was attributed to the additional energy necessary to rearrange added solvent molecules (15, 32). In the case of our samples, CdSe–MO films in vacuum, one would expect system reorganizational energies to be very small, with only ligand molecules on the QD surface or vibrational modes contributing. Therefore, our reported value of λ = 10 meV for an evacuated system is in good agreement with previous observations (33).

The defect width, Δ, is an estimation of how far trap states extend below the conduction band edge. For dye–MO systems, this value was previously estimated to be 100 meV (19, 20). Graphically, defect width corresponds with the slope of the k_ET vs. ΔG trace at values near λ, where a larger slope is suggestive of fewer MO trap (or surface) states participating in the electron transfer reaction. In our analysis, this feature appears to be indistinguishable within experimental error for the two MO accepting species which posses electron transfer driving energies close to λ. Our reported value of Δ = 50 meV indicates that the majority of accepting states participating in QD to MO electron transfer are bulk-like in nature.

There exists some uncertainty regarding the effective electronic masses for the three MO acceptor species under investigation, as discussed further in the SI Text. Using effective masses of 0.33, 1.0, and 0.26m₀, for SnO₂, TiO₂, and ZnO, respectively, which represent an average of those reported in the literature, approximations of 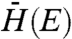were found to be 0.025, 0.0071, and 0.011 cm^-1 for SnO₂, TiO₂, and ZnO, respectively. It is interesting to note that, in contrast with electron transfer studies conducted on dye–MO systems (15, 19, 20, 34), we found no strong electron transfer rate dependence on MO species. Such an observance highlights the unique nature of QD–MO junctions and further experiments need to be conducted to better understand this discrepancy. One possible reason for the observed difference is that dye–MO studies often probe electron transfer from unthermalized “hot” dye electron donating states. In the following section, we investigate the role of hot injection in QD–MO systems.

Lack of Hot-Electron Transfer.

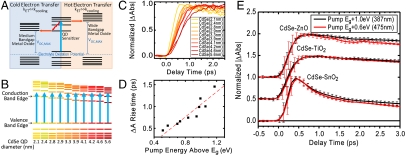
Because of the quasi-continuum of states which make up the conduction band of semiconducting QDs, the absorption of photons with energies greater than that of the bandgap results in the population of states energetically above the conduction band edge. These so-called hot electrons then relax to the conduction band edge with characteristic rate constant, k_cooling. In terms of a photovoltaic device, cooling translates into lost energy that could otherwise be used to contribute to maximum open circuit photovoltage, V_oc, max. The concept of harvesting band edge “cold” versus thermally excited hot electrons and its ramifications in a photovoltaic device are illustrated in Fig. 4A.

Fig. 4.

Schematic diagram of hot versus cold electron injection and its effect on maximum obtainable open circuit voltage (V_oc,MAX) in a photovoltaic device (A). Depiction (B) and ultrafast transient rise times (C) of multiple sizes of CdSe quantum dot excited at various heights above the band edge utilizing a single pump energy. Rise time of transient versus energy differential between quantum dot bandgap and pump pulse (D) and demonstration of a lack of hot-electron injection in CdSe-SnO₂, CdSe-TiO₂, and CdSe-ZnO systems (E). Note, C and D collected from CdSe in toluene solution.

In a QDSSC, hot electrons will only contribute to overall photocurrent if the rate constant of electron transfer is much greater than that of carrier cooling (k_ET≫k_cooling). The rate at which carrier cooling occurs has been investigated previously using first excitonic peak rise times in ultrafast transient absorption measurements, and has been found to be subpicosecond in nature (23, 35–37). To demonstrate typical k_cooling rates in the CdSe QDs utilized in this study, we synthesized 10 small batches of QDs with diameters ranging from 2.1 to 5.6 nm. Because of the high ratio of effective hole/electron mass in CdSe, most of the energy transferred to a QD from an absorbed photon is manifested within the conduction band. By collecting transient absorption traces with a constant pump energy of 387 nm (3.2 eV), we were able to pump electrons into thermally excited conduction band states at various energies above the QD conduction band edge (Fig. 4B). Carrier cooling was then monitored through the rise time of the transient bleach, where the maximum bleach corresponds with the maximum population of electrons at the conduction band edge. The rise of this peak for all 10 samples and the time constants for each trace are shown in Fig. 4 C and D. A linear best fit for the data shown in Fig. 4D gives a slope of ∼1.3 ps/eV, which is in reasonable agreement with previously reported carrier cooling rates (23, 37).

In terms of electron transfer rate constants measured in this study, which were found to range from 1.9 × 10¹⁰ to 2.8 × 10¹¹ s^-1, transfer to MO species is not fast enough to compete with the observed subpicosecond electron cooling time. Therefore, we do not expect hot-electron injection to make a measurable contribution to the total electron transfer rate within the CdSe–MO system, or further, to any photocurrent obtained from a photovoltaic device constructed with a CdSe–MO working electrode. To further investigate the effects of hot-electron injection in prepared CdSe–MO systems, we compared transient absorption decay traces of CdSe-SnO₂, CdSe-TiO₂, and CdSe-ZnO systems pumped by both a 387-nm (1 eV above band edge) and a 475-nm (0.6 eV above band edge) source. A kinetic comparison between the two excitation energies in the three aforementioned systems is shown in Fig. 4E. If hot-electron injection was to contribute to the total electron transfer, one would expect more hot-electron injections with the higher energy 387-nm pump in comparison to the 475-nm pump, due to the increased time spent in a thermally excited state. Further, any contribution from hot electrons would occur on a timescale no longer than a few picoseconds. However, as shown in Fig. 4E, the transient decay traces are indistinguishable in all three systems, suggesting that electron transfer processes from CdSe QDs to the three MOs are independent of excitation energy or, more specifically, independent of electron cooling within the QD conduction band.

Previously, hot-electron injection has been demonstrated in systems composed of TiO₂ sensitized with ruthenium based dyes (17, 38, 39) which utilize multiple carboxylic acid functional groups to couple strongly with MO surfaces, resulting in strong spatial coupling between the dye excited state and TiO₂ conduction band states. This intimate contact results in electron injection from nonthermalized hot dye states into TiO₂ with time constants on the order of hundreds of femtoseconds (40). The likely reason for the observation of hot injection in these systems is the relatively larger ratio of k_ET/k_cooling in dye-sensitized TiO₂ moieties. Typical k_cooling timescales in these systems are on the order of tens of picoseconds (41), which yields k_ET/k_cooling ratios on the order of 100. Comparatively, the CdSe–MO systems studied here were found to have k_ET/k_cooling ratios ranging from 0.02 to 0.5, roughly 2–3 orders of magnitude smaller than their dye-sensitized counterparts.

Although hot-electron injection was not observed in the QD–MO systems studied here, such was recently reported by Tisdale et al. in PbSe–TiO₂ systems (42). However, hot-injection was only observed at 80 K in QDs which had received surface treatment, both conditions which were shown to slow k_cooling in quantized systems. Additionally, this study was performed with single crystal rutile TiO₂ as the accepting species, a material which has a larger density of states than the nanoparticulate anatase TiO₂ utilized here. Although the realization of hot-electron transfer in QD–MO systems is an important step toward beating the Shockley–Queisser limit in photovoltaic devices (43), further work needs to be completed in order to exploit this phenomenon in real-world devices, as evidenced by the lack of hot-injection observed here. In the final section, we explored a practical application of QD–MO systems by employing the aforementioned films as working electrodes within an electrolyte filled QDSSC.

Application—Photovoltaic Devices.

One promising application for QD–MO systems is as a sensitizer-electron transporter in solar cells. Although extensive research has been performed regarding the use of QD–MO junctions in both solid-state and electrolyte-based photovoltaic devices, such systems have yet to achieve efficiencies to make them competitive with current energy sources, renewable or otherwise. It is useful then to compare the electron transfer rate results presented here with performance of those same materials in photovoltaic devices.

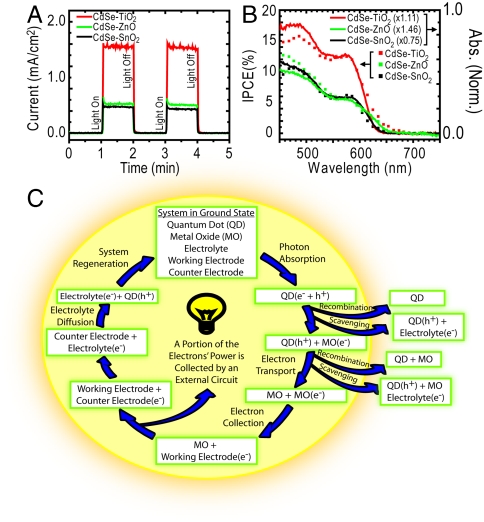
Working electrodes were constructed under the same protocol used to construct the thin films utilized in the spectroscopic portion of this study. Although electing to sensitize metal oxides with CdSe QDs in a linkerless fashion limits the film loading density of QDs—and therefore limits performance of a device constructed from that film—doing so allows a direct comparison between electron transfer and photovoltaic datasets. To perform photovoltaic characterizations, a separate batch of CdSe QDs was synthesized (d = 4.3 nm) and anchored to SnO₂, TiO₂, and ZnO nanoparticulate thin films supported by transparent conducting fluorine doped tin oxide glass. These films were inserted into an aqueous 0.1 M Na₂S electrolyte solution as working electrodes with a Cu₂S-coated nickel wire counter electrode. The short circuit current profiles and incident photon-to-carrier generation efficiency traces of these films are shown in Fig. 5 A and B, respectively, whereas I–V curves and a numerical summary of common photoelectrochemical parameters are provided in Fig. S3 and Table S2, respectively. Of the three metal oxides studied, the consistent trend in rate of electron transfer for all dot sizes was k_ET,CdSe-SnO2 > k_ET,CdSe-TiO2 > k_ET,CdSe-ZnO. It is surprising then, to see that both the short circuit photocurrent (I_SC) and the power conversion efficiency (η) were greatest in the CdSe-TiO₂ device. In a previous comparison between electron transfer rates and device performance, a similar trend of faster electron transfer yet smaller I_SC was reported in a comparison between SnO₂ (larger k_ET) and TiO₂ (larger I_SC) dye-sensitized solar cells (44). This trend was attributed to faster electron scavenging by the redox couple in SnO₂. Consequently, similar phenomena are affecting device performance in CdSe–MO cells. An outline of specific processes which may be hindering performance in our devices is discussed in the following paragraphs.

Fig. 5.

Photovoltaic characteristics of films prepared in an identical manor as those described in the spectroscopic portion of the study. Transient current (A) and incident photon-to-carrier generation efficiency (IPCE) (B) measurements both show improved performance in the CdSe-TiO₂ working electrode. Electron transfer reaction cycle in liquid junction QDSSC (C). Processes which result in loss of performance are depicted as arrows leading away from the center of the cycle.

The ability of a photovoltaic device to effectively generate current hinges on its capacity to robustly undergo electron transfer. Although this study focuses primarily on electron transfer from the CdSe QD sensitizer to the MO electron shuttling material, it is important to note that other electron transfer and transport events must occur in order to generate current, each of which can independently affect device performance. Namely, to complete a circuit in a liquid junction QDSSC, a photoexcited electron takes the following path: transfer from the QD sensitizer to the MO, transport through the MO framework, transfer to the working electrode surface, through an external load, into the counter electrode, into the electrolyte, and ultimately back into the sensitizer from which it originated. If this cycle—and this cycle only—occurred continuously, it would result in a high-efficiency device. However, device performance is limited due to various reactions which compete with this ideal cycle, which could include, but are not necessarily limited to, electron-hole recombination within the QD (or between the QD and MO) and electron recombination (scavenging) of free electrons by the electrolyte. An illustration of these processes is shown in Fig. 5C.

In order to explain the mismatched trends between QD to MO electron transfer rate and device performance, it is important to consider all reactions within Fig. 5 which are dependent on MO species. In addition to QD to MO electron injection, additional reactions satisfying this criterion include QD to MO back electron transfer, intra-MO transport, and electron scavenging from the MO by the electrolyte. Previously, Xie et al. demonstrated a direct correlation between short circuit current and intra-MO transport in polymer-TiO₂ devices, noting higher current in devices with larger photoconductivity (45). Further, in comparison with nanoparticulate films, multiple studies have noted larger I_SC in tubular TiO₂ architectures designed to reduce grain boundary resistance (25, 46, 47). Although a full understanding of the relationship between MO species and QDSSC performance would only be achieved by a comprehensive study on all electron transfer reaction rates involving MOs, as previous studies demonstrate, poor intra-MO transport and electrolyte electron scavenging from the MO can directly affect short circuit photocurrent and are most likely the reason for the discrepancy between electron transfer rates and device performance observed in this study. A full characterization of these and other electron transfer reactions in QDSSCs is currently underway.

Conclusion

This comprehensive study of the energy dependence of electron transfer rates in quantum dot sensitized metal oxide systems highlights its implications in photovoltaic devices. Utilizing ultrafast transient absorption spectroscopy, we measured electron transfer rates from four different sizes of CdSe quantum dots to three unique metal oxide species. Electron transfer rates ranged from 1.9 × 10¹⁰ to 4.6 × 10¹¹ s^-1 and trends generally agreed with Marcus theory. Such agreement highlights the accuracy of the many-state Marcus model, in conjunction with our determination of change in free energy for QD to nanoparticulate MO electron transfer, over a range of CdSe QD sizes and MO accepting species. In contrast with dye-sensitized metal oxide films, no room temperature hot-electron injection was observed in our quantum dot sensitized films. A comparison between measured electron transfer rates and measured photovoltaic device performance showed no correlation, suggesting that other loss mechanisms, such as electron scavenging from the metal oxide by electrolyte, are limiting the performance of quantum dot sensitized solar cells.

Materials and Methods

All materials used in this study, including vendor source and purity, are provided in the SI Text with a detailed description of synthetic and experimental methods. Below, we present an abbreviated version which allows one to sufficiently follow and reproduce the aforementioned findings.

CdSe quantum dots were synthesized as previously described using the one-pot, coordinating solvent method, resulting in < 10% size distribution per batch (31). Dots were washed three times in a nitrogen environment using methanol as a flocculating agent and stored in the dark as a nitrogen-purged toluene suspension to prevent surface oxidation (37).

Semitransparent nanopaticulate MO thin films were made by either doctor blading or spin-coating suspensions of native MO nanoparticles (SiO₂, SnO₂, TiO₂, or ZnO; see X-ray diffraction patterns in Fig. S4) onto either glass microscope slides (spectroscopic measurements) or transparent conducting electrodes (photoelectrochemical measurements). Sensitization with QDs was achieved through 48-h immersion within a > 1 μM (number of QDs per liter) solution under nitrogen. Films intended for optical measurements were placed inside of a sealed optical cell, removed from the glove box, and evacuated, whereas those intended for photoelectrochemical measurements were removed from the glove box and characterized. A pictorial scheme of sensitization strategy is provided in Fig. S2.