Pressure-induced superconductivity in topological parent compound Bi₂Te₃

Abstract

We report a successful observation of pressure-induced superconductivity in a topological compound Bi₂Te₃ with T_c of ∼3 K between 3 to 6 GPa. The combined high-pressure structure investigations with synchrotron radiation indicated that the superconductivity occurred at the ambient phase without crystal structure phase transition. The Hall effects measurements indicated the hole-type carrier in the pressure-induced superconducting Bi₂Te₃ single crystal. Consequently, the first-principles calculations based on the structural data obtained by the Rietveld refinement of X-ray diffraction patterns at high pressure showed that the electronic structure under pressure remained topologically nontrivial. The results suggested that topological superconductivity can be realized in Bi₂Te₃ due to the proximity effect between superconducting bulk states and Dirac-type surface states. We also discuss the possibility that the bulk state could be a topological superconductor.

Utilizing high pressure can be a very powerful method to generate new materials states, as demonstrated by either high-pressure synthesis of new compounds, or pressure-tuned unique electronic states, such as insulator metal transitions. High pressure is particularly effective in tuning superconductivity as it is well documented that the record high superconducting transition temperature T_c for either elements (1) or compounds (2) is created with the application of pressure. Recently, topological insulators (TIs) have generated great interest in the area of condensed matter physics (3–8). These materials have an insulating gap in the bulk, while also possessing conducting gapless edges or surface states in the boundaries that are protected by the time-reversal symmetry (8, 9). Similar to TIs, topological superconductors have a full pairing gap in the bulk and gapless Majorana states on the edge or surface (10–13, 18). Majorana Fermions (14), half of ordinary Dirac fermions, could be very useful in topological quantum computing (15–17), which is proscriptive for new concept information technology. To reach such a situation, two criteria should be satisfied: (i) superconductivity in the bulk states of TI; and (ii) well defined Dirac-type surface states that can be well distinguished from the bulk states around the Fermi energy. Although many materials have been realized as TIs, such as HgTe/CdTe superlattice (3), Bi_1-xSb_x (5), and Bi₂Te₃, Bi₂Se₃, Sb₂Te₃ (6), the search for topological superconductors remains a challenge. Due to the nontrivial band structure of TIs, the realization of superconductivity in topological compounds is regarded as an important step towards such possible topological superconductors. In the usual case, introducing bulk carriers that is a necessary but insufficient condition for the bulk superconductivity pushes the Fermi level into the bulk states, in which the topologically protected surface states are ill defined. The combination of both conditions imposes a stringent constraint, which may not be easily realized in the Cu_xBi₂Se₃ superconductor where n-type carriers have been observed (19). In this report, we show that both superconductivity and well defined surface states can be realized simultaneously in a p-type topological compound Bi₂Te₃ through the application of pressure.

Results and Discussion

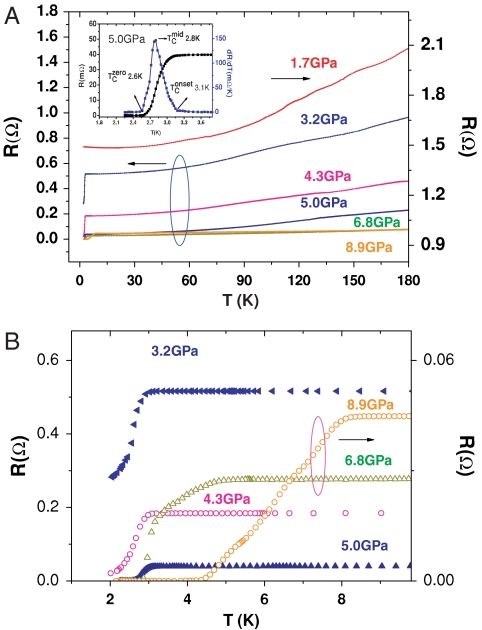
The Bi₂Te₃ single crystal was grown using flux method based on Bi₂Te₃ stoichiometry (20), while the diamond anvil cell technique was used for the high-pressure measurements. Fig. 1 shows the evolution of resistance as a function of the temperature of the Bi₂Te₃ single crystal at various pressures. For a pressure above 3.2 GPa, a clear superconducting transition was observed, with the transition temperature maintaining almost a constant up to 6.3 GPa before a crystal structure phase transition occurred (will be discussed further in the high-pressure structure part of this paper). The data collected at 5.0 GPa showed that resistance dropped to zero at low temperature, while the transition temperatures of onset, midpoint, or zero resistance were defined based on the differential of resistance over temperature (dR/dT) (inset of Fig. 1A). The superconducting transition was sharp with the transition width (from 10%–90%) of the normal state resistance at T^onset) around 0.3 K, indicating the good homogeneity of the superconducting phase. Although the high-pressure phase (> 6.3 GPa) of Bi₂Te₃ is structurally different, it is also superconducting with higher 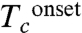(> 8 K) (see Fig. 1B). Such superconducting high-pressure phase (> 6.3 GPa) has been reported previously (21); however, the different transition temperatures that are above 8 K in our measurement and around 2 K as reported in ref. 21 may originate from the different carrier types or densities of the samples as addressed in this paper. The major result of our paper is the discovery of the superconducting phase between 3.2–6.3 GPa, with the crystal structure being the same as in the ambient phase, in which the topological insulator behavior has been predicted and observed.

Fig. 1.

(A) (Upper) The resistance of the Bi₂Te₃ single crystal as a function of temperature at various pressures showing a superconducting transition above 3 K at 3.2 GPa. The inset is the resistance near the critical temperature T_c with the differentiation of dR/dT showing the definition of 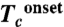, , 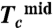and 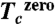, respectively; (B) (lower) The enlarged (low temperature) part of the measured resistance, indicating the almost constant T_c for the states between 3.2–5.0 GPa, while a much higher T_c of 8.1 K appears at 8.9 GPa that is structurally different from the ambient phase. A broad superconducting transition has been observed for the intermediated pressure range, such as the data shown for 6.8 GPa.

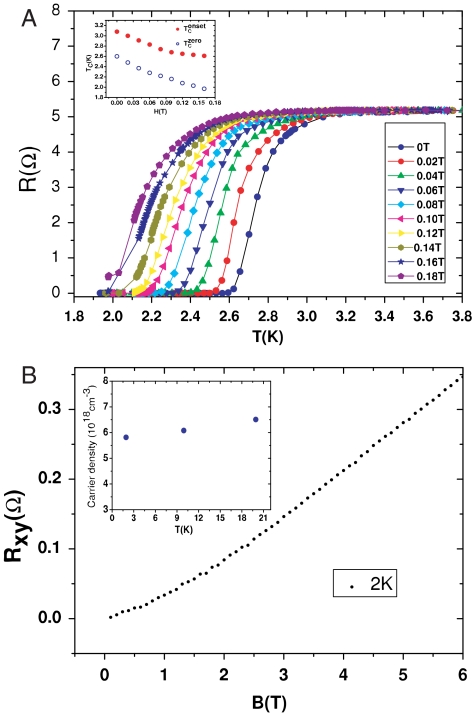
To assure what has been observed in Fig. 1 is indeed a superconducting transition, we further conducted the measurements around the transition temperature at variant external magnetic field. Fig. 2A shows the measured resistance at 6.1 GPa with applied magnetic H. The transition temperature T_c decreased with increasing magnetic field, indicating strong evidence that the transition is superconductivity in nature. The inset of Fig. 2A shows the change of T_c with magnetic field H. Using the Werthdamer-Helfand-Hohenberg formula (22) of H_c2(0) = -0.691[dH_c2(T)/dT]_T=Tc•T_c, the upper critical field H_c2(0) was extrapolated to be 1.8 Tesla for H_‖c, where the single crystal was placed inside the diamond anvil cell with magnetic H direction perpendicular to ab-plane.

Fig. 2.

(A) (Upper) The superconducting transition of the Bi₂Te₃ single crystal at 6.1 GPa with applied magnetic field H perpendicular to the ab-plane of single crystal. Inset shows the change of T_c with H. (B) (Lower) The Hall resistance of the Bi₂Te₃ single crystal with magnetic field H perpendicular to the ab-plane of the single crystal. Inset shows the carrier density deduced from the linear part of Hall resistance at various temperatures at ambient pressure.

The Hall coefficient measurements indicated the p-type carrier nature of the Bi₂Te₃ as grown single crystal (Fig. 2B). The carrier density calculated from the linear part at high magnetic field H was approximately 3 ∼ 6 × 10¹⁸ /cm³ as deduced for several measurements at ambient pressure. The carrier density changed slightly from high to low temperature (inset of Fig. 2B). Both p-type and n-type carriers have been reported to exist in Bi₂Te₃ as grown single crystal depending on the growth conditions and the elements ratio of Bi over Te in the starting materials. In our samples, the single crystal is a p-type compound. This type is different from Cu_xBi₂Se₃ superconductor where n-type carriers have been observed (19). Conducting direct Hall measurement at high pressure had been difficult; however primary measurements indicated little change in the carrier density from ambient to 1.0 GPa (Fig. S1). In addition, the relative change of carrier density with pressure can be estimated from the transport data. The resistivity at fixed temperature (10 K) was only changed by a factor of 3 from ambient pressure to 3.2 GPa wherein superconductivity occurs. Therefore, we do not expect the dramatic change of carrier density at the superconducting pressure.

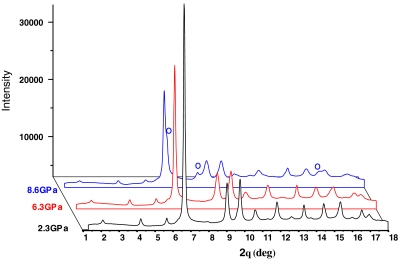
To check whether the superconducting phase transition was not caused by crystal structure phase transition under pressure, we further conducted synchrotron X-ray diffraction experiments with pressure from ambient to above 30 GPa in an average 2 GPa step at room temperature. Fig. 3 shows the X-ray diffraction patterns of Bi₂Te₃ polycrystalline (ground from the single crystal) at several selected pressure levels. The ambient phase remained stable up to 6.3 GPa, while the results of the resistance measurements indicated an intermediate phase occurred at 6.8 GPa (Fig. 1B), above which a structure phase transition was observed (Fig. 3) for X-ray data at 8.6 GP. This finding is consistent with that of previous report (21). Therefore, the superconductivity observed in our experiments has been verified to be coming from the parent structure of Bi₂Te₃, which preserves the topological property. This situation will be shown later in the electronic structure calculation. We further refined the crystal structure at high pressure using Rietveld method with GSAS package to determine the lattice parameters and atomic positions (Fig. S2).

Fig. 3.

The synchrotron X-ray diffraction patterns of Bi₂Te₃ samples at selected pressures showing that the ambient structure is stable at least up to 6.3 GPa, while a structurally different phase appears at 8.6 GPa (the circle indicating the peaks from new structure).

Stoichiometric Bi₂Te₃ has a layered hexagonal structure with unit cells consisting of five atomic layers forming a so called quintuple-layer (QL) as shown in Fig. S3. The topological property of Bi₂Te₃ has been theoretically predicted from first-principles calculations and analytical models (6) and is confirmed by the Angle Resolved Photon Electron Spectroscopy (ARPES) measurement of surface states (4, 23). Due to the strong spin-orbit coupling, the band structures around the Γ point of the Brillouin zone (BZ) are inverted, similar to the case of HgTe quantum wells (3), which gives rise to the TI behavior.

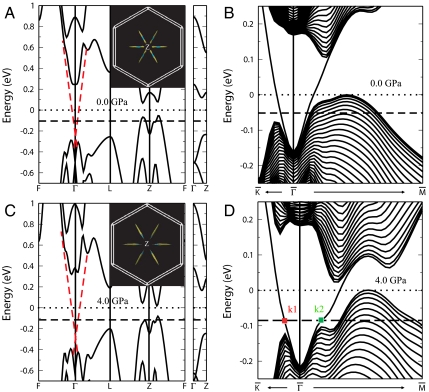
Using the first-principles calculations based on density functional theory and the generalized gradient approximation, we performed full relativistic electronic structure calculations for Bi₂Te₃ at both 0 and 4 GPa, using the experimental lattice parameters and atomic positions obtained from the X-ray refinement (Table S1). We also relaxed the lattice constants and internal atomic sites theoretically for both cases and confirmed that all features of the electronic structures discussed here did not change. For the calculations of surface states, we used a thick slab consisting of 40 QLs. For the 0 GPa phase, our calculations well reproduced those found in earlier results (6, 23) (Fig. 4 A and B). In particular, the calculated surface states can be well compared with the ARPES measurement (4, 23). Given the small changes of lattice parameters and atomic positions at 4 GPa, we do not expect a dramatic change in its electronic structure. Indeed, the electronic structure at 4 GPa was quite similar to that at 0 GPa (Fig. 4 C and D). Most importantly, by calculating the Z₂ number from parity analysis and the surface states, we confirmed that the compound remained topologically nontrivial at 4 GPa.

Fig. 4.

The calculated bulk electronic structures (left) and surface states (right) of the Bi₂Te₃ at 0 GPa (A) and (B) and 4 GPa (C) and (D), respectively. The chemical potential corresponding to the experimental hole concentration (5.8 × 10¹⁸ /cm³) are indicated as horizontal dashed lines, while the corresponding Fermi surfaces are also shown as insets. In order to understand the k-space separation of bulk and surface states, we also show the surface states schematically in the bulk band structures (left).

Bi₂Te₃ has the particular property, in which the surface states are located around the Γ point, while both conduction band minimum (CBM) and valence band maximum of bulk states are located away from the Γ point. In other words, for the low energy range, the surface states and bulk states were well separated in the momentum space (Fig. 4). The direct band gap at Γ point was much bigger than the indirect bulk band gap, which was formed from states around the Z point of the bulk BZ. Such character is crucial for the criteria discussed at the beginning to realize the bulk-to-surface proximity effect. Using the rigid band model, we estimated the Fermi level position as functions of carrier concentration and found that the surface states remained well defined even if the carrier density was as high as 10²¹ /cm³ (hole type). For our experimental situation, where superconductivity was observed, the carrier density (of the order of 10¹⁸ /cm³) was much smaller than this level. The electronic structures at 4 GPa were, in fact, quantitatively different with that of 0 GPa. The differences are as follows: (i) the direct gap at Γ point is enhanced while the indirect bulk band gap is reduced and (ii) the separation between surface states and bulk states at the Fermi level is further enhanced. We have also analyzed the penetration depth of surface states around the Fermi energy as determined by the experiments (k1 and k2 points shown in Fig. 4D). We found that the surface states were exponentially localized to the surface region with half-widths of about 3 QLs. In contrast to Bi₂Te₃, for the electron-doped Bi₂Se₃, the CBM of bulk states were located around the Γ point, very close to the surface states. Both facts support our conclusion that the topological surface states can maintain their character in the presence of the p-type bulk carriers. Therefore, the resulting proximity effect with the bulk superconducting carriers can give rise to Majorana fermions in the surface state.

We now turn to the exciting possibility that the bulk superconducting state in Bi₂Te₃ could be a topological superconductor (10–13, 24–27). In insets of Fig. 4 A and C, we see that with p-type doping, holes form disconnected pockets. Pairing amplitude on a given hole pocket could be largely determined by the phonon contribution mediated at the small momentum transfer, and a uniform pairing order parameter could be established on each hole pocket. The relative pairing amplitude among the different hole pockets would be determined by the large momentum transfer, where the Coulomb repulsion plays a more dominant role. Such a repulsive interaction generally favors opposite pairing amplitudes on different Fermi pockets, leading to a negative Josephson coupling among the neighboring hole pockets. However, due to the threefold symmetry of the Fermi surface, such a coupling is frustrated, so that the pairing order parameter in the ground state may become complex. A natural choice of such a complex orbital pairing symmetry without breaking the time-reversal symmetry is a triplet pairing symmetry similar to the Balian and Werthamer state in He3-B-phase. Such a pairing state has been shown on general grounds to be a topological superconducting state respecting the time-reversal symmetry (10–13, 24–27).

In summary, we have experimentally observed superconductivity in the Bi₂Te₃ parent phase driven by pressure from 3 to 6 GPa, in which the crystal structure is maintained as the ambient topological phase. Topological surface states remained well defined under pressure in the presence of bulk p-type carriers. The results could be a substantial step towards the realization of topological superconductivity.

Methods

Physical Properties Characterization at High Pressure.

The superconducting measurements induced via high pressure were conducted using diamond anvil cell technique as previously described (28). The diamond culet was 300 μm in diameter. A plate of T301 stainless steel covered with MgO fine powders that is to protect the electrodes leads from short circuit was used as gasket. The gasket, which was preindented from the thickness of 300 to 60 μm, was drilled with a hole of 180 μm diameter. Into this hole, MgO fine powders were pressed and further drilled into a center hole with a diameter of 100 μm to serve as sample chamber wherein a Bi₂Te₃ single crystal with a dimension of 60 μm × 30 μm × 10 μm was inserted with soft hBN fine powder as a pressure-transmitting medium that can provide a good hydrostatic pressure environment. A tiny ruby was placed aside the specimen. Pressure was measured using ruby florescent method (29). We used slim Au wire of 10 μm diameter as electrodes. The four-probe method was adapted to measure the resistivity. A screw-type diamond anvil cell made of BeCu was then used to conduct low temperature experiments. The diamond anvil cell was put inside a Mag lab system upon loading. The temperature was automatically program controlled via the Mag Lab system. A thermometer was specially mounted around the sample in the diamond anvil cell to monitor the sample temperature. Data were collected at each equilibrium point of temperature. The high-pressure Hall effects were measured based on Van der Pauw method using a piston cylinder-type instrument that was inserted into the Mag Lab system.

Crystal Structure Determination at High Pressure.

The X-ray diffraction experiments at high pressure with synchrotron radiation were done at the HPCAT of Advanced Photon Source of Argonne National Lab with a wavelength 0.368 Å using a symmetric Mao Bell diamond anvil cell at room temperature. The crystal structures were refined using GSAS package (30).

Electronic Structure Calculations at High Pressure.

We calculated the electronic structures of Bi₂Te₃ with experimental crystal structures (Table S1). The first-principles calculations were performed using OpenMX package (31) based on a linear combination of pseudoatomic orbital (PAO) method (32). The PAOs were generated by a confinement potential scheme (33) with cutoff radii of 9.0 and 7.5 a.u. for Bi and Te, respectively. Basis sets with s2p2d2f1 PAOs for Bi and s2p2d3 for Te were found to be good enough to describe our system. The j-dependent pseudopotentials for Bi and Te were generated from full relativistic calculations, and spin-orbit coupling was included in electronic self-consistent calculations. The exchange correlation energy functional within the generalized gradient approximation as parameterized by Perdew, Burke, and Ernzerhof (34) was used. The BZ was sampled with 10 × 10 × 4 grids. We relaxed the lattice constants and internal atomic sites theoretically starting with the experimental structures for both 0.0 and 4.0 GPa. The optimized geometrical structures were nearly the same as those in the experimental ones (Table S1). We also confirmed that all features of the electronic structures discussed here hardly changed after relaxation. We constructed the projected atomic Wannier (PAW) functions (35) for the s and p orbitals of both Bi and Te (36). With this set of PAW bases, an effective model Hamiltonian for slab of 40 QLs was established, and the topologically nontrivial surface state were obtained from it.