Redrawing the Ramachandran plot after inclusion of hydrogen-bonding constraints

Abstract

A protein backbone has two degrees of conformational freedom per residue, described by its φ,ψ-angles. Accordingly, the energy landscape of a blocked peptide unit can be mapped in two dimensions, as shown by Ramachandran, Sasisekharan, and Ramakrishnan almost half a century ago. With atoms approximated as hard spheres, the eponymous Ramachandran plot demonstrated that steric clashes alone eliminate ¾ of φ,ψ-space, a result that has guided all subsequent work. Here, we show that adding hydrogen-bonding constraints to these steric criteria eliminates another substantial region of φ,ψ-space for a blocked peptide; for conformers within this region, an amide hydrogen is solvent-inaccessible, depriving it of a hydrogen-bonding partner. Yet, this “forbidden” region is well populated in folded proteins, which can provide longer-range intramolecular hydrogen-bond partners for these otherwise unsatisfied polar groups. Consequently, conformational space expands under folding conditions, a paradigm-shifting realization that prompts an experimentally verifiable conjecture about likely folding pathways.

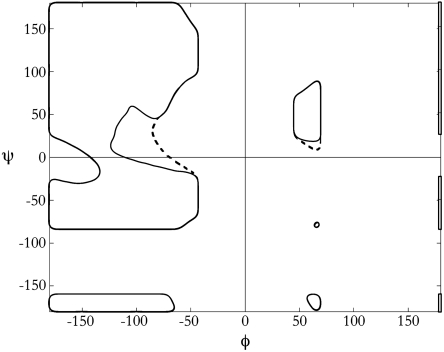
No general biochemistry textbook is complete without a φ,ψ-map of the alanine dipeptide (1, 2). This iconic plot is a compact representation of a profound organizing idea, one that ranks among the fundamentals of structural biochemistry (3–5). In particular, each peptide unit has only two degrees of freedom, specified by its backbone torsion angles φ and ψ, so all sterically allowed conformations of the alanyl dipeptide can be described by a two-dimensional plot (Fig. 1). Based on a hard sphere atomic model, which approximates the steeply repulsive term in a Lennard–Jones 6-12 potential (6), a given conformation is “disallowed” if it results in an atomic clash. Applying this enormously simplified energy function to the alanyl dipeptide eliminates 73% of its conformational space, a result that has since been validated by experiment in tens of thousands of structures (7), to the extent that significant deviations from the theory are now regarded as probable errors in the data (8).

Fig. 1.

The Ramachandran plot. For a blocked peptide unit, steric clash alone winnows allowed conformational space to the outlined regions. The bridge is defined as the isthmus on the left side of the plot (ϕ < 0), situated around ψ ≈ 0. The addition of hydrogen-bonding constraints eliminates two additional segments of φ,ψ-space (8%), a major segment in the bridge (inside the dashed region) and a minor segment in α_L (inside the dashed region).

Here, we refine the conventional Ramachandran plot by applying a hydrogen-bonding requirement as an additional energetic criterion. A conformation for which any backbone polar group, either N─H or C═O, is shielded from solvent access and therefore deprived of a hydrogen-bond partner would be disfavored by approximately 5 kcal/mol relative to other sterically allowed conformations. This energy penalty is sufficient to deplete the map of such conformations (9), effectively eliminating a major fraction of the bridge region from the familiar map (Figs. 1 and 2) (10).

Fig. 2.

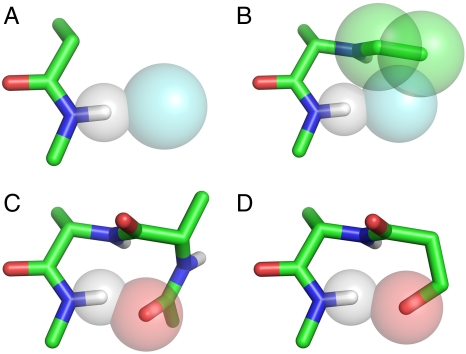
Peptides with φ,ψ-angles in the bridge. (A) A clash-free amide-water hydrogen bond. (B) A Ramachandran dipeptide with φ,ψ-angles in the bridge causes unavoidable steric clashes between acetyl carbons (green spheres) and water (aqua sphere), rendering the N-methyl hydrogen solvent-inaccessible and depriving it of a hydrogen-bond acceptor. Clashing atoms are shown as overlapping van der Waals spheres; the backbone chain is shown as a stick model. (C) A type I turn, illustrating how a longer range, intramolecular hydrogen-bond acceptor can satisfy the amide hydrogen without steric interference. (D) A local side chain (serine)—backbone hydrogen bond can also satisfy the amide hydrogen without steric interference. Atom color code: carbon: green; peptide oxygen: red; nitrogen: blue; hydrogen: white; water: aqua.

The existence of the disfavored bridge has implications that extend well beyond a technical adjustment to the Ramachandran plot. Intrapeptide H bonds are disfavored under unfolding conditions but favored under native conditions (11). Consequently, accessible φ,ψ-space is enlarged upon shifting to native conditions because residues can then occupy this otherwise disfavored region. Conversely, elimination of this region under unfolding conditions will inhibit type I turn formation. Given that almost all non-glycine-based β-turns in proteins are type I (12), this conformational restriction is expected to promote dramatic chain expansion in the unfolded population (13–15). These changes in solvent or temperature conditions modulate occupancy of the disfavored bridge and, in turn, affect the overall U(nfolded)⇌N(ative) equilibrium.

Why has this “forbidden” bridge region been overlooked in previous versions of the ubiquitous plot? In fact, some early simulations of the alanine dipeptide in water did show a narrowing of this region: See, for example, ref. 16. However, such results failed to inform textbook representations of the map, most likely because the observed distribution of φ,ψ-angles from solved structures falls almost entirely within sterically allowed boundaries, including the disfavored bridge.

This long-standing paradox has gone unnoticed because its resolution rests on such familiar ground. When a residue at position i is situated in the disfavored bridge, the N─H at (i + 1) is rendered inaccessible to solvent (Fig. 2B). However, when experimentally determined structures are analyzed, residues that populate this region are found to participate in one of three possible hydrogen-bonded motifs, obviating the need for an H bond to solvent. Two of these motifs are β-turns—either type I or type II′ (17)—and the third involves backbone:side chain hydrogen bonds (Figs. 2 C and D).

A plot of backbone dihedral angles from solved structures traces a revealing corridor through φ,ψ-space, linking the northwest quadrant to the α-basin across the disfavored bridge. Under unfolding conditions, conformers within this region are suppressed, but they are enhanced in solved structures because folding conditions, which favor intramolecular hydrogen bonding, shift this region from a high-energy plateau to a low-energy basin. This trail from solved structures suggests the existence of an actual pathway. Guided along this trail, we present a hypothesized folding pathway from the northwest quadrant to the α-basin via consecutive intermediates that can successfully maintain an unbroken series of intramolecular hydrogen bonds.

Results

Using the conventional alanyl dipeptide^† (2), the disfavored bridge was mapped in detail via exhaustive Monte Carlo simulations, with the Metropolis criterion set to reject conformations having a steric clash or lacking a hydrogen-bond partner. The resultant φ,ψ-map was then compared with φ,ψ-angles drawn from a nonredundant set of high-resolution X-ray elucidated proteins. This set included 30,924 residues in the disfavored bridge; almost all could be classified readily into one of three local hydrogen-bonded motifs. A complicating factor that may have hindered earlier recognition of the clear-cut result presented here is that approximately 12% of these residues ostensibly lacked H-bond partners. However, similar to a previous study (18), we found that local torsional angle minimization, which induces only minor conformational changes, shifts all but 0.1% of these outliers into acceptable water-accessible geometry. These results are now described in detail.

The Disfavored Bridge.

Inclusion of a hydrogen-bonding constraint eliminated two additional regions (8%) of the conventional φ,ψ-plot: (i) the bottom sliver of the α_L-basin and (ii) a large fraction of the bridge (Fig. 1). Here, we focus on the bridge.

Specific interactions involved in winnowing the bridge were identified in further simulations: When the H-bond requirement for the N-methyl amide (Nme) hydrogen was suppressed, the bridge was fully restored. This test confirmed that the Nme hydrogen is water-inaccessible because the only other H-bonding alternative, an intrapeptide hydrogen bond, is not possible in a blocked monomer with φ,ψ-angles in the bridge. Additionally, when the van der Waals radius of acetyl carbons was set to 0, the bridge was again fully restored, demonstrating that these atoms are solely responsible for shielding the Nme hydrogen from solvent access when φ,ψ-angles are in this disfavored region (Fig. 2).

Comparison with the Protein Data Bank (PDB).

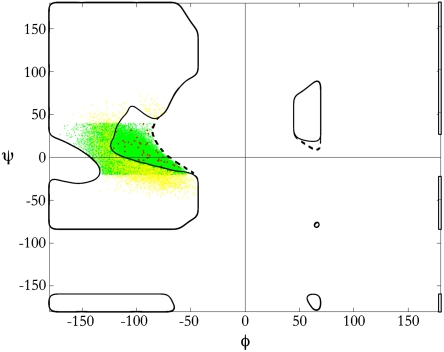
All φ,ψ-angles were determined in a nonredundant set of high-resolution X-ray crystal structures (19), and those within the bridge region were compared with results from simulations (Fig. 3). Specifically, the bridge comprised 47,401 residues, with 30,924 in the disfavored region. Three local hydrogen-bonded motifs (Fig. 2) were sufficient to classify the majority (88%) of those in this region: type I β-turns (18,762 total), type II′ β-turns (947 total), and local side chain-backbone hydrogen bonds (7,453 total). By definition, the ith residue of a type I or type II′ β-turn is situated in the disfavored bridge (20), and the water-inaccessible N─H_i+1 forms an H bond with the C═O_i-2 acceptor. In the third case, the water-inaccessible N─H_i+1 forms an H bond with a nearby side chain acceptor, predominantly at the i - 1 position.

Fig. 3.

Experimentally determined φ,ψ-angles in the bridge. A total of 47,401 bridge residues—both solvent-accessible and solvent-inaccessible—from high-resolution structures is shown as a scatter plot. Sterically allowed but solvent-inaccessible regions are inside the dashed boundary. Most bridge residues (green points) either fall within the water-accessible bridge or provide an intramolecular hydrogen-bond partner for the otherwise unsatisfied water-inaccessible amide hydrogen. Outliers (yellow points) are classified as bridge residues having φ,ψ-angles that were successfully minimized into the water-accessible bridge while remaining within 1.0-Å root-mean-squared deviation from the starting X-ray structure. Remaining points (red) that evaded such minimization constitute 0.1% of the entire bridge population.

Residue Preferences.

The two β-turn types have marked residue preferences, as noted earlier (12). For type I, Pro, Ala, Glu, and Ser constitute 45% of all residues in the i - 1st position, whereas Asn and Asp constitute 25% of residues at the ith position. For type II′, Gly constitutes 74% of residues at i - 1, whereas Asp, Asn, and Ser constitute 48% at i. For the backbone:side chain motif, Pro is found most frequently at the ith position along with Asp, Ser, and Thr; together they constitute 41% of residues at this position. Ser, Asp, Asn, Thr, and Gly constitute 81% of residues at the adjacent i - 1st position. These residue preferences in the disfavored bridge are more pronounced than those in any other locale on the φ,ψ-map.

Simulations with Intrapeptide Hydrogen Bonds.

Occupation of the disfavored bridge requires an intrapepide H-bond acceptor for the water-inaccessible N─H, a requirement that cannot be satisfied by the conventional alanyl dipeptide (i.e., a blocked monomer). Accordingly, the three motifs observed in solved structures were modeled in Monte Carlo simulations of blocked dipeptides, Acetyl₁-Xaa₂-Ala₃-Nme₄, long enough to form an intrapeptide H bond. To model a turn with Ala₃ situated in the disallowed bridge, either an Ala or a Gly was introduced as Xaa₂ and allowed to randomly sample those regions of φ,ψ-space specific to the corresponding residue in a type I or a type II′ β-turn, respectively. To model side chain acceptors, a serine was introduced as Ser₂ and allowed to randomly sample allowed φ,ψ-space excluding the turn regions sampled previously. In all three cases, Ala₃ randomly sampled the entire Ramachandran plot and conformations with a steric clash or without a hydrogen-bond partner were rejected. Each model successfully recapitulated its structural correlate in solved proteins.

Minimization of Outliers.

From a total of 30,924 residues in the disfavored bridge, 3,762 residues (12%) appear to lack H-bond partners, an energetically implausible finding (9, 18). However, over 98% of these outliers could be minimized into water-accessible bridge conformations with only minor shifts in backbone geometry (see Methods summary). In particular, 81% of the outliers were successfully minimized into clash-free, hydrogen-bond-satisfied conformations within 0.5 Å (root-mean-square deviation) of the starting X-ray structure, and an additional 17% were included upon extending this threshold to 1.0 Å. Following minimization, only 50 of the 47,401 bridge residues (0.1%) remained unclassified.

Navigating the φ,ψ-Map

The φ,ψ-map subdivides into naturally formed discrete basins upon plotting φ,ψ-angles from proteins of known structure (21, 22). Accordingly, it is often assumed that basin hopping is a barrier process that occurs in the absence of populated intermediates, with interbasin crossings controlled by barrier heights (23).

Suggestively, when the map is modified to include hydrogen bonding, most of the population in the bridge is observed to fall within the disfavored region. This population distribution prompts a conjecture that the major flux from the northwest quadrant to the α-helix follows a direct route, passing through this region. A related question is raised by the finding of substantial polyproline II (P_II) conformation under unfolding conditions (24). Upon shifting to folding conditions, how does a structure like P_II conformation, from the left-handed region of φ,ψ-space, surmount the ostensibly high-energy barrier when switching handedness to a right-handed helical structure, like an α-helix?

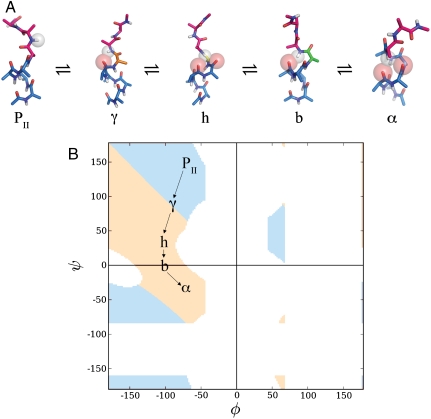
We hypothesize that conformers distributed across the southwest quadrant preferentially follow a low-energy pathway of hydrogen-bonded intermediates that traverse the disfavored bridge, as illustrated in Fig. 4. These intermediate “stepping-stones” form a progressive continuum that spans the main H-bonded backbone structures on the left side of the map: β-turns, 3₁₀ helices, and α-helices.

Fig. 4.

Proposed low-energy pathway for helix formation. (A) Trajectory from P_II to the α-basin via hydrogen-bond-preserving intermediates. The color-coded φ,ψ-angles of a probe residue are tracked from P_II (pink,ϕ,ψ = -60,150)⇌inverse γ-turn (γ) (orange,ϕ,ψ = -75,80)⇌hybrid turn (h) (yellow,ϕ,ψ = -90,35)⇌bridge turn (b) (green,ϕ,ψ = -90,0)⇌α-helix (α) (blue, φ,ψ = -60, -40). Along this pathway, the N─H donor of interest forms consecutive hydrogen bonds with C═O acceptors as indicated: P_II (none)⇌γ(i → i - 2)⇌h(i → i - 2 & i → i - 3)⇌b(i → i - 3)⇌α(i → i3 & i → i - 4). (B) Helical handedness in the Ramachandran plot. Repeated φ,ψ-angles give rise to either left-handed (blue region) or right-handed (peach region) helices. The low-energy pathway proposed here transits from left-handed polyproline II conformation to right-handed α-helical conformation, passing through an inflection point at the centroid of the γ-basin (φ,ψ = -80°, +80°). Map labels correspond to the φ,ψ-angles of conformers in A.

Changing Hands Without Letting Go.

The φ,ψ-map separates cleanly into left-handed and right-handed structures on either side of a main diagonal that originates in the northwest corner. Emanating from the P_II-basin (centered at φ,ψ = -65, 141), a hydrogen-bonded path connects the P_II and α-helical basins (Fig. 4), passing through the γ-basin (C₇ equatorial, centered at φ,ψ = -85, 78). The γ-basin adjoins the P_II-basin, but unlike a three-residue turn of P_II helix, which lacks intramolecular hydrogen bonds, a residue in γ-conformation at position i engenders a three-residue, hydrogen-bonded inverse γ-turn: NH(i + 1)⋯O═C(i - 1) (17). The diagonal divide between left-handed and right-handed conformers (Fig. 4A) passes precisely through the centroid of the γ-basin, with an inflection point near φ,ψ = -80°, +80°. Helices having backbone dihedral angles above this diagonal (upper-γ) are left-handed, whereas those having backbone dihedral angles below the diagonal (lower-γ) are right-handed. At the inflection point, the conformation is flat. Unlike classical four-residue β-turns, in which switching between right- and left-handed isomers (e.g., type I vs type I′) requires a peptide chain flip (17), an inverse γ-turn is poised near its chiral inflection point and can undergo a smooth transition between right- and left-handed isomers with identical peptide backbone orientation and only modest adjustment of its φ,ψ angles.

Following the H-Bonded path.

Transit from P_II to upper-γ, then lower-γ, can then continue toward types I, II′, and III β-turns and 3₁₀ helix. Bifurcated hydrogen bonds form as the conformation shifts from a three- to four-residue turn (i.e., γ-turn to β-turn) but then resolve into i → i - 3 hydrogen bonds. Bifurcated hydrogen bonds form once again as the conformation shifts from β-turns to α-helix but then resolve yet again into the familiar i → i - 4 pattern in α-helix. This trajectory is mapped in Fig. 4B.

Thus, upon descent from the P_II-basin, hydrogen bonding can be maintained along the entire path from an inverse γ-turn to an α-helical turn, with partner exchange facilitated via bifurcated intermediates, not barrier-limited bond-breaking/remaking. Notably, hydrogen-bond exchange in liquid water seems to follow a similar “hand-over-hand” mechanism according to the dynamic picture that emerges from femtosecond infrared spectroscopy (25) coupled with simulations (26, 27). The detailed mechanism of helix nucleation is unknown. The mechanism hypothesized here would require an initiating residue to be situated in the α-basin, promoting nucleation at the N terminus.

Conclusion

Steric restriction has long been recognized as a major organizing force in protein structure. As revealed in both the Ramachandran plot (2) and Corey–Pauling–Koltun models (28), the fact that nonbonded atoms cannot occupy the same space at the same time results in a substantial reduction of accessible conformational space. Along with sterics, hydrogen-bonding constraints also impose substantial restrictions on accessible conformational space; a conformer with a completely unsatisfied hydrogen-bonding group would be strongly disfavored (9). The imposition of steric and hydrogen-bonding constraints was sufficient to deduce the structures of α-helix and β-sheet once Pauling had realized that the peptide unit is planar (29, 30). Curiously however, hydrogen-bond satisfaction has not been incorporated into the ubiquitous Ramachandran plot. When included, it becomes evident immediately that folding conditions, which favor intramolecular H bonding, result in an expansion of accessible conformational space, contrary to intuitive expectations. Conversely, unfolding conditions would deplete the population in the disfavored bridge, an experimentally verifiable proposition.

Unlike an ordinary chemical reaction, no covalent bonds are made or broken when a protein folds. Instead, the population simply reequilibrates in response to changed chemical and/or physical conditions, and the resultant equilibrium is established via three main factors: conformational entropy, the hydrophobic effect, and hydrogen bonding. Conformational entropy always favors the unfolded state. In opposition, the hydrophobic effect favors the folded state across a broad range of aqueous solvent conditions. Of these three, hydrogen-bonding is uniquely pivotal, favoring the folded state in poor solvent and/or at physiological temperature and the unfolded state in good solvent and/or at high temperature (11). Such conditions serve to control occupancy of the disfavored bridge. It is our conjecture that a shift to conditions that favor intramolecular hydrogen bonding would open the bridge to occupancy, facilitating a flux from the northwest quadrant to the repertoire of hydrogen-bonded backbone structures that populate the southwest quadrant: β-turns, 3₁₀ helices, and α-helices. This conjecture is amenable to experimental assessment.

Methods

High-resolution X-ray crystal structures (resolution ≤ 1.5 Å, R ≤ 0.25, sequence identity < 90%) were extracted from the PDB based on a PISCES list (19) (04/07/10). Bridge residues were defined as [(ϕ,ψ)|ϕ ≤ 0° and 20° ≤ ψ ≤ 40°], but excluding angles outside the standard Ramachandran plot.

Ramachandran plots were generated from computed φ-ψ distributions, which were then binned with a grid size of 2° × 2° (180 × 180 bins). Populated bins were displayed in plots. PDB-derived residues with φ,ψ-angles in an unpopulated bin were classified as outliers.

Local torsional angle minimization was attempted for residues having φ,ψ-angles in the water-inaccessible bridge but lacking intrapeptide hydrogen bonds. In such cases, a nine-residue fragment centered around the residue in question was excised from its parent X-ray structure, and all residues except glycine and proline were mutated to alanine. The φ,ψ-angles of the central residue were then reassigned to the closest populated bin, after which the entire fragment was minimized by searching exhaustively for a nearby, acceptable (i.e., clash-free, hydrogen bond-satisfied, and within the bridge) structure. Specifically, the φ,ψ-angles of all nine residues were varied at random within n_1° of their PDB values until an acceptable conformation with an rmsd less than n₂ from the original fragment was found or until termination after n₃ unsuccessful attempts; ω-angles were held fixed at their original values throughout. The three search constraints, (n₁, n₂, n₃), were relaxed incrementally in up to four steps, with successive values of (20°, 0.5 Å, 10³ trials), (30°, 0.5 Å, 10⁴ trials), (30°, 1.0 Å, 10⁴ trials), and (40°, 1.0 Å, 3 ∗ 10⁴ trials).

Geometric criteria for backbone:backbone H bonds were (i) N─H⋯O═C distance ≥3.5 Å, (ii) C─O─H scalar angle ≥90°, and (iii) N─H─O scalar angle ≥100° (31). For side chain–backbone H bonds, conditions (ii) and (iii) were either (45°, 90°) or (90°,45°) (32). Atoms were treated as hard spheres with radii scaled to 95% of their van der Waals values: C(sp³) = 1.64 Å, C(sp²) = 1.5 Å, O(sp²) = 1.35 Å, N(sp²) = 1.35 Å, H = 1.0 Å (31). Hydrogen bonds with solvent were assessed using a spherical water probe with a radius of 1.4 Å (10).

Metropolis Monte Carlo simulations (33) were performed using blocked, all-atom monomers and dimers (34), as indicated in the text. Accessible φ,ψ,ω,χ-conformational space was sampled uniformly in runs ranging between 3 ∗ 10⁷–10⁸ trials. Sampling was residue-specific for both backbone (2) and side chain (35) conformers; ω-sampling was Gaussian-distributed around a mean of 180° ± 5°. Conformations having a steric clash, an unsatisfied hydrogen bond, or |ω| < 170.1° were rejected.