A network model for plant–pollinator community assembly

Abstract

Community assembly models, usually constructed for food webs, are an important component of our understanding of how ecological communities are formed. However, models for mutualistic community assembly are still needed, especially because these communities are experiencing significant anthropogenic disturbances that affect their biodiversity. Here, we present a unique network model that simulates the colonization and extinction process of mutualistic community assembly. We generate regional source pools of species interaction networks on the basis of statistical properties reported in the literature. We develop a dynamic synchronous Boolean framework to simulate, with few free parameters, the dynamics of new mutualistic community formation from the regional source pool. This approach allows us to deterministically map out every possible trajectory of community formation. This level of detail is rarely observed in other analytic approaches and allows for thorough analysis of the dynamical properties of community formation. As for food web assembly, we find that the number of stable communities is quite low, and the composition of the source pool influences the abundance and nature of community outcomes. However, in contrast to food web assembly, stable mutualistic communities form rapidly. Small communities with minor fluctuations in species presence/absence (self-similar limit cycles) are the most common community outcome. The unique application of this Boolean network approach to the study of mutualistic community assembly offers a great opportunity to improve our understanding of these critical communities.

The development of communities has been, and continues to be, a major research topic in ecology. Because of its dynamic nature, its unpredictability, and the timescales involved, most studies of the assembly process are theoretical. Existing models primarily focus on the assembly of food webs. Most of them explore assembly in the context of ecological succession (but see, e.g., refs. 1 and 2), with either finite (e.g., ref. 3) or infinite (e.g., ref. 4) source pools of candidate species. Models of colonizations and extinctions are generally based on Lotka–Volterra predator–prey dynamics (e.g., refs. 3 and 5, but see ref. 6). Many methods have been developed to determine when equilibrium (maximum biodiversity) is attained, including biomass thresholds (e.g., ref. 7), dynamical constraints (e.g., permanence; ref. 3), and resistance to invasion (e.g., ref. 4).

We lack similar models for mutualistic community assembly. Plant–pollinator mutualisms are of particular concern, given the growing documentation of changes in pollinator communities worldwide (8–10). Models of food web assembly have yielded many insights; for example, food web assembly models suggest that communities assembled from the same potential species pool may converge (e.g., ref. 4) or diverge into alternative stable states (e.g., ref. 11). Early composition and conditions, as well as order of species introduction, may affect future composition (12, 13) and thereby affect the resilience of a system to invasion (14). Mutualistic communities may also follow these patterns of food web assembly; however, given the nature of mutualistic interactions, key differences will likely come to light. For instance, the smallest possible plant–pollinator community must include both a plant and a pollinator, in contrast to the smallest food web possible (i.e., one plant).

Much of the difficulty in synthesizing the study of community assembly lies with the challenge of identifying organizing principles that accommodate the wide variation in complex, natural systems. Although food web assembly models can be based on Lotka–Volterra predator–prey population dynamics, we cannot easily model the mutualistic interdependence of multiple species in a similar fashion. Adapting Lotka–Volterra population models for mutualism yields dynamics that are unrealistic, are destabilizing, and/or feature infinite growth (15–17), unless other interactions (e.g., refs. 17–22) or functional responses (23) are present. A potentially unifying approach to studying community assembly is network theory. Networks are useful representations of complex systems (e.g., refs. 24–26) and have been instrumental in the development of recent community assembly models for food webs (4, 6, 27–30). In this work, we build on the growing literature on mutualistic network models (18, 31–38) by introducing a dynamic Boolean network framework to simulate the process of repeated colonizations and extinctions inherent in the real process of community assembly.

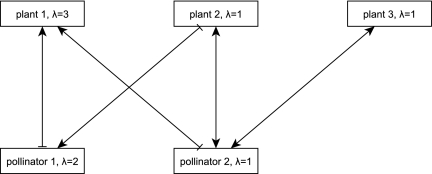
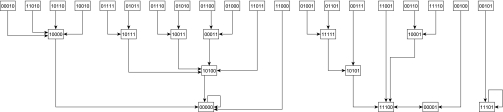
A plant–pollinator community can be represented by a bipartite network, with the plant and pollinator species as nodes and their interactions as edges (39–41). We show such an interaction network for a highly simplified community in Fig. 1. Unlike most interactions in a food web, interactions in a mutualistic community are bidirectional (18, 42, 43). As plant species colonize or become extinct from the patch, pollinator species that are dependent upon them may also be able to colonize or be driven extinct. However, not all plant–pollinator interactions may result in equal benefit for both partners (e.g., ref. 44). In our model, the benefit from an interaction, and therefore the effect of the interaction on colonization and extinction, depends upon empirically based values of the length of the pollinator's proboscis compared with the plant's nectar depth. As a new ecological community is colonized by species from all of the surrounding communities, we simulate assembly via (a) repeated invasion attempts from finite, regional source pools and (b) interactions between species that have successfully invaded. Thus, although the amalgamated source pool does not represent a stable community in and of itself, it may give rise to new, stable communities of species. We simplify population dynamics by using a synchronous Boolean network framework (45, 46) and consider the colonization and extinction of a species as changes to its presence and absence. A similar method was previously used to develop a simple model of food web assembly (6) and enables us to map all possible successional trajectories (4, 6) in a separate network that we refer to as the state transition network (Fig. 2). In this framework, stable communities (the “attractors” of the state transition network) are either steady states (SSs), wherein species do not change from present to absent or vice versa as time advances, or limit cycles (LCs), wherein the presence and absence of some species vary cyclically and predictably. In the context of our Boolean framework, LCs indicate that some of the species fluctuate across a population threshold. Realistic LCs (unlike the example depicted in Fig. 2) should possess states that are nearly identical. Such LCs can be considered very similar biologically to SSs.

Fig. 1.

A simple example plant–pollinator interaction network consisting of three plant species and two pollinator species. A pointed (flat) tip indicates a positive (negative) interaction. Pollinator 2 is a generalist in that it successfully pollinates all three plants, although it cannot feed from plant 1, as its proboscis length (λ) is significantly shorter than the nectar depth (λ) of plant 1.

Fig. 2.

The state transition network that corresponds to the interaction network shown in Fig. 1. Dynamically, the presence or absence of a species at time 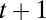is determined by the species that target it and are present at time t. Here, the effect of a negative edge is equal to that of a positive edge, and a species must have more active positive incoming edges than negative at time t to be present at time t + 1 (Materials and Methods). The 32 possible community states are identified with a binary number (present = 1, absent = 0) where the values correspond to (from left to right) plant 1, 2, 3 and pollinator 1, 2. Edges indicate the succession of the system's states in the absence of outside influence. The system admits two steady states, 00000 (presence of no species) and 11101 (absence only of pollinator 1), and one cycle of length 2, 11100 ↔ 00001 (the system oscillates between all plants and no pollinators and only pollinator 2). Note that due to the artificial nature of this example interaction network, this limit cycle is highly unrealistic, and such limit cycles are extremely uncommon in larger, more realistic interaction networks.

We simulated the process of community assembly from ensembles of regional source pools (i.e., interaction networks) with a wide range in size (species richness) and ratio of plant to pollinator species. We first consider the overall topology of the state transition networks in each ensemble and then discuss the properties of their attractors. Although the effect of positive interactions in existing communities has been explored (47), the relative influence of a positive interaction compared with a negative interaction during community assembly is poorly understood, and thus we fixed the weight of a negative interaction and repeated our analysis for a range of positive edge weights (PEWs).

Results

We compare a property across ensembles by reporting mean values whenever doing so does not constitute an oversimplification of the behavior. Varying the plant–pollinator ratio from 1 in our simulations (Materials and Methods) typically had little effect on the resulting behavior, so for simplicity we report on ensembles where the ratio is equal to 1, except where noted. We did not consider interaction networks where the ratio is highly skewed because they are rarely seen in nature (48).

State Transition Network Topology.

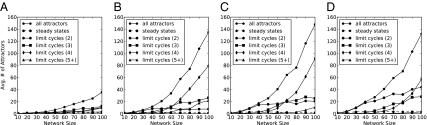
The total number of attractors (distinct community outcomes) grows with the size of the source pool; increasing the PEW beyond 1 results in a significant increase in the rate of this growth (Fig. 3). Nevertheless, because the total number of states grows much more rapidly than the number of attractors, the fraction of states that exist in an attractor becomes vanishingly small as the number of species increases. The number of LCs grows with source pool size, whereas the number of SSs is relatively constant. The dominance of LCs is expected in light of the fact that the probability that an attractor will have no fluctuation in any species decreases as the species pool increases.

Fig. 3.

The average number of attractors for ensembles of 1,000 randomly generated networks with equal numbers of plants and pollinators. A–D correspond to positive edge weights of 1–4, respectively. Most limit cycles consist of two, three, or four states. Their abundance increases with network size, whereas the number of steady states is comparatively constant.

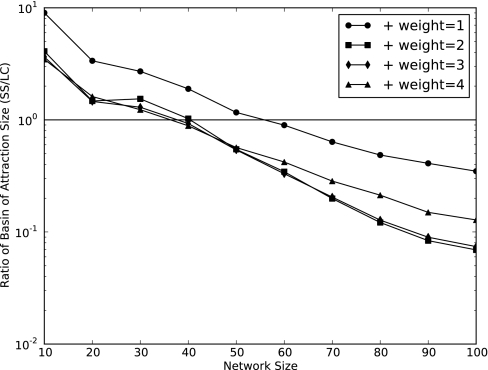
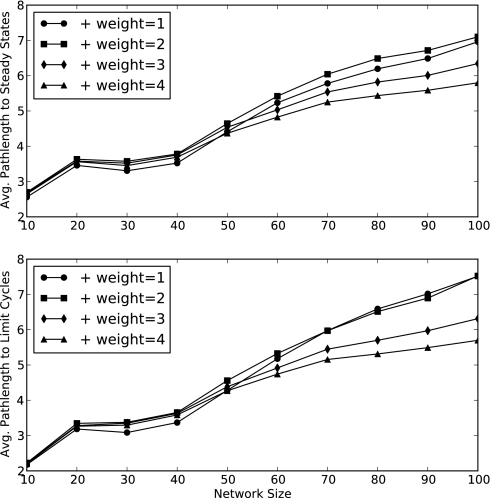
The states that lead to a particular attractor make up its basin of attraction; the size of an attractor's basin of attraction indicates the probability that a randomly selected starting state will eventually lead to that attractor. We find that the net size of the SS and LC basins of attraction scales with their relative abundances (Fig. 4). The existence of multiple basins of attraction indicates that outcomes are conditional on successional history. In addition, the average path length (i.e., the number of time steps required to reach an attractor) grows very slowly compared with the size of the state space (Fig. 5). Larger PEWs lead to more LCs and slightly shorter average path lengths.

Fig. 4.

A randomly chosen starting state will lead to a steady state more often than a limit cycle for small networks, but the converse is true for larger networks. This behavior corresponds to the relative abundance of steady states (limit cycles) for small (large) networks (Fig. 3).

Fig. 5.

The average number of time steps required to reach an attractor grows with network size, albeit at a much slower rate than the total size of the state space [the average path length lies in the range (2, 8), whereas the number of states ranges from 2¹⁰ to 2¹⁰⁰]. If the positive edge weight is larger, the greater abundance of attractors (Fig. 3) results in a wider but shallower distribution of transitional states, which leads to a smaller average path length.

Properties of Attractors.

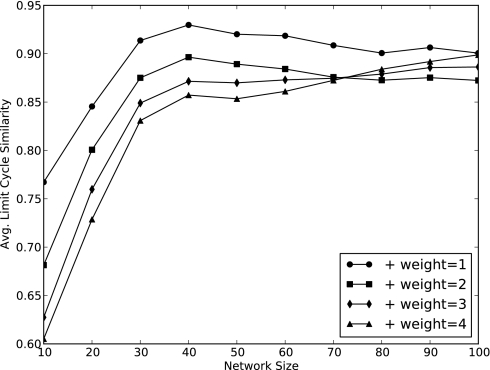
Most LCs contain few states (Fig. 3); moreover, very few species change from present to absent or vice versa within a LC (Fig. 6). For instance, the LC 1101 ↔ 1111 has two states; three of the four species have the same expression level in both states; we refer to this as 75% similar. Thus, despite the fact that the LCs greatly outnumber the SSs in large networks, most behave much like SSs, with only a few species fluctuating about the presence/absence threshold.

Fig. 6.

The average normalized agreement in the present/absent state of each species for the states in a limit cycle. The agreement is determined by computing the average of all pairwise combinations of the states in a limit cycle. We report the average over all observed limit cycles. Limit cycles in small networks tend to have greater fluctuation (although the agreement is still >60%), whereas the agreement in larger networks stabilizes above 85%.

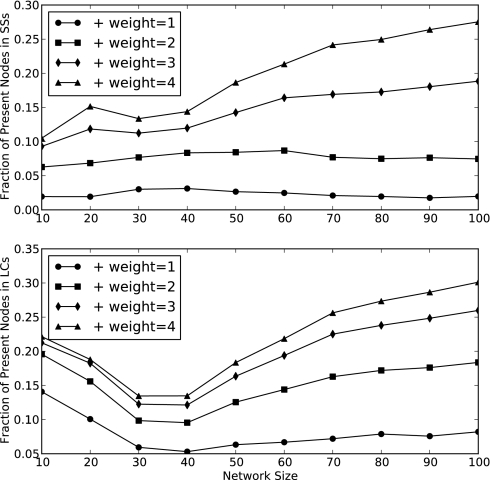
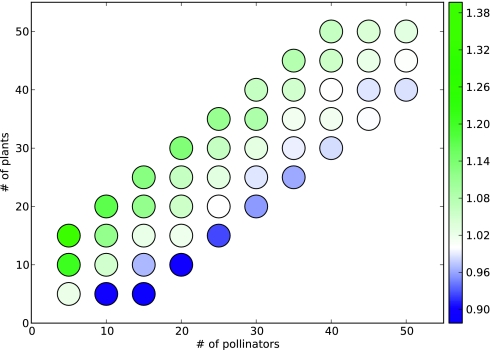
The fraction of species that is present in the attractors is typically low (Fig. 7): The average fraction is <25% for SSs and <30% for LCs. Increasing the PEW raises the percentage: As the relative strength of a negative edge is weakened, the tendency of species to be present is increased, and end-point communities can become larger. The abundance of species is inflated for LCs in small networks due to inherent complexity requirements: Some species are required to fluctuate in a LC, and in a small network, only a few species fluctuating increases the reported value significantly. The abundance of plants and pollinators is roughly equivalent except when the source pool itself contains unequal quantities (Fig. 8).

Fig. 7.

The fraction of species present in steady states (Upper) and limit cycles (Lower). Greater values for larger networks indicate that large source pools are capable of sustaining disproportionately larger communities. We attribute the increased percentage of present nodes in small network limit cycles to minimum complexity requirements for limit cycles.

Fig. 8.

The ratio of present plants to present pollinators in steady states for positive edge weight = 1. The ratio scales with the source pool composition.

Discussion

The complex process by which mutualistic communities are formed is not well understood, despite the significant corpus of literature that exists on the topic (reviewed in refs. 49–53). In this report, we used a network theory approach with a synchronous Boolean framework to model the formation of plant–pollinator communities. Our results give insight into the dynamics of community formation while simultaneously eliminating the need for extensive parameter estimation.

In our model, communities are formed by constant invasion attempts from species in neighboring communities. By assigning interactions according to ecologically realistic properties, we ensure our networks are statistically similar to real networks. A stable community (attractor) is formed when the system goes to (a) a SS, where the composition of species ceases to change as time advances, or (b) a LC, where the composition of species changes periodically and predictably. Whether a species successfully invades in the new community depends upon the species already present; e.g., a plant species will not survive if it cannot be pollinated. Because an interaction may be beneficial for one participating species but detrimental for the other, we consider each as a pair of directed interactions. In this report, we required a significant degree of matching between the plant nectar depth and pollinator proboscis length for both interactions to be considered positive. As a result, only 7.7% of interaction pairs (on average) are mutually beneficial in our simulated networks. Surprisingly, stable community formation is possible despite this relatively low value.

Our simulations indicate that plant–pollinator communities assemble quickly and that the species richness that is attained is relatively small compared with the species richness of the regional source pool. Communities rapidly advance to an attractor even though the majority of the possible community compositions do not exist in an attractor. Relatively few (<30%) species from the source pool exist in the attractors, and LCs are more prolific than SSs for all but the smallest networks. Most LCs are relatively simple in that they contain few (typically less than five) states and the states themselves exhibit little fluctuation (<15% for large networks). LCs with many constituent states that vary wildly in their species compositions are rarely observed. Our results suggest that LCs are a natural extension of complex community dynamics, as has been shown with food web models (54, 55).

Our model suggests that for plant–pollinator communities, the properties of the regional source pool are important for the assembly process, as found by food web models (27, 56, 57). More stable communities are possible when more species are available to colonize from the source pool, but there is a diminishing return because the total number of communities increases more rapidly. The duration of assembly also increases with source pool size, although the process generally takes few steps (in contrast to food web assembly model communities, which typically form over much longer periods). In addition, the ratio of plants to pollinators in the stable communities reflects the ratio present in the source pool. Finally, although species richness in the attractors is low in comparison with that of their source pools, larger stable communities are possible with increased source pool size.

Higher PEWs make it easier for species to invade and survive in the community and lead to an increase in attractor abundance and complexity. It is reasonable to assume that negative interactions are less significant than positive interactions; e.g., a pollinator wasting some time at a plant where it cannot feed does not completely negate feeding elsewhere. Our model results were similar for higher PEWs, compared with when the weights were equal. The consistency in behavior for PEWs >1 suggests that the range of PEWs is less important than the minimum value. Although we use a universal threshold for presence/absence in this study, assigning unique threshold value(s) for each species would be a straightforward extension (e.g., plant A is hardier than plant B and can persist more easily).

As in some food web assembly models (11), we find that both convergence and divergence of successional trajectories can occur, although convergence of mutualistic community trajectories is more likely to result from assembling from small, rather than large source pools. Because of the existence of divergent trajectories (multiple basins of attraction), we confirm the importance of successional history as identified for food webs (6, 12). Interestingly, our model shows mutualistic assembly to be rapid, unlike other network-based community assembly models, which require very long duration to reach the end point (4, 6).

It is possible to use the framework that we described here to explore how interaction complexity develops and how specific properties, such as species specialization, contribute to assembly. Because generalists can in theory support many interactions, we would expect them to be very important in the assembly process. Additionally, there are transient species in every species pool that do not participate in any stable communities. We expect these species to typically be specialists, rather than generalists. However, experience with other types of biological networks indicates that the number of interactions alone is not a perfect indicator of a node's criticality for the system's stability (58–60).

In addition, our framework can be applied to examine issues related to pollinator conservation and management, such as the effect of pollinator loss and the introduction or eradication of invasive species. For example, we can investigate the ability of locally extinct species to recolonize communities and the effect of global extinctions on the stability of communities. Local extinction of a species can be represented in the model by temporarily removing a species from a stable community (attractor) and allowing it to potentially recolonize from the regional species pool. We hypothesize that although a return to the original stable community would be possible, local extinction of species may nevertheless force the community into another stable state. Global extinction, on the other hand, would be expected to be a stronger perturbation, with a higher chance to force the community into a very different stable state and a greater likelihood of catastrophic failure in which all species go extinct. We can similarly explore the effect of introducing novel species to communities.

Many advances in the study of mutualisms have originated from network approaches, especially the understanding of interaction complexity (e.g., refs. 18, 31–35, 40, 61, and 62). As quantitative information becomes more available, more specific network models, such as asynchronous Boolean and continuous/Boolean hybrid models, may offer additional insight (60–65). We anticipate that this unique approach to modeling mutualistic communities will also be applied to a range of other ecological questions.

Materials and Methods

Formation of Plant–Pollinator Interaction Networks.

In the language of network theory, each species is a node in the plant–pollinator interaction network, and each plant–pollinator interaction is an edge between two nodes. However, we use the term “species” rather than “node” and “interaction” rather than “edge” when we discuss the plant–pollinator interaction network, to clearly distinguish it from the state transition network (see next section).

An interaction between plant species A and pollinator species B means that if both are present in an ecosystem, B will attempt to feed on A, and A may or may not be pollinated during the process. The network is bipartite: Direct interactions never exist between two plants or two pollinators. The probability of a plant interacting with k pollinators (and vice versa) is assigned from an exponentially cut off power law, as is commonly observed in real ecosystems, with properties drawn from the literature (56). As in some other studies (31, 33, 34), we assign trait values to the species to characterize the beneficial or detrimental nature of their interactions. When trait values are used to determine whether interactions exist, recapitulation of real network properties is possible only if multiple dimensions of characteristics are considered (31). Here, we choose an alternative route and impose the interactions by following a known degree distribution and use a single characteristic value to categorize interactions into three types.

Ecologically, a plant–pollinator interaction may be (a) beneficial to both species or (b) beneficial to one and detrimental to the other. The categorization depends upon the length of the pollinator's proboscis (λ_po) compared with the plant's nectar depth (λ_pl). The λ-values are drawn from skew normal distributions reported in the literature (37).

The λ-values determine the effect of each interaction on the participating species:

• (i) If λ_po and λ_pl are roughly equal (here defined as having percentage of difference ≤10), the interaction is beneficial to each species: The pollinator can effectively draw sustenance from the plant, and the plant is pollinated in the process.

• (ii) If λ_pl > λ_po, the plant is pollinated but the pollinator fails to draw any sustenance from it. The interaction is beneficial for the plant, but detrimental to the pollinator (because it spends time and energy in an unsuccessful attempt to feed from the plant).

• (iii) If λ_pl < λ_po, the plant is not pollinated, but the pollinator is able to feed on it. The interaction is detrimental for the plant (which loses nectar and time available for other pollinators), but beneficial for the pollinator.

A beneficial (detrimental) interaction is assigned a positive (negative) weight. Interaction asymmetry is a fundamental feature of mutualistic interaction networks, and thus these networks are best viewed in terms of directed interactions, because assigning two weights to a single undirected edge is ambiguous (43). In this framework, an interaction A → B (B → A) corresponds to the influence of A on B (B on A). Each interaction has only one weight, and the directionality is clear.

To completely describe an interaction network, it is sufficient to consider only the species, their interactions, and the effect of those interactions (the interaction weights).

Community Assembly on the State Transition Network.

In this section we describe methods for simulating population dynamics on the interaction networks described above. Our method makes two simplifying assumptions. First, the population of each species may be considered either present or absent (i.e., above or below a threshold value). In Boolean models, the presence or absence of a node (here, a species) is identified as ON or OFF or equivalently with binary values 1 and 0. Second, we may capture salient properties of the network dynamics within the framework of discrete advances in time. These properties are common assumptions that characterize the synchronous Boolean family of discrete dynamic network models (45, 46).

Because each species is categorized as present or absent for each time step, an interaction network with n species has 2ⁿ possible configurations. We refer to each of these configurations as a “state” of the interaction network. Each state corresponds to a unique community composition: the set of species that are present and the interactions between them. The state of the network varies as time steps are taken. Every species that is present (absent) at time t attempts to persist (invade) as the community transitions to time t + 1; if it is successful (unsuccessful), it will be present (absent) at time t + 1.

The state of each species at time t + 1 is determined by the total influence of its active interactions at time t (an interaction is considered active at time t if its source species is present at time t). Quantitatively, for a species to be present at time t + 1 we require the sum of the weights of active incoming interactions to be above a threshold, T, at time t:

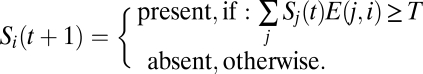In the above, 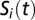is the state (present = ON = 1; absent = OFF = 0) of node i at time t, and 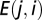is the weight of the interaction from node j to node i (nonexistent interactions have weight 0 by definition). In this report, we use T = 1, which requires the interactions of a species to be a net positive for it to successfully colonize or persist in the system. This is an obvious and common choice for T, although some studies allow for a third outcome when 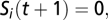wherein the species retains its state from 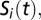(e.g., ref. 58). Our choice to explicitly require a net positive influence to maintain a species’ presence serves to remove any ambiguity in the strength of any observed attractors. Negative interactions are assigned a weight of −1, and the positive interaction weight is systematically varied from 1 to 4. Positive interaction weights of +1 effectively force a node to have more active positive incoming interactions than active negative incoming interactions to exist as present in the network; increasing the value of positive interaction weights allows a node to exist as present with more active negative interactions.

In addition to its computational simplicity, this framework unambiguously determines the state of the network at any time t, given an initial configuration at time t_i. Thus, we are able to map out all possible trajectories of community assembly for any interaction network. This second network consists of the states of the interaction network (as nodes) and their transitions (as edges) and is referred to as the “state transition network.” Every possible community assembly trajectory corresponds to a directed walk on the state transition network. To illustrate the relationship between the interaction network and the state transition network in our assembly model, we show a highly simplified interaction network (source pool of species and their interactions) in Fig. 1 and the corresponding state transition network (all possible trajectories of species abundances) in Fig. 2.

Each node in the state transition network has one outgoing edge (e.g., Fig. 2). Nodes without an incoming edge can be only starting nodes of any directed walk on the state transition network (e.g., top row in Fig. 2). Nodes with an outgoing edge directed to itself (e.g., 11101 → 11101 in Fig. 2) are SSs of the system (i.e., stable communities): If the species reach this configuration, no further absent/present or present/absent transitions will be observed. All other nodes have one incoming edge and do not form a loop with their outgoing edge. These states may exist in a LC (e.g., 11100 ↔ 00001 in Fig. 2) and are otherwise classified as transient.

Simulations.

We describe the population dynamics of an interaction network by determining its state transition network. We investigated networks ranging in size from 10 to 100 species, with both equal and slightly unequal numbers of plants and pollinators. Because the influence of a positive plant–pollinator interaction is poorly understood, we repeated all analyses with the value of a positive edge incremented between 1 and 4. To characterize model features, we generated a series of interaction network ensembles. Each ensemble consists of 1,000 interaction networks with a fixed network size (i.e., the size of the species pool) and composition (i.e., the distribution of plants and pollinators); the degree distribution and characteristic lengths vary between networks and are obtained from the distributions as described above.

Due to the size of the state transition networks (a single 100-species interaction network has 2¹⁰⁰ states), we implemented a Monte Carlo method to probe the state space of the state transition networks (66). Monte Carlo methods are ideally suited for determining an average property (e.g., the number of time steps required to advance to an attractor), but are less effective when determining a cumulative property (e.g., the total number of attractors in a state transition network). For a fixed Monte Carlo sample size, this method results in an increasing probability of undercounting as the state space grows. This method does not change any of our qualitative results, but given a complete characterization of the state transition networks, we expect the curves in Fig. 3 to increase more rapidly than is shown.