Automated sampling assessment for molecular simulations using the effective sample size

Abstract

To quantify the progress in the development of algorithms and forcefields used in molecular simulations, a general method for the assessment of the sampling quality is needed. Statistical mechanics principles suggest the populations of physical states characterize equilibrium sampling in a fundamental way. We therefore develop an approach for analyzing the variances in state populations, which quantifies the degree of sampling in terms of the effective sample size (ESS). The ESS estimates the number of statistically independent configurations contained in a simulated ensemble. The method is applicable to both traditional dynamics simulations as well as more modern (e.g., multi–canonical) approaches. Our procedure is tested in a variety of systems from toy models to atomistic protein simulations. We also introduce a simple automated procedure to obtain approximate physical states from dynamic trajectories: this allows sample–size estimation in systems for which physical states are not known in advance.

1 Introduction

The field of molecular simulations has expanded rapidly in the last two decades and continues to do so with progressively faster computers. Furthermore, significant effort has been devoted to the development of more sophisticated algorithms^1–5 and forcefields^6–10 for use in both physical and biological sciences. To quantify progress – and indeed to be sure progress is occurring – it is critical to assess the efficiency of the algorithms. Moreover, if the quality of sampling is unknown, we cannot expect to appreciate fully the predictions of molecular mechanics forcefields: after all, statistical ensembles, whether equilibrium or dynamical, are the essential output of forcefields. These issues demand a gauge to assess the quality of the generated ensembles¹¹ – one which is automated, non–subjective, and applicable regardless of the method used to generate the ensembles.

Ensembles are of fundamental importance in the statistical mechanical description of physical systems: beyond the description of fluctuations intrinsic to the ensembles, all thermodynamic properties are obtained from them.¹² The quality of simulated ensembles is governed by the number of uncorrelated samples present in the ensemble. Due to significant correlations between successive frames in, say, a dynamics trajectory, the number of uncorrelated samples cannot be directly gauged from the total number of frames. Rather, the number of statistically independent configurations in the ensemble (or the effective sample size, ESS) is required.^13–16 This effective sample size has remained difficult to assess for reasons described below. In this work, we present a straightforward method to determine the ESS of an ensemble – regardless of the method used to generate the ensemble – by quantifying variances in populations of physical states.

A conventional view of sample size based on a dynamical simulation is given by the following equation:

$$\mathrm{ESS}=\frac{t_{\mathrm{sim}}}{t_{\mathrm{corr}}\left[f\right]}$$ (1)

where t_sim is the simulation time, and t_corr[f] is the correlation time¹⁶ for the observable f, which is presumed to relax most slowly. However, the estimation of the correlation time is data intensive and potentially very sensitive to noise in the tail of the correlation function.¹⁷ Other approaches for assessing correlations have, therefore, been proposed. For example, Mountain and Thirumalai^18,19 introduced the “ergodic measure”, which quantifies the time required for the observable to appear ergodic. Flyvbjerg and Petersen¹⁷ developed a block averaging method which can be adapted to yield a correlation time and ESS.²⁰

The key challenge in applying Eq. (1), however, is the choice of an observable f which consistently embodies the slowest motions across the incredible variety of molecular systems. Indeed, it is well appreciated that different observables exhibit different correlation times. (e.g., Ref. 21) For example, in a typical molecule, bond lengths become decorrelated faster than dihedral angles. Nevertheless, apparently fast observable rarely are fully decoupled from the rest of the system: slower motions ultimately couple to the fast motions and influence their distributions in typical cases.²¹ On the whole, there is significant ambiguity in the use of a hand–picked observable to estimate “the” correlation time – not to mention, subjectivity. Moreover, the ultimate goal of simulation, arguably, is not to compute a particular ensemble average but to generate a truly representative ensemble of configurations, from which any observable can be averaged.

Several years ago, Lyman and Zuckerman proposed that the configuration–space distribution itself could be used as a fundamental observable.²² In particular, it was pointed out that if configuration space is divided into different regions or bins, then the resulting “structural histogram” of bin populations could be a critical tool in assessing sampling. The idea was subsequently used to quantify sample size in at least two studies: Lyman and Zuckerman developed a scheme to quantify ESS for trajectories with purely sequential correlations based on variances in the bins of the structural histogram;¹⁶ Grossfield and coworkers suggested a bootstrapping approach for estimating ESS based on structural histograms.¹⁵ The present work expands on ideas from these studies. There has been related work for sequentially correlated Markov chains.^23,24

This study extends the earlier structural–histogram approaches by focusing on physical or metastable states. Qualitatively, a physical state can be defined as a region of configuration space for which the internal timescales are much shorter than those for transitions between different states.²⁵ The populations of physical states seem an intuitive choice for quantifying sampling quality, since they reflect slow timescales by construction. Indeed, the state populations along with state definitions (addressed in Sec. 2.1) can be said to embody the equilibrium ensemble. This type of argument can be made semi–quantitative by noting that any ensemble average 〈f〉 can be expressed in terms of state populations p_i and state-specific averages 〈f〉_i for state i, because 〈f〉 = Σ_ip_i〈f〉_i. Thus, the goal of sampling can be described as obtaining both (i) state populations and (ii) well-sampled ensembles within each state.

Statistical mechanics principles strongly suggest, moreover, that state populations should be viewed as the most critical slow observables. To see why, consider states i and j defined by regions of configuration space V_i and V_j. The ratio of state populations is given by the ratio of state partition functions:

$$\frac{p_i}{p_j}=\frac{Z_i}{Z_j}=\frac{{\int }_{V_i}d\mathbf{r}\exp (-U\left(\mathbf{r}\right)∕k_{\mathrm{B}}T)}{{\int }_{V_j}d\mathbf{r}\exp (-U\left(\mathbf{r}\right)∕k_{\mathrm{B}}T)}$$ (2)

where Z_i is the partition function for state i, U is the potential energy of the system, T is the temperature, and r represents all configuration–space coordinates. Eq. (4) indicates that state populations cannot be determined without good sampling within each state. In other words, it would seem impossible for an algorithm (which is correct for arbitrary systems) to predict state populations without having already sampled correctly within states (see Fig. 1). For this reason, the state populations can be considered the fundamental set of slow observables – a physically motivated choice of structural histogram. We will use variances in state populations to estimate ESS, an approach which applies to both dynamic and non-dynamic (e.g., exchange) simulations.

Figure 1.

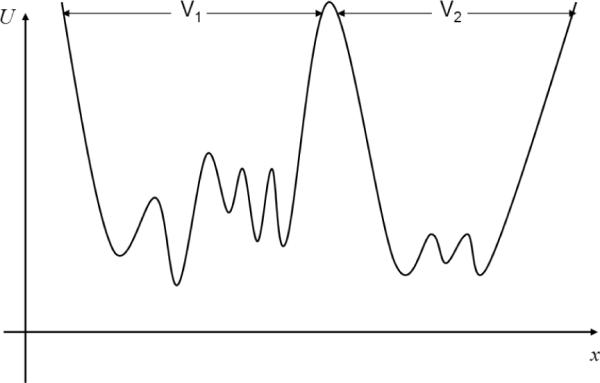
A schematic two-state potential energy landscape from Eq. (4). The states are defined by the “volumes” V₁ and V₂. The distributions of configurations within each states help to determine the overall ratio of state populations in Eq. (4).

Accordingly, an important prerequisite for the estimation of ESS is the determination of physical states. In this work, we use a particularly simple method for the approximation of physical states that uses information present in a dynamics trajectory regarding the transition rates between different regions. Regions showing high transition rates with each other belong in the same physical state. Further, this procedure also highlights the hierarchical nature of the energy landscape. Our state approximation scheme is based on ideas of Chodera et al.²⁵ who developed approximated physical states by determining a division of the total configuration space that maximizes the self transition probabilities (i.e., the divisions represent metastable states.) See also Ref. 26. Our state–approximation method can also be used with short dynamics trajectories initiated from configurations obtained from non–dynamic simulations.

We emphasize, nevertheless, that our procedure for ESS estimation can be used with states discovered by different means.

The manuscript is organized as follows. First, we describe in detail the procedure we use to estimate the effective sample size. Then, we present results for several models with different levels of complexity – a two–state toy model, butane, calmodulin, di–leucine, and Met–enkaphalin. Our ESS results are compared with the previous “decorrelation time” approach.²⁷ We also analyzed multi-μsec atomistic simulations for the membrane protein rhodopsin.¹⁵ We then discuss the practical aspects of the procedure and present conclusions. Further, in the Appendix, we describe the simple, automated procedure used to determine approximate physical states.

2 Methods and systems

We have argued above that the populations of physical states are fundamental observables for assaying the equilibrium ensemble. We therefore propose that the statistical quality of an equilibrium ensemble be quantified using variances in state populations. As usual, the variances will decrease with better sampling. Importantly, however, simple binomial statistics permit a fairly precise quantification of the ESS - i.e., the number of statistically independent configurations to which an ensemble is equivalent - regardless of the number of configurations in the original ensemble. Below, we will address the issues of computing variances from dynamical and non–dynamical simulations, as well as methods for approximating physical states.

The key technical idea in connecting the variance in a state's population to the ESS follows work presented in Ref. 16: an analytic estimate for the variance can be computed based on a known number of independent samples. If one “turns around” this idea, given the observed variance, an estimate for the number of independent samples can be immediately obtained. In particular, given a region j of configuration space with fractional population p_j, the variance in p_j based on N independent samples is ${\sigma }_j^2=p_j(1-p_j)∕N$. In practice, this variance is estimated from repeated independent simulations, each yielding a value for p_j. The ESS based on populations recorded for region j can therefore be estimated via

$$N_j^{\mathrm{eff}}=\frac{{\stackrel{‒}{p}}_j(1-{\stackrel{‒}{p}}_j)}{{\sigma }_j^2}$$ (3)

where ${\stackrel{‒}{p}}_j$ is the observed average population in region j.

Both ${\stackrel{‒}{p}}_j$ and ${\sigma }_j^2$ can be computed from N_obs repeated simulations:

$${\stackrel{‒}{p}}_j=\frac{1}{N_{\mathrm{obs}}}\sum _i^{N_{\mathrm{obs}}}{p}_j^{\left(i\right)},{\sigma }_j^2=\frac{1}{N_{\mathrm{obs}}}\sum _i^{N_{\mathrm{obs}}}{(p_j^{\left(i\right)}-{\stackrel{‒}{p}}_j)}^2.$$ (4)

Two important points are implicit in these estimators (both of which are discussed further, below). First, our analysis assumes reasonable ${\stackrel{‒}{p}}_j$ values have been obtained in the simulations to be analyzed – although a low value of N^eff can suggest additional sampling is advisable. Second, our effective sample size will have the lower bound N^eff > N_obs, so in practice estimates such that N^eff > N_obs suggest poor sampling.

As noted in Ref. 16, Eq. (3) is actually a limiting form appropriate for large N. Although it is straightforward to include corrections accounting for the fact that only N − 1 observations are independent (because ${\stackrel{‒}{p}}_j$ is the observed average among the p_j values used in estimating the variance), the effect is unimportant compared to the intrinsic fluctuations in N^eff.

Each region or state will yield its own estimate for the ESS via Eq. (3), but we are interested in the smallest ESS reflecting the slowest timescales. As described below, in this report, we use a hierarchical decomposition of configuration space which leads to only two states at the top level by construction. In turn, these two states yield identical ESS values by Eq. (3). Alternatively, if a full hierarchy is not constructed, one can simply select the lowest ESS value as the best quantification of sampling, reflecting the worst bottleneck encountered; in such cases, it may be of interest to set a minimum ${\stackrel{‒}{p}}_j$ value for the governing state (e.g., 0.01–0.05) to avoid the ESS being dominated by a relatively minor state.

We noted that, based on Eq. (3), the minimal value which can be determined is one, and generally $N_j^{\mathrm{eff}}>1$. Thus, a value of O(1) is strongly suggestive of inadequate sampling.

The current approach, in essence, uses a block-averaging strategy^17? and can be contrasted with the previous work of Lyman and Zuckerman for dynamical trajectories.¹⁶ The present work computes block-style variances of quantities (the state populations) whose statistical behavior is straightforward to analyze - e.g., via eq 3. The earlier approach, in contrast, directly exploited sequential correlations to do “hypothesis testing”: Do the snapshots of a trajectory separated by a fixed time interval behave as though independent?¹⁶ The earlier work also used population variances and an analog of eq 3; however, physical states were not required because individual configurations were used, rather than block averages as in the present work - which tend to convolute timescales (Sections 3.5 and 4.3).

2.1 Hierarchical approximation of physical states

The approximation of physical states has previously been addressed in some detail, particularly in the context of developing Markov models.²⁵ Below, and in the Appendix, we describe a simpler approach used in this work. As we elaborate in the Discussion, it appears that our ESS analysis does not require a particularly precise specification of physical states. Because our prescription is to find the slowest timescale (i.e., smallest ESS) among the many which may be present, and because our physical states are reasonable, the approach works reliably. On the other hand, although Eq. (3) can be applied to an arbitrary region in principle, it can “get fooled” into over–estimating the ESS if only a small part of a state is considered: see Sec. 4 for details.

We emphasize that our ESS analysis described above is distinct from the states analyzed, and other reasonable state decomposition procedures can be used.

The Appendix details the hierarchical state approximation scheme adopted here, which is closely related to the work of Chodera et al.²⁵ In brief, given the best data available, we first divide configuration space into small regions or bins (following Refs. 16 and ²⁸), which do not necessarily correspond to energy basins. Based on one or more dynamical trajectories (perhaps those being analyzed for ESS), we estimate rates among each pair of regions. Starting from the fastest pairwise rates, the bins are combined into state–like aggregated regions. By construction, all pairwise rates within each aggregate are faster than rates between aggregates. The process is continued to construct a full hierarchy until all aggregates are combined (see Figures A2 and A3 in the Appendix). The approximate states used to estimate the ESS are based on the top (i.e., two–state) level of the hierarchy, which reflects the slowest timescales as desired.

Our rate estimation procedure is well–suited to our purpose of ESS estimation. First, it is fairly simple and typically requires a small fraction of the computational cost of the simulation being analyzed. More importantly, as noted in the Discussion, it performs as well as a somewhat more complex approach we implemented (data not shown). Although our procedure (and others²⁵) requires dynamical trajectories to estimate inter–bin transition rates, this does not mean prohibitively expensive dynamics simulations must be performed, as we now discuss.

2.1.1 State approximation from non–continuous dynamical trajectories

Because our state approximation scheme depends on continuous dynamical trajectories, the question arises as to how states can be obtained when sampling has been performed using a non–dynamical method such as replica exchange.^3,29,30 Although exchange simulations use continuous trajectories which contain the necessary information for estimating rates among local regions,³¹ other sampling methods may not employ dynamical trajectories at all (e.g., see Ref. 28).

In fact, states can be approximated based on a set of short dynamics trajectories run after a possibly costly non–dynamical trajectory. In particular, a set of M trajectories (we use M = 20 below) can be initiated from random configurations selected from the non–dynamical simulation. These short trajectories need only be long enough to permit exploration within states. There is no need for transitions between states. The only modification to the state approximation scheme described previously is that it may not be possible to iterate the combination procedure until all states are combined. Rather, the process will terminate after regions with measurable transition rates are combined. A set of approximate states will remain for which no inter–state transitions have been recorded. For each of these remaining states, an ESS estimate can be obtained via Eq. (3). Because of our interest in the slowest timescales, the overall ESS will be taken as the minimum among the various state values.

The scheme just described is tested below, and compared with the use of longer trajectories for state approximation.

We, again, emphasize that short dynamic trajectories are only used to approximate states, whereas ESS is, subsequently, computed from the much longer non–dynamic trajectories. The non-dynamic trajectories are presumed to sample all the relevant states.

2.2 A caveat: Self–consistent but not absolute ESS

Without prior knowledge or assumptions about a landscape, it would appear impossible to know whether every important state has been visited in a given simulation. This is not a limitation of our analysis per se, but of any attempt to estimate ESS based on simulation data. Nevertheless, it is important to make this caveat clear.

Therefore, the goal of the present analysis is not to assess the coverage of configuration space, but to self–consistently assess sampling quality given the states visited in the simulation. In other words, we answer, “What is the statistical quality of the sampling based on the configurational states visited in a given set of simulations?” Our ESS estimation can therefore be viewed as an upper bound to the true ESS based on the full configuration space. ESS estimation, nevertheless, is essential for assessing efficiency in algorithms and precisely specifying the predictions of modern forcefields.

On the other hand, so long as a state has been visited in a simulation, it can greatly affect the sample size. For instance, if a state has been visited only once, the estimate of its population variance will be large and lead (correctly) to a small ESS.

2.3 Estimating variances in state populations

The heart of our approach is to estimate ESS based on variances in state populations using Eq. (3). Clearly, then, without reliable variance estimates, we cannot expect ESS values to be reliable.

For dynamical simulations - i.e., simulations yielding trajectories in which correlations are purely sequential, such as MD and “ordinary” (Markov chain) MC - there is more than one way to estimate a variance suitable for ESS calculation via Eq. (3). Ideally, a number of independent dynamics runs would be started from significantly different initial conditions. Nevertheless, multiple simulations started from the same configuration will also reveal the variance associated with the duration of each run: for instance, if only one simulation makes a transition to an alternative basin, a large variance and small ESS estimate will result, appropriately. It is important to note that the ESS thus calculated is characteristic of one of the simulation trajectories, so that M independent trajectories imply an ESS which is M times as large. This discussion also indicates that a single long trajectory can be divided into M segments (“blocks”) which can be used for variance estimation.

More complex simulation methods, such as replica exchange,^3,29,30 may require multiple independent runs for careful variance estimation. To see why in the case of replica exchange, note that continuous trajectories will traverse a ladder of different “conditions” (e.g., temperatures or forcefields), but often only a single condition is of interest. By the construction of such an algorithm, configurations appearing at one time at the condition of interest may be strongly correlated with configurations occurring later on - but not with configurations in between, when a different trajectory may have occupied the condition of interest. In sharp contrast to dynamics simulation, correlations may be non–sequential. This absolutely precludes estimating the variance by simply cutting up the equilibrium ensemble into blocks or segments. Such a variance may not reflect sampling quality, and could misleadingly reflect only diffusivity among ladder levels.²¹ We note that subtleties in estimating uncertainties in replica exchange simulations have been noted previously.^32–34 Further, it may be possible to use the independent continuous trajectories from one replica exchange run to provide ${\stackrel{‒}{p}}_j$ values in eq 4; see also Ref 16.

For a non-dynamical simulation method, the only sure way to estimate a variance which reflects the underlying ESS is by multiple independent runs. The extra cost could be modest if each run is sufficiently short and such runs would, of course, enhance sampling.–i.e., they would “pay for themselves.” In any case, the cost seems worthwhile when it permits careful quantification of the results.

2.4 Systems studied

We study several systems using the ESS procedure described above to establish correctness and robustness of the procedure. The systems range from toy models and small molecules to coarse-grained and atomistic proteins.

Toy models with known sample size

First, we study simple toy models for which the correct sample size is known in advance, to establish the correctness of the procedure. The toy system has n idealized “states” that correspond to pre-set values of independently drawn random numbers. The sample size in such toy models is simply the number of random numbers drawn by construction. We use two such toy models: n = 2 (and both states with equal population), and n = 5 (with state probabilities 0.1, 0.15, 0.2, 0.25, 0.3). An application of Eq. (3) to the two–state system yields, by construction, the same sample size in both the states. On the other hand, the effective sample sizes obtained may, in general, be different when the number of states is greater than 2. Thus, the five–state toy model is useful in determining the consistency in the sample sizes obtained in the different states.

The sampling in these toy models is nondynamic and uncorrelated. Thus, the use of such models illustrate the applicability of the effective sample size determined by Eq. (3) to nondynamic sampling. Results for the toy models and all other systems are given in Sec. 3.

Systems with a priori known physical states

In contrast to independent sampling in the toy models, dynamics-based sampling in molecular systems is not typically independent and the sample size is not known in advance. Nevertheless, a knowledge of physical states allows for an independent estimate of the ESS by computing the variances in the known physical states and comparing with the estimate obtained via approximate hierarchical states. Thus, the robustness of the procedure described in Sec. 2 with regard to definitions of physical states can be checked. We study two such systems with a priori known states: butane and calmodulin. A second, independent ESS estimate for these systems is derived from a time correlation analysis.¹⁸

We study a standard all–atom butane model using the OPLSAA forcefield.⁷ This system has three well–known states: trans, gauche+, and gauche−. The 1 μsec dynamical trajectory is generated at 298K using Langevin dynamics (as implemented in Tinker v. 4.2.2) in vacuum with friction constant 91/ps.

We also study the N-terminal domain of calmodulin, which has the two known physical states: the apo form (PDB id – 1CFD) and the holo form (PDB id – 1CLL). A long trajectory (5.5×10⁷ MC sweeps) was generated by using “dynamic” Monte Carlo (small, single-atom moves only) as previously described.³⁵ To permit transitions, we use a simple alpha–carbon model with a double–Gō potential to stabilize the two physical states. Full details of this model are given elsewhere.³⁵

Systems with unknown physical states

For most biomolecular systems, the physical states are not known in advance. For this reason, we test our method on several such systems, starting with two peptides: leucine dipeptide (acetaldehyde–(leucine)₂–n–methylamide) and Met–enkaphalin (${\mathrm{NH}}_3^{+}-\mathrm{Tyr}-{\left[\mathrm{Gly}\right]}_2-\mathrm{Phe}-\mathrm{Met}-{\mathrm{COO}}^{-}$). We use the Charmm27 forcefield for leucine dipeptide and OPLSAA forcefield for Met-enkaphalin and generate trajectories using over-damped Langevin dynamics (in Tinker v 4.2.2) at 298 K with a friction constant of 5/ps for both. For leucine dipeptide we use a uniform dielectric of 60, and the GB/SA solvation for Met-enkaphalin.^36,37 For each system, a 1 μs simulation is performed with frames stored every 1 ps for Met-enkaphalin and every 10 ps for leucine dipeptide.

We then study a much more complex system – rhodopsin.^15,38 We analyze 26 independent 100 ns molecular dynamics simulations of rhodopsin in a membrane containing 50 1-stearoyl-2-docosahexaenoyl-phosphatidylethanolamine (SDPE) molecules, 49 1-stearoyl-2-docosahexaenoyl-phosphatidylcholine (SDPC) molecules, and 24 cholesterols. There is an explicit water environment embedded in a periodic box. The all-atom CHARMM27 force field was used. We analyze only protein coordinates under the assumption that these will include the slowest timescales.

2.5 Independent ESS estimates

We would like to compare ESS estimates obtained from our new procedure to independent “reference” results. Independent ESS estimates can be obtained in several ways, depending on the system and simulation method to be analyzed.

For uncorrelated sampling in the toy models, the ESS is known in advance: it is simply the number of samples used to obtain the state variance. In this case, we merely check that knowledge of the variances along is sufficient to recover the number of samples.

In some molecular systems, such as butane and calmodulin in this study, physical states are known in advance. Independent variance (and hence ESS) estimates are then obtained using the “exact states”. These are compared to ESS estimates obtained fully automatically based on states approximated from trajectories. In systems with a small number of states, additional ESS estimates can be approximately obtained simply by counting transitions.

Whether or not physical states are known, if a dynamics (or Markov Chain MC) trajectory is analyzed, independent ESS estimates can be obtained using our previously developed structural decorrelation time analysis¹⁶ and Eq.1. This approach uses a t_corr reflecting the time to sample the whole distribution. In work with model one-dimensional systems (data not shown), we have found that the ESS is estimated within a factor of 2 using the method of Ref. 16; therefore ESS estimates based on decorrelation time are shown as ranges.

3 Results

3.1 Non–dynamic toy systems

First, we establish the formal correctness of our method for estimating N^eff. For this purpose, we study the toy models described in Sec. 2.3 for which the sample size is known in advance. For each toy model, we draw N independent samples and estimate the sample size using the procedure described in Sec. 2.

To determine whether an accurate estimate of N^eff (≡ N) is obtained, we also compute both the mean value and standard deviation of N^eff based on many repeats. As suggested by Eq. (3), the N^eff variation depends on variances of both the mean population and the population variance (these quantities are equal across the states for a two–state system). Further, care must be taken to account for the nonlinear dependence of N^eff on the state variance in Eq. (3).

For the two–state model, with N = 2000, we obtain a mean value of 〈N^eff〉 = 2004, with a standard deviation of 57.4. Similarly, for N = 4000, we obtain a mean 〈N^eff〉 = 4041 with a standard deviation 117.6. This confirms our basic premise of using Eq. (3) based on the binomial distribution. The intrinsic fluctuations in the estimates, about 3% in both cases, presumably do not decrease with increasing N due to the non–linearity of Eq. (3).

In the five–state model estimates of the sample sizes in each state are different (see Sec. 2), and such a model is a further step in confirming Eq.3 in a mere heterogeneous case. Using N = 2000, and states with fractional populations 0.1, 0.15, 0.2, 0.25, and 0.3, the mean sample sizes (standard deviations) are obtained as 2007 (70), 1998 (57), 1974 (35), 1966 (79), and 1986 (63), respectively. There is a good agreement across the states, as well as with the correct sample size N = 2000.

3.2 Systems with a priori known physical states

We turn next to molecular systems with known physical states for which long dynamics trajectories are available. This is essentially the simplest case for a molecular system, because two independent estimates of ESS can be obtained, as described below. Comparison of our blind, automated procedure to these independent estimates further establishes the correctness and robustness of the procedure. Additionally, because our automated state-construction procedure is somewhat stochastic (see Appendix), we repeat the procedure to understand the fluctuations in our ESS estimates.

We obtained multiple estimates of ESS as described above using a single long trajectory for each of the two systems with known physical states – butane and calmodulin. Table 1 shows results for N^eff for the two systems, including three different estimates of N^eff from Eq. (3) based on different sets of approximate states. Comparison is also made to the use of Eq. (3) based on known physical states, and to the range of effective sample sizes obtained using time correlation analysis. For both butane and calmodulin, the procedure is very “robust” in estimating N^eff, as different binning procedures give similar estimates. These estimates also agree with the range of sample sizes suggested by the correlation time analysis and with counts of transitions. For butane, the total number of transitions among the three state is about 6000. For calmodulin, the total number of transitions is 80. These results also agree with the estimates in Table 1.

Table 1.

Automated and independent effective sample sizes for butane and calmodulin. ESS estimates obtained from Eq. (3) using three different sets of approximate physical sets are shown in Columns 2–4. Also shown are ESS estimates from Eq.3 and the known physical states (column 5), the structural decorrelation time analysis¹⁶ (column 6) and from counting the number of transitions (column 7).

	approx. states			known states	time correlation	counting
	1	2	3
butane	6064	6236	6200	5865	5000–10000	6000
calmodulin	93	90	92	91	80–160	80

3.3 Systems with unknown physical states

Exact physical states are not known in advance for most biomolecular systems. Thus, we test the approach described in Sec. 2 to determine ESS in three such systems - dileucine, Met–enkaphalin and rhodopsin. Because the physical states are not well defined, we can only obtain independent estimates from the time correlation analysis. A single 1 μsec trajectory is analyzed for each of the peptide, whereas 26 trajectories of 100 nsec each are studied for rhodopsin.

Table 2 shows repeated ESS estimates using our approximate states with Eq.3 as well as the time–correlation analysis for both dileucine and Met–enkaphalin. There is good agreement between our variance-based estimates and those from time correlation analysis for both systems.

Table 2.

Effective sample sizes for di–leucine and Met–enkaphalin. Eq. (3) is used on the final two states in the hierarchical picture obtained by three different repetitions of the binning procedure (Columns 2–4), and the ESS is independently estimated from the structural decorrelation time correlation (Column 5).

	approx. states			time correlation
	1	2	3
di–leucine	1982	1878	1904	1100–2200
Met–enkaphalin	416	362	365	250–500

We proceed to analyze the sample size of 26 rhodopsin trajectories based on our approximate states with Eq.3. Our analysis gives three physical states, with sample sizes 1.93, 1.99, 2.73, respectively, per 100 nsec trajectory. The three states are never further connected in full hierarchy, since transitions are not observed between some bin pairs. The three N^eff estimates, nevertheless, are quite similar and all are O(1). However, Eq. (3) always yields a value ≥ 1, indicating that the 100 nsec rhodopsin values are effectively minimal and reflect inadequate sampling. In Ref. 15, Grossfield and coworkers examined the same trajectories with principal components and cluster populations. They concluded, similarly, that rhodopsin's fluctuations are not well described by 100 ns of dynamics, and that the sampling is not fully converged even for individual loops.

3.4 Application to discontinuous trajectories

Although sample size estimation using Eq. (3) is applicable to non–dynamical simulation methods, the underlying physical states, approximated from transition rates between regions of configuration space: see Appendix, may not be easy to calculate from non–dynamical trajectories. We therefore investigate the feasibility of running short dynamics trajectories starting from configurations previously obtained from non–dynamic simulations and then estimating ESS based on states from the short dynamics simulations.

For this purpose, we ran a series of 20 short Langevin simulations for both dileucine and Met-enkaphalin, starting from configurations obtained in the original long trajectories which serve as proxies for well-sampled ensembles by an arbitrary method. For both systems, we approximated states as described in Sec. 2.1, and estimated the ESS as $\min \left\{N_j^{\mathrm{eff}}\right\}$. For simulation segments as short as 200 psec we could obtain the correct ESS within a factor of 2 (di-leucine) or 3 (Met-enkaphalin), whereas the longest timescales (i.e., decorrelation time) in these systems exceed a nsec.¹⁶ However, a precise estimate of the ESS required 1–3 nsec segments.

We note that Chodera et al²⁵ also used discontinuous trajectories in their state approximation scheme. As noted in the Appendix, our scheme is a simplified version of theirs.

3.5 Spurious results from un–physical states

Thus far, we have focused on using physical states with Eq.3, based on the arguments presented in the Introduction. In principle, however, Eq. (3) can be applied to an arbitrary region. To confirm the need for using states, here we investigate what happens when only part of a state is used. We will see that spurious ESS estimates results.

The system we examine is butane. We divide the configuration space into 10 “bins” using Voronoi cells,³⁹ and perform no combination into physical states. We estimate the effective sample size using Eq.3 for each bin. We examine a 300 nsec trajectory, for which N^eff ≃ 2000.

Table 3 shows estimates of ESS obtained for each of the 10 arbitrary bins, which are not approximate states. The estimates shows a dramatic bin dependence.

Table 3.

Spurious ESS estimates when physical states are not used. Butane sample size is estimated in each of 10 arbitrary regions of configuration space. The actual sample size is ~6000, based on a 1 μs Langevin dynamics trajectory.

Bin number	ESS
1	12567
2	61380
3	82080
4	91820
5	292640
6	71180
7	240200
8	5600
9	162720
10	310260

The problem with using bins rather than states results for simulations which use dynamics. In fact, arbitrary bins can be used in Eq.3 if sampling is fully uncorrelated; we verified this using a fixed number of butane configurations which were essentially uncorrelated. However, when dynamics are present, the variance of one bin is a convolution of state variances and fast processes. We discuss this in more details below.

4 Discussion

4.1 Is the ESS measure too strict?

It certainly can be argued that many observables of interest will “converge” to satisfactory accuracy and precision even with small sample sizes. However, the ESS measure should be valuable in two important regards: (i) as an objective measure of sampling quality that can be applied to any method to enable unbiased comparison, and (ii) as a measure of the quality of ensemble generated, which can be expected to embody structural details of interest in biomolecular simulation.

4.2 Diagnosing poor sampling

A key outstanding issue is how to know when sampling is inadequate, at least in the self-consistent sense of Sec. 2.2. The “diagnosis” of poor sampling is intimately connected with the idea of estimating ESS by subdiving a dynamics trajectory into smaller, equal segments.

First, consider subdividing a dynamics trajectory into smaller, equal segments to estimate the population mean and variances. If the trajectory is very long compared to all corelation times, no serious problems will arise. If the sample size estimate for each of these segments is O(1), however then the method does not reliably give the estimate of the sample size of the total trajectory, and likely overestimates it. For example, if the correct total number of independent configurations in the full trajectory is 10, and we subdivide it into 20 equal segments, then each of the segment will give a sample size of 1, which is the minimum number possible using Eq. 3. This leads to an overestimate of the sample size. But the problem is easily diagnosed by ESS ~ 1 for each segment. If division into fewer segments still leads to ESS ~ 1, sampling is likely inadequate.

It is of interest to consider a special case of poor sampling, where trajectories started from different initial conditions visit mutually exclusive states – i.e., have no overlap. In this case, the ${\stackrel{‒}{p}}_j$ values in eq 3 will not be know correctly. Nevertheless, because some $p_j^{\left(t\right)}$ values in eq 4 will be zero, the analysis will correctly “sense” a maximal variance with ESS~O(1) for each simulation. In other words, poor sampling can still be diagnosed.

4.3 The inadequacy of arbitrary regions for ESS estimation

It is somewhat difficult to understand the reason for spurious results for ESS obtained using a correlated dynamics trajectory from bins that are a small part of a physical state as in Sec. 3.5. A two-state thought experiment is instructive. Consider a system with two basins, A and B, separated by a barrier. Imagine that we divide the full space into many bins, of which the seventh is a small part of state A and has the (true) probability of p₇. In ideal uncorrelated sampling, the observed outcomes should be in the bin with probability p₇ and out of the bin with probability 1-p₇. However, in dynamical sampling, if the system is trapped in state A (with a fractional population p_A) for the observation time, the observed probability in the bin turns out to be p₇/p_A instead of p₇. Conversely, if a trajectory segment is trapped in state B, the observed population of bin 7 is zero. The variance of this observed distribution when p₇ ⪡ p_A is much lower than the binomial case; physically, the fast timescales within state A act to “smooth out” population variation within a small part of the state. The estimated ESS obtained using a correlated (i.e.,dynamical) trajectory thus will typically appear to be larger based on such a bin. This is seen in Table 3, except for one bin which corresponds, roughly, to a physical state.

5 Conclusions

We have developed a new method to assess the effective sample size, which quantifies the degree of sampling in molecular simulations. Our approach is based on the fundamental role of physical states and hence of variances in their populations. A major feature of the method is that it is applicable both to dynamical and non–dynamical simulation methods, and gives a tool to compare sampling and efficiencies of different molecular simulation algorithms. Our previous approach was applicable only to dynamical (sequentially correlated) molecular simulation algorithms.¹⁶ Another feature of the new procedure is that it is applicable to discontinuous trajectories as well. We also demonstrated that our procedure is fairly insensitive to the precise definitions of physical states – a fact that is expected to be of importance for systems for which actual physical states are not known in advance. We applied the approach to systems ranging from discrete toy models to an all-atom treatment of rhodopsin.

To supplement the estimation of the effective sample size, we also developed a simple procedure for the automated determination of physical states, which is based on previous work.²⁵ This procedure yields, in a natural way, a hierarchical picture of the configurational space, based on transition rates between regions of configurational space.

Method

Use of rates to describe conformational dynamics

Our approximate states are constructed based on rates between regions of configuration space, which are a fundamental property that emerges uniquely from the natural system dynamics. Following Ref. 25, we first decompose the conformational space into multiple bins as detailed below. Subsequently, we combine bins that have the highest transition rates between them, iterating to create a hierarchical description. This procedure is based on the physical idea of separation of time scales: there are faster timescales (high transition rates) associated with regions within a single physical state, and slower timescales for transitions between states. Furthermore, “fast” and “slow” timescales are not absolute, necessitating a hierarchical description following precedents.^40,41

Binning decomposition of the configurational space

We divide the whole configuration space into m bins, and determine the physical states by combination of these regions. All data reported here used m = 20. The value m = 20 was motivated by our intuition that regions with less than 5% population should not be allowed to dominate ESS. However, we obtained very similar results using larger m values of 40 and 60.

The procedure to decompose the whole configurational space (with N configurations) into m bins is as follows:²⁸

1. A reference configuration i is picked at random from the trajectory.

2. The distance of the configuration i to to all remaining configurations in the trajectory is then computed, based on an appropriate metric discussed later.

3. The configurations are sorted according to distance, and the closest N/m configurations are removed.

4. Steps 1–3 are repeated m−1 times on the progressively smaller set of remaining configurations, resulting in a total of m reference configurations.

For the distance metric, we select the root-mean squared deviation (RMSD) of the full molecule, estimated after alignment. We note that using just the backbone RMSD may be a poor distance metric for peptides as it ignores side chain kinetics. However, other metrics may prove useful.

After reference structures are selected, we decompose the whole space into bins based on a Voronoi construction. That is, for each configuration, we calculate the RMSD of this configuration to each of the m reference structures. We assign the configuration to the bin associated with the reference structure, with which the configuration has the smallest RMSD.

Calculation of rates among bins and bin combination

We compute the mean first passage time (MFPT) from each bin, i, to every other bin, j, using a continuous dynamical trajectory or a set of trajectories. The rate from bin i to bin j is the inverse of that MFPT. In general, the rate from bin i to bin j is not the same as the rate from bin j to bin i – and we take a linear average of these two rates to define an effective rate between bin i and bin j, $k_{ij}^{\mathrm{eff}}$. The effective rates are then used to construct a hierarchy of states. Rates may also be computed via alternate methods such as via transition matrices, and these different definitions may lead to somewhat different approximate physical states; however, the estimates of the effective sample size should be fairly robust, based on our experience varying other parameters.

Hierarchy

In essence, we perform hierarchical clustering.⁴² We construct a hierarchy of states by combining bins together if all pairs of rates $k_{ij}^{\mathrm{eff}}$ exceed a cutoff, k_c. The cutoff is then decreased. We start with k_c = 1/min(MFPT) and progressively decrease k_c (or, equivalently, increase the transition time cutoff) until the next smallest $k_{ij}^{\mathrm{eff}}$ value is reached. The new set of $k_{ij}^{\mathrm{eff}}$ is, then, calculated between the new set of bins. With a decrease in k_c, more bins are combined resulting fewer states. Ultimately all bins are combined if transitions among all bin pairs are present in the trajectories which are analyzed. See Results below.

The rule of unanimity – the requirement for fast transitions among all bin pairs in a state – is important for ESS estimation. In physical terms, it prevents a bin which “straddles” two states from combining with bins on both “sides” of the straddled barrier (until a suitably low k_c is employed). In turn, this absence of straddling prevents anomalous ESS estimates.

We note that the hierarchical picture can be significantly affected by the time interval between snapshots underlying the MFPT calculations. For example, although a trajectory may have a low likelihood (hence a low rate) to cross over the 2k_BT barrier in Fig. A1 in time τ₁, it may easily cross that barrier for a long enough time interval, τ₂. Thus, a hierarchical picture at the lowest level can differentiate the two left states of Fig. A1 if the rates are computed from the dynamic trajectory with snapshots at every τ₁ interval. On the other hand, if the rates are computed using the τ₂ interval, 2k_BT barrier cannot be resolved at the lowest hierarchical level. As an extreme case, if the interval between snapshots is longer than the largest correlation time in the system, then the rates to bin i from any other bin is simply proportional to the equilibrium population of bin i – and the application of the procedure described above is not appropriate.

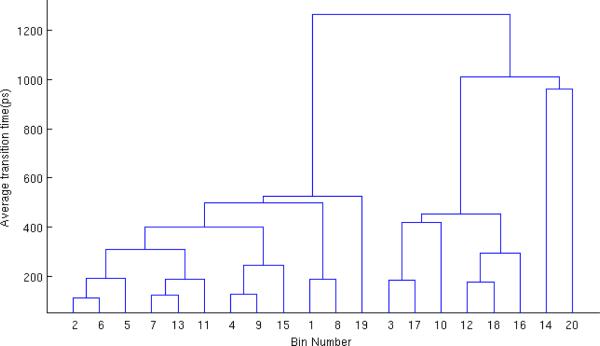
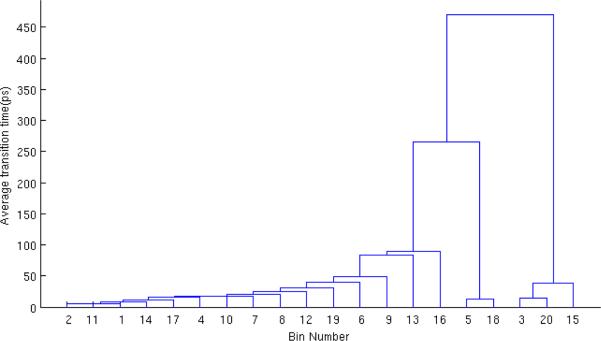
Fig. A2 and A3 show the hierarchical physical for dileucine and butane, respectively. Both start with m = 20 initial bins, and combine all the way to a single state. The effective sample size is calculated from the two-state level of the hierarchy as described in Sec. 2.

Appendix: A simple hierarchical scheme for approximating physical states from dynamical trajectories

In this Appendix, we describe our physical state discovery method and its results. In this method, bins or regions in configurational space are combined to give the physical states, as discussed below in more detail. Our method is based on the work of Chodera et al.²⁵, but is simpler. There is no Markovian requirement on the selection of bins. Indeed, a typical bin in a configurational space for a large multidimensional system may itself encompass several separate minima. We emphasize that our procedure is designed solely for the purpose of estimating sample size and is not claimed to be an extremely precise description of states.

Our approach explicitly shows the hierarchical nature of the configurational space,⁴⁰,⁴¹ and focuses on the slowest timescale – which is of paramount importance for the estimation of the effective sample size in the main text.

Figure A1.

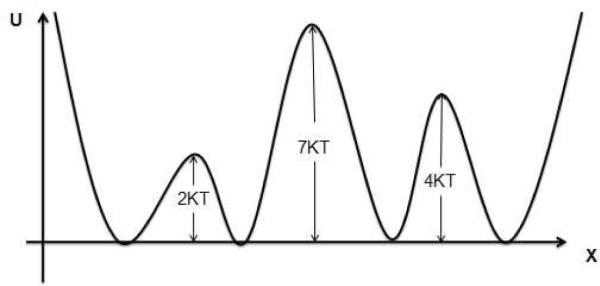
A one–dimensional potential energy landscape with four basins separated by three barriers.

Figure A2.

Hierarchical physical states for dileucine shown via the average transition time required for transition among bin pairs. Bin pairs that combine “faster” (i.e., have shorter transition time) are combined at a lower level of the hierarchy.

Figure A3.

Hierarchical physical states for butane shown via the average transition time ($1∕k_{ij}^{\mathrm{eff}}$)required for transition among bin pairs. Bin pairs that combine “faster” (i.e., have shorter transition time) are combined at a lower level of the hierarchy.