Review of biomaterial thermal property measurements in the cryogenic regime and their use for prediction of equilibrium and non-equilibrium freezing applications in cryobiology

Abstract

It is well accepted in Cryobiology that the temperature history and cooling rates experienced in biomaterials during freezing procedures correlate strongly with biological outcome. Therefore, heat transfer measurement and prediction in the cryogenic regime is central to the field. Although direct measurement of heat transfer can be performed, accuracy is usually achieved only for local measurements within a given system and cannot be readily generalized to another system without the aid of predictive models. The accuracy of these models rely upon thermal properties which are known to be highly dependent on temperature, and in the case of significant cryoprotectant loading, also on crystallized fraction. In this work we review the available thermal properties of biomaterials in the cryogenic regime. The review shows a lack of properties for many biomaterials in the subzero temperature domain, and especially for systems with cryoprotective agents. Unfortunately, use of values from the limited data available (usually only down to −40 °C) lead to an underestimation of thermal property change (i.e. conductivity rise and specific heat drop due to ice crystallization) with lower temperatures. Conversely, use of surrogate values based solely on ice thermal properties lead to an overestimation of thermal property change for most biomaterials. Additionally, recent work extending the range of available thermal properties to −150 °C has shown that the thermal conductivity will drop in both PBS and tissue (liver) due to amorphous/glassy phases (vs. ice) of biomaterials with the addition of cryoprotective additives such as glycerol. Thus, we investigated the implications of using approximated or constant property values versus measured temperature-dependent values for predicting heat transfer in PBS (phosphate buffered saline) and porcine liver with and without cryoprotectants (glycerol). Using measured property values (thermal conductivity, specific heat, and latent heat of phase change) of porcine liver, a standard was created which showed that values based on surrogate ice properties under-predicted cooling times, while constant properties (i.e. based on limited data reported near the freezing point) over-predicted cooling times. Additionally, a new iterative numerical method that accommodates non-equilibrium cooling effects as a function of time and position (i.e. crystallization vs. amorphous phase) was used to predict heat transfer in glycerol loaded systems. Results indicate that in addition to the increase in cooling times due to the lowering of thermal diffusivity with more glycerol, non-equilibrium effects such as the prevention of maximal crystallization (i.e. amorphous phases) will further increase required cooling times. These results affirm the need to use accurate thermal properties that incorporate temperature dependence and crystallized fraction. Further studies are needed to extract thermal properties of other important biomaterials in the subzero temperature domain and to develop accurate numerical methods which take into account non-equilibrium cooling events encountered in cryobiology when partial or total vitrification occurs.

1. Introduction

Technologies associated with cryobiology focus on two central applications: cryopreservation, the freeze-banking of cells and tissues for later use; and cryosurgery, the use of freezing to destroy biological materials including tumors. Several reviews are available on the engineering aspects of cryopreservation and cryosurgery [1] [2] [3] [4] [5] [6] along with specific discussions related to heat transfer solution techniques [7] [8] [9] [10]. The central engineering tasks associated with these applications are related to being able to measure or calculate the heat (and mass) transfer during freezing-induced phase change in biosystems and then correlating the observed transport phenomena with the biological outcome. The direct measurement of heat transfer of biosystems is often difficult in many situations due to access and/or practical measurement issues. For situations when direct measurement of transport becomes difficult, analytical or numerical methods [11] [12] become valuable alternatives in allowing us to predict the outcome of a cryobiological procedure. Additionally, such predictions also aid in reducing the experimental load required in optimizing the freezing procedure for a cryobiological objective. The reliability of predictions depends on employing an appropriate heat transfer model and usage of accurate thermal properties for the biosystems of interest. Thermal properties needed for performing numerical predictions of cryobiological applications include specific/latent heats, density, and thermal conductivity/diffusivity. While analytical predictions may be possible for certain cases, numerical methods are necessary when the analysis pertains to systems with thermal properties that are strongly dependent upon temperature, when the change of phase deviates from equilibrium conditions, and with challenging geometries.

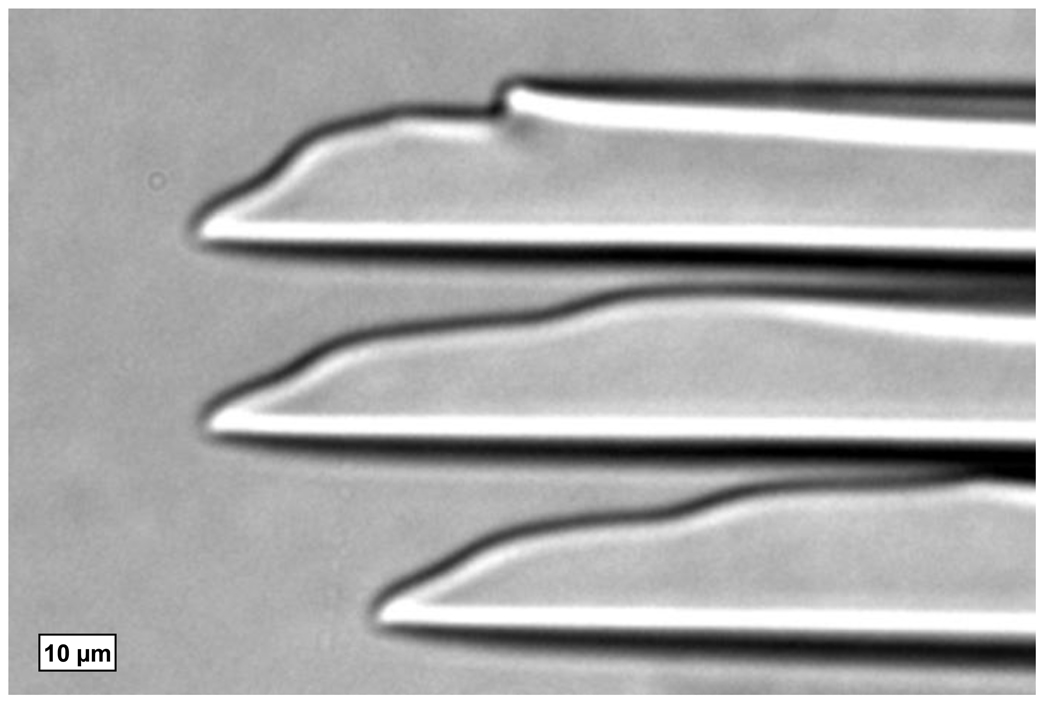
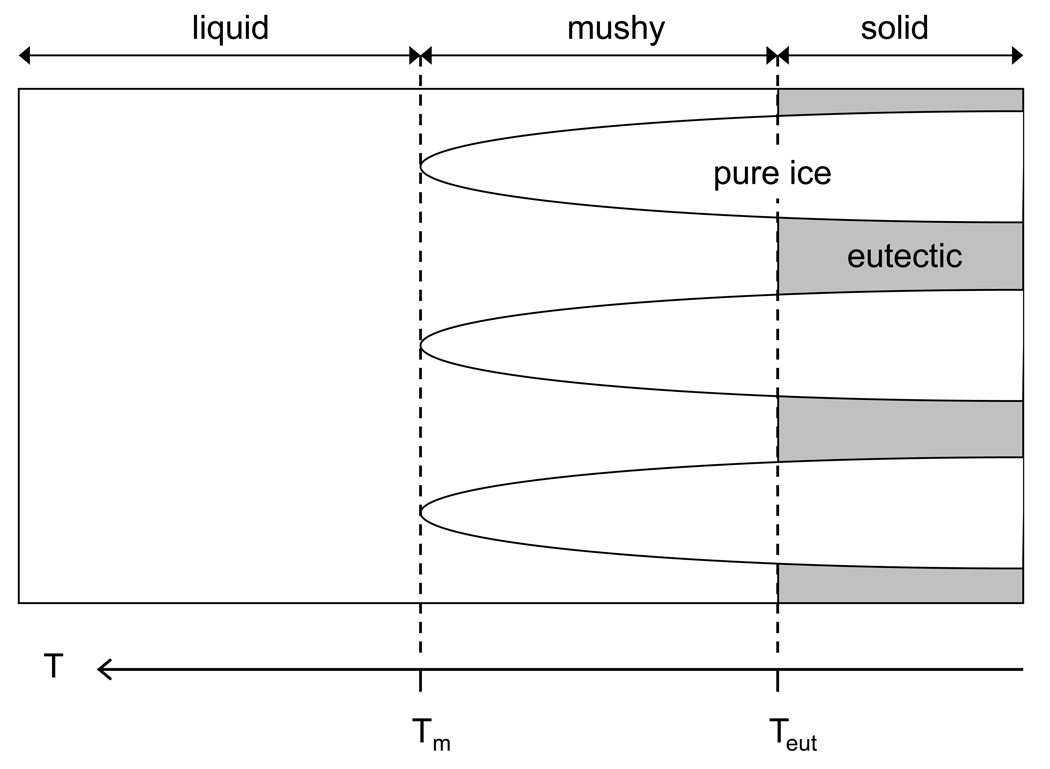
The conditions under which a numerical prediction of a cryobiological procedure can be performed need to be clearly understood. One such condition which needs to be considered is the spatial resolution at which calculations will be performed. Fig. 1 shows the dendritic ice formation and growth with further cooling in isotonic saline due to directional freezing, where the crystallization of water into ice will expel solutes into the remaining unfrozen liquid channels between the dendritic “cells” and the bulk liquid further from the cooling source. Therefore, depending on how the size scale is chosen, the local composition will be comprised of pure ice, unfrozen freeze-concentrated liquid, or both. If the size scale were to be chosen sufficiently large, the local composition can be considered a homogenate, composed of multiple regions of liquids and/or solids. For solutions which can be considered as simple binary systems such as saline, the change in phase will occur over a finite temperature range as shown in Fig. 2. At temperatures above the liquidus temperature T_m, the system remains in liquid form and at its original solute concentration C_o. Upon freezing, primary ice will form and grow with a reduction in temperature while the concentration of the adjacent unfrozen region will increase until the eutectic concentration C_eut is reached at the corresponding eutectic temperature T_eut. This temperature range in which both phases exist is often referred to as the mushy zone. At temperatures below T_eut the concentrated liquid will undergo eutectic solidification. It is noted that the temperatures described here are based on conditions when supercooling does not occur.

Fig. 1.

Microscope image of the advancing ice front due to the directional freezing of isotonic saline.

Fig. 2.

Schematic representation of directional freezing in a saline system. The system is divided into three regions depending on temperature as 1) liquid above the liquidus temperature T_m, 2) mushy below T_m and above the eutectic temperature T_eut, and 3) solid below T_eut.

Due to the fact that a solute concentration gradient forms between frozen and unfrozen in a biosystem it becomes necessary to perform a simultaneous analysis of both heat and mass transfer in which a higher concentration of solutes than its original value should accumulate in regions furthest from the cooling source [13] [14]. However, mass transfer can be neglected for many practical situations in cryobiology where heat diffusivity is orders of magnitude higher than mass diffusivity. If we consider as an example values for saline systems at subzero temperatures, thermal diffusivity is in the order of 10⁻⁶ m²/s while mass diffusivity values are in the order of 10⁻⁹ m²/s [15] [16] [17]. The difference in diffusivities becomes greater for solutions with cryoprotective agents (CPA) such as glycerol [18] [19] [20]. This implies that the ratio of the characteristic thermal versus mass diffusion lengths over a unit time will be sufficiently large as to assure that observed changes in systems will be largely dictated due to thermal perturbations (as experimentally confirmed [21] [14]). This high ratio of diffusivities along with the selection of the scale of analysis to be much greater than the spacing between crystalline structures (for dendritic ice growth, ~10⁻⁵ m [22]) become the conditions under which an uncoupled heat-transfer-dominated analysis can be performed, and where the local solute concentration can subsequently be determined with reasonable accuracy by assuming that the concentration of solutes in the local unfrozen fraction depends on the temperature based on the equilibrium phase diagram [23] [24] [25] [8]. Such an assumption implies that all solute movement is solely in the direction perpendicular to the thermal gradient (and crystal growth) in Fig. 2. Additionally, the selection of the scale of analysis to be sufficiently large allows for the assumption that the thermal properties of the local region can be represented as the weight averaged values of the individual constituents which do not depend on the adjacent compositions and are a function only of the local temperature. These are the assumptions which were applied to the subsequent numerical predictions performed in this paper.

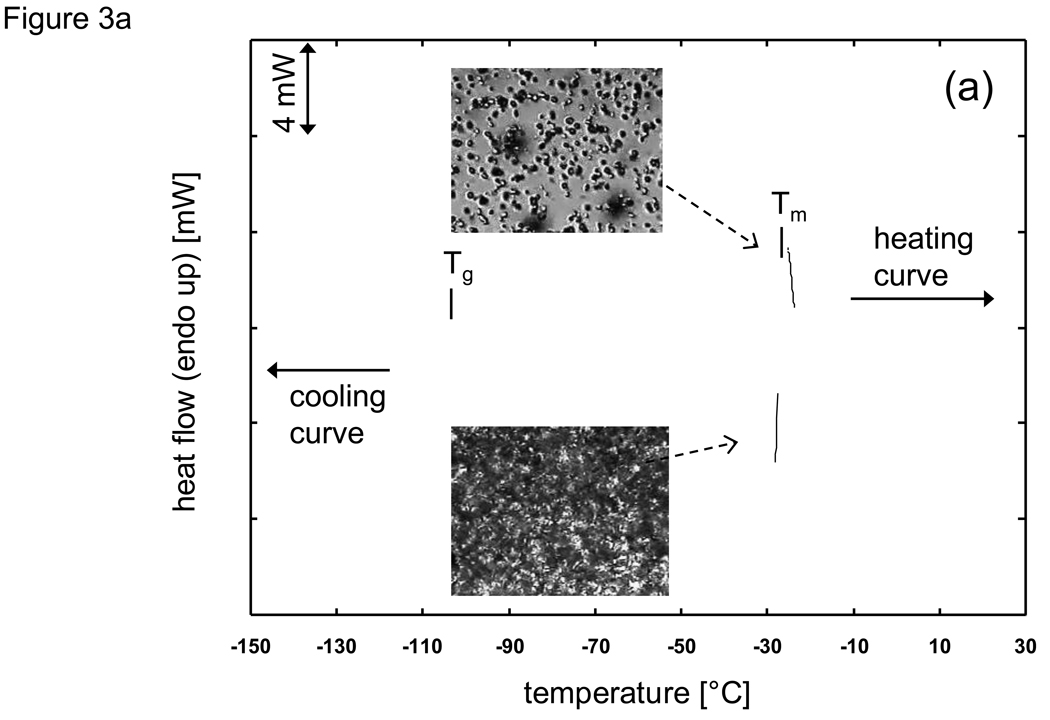
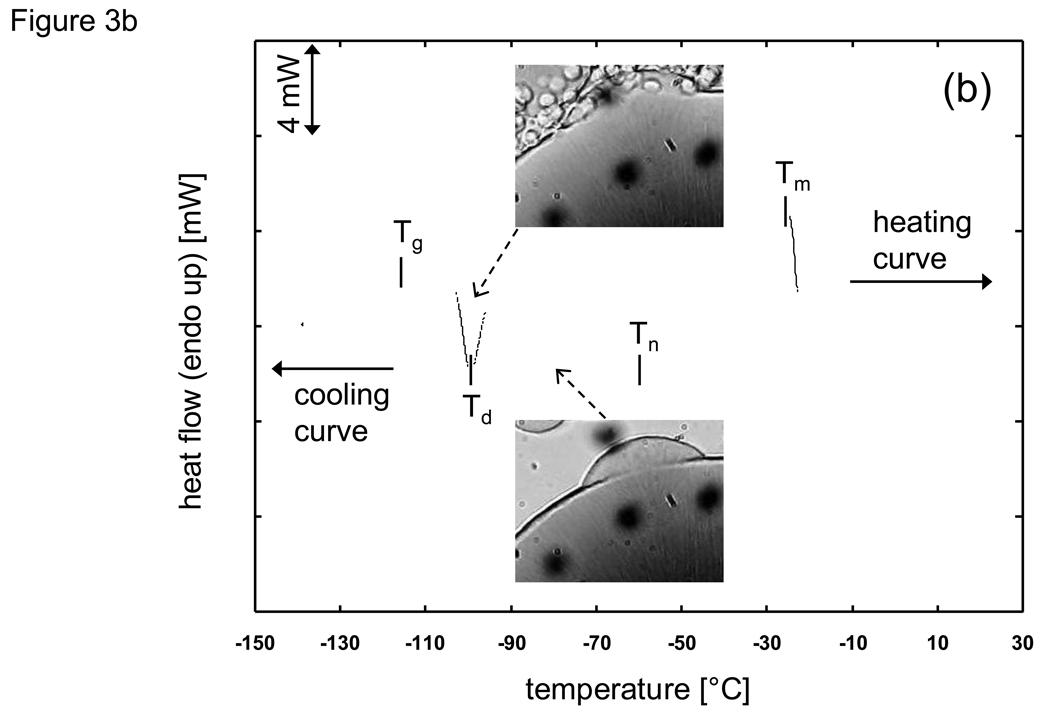
While freezing events and the ensuing phase change are often correlated to the equilibrium phase diagram (based on the assumption that a quasi-equilibrium cooling occurs), there are many situations in cryobiology where the cooling protocol will result in deviations due to the existence of non-equilibrium cooling (and heating) events manifested in the form of supercooled nucleation, the absence of eutectic formation, and devitrification, to name a few. Fig. 3 shows the cooling and heating history of 1×PBS (phosphate buffered saline) + 6M glycerol as observed with a DSC (Differential Scanning Calorimeter) employing a 5 °C/min scanning rate. Under pre-nucleated conditions (Fig. 3a) where small amounts of ice exist just below the melting temperature (T_m), there is good correlation between the exothermic cooling and endothermic heating thermograms. Cryomicroscopy images under similar conditions show that crystal growth is rapid during cooling while the individual crystals are numerous but small in size. These results show that under pre-nucleated conditions, the cooling history can be predicted using quasi-equilibrium and homogeneous assumptions. However, during non-pre-nucleated cooling (Fig. 3b) the crystallization of ice begins at a supercooled heterogeneous nucleation temperature (T_n) far below the melting point (T_m) and only a fraction of the maximal amount of ice crystallization which is possible occurs prior to reaching the glass transition temperature (T_g). Subsequent heating results in the crystallization of water which did not freeze during cooling and appears in the DSC thermogram in the form of a devitrification peak (T_d). It is only beyond the end of devitrification when the system can be considered to approach any resemblance of a quasi-equilibrium state. Cryomicroscopy images confirm the trends shown with the DSC that crystal growth slows and is limited during cooling and that the individual crystals are few but are relatively larger in size compared to pre-nucleated conditions.

Fig. 3.

DSC (Differential Scanning Calorimeter) thermogram for cooling and heating of PBS (phosphate buffered saline) + 6M glycerol at a scanning rate of 5 °C/min under a) prenucleated quasiequilibrium and b) supercooled nonequilibrium conditions. T_m: melting peak temperature, T_g: glass transition, T_n: onset of supercooled heterogeneous nucleation, T_d: devitrification peak. Inset slides are cryomicroscpoy images under the same conditions (dark unfocused spots are lens artefacts).

This example with PBS with a high concentration of glycerol (Fig. 3b) shows the level of non-equilibrium conditions that may exist in relevant systems and the need to address these effects in heat transfer analyses in order to obtain more accurate predictions for cryobiological procedures. The fact that thermal properties are usually measured under quasi-equilibrium states further hinders analyses in which non-equilibrium effects need to be accounted for.

Cryobiological analysis using heat transfer models will often require the accounting of the change of phase experienced by the biosystem and the corresponding latent heat effects. While the latent heat of pure substances such as water will be released at a constant temperature (isothermal freezing), biological aqueous solutions and tissues will undergo phase change over a range of temperatures (mushy zone, Fig. 2). Several models have been used to account for the effect of this latent heat release on thermal modeling and reviewed elsewhere [10] (Table 1).

Table 1.

Phase change formulations of the heat equation

Method	Equation	Conditions	Comments
Front Tracking [26] [27] [11] [28] [29] [30]	${\rho }_i{c}_i\frac{\partial T}{\partial t}=\nabla \cdot (k_i\nabla T)$	${k_s\frac{\partial T}{\partial r}|}_{r_{\text{int}}^{-}}-{k_l\frac{\partial T}{\partial r}|}_{r_{\text{int}}^{+}}=\rho \mathrm{\Lambda }\frac{\partial r_{\text{int}}}{\partial t}$	Intrinsic error in interface tracking
Enthalpy [11] [12] [31]	$\frac{\partial [\rho h]}{\partial t}=\nabla \cdot (k\nabla T)$	h = cT, T < Tph h = cT + (1 − fc)Λ, T = Tph h = cT + Λ, T > Tph	Most used, need a priori knowledge of h
Apparent Heat Capacity [32] [33] [34] [35] [25] [7] [36]	$\rho \left[c+\frac{\partial \mathrm{\Lambda }}{\partial T}\right]\frac{\partial T}{\partial t}=\nabla \cdot (k\nabla T)$	$\frac{\partial \mathrm{\Lambda }}{\partial t}=\frac{\partial \mathrm{\Lambda }}{\partial T}\cdot \frac{\partial T}{\partial t}$	Can link Λ to phase diagram
Source Term [35] [37] [38] [39]	$\frac{\partial (\rho cT)}{\partial t}=\nabla \cdot (k\nabla T)+S$	$\begin{array}{c}S=\rho \mathrm{\Lambda }\frac{\partial f}{\partial t},T=T_{\mathit{\text{ph}}}\hfill \\ S=0,T\ne T_{\mathit{\text{ph}}}\hfill \end{array}$	Most general, can link S to any release pattern

ρ: density, c: specific heat, T: temperature, t: time, k: thermal conductivity, r: length, Λ: latent heat, h: enthalpy, f_c: fractional release of latent heat (crystallized fraction), S: source term, subscripts: i: solid(s) or liquid(l), int: interface, ph: phase change region (temperature range)

The front tracking (or moving boundary) method makes use of an interface separating the frozen and unfrozen regions and tracking its location with the passage of time [26] [27] [11] [28] [29] [30] [10]. The enthalpy method uses enthalpy to represent the energy stored in the region of interest and is more applicable for use with systems having a mushy zone [11] [12] [31]. The apparent heat capacity method uses an equivalent heat capacity which takes into account the effects of both sensible and latent heat in a single term applicable for use with standard heat transfer numerical codes [32] [33] [34] [35] [25] [7] [36]. The source term method represents the latent heat during phase change as a source term and is advantageous when implementing time-dependent biophysical events into the thermal model [35] [37] [38] [39] including the conditions of non-equilibrium phase transitions.

While not the focus of this paper, for cooling analysis of in vivo biosystems the roles of blood flow and metabolic heat generation need to be taken into account in addition to the phase change formulations shown above [8] [40]. The Pennes bioheat equation [41] is often used for its simplicity and applicability to a wide range of biosystems and conditions. Subsequent investigators have introduced equations which address some of its limitations including the assumption of thermal equilibrium between perfused blood and local tissue in smaller vessels[42], and those which take into account the countercurrent nature of tissue vasculature [43] [44]. A summary of perfusion models developed by investigators is available in [45] [9].

The current paper will focus on reviewing the methods used to measure thermal properties of biological materials and the availability of thermal properties in the subzero temperature domain. The results of a series of cooling predictions of biosystems based on the enthalpy method previously described will be shown, and the implications of the changes in outcome due to differences in scale (size of the system), material (solution vs. tissue, with/without glycerol), and state (equilibrium vs. non-equilibrium) will be discussed.

2. Thermal Properties of Biomaterials

Methods for measuring thermal properties of biomaterials have been reviewed previously [46] [47] [48] [9]. Specific and latent heats are measured using calorimetric methods, often utilizing a Differential Scanning Calorimeter. Density measurements are obtained through displacement methods or other indirect methods when displacement methods cannot be applied. For instance, X-ray computer tomography can be used to map crystalline and amorphous phases in frozen biomaterials in which the local density is correlated to Hounsfield unit measurements [49]. Thermal conductivity and diffusivity have been measured using a large variety of methods, and we discuss the most representative methods here.

Representative methods to measure thermal conductivity with their advantages and disadvantages are summarized in Table 2. The steady state longitudinal heat flow (guarded hot plate) method [50] determines thermal conductivity at steady state using a 1-D heat flow model and knowledge of the heat flow and temperature gradient. The thermal comparator method [51] [52] [53] uses two different materials at different initial temperatures and analyzes the temperature changes when they are brought together. In the heated thermocouple method [54], the thermocouple is used both to measure the sample temperature and to apply heat to the sample by applying a prescribed current. A spherical source of heat dissipating a constant amount of heat into an infinite medium is assumed. The self heated thermistor technique has been used in several configurations to determine thermal conductivity/diffusivity [55] [56] [46] [47] [57] [58]. For the configuration in which a step change in temperature is brought about by controlling the heating, the decreasing power input required to maintain temperature can be correlated to the thermal diffusivity of the sample [57]. If the thermal conductivity of the sample is not significantly lower than that of the thermistor probe, the thermistor cannot be considered as a lumped mass and the coupled thermal response of both the thermistor and the sample must be solved [56] [58] [47]. The pulse decay method utilizes a pulsed heat input which is assumed as a spherical point heat source and monitors the subsequent temperature decay in order to determine the sample thermal diffusivity [55]. Measurement errors are reduced compared to step change configurations due to the fact that the region of the steepest thermal gradient is not adjacent to the probe (i.e. the probe lies in a region of relatively uniform temperature) and allows the effect of finite probe radius to be negligible when a sufficient amount of time has expired since the end of pulsing. A cylindrical model of the pulse decay method was also explored in [59]. In addition to the above-described methods various other methods exist, including hot wire methods (similar to the heated thermocouple method, but cylindrical in assumed geometry) [60] [47], Differential Scanning Calorimetry (DSC) operational methods [61] [62] [63], surface measurement techniques [64] [65] [66], and MRI thermometry methods [67].

Table 2.

Summary of representative methods used to measure thermal conductivity of biomaterials

Method	Pros	Cons	Schematics and Model
Steady state longitudinal heat flow method (Guarded hot plate) [50]	k is directly measured Other properties not Required	Guarding necessary for 1-D heat flow Long measurement times (steady) Requires temperature controller
Thermal comparator method (Cooper & Trezek’s probe) [53]	No heating mechanism Transient Measurement	High length-to-diameter ratio necessary Extensive data processing required Large ΔTinit results in an averaged k value Inapplicable with hard materials
Heated thermocouple method (Grayson’s probe) [54]	Simple probe and analysis k is directly measured Simple data processing	Sensor geometry may not satisfy 1-D assumption Long measurement times (steady) Requires heat controller
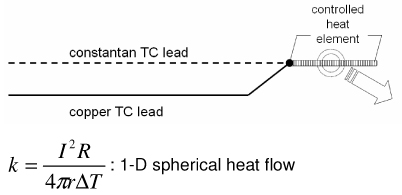Thermistor w/step temperature change (Chato’s probe) [47]	Simple probe k is directly measured Simple data processing	Equivalent probe radius used Temperature control at probe interface difficult Requires heat controller
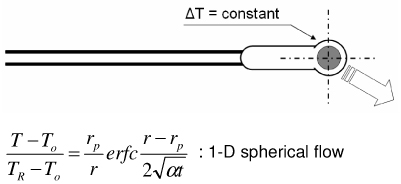Thermistor w/ pulse heat input (Pulse decay method) [55]	Simple probe & heating method Simple data processing	Volumetric heat capacity required to determine k Thermistor response / sensitivity issues

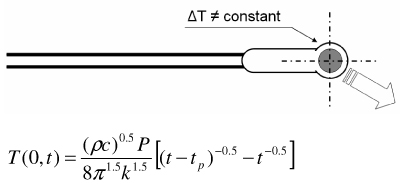Selection of a measurement method would depend on numerous factors, including considerations for the sample size, temperature range to be measured, whether an in vivo measurement would be possible, and whether time constraints need to considered (transient vs. steady). The steady state longitudinal heat flow method has its advantages in the fact that thermal conductivity is directly measured without the need to know heat capacity. However, the necessary guarding to assure 1-D heat flow may be challenging and in vivo measurements would not be feasible. The thermal comparator method is relatively easy to devise and does not require any heating mechanisms. The requirement of a sufficiently large temperature difference that can be measured is a disadvantage and will render the measured property as a temperature averaged value. Problems are also foreseeable when it is used to measure solid (frozen) materials since plunging the probe would be difficult. Although the heated thermocouple method employs a simple probe design and can directly measure thermal conductivity it also requires an elaborate heating mechanism and the 1-D spherical assumption may not be valid for certain situations. The thermistor method with a step temperature change also allows direct measurement of thermal conductivity, but an equivalent radius needs to be determined for analysis and there is also a heat control component. The pulse decay thermistor method requires minimal calibration and requires a simple heating mechanism, but the volumetric heat capacity needs to be separately determined in order to find thermal conductivity and thermistor response can become an issue.

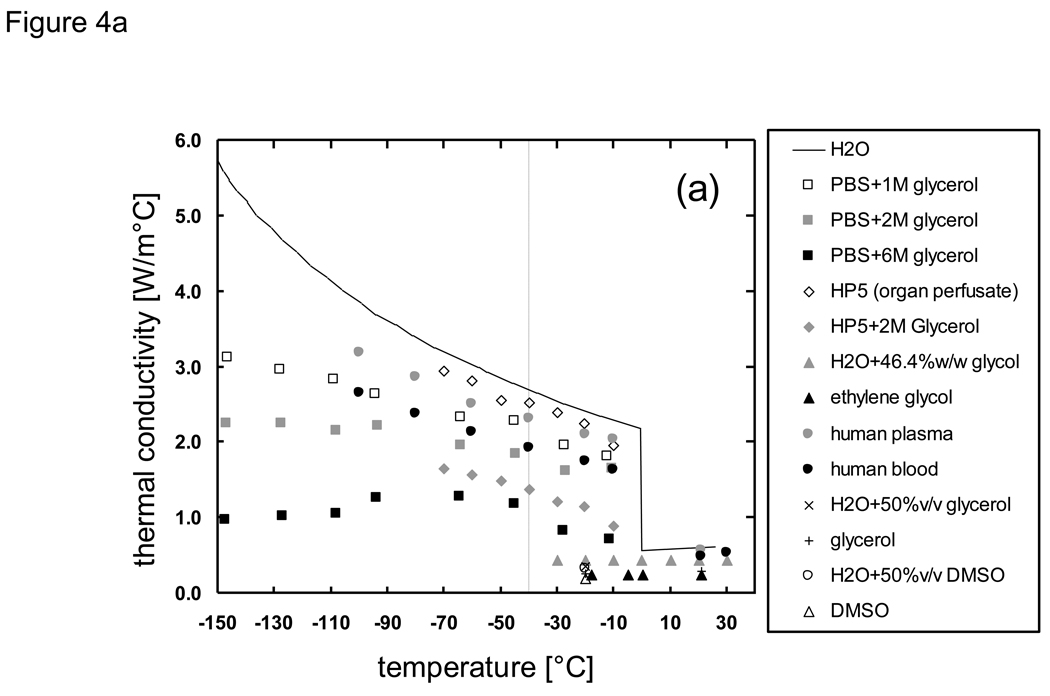
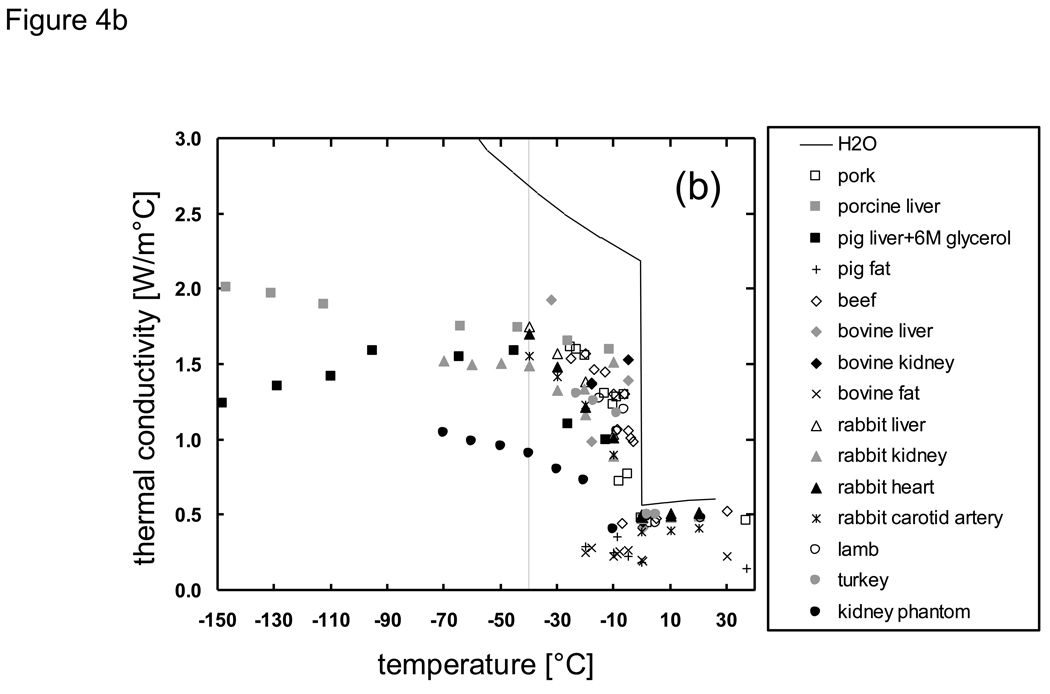
Thermal property data of biomaterials have been reviewed and summarized previously [9] [68] [69] [46] [70] [71], but there is a lack of available values in the subzero temperature domain. In the absence of available property data, values are often estimated based upon known values for pure ice [72] [73] [74]. An estimation based upon the thermal property models of a material’s major constituents (water/ice, protein, fat, carbohydrate, fiber, and ash) [75] and the averaging of the thermal properties of the constituents based on weight percentage [68] is also employed. The available thermal properties of biomaterials in the subzero temperature domain are summarized in the Appendix. Of the reported thermal properties in the literature, thermal conductivity and diffusivity have been measured most extensively with the methods described above. However, it is evident from Fig. 4 that other than for a few types of biomaterials little is known at temperatures below −40 °C. The general trend for thermal conductivity shows that higher values are obtained with lower temperatures presumably due to the ice composition within the biomaterial, and that this effect decreases when there is less ice composition.

Fig. 4.

Thermal conductivity of biologically relevant a) solutions and liquids b) tissues and solid materials in the subzero temperature domain. Data sources are described in the Appendix. Dashed line indicates lack of available data below −40 °C.

Due to the lack of available property values in the literature, we have recently measured and reported on the properties of phosphate buffered saline with glycerol [20] and porcine liver with glycerol [76]. The studies were focused on extending the knowledge of biomaterial properties (thermal conductivity, melting point, latent heat, and specific heat) down to very low temperatures (−150 °C) and additionally on understanding the effects of the formation of glass on the trend of the property values. The measured results for thermal conductivity k (Fig. 4) indicate that the drastic increase in k at low temperatures observed in H₂O and PBS systems become less pronounced with the addition of glycerol, and that the formation of glass due to glycerol counteracts the rise in k values. Therefore it was evident that an approximation using H₂O values would be largely inappropriate, and that a weight averaging of H₂O and glycerol properties would fail to identify the downward inflection in k values that was observed from measured data. Based on such findings, it became clear that substantial differences would exist in cooling predictions based on assumed versus measured property values. The following sections will discuss the cooling analyses which were performed to confirm such differences.

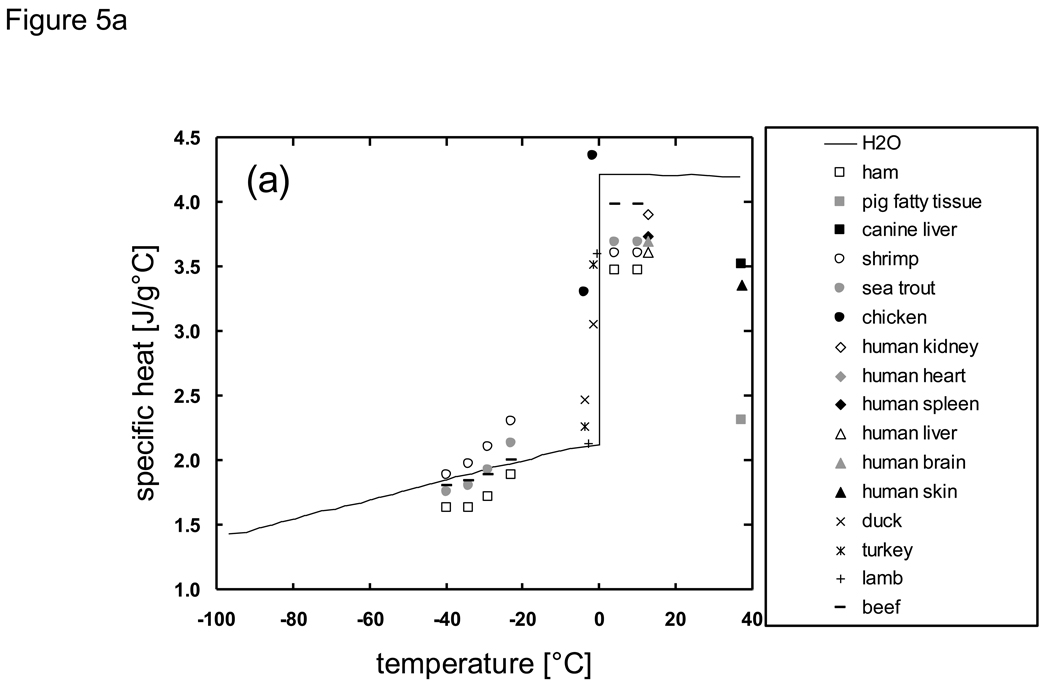
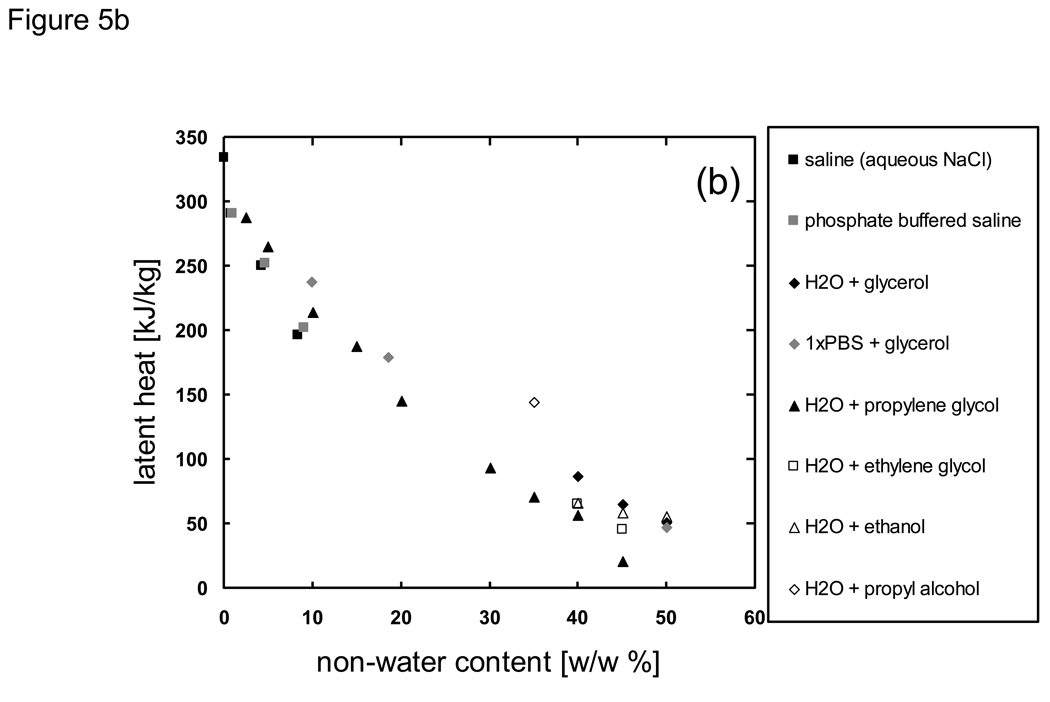
Despite the relative simplicity and ease with which specific/latent heats can be measured compared to thermal conductivity/diffusivity, a search in the literature for biologically relevant materials in the subzero temperature range revealed very little available data (Fig. 5). It should be noted that although the specific and latent heats are considered separately in this paper, investigators often tabulate specific heat values in which the latent heat related to phase change is not separated. Additionally, for heat transfer calculations it is often more advantageous to use enthalpic tabulations, as discussed further in subsequent sections. The latent heat values of biologically relevant solutions and materials associated with primary ice formation/melting have been found to be less than that of pure water (~334 J/g, Fig. 5b) and have been correlated with the material’s overall water content [69]. The latent heat of foods has been calculated by multiplying the food’s water content by the latent heat of water in [68]. A recent study with saline solutions has shown that the latent heats of both water/ice and eutectic phase change do not correlate with the overall water content, but correlate with the amounts of water and solute that participate in either of the phase changes (i.e. water/ice or eutectic) respectively [77].

Fig. 5.

Available literature values of a) specific heat and b) latent heat of phase change for biologically relevant materials in the subzero temperature domain. Data sources are described in the Appendix.

3. Numerical predictions of cryobiological applications

It is evident from Figure 4 and Figure 5 and tabulated thermal property data in the Appendix that a substantial difference exists between the thermal properties of water/ice versus actual solutions/tissues. Furthermore, the deviation of thermal properties from that of water/ice due to the non-water component as well as the formation of eutectics or glassy amorphous phases is expected to bring about a change in the thermal history of biomaterials during cooling. In this section, the results of using the enthalpy method in predicting the 1-D thermal history of bulk systems while applying different thermal property data is discussed. Nonequilibrium phase change events and their effect on cooling outcome are also discussed.

Of the methods described in Table 1, the enthalpy method was used due to the simplicity of the governing equation and its applicability to systems which undergo phase change over a range of temperatures (termed the “mushy zone”). The governing equation in one-dimensional in vitro form is:

$$\rho \frac{\partial H}{\partial t}=k\frac{{\partial }^{2}T}{\partial x^2}$$ (1)

where ρ is density, H is enthalpy, t is time, k is thermal conductivity, T is temperature, and x is length. Discretization and reorganization gives [31]:

$$H_i^{n+1}=H_i^n+\frac{k}{\rho }\cdot \frac{\Delta t}{{\mathit{(}\Delta x\mathit{)}}^2}\left(T_{i-1}^n-2T_i^n+T_{i+1}^n\right)$$ (2)

where a central differencing method is employed in the spatial domain. The superscript n denotes time steps while the subscript i indicates node steps. Eq. (2) allows the determination of enthalpy at the next time step based on an explicit Forward Euler analysis in the temporal domain. Due to the fact that thermal properties can experience an abrupt change in value with phase change, half-node values based on harmonic averaging of adjacent true nodes were employed and the discretized governing equation was further modified as:

$$H_i^{n+1}=H_i^n+\frac{\mathrm{\Delta }t}{{(\mathrm{\Delta }x)}^2}\left[\frac{k_{i-1/2}}{{\rho }_{i-1/2}}\left(T_{i-1}^n-T_i^n\right)-\frac{k_{i+1/2}}{{\rho }_{i+1/2}}\left(T_i^n-T_{i+1}^n\right)\right]$$ (3)

Although time steps and spatial resolution were initially chosen satisfying the stability (convergence) criteria (eq. 4) of the enthalpy equation [31], Δx needed to be reduced further in order to remove oscillatory instabilities with their source in the nodes corresponding to the mushy zone [78].

$$0<\frac{\alpha \mathrm{\Delta }t}{{(\mathrm{\Delta }x)}^2}\le \frac{1}{2}$$ (4)

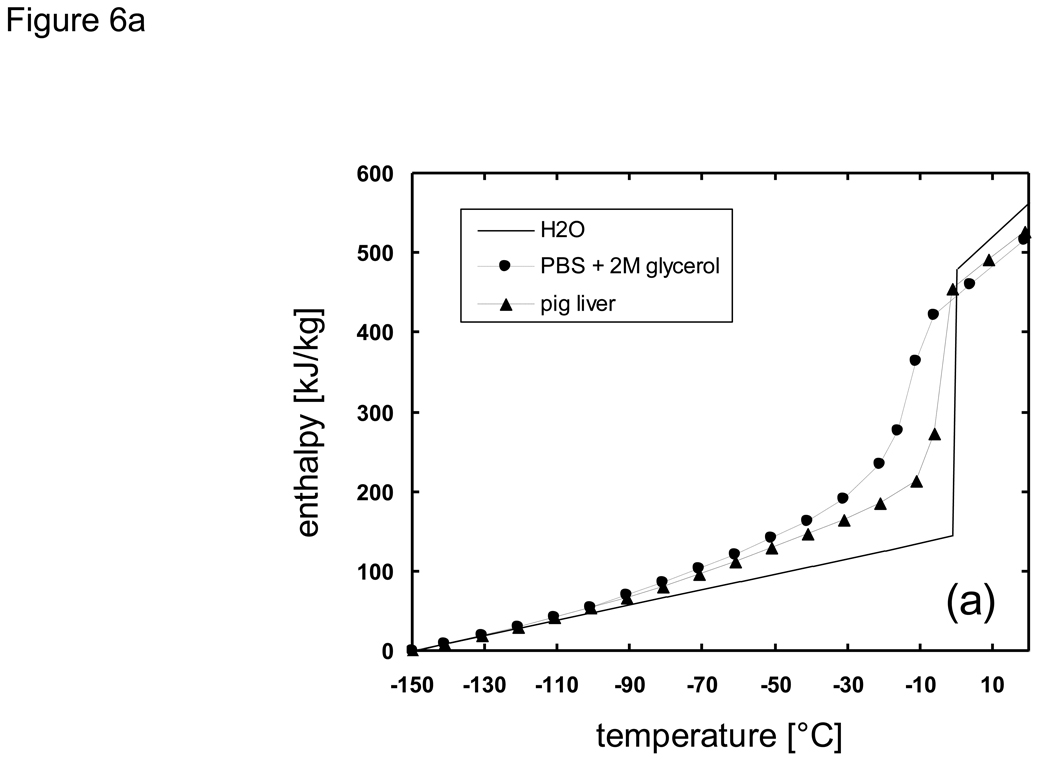
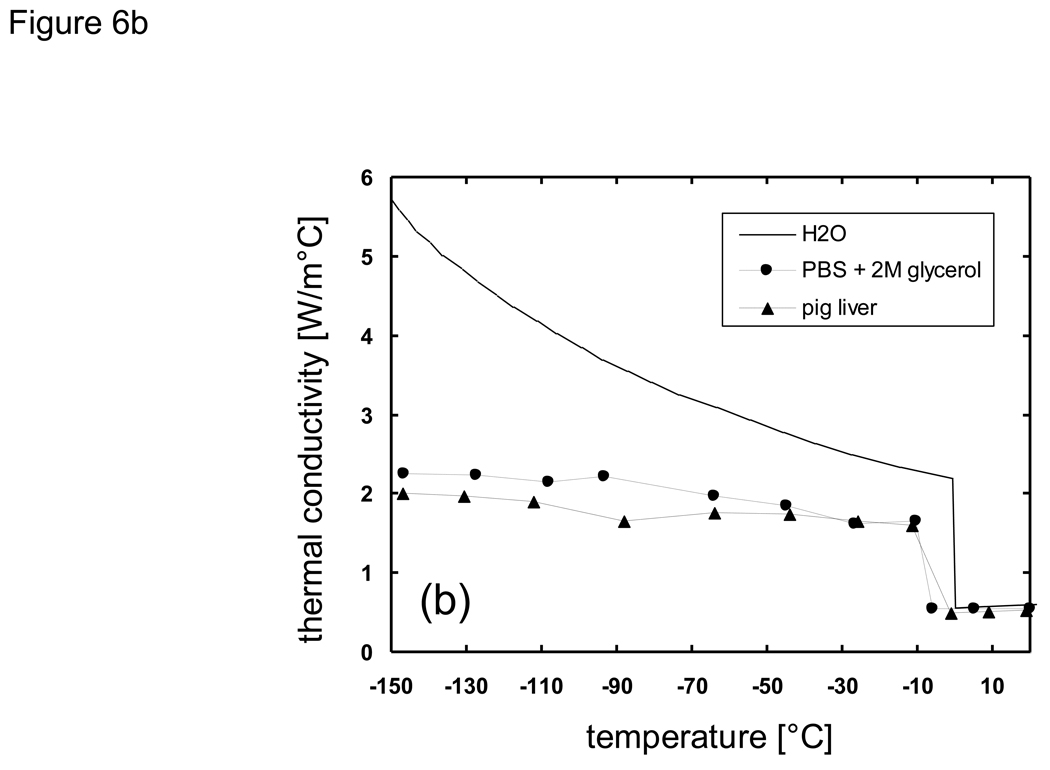
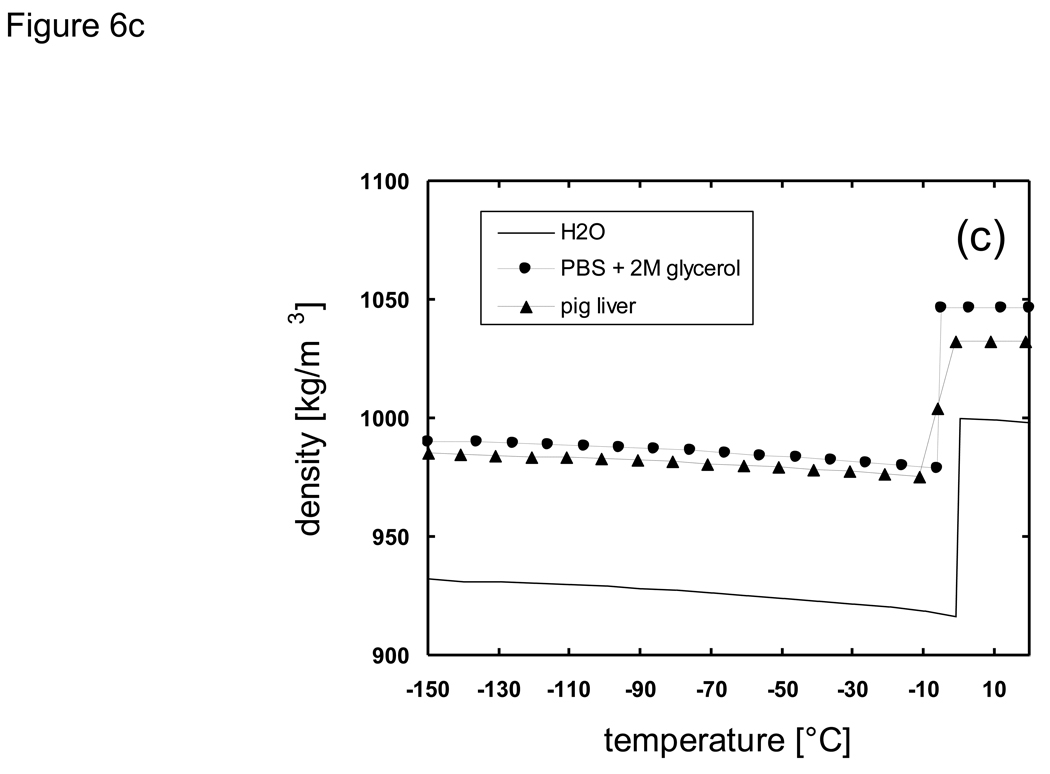
The node spacing (Δx) was also chosen so that the diffusion of solutes due to the formation of ice would be limited to be within a single node spacing in order to justify the decoupling of the heat and mass transfer analysis, as discussed previously. That is, in the time frame during which a node space is in a mushy state, the solute would not diffuse into adjacent nodes if the characteristic diffusion length was less than the node spacing. As an example, for the analysis of the system PBS + 2M glycerol, by assuming D_glycerol ~ 10⁻⁷ cm²/s [18] [79] in the mushy temperature range the diffusion length would be less than 10⁻³ cm over 1 second. Therefore, by setting the node spacing to be greater than 10⁻² cm mass transport to adjacent nodes would become significant only after accumulated times of ~ 10³ s, which is well beyond the time frame in which the local composition remains in a mushy state. Heat absorption ratios of melting (HR) over the mushy temperature range were determined from percent area curves of DSC thermograms [77] [20] [76], multiplied with the overall latent heat value, and added to sensible heat values in defining enthalpy values (e.g. Fig. 6a). Enthalpy values were tabulated at 5 °C intervals and linear interpolation was used for determining temperature values from enthalpy values which existed between two defined enthalpy points. The finite difference scheme was prepared using a FORTRAN 77 compiler under Sun Microsystems UNIX environments. A one-dimensional Cartesian geometry (infinite slab) was employed in which the thickness of the slab was varied from 1 ~ 100 mm. These dimensions were chosen to represent actual sizes of bulk cryobiological systems which range from freezing tubes to organs. Additionally, difference in system size was expected to bring about large differences in the predicted local cooling rate, and overall crystallized fractions under non-equilibrium cooling conditions due to high glycerol concentrations. It was assumed that the systems were initially at 20 °C, and then subject to constant temperature conditions of −150 °C at the outer boundaries.

Fig. 6.

Thermal properties of H₂O, Phosphate buffered saline + 2M glycerol, and porcine liver used for cooling predictions using the enthalpy method: a) enthalpy, b) thermal conductivity, c) density.

3.1 Effects of varying thermal properties

Thermal properties of biomaterials in the subzero temperature range have a large dependence on temperature and/or concentration. In order to assess the effects of applying different thermal property values in the outcome of thermal history the properties of H₂O, PBS + 2M glycerol, and pig liver were chosen for comparison. Latent heat, specific heat, heat absorption ratio, and thermal conductivity values reported previously in [20] [76] were used. Density values were derived based on the results of X-ray tomography studies at low temperatures from [49]. Values for thermal conductivity, density, and enthalpy used with the enthalpy code are shown in Fig. 6.

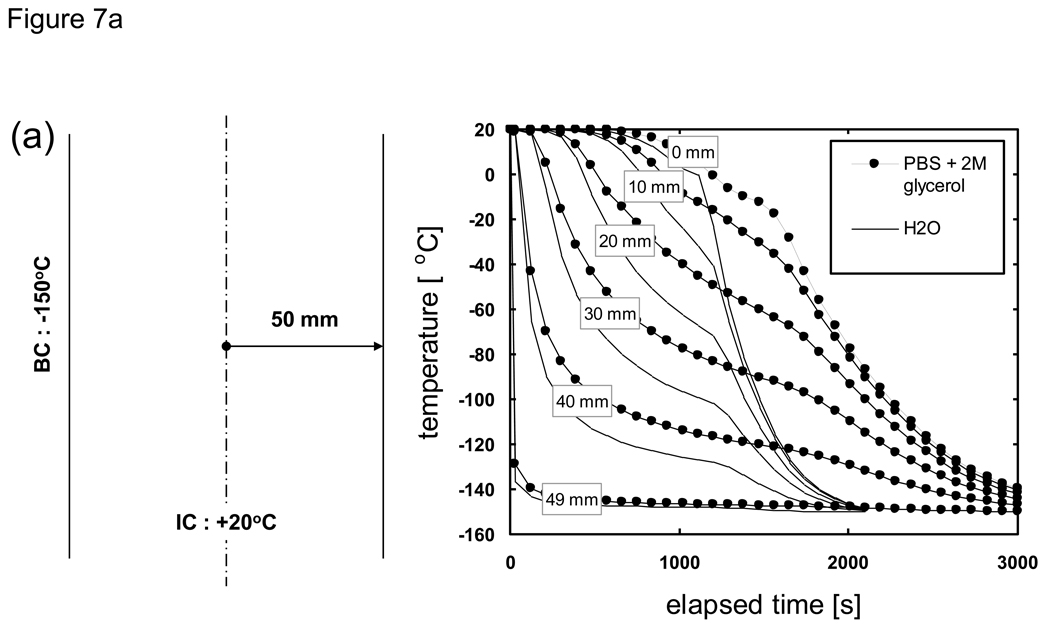
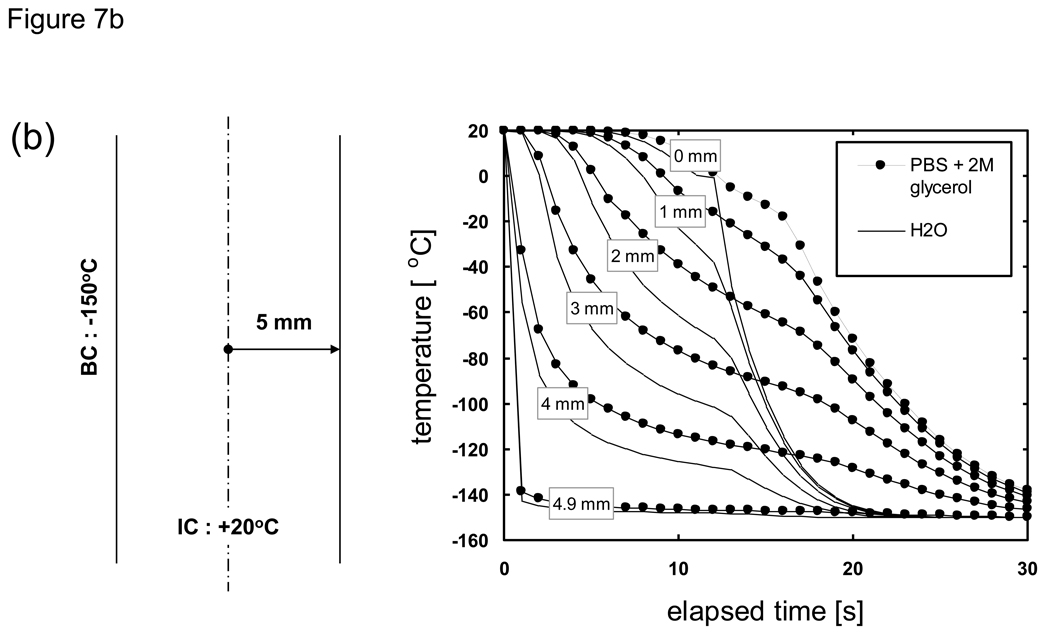
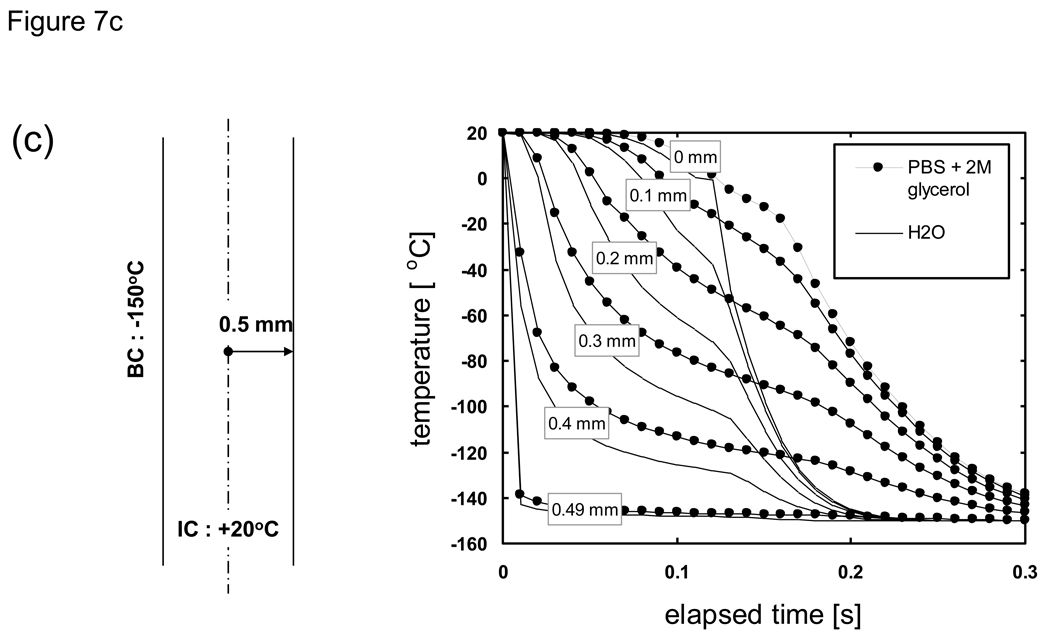
When the thermal property values of a material of interest are not known H₂O values are often substituted. Here we consider the implications of substituting thermal property values by comparing the predicted cooling histories for PBS + 2M glycerol (our system of interest with “unknown” properties) versus H₂O (our “surrogate” system). As shown in Fig. 7 the cooling history of both materials can be divided into two sections; an initial cooling curve which slows down in rate with the passage of time, followed by a secondary rapid drop in temperature when the centerline (0 mm) location (and thus the entire system) completes phase change. The cooling rates also varied greatly depending on the location within the sample, as was observed previously in studies which focused on understanding the spatial distribution of thermal histories and the range of cooling rates experienced during the freezing of biological solutions [37] [23] [80] [35] [25] [24] [7]. It is apparent from these results that predictions based on using thermal properties of water/ice will result in a more rapid cooling to the end temperature. A comparison of the cooling histories at specific spatial locations reveal that the effect of differences in thermal property values is minor near the outer boundary while there are larger time differences in reaching the final end temperature further inward. That is, the effect of differences in thermal property values on the cooling history will accumulate with the increase in distance from the cooling source (surface). It is clear that the temperature histories for all thicknesses exhibit the same trend and will collapse into a single curve by normalizing the elapsed time with respect to the squared value of the characteristic length. What is important in practical terms is that for cooling analyses the errors associated with the predicted time to reach a milestone temperature or traverse a critical temperature region for a given cryobiological application will be amplified for larger (or radial) systems if the correct thermal property values are not applied [20] [76].

Fig. 7.

Comparison of the predicted cooling history of PBS + 2M glycerol (filled symbols) versus H₂O (lines). Samples are assumed to be initially at 20 °C and cooled with a constant outer surface temperature of −150 °C. Geometry is a 1-D Cartesian infinite slab with a thickness of a) 100, b) 10, and c) 1 mm. Length descriptors indicate the node distance from the centerline.

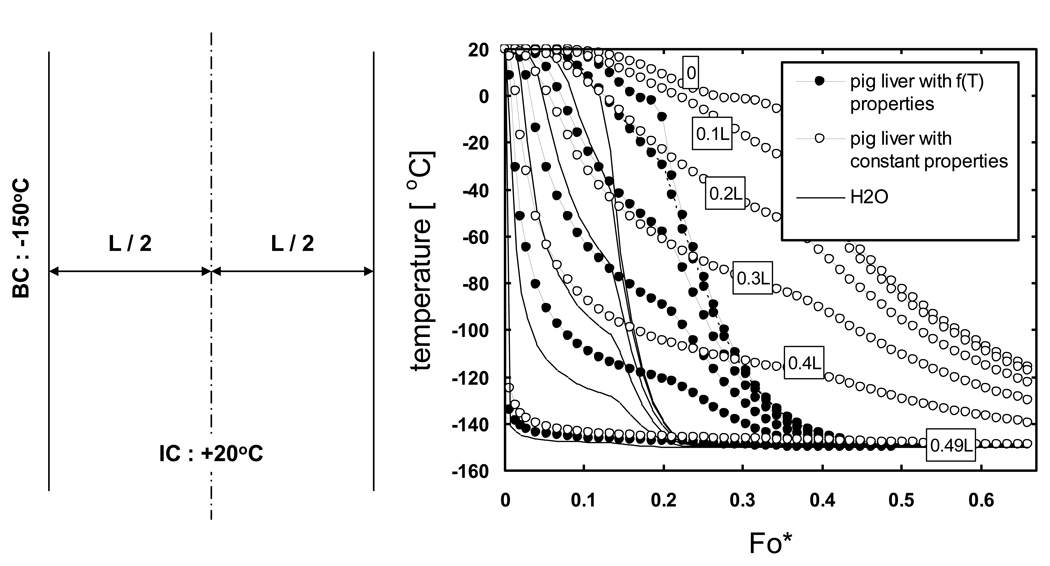
Another situation which often occurs when performing cooling predictions of biomaterials is when the thermal properties for the material of interest are known only over a limited temperature range or at a single point. In order to understand the implications of performing predictions when only a limited amount of thermal property values are known for a biomaterial, the cooling history of pig liver using constant property values (one each for suprazero and subzero temperatures) was compared to results for pig liver using known thermal property values in the entire temperature range of interest as well as to results for H₂O. From Fig. 8 it is clear that while predictions based on H₂O properties will underestimate cooling times for pig liver the use of constant property values will result in the opposite effect, an overestimation of cooling times which has a larger magnitude of error in reaching end temperatures compared to the surrogate use of H₂O properties.

Fig. 8.

Comparison of the predicted cooling history of pig liver using thermal properties as a function of temperature (filled symbols) versus liver with a constant property value per phase (unfilled symbols). Results using property values of H₂O are also shown (lines). Samples are assumed to be initially at 20 °C and cooled with a constant outer surface temperature of −150 °C. Geometry is a 1-D Cartesian infinite slab with a thickness of L. Length descriptors indicate the node distance from the centerline. Elapsed time is non-dimensionalized using Fo* = α_o ⋅ t/L², where α_o is the thermal diffusivity of ice at 0 °C.

It should be noted that all of the numerical predictions discussed until now used thermal properties measured under quasi-equilibrium states and assumed equilibrium freezing conditions including the assumption that the onset of crystallization correlates with the melting temperature (T_m) of the system. Moreover, the maximum amount of ice crystallization possible was assumed to occur during the freezing process for systems containing glycerol. For PBS + 2M glycerol, this was indirectly confirmed by using the DSC (as shown in Fig. 3a) to compare the latent heat during cooling at various rates (5 ~ 50 °C/min) and finding little difference in the calculated value. Additionally, some of the samples for DSC analysis (~10 mL) were initially plunged into liquid nitrogen (−196 °C) and then quickly placed in the DSC preset at −180 °C (transient temperatures never went above −50 °C) to see if devitrification would occur^†. However, peaks indicative of the occurrence of devitrification were never observed. Although the maximum amount of crystallization possibly does occur during cooling, the amount of crystal formed at a given temperature may slightly differ, depending on the cooling rate. However, the impact of these differences on the temperature history is expected to be minimal.

3.2 Effects of non-equilibrium processes

While many cryobiological applications can be modeled as undergoing a quasi-equilibrium cooling process, there are situations when non-equilibrium effects need to be considered. An example would be when a system undergoes supercooled nucleation during the freezing process. The addition of cryoprotective agents such as glycerol may also bring about deviations from equilibrium cooling conditions [20]. Unlike systems with low glycerol content, the numerical prediction of cooling systems with high glycerol content cannot directly utilize thermal property values which were measured under quasi-equilibrium states. This is due to the fact that the amount of crystallization which occurs may not be maximal, but reduces as a function of the cooling rate. The crystallization kinetics of CPA solutions have been studied by numerous investigators and parameters related to the formation of ice in high concentration glycerol solutions are available [81] [82] [83] [84] [85] [86] [87]. Theoretical models based on the findings are also available [88] [89]. Therefore, under such non-equilibrium conditions the thermal properties need to be modified from a function of temperature to a function of temperature and cooling rate (or crystallized fraction). Here we present results of employing the modified enthalpy method to two systems with high glycerol content; a solution system comprised of PBS + 6M glycerol and a tissue system comprised of pig liver + 6M glycerol.

Based on their DSC measurements of high concentration glycerol solutions during freeze-thaw [90] [91] [92] Boutron et al. formulated an empirical equation which predicts the rate of ice crystallization for high concentration aqueous glycerol (>5M glycerol) [82]:

$$\frac{{\mathit{\text{df}}}_c}{\mathit{\text{dt}}}=k_1\times f_c^{2/3}(1-f_c)\times (T_m-T)\text{exp}\left(-\frac{Q_A}{\mathit{\text{RT}}}\right)$$ (5)

where f_c (from Table 1) is the crystallized fraction (i.e. the amount of water which has crystallized over the maximum amount of water which can possibly crystallize), t is time, k₁ is the crystallization rate constant (dependent on sample and concentration), T_m is the melting point (or liquidus) temperature, T is temperature, Q_A is the activation energy (dependent on sample and concentration), and R is the gas constant. For 50% w/w (= 6M) aqueous glycerol the values are: k₁ = 5.783 × 10⁸ [1/sK] and Q_A = 11.6 [kcal/mol]. Discretization of the above equation was done as:

$$\Delta x=k_1\times {\left(x^{2/3}\right)}_i^{n-1}\mathit{(}1-x_i^{n-1}\mathit{)}\times \mathit{(}{T}_m-T_i^n\mathit{)}\mathit{\text{exp}}\left(-\frac{Q_A}{{\mathit{\text{RT}}}_i^n}\right)\times \frac{\left(T_i^{n-1}-T_i^n\right)}{\mathit{\text{CR}}}$$ (6)

where CR is the cooling rate. The discretization of equation 5.6 is expected to bring about errors which depend on the time step. The time steps chosen (4 ms or less) were found to provide a stable value for calculated values of Δx, which did not change with smaller time steps. It is noted that the current nonequilibrium method of analysis assumes the heterogeneous nucleation and subsequent crystal growth in a given node is not affected by adjacent nodes due to impingement, and by defining the node spacing to be sufficiently larger than the characteristic diffusion length of glycerol (as discussed earlier in Section 3) the change in concentration brought about by crystal growth is localized and does not affect the original glycerol concentration of adjacent nodes.

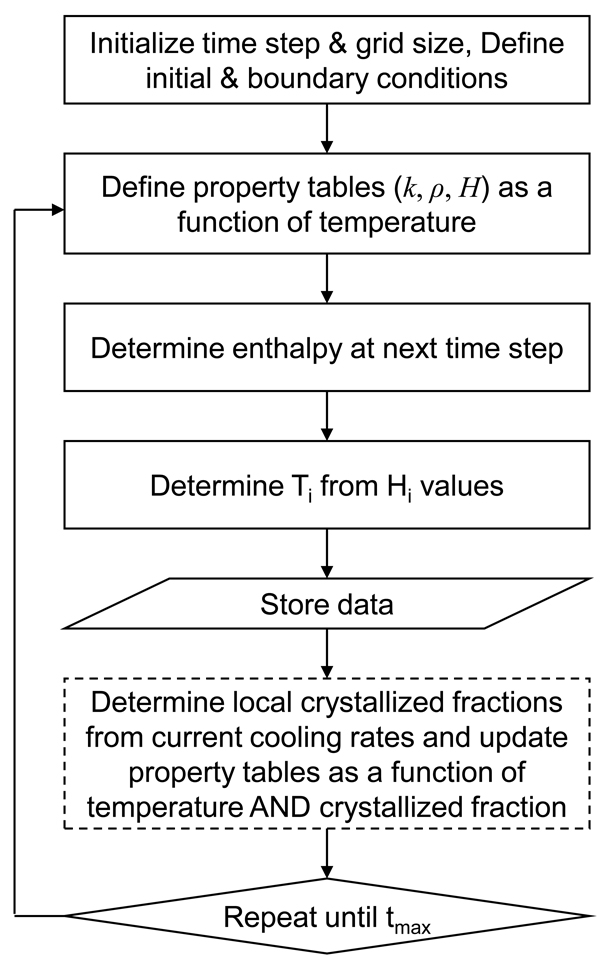
The original enthalpy code used in the previous section for analysis under equilibrium cooling conditions was modified (Fig. 9) so that the cooling rate per node location would be monitored and the crystallized fraction per node location would be updated accordingly. Based on the crystallized fractions, local thermal property values needed to be modified due to the difference in the water/ice ratio at a given temperature compared to quasi-equilibrium values. Thermal conductivity was redefined as a function of both temperature and cooling rate (or crystallized fraction):

$$k(T,f_c)=w_{H2O}\{f_c\cdot k_{\mathit{\text{ice}}}(T)+[1-f_c]\cdot k_{\mathit{\text{wat}}}\}+w_{\mathit{\text{gly}}}\cdot k_{\mathit{\text{gly}}}(T)+w_{\mathit{\text{NW}}}\cdot k_{\mathit{\text{NW}}}$$ (7)

where w_H20 is the weight fraction of water, k_ice is the thermal conductivity of ice, k_wat is the thermal conductivity of water, w_gly is the weight fraction of glycerol, k_gly is the thermal conductivity of glycerol, w_NW is the weight fraction of the non-water tissue components, and k_NW is the thermal conductivity of the non-water tissue components. k_gly values were obtained from [93] [94] while k_NW for pig liver was determined from the relationship:

$$k(T)=w_{6\mathit{\text{MG}}}\cdot k_{6\mathit{\text{MG}}}(T)+(1-w_{6\mathit{\text{MG}}})\cdot k_{\mathit{\text{NW}}}$$ (8)

which implies that the thermal conductivity of pig liver treated with 6M glycerol [76], k(T), is a weight averaged value of the PBS + 6M glycerol solution [20], k_6MG(T), and the non-solution tissue component, k_NW. Fig. 10 shows the range of k values (using eqn. 7) possible for porcine liver treated with PBS + 6M glycerol bracketed by cases when no crystallization occurs due to a sufficiently high cooling rate and when maximal crystallization occurs under slow (quasi-equilibrium) cooling conditions. The local regions in the system of analysis will experience a cooling condition in between these two extremes. The change in k value if a region experiences a constant cooling rate of 10 °C/min and undergoes heterogeneous nucleation at −50 °C is also shown as an example. Definitions similar to those used for thermal conductivity were also used to define density and specific heat as a function of temperature and cooling rate (or crystallized fraction). The change in enthalpy values due to the change in crystallized fraction values was determined as (Table 1):

$$\mathrm{\Delta }{h}_i=h_i^{n-1}+c_i^n\left(T_i^n-T_i^{n-1}\right)+f_{c,i}^n\cdot \mathrm{\Lambda }-f_{c,i}^{n-1}\mathrm{\Lambda }$$ (9)

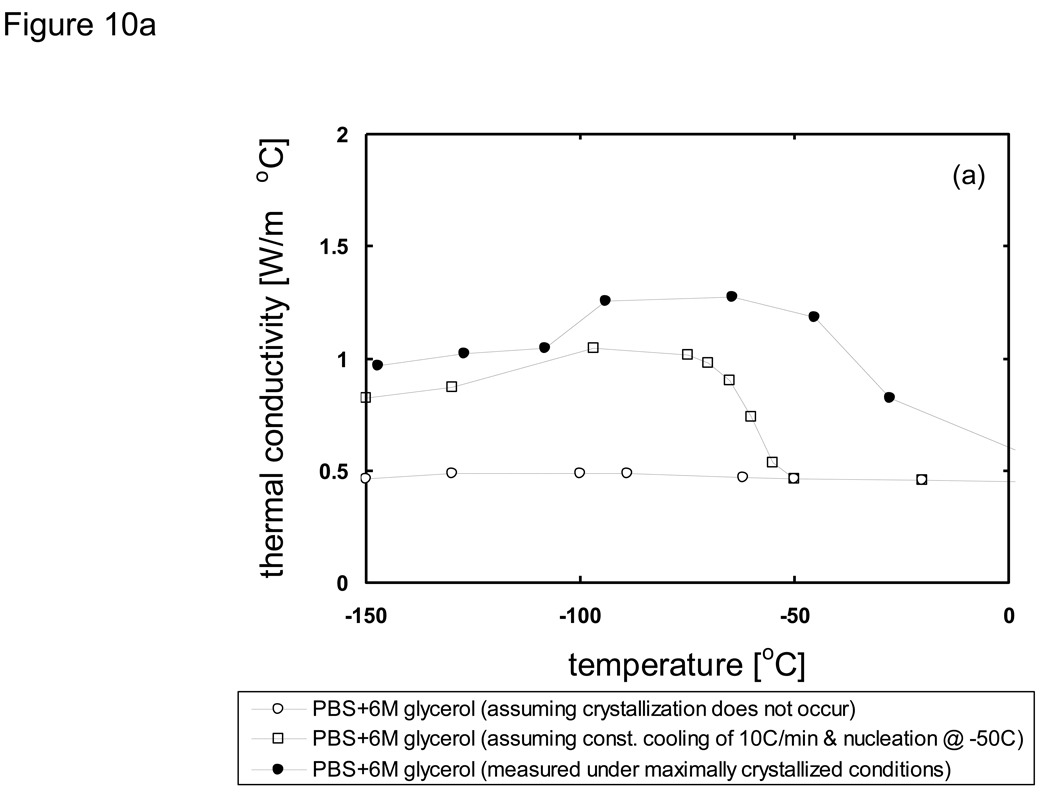
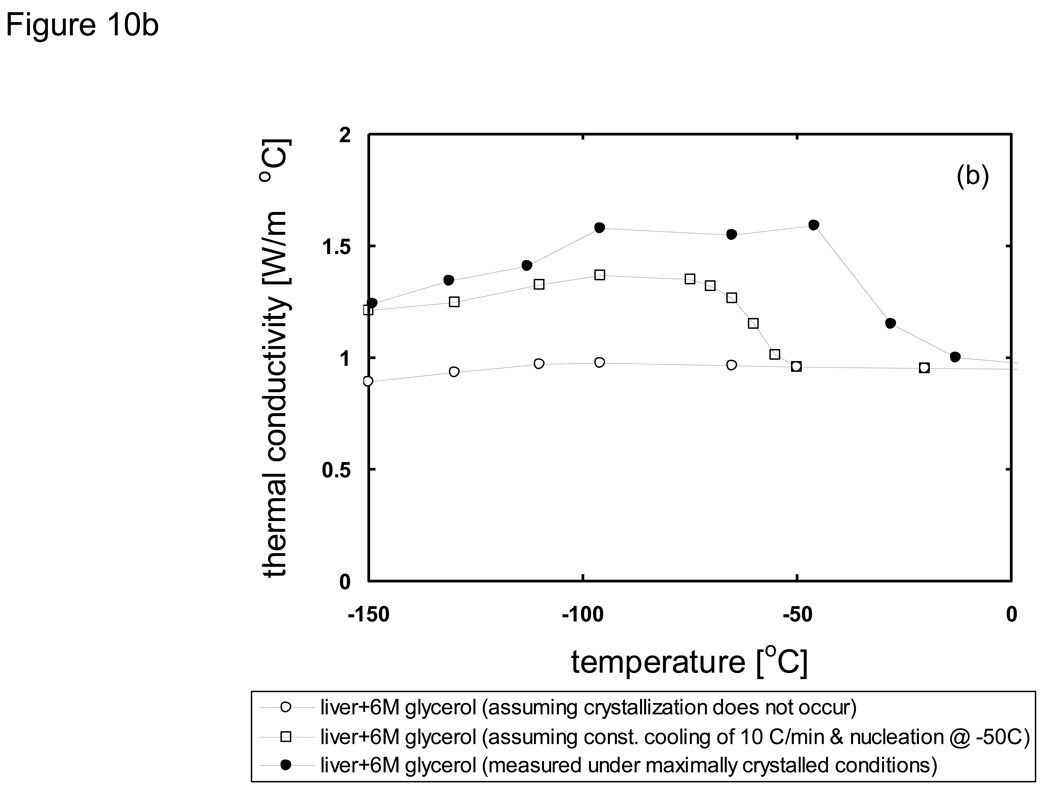
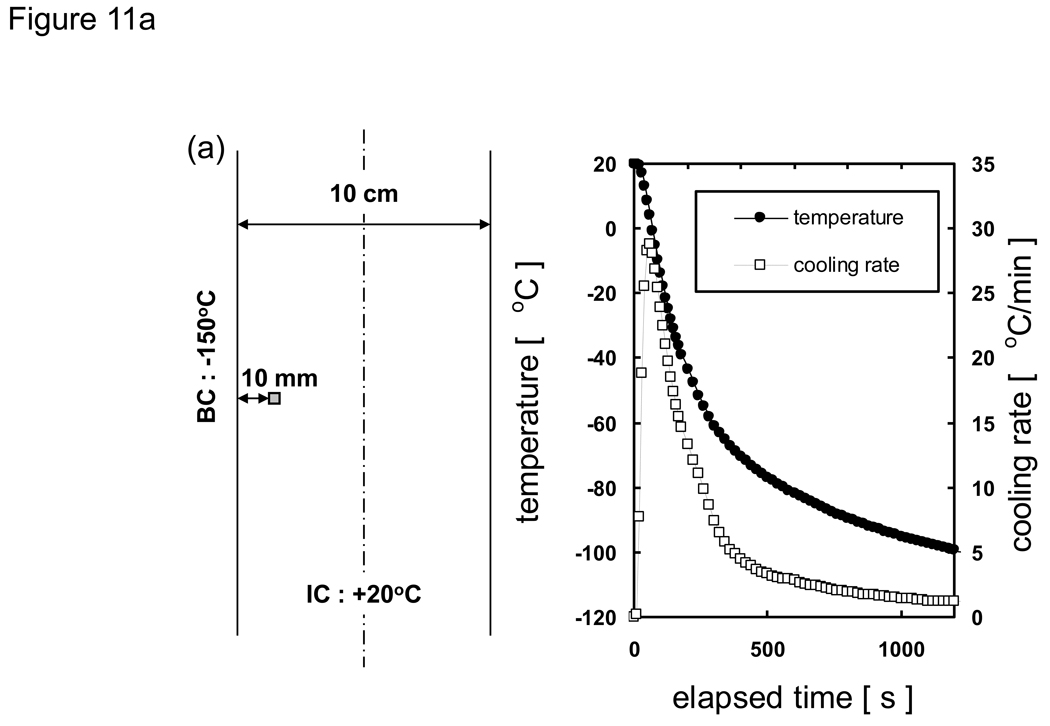
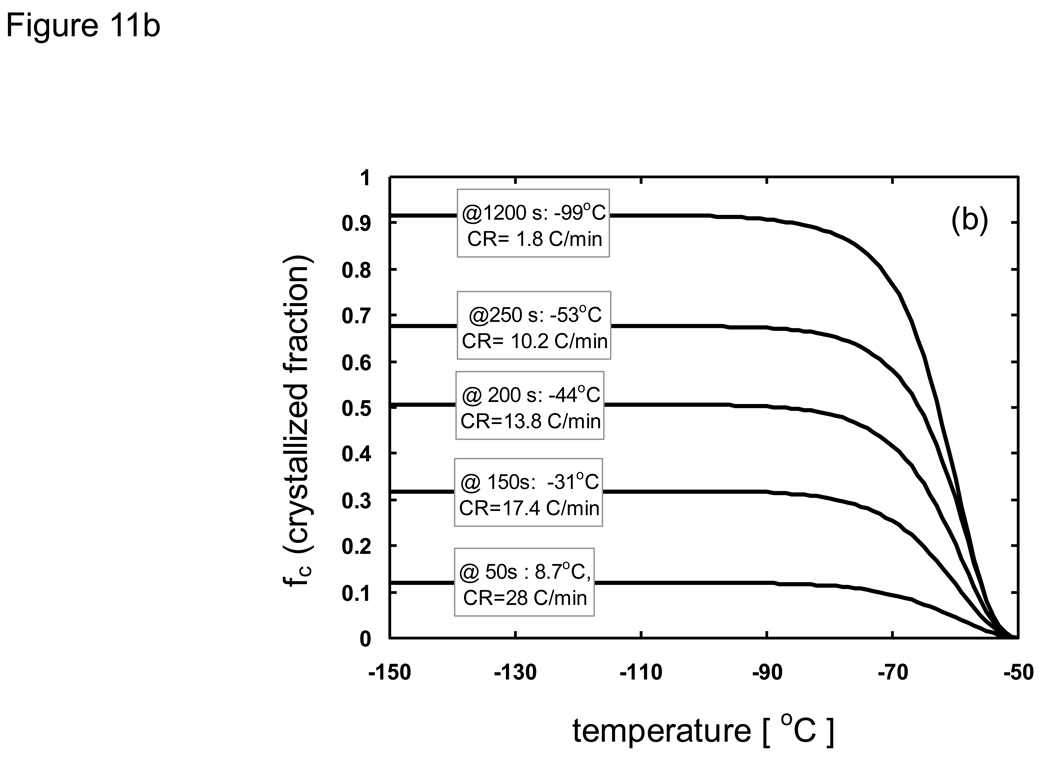
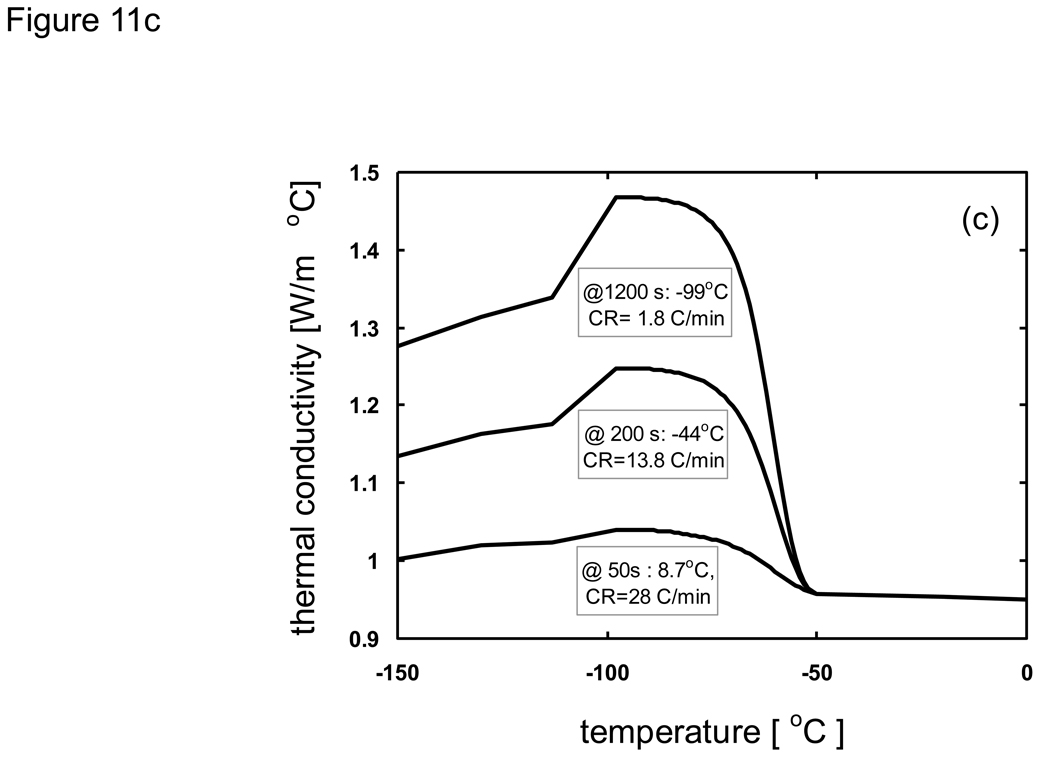
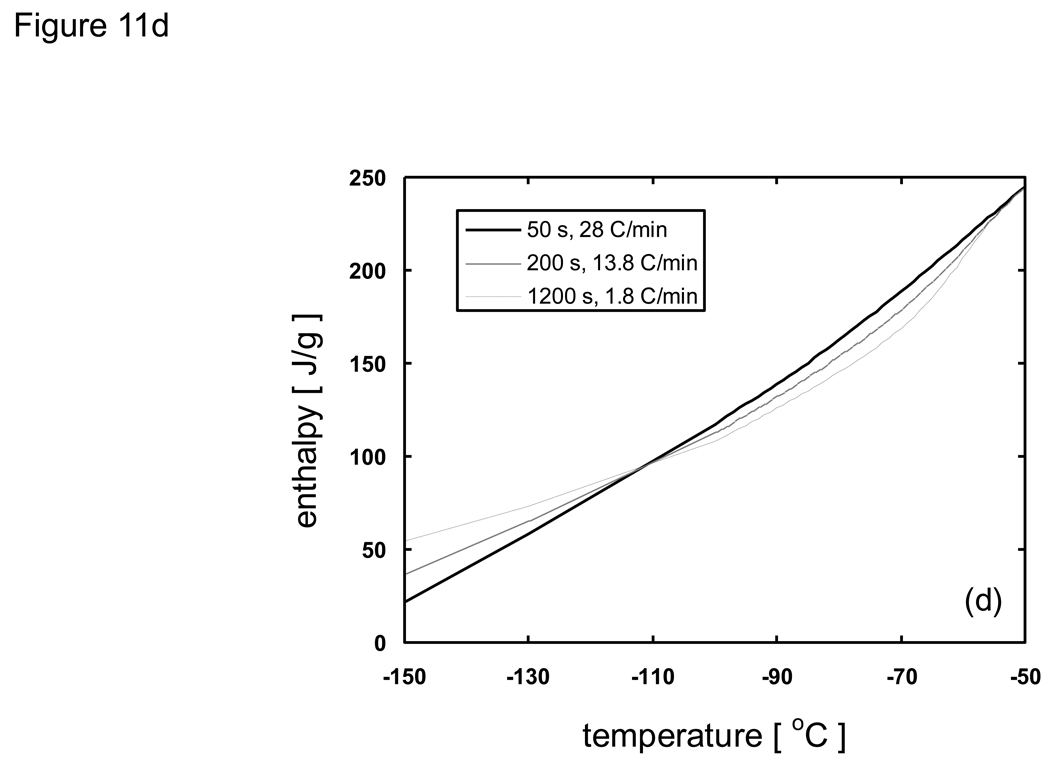
where h is the specific enthalpy, c is the specific heat, and Λ is the latent heat. As an example that illustrates how the modified enthalpy method determines the thermal history of a system of interest, observe the changes at the node corresponding to the location 10 mm from the cooling surface of a 10 cm-thick sample of porcine liver treated with PBS + 6M glycerol as shown in Fig. 11. The thermal history is the result of continuously updating the local cooling rate to determine the crystallized fraction as a function of temperature, and subsequently updating the enthalpy vs. temperature table as well as the thermal properties. It is seen based on the temperature profile (Fig. 11a) that the local area experiencing fast cooling rates at early times reduced with the passage of time. The crystallized fraction is then defined as a function of temperature (eqn. 6) and continuously updated with the passage of time. Fig. 11b plots show predicted f_c values based on cooling information (i.e. rates) available up to designated times. Later times show slower cooling rates and the values consequently increase dramatically. Since it was assumed (based on experimental observations [82] [20]) that heterogeneous nucleation occurs at −50 °C crystallized fraction values above this temperature were not updated. Additionally, f_c values only below the current temperature were updated (since higher temperatures were already traversed based on the f_c values at earlier times), and further crystal growth was assumed not to occur below T_g (~ −100 °C). It is noted that an f_c value of unity does not imply that the entire volume element has crystallized, but rather that the maximum possible amount of crystallization has occurred (which is assumed to be ~ 11% of the entire volume for porcine liver treated with 1×PBS + 6M glycerol).

Fig. 9.

Flowchart of the enthalpy method used in the current study to determine the cooling history of various biomaterials. The dashed box is the additional modification step applied in solving non-equilibrium cooling problems.

Fig. 10.

Predicted thermal conductivity of a) PBS + 6M glycerol and b) porcine liver treated with PBS + 6M glycerol under various cooling conditions. Values will depend upon the crystallized fraction which is determined from the cooling rate and nucleation temperature.

Fig. 11.

Predicted a) thermal history/property of cooling pig liver treated with PBS + 6M glycerol at the location 10 mm from the cooling surface (1-D Cartesian, thickness = 10 cm, initially at 20 °C, subject to boundary temperatures of −150 °C). b) Crystallized fraction f_c (as a function of temperature) is continuously updated based on the current local cooling rate. c) Thermal conductivity, density (not shown), specific heat (not shown), and d) enthalpy are also continuously updated (as a function of temperature) due to the change in cooling rate (and thus f_c) with the passage of time.

Enthalpy versus temperature tables were updated (using eqn. 9) based on the local cooling rates (which changes with time) as shown in Fig. 11d. Enthalpic values above T_n (−50 °C) will not change depending on the cooling rate since crystals are assumed not to occur. With lower cooling rates (more crystallization) there was a larger change in enthalpic values between −50 and −100 °C due to latent heat effects. However, the overall change in enthalpy (difference between −50 and −150 °C) was less compared to faster cooling rates due to the reduction in specific heat with more crystallization which leads to a reduction in the change in the sensible heat. The opposite effect was noticed when the cooling rates were high, where enthalpic changes due to crystallization/latent heats was minimized while enthalpic changes associated with the change in sensible heat became large.

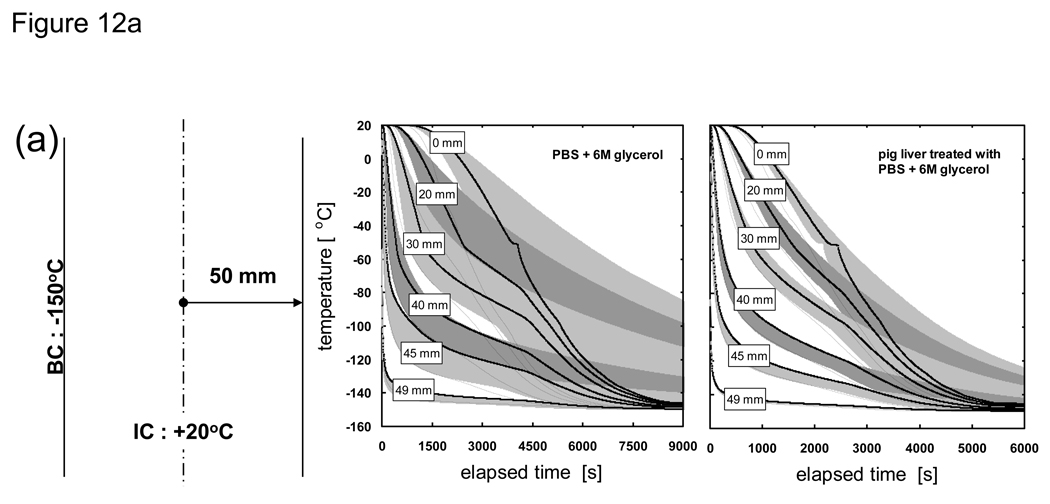
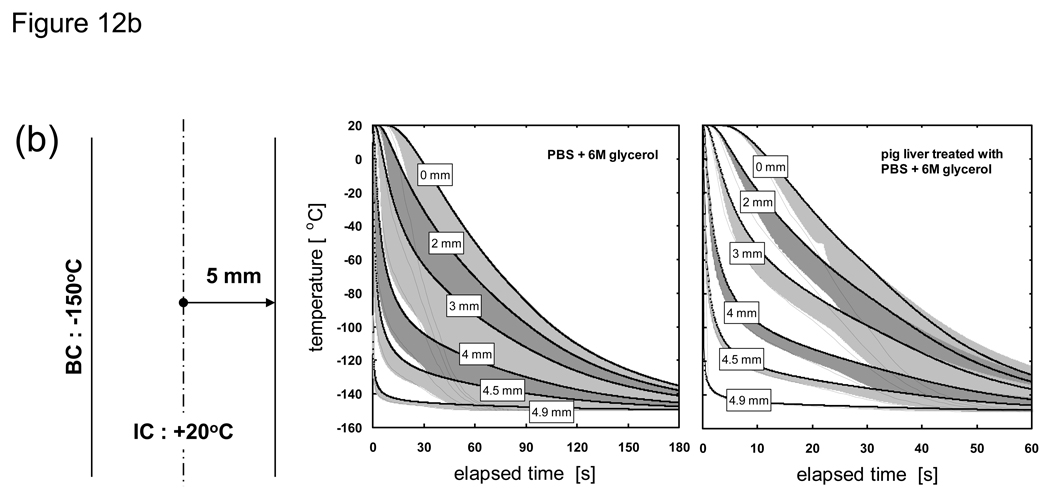
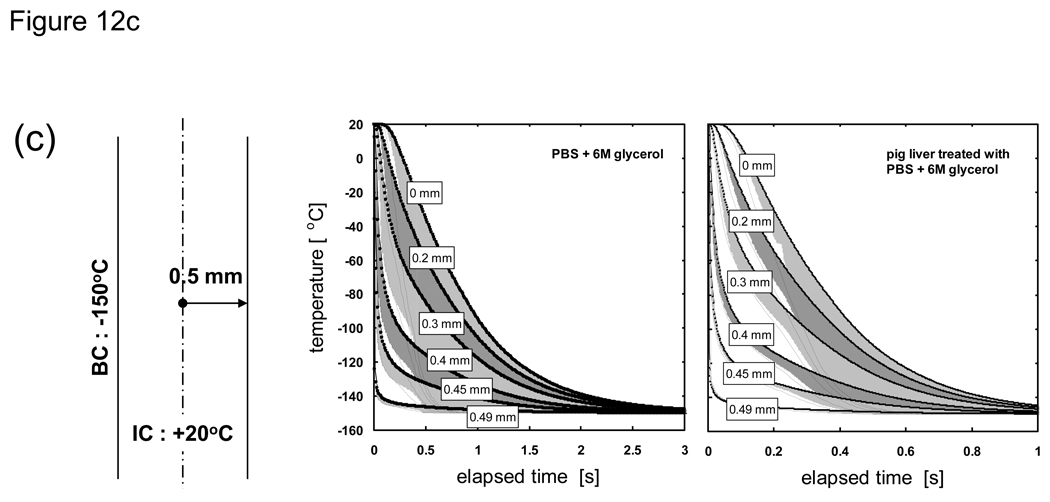
Fig. 12 shows the cooling history of PBS + 6M glycerol and pig liver treated with PBS + 6M glycerol under varied thickness conditions. The solid lines are the result of an analysis in which the thermal properties are allowed to change based on the local cooling rate and take into account non-equilibrium crystallization effects. The dotted lines are based on measured (quasi-equilibrium) thermal property values and do not take into account non-equilibrium effects. The onset of crystallization for the quasi-equilibrium case is −26 °C (T_m) while the cooling rate-dependent case nucleates at a heterogeneous nucleation point of −50 °C. The edges of the bands surrounding the solid lines indicate cases when the crystallized fraction was forced to be either zero (right edge of shaded region) or unity (left edge of shaded region) and bracket the expected temperature distribution for the system at that location.

Fig. 12.

Thermal history of PBS + 6M glycerol and porcine liver treated with PBS + 6M glycerol at the indicated distances from the centerline. Solid lines represent non-equilibrium cooling conditions with supercooled nucleation at −50 °C (as measured in [82] [20]) where thermal properties are dependent on temperature and cooling rate (or crystallized fraction). Dotted lines represent quasi-equilibrium cooling conditions with nucleation at the melting point (−26 °C) where thermal properties are measured values from [20] [76] and depend on temperature only. Shaded regions around solid lines indicate the extent of temperature deviation possible if the crystallized fraction is forced to zero or unity at the nucleation point regardless of the cooling rate. Samples are assumed to be initially at 20 °C and cooled with a constant outer surface temperature of −150 °C. Geometry is a 1-D Cartesian infinite slab with a thickness of a) 100, b) 10, and c) 1 mm.

It can be seen from Fig. 12 that a consideration of cooling rate dependency is not necessary near the outer boundary (solid and dotted lines show similar history) but becomes critical as locations closer to the centerline are interrogated. It is also evident from the 100 mm-thick samples that the cooling rate dependent (solid) lines near the outer boundary are offset to the right edge of their shaded bands, which indicates that a minimal amount of crystallization occurs. However, the solid lines start moving leftward within their shaded bands at locations deeper into the sample, which indicates that more and more crystallization occurs at these locations due to a drop in cooling rates experienced in these regions. These shifts are minimally observed for the 10 and 1 mm-thick samples, indicating that they experienced high cooling rates throughout and that crystallization was minimal. It is also clear from the thermal history of different thicknesses that normalization with respect to the characteristic length of the system will not allow the temperature curves to collapse into a single line due to the amplified effect of non-equilibrium cooling and crystallization on the outcome of larger (i.e. in thickness) systems.

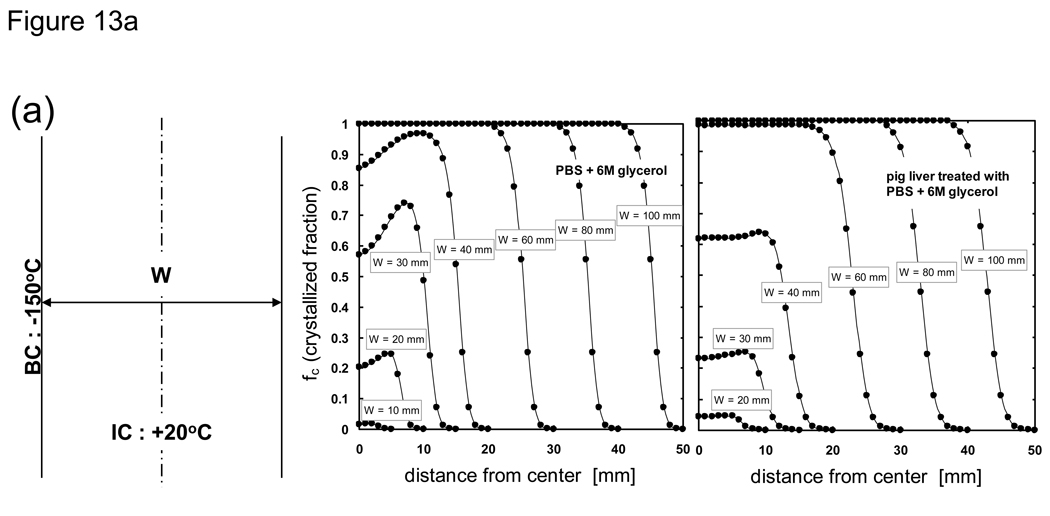
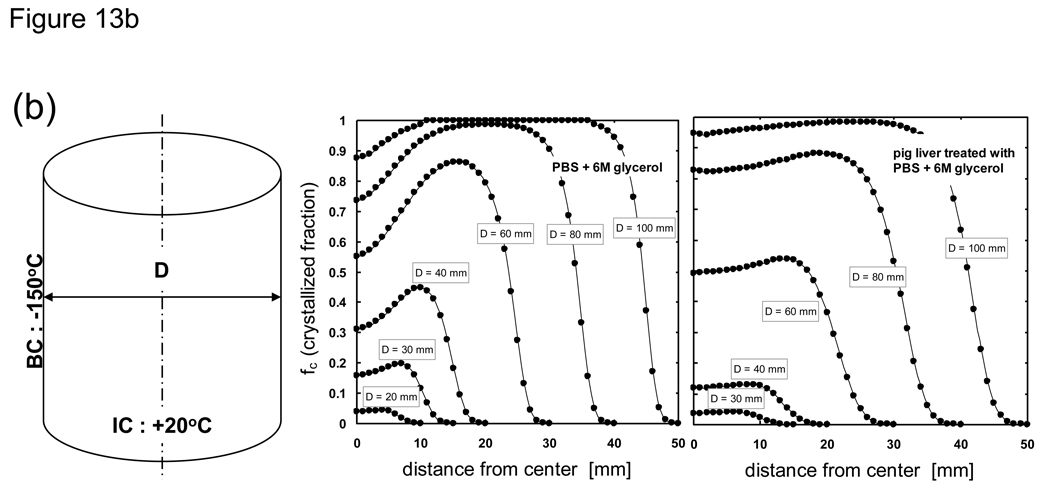
Based on the above results further analyses were performed by varying the sample thickness in order to gauge the size under which significant crystallization would occur. Fig 13 shows the crystallized fraction distribution of PBS + 6M glycerol and pig liver treated with PBS + 6M glycerol post-cooling based on 1-D Cartesian and cylindrical geometries. It can be seen that for the largest thickness investigated (100 mm) a majority of the system achieves maximum crystallization (f_c = 1). The centerline achieves maximum crystallization for Cartesian systems, but a reduction in f_c values is observed in cylindrical systems due to more rapid cooling near the core brought about from geometric differences. As the system size becomes less, the system overall achieves less crystallization and f_c becomes negligible for widths less than 10 mm. It is interesting to note that even for Cartesian geometries, the peak location corresponding to a maximum amount of crystallization at a given width is not at the center but located somewhere between the center and outer surface. This can be attributed to the fact that these mid-locations experienced slower cooling rates overall compared to center locations, and is similar to findings from [23] in which it was shown that for a 2 cm slab of pure water the cooling rates close to the center of the slab are higher than those midway between the outer cooling surface and the center of the slab. Additionally, current findings concerning the peak location of crystallization is in agreement with the results from [95] in which it was shown that there is a smaller probability of crystallization in the center compared to the regions nearer to the outer surface of a rectangular slab of water.

Fig. 13.

Post-cooling crystallized fraction distribution of PBS + 6M glycerol and porcine liver treated with PBS + 6M glycerol. Samples are assumed to be initially at 20 °C and cooled with a constant outer surface temperature of −150 °C. Geometry is a 1-D a) infinite slab or b) infinite cylinder with varying thickness values (labeled as width or diameter).

It should be noted that the current numerical study focused on understanding the thermal history of biomaterials using a heat transfer analysis which is essentially decoupled from the mass transfer of the system. That is, the solute flux associated with crystal growth and microstructure formation was neglected based on the fact that mass diffusivity is several orders of magnitude less than the heat diffusivity of the system. Therefore, although the numerical predictions are based on thermal properties of relevant biomaterials, the results should be treated as an ‘idealized state’ in which the mass transfer of solutes will be confined to the dimensions of the nodes used and crystal growth is solitary and without impingement.

4. Summary

An important engineering task in cryobiology is to measure or calculate the heat transfer during freezing-induced phase change in biosystems and then correlate this with the biological outcome. For situations when direct measurement of thermal transport becomes difficult and simplified analytical approaches are inadequate, numerical calculation becomes a valuable alternative in allowing us to predict the outcome of a cryobiological procedure. A survey of thermal properties of biomaterials available in the literature has shown that while there is a large database available in the suprazero temperature domain there is a lack of data in the subzero temperature domain. The fact that reliable numerical predictions depend on the use of appropriate thermal properties (as shown here for two cases; PBS + glycerol and liver + glycerol) advocates the need for the further tabulation of thermal properties in the subzero temperature domain. The implications of using approximated (as H₂O) or limited (assumed constant over a wide temperature range) property values versus actual values were gauged by performing cooling predictions. The use of H₂O properties resulted in the significant underestimation of required cooling times while the use of constant properties for biomaterials resulted in the significant overestimation of cooling times. The addition of glycerol to biological solutions or tissue resulted in thermal histories which required significantly greater times to cool compared with those for H₂O. A modified numerical scheme was developed for systems with high glycerol content to accommodate non-equilibrium cooling effects in which an empirical crystallization model was employed and thermal properties were dependent on both temperature and cooling rate. Temperature-vs.-time predictions based on non-equilibrium properties showed large differences compared with results using quasi-equilibrium properties (which are generally reported in the literature) for systems with large dimensions. Additionally, the region between the center and the outer surface experienced the lowest cooling rates, and correspondingly had the largest amount of crystallization.

Appendix A1.

Thermal properties of biologically relevant liquids and chemicals in the subzero temperature domain^*

Material	Thermal Conductivity [W/mK]	Thermal Diffusivity ×107 [m2/s]	Specific Heat [J/gK]	Latent Heat (ice) [J/g]	Reference
Blood					[96]
packed cells	1.24 (−10 °C)	6.8(−10 °C)
	1.51 (−40 °C)	11.0(−40 °C)
	1.98 (−80 °C)	17.2(−80 °C)
	2.26 (−100 °C)	20.4 (−100 °C)
plasma	2.03 (−10 °C)	9.7 (−10 °C)
	2.31 (−40 °C)	15.1 (−40 °C)
	2.86 (−80 °C)	22.9 (−80 °C)
	3.19 (−100 °C)	26.9 (−100 °C)
Whole	1.64 (−10 °C)	8.7 (−10 °C)
	1.92 (−40 °C)	13.6 (−40 °C)
	2.38 (−80 °C)	20.4 (−80 °C)
	2.66 (−100 °C)	23.7 (−100 °C)
DMSO (dimethyl sulphoxide)					[97]
100%	0.2 (−20 °C)
75% (v/v)	0.243 (−20 °C)
50% (v/v)	0.318 (−20 °C)
Ethanol					[92]
50% (w/w)				55.3
45% (w/w)				58.3
40% (w/w)				65.7
Ethylene glycol
100%	0.242	0.934			[48]
	(−5 ~ −20 °C)	(−5 ~ −20 °C)
45% (w/w)				44.9	[91]
40% (w/w)				65.3
27% (w/w) + glycerol (18%)				53.3
Glycerol					[97]
100%	0.258 (−20 °C)
75% (v/v)	0.299 (−20 °C)
50% (v/v)	0.362 (−20 °C)
50% (w/w)				50.6	[92]
40% (w/w)				86.8
40% (w/w) + ethanol (10%)				48.9
30% (w/w) + ethanol (20%)				39.9
20% (w/w) + ethanol (30%)				41.9
10% (w/w) + ethanol (40%)				38.9
					[20]
6M + 1× PBS	0.82 (−28 °C)		2.984 (−20 °C)	47.1
	1.27 (−65 °C)		1.996 (−73 °C)
	1.05 (−108 °C)		1.114 (−110 °C)
	0.97 (−147 °C)		0.834 (−148 °C)
2M + 1× PBS	1.61 (−27 °C)		3.781 (−5 °C)	178.6
	1.96 (−64 °C)		1.712 (−73 °C)
	2.15 (−108 °C)		1.206 (−110 °C)
	2.25 (−147 °C)		0.903 (−148 °C)
1M + 1× PBS	1.95 (−28 °C)		3.969 (0 °C)	238.2
	2.33 (−64 °C)		1.641 (−73 °C)
	2.83 (−109 °C)		1.216 (−110 °C)
	3.11 (−146 °C)		0.959 (−148 °C)
Glycol					[97]
100%	0.253 (−20 °C)
46.4% (w/w)	0.43 (0 °C)
	0.441 (−10 °C)
	0.437 (−20 °C)
	0.439 (−30 °C)
HP5 (organ perfusate)					[98]
whole	1.962 (−10.3 °C)
	2.394 (−30 °C)
	2.556 (−50 °C)
	2.936 (−70 °C)
+ 2M glycerol	0.896 (−10.3 °C)
	1.221 (−30 °C)
	1.486 (−50 °C)
	1.65 (−70 °C)
Milk (whole)				289.8	[68]
Propyl alcohol					[99]
35% (w/w)				144.1
Propylene glycol					[97]
100%	0.193 (−20 °C)
75% (v/v)	0.286 (−20 °C)
50% (v/v)	0.36 (−20 °C)
40% (w/w)				57	[100]
30% (w/w)				93.8	[99]
20% (w/w)				145.7
10% (w/w)				214.4
28% (w/w) + ethanol (7%)				65
36% (w/w) + glycerol (9%)				26.1
27% (w/w) + glycerol (18%)				50.3
14% (w/w)				92.5
+ propyl alcohol (21%)

^*weight and volume ratios are with respect to H₂O unless indicated otherwise.

A2.

Thermal properties of biological tissues and materials in the subzero temperature domain

Material	Thermal Conductivity [W/mK]	Thermal Diffusivity ×107 [m2/s]	Specific Heat [J/gK]	Latent Heat (ice) [J/g]	Ref.
Beef
bovine fat	0.193 (+0.1 °C)a	0.59 (+0.1 °C)a	2.3 (−40 °C)c		[48]a
	0.266 (−5 °C)a	0.98 (−5 °C)a	1.55 (−80 °C)c		[57]b
	0.216 (−7.6 °C)b	1.54 (−18 °C)a	1.00 (−120 °C)c		[101]c
	0.3 (−9.4 °C)b		0.85 (−160 °C)c
	0.28 (−18 °C)a
bovine fat (74.5% water, per-  pendicular to fiber)	0.478 (0 °C)	1.36 (−20 °C)			[102]
	0.930 (−5 °C)
	1.20 (−10 °C)
	1.43 (−20 °C)
bovine meat	0.417 (−7.3 °C)a		3.977 (+4 °C)b	205.8	[57]a
	0.448 (−7.5 °C)a		3.68 (−22 °C)c	~ 256.2d	[69]b
			2.0 (−23 °C)b		[101]c
			1.884 (−29 °C)b		[68]d
			1.842 (−34 °C)b
			2.43 (−34 °C)c
			1.8 (−40 °C)b
			1.88 (−57 °C)c
			1.63 (−87 °C)c
			1.05 (−169 °C)c
bovine meat (74.5% water)			3.6 (0 °C)		[103]
			2.5 (−20 °C)
			2.1 (−30 °C)
			1.9 (−40 °C)
bovine meat (75% water, 0.9%  fat, parallel to fiber)	0.480 (0 °C)				[104]
	1.36 (−10 °C)
	1.54 (−25 °C)
bovine meat (78.5% water)					[102]
			3.81 (0 °C)
			3.31 (−20 °C)
			2.89 (−30 °C)
bovine meat, lean					[102]
	0.480 (0 °C)	4.72 (−20 °C)
	1.06 (−5 °C)
	1.35 (−10 °C)
bovine meat, lean, neck	1.57 (−20 °C)				[46]
bovine muscle	0.415 (−7 °C)				[48]
	0.425 (+0.1 °C)	1.05 (+0.1 °C)
	1.393 (−5 °C)	5.37 (−5 °C)
eye loin, 69% water aged	1.076 (−18 °C)	6.84 (−18 °C)			[105]
	0.294 (0 °C)
	0.990 (−3 °C)
	1.04 (−10 °C)
flank, lean, 3.4% water	1.07 (−17 °C)				[104]
	1.07 (−10 °C)
round, 76% H2O, 3% fat	1.21 (−25 °C)				[50]
	0.47 (+2 °C)
	0.88 (−4 °C)
udder, 9% H2O, 89% fat	1.12 (−13 °C)				[104]
	0.21 (+2 °C)
	0.29 (−7 °C)
	0.29 (−12 °C)
Bone (femur, cow)	0.33 (−19 °C)				[106]
Chicken			4.354 (−1.8 °C)		[68]
			3.3 (−3.8 °C)
Duck			3.056 (−1.8 °C)		[68]
			2.47 (−3.8 °C)
Eggs				222.6	[68]
Fish	0.43 (0 °C)a			205.8	[107]a
	1.22 (−10 °C)a			~ 285.6b	[68]b
	1.37 (−20 °C)a
sea trout			3.684 (+4 °C)		[69]
			2.135 (−23 °C)
			1.926 (−29 °C)
			1.8 (−34 °C)
			1.758 (−40 °C)
Fruits				252	[68]
				~ 306.6
Gelatin					[104]
20%	1.57 (−10 °C)
	1.56 (−30 °C)
12%	1.89 (−10 °C)
	2.08 (−30 °C)
6%	2.09 (−10 °C)
	2.28 (−30 °C)
Kidney
79.8% water			4.1 (0 °C)		[108]
			2.14 (−23 °C)
			1.63 (−40 °C)
bovine, cortex	0.454 (+0.1 °C)	1.18 (+0.1 °C)			[48]
	1.535 (−5 °C)	4.71 (−5 °C)
	1.372 (−18 °C)	6.84 (−18 °C)
Lamb	1.77 (−19 °C)a		3.6 (−0.9 °C)b	201.6	[106]a
			2.135 (−2.9 °C)b	~ 231b	[68]b
64.9% water			3.39 (0 °C)		[108]
			1.93 (−23 °C)
			1.3 (−40 °C)
leg, 71.8% H2O, 8.7% fat	0.45 (+5.5 °C)				[50]
	1.05 (−8.5 °C)
	1.13 (−14.5 °C)
Liver
bovine	0.417 (+0.1 °C)a	1.05 (+0.1 °C)a			[48]a
	1.396 (−5 °C)a	4.77 (−5 °C)a			[109]b
	0.989 (−18 °C)a	5.71 (−18 °C)a
	1.93 (−32 °C)b
Porcine	1.6 (−11 °C)		3.659 (0 °C)	223.4	[76]
	1.75 (−64 °C)		1.522 (−73 °C)
	1.9 (−112 °C)		1.192 (−109 °C)
	2.01 (−147 °C)		0.941 (−147 °C)
porcine, treated with	1.56 (−10 °C)		3.394 (−4 °C)	146.4
1× PBS + 2M glycerol	1.68 (−64 °C)		1.611 (−73 °C)
	1.78 (−108 °C)		1.135 (−109 °C)
	1.73 (−146 °C)		0.872 (−147 °C)
porcine, treated with	1.0 (−13 °C)		2.807 (−24 °C)	35.9
1× PBS + 6M glycerol	1.55 (−64 °C)		1.993 (−74 °C)
	1.42 (−110 °C)		1.152 (−110 °C)
	1.24 (−148 °C)		0.809 (−148 °C)
porcine, treated with	0.65 (−10 °C)		2.688 (−23 °C)	40.1
1× PBS + 8M glycerol	1.27 (−64 °C)		1.969 (−75 °C)
	1.07 (−109 °C)		1.19 (−111 °C)
	0.86 (−149 °C)		0.781 (−148 °C)
Pork				117.6	[68]
				~ 138.6
ham			3.475 (+4 °C)		[69]
			1.884 (−23 °C)
			1.717 (−29 °C)
			1.633 (−34 °C)
			1.633 (−40 °C)
pig fat	0.360 (−9.1 °C)a		1.6 (−40 °C)b		[57]a
	0.366 (−10 °C)a		1.21 (−80 °C)b		[101]b
			1.03 (−120 °C)b
			0.88 (−160 °C)b
pig fat (3.1% water)	0.186 (0 °C)				[102]
	0.227 (−5 °C)
	0.254 (−10 °C)
	0.291 (−20 °C)
pig, lean, 6.1% fat, 72% water,	1.43 (−10 °C)				[104]
parallel to fiber	1.61 (−25 °C)
pig, lean, 6.1% fat, 72% water,	1.23 (−10 °C)				[104]
parallel to fiber	1.38 (−25 °C)
pig, lean, 76.8% water,	0.478 (0 °C)	3.89 (−20 °C)			[102]
perpendicular to fiber	0.767 (−5 °C)
	0.990 (−10 °C)
pig, lean, neck	1.29 (−20 °C)				[57]
	0.783 (−8 °C)
	0.835 (−8.4 °C)
pork, exterior,	0.408 (−9 °C)				[104]
6% H2O, 93% fat	0.21
pork, leg,	(+3 ~ −24 °C)				[50]
75.9% H2O, 6.7% fat	0.49 (+6 °C)
	1.28 (−8 °C)
	1.3 (−14 °C)
Seal					[104]
blubber, 4.3% H2O, 95% fat	0.19 (+5 °C)
	0.21 (−11 °C)
	0.21 (−22 °C)
Shrimp			3.6 (+4 °C)		[69]
			2.3 (−23 °C)
			2.1 (−29 °C)
			1.968 (−34 °C)
			1.884 (−40 °C)
Turkey			3.517 (−1.8 °C)		[68]
			2.26 (−3.8 °C)
Veal	0.48 (+6 °C)				[50]
leg, 75% H2O, 2.1% fat	1.3 (−9.5 °C)
Vegetables				218.4	[68]
				~ 319.2