Abstract
The influence of muscle fiber motion during exercise on diffuse correlation spectroscopy (DCS) measurements of skeletal muscle blood flow is explored. Isotonic (with muscle fiber motion) and isometric (without muscle fiber motion) plantar flexion exercises were performed at 30% of maximal force on a dynamometer, and muscle blood flow was continuously monitored on the medial gastrocnemius (calf) muscle of a healthy volunteer using DCS. During exercise, dynamometer recordings including footplate position, footplate angular velocity, and plantar flexion torque were obtained. Muscle fiber motions introduced artifacts into the DCS signals, causing an overestimation of blood flow changes. We show how proper co-registration of dynamometer recordings and DCS measurements enables separation of the true blood flow responses during exercise from those affected by the motion artifacts.
OCIS codes: (170.0170) Medical optics and biotechnology; (170.3660) Light propagation in tissues; (170.3880) Medical and biological imaging; (170.6480) Spectroscopy, speckle
1. Introduction
The study of blood flow responses to exercise may provide useful information for diagnosis of vascular diseases. However, assessment of skeletal muscle blood flow during exercise is a complex task, and in the past, assessment schemes have often required the use of invasive, expensive, and less than precise measurement techniques. Doppler ultrasound and magnetic resonance angiography (MRA) have been used for this purpose, but they are limited to assessment of blood flow within large vessels. Microvascular blood flow evaluation techniques include capillaroscopy [1], laser Doppler flowmetry (LDF) [1,2], skin perfusion pressure [3], and optical coherence tomography [4]; generally, however, these techniques are limited to measuring blood flow at the skin level. Recent technical advances (e.g., positron emission tomography (PET) [5], arterial-spin labeled MRI (ASL-MRI) [6]) have made it possible to monitor microvascular blood flow in deep tissues, but these imaging modalities require large and costly instrumentation that limits their routine use in exercise and other clinical settings.
To date, diffuse optical techniques probing tissue oxy- and deoxy-hemoglobin concentrations (called Diffuse Optical Spectroscopy (DOS) or Near-infrared Spectroscopy (NIRS)) have shown promise for noninvasive measurement of blood oxygenation in deep muscle tissues [7–11]. Unlike Doppler ultrasound and MRA, DOS is sensitive to small vessels such as arterioles, capillaries, and venules, and researchers have applied DOS to investigate tissue oxygenation changes in skeletal muscles during different types of exercise. DOS research has found that muscle oxygenation responses to exercise can be associated with the severity of various vascular diseases [11–16]. DOS has also been used to indirectly estimate skeletal muscle blood flow at several discrete time-points by applying venous occlusion to an arm or limb [13,17,18]. Unfortunately, the occlusion interrupts blood flow, making the measurements difficult during exercise.
Recently a related optical technology, diffuse correlation spectroscopy (DCS), has been employed non-invasively in the near-infrared for direct measurement of the relative change of blood flow (rBF) in deep tissues [19–31], including skeletal muscles [32–37]. DCS uses the rapid temporal fluctuations of NIR light intensity to directly detect the motion of moving scatterers (e.g., red blood cells) in the microvasculature of biological tissues. In contrast to venous occlusion DOS/NIRS, DCS does not require the interruption of blood flow during measurement and permits continuous assessment of muscle blood flow during exercise. DCS measurements of tissue blood flow variation have been validated by other standards, including Doppler ultrasound [32,38,39], laser Doppler [40], Xenon-CT [41], and arterial-spin-labeled MRI (ASL-MRI) [22,33]. One validation study [33], related to the present research, concurrently compared blood flow in human calf muscle during cuff inflation and deflation using DCS and ASL-MRI.
Researchers have thus begun to explore the use of DCS in muscle during exercise [32] and electrical stimulation [34,35]. These blood flow measurements, however, can be adversely influenced by the overall motions of scatterers in the vasculature and muscle structures during exercise/stimulation [34] (e.g., motions of cell nuclei and mitochondria inside muscles [42], among other factors). Clearly, improved understanding and characterization of these motion artifacts are needed, if the DCS technique is to be optimally used during exercise. The goal of the present study is to investigate the influence of motion artifacts on DCS measurements during exercise, and then to introduce protocols that help separate DCS blood flow signals from those affected by the motion artifacts.
To estimate the influence of these motion artifacts, we compared DCS signals measured from the medial gastrocnemius muscle during two types of plantar flexion exercise on a dynamometer: isotonic plantar flexion (with muscle fiber motion) and isometric plantar flexion (without muscle fiber motion). We found that muscle fiber motions caused a substantial increase in the DCS ‘blood flow’ signals during exercise. We also recorded the footplate position, footplate angular velocity, and plantar flexion torque during the exercises. We show how proper co-registration of dynamometer recordings and the DCS measurements enables separation of the true blood flow responses during exercise from those affected by the motion artifacts. Potentially, with these improvements, the study of blood flow responses to exercise by DCS may provide useful information for diagnosis of muscle vascular diseases.
2. Methods and materials
One healthy male volunteer participated in this study with IRB approval and appropriate consent. Measurements were conducted at the Graduate Center for Gerontology, University of Kentucky. Three exercise protocols of plantar flexion were used to investigate the muscle fiber motion artifacts on DCS measurements, including isotonic/isometric exercises on a dynamometer and toe up/down on the ground. A fiber-optic probe was taped on top of medial gastrocnemius muscle for continuous DCS measurements during exercise. The measurement techniques, experimental protocols and data analyses are described in the following subsections.
2.1 Near-infrared diffuse correlation spectroscopy
Details of the optical instrument for DCS [see Fig. 1(d) ] are described elsewhere [32,33,36,43]. Briefly, a narrowband continuous wave laser diode working at 785 nm (Crystalaser Inc., NV, USA) with long coherence length (> 5 meter), four fast photon-counting avalanche photodiodes (APDs) (Pacer Components Inc., UK), and a 4-channel autocorrelator board (Correlator.com, NJ, USA) facilitate measurements of blood flow.
Fig. 1.
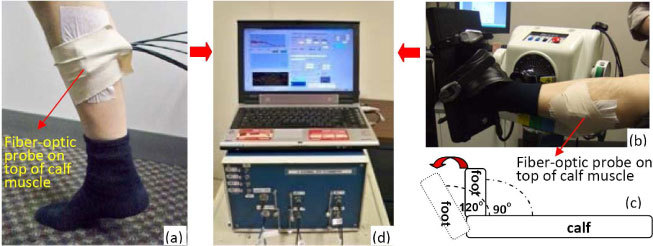
(a) Toe up/down plantar flexion (PF) exercise on the ground. (b) Isotonic and isometric PFs on a dynamometer. (c) The foot position changes (90° ←→ 120°) during isotonic PF. (d) 4-channel DCS device.
Output from the laser is delivered to the tissue through a multimode optical fiber (diameter = 200 µm). A single-mode fiber (diameter = 7 µm) is used to collect photons from a single speckle emitted from the tissue surface. The light intensity fluctuations are detected by the APD connected with the single-mode fiber. The autocorrelator takes the APD output and computes the light intensity temporal autocorrelation function. From the normalized light intensity temporal autocorrelation function, the electric field temporal autocorrelation function G1(r, τ) is derived. This correlation function is related to motions of scatterers in media that multiply scatter light [44,45]. For tissue studies, it has been demonstrated that this correlation function satisfies the correlation diffusion equation in highly scattering media [19,30–32,43,46,47]. Solutions of the correlation diffusion equation can have different forms depending on the nature and heterogeneity of the scatterer motion. In semi-infinite homogeneous media, G1(r, τ) is a function of the distance between the source and detector fibers, the medium absorption coefficient µa, the reduced scattering coefficient µs’, the effective reflection coefficient Reff, and the mean-square displacement of the moving scatterers in the medium <Δr2(τ)> [31,40]. The mean-square displacement <Δr2(τ)> directly characterizes the scatterer movement. For the case of diffusive motion, <Δr2(τ)> = 6DBτ, where DB is an effective diffusion coefficient of the moving scatterers. In this case the correlation function G1(r, τ) decays approximately exponentially in the decay time τ. Its decay rate, Γ (sec−1), depends on a parameter α (proportional to the tissue red blood cell volume fraction), and on the extent of motion of the blood cells. The blood flow-index (αDB) is then derived by fitting the autocorrelation curve to the solution of G1(r, τ) [19,31,33], and assuming the µa, µs’ and Reff based on the reported muscle tissue optical properties [12,16,32,40]. Although the units of αDB (cm2/s) differ from the traditional blood perfusion unit [ml/min/100 g], changes in αDB have been found to correlate quite well with other blood flow as measured by other modalities [30,33,38–41].
DCS can be used in many physiological situations requiring diverse probe designs [21,22,25,32]. In this study we tightly bundled four single-mode fibers to detect light from multiple speckles simultaneously [25]. The separations between the source (200 µm) and four detector fibers (7 µm) were ~2.5 cm. The four-channel autocorrelator was connected to four detectors and generated four autocorrelation curves every 44 ms. Seven consecutive autocorrelation curves from each channel were then averaged respectively to get one smoothed correlation curve. The signal-to-noise ratio was increased by averaging these four smoothed autocorrelation functions. With adequate signal-to-noise, the data sampling rate of DCS was 2.2 Hz.
2.2 Dynamometer
The isotonic and isometric plantar flexion exercises (see Section 2.3) were performed on a Biodex multi-joint dynamometer (System 4, Biodex Medical Systems, Shirley, New York, USA) [see Fig. 1(b)]. The participant sat in a reclined position with a hip angle of approximately 85°, a knee angle of approximately 120°, and his leg was aligned parallel to the ground [see Fig. 1(b)]. A Velcro strap across the thigh, an adjustable seat belt across the waist, and two shoulder straps were employed to minimize hip flexion and upper body movement. Strapping across the toes and the top of the foot secured the participant foot to the dynamometer footplate. Dynamometer recordings, including footplate position, footplate angular velocity, and plantar flexion torque, were obtained at high sampling rate (100 Hz) using the Biodex Advantage software version 4.0. The dynamometer recordings were synchronized with DCS measurements and used to determine skeletal muscle status (e.g., contracting or non-contracting, see Section 2.4).
2.3 Experimental protocols
Plantar flexion exercise was selected in this study because it selectively works the gastrocnemius muscle and can be performed by both healthy subjects and most of the patients with muscle vascular diseases (e.g., peripheral arterial disease).
Three exercise protocols of plantar flexion were used in this study, including toe up/down on the ground and isotonic/isometric exercise on a dynamometer.
Protocol #1: toe up/down plantar flexion exercise on the ground [see Fig. 1(a)]. The subject remained in a stable standing position during the test protocol. Both legs were positioned shoulder width apart. A skinfold caliper (Beta Technology Inc., Santa Cruz, California, USA) was used to mechanically measure the thickness of the upper layers (skin and adipose) above medial gastrocnemius muscle. The optical probe was then placed over the calf (medial gastrocnemius) and secured with an elastic bandage. After a 3-minute baseline, the subject performed 15 plantar flexion exercises (2-second toe-up and 2-second toe-down) within one minute, followed by a 3-minute recovery measurement.
Protocol #2: isotonic plantar flexion exercise on a dynamometer [see Fig. 1(b) and 1(c)]. Once positioned in the Biodex chair, the participant was given a verbal description of the maximal voluntary isometric contraction (MVIC) to be performed. The participant then performed three practice contractions (ankle angle = 90°) with a 2-minute rest period between each contraction. After practicing, the participant performed three test contractions (3 MVICs, 2 minutes rest between contractions) and was instructed to contract as hard and as fast as possible, while the highest peak torque value was recorded.
The optical probe was then placed and secured over the medial gastrocnemius. After 3-minute resting baseline measurement (the foot at 90° position), the participant was asked to perform an isotonic protocol, involving 10 isotonic plantar flexion contractions (pushing the footplate from 90° to 120°) at 30% of the participant’s highest MVIC value. At the completion of each plantar flexion contraction the participant held the contraction for three seconds (ankle angle = ~120° plantar flexion). The participant’s foot was then passively returned to the starting position (ankle angle = 90°) and held for three seconds. The participant performed 10 isotonic exercises repeatedly within ~1.5 minutes. The recovery DCS measurement after exercise was made for approximately 3 minutes.
Protocol #3: isometric plantar flexion exercise on a dynamometer [see Fig. 1(b)]. The measurement configurations were similar to those described in the Protocol #2, except the footplate was fixed at an angle of 90° during the isometric plantar flexion exercise. After 3 minutes of DCS baseline measurement, the participant was asked to perform an isometric protocol, involving 10 isometric contractions at 30% of the participant’s highest MVIC value (ankle angle = 90°). Each isometric contraction was held for three seconds and a rest period of three seconds was given between each isometric contraction. This contraction-rest period was repeated for 10 times within ~1 minute. After the exercise protocol was completed, the recovery DCS measurement was continued for ~3 minutes.
2.4 Co-registration of DCS measurements and dynamometer recordings
During isotonic and isometric exercises, the start time of dynamometer recordings (footplate position, footplate angular velocity, and plantar flexion torque) was marked and recorded in DCS control panel [see Fig. 1(d)], from which we synchronize the dynamometer recordings and DCS data.
The status of muscle fibers (i.e., static, movement, contracting, non-contracting) during exercise was determined by the dynamometer recordings. For isotonic exercise, the footplate angular velocity and position were used to separate the muscle fiber states: the term “PF” (plantar-flexion) represents the footplate moving forward from 90° to 120° (footplate angular velocity > 0); the term “DF” (Dorsi-flexion) represents the footplate moving backward from 120° to 90° (footplate angular velocity < 0); the term “PF-120°” represents the footplate being held by the muscles (muscle contracting) at 120° (footplate angular velocity = 0 and footplate position = 120°); the term “Non-contracting” represents the muscle relaxation status (no contracting) positioning at 90° (footplate angular velocity = 0 and footplate position = 90°).
The footplate position was kept at 90° for isometric exercise, and the plantar flexion torque was used to separate the muscle fiber statues (i.e., contracting, non-contracting): “PF-90° represents the footplate being held by the contracting muscle (torque > 0) and “Non-contracting” represents the muscle relaxation status (torque = 0).
The magnitude of the DCS signal decay rates (i.e., αDB) depend on the status of muscle fibers and can be classified into three groups: (1) blood flow mixed with motion artifacts (i.e., PF and DF in isotonic protocol), (2) blood flow during muscle contracting without fiber motions (i.e., PF-120° in isotonic protocol and PF-90° in isometric protocol), and (3) blood flow during muscle relaxation (non-contracting) without fiber motions in both protocols. Grouping of DCS signals permits us to evaluate and separate the true blood flow signals from the “motion-contaminated” flow responses to exercise.
To quantify the relative changes of DCS signals throughout exercise, the time course of the blood flow indices derived from DCS data (i.e., αDB) are normalized to the 2-minute average baseline value before exercise (assigned to be 100%). The normalized time course of DCS data within each exercise trial (1st, 2nd,…, 10th) are averaged respectively for each muscle status (i.e., PF, DF, PF-120°, PF-90°, and non-contracting). The ten mean values of αDB for each muscle status are then averaged respectively, and the means ± standard errors (SE) are presented as during-exercise responses [see Fig. 3(b) and Fig. 5 ]. The post-exercise responses are calculated by averaging the 2-minute DCS data after exercise, and presented as mean ± standard deviation (SD) (see Fig. 6 ).
Fig. 3.
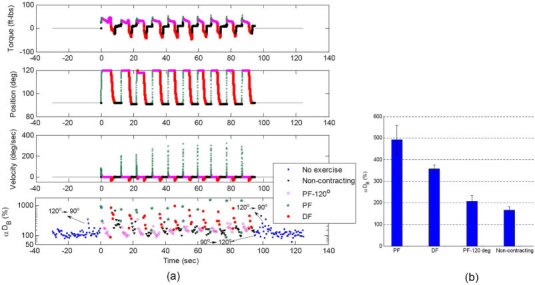
(a) Dynamometer recordings (plantar flexion torque, footplate position and angular velocity) and DCS signals (αDB) during 10 isotonic exercises. Data are presented with different colors and symbols based on the exercise status of muscle fibers; i.e., no-exercise (pre- and post-exercises without muscle fiber motion, ■), non-contracting (muscle relaxation at 90° without fiber motion, ▼), PF-120° (muscle contraction at an angle of 120° without fiber motion, ◇), PF (footplate moving forward with muscle fiber motions,★) and DF (footplate moving backward with muscle fiber motions, ●). The muscle exercise status was determined by the footplate position and angular velocity. Note that several motion-induced spikes appeared in DCS measurements before and after exercise when the angle of footplate was adjusted (i.e., 90° → 120° or 120° → 90°) for setting up the dynamometer. Those artifacts were excluded from our data analysis. (b) Average increases [mean ± standard error, n = 10 (trials)] in DCS data (αDB) during muscle fiber motion (PF or DF) and during static status of muscles (PF-120° or non-contracting). The muscle fiber motion (i.e., PF and DF) created higher αDB than that without motion (i.e., PF-120° and Non-contracting), and muscle fiber contraction (PF-120°) caused an increase in blood flow compared to that without the muscle contracting.
Fig. 5.
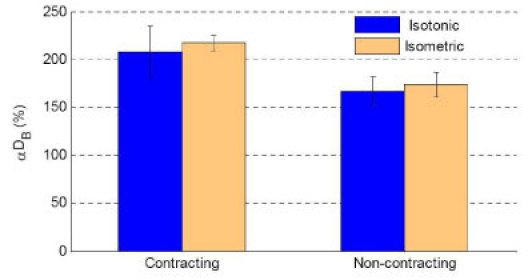
Comparison of average DCS signals (αDB) [mean ± SE, n = 10 (trials)] during isotonic and isometric exercises. Here the “Contracting” data during isotonic/isometric exercise represents the PF-120°/PF-90°, and “Non-contracting” represents the muscle in a relaxed status for both exercises. DCS data presented here are not influenced by any known motion artifacts, and therefore these signals are believed to originate from the muscle blood flow. Without motion artifacts the isotonic exercise produced similar level DCS flow signals compared to the isometric exercise, when the exercise intensity was set up at the same level (30% of highest MVIC) and the muscle worked in the same way (contracting or non-contracting).
Fig. 6.
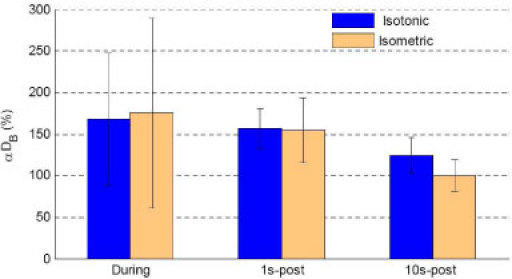
Comparison of during- and post- exercise DCS (αDB) responses in medial gastrocnemius muscle. The mean and standard deviation (SD) of DCS flow data (αDB) during 10 isotonic exercise [n = 75 (data points)] and isometric exercise [n = 68 (data points)] when muscle was under relaxation status (no motion and non-contracting) were calculated respectively, and presented as during-exercise blood flow responses. The 1s-post blood flow data was calculated by averaging the 1st~3rd-sec DCS data [n = 5 (data points)] immediately after the end of last (10th) PF. The 10s-post blood flow data was calculated by averaging the 2-minute DCS data [n = 264 (data points)] started at 10-second after the end of last PF. A small flow decrease immediately after the exercise (1s-post) was observed compared to during exercise, followed by a rapid and substantial drop at 10-second (10s-post) after isotonic/isometric exercise.
3. Results
Skin and adipose tissue layers generally lie above muscle. The thickness of the upper layers (skin and adipose tissues) above the participant’s medial gastrocnemius muscles (measured by the skinfold caliper) was 4 mm. From diffusion theory, maximum penetration depth of diffuse light in tissue depends on tissue optical properties and source-detector separation, and is roughly one-half of the separation. According to multi-layer theoretical models of diffusion theory [48–50] and our previous study [32], the signals detected by the source-detector pairs with a separation of 2.5 cm derive mainly from the muscles when the thickness of upper layers is small (e.g., < 5 mm). Note, however, even at this relatively large source-detector separation, there is always some contribution to the signal from the overlaying tissues.
3.1 Protocol #1: toe up/down plantar flexion exercise
Figure 2 shows the measured DCS signals (αDB) on medial gastrocnemius muscles throughout the toe up/down exercise. Each period of toe up/down was marked manually at the control panel of DCS device. A 3 to 8 fold increase in DCS signals was found during the toe/up down exercise. Since this protocol cannot quantify the muscle motions during exercise, it is impossible to precisely separate blood flow changes associated with the motion artifacts caused by the moving muscle fibers.
Fig. 2.
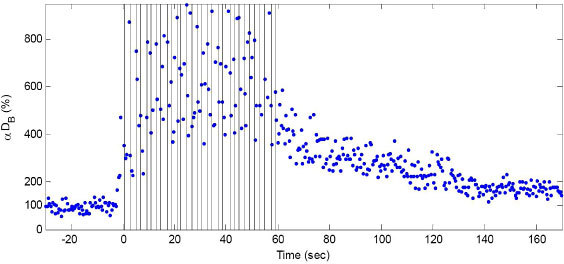
Time course of the DCS signals (αDB) during 15 toe up/down plantar flexion (PF) exercise. The vertical lines indicate beginning and end of each PF period. DCS data were normalized to the averaged 2-minute baseline before exercise. The baseline value was assigned 100%. The exercise creates both muscle fiber motion and blood flow changes, which in turn result in significant increases in DCS signal decay rates. No objective way exists to separate the blood flow contributions to the DCS signal from the motion artifacts contributions using this protocol.
The 2-minute average post-exercise DCS signal (164%) was higher than its 2-minute pre-exercise value (100%), indicating the exercise-induced increase in muscle blood flow. Note that there were no motion artifacts before and after exercise.
3.2 Protocol #2: isotonic plantar flexion exercise
In contrast to the toe up/down protocol, blood flow information can be precisely extracted in the present case by synchronizing the DCS data with the dynamometer recordings during the isotonic plantar flexion exercise. Figure 3 shows the DCS data and dynamometer recordings during the isotonic exercise. As described in Section 2.4, the footplate angular velocity and position was used to separate the muscle fiber status (i.e., static, movement, contracting, non-contracting). Clearly [see Fig. 3(b)], muscle fiber motion (i.e., PF and DF) created higher DCS signal decay rates than those without motion (i.e., PF-120° and Non-contracting).
The angular velocities of PFs (derived from the angle changes of the footplate per unit time from 90 ° to 120°) were much larger (average 40.6 deg/sec) than that of DFs (average 15.2 deg/sec) [see Fig. 3(a)], thus generating larger motion effects on the DCS measurements [see Fig. 3(b)]. The DCS signal (208 ± 27%) without motion but with the muscle contracting (PF-120°) is slightly higher than that (167 ± 16%) without the muscle contracting [see Fig. 3(b)]; this observation suggests that muscle fiber contraction may cause an increase in blood flow (see discussion in Section 4).
3.3 Protocol #3: isometric plantar flexion exercise
Figure 4 shows the DCS data and dynamometer recordings during 10 isometric plantar flexion exercises. As described in Section 2.4, the plantar flexion torque was used to separate the muscle fiber statues. The DCS signal (217 ± 8%) during muscle contraction (PF-90°) was higher than that (174 ± 13%) during non-contracting, consistent with observations of isotonic exercise (see Section 3.2).
Fig. 4.
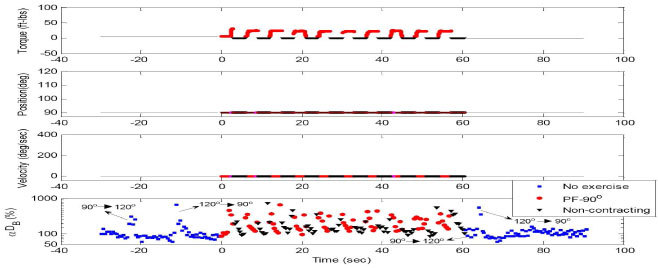
Dynamometer recordings (plantar flexion torque, footplate position and angular velocity) and DCS signals (αDB) during 10 isometric exercises. Data are presented with different colors and symbols based on the exercise status of muscle fibers; i.e., no exercise (pre- and post- exercise without muscle fiber motion, ■), non-contracting (muscle relaxation at 90° without fiber motion, ▼), and PF-90° (muscle contraction at 90° without fiber motion, ●). The muscle exercise statues are determined by the plantar flexion torque. Note that several motion-induced spikes appeared in DCS measurements before and after exercise when the angle of footplate was adjusted for setting up the dynamometer. Those artifacts were excluded from our data analysis. Similar to the isotonic exercise, the muscle fiber contraction (PF-90°) caused an increase in blood flow compared to that without the muscle contracting. The average results of DCS data (αDB) during exercise are presented in Fig. 5.
3.4 Comparison of blood flow responses during isotonic and isometric exercises
Figure 5 shows the comparison of DCS signals without motion artifacts obtained from the medial gastrocnemius muscle with and without muscle contraction during the isotonic and isometric exercises. As expected, when the muscle works in the same way (contracting or non-contracting) with the same power output (30% of highest MVIC value), the increases in static DCS signals (blood flow) are approximately the same order for both isotonic and isometric exercise. Muscle contraction appears to cause a slightly larger increase in blood flow compared to the non-contracting status.
To investigate exercise-created blood flow changes throughout the whole exercise procedure (before, during, and after exercise), we compared DCS flow signals only derived when the muscle was in the relaxed states (i.e., no motion or non-contracting) before, during and after exercise. The immediate post-exercise flow response (1s-post) was calculated by averaging the 1st~3rd-second DCS data immediately after the last (10th) plantar flexion contraction. The 10s-post blood flow response was calculated by averaging the 2-minute data started at 10-second after exercise. As shown in Fig. 6, muscle blood flow increased to ~160% during both isotonic and isometric exercise. There was a small flow decrease immediately after the exercises (1s-post) compared to during exercise. However, the blood flow dropped rapidly and dramatically at 10-second after isotonic and isometric exercise (10s-post); blood flow recovered faster towards its baseline value after isometric exercise compared to the flow recovery after isotonic exercise.
4. Discussion and conclusions
Diffuse correlation spectroscopy (DCS) is an emerging technique which detects the motion of moving scatterers inside biological tissues. It has been experimentally verified that DCS signals originate primarily from the motion of red blood cells (blood flow) in the microvasculature of biological tissues [30,33,38–41]. These studies were carried out on tissues that were essentially static. However, the motions of nuclei and mitochondria inside muscle cells/fibers during exercise may significantly contribute to the DCS signal decay rates and consequently affect blood flow measurements in moving muscles. In this study, we evaluated and separated the true blood flow signals and those affected by the muscle fiber motion artifacts using three plantar flexion exercise protocols.
The toe up/down plantar flexion exercise (Protocol #1) can be easily performed without the need of dynamometer. Since the toe up/down plantar flexion supports the entire body weight, its intensity is likely higher than the 30% MVIC isotonic or isometric exercise. Moreover, the frequency of toe up/down plantar flexion exercise (1/4 Hz) was higher than those of isotonic (1/9 Hz) and isometric (1/6 Hz) exercises. The high intensity and high frequency of toe up/down plantar flexion exercise should cause more obvious increase in DCS signals seen in Fig. 2 compared to those seen in Fig. 3 (isotonic exercise) and Fig. 4 (isometric exercise). With protocol #1, however, it is impossible to accurately determine and separate motion artifacts from true blood flow signals (see Fig. 2), because the muscle status (i.e., static, movement, contracting, and non-contracting) cannot be precisely tracked. In fact, these motion artifacts during exercise led to blood flow quantification errors in our previous study using this exercise protocol [32]. In addition, the exercise intensity of toe up/down flexion may vary between subjects.
The isotonic and isometric plantar flexion exercises (Protocols #2 and #3) require a dynamometer, which increases the complexity and cost of measurements. However, the dynamometer provides precise recordings of the muscle status during exercise. Furthermore, compared to the isometric exercise (Protocol #3), the isotonic exercise of pushing the footplate (Protocol #2) is more naturally similar to the toe up/down exercise, and its intensity can be precisely and objectively controlled.
The precise co-registration of the dynamometer recordings and DCS data during isotonic exercise enabled us to evaluate and separate the contributions of muscle fiber motion artifacts from DCS determined blood flow indices. During the isotonic exercise, the muscle fiber motions created larger DCS signal decay rates than those without motion [see Fig. 3(b)]. The difference between the static and moment DCS signals clearly demonstrates the effect of motion artifacts. Furthermore, larger angular velocity PF generated larger motion artifacts than that of smaller angular velocity DF [see Fig. 3(b)], verifying the motional sensitivity of the DCS measurements. By contrast, DCS data obtained when the muscle was under static status during isotonic and isometric exercise (see Fig. 3–5) were not significantly influenced by any motion artifact. Therefore, we believe the latter ‘static’ DCS signals originate primarily from the muscle blood flow.
The muscle exercise activity has two different phases (contracting and non-contracting (relaxation)), which affect the muscle blood flow level [51]. Each time the muscles contract, arterial inflow decreases due to extravascular compression, and then arterial inflow increases as the muscles relax. If blood flow were measured in the outflow vein, the venous outflow would increase during contraction and decrease during relaxation; the opposite of what occurs on the arterial side of the circulation. In this study a higher level of DCS blood flow was observed during muscle contraction compared to that during muscle relaxation (see Fig. 5), which is most likely due to the large increase in venous outflow when the muscles contracted. Since DCS measures blood flow in muscle microvasculature including arterioles, capillaries and venules, the blood volume (65–70% at rest) residing in the venous vasculature [52] may contribute more to DCS measurements than that in the arterial vasculature.
As expected, without motion artifacts the isotonic exercise (Protocol #2) produced similar level DCS signals compared to the isometric exercise (Protocol #3) (see Fig. 5) when the exercise intensity was set up at the same level (30% of highest MVIC). This observation further verifies that DCS measures blood flow in muscles.
Because of the lack of adequate technologies for continuous monitoring of blood flow during exercise, researchers previously focused on the evaluation of post-exercise blood flow responses in muscles [16,17]. DCS can continuously monitor muscle blood flow before, during and after exercise with relatively high temporal resolution and without interrupting blood flow. These advantages are critical not only for continuous monitoring of flow responses during exercise, but also for tracking of the rapid and dramatic flow immediately after exercise (see Fig. 6). In addition, the substantial difference in post-exercise flow responses between the toe up/down exercise and isotonic/isometric exercise is most likely due to the different intensities and frequencies of the exercises. Although it is unclear why the flow recovery towards baseline at 10-second post isotonic exercise is slower than that of post isometric exercises (see Fig. 6), the muscle fiber response due to the contraction type (i.e., isotonic vs. isometric) may have contributed to the difference observed. Further investigations are needed to understand these differences.
We note that while our findings are encouraging, measurements with a larger sample size is desirable to confirm observations. Finally, the relatively low temporal resolution (2.2 Hz) of our DCS system has restricted the highest frequency of exercise. However, it is expected that with faster DCS systems (e.g. ~100 Hz [25,34]) we should be able to monitor exercise at high speed (e.g., plantar flexion exercise at 1 Hz) in the future, and the DCS approach will therefore offer even more possibilities for monitoring natural muscle activities. Of course, as we have demonstrated in the present paper, the DCS measurements can be gated via monitoring of muscle status by a dynamometer to derive more accurate blood flow information.
In conclusion, this case study demonstrates that muscle fiber motions during exercise introduce artifacts into traditional (low repetition rate, ~1 Hz) DCS measurements of muscle blood flow responses to exercise. However, we show that the DCS signals due solely to blood flow can be precisely separated from those affected by motion artifacts using concurrent and co-registered dynamometer recordings with DCS data during exercise.
Acknowledgments
We acknowledge funding support from the National Institutes of Health (NIH) [HL-083225 (GY), HL-PA08162 (GY), HL-077699 (AGY), RR-02305 (AGY)], National Heart Association (AHA) 0665446U (GY), and University of Kentucky Research Foundation (GY).
References and links
- 1.Ubbink D. T., Kitslaar P. J., Tordoir J. H., Reneman R. S., Jacobs M. J., “Skin microcirculation in diabetic and non-diabetic patients at different stages of lower limb ischaemia,” Eur. J. Vasc. Surg. 7(6), 659–6 (1993). 10.1016/S0950-821X(05)80713-3 [DOI] [PubMed] [Google Scholar]
- 2.Wahlberg E., Olofsson P., Swedenborg J., Fagrell B., “Level of arterial obstruction in patients with peripheral arterial occlusive disease (PAOD) determined by laser Doppler fluxmetry,” Eur. J. Vasc. Surg. 7(6), 684–689 (1993). 10.1016/S0950-821X(05)80717-0 [DOI] [PubMed] [Google Scholar]
- 3.Yamada T., Ohta T., Ishibashi H., Sugimoto I., Iwata H., Takahashi M., Kawanishi J., “Clinical reliability and utility of skin perfusion pressure measurement in ischemic limbs--comparison with other noninvasive diagnostic methods,” J. Vasc. Surg. 47(2), 318–323 (2008). 10.1016/j.jvs.2007.10.045 [DOI] [PubMed] [Google Scholar]
- 4.Chen Z. P., Milner T. E., Wang X. J., Srinivas S., Nelson J. S., “Optical Doppler tomography: imaging in vivo blood flow dynamics following pharmacological intervention and photodynamic therapy,” Photochem. Photobiol. 67(1), 56–60 (1998). 10.1111/j.1751-1097.1998.tb05165.x [DOI] [PubMed] [Google Scholar]
- 5.Baron J. C., “Mapping the ischaemic penumbra with PET: implications for acute stroke treatment,” Cerebrovasc. Dis. 9(4), 193–201 (1999). 10.1159/000015955 [DOI] [PubMed] [Google Scholar]
- 6.Schmitt P., Kotas M., Tobermann A., Haase A., Flentje M., “Quantitative tissue perfusion measurements in head and neck carcinoma patients before and during radiation therapy with a non-invasive MR imaging spin-labeling technique,” Radiother. Oncol. 67(1), 27–34 (2003). 10.1016/S0167-8140(03)00024-0 [DOI] [PubMed] [Google Scholar]
- 7.Fantini S., Hueber D., Franceschini M. A., Gratton E., Rosenfeld W., Stubblefield P. G., Maulik D., Stankovic M. R., “Non-invasive optical monitoring of the newborn piglet brain using continuous-wave and frequency-domain spectroscopy,” Phys. Med. Biol. 44(6), 1543–1563 (1999). 10.1088/0031-9155/44/6/308 [DOI] [PubMed] [Google Scholar]
- 8.Strangman G., Franceschini M. A., Boas D. A., “Factors affecting the accuracy of near-infrared spectroscopy concentration calculations for focal changes in oxygenation parameters,” Neuroimage 18(4), 865–879 (2003). 10.1016/S1053-8119(03)00021-1 [DOI] [PubMed] [Google Scholar]
- 9.Duncan A., Meek J. H., Clemence M., Elwell C. E., Tyszczuk L., Cope M., Delpy D. T., “Optical pathlength measurements on adult head, calf and forearm and the head of the newborn infant using phase resolved optical spectroscopy,” Phys. Med. Biol. 40(2), 295–304 (1995). 10.1088/0031-9155/40/2/007 [DOI] [PubMed] [Google Scholar]
- 10.Song Y. L., Kim J. G., Mason R. P., Liu H. L., “Investigation of rat breast tumour oxygen consumption by near-infrared spectroscopy,” J. Phys. D Appl. Phys. 38(15), 2682–2690 (2005). 10.1088/0022-3727/38/15/021 [DOI] [Google Scholar]
- 11.McCully K. K., Halber C., Posner J. D., “Exercise-induced changes in oxygen saturation in the calf muscles of elderly subjects with peripheral vascular disease,” J. Gerontol. 49(3), B128–B134 (1994). [DOI] [PubMed] [Google Scholar]
- 12.Wallace D., Michener B., Choudhury D., Levi M., Fennelly P., Hueber D., Barbieri B., “Summary of the results of a 95 subject human clinical trial for the diagnosis of peripheral vascular disease using a near infrared frequency domain hemoglobin spectrometer,” Proc. SPIE 3597, 300–316 (1999). [Google Scholar]
- 13.Wolf U., Wolf M., Choi J. H., Levi M., Choudhury D., Hull S., Coussirat D., Paunescu L. A., Safonova L. P., Michalos A., Mantulin W. W., Gratton E., “Localized irregularities in hemoglobin flow and oxygenation in calf muscle in patients with peripheral vascular disease detected with near-infrared spectrophotometry,” J. Vasc. Surg. 37(5), 1017–1026 (2003). 10.1067/mva.2003.214 [DOI] [PubMed] [Google Scholar]
- 14.Cheatle T. R., Potter L. A., Cope M., Delpy D. T., Smith P. D. C., Scurr J. H., “Near-infrared spectroscopy in peripheral vascular disease,” Br. J. Surg. 78(4), 405–408 (1991). 10.1002/bjs.1800780408 [DOI] [PubMed] [Google Scholar]
- 15.Kooijman H. M., Hopman M. T. E., Colier W. N. J. M., van der Vliet J. A., Oeseburg B., “Near infrared spectroscopy for noninvasive assessment of claudication,” J. Surg. Res. 72(1), 1–7 (1997). 10.1006/jsre.1997.5164 [DOI] [PubMed] [Google Scholar]
- 16.L. A. Paunescu, “Tissue blood flow and oxygen consumption measured with near-infrared frequency-domain spectroscopy,” Degree of Doctor of Philosophy (University of Illinois, Urbana, 2001). [Google Scholar]
- 17.Ferrari M., Binzoni T., Quaresima V., “Oxidative metabolism in muscle,” Philos. Trans. R. Soc. Lond. B Biol. Sci. 352(1354), 677–683 (1997). 10.1098/rstb.1997.0049 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Blasi R. A., Cope M., Elwell C., Safoue F., Ferrari M., “Noninvasive measurement of human forearm oxygen-consumption by near-infrared spectroscopy,” Eur. J. Appl. Physiol. 67(1), 20–25 (1993). 10.1007/BF00377698 [DOI] [PubMed] [Google Scholar]
- 19.Cheung C., Culver J. P., Takahashi K., Greenberg J. H., Yodh A. G., “In vivo cerebrovascular measurement combining diffuse near-infrared absorption and correlation spectroscopies,” Phys. Med. Biol. 46(8), 2053–2065 (2001). 10.1088/0031-9155/46/8/302 [DOI] [PubMed] [Google Scholar]
- 20.Gagnon L., Desjardins M., Jehanne-Lacasse J., Bherer L., Lesage F., “Investigation of diffuse correlation spectroscopy in multi-layered media including the human head,” Opt. Express 16(20), 15514–15530 (2008). 10.1364/OE.16.015514 [DOI] [PubMed] [Google Scholar]
- 21.Yu G., Durduran T., Zhou C., Zhu T. C., Finlay J. C., Busch T. M., Malkowicz S. B., Hahn S. M., Yodh A. G., “Real-time in situ monitoring of human prostate photodynamic therapy with diffuse light,” Photochem. Photobiol. 82(5), 1279–1284 (2006). 10.1562/2005-10-19-RA-721 [DOI] [PubMed] [Google Scholar]
- 22.Durduran T., Yu G., Burnett M. G., Detre J. A., Greenberg J. H., Wang J. J., Zhou C., Yodh A. G., “Diffuse optical measurement of blood flow, blood oxygenation, and metabolism in a human brain during sensorimotor cortex activation,” Opt. Lett. 29(15), 1766–1768 (2004). 10.1364/OL.29.001766 [DOI] [PubMed] [Google Scholar]
- 23.Durduran T., Zhou C., Edlow B. L., Yu G., Choe R., Kim M. N., Cucchiara B. L., Putt M. E., Shah Q., Kasner S. E., Greenberg J. H., Yodh A. G., Detre J. A., “Transcranial optical monitoring of cerebrovascular hemodynamics in acute stroke patients,” Opt. Express 17(5), 3884–3902 (2009). 10.1364/OE.17.003884 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Li J., Ninck M., Koban L., Elbert T., Kissler J., Gisler T., “Transient functional blood flow change in the human brain measured noninvasively by diffusing-wave spectroscopy,” Opt. Lett. 33(19), 2233–2235 (2008). 10.1364/OL.33.002233 [DOI] [PubMed] [Google Scholar]
- 25.Dietsche G., Ninck M., Ortolf C., Li J., Jaillon F., Gisler T., “Fiber-based multispeckle detection for time-resolved diffusing-wave spectroscopy: characterization and application to blood flow detection in deep tissue,” Appl. Opt. 46(35), 8506–8514 (2007). 10.1364/AO.46.008506 [DOI] [PubMed] [Google Scholar]
- 26.Zhou C., Eucker S. A., Durduran T., Yu G., Ralston J., Friess S. H., Ichord R. N., Margulies S. S., Yodh A. G., “Diffuse optical monitoring of hemodynamic changes in piglet brain with closed head injury,” J. Biomed. Opt. 14(3), 034015 (2009). 10.1117/1.3146814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sunar U., Quon H., Durduran T., Zhang J., Du J., Zhou C., Yu G., Choe R., Kilger A., Lustig R., Loevner L., Nioka S., Chance B., Yodh A. G., “Noninvasive diffuse optical measurement of blood flow and blood oxygenation for monitoring radiation therapy in patients with head and neck tumors: a pilot study,” J. Biomed. Opt. 11(6), 064021 (2006). 10.1117/1.2397548 [DOI] [PubMed] [Google Scholar]
- 28.Culver J. P., Durduran T., Furuya D., Cheung C., Greenberg J. H., Yodh A. G., “Diffuse optical tomography of cerebral blood flow, oxygenation, and metabolism in rat during focal ischemia,” J. Cereb. Blood Flow Metab. 23(8), 911–924 (2003). 10.1097/01.WCB.0000076703.71231.BB [DOI] [PubMed] [Google Scholar]
- 29.Zhou C., Choe R., Shah N., Durduran T., Yu G., Durkin A., Hsiang D., Mehta R., Butler J., Cerussi A., Tromberg B. J., Yodh A. G., “Diffuse optical monitoring of blood flow and oxygenation in human breast cancer during early stages of neoadjuvant chemotherapy,” J. Biomed. Opt. 12(5), 051903 (2007). 10.1117/1.2798595 [DOI] [PubMed] [Google Scholar]
- 30.Yu G., Durduran T., Zhou C., Wang H. W., Putt M. E., Saunders H. M., Sehgal C. M., Glatstein E., Yodh A. G., Busch T. M., “Noninvasive monitoring of murine tumor blood flow during and after photodynamic therapy provides early assessment of therapeutic efficacy,” Clin. Cancer Res. 11(9), 3543–3552 (2005). 10.1158/1078-0432.CCR-04-2582 [DOI] [PubMed] [Google Scholar]
- 31.Durduran T., Choe R., Baker W. B., Yodh A. G., “Diffuse optics for tissue monitoring and tomography,” Rep. Prog. Phys. 73(7), 076701 (2010). 10.1088/0034-4885/73/7/076701 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yu G., Durduran T., Lech G., Zhou C., Chance B., Mohler E. R., 3rd, Yodh A. G., “Time-dependent blood flow and oxygenation in human skeletal muscles measured with noninvasive near-infrared diffuse optical spectroscopies,” J. Biomed. Opt. 10(2), 024027 (2005). 10.1117/1.1884603 [DOI] [PubMed] [Google Scholar]
- 33.Yu G., Floyd T. F., Durduran T., Zhou C., Wang J. J., Detre J. A., Yodh A. G., “Validation of diffuse correlation spectroscopy for muscle blood flow with concurrent arterial spin labeled perfusion MRI,” Opt. Express 15(3), 1064–1075 (2007). 10.1364/OE.15.001064 [DOI] [PubMed] [Google Scholar]
- 34.M. Belau, M. Ninck, G. Hering, and T. Gisler, “Non-invasive measurement of skeletal muscle contraction with time-resolved diffusing-wave spectroscopy,” in Conference on Biomedical Optics and 3D Imaging, Technical Digest (CD) (Optical Society of America, 2010), paper BSuD70. http://www.opticsinfobase.org/abstract.cfm?uri=BIOMED-2010-BSuD70
- 35.Y. Shang, Y. Zhao, R. Cheng, L. Dong, D. Irwin, K. R. Swartz, S. S. Salles, and G. Yu, “Diffuse optical spectroscopies for evaluation of muscle hemodynamic enhancements by electrical stimulation,” in Conference on Biomedical Optics and 3D Imaging, Technical Digest (CD) (Optical Society of America, 2010), paper BSuD80. http://www.opticsinfobase.org/abstract.cfm?URI=BIOMED-2010-BSuD80
- 36.Shang Y., Zhao Y., Cheng R., Dong L., Irwin D., Yu G., “Portable optical tissue flow oximeter based on diffuse correlation spectroscopy,” Opt. Lett. 34(22), 3556–3558 (2009). 10.1364/OL.34.003556 [DOI] [PubMed] [Google Scholar]
- 37.X. Xing, E. R. Mohler, C. Zhou, T. Durduran, G. M. Lech, Y. Shi, R. Wilensky, J. Moore, A. G. Yodh, and G. Yu, “Hemodynamic changes in diabetic pig muscle,” SVMB 18th Annual Meeting (2007). [Google Scholar]
- 38.N. Roche-Labarbe, S. A. Carp, A. Surova, M. Patel, D. A. Boas, P. E. Grant, and M. A. Franceschini, “Noninvasive optical measures of CBV, StO2, CBF index, and rCMRO2 in human premature neonates' brains in the first six weeks of life,” Hum. Brain Mapp. online, 1–12 (2009). [DOI] [PMC free article] [PubMed]
- 39.Buckley E. M., Cook N. M., Durduran T., Kim M. N., Zhou C., Choe R., Yu G., Schultz S., Sehgal C. M., Licht D. J., Arger P. H., Putt M. E., Hurt H. H., Yodh A. G., “Cerebral hemodynamics in preterm infants during positional intervention measured with diffuse correlation spectroscopy and transcranial Doppler ultrasound,” Opt. Express 17(15), 12571–12581 (2009). 10.1364/OE.17.012571 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.T. Durduran, “Non-invasive measurements of tissue hemodynamics with hybrid diffuse optical methods,” Degree of Doctor of Philosophy (University of Pennsylvania, 2004). [Google Scholar]
- 41.Kim M. N., Durduran T., Frangos S., Edlow B. L., Buckley E. M., Moss H. E., Zhou C., Yu G., Choe R., Maloney-Wilensky E., Wolf R. L., Grady M. S., Greenberg J. H., Levine J. M., Yodh A. G., Detre J. A., Kofke W. A., “Noninvasive measurement of cerebral blood flow and blood oxygenation using near-infrared and diffuse correlation spectroscopies in critically brain-injured adults,” Neurocrit. Care 12(2), 173–180 (2010). 10.1007/s12028-009-9305-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.L. V. Wang, H. I. Wu, and W. Wang, Biomedical optics: principles and imaging, (Wiley-Interscience, 2007). [Google Scholar]
- 43.Durduran T., Choe R., Yu G., Zhou C., Tchou J. C., Czerniecki B. J., Yodh A. G., “Diffuse optical measurement of blood flow in breast tumors,” Opt. Lett. 30(21), 2915–2917 (2005). 10.1364/OL.30.002915 [DOI] [PubMed] [Google Scholar]
- 44.Maret G., Wolf P. E., “Multiple light-scattering from disordered media - the effect of brownian-motion of scatterers,” Z. Phys. B 65(4), 409–413 (1987). 10.1007/BF01303762 [DOI] [Google Scholar]
- 45.Pine D. J., Weitz D. A., Chaikin P. M., Herbolzheimer E., “Diffusing wave spectroscopy,” Phys. Rev. Lett. 60(12), 1134–1137 (1988). 10.1103/PhysRevLett.60.1134 [DOI] [PubMed] [Google Scholar]
- 46.Boas D. A., Campbell L. E., Yodh A. G., “Scattering and imaging with diffusing temporal field correlations,” Phys. Rev. Lett. 75(9), 1855–1858 (1995). 10.1103/PhysRevLett.75.1855 [DOI] [PubMed] [Google Scholar]
- 47.Boas D. A., Yodh A. G., “Spatially varying dynamical properties of turbid media probed with diffusing temporal light correlation,” J. Opt. Soc. Am. A 14(1), 192–215 (1997). 10.1364/JOSAA.14.000192 [DOI] [Google Scholar]
- 48.Kienle A., Glanzmann T., “In vivo determination of the optical properties of muscle with time-resolved reflectance using a layered model,” Phys. Med. Biol. 44(11), 2689–2702 (1999). 10.1088/0031-9155/44/11/301 [DOI] [PubMed] [Google Scholar]
- 49.Farrell T. J., Patterson M. S., Essenpreis M., “Influence of layered tissue architecture on estimates of tissue optical properties obtained from spatially resolved diffuse reflectometry,” Appl. Opt. 37(10), 1958–1972 (1998). 10.1364/AO.37.001958 [DOI] [PubMed] [Google Scholar]
- 50.van Beekvelt M. C. P., Borghuis M. S., van Engelen B. G. M., Wevers R. A., Colier W. N. J. M., “Adipose tissue thickness affects in vivo quantitative near-IR spectroscopy in human skeletal muscle,” Clin. Sci. 101(1), 21–28 (2001). 10.1042/CS20000247 [DOI] [PubMed] [Google Scholar]
- 51.R. E. Klabunde, “Cardiovascular physiology concepts,” (2007) http://www.cvphysiology.com/Blood%20Flow/BF015.htm
- 52.P. O. Astrand, K. Rodahl, H. Dahl, and S. Stromme, Textbook of work physiology, (Human Kinetics, 2003). [Google Scholar]


