Next-generation acceleration and code optimization for light transport in turbid media using GPUs

Abstract

A highly optimized Monte Carlo (MC) code package for simulating light transport is developed on the latest graphics processing unit (GPU) built for general-purpose computing from NVIDIA - the Fermi GPU. In biomedical optics, the MC method is the gold standard approach for simulating light transport in biological tissue, both due to its accuracy and its flexibility in modelling realistic, heterogeneous tissue geometry in 3-D. However, the widespread use of MC simulations in inverse problems, such as treatment planning for PDT, is limited by their long computation time. Despite its parallel nature, optimizing MC code on the GPU has been shown to be a challenge, particularly when the sharing of simulation result matrices among many parallel threads demands the frequent use of atomic instructions to access the slow GPU global memory. This paper proposes an optimization scheme that utilizes the fast shared memory to resolve the performance bottleneck caused by atomic access, and discusses numerous other optimization techniques needed to harness the full potential of the GPU. Using these techniques, a widely accepted MC code package in biophotonics, called MCML, was successfully accelerated on a Fermi GPU by approximately 600x compared to a state-of-the-art Intel Core i7 CPU. A skin model consisting of 7 layers was used as the standard simulation geometry. To demonstrate the possibility of GPU cluster computing, the same GPU code was executed on four GPUs, showing a linear improvement in performance with an increasing number of GPUs. The GPU-based MCML code package, named GPU-MCML, is compatible with a wide range of graphics cards and is released as an open-source software in two versions: an optimized version tuned for high performance and a simplified version for beginners (http://code.google.com/p/gpumcml).

1. Introduction

Modelling light propagation in biological tissue both accurately and efficiently is a problem of great importance in biomedical optics. Macroscopic transport of light in scattering materials, such as tissue, can be described by the Radiative Transport Equation (RTE), which has proven difficult to solve analytically without introducing severe approximations and simplifications. To solve the RTE numerically, Wilson and Adam [1] introduced the Monte Carlo (MC) method. Owing to its accuracy and its ability to handle heterogenous optical properties, the MC method is currently widely accepted as the gold standard approach for photon migration modelling. In particular, the MC implementation by Wang et al. (MCML) [2] has been accepted as a gold standard tool for simulating light propagation in multilayered turbid media. The MCML code package has since then been used for validation of numerous photon migration modelling schemes and as a starting point for custom-developed MC solutions. Further, Boas et al. extended the code capabilities by releasing the tMCimg code for time-resolved and steady-state MC-based photon migration in arbitrary, 3-D voxelized media [3].

The main drawback of the MC method is the heavy computational burden, causing MC simulation times to become prohibitively long. Owing to this limitation, MC simulations have so far mainly been used for forward modelling—that is, calculating the photon density distribution given a defined geometry of photon sources and tissue structures as well as their optical properties. A few examples of inverse modelling have been published [4–8], but these methods have relied on either rescaling the results of Monte Carlo simulations or building databases of simulation results, both methods constraining the evaluation space in terms of optical properties and geometrical complexity. The ability to directly use MC simulations for complex, inverse optimization problems would benefit numerous important biomedical applications, ranging from diffuse optical tomography [9, 10] to treatment planning for photodynamic therapy [11–13].

To enable the use of MC simulations for solving inverse problems, the graphics processing unit (GPU) has recently emerged as a promising solution, achieving speedups of up to 3 orders of magnitude over CPU-based codes [14]. However, several previous attempts to use the GPU for accelerating MC simulations have shown limited success, probably due to the difficulty of optimizing the GPU code for high performance. These previous attempts [15–19] and preliminary observations highlight the need for a new optimization approach to avoid performance bottlenecks in order to harness the full potential of the GPU. To tackle this computational challenge, we present a highly optimized implementation of MCML on GPUs, called GPU-MCML, which represents the fusion of and a significant improvement on our earlier, preliminary implementations. In addition, this work focuses on various GPU optimizations enabled by the latest Fermi GPU architecture and analyzes how they dramatically affect the performance of MC simulations for photon migration on GPUs. In particular, we propose a solution to tackle the major performance bottleneck caused by the inefficiency of atomic access to the GPU memory. The proposed solution is applicable to both 2-D and 3-D cases; it is also favored by the latest architectural improvements on the Fermi GPUs.

In addition to solving major bottlenecks, the current GPU-MCML code is designed to support a wide range of NVIDIA graphics cards, including those with multiple GPUs. With this scalability, the code can be extended to run on a GPU cluster and be used for solving complex inverse problems in the future. A generalized version of the GPU-MCML code is also presented, which serves as a starting point for scientists and programmers interested in developing their own custom GPU-accelerated MC code. This version is a familiar, well-documented starting point and it shares many similarities with the well-known MCML package. The GPU-MCML code has been thoroughly validated against the original CPU version and can be downloaded from http://code.google.com/p/gpumcml.

2. Background

2.1. MCML.

The MCML algorithm [2] models steady-state light transport in multi-layered turbid media using the MC method. A pencil beam perpendicular to the surface is modelled; more complex sources can be modelled with modifications or with other tools [20]. The implementation assumes infinitely wide layers, each described by its thickness and its optical properties, comprising the absorption coefficient, scattering coefficient, anisotropy factor, and refractive index.

In the MCML code, three physical quantities - absorption, reflectance, and transmittance - are calculated in a spatially-resolved manner. Absorption is recorded in a 2-D array called A[r][z], which stores the photon absorption probability density [cm^-3] as a function of radius r and depth z for the pencil beam (or impulse response). Absorption probability density can be converted into more common quantities, such as photon fluence (measured in cm^-2 for the impulse response) which is obtained by dividing A[r][z] by the local absorption coefficient.

The simulation of each photon packet consists of a repetitive sequence of computational steps and can be made independent of other photon packets by creating separate absorption arrays and, importantly, decoupling random number generation using different seeds. Therefore, a conventional software-based acceleration approach involves processing photon packets simultaneously on multiple processors. Figure 1 shows a flow chart of the key steps in an MCML simulation, which includes photon initialization, position update, direction update, fluence update, and photon termination. Further details on each computational step may be found in the original papers by Wang et al. [2].

Fig. 1.

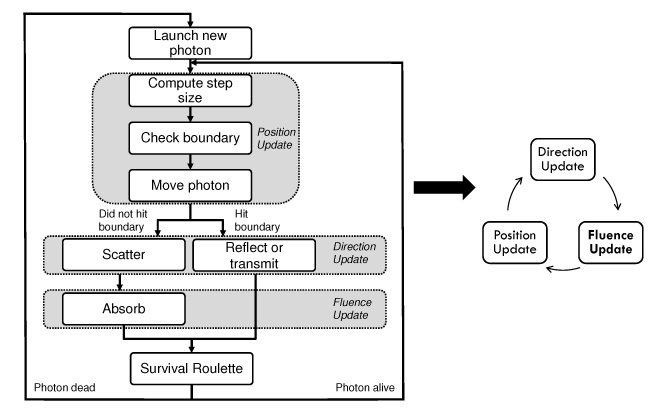
Left: Flow-chart of the MCML algorithm. Right: Simplified representation used in subsequent sections.

2.2. Programming Graphics Processing Units.

This section introduces the key terminology for understanding the NVIDIA GPU hardware and its programming model. This learning curve is required to fully utilize this emerging scientific computing platform for this and other related applications.

Fig. 2.

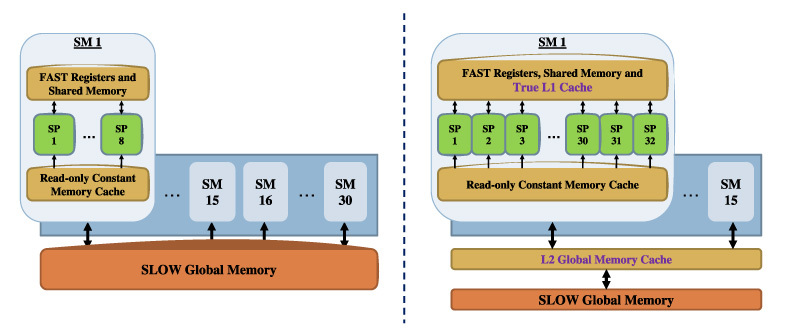
Simplified representation of the GPU architecture for NVIDIA GTX 280 (left) and GTX 480 (right). Each GPU consists of a number of streaming multiprocessors (SMs), each of which has a number of scalar processors (SPs). GTX 280 has 16KB of shared memory per SM, while GTX 480 has up to 48KB.

2.2.1. CUDA.

GPU-accelerated scientific computing is becoming increasingly popular with the release of an easier-to-use programming model and environment from NVIDIA (Santa Clara, CA), called CUDA, short for Compute Unified Device Architecture [21]. CUDA provides a C-like programming interface for NVIDIA GPUs and it suits general-purpose applications much better than traditional GPU programming languages. However, performance optimization of a CUDA program requires careful consideration of the GPU architecture.

In CUDA, the host code and the device code are written in a single program. The former is executed sequentially by a single thread on the CPU, while the latter is executed in parallel by many threads on the GPU. Here, a thread is an independent execution context that can, for example, simulate an individual photon packet in the MCML algorithm. The device code is expressed in the form of a kernel function. It is similar to a regular C function, except that it specifies the work of each GPU thread, parameterized by a thread index variable. Correspondingly, a kernel invocation is similar to a regular function call except that it must specify the geometry of a grid of threads that executes the kernel, also referred to as the kernel configuration. A grid is first composed of a number of thread blocks, each of which then has a number of threads.

2.2.2. NVIDIA GPU Architecture.

CUDA-enabled NVIDIA GPUs have gone through two generations; an example for each generation includes Geforce 8800 GTX and Geforce GTX 280, respectively. The third generation, named Fermi and represented by Geforce GTX 480, was released recently (in the second quarter of 2010). Figure 2 compares the underlying hardware architecture of GTX 280 and GTX 480, showing both a unique processor layout and memory hierarchy [21].

GTX 280 has 30 streaming multiprocessors (SMs), each with 8 scalar processors (SPs). Note that the 240 SPs (total) are not 240 independent processors; instead, they are 30 independent processors that can perform 8 similar computations at a time. From the programmer’s perspective, each thread block is assigned to an SM, and each thread within it is further scheduled to execute on one of the SPs. Compared to GTX 280, the Fermi-based GTX 480 has half the number of SMs, but each SM contains four times the number of SPs, resulting in a total of 480 SPs.

Apart from the processor layout, the programmer must understand the different layers and types of memory on the graphics card, due to the significant difference in memory access time. At the bottom layer resides the off-chip device memory (also known as global memory), which is the largest yet slowest type of GPU memory. Closer to the GPU are various kinds of fast on-chip memories. Common to both GTX 280 and GTX 480 are registers at the fastest speed, shared memory at close to register speed, and a similarly fast cache for constant memory (for read-only data). On-chip memories are roughly a hundred times faster than the off-chip global memory, but they are very limited in storage capacity. Finally, there is a region in device memory called local memory for storing large data structures, such as arrays, which cannot be mapped into registers by the compiler. Compared to GTX 280, GTX 480 has up to triple the amount of shared memory for each SM. Most importantly, it includes two levels of hardware-managed caches to ameliorate the large difference in access time of on-chip and off-chip memories. At the bottom, there is an L2 cache for the global memory with roughly half the access time. At the top, there is an L1 cache within each SM, at the speed of the shared memory. In fact, the L1 cache and the shared memory are partitions of the same hardware. The programmer can choose one of two partitioning schemes for each kernel invocation. Even with these improvements in GTX 480, it is still important to map the computation efficiently to the different types of memories for high performance.

2.2.3. Atomic Instructions.

CUDA also provides a mechanism to synchronize the execution of threads using atomic instructions, which coordinate sequential access to a shared variable (such as the absorption array in the MCML code). Atomic instructions guarantee data consistency by allowing only one thread to update the shared variable at any time; however, in doing so, it stalls other threads that require access to the same variable. As a result, atomic instructions are much more expensive than regular memory operations. Although their speed has been improved on Fermi-based GPUs [22], it is still very important to optimize atomic accesses to global memory, as explained in the following section.

3. GPU-accelerated MCML Code (GPU-MCML)

This section presents the implementation details of the GPU-accelerated MCML program (named GPU-MCML), highlighting how a high level of parallelism is achieved, while avoiding memory bottlenecks caused by atomic instructions and global memory accesses. The need to carefully consider the underlying GPU architecture, particularly the differences between the pre-Fermi and Fermi GPUs, is discussed.

3.1. Features.

Before describing the implementation details, several features of the GPU-MCML program are highlighted below:

1. Compatibility with a wide range of NVIDIA graphics cards (Fermi and pre-Fermi): The GPU-MCML program has been tested on the latest NVIDIA Fermi graphics cards such as GTX 480 (Compute Capability 2.0) and is backward compatible with pre-Fermi generations such as GTX 280 and 8800 GT (Compute Capability 1.1–1.3). This compatiblity is achieved by automatically enabling different set of features based on the Compute Capability of the GPU detected.

2. Multi-GPU execution mode: The program can be executed on multi-GPU systems by specifying the number of GPUs at runtime to open up the possibility of GPU cluster computing.

3. Optimized version and simplified version: Two versions of the GPU-MCML program are released. The optimized version automatically detects the GPU generation and chooses the proper set of architecture-specific optimizations based on the features supported. The simple version aims for code readability and reusability, by removing most optimizations. The simplified code is designed to look very similar to the original CPU MCML program to ease the learning curve for novice CUDA programmers.

3.2. Implementation Overview.

One important difference between writing CUDA code and writing a traditional C program (for sequential execution on a CPU) is the need to devise an efficient parallelization scheme for the case of CUDA programming. Although the syntax used by CUDA is, in theory, very similar to C, the programming approach differs significantly. Compared to serial execution on a single CPU where only one photon packet is simulated at a time, the GPU-accelerated version can simulate many photon packets in parallel using multiple threads executed across many scalar processors. The total number of photon packets to be simulated are split equally among the threads.

The GPU program or kernel contains the computationally intensive loop in the MCML simulation (the position update, direction update, and fluence update loop). Other miscellaneous tasks, such as reading the simulation input file, are performed on the host CPU. Each thread executes the same loop, except using a unique random number sequence. Also, a single copy of the absorption array is allocated in the global memory, and all the threads update this array concurrently using atomic instructions. Although it is, in theory, possible to allocate a private copy of the array for each thread, this approach greatly limits the number of threads that can be launched when the absorption array is large, especially in 3-D cases. Therefore, a single copy is allocated by default (and the program provides an option to specify the number of replicas).

The kernel configuration, which significantly affects performance, is set based on the generation of the GPU detected at runtime. The number of thread blocks is chosen based on the number of SMs detected, while the number of threads within each block is chosen based on the Compute Capability of the graphics card. For example, the kernel configuration is specified as 15 thread blocks (Q=15), each containing 896 threads (P=896), for GTX 480 with a Compute Capability of 2.0. As shown in Fig. 3, each thread block is physically mapped onto one of the 15 multiprocessors and the 896 threads interleave its execution on the 32 scalar processors within each multiprocessor on GTX 480.

Fig. 3.

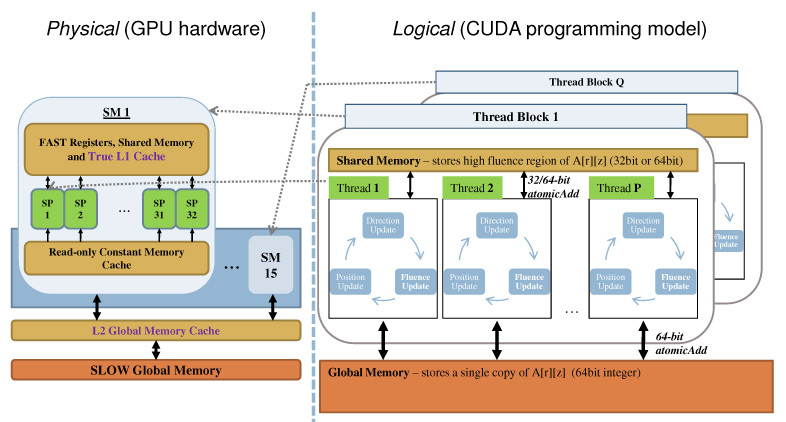
Parallelization scheme of the GPU-accelerated MCML code. Note that the number of thread blocks Q is matched to the number of SMs available and the number of threads P in each block is a many-to-one mapping (in this case, Q=15 and P=896 for GTX 480).

The choice of the kernel configuration is complicated by a series of competing factors. In general, maximizing the number of threads per block is preferred since this maximizes GPU resource utilization and helps hide the global memory latency. However, in this case, increasing the number of threads also worsens the competition for atomic access to the common A[r][z] array. Therefore, the maximum number of threads (i.e., 1024 for Fermi GPUs with a Compute Capability of 2.0) was not chosen. Similar reasoning applies to the choice of the number of thread blocks. Specifying fewer than 15 thread blocks would under-utilize the GPU resources available since there are 15 multiprocessors on GTX 480. A larger number, such as 30 thread blocks, would increase competition for atomic access and decrease the shared memory available to each thread block. The need to improve the efficiency for atomic access is discussed in detail next.

3.3. Key Performance Bottleneck.

As all threads need to atomically access the same absorption array in the global memory during every fluence update step, this step becomes a major performance bottleneck when thousands of threads (13440 threads in example shown in Fig. 3) are present. In CUDA, atomic addition is performed using the atomicAdd() instruction. However, using atomicAdd() instructions to access the global memory is particularly slow, both because global memory access is a few orders of magnitude slower than that of on-chip memories and because atomicity prevents parallel execution of the code (by stalling other threads in the code segment where atomic instructions are located). This worsens with increasing number of threads due to the higher probability for simultaneous access to an element, also known as contention.

3.4. Solution to Performance Bottleneck.

To reduce contention and access time to the A[r][z] array, two memory optimizations were applied:

1. Storing the high-fluence region in shared memory: The first optimization, illustrated in Fig. 3, is based on the high access rate of the A[r][z] elements near the photon source (or at the origin in the MCML model), causing significant contention when atomic instructions are used. Therefore, this region of the A[r][z] array is cached in the shared memory. Namely, if a photon packet is absorbed inside the high-fluence region, its weight is accumulated atomically into the shared memory copy. Otherwise, its weight is added directly into the global memory atomically. At the end of the simulation, the values temporarily stored in the shared memory copy are written (flushed) to the master copy in the global memory.

   This optimization has two significant implications. First, the shared memory copy of the array is now only updated atomically by the threads within each thread block, instead of all the threads across all thread blocks. Second, memory accesses to the shared memory are ~30-fold faster than those to the global memory.

   A point of complexity of this optimization involves maximizing the number of high-fluence elements that can be stored in shared memory. To achieve this, the size of each A[r][z] element in shared memory can be reduced (from 64 bits for the master copy in the global memory). In fact, the default setting in GPU-MCML for pre-Fermi GPUs is to declare an array of 32-bit elements in the shared memory since the 64-bit atomicAdd operation to shared memory is only supported on Fermi GPUs. However, reducing the size of the shared memory entries to 32 bits requires the explicit handling of arithmetic overflow. When the accumulated weight approaches ~2³² and overflow becomes imminent, the value needs to be flushed to global memory. Since the overhead of overflow handling can be significant (especially if overflow occurs frequently in highly absorbing media), the default setting for Fermi GPUs is to declare a 64-bit shared memory array instead.

   The overall effect of this optimization clearly depends on both the size of the shared memory on the GPU and the selection of the cached region from the A[r][z] array. Fortunately, the latest Fermi GPUs have triple the amount of shared memory (48 kB on GTX 480) compared to pre-Fermi GPUs (16 kB on GTX 280). Hence, Fermi GPUs (and likely future generations of GPUs with even larger shared memory) can greatly benefit from this optimization. As for the selection of the optimal dimensions of the cached region, this is currently specified manually as this selection is input-dependent (i.e., the shape of the high-fluence region depends on such simulation inputs as the tissue optical properties and absorption grid resolution). However, this selection can, in theory, be automated in the future by running a short simulation with the input parameters and then extracting the locations and shape of the region with the highest fluence.

2. Caching photon absorption history in registers: To further reduce the number of atomic accesses (even to the shared memory), the recent write history, representing previous absorption events, can be stored privately in registers by each thread. It was observed that consecutive absorption events can happen at nearby, or sometimes the same, locations in the A[r][z] array, depending on the absorption grid geometry and optical properties of the layers. To save on register usage, the current GPU-MCML code only stores the most recent write history using 2 registers - one for the last memory location and one for the total weight. For each thread, consecutive writes to the same location of the A[r][z] array are accumulated into these registers until a different memory location is computed. Once a different location is detected, the accumulated weight is flushed to shared (or global) memory using an atomicAdd instruction and the whole process is repeated.

As an additional optimization to avoid atomic accesses, in the GPU version, photon packets at locations beyond the coverage of the absorption grid (as specified through the input parameters dr, dz, nr, and nz) no longer accumulate their weights at the perimeter of the grid, unlike in the original MCML code. Note that these boundary elements were known to give invalid values in the original MCML code [2]. This optimization does not change the correctness of the simulation, yet it ensures that performance is not degraded if the size of the detection grid is decreased, which forces photon packets to be absorbed at boundary elements (significantly increasing contention and access latency to these elements in the A[r][z] array).

3.5. Alternative Solution: Reflectance/transmittance-only Mode.

GPU-MCML offers an alternative way to overcome the performance bottleneck. In some cases, the user is not interested in the internal absorption probability collected in the A[r][z] array. As the major performance bottleneck is caused by the atomic update of the A[r][z] array for almost every step for each photon, ignoring the array update (while still reducing the photon packet weight after each scattering event) causes a major performance boost while still retaining valid reflectance and transmittance outputs. The maximum number of atomic memory operations is reduced to the total number of photon packets launched (since reflectance/transmittance is recorded atomically only upon exiting the tissue, which happens once per photon packet) and these operations are spread out over the entire simulation. Also, the small number of memory operations compared to arithmetic operations allows the GPU to “hide” the cost of memory operations. Note that this way of recording simulation output is similar to that presented in [14]. The option to ignore the A[r][z] array detection is enabled by passing a -A flag to GPU-MCML at runtime.

3.6. Parallel pseudo-random number generation.

Efficiently generating uncorrelated pseudo random numbers is a non-trivial, albeit critical, task for parallelized MC simulations. Unless each thread uses a unique sequence of random numbers, there is a risk that multiple threads will simply re-calculate one another’s results, which would affect the signal-to-noise ratio in the resulting simulation output. Simply seeding the PRNG state differently for each thread, an approach taken in [11, 16, 18], is not sufficient to ensure against inter-thread correlation of random numbers. The GPU implementation of the Mersenne Twister (MT) PRNG used by Fang and Boas [16] provides unique random numbers for threads within a block but still potentially suffers from correlation between different thread blocks. In addition, continuously reseeding the PRNG state, for example in [16], is highly inappropriate and may increase the risk of correlating random numbers. Furthermore, the GPU version of MT PRNG uses a significant amount of the limited shared memory which may be put to better use as described in Section 3.4. Therefore, the PRNG solution used by Alerstam et al. in [14] and [19]—the Multiply-With-Carry (MWC) algorithm by Marsaglia [23]—is instead used in GPU-MCML. In addition to assigning each thread a unique seed, the MWC PRNG also allows each thread to use a unique multiplier in the algorithm, ensuring that the PRNG sequence calculated by each thread is unique. The MWC PRNG uses only 3 registers per thread and features a period of ~2⁶⁰.

3.7. Scaling to Multiple GPUs.

To scale the single-GPU implementation to multiple GPUs, multiple host threads were created on the CPU side to simultaneously launch multiple kernels, to coordinate data transfer to and from each GPU, and to sum up the partial results generated by the GPUs for final output. The same kernel and associated kernel configuration were replicated N times where N is the number of GPUs, except that each GPU initializes a different set of seeds and multipliers for the random number generator and declares a separate absorption array. This allows the independent simulation of photon packets on multiple GPUs, opening up the possibility of GPU-based cluster computing.

4. Performance

4.1. Test Platform and Test Cases.

The execution time of the GPU-accelerated MCML program (named GPU-MCML) was measured on a variety of NVIDIA graphics card to test for compatibility across different generations. This selection includes the latest NVIDIA Fermi graphics card (GeForce GTX 480) and the pre-Fermi GTX 200 series graphics cards (GeForce GTX 280 and GTX 295). The code was also tested on a heterogeneous, multi-GPU system consisting of GTX 200 series graphics cards (GTX 280 and GTX 295). This setup contains a total of 960 scalar processors. The final GPU-MCML in single-precision was compiled using the latest CUDA Toolkit (version 3.0) and tested on three different operating systems: Linux (Ubuntu 8.04), Mac OS X and Windows (Visual Studio). The Linux version was used for simulation time measurement in all cases except the multi-GPU setup (which was configured on a Windows XP system). The number of GPUs can be varied at run-time and the simulation is split among the specified number of GPUs.

For baseline performance comparison, a high-performance Intel Core i7 processor (Core i7 920, 2.66 GHz) was selected, using one of the four available processor cores. The original CPU-based MCML program in double-precision (named here CPU-MCML) was compiled with the highest optimization level (-O3 flag) using gcc 4.3.4 on Ubuntu 9.10. During simulations both HyperThreading and SpeedStep was turned off for simulation time consistency and for easily interpretable results. Also this allows simple extrapolation of the single core results to multiple core results. Due to the slow and statistically bad PRNG used in the original MCML implementation [11, 24], the PRNG was exchanged for the well-known double precision, SIMD-oriented Mersenne Twister random number generator [25, 26]. This modification resulted in ~10% improvement in the execution time of CPU-MCML.

To standardize performance measurement and validation, a seven-layer skin model at λ =600 nm (shown in Table 1) [27] was used as the simulation geometry. A second model, modelling a a thick, homogeneous slab with 10% intralipid (μ_a=0.015 cm^-1, μ_s=707.7 cm^-1, n=1.33, g=0.87, thickness=100 cm, λ =460 nm) [28] was also used. Unless otherwise noted, all simulations were performed with an absorption grid resolution of 20 μm × 100 μm (z- and r-direction, respectively) using a 500×200 detection grid (z- and r-direction, respectively) and 30 angular bins for reflectance and transmittance detection. Similarly, unless explicitly specified, the maximum amount of shared memory available was used for caching of the high-fluence region of the A[r][z] array.

4.2. Effect of GPU Architecture.

To demonstrate the compatibility of the GPU-MCML software on different graphics cards, Table 2 shows the execution times measured on a pre-Fermi GPU (GTX 280) and the latest Fermi GPU (GTX 480). Note that different architecture-specific optimizations are applied through the automatic detection of GPU compute capability (which dictates what features are supported and hence which optimizations can be applied). For example, the GPU-MCML program takes advantage of the larger shared memory size of the Fermi architecture by declaring a larger shared absorption array.

4.3. Effect of Shared Memory Size.

Figure 4 demonstrates the effect of increasing the shared memory size, used for caching the high-fluence region of the A[r][z] array, on the simulation time. The amount of shared memory (per SM) is limited to 16KB on pre-Fermi architecture and 48KB on Fermi. As the amount of shared memory is increased from 0 to the upper limit for each platform, the code executes ~2x faster on GTX 280 and ~2.4x faster on GTX 480. In the GTX 480 simulation where 0 kB is used for caching, each SM was configured with 48 kB true L1 cache and 16 kB of shared memory (although this memory was not used for caching). In all other cases, each SM was configured to use 48 kB for shared memory and 16 kB for true L1 cache. The fact that the speedup increased from ~260x (without using shared memory) to ~620x (with shared memory) on the Fermi platform shows that the true cache alone is not sufficient to attain the best possible performance. Note that, given a fixed amount of shared memory, changing the shape of the cached array region also has an impact on performance. Figure 5 shows the speedups for using all possible shapes that take 45 KB of shared memory on GTX 480. The speedups for the best and the worst shape configurations differ by a factor of 1.6.

Fig. 4.

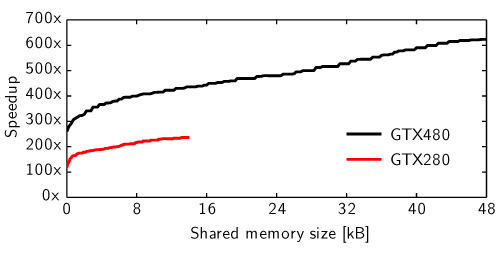
The simulation time dependance on the shared memory size used for caching of the high-fluence region of the A[r][z] array. The speedup is compared to the CPU-MCML execution time of 14418 s or ~4 h.

Fig. 5.

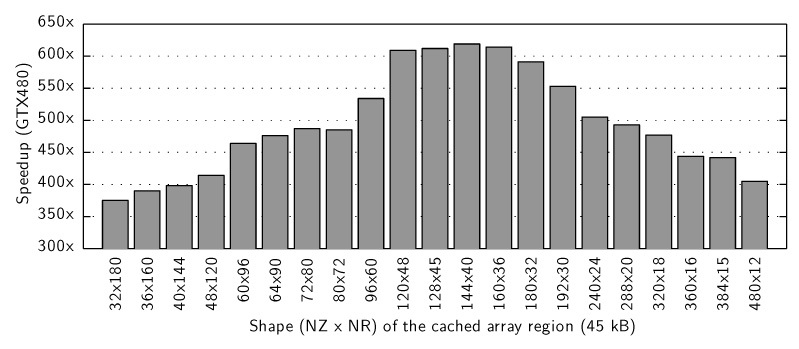
The simulation time dependance on the shape of the region of array A[r][z] that is cached in the shared memory. Here, NR and NZ are the number of voxels in the r and z dimensions of the cached region respectively. The speedup is compared to the CPU-MCML execution time of 14418 s or ~4 h.

In general, the highest speedup is achieved when the greatest number of high-fluence voxels are cached in the fast, shared memory space. Although decreasing the capacity of each shared memory element (e.g., from 64 bits to 32 bits) allows more high-fluence voxels to be cached, this also causes more frequent arithmetic overflow, which slows down the simulation. Since the frequency of overflow depends on parameters such as the absorption coefficient, the GPUMCML provides the option to toggle between 64-bit and 32-bit shared memory entries, as an additional optimization.

4.4. Effect of Grid Geometry.

The thick, homogeneous slab model was used to test the effect of the absorption grid resolution and the number of voxels on simulation time. The four rows of Table 3 show the execution times (and speedup) of GPU-MCML and CPU-MCML for four different grid resolutions, while keeping the volume of the cylindrical region of interest constant at 1 cm in radius and 1 cm in depth. As the grid resolution (specified by dr and dz) increases from 1 cm to 0.001 cm, the execution time of GPU-MCML increases by 34%. This is anticipated because the number of voxels (specified by nr and nz) increases with the resolution, and most importantly, the number of voxels located near the photon source (i.e., in the high-fluence region) increases proportionally. Since the shared memory can only cache a fixed number of voxels due to its limited size, having more voxels in the high-fluence region means that a larger portion of the region cannot be cached in the shared memory, leading to more atomicAdd() operations for writing to the slow global memory. Also, GPU-MCML performs equally well when the resolutions are set at 1 cm and 0.1 cm because all voxels are cached in the shared memory. Note that increasing the resolution in CPU-MCML has a significant impact on the simulation time. Also, the GPU-MCML code runs faster in a single-layered geometry compared to a multilayered geometry, likely due to reduced code divergence.

Table 3.

Effect of absorption grid resolution (dr, dz) and grid dimensions (nr, nz) on simulation time, simulating 10⁷ photon packets in the thick homogeneous slab model. The GPU-MCML results were measured on the GTX 480 GPU

dr and dz (cm)	nr	nz	GPU-MCML (s)	CPU-MCML (s)	Speedup
1	1	1	23.5	21817	928x
0.1	10	10	23.2	22708	979x
0.01	100	100	26.0	22624	870x
0.001	1000	1000	31.5	22813	724x

4.5. Scaling to Multiple GPUs.

Table 4 shows the possibility of running the GPU-MCML software on a multi-PU system and the linear reduction in execution time as the number of GPUs was increased at runtime. In this case, four GTX 200 series GPUs (two GTX280 graphics cards each with 1 GPU and one GTX295 graphics card with 2 GPUs) were used as the test platform and the skin model was used for performance measurements here. Each GPU contains 30 multiprocessors and a total of 240 scalar processors. Therefore, the kernel configuration for each GPU was set at 30 thread blocks and 256 threads per block. Using all 4 GPUs or equivalently 960 scalar processors, the simulation time for 100 million photon packets in the skin model was reduced from approximately 4 h on an Intel processor to only 19 s on 4 GPUs. This represents an overall speedup of 775x, with all the simulation outputs enabled.

Table 4.

Speedup as a function of the number of GPUs for simulating 10⁸ photon packets in a skin model (λ =600 nm). The speedup is compared to the CPU-MCML execution time of 14418 s or ~4 h. Values in brackets were generated without tracking absorption; only reflectance and transmittance were recorded

Number of GPUs	Platform Configuration	Time (s)	Speedup
1	GTX 295 (using 1 of 2 GPUs)	73.3 (45.9)	197x (314x)
2	GTX 295 (using both GPUs)	37.2 (23.4)	388x (616x)
3	GTX 295 (2 GPUs) + GTX 280	24.8 (15.7)	581x (918x)
4	GTX 295 (2 GPUs) + 2 x GTX 280	18.6 (11.9)	775x (1212x)

4.6. Performance of Simplified Version.

Table 5 shows the performance of the simplified version of GPU-MCML (described in Section 3.1) for the 7-layer skin model specified in Table 1, with and without tracking the absorption. With absorption calculations, the simpler version is ~4x slower on GTX280 and ~6x slower on GTX480. In the reflectance/transmittance-only mode, the simpler version achieves similar performance.

Table 5.

Execution time of the simplified version of GPU-MCML for 10⁸ photon packets. The speedup is compared to the CPU-MCML execution time of 14418 s or ~4 h. Values in brackets were generated without tracking absorption; only reflectance and transmittance were recorded

Platform	Simplified GPU-MCML (s)	Speedup
GeForce GTX 280	225.8 (38.3)	64x (376x)
GeForce GTX 480	147.9 (17.5)	97x (824x)

Table 1.

Tissue optical properties of a seven-layer skin model (λ =600 nm)

Layer	n	μa (cm-1)	μs (cm-1)	g	Thickness (cm)
1. stratum corneum	1.53	0.2	1000	0.9	0.002
2. living epidermis	1.34	0.15	400	0.85	0.008
3. papillary dermis	1.4	0.7	300	0.8	0.01
4. upper blood net dermis	1.39	1	350	0.9	0.008
5. dermis	1.4	0.7	200	0.76	0.162
6. deep blood net dermis	1.39	1	350	0.95	0.02
7. subcutaneous fat	1.44	0.3	150	0.8	0.59

4.7. Performance in Reflectance/transmittance-only Mode.

The results of running GPU-MCML in reflectance/transmittance-only mode, by enabling the -A flag, are shown in parentheses in Tables 2, 4, and 5. In summary, the additional speedup factor is ~1.4x and ~1.6x (multiplicatively) on GTX 480 and GTX 280, respectively. The cause of the discrepancy is the larger cache on Fermi GPUs, as illustrated in Fig. 4. The simple GPU-MCML version achieves similar performance as the optimized version in reflectance/transmittance-only mode as shown in Table 5, since atomic access is not a bottleneck in this mode and optimizations targeted at atomic access are expected to have minimal effect.

Table 2.

Effect of GPU architecture on simulation time for 10⁸ photon packets. The speedup was calculated in comparison to the CPU-MCML execution time of 14418 s or ~4 h. Values in brackets were generated without tracking absorption; only reflectance and transmittance were recorded

Platform (Compute Capability)	No. of SMs	No. of SPs	GPU-MCML (s)	Speedup
GeForce GTX 280 (1.3)	30	240	60.3 (38.6)	239x (374x)
GeForce GTX 480 (2.0-Fermi)	15	480	23.2 (16.6)	621 x (869x)

Investigating the effects of removing absorption tracking in CPU-MCML revealed a ~ 10% performance boost, which reduced the simulation time for 10⁸ photon packets in the skin model from 14418s to 12824s.

5. Validation

In this section, the validation results of GPU-MCML vs. CPU-MCML are presented. Although all output parameters of GPU-MCML have been validated using several different GPUs (both single and multiple GPU configurations) and different test cases, only the representative results are included here. The fastest GPU platform available (NVIDIA GTX 480 - Fermi architecture) was selected to generate the GPU results and the standard skin model (10⁸ photon packets) from Table 1 was used as the test case geometry.

All the validation tests indicate that the simulation outputs of GPU-MCML are statistically equivalent to those of CPU-MCML.

5.1. Fluence Distribution.

Figure 6 shows the simulated fluence distribution and the corresponding isofluence plots. The outputs produced by the GPU-MCML and CPU-MCML programs matched very well. To further quantify any potential error introduced in the implementation, the relative error E[i_r][i_z] is computed for each voxel using Eq. (1).

Fig. 6.

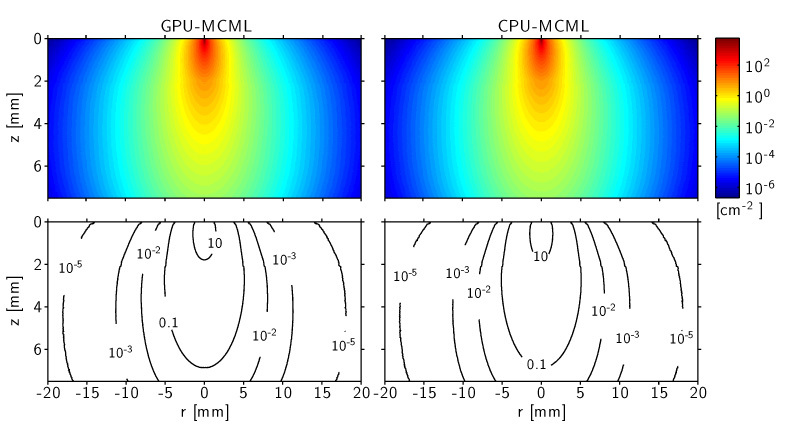
Simulated fluence distribution and corresponding contour plots in the skin model (10⁸ photon packets) for the impulse response: generated by GPU-MCML (left) and by generated by CPU-MCML (right). Note the logarithmic scale. The first layers are thin and cannot be fully appreciated in this scale, especially as the optical properties are rather similar. Both simulations provide, within statistical uncertainties, the same results.

$$E\left[i_r\right]\left[i_z\right]=\frac{\mid A_{\mathit{gpu}}\left[i_r\right]\left[i_z\right]\mid -A_{\mathit{cpu}}\left[i_r\right]\left[i_z\right]}{A_{\mathit{cpu}}\left[i_r\right]\left[i_z\right]}$$ (1)

where A_cpu is the gold standard absorption array produced by the CPU-MCML software while A_gpu contains the corresponding elements produced by the GPU-MCML program.

Figure 7 plots the relative error as a function of position, showing that the differences observed are within the statistical uncertainties between two simulation runs of the gold standard CPU-MCML program using the same number of photon packets.

Fig. 7.

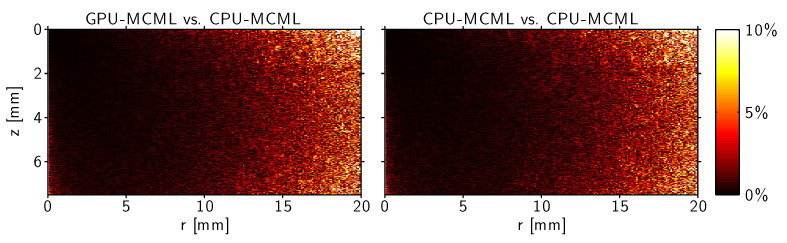
Distribution of relative error for the skin model (10⁸ photon packets). Left: GPUMCML vs. CPU-MCML. Right: CPU-MCML vs. CPU-MCML. Color bar represents percent error from 0% to 10%.

6. Discussion and Conclusions

The rapid evolution of the GPU, particularly with the recent release of the NVIDIA Fermi GPU built for general-purpose computing, has made GPU-based scientific computing an attractive alternative to conventional CPU-based cluster computing. However, several previous attempts to use the GPU for accelerating MC simulations by other groups have shown limited success due to the difficulty of optimizing the GPU code for high performance. This makes the GPU seem less than ideal, especially for complex inverse problems where high performance is an important criterion.

For example, two groups have recently presented attempts to use GPUs for MC-based photon simulations in arbitrary 3-D geometry, but both groups reported challenges optimizing GPU code for high performance. Ren et al. only achieved a 10x speedup compared to a 2.4-GHz Intel Xeon CPU, despite using a modern GPU (NVIDIA GTX 260 with 192 scalar processors). Their simulation involved modelling heterogenous tissue using triangular meshes [15]. Although an earlier 3-D, voxel-based implementation by Fang and Boas [16] reported a higher speedup (300x on an NVIDIA 8800GT graphics card with 112 scalar processors compared to a 1.86GHz Intel Xeon CPU), this was achieved without using atomic instructions, possibly compromising data integrity. The speedup dropped to 75x, or 4 times slower, when atomic instructions were used. Note that atomic instructions are required to avoid race conditions [29]. Race conditions can compromise the stability and accuracy of the simulation results, both of which are crucial to the use of the MC method as a gold standard. Finally, Badal and Badano obtained a 27x speedup when using a modern GTX 295 GPU (utilizing 240 out of 480 scalar processors) to accelerate the simulation of high-energy photons in voxelized media for X-ray imaging [17]. Based on these previous attempts, Shen and Wang developed a tetrahedron-based, inhomogeneous MC simulator utilizing multiple cores in modern CPUs, arguing that the speedup obtained using mid-range GPUs was insufficient to motivate a complicated, GPU-based implementation [24].

In contrary, our earlier work showed that the GPU has the potential to significantly accelerate MC simulations for photon migration. Alerstam et al. introduced GPU-accelerated MC to the field by demonstrating a massive speedup for simulating time-resolved photon reflectance in a homogenous semi-infinite medium [14], which requires atomic access to a 1-D histogram array. Lo et al. presented both an FPGA-based [11] and a GPU-based solution [18] to simulate steady-state photon migration in multilayered media. Notably, this preliminary GPU implementation demonstrated the importance of optimizing atomic access to the 2-D absorption array. Simultaneously and independently, Alerstam et al. presented a more versatile, albeit less optimized, code solving the same problem using GPU hardware [19] and observed a similar performance bottleneck caused by atomic access.

In this paper, we point out a major performance bottleneck preventing several GPU-MC codes for photon migration from fully exploiting the computing power in modern GPUs [16] and present a solution based on caching the high-fluence region in the on-chip shared memory. This is illustrated by implementing a GPU-accelerated version of the well-known MC program MCML [2] and showing that an approximate 600x speedup can be achieved on a single NVIDIA GTX 480 Fermi graphics card compared to a high-performance Intel Core i7 processor. This speedup should be put into perspective by considering the equivalent performance figure for the naive solution as presented in Table 5 where a mere 97x speedup is achieved on the same setup. In other words, the optimized implementation is more than 6x more efficient than the naive solution. The effect of the size and shape of the cached region is investigated and it is found that more shared memory results in better performance, giving the new Fermi architecture an advantage over the pre-Fermi architectures. Although Fermi features an L1 cache, the performance when using this implicit (true) caching method is found to be significantly inferior to the explicit caching scheme which configures the GPU to use 48 kB of shared memory.

In addition to presenting a cache-based solution to the key bottleneck, we present an alternative solution which may be of great use for some applications. As illustrated by the simplified GPU-MCML code, representing the naive solution, the major bottleneck is the atomic memory operation performed by every thread in every iteration of the main loop. Simply ignoring the scoring of the internal absorption distribution (by not storing this data in memory) reduces the need for atomic memory operations to a maximum of one per photon packet. Note that this is very similar to the simulation performed by Alerstam et al. [14] and Carbone et al. [30]. Considering the differences in the hardware used, the performance of the codes agree well. This is an important result as almost all current methods of evaluating optical properties, including optical tomography methods, are based on either monitoring spatial/temporal distributions of light exiting the boundary of a scattering medium or monitoring one or a few discrete points inside the medium. Both of these cases are covered by the alternative solution. In addition, this result illustrates the strength of GPU-based calculations; GPUs are good at handling organized (coalesced) memory operations (which is hard to achieve in MC applications), but perform poorly with random memory operations and atomic memory operations. However, when the ratio of arithmetic operations to memory operations is high, the GPU may “hide” the memory latency by using the waiting time to do calculations with other threads. Consequently, the simplified/naive GPU-MCML version performs almost as well as the highly optimized code when ignoring the internal absorption array detection while the code is much simpler.

The great speedup of MC applications for simulating photon migration on GPUs are mainly attributed to their parallelizable nature, as the results of each photon packet can be computed independently of all the other photon packets and thus all other threads. A simple and effective way to accelerate CPU-based Monte Carlo simulations would be to make use of the many cores in moderns CPUs. The Intel Core i7 CPU used for performance comparison in this paper has four cores and one may expect up to four times the performance if all cores were used for the simulation. Additional CPU-based optimizations can be applied, such as vectorizing the MC code, making use of Streaming SIMD Extensions (SSE), and using faster arithmetic libraries. This was attempted, for example, by Shen and Wang who demonstrated a 30–50% improvement in speed [24]. Although optimizing the CPU code would decrease the relative gain of using GPUs for accelerating MC simulations, one should keep in mind that the effort to write optimized CPU code may be similar, or even greater, than writing optimized GPU code while the GPU code most likely still would be significantly faster. While many current MC codes may benefit significantly from GPU-based acceleration, it should be mentioned that not all implementations may be suitable for massive parallelization. In particular, calculations with more inter-thread dependancies may not be possible to efficiently implement on GPUs and CPU-based MC may remain competitive for certain complex MC algorithms.

The scalability of the GPU-based implementation was also demonstrated using four GTX 200 series graphics cards. With this scalability, the performance can be further improved using a GPU-based computing cluster, such as the NVIDIA Tesla S1070 system with 960 scalar processors which can be stacked in a cluster configuration.

In conclusion, we demonstrate a highly optimized, scalable and flexible GPU-accelerated implementation of the well-known MCML package, named GPU-MCML. GPU-MCML features two ways of utilizing the hardware to achieve the best possible performance, either by caching the high-fluence region in the on-chip shared memory or by only tracking the distribution of the photon packets exiting the medium. Both these solutions illustrate the need to understand the underlying GPU architecture for high performance, even on the latest Fermi GPU designed for general-purpose computing. The dramatic reduction in computation time opens up the possibility of using MC simulations for solving inverse problems in biomedical optics in the future. A generalized and simplified code is released along GPU-MCML which intends to provide a good starting point for scientists and programmers interested in learning or using GPU-accelerated MC. This code aims to ease the learning curve for anyone familiar with MCML and provides a foundation built on good GPU programming practices. The GPU-MCML code package has been released as an open-source software on this website: http://code.google.com/p/gpumcml.