Spectral and spatial dependence of
diffuse optical signals in response to
peripheral nerve stimulation

Abstract

Using non-invasive, near-infrared spectroscopy we have previously reported optical signals measured at or around peripheral nerves in response to their stimulation. Such optical signals featured amplitudes on the order of 0.1% and peaked about 100 ms after peripheral nerve stimulation in human subjects. Here, we report a study of the spatial and spectral dependence of the optical signals induced by stimulation of the human median and sural nerves, and observe that these optical signals are: (1) unlikely due to either dilation or constriction of blood vessels, (2) not associated with capillary bed hemoglobin, (3) likely due to blood vessel(s) displacement, and (4) unlikely due to fiber-skin optical coupling effects. We conclude that the most probable origin of the optical response to peripheral nerve stimulation is from displacement of blood vessels within the optically probed volume, as a result of muscle twitch in adjacent areas.

1. Introduction

Near-infrared spectroscopy is a diffuse optical technique that allows for the non-invasive investigation of biological tissues (skeletal muscle, brain, breast, etc.) on a macroscopic scale of several millimeters to several centimeters. Recently, we have reported that fast (~0.1 ms) electrical stimulation of peripheral nerves triggers a non-invasively detected optical response co-localized with the stimulated nerve on a time scale of ~100 ms in human subjects [1]. We have then investigated the spatial characteristics as well as the diagnostic potential of such optical response to peripheral nerve stimulation, finding a co-localization with the sensory nerve action potential (SNAP) [2], and a delayed response in patients affected by diabetic neuropathy [3]. In the present work, we report further studies on the spatial and spectral dependence of these optical signals in an effort to better characterize them and to advance our understanding of their origins.

Whereas in this article we report optical signals in tissue regions containing or immediately adjacent to the stimulated peripheral nerves, there have been several studies of optical signals induced by peripheral nerve stimulation on the central nervous system, either on the brain, in animal models [4] or human subjects [5–8], or on the spinal cord in animal models [9–11]. These studies aimed at detecting optical responses to peripheral nerve stimulation in the central nervous system that are associated either with a hemodynamic response on a time scale of seconds [4,6,8,10,11], or with a faster process on a time scale of ~100 ms that may be closely linked with electrical neuronal activity [4,5,7]. Measurements of the average changes in oxygenation and optical scattering properties of the rat spinal chord during a train of peripheral nerve stimulations (1 Hz frequency) may be sensitive to both hemodynamic and neuronal activation effects [9]. While the slower hemodynamic response measured in the brain has been widely accepted as resulting from an increased cerebral blood flow, the reliability of measurements of the faster optical signal through the intact human head is still debated [12,13].

There has been a previous non-invasive study of optical signals in response to peripheral nerve stimulation specifically aimed at detecting an optical response on the same time scale (~ms) of the median nerve action potential [14]. In this study, Lebid et al. presented concurrent electrical and optical measurements with a sampling rate of 2 kHz, but were not able to detect an optical signal on the millisecond time scale of the sensory nerve action potential [14].

We have investigated the spectral and spatial dependence of the optical signals measured on tissues containing or in close proximity to peripheral nerves following their stimulation. Specifically, we have measured the wavelength dependence of the optical signals in experiments using two discrete wavelengths (690 and 830 nm) or broadband spectroscopy (650-900 nm). Spatial dependence was assessed by measuring the optical signals at twelve locations around a fixed optical collection point. In addition to studying the spectral and spatial dependence of optical responses to nerve stimulation to obtain indications on their origins, we also introduce controlled hemodynamics and oxygenation changes in the tissues under study by means of vascular occlusions. This is accomplished in the human forearm by placing a pressure cuff around the upper arm and inflating the cuff above venous pressure (typical inflation pressure: 50-60 mmHg) to achieve venous occlusion [15–17], or above systolic arterial pressure (typical inflation pressure: 200-260 mmHg or lower, depending on individual systolic pressure values [16]) to achieve arterial occlusion [16,18–20]. Near-infrared spectroscopy studies have characterized the effects of venous occlusion and arterial occlusion on muscle hemodynamics. Specifically, venous occlusion results in increases in muscle concentration of both oxy-hemoglobin, [HbO₂], and deoxy-hemoglobin, [Hb] [19,21], and a relatively small decrease in muscle tissue oxygen saturation on the order of a few percent [11]. Arterial occlusion results in a strong oxygen desaturation of muscle tissue (~20-30%), an increase in [Hb] and a decrease in [HbO₂] [16,19]. Because most of the blood flow changes due to venous and arterial occlusion in muscle are exhibited in the capillary bed or small vessels, we used these established hemodynamic and oxygenation changes, with their associated spectrally dependent changes in optical properties, to investigate their effects on the optical response to nerve stimulation.In this work, we investigate several possible origins for the optical response to electrical stimulation of peripheral nerves: (1) hemodynamic changes involving hemoglobin in the capillary bed and small blood vessels, (2) vascular dilation or contraction, (3) displacement of individual blood vessel(s), (4) changes in the efficiency of optical coupling between the skin and the illumination/collection optical fibers.

We have characterized the optical response to nerve stimulation in terms of its spatial dependence, wavelength dependence, and changes induced by vascular occlusions (venous or arterial occlusion). Our measurements show repeatable, spatially dependent optical signals with spectral features that are unaffected by vascular occlusions and are consistent with those of hemoglobin. While it is possible that changes in optical coupling between optical fibers and skin may contribute to the optical signals, they cannot fully account for them. Based on the results of our studies, we conclude that the most likely origin of the optical response to electrical stimulation of peripheral nerves is a nerve-stimulation-induced displacement of relatively large blood vessel(s) in the probed volume.

2. Methods

We have performed studies according to three separate protocols: spatially resolved measurements (at two wavelengths: 690 and 830 nm) on the sural nerve, measurements before-during-after vascular occlusions on the median nerve (also at 690 and 830 nm), and broadband spectral measurements (650-900 nm) on the median nerve. Table 1 shows a list of the investigated subjects, the peripheral nerve studied, and the experimental protocols performed. By studying two distinct nerves, we can show that there are optical responses to electrical stimulation in different peripheral nerves, one with both motor and sensory function (median) and one with solely sensory function (sural). Both nerves are superficial at the locations of measurement (2-6mm depth), allowing for good optical sensitivity There are, however, practical reasons to prefer one nerve over the other in each of the three protocols reported in this manuscript, and this justifies the investigation of one or the other nerve in each protocol, as reported in Table 1.

Table 1. Summary of subjects, peripheral nerves examined, and experimental protocols performed.

Subject	Age (y)	Sex	Nerve Investigated	Protocol
1	26	M	right sural	spatial dependence
2	28	M	right sural	spatial dependence
3	25	F	right sural	spatial dependence
4	26	M	right sural	spatial dependence
5	34	F	right sural	spatial dependence
6	43	M	right median	vascular occlusion
6	43	M	left median	broadband spectroscopy
7	51	M	left median	vascular occlusion
8	33	F	right median	vascular occlusion
9	24	M	right median	vascular occlusion

2.1 Instrumentation for measurements on the median and sural nerves

Figure 1 shows the experimental setup used in this study for median nerve investigations where surface stimulating electrodes were placed on the palmar branch of the median nerve between the pointer and middle fingers, whereas the optical probe was placed in proximity to the median nerve on the wrist area. Figure 2 shows the instrumental setup for sural nerve measurements where the stimulating electrodes were placed about 10 cm proximal to the optical probe, which was applied below the lateral malleolus where the sural nerve bends to run along the lateral side of the foot. Before performing optical measurements, recording electrodes were placed in the same area as the optical probe shown in Figs. 1 and 2 to measure the sensory nerve action potential (SNAP). After the SNAP was measured, the recording electrodes were removed and replaced by the optical probe. An electromyogram (EMG) system (TECA Synergy, Viasys Healthcare, Conshohoken, PA or Sierra II Wedge, Cadwell Laboratories, Inc., Kennewick, WA) provided the electrical stimulation at current levels set by the operator. An electrical pulse of 0.1 ms duration, at a repetition rate of 1.5 Hz, was used at the highest level of current below the threshold of any visible skin motion to avoid potential motion artifacts and minimize contributions to the optical data from changes in optical coupling between skin and illumination/collection optical fibers. Stimulation current levels ranged from 5 to 15 mA.

Fig. 1.

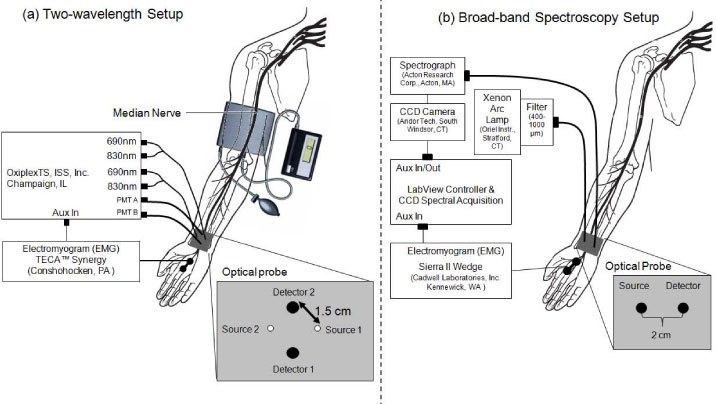
Experimental setup for electrical stimulation and optical recordings on the median nerve. Optical recordings were performed with: (a) a two-wavelength (690 and 830 nm) tissue spectrometer in the vascular occlusion protocol (PMT: photomultiplier tube detector); (b) a spectral setup for broadband spectral measurements (over the wavelength range 650-900 nm) in the spectral characterization study (CCD: charge coupled device).

Fig. 2.

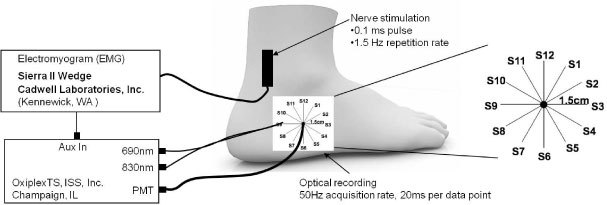
Experimental setup for electrical stimulation and optical recordings on the sural nerve, including an expanded schematic of the spatially resolved probe (right), where S1–S12 denote the twelve sequential positions of the illumination optical fibers and the black circle represents the fixed detector position.

Optical measurements at discrete wavelengths were performed with a commercial near-infrared tissue spectrometer (OxiplexTS, ISS Inc., Champaign, IL) featuring time-multiplexed laser diodes emitting at 690 and 830 nm, and two independent optical detection channels based on two photomultiplier tubes (PMT’s) [see Fig. 1(a) and Fig. 2]. Although the OxiplexTS is a frequency-domain instrument, we could not detect any phase signals associated with nerve stimulation in our initial measurements, therefore, we only recorded and report continuous-wave intensity data, in this manuscript. A portion of the stimulating electrical pulse was coupled to an auxiliary input of the near-infrared tissue spectrometer to synchronize the electrical stimulation and the acquisition of optical data. The optical probes for measurements on the median nerve [Fig. 1(a)] and sural nerve (Fig. 2) consisted of 400 μm-diameter illumination optical fibers (coupled to the laser diodes) and 2 mm-diameter collection optical fiber bundles (coupled to the PMT’s), arranged according to geometries specific to the various measurement protocols, as described below. The laser diodes were multiplexed at a rate of 100 Hz to turn them on and off in sequence every 10 ms, so that data from each individual light source were collected for 10 ms. This results in a time resolution of 20 ms for measurements at two wavelengths and one illumination point (spatial dependence study, see Fig. 2), or 40 ms for measurements at two wavelengths and two illumination points [vascular occlusion protocol, see Fig. 1(a)]. The optical power coupled from the laser diodes into the 400 μm diameter illumination fibers is on the order of 2 mW. In the vascular occlusion protocol [Fig. 1(a)] and in the spatial dependence study (Fig. 2), we have used a separation of 1.5 cm between the illumination and collection optical fibers.

The light source for broadband spectral measurements was a xenon arc lamp (Model 6258, Oriel Instruments, Stratford, CT), which was band-pass filtered over the wavelength band 400-1000 nm [see Fig. 1(b)]. Two 2 mm diameter optical fibers served as illumination and collection fibers, respectively, delivering light from the arc lamp to the tissue and collecting light from the tissue to a spectrograph (ModelSP-150, Acton Research Corp., Acton, MA) with a 300 g/mm grating and 700 nm blaze wavelength. We detected spectrally dispersed light with a charged coupled device (CCD) camera (Model DU420A-BR-DD, Andor Technology, South Windsor, CT). The distance between illumination and collector fiber on the tissue was set to 2 cm for the broadband spectral measurements [Fig. 1(b)]. The different source-detector separations (with respect to 1.5 cm used in the discrete wavelength measurements) were dictated by practical issues associated with the need to shield the detector optical fiber from specular reflections at the tissue/phantom surface. The larger source-detector separation may result in a slightly reduced sensitivity to the superficial nerve, but should not impact the wavelength dependence of the detected optical signal. A LabView program controlled the CCD collection and synchronized the spectral acquisition with the electrical stimulation to collect 30 consecutive spectra following each stimulation pulse, at an acquisition time per spectrum of 18.3 ms. A schematic diagram of the broadband spectral setup for measurements on the median nerve is shown in Fig. 1(b).

2.2. Spatial dependence study (sural nerve)

Five human subjects [subjects 1-5 in Table 1, three males, two females, age range 25-34 y] were measured to investigate the spatial dependence of the optical response to sural nerve stimulation. Only the right sural nerve was used for spatial dependence studies because the tissue surrounding the sural nerve in the measurement area is more homogeneous than that surrounding the median nerve and includes no skeletal muscle. For this protocol, the set of two illumination optical fibers (one for 690 nm and one for 830 nm) was sequentially placed at each source location (S1-S12) as shown in Fig. 2. The illumination fibers were held at one specific source location for 30 s before moving to the next location, for a total acquisition time of 6 min for all twelve locations. The collection optical fiber was placed at a fixed location, centered with respect to the sequential source fibers locations. Because of the circular arrangement of the sequential illumination locations S1-S12, we refer to them as 1-12 o’clock positions.

2.3. Vascular occlusion protocol (median nerve)

Four human subjects [subjects 6-9 in Table 1, three males, one female, age range 24-51 y] were measured to study the effects of vascular occlusions on the optical response to median nerve stimulation. We opted to study the median nerve in the vascular occlusion protocol because vascular occlusion is less practical (although feasible) and induces more discomfort in the lower limbs than in the upper limbs. Vascular occlusion was induced by a pneumatic pressure cuff placed on the upper arm and pressurized to 50 mmHg for venous occlusion and either 150 mmHg (subjects 6-7) or 220 mmHg (subjects 8-9) for arterial occlusion. The four phases of each trial are as follows: (phase 1) 2 min baseline with no nerve stimulation, (phase 2) 2 min period with nerve stimulation and no vascular occlusion, (phase 3) nerve stimulation during vascular occlusion (venous occlusion: 5 min; arterial occlusion: 5 min for subjects 6-7, 2 min for subjects 8-9), and (phase 4) 5 min of nerve stimulation after release of vascular occlusion.

As shown in Fig. 1(a), we used two illumination positions and two collection positions (distributed over an area of ~3 cm²), so that we collected data with four distinct source-detector pairs, corresponding to four separate tissue volumes. We examined the power spectrum of the optical signals measured during the two-minute stimulation period preceding occlusion (phase 2) to determine which source-detector pair detected the signal with the largest 1.5 Hz stimulation frequency contribution. The data from such source-detector pair is the one that we report, being the one that is most sensitive to the optical response to nerve stimulation.

2.4 Broadband spectral measurements (median nerve)

One human subject [subject 6 in Table 1, male, age 43 y] was investigated with the setup shown in Fig. 1(b) to study the spectral features of (A) optical responses to median nerve stimulation, and (B) optical signals associated merely with a change in the optical coupling between optical fibers and skin. In particular, we studied the optical signals in response to nerve stimulation under conditions in which the illumination and collection optical fibers were both in contact with the skin (contact configuration) or neither in contact with the skin (non-contact configuration). The need for fine adjustment of the relative position of optical fibers and tissue made it more practical to measure the median nerve (wrist area) rather than the sural nerve (ankle area). In the contact configuration, we measured the change in optical irradiance caused by pushing the collection optical fiber by 125 μm into the skin by means of a finely controlled linear stage. We have also collected similar data on a tissue-like phantom made of silicon, featuring optical properties similar to those of tissue (μ_a~0.15 cm⁻¹, μ_s'~5 cm⁻¹) in the wavelength band considered in this study (650-900 nm).

2.5 Data analysis

The relative change in optical irradiance associated with electrical stimulation of peripheral nerves is expressed as δI_stim(t)/I(t₀), where I(t₀) is the measured irradiance at the onset of stimulation, occurring at a time identified as t₀, and δI_stim(t) = I(t) – I(t₀). Since we apply multiple stimulations (at a 1.5 Hz repetition rate), we may denote each individual stimulation with the index i, so that the optical response to the i-th stimulation is written δI_{stim_i}(t)/I(t_0i), where t_0i is the onset time for the i-th stimulation. The average response over N stimulations is then written as $<\delta I_{\text{stim}}(t)/I(t_0){>}_N=\frac{1}{N}{\displaystyle {\sum }_{i=1}^N\delta I_{\text{stim\_}i}(t)/I(t_{0i})}$. In the study of the optical response to nerve stimulation in the vascular occlusion protocol, we have measured the maximum optical response (with sign) for each individual stimulation (i.e. δI_stim(t_max)/I(t₀), where t_max is defined as the time at which |<δI_stim(t)/I(t₀)>| is maximum). We obtain a time trace for the maximal optical response for phases 2-4 of the protocol by applying a 20 point moving average (corresponding to a time of 20 × 0.67 s ≈ 13 s), sliding each 13 s time period by one point (or 0.67 s) in succession.

We express the change in optical irradiance measured during the vascular occlusion protocol as ∆I_occl(t)/I₀, where I₀ is the average irradiance over the two-minute baseline period (phase 1), and ∆I_occl(t) = I_occl(t) – I₀ is the difference between the detected irradiance during the occlusion protocol, I_occl(t), and I₀. Such change in optical irradiance (∆I_occl(t)/I₀) reflects the changes in tissue hemoglobin concentration and saturation over the optically probed volume.

The relative change in optical irradiance associated with changes in optical coupling between optical fibers and tissue is indicated as ∆I_coupling/I₀ where ∆I_coupling = I - I₀ is the difference between the detected irradiance after (I) and before (I₀) the change in optical coupling.

2.6 Diffusion model for optical signals due to blood vessel displacement

To model the optical signals associated with geometrical changes (dilation, contraction, displacement) of a blood vessel within tissue, we have used a previously published perturbation approach for diffusion theory [22], which is applicable to a localized optical inhomogeneity embedded within a semi-infinite turbid medium. In a coordinate system (x,y,z) where the x axis is perpendicular to the medium boundary (set at x = 0), and the y axis is along the source-detector direction, we set the source at (1/μ_s',0,0), where μ_s' is the reduced scattering coefficient of the medium, and the detector at (0,15,0) mm. The portion of a blood vessel intersecting the optically probed volume is modeled as a rectangular rod with the long axis perpendicular to the source-detector line, i.e. along the z axis (Fig. 3 ). The mean path-length traveled by detected photons through the volume occupied by the blood vessel (<l_bv>) is computed by previously described methods from diffusion theory [22], using a 10x10x100 element mesh of the rod, and assuming background absorption and reduced scattering coefficients (µ_a0,µ_s0'), blood vessel size, and blood vessel position.

Fig. 3.

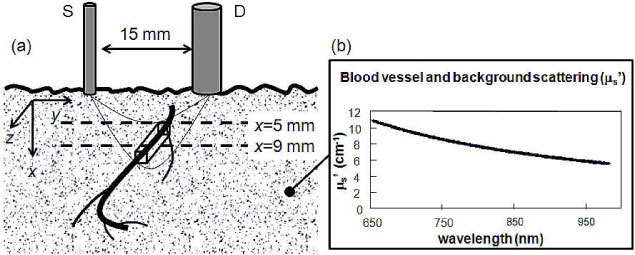
Pictorial representation of the vascular displacement model showing (a) the rectangular modeled portion of a blood vessel passing through the optically probed volume and (b) the assumed reduced scattering spectrum for both the blood vessel and the surrounding tissue.

The change in optical irradiance due to the presence of a blood vessel at position r is written ∆I_bv(r)/I₀, where I₀ is defined as the irradiance measured in the medium with no blood vessel, I_bv(r) is the irradiance measured with blood vessel at position r, and ∆I_bv(r) = I_bv(r) - I₀. Relative changes in irradiance ∆I_bv(r)/I₀ are calculated by a truncated McLaurin series [23]:

$$\frac{\Delta I_{bv}\left(r\right)}{I_0}~-\langle l_{bv}\rangle \Delta {\mu }_{a,bv}+\frac{1}{2!}\langle l_{bv}^2\rangle \Delta {\mu }_{a,bv}^2-\frac{1}{3!}\langle l_{bv}^3\rangle \Delta {\mu }_{a,bv}^3+\frac{1}{4!}\langle l_{bv}^4\rangle \Delta {\mu }_{a,bv}^4$$ (1)

where the coefficients of the series $\langle l_{bv}^n\rangle$are the moments of order n (n = 1,2,3,4) of the partial path-length distribution l_bv, and ∆µ_a,bv is the absorption contrast between blood vessel and background. After assuming the concentration and saturation of hemoglobin in the background tissue and in the blood vessel, ∆µ_a is calculated using hemoglobin molar extinction coefficients:

$$\Delta {\mu }_{a,bv}=\Delta \left[Hb{O}_2\right]{\epsilon }_{Hb{O}_2}+\Delta \left[Hb\right]{\epsilon }_{Hb}$$ (2)

where ∆[HbO₂] (∆[Hb]) is the difference of the concentrations of oxy-hemoglobin (deoxy-hemoglobin) inside and outside of the blood vessel, and ε_HbO2 (ε_Hb) is the molar extinction coefficient of oxy-hemoglobin (deoxy-hemoglobin). We assumed previously published background coefficients of absorption and reduced scattering coefficients (µ_s’) in forearm tissue under rest conditions [24]. The assumed spectrum µ_s’(λ) is shown in Fig. 3(b) over the wavelength band 650-960 nm. The tissue is assumed to have 75% oxygen saturation of hemoglobin (StO₂) [25] and 100 µM total hemoglobin concentration [HbT] [25] under rest conditions. Under sustained arterial occlusion, we assume an StO₂ of 40% [26] and an [HbT] of 100 µM [25]. Arterial blood is assumed to have a hemoglobin saturation of 98% [27] and a total hemoglobin concentration of 2.3 mM [28]. Venous blood is assumed to have a hemoglobin saturation of 75% [29] and a total hemoglobin concentration of 2.3 mM [28]. Tissue oxygen saturation is denoted as S_tO₂ and blood vessel oxygen saturation is denoted as S_bvO₂. In these models, we did not assume a scattering contrast between background tissue and blood vessel. The McLaurin series [Eq. (1)] can be estimated by Padé approximants, which are ratios of rational functions of ∆µ_a,bv, as follows [23]:

$$\frac{\Delta I_{bv}\left(r\right)}{I_0}~P_{\frac{M}{N}}\left(\Delta {\mu }_{a,bv}\right)=\frac{{\displaystyle \sum _{k=0}^M{a}_k\Delta {\mu }_{a,bv}^k}}{1+{\displaystyle \sum _{k=1}^N{b}_k\Delta {\mu }_{a,bv}^k}}$$ (3)

Equation (3) was used with M = N = 2, and provides a more accurate expression than the fourth order McLaurin expansion of Eq. (1) The coefficients a_k and b_k in Eq. (3) are obtained by imposing that the right hand sides of Eqs. (1) and (3), and their first four derivatives, coincide for ∆µ_a,bv = 0 [23,30]. The Padé Approximants methods of Eq. (3) is computationally fast and lends itself to multi-wavelength estimation of optical signals. In fact, the total computation time for 351 wavelengths was about 5 s on a Pentium^®4, 3.2GHz processor with 2GB of RAM. The change in optical irradiance, or optical signal, due to blood vessel displacement from position r₁ to position r₂ is obtained by taking the difference between the changes in irradiance measured at r₂ and r₁ and multiplying by $I_0/I_{r_1}$:

$$\frac{\Delta I_{bv}\left(r_1\to r_2\right)}{I_{r_1}}=\left[\frac{\Delta I_{bv}\left(r_2\right)}{I_0}-\frac{\Delta I_{bv}\left(r_1\right)}{I_0}\right]\frac{I_0}{I_{r_1}}$$ (4)

where $I_{r_1}$is the intensity measured when the blood vessel is at position r_1.

3. Results

3.1 Time scales of SNAP and of the optical response to nerve stimulation

Figure 4(a) shows a typical sensory nerve action potential (SNAP), measured on the sural nerve of subject 4, peaking at ~2 ms post stimulus. Figure 4(b) shows the corresponding optical signals at 690 and 830 nm, averaged over 45 stimulation responses, which peak about 100 ms post stimulus. The error bars in Fig. 4(b) are the standard errors of the responses over 45 stimulations. The two orders of magnitude difference between the time scales of the SNAP and the optical response demonstrate that the optical signals measured by us are not directly associated with the electrical signals of the nerve action potential. Of course, because our experimental setup only had a temporal resolution of 20 ms (40 ms in the vascular occlusion protocol), it could not be sensitive to an optical signal on the millisecond time scale of the SNAP, even if such an optical signature directly associated with the SNAP was there.

Fig. 4.

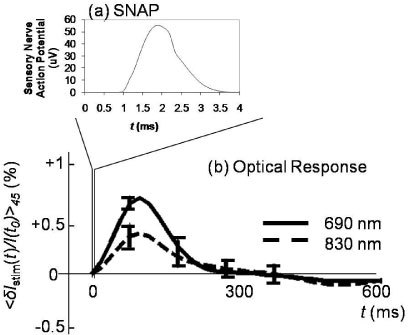
(a) Typical sensory nerve action potential (SNAP) and (b) typical optical signals at 690 and 830 nm measured on the sural nerve in response to electrical stimulation. Note the significantly different timescale of the SNAP and the optical response.

3.2 Spatial dependence of the optical response (sural nerve)

Figure 5 shows a schematic diagram of the optical probe for spatially-resolved measurements [panel (a)] and the spatial dependence of the stimulated optical response, <δI_stim/I(t₀)>₄₅, for subjects 1-5 [panels (b)-(f)]. Each time trace is a block average of 45 stimulation responses (with standard errors indicated by the error bars) over the time range 0-600 ms, where the electrical stimulation is at time 0. A result consistently observed across all five subjects is that positive optical responses are mainly exhibited in the upper-right quadrant associated with illumination positions S12 to S3 (clockwise, 12 o’clock to 3 o’clock), whereas the other three quadrants exhibit negative or flat optical responses. The reproducibility of these findings across subjects suggests an anatomical origin related to the location of the optical probe with respect to the sural nerve, blood vasculature, and adjacent skeletal muscles.The fact that the optical responses are positive (increase in optical irradiance) at some locations, and negative (decrease in optical irradiance) at others, indicates that they cannot result solely from vascular contraction (which would always induce positive optical responses) or dilation (which would always induce negative optical responses). These findings are consistent with known anatomical principles. In fact,the typical anatomical arrangement of nutrient vascular supply to a peripheral nerve includes branches from adjacent axial arteries, or fasciocutaneous or muscular arteries, that anastomose to form continuous longitudinal arteries that travel in the endoneurium of a nerve [31].

Fig. 5.

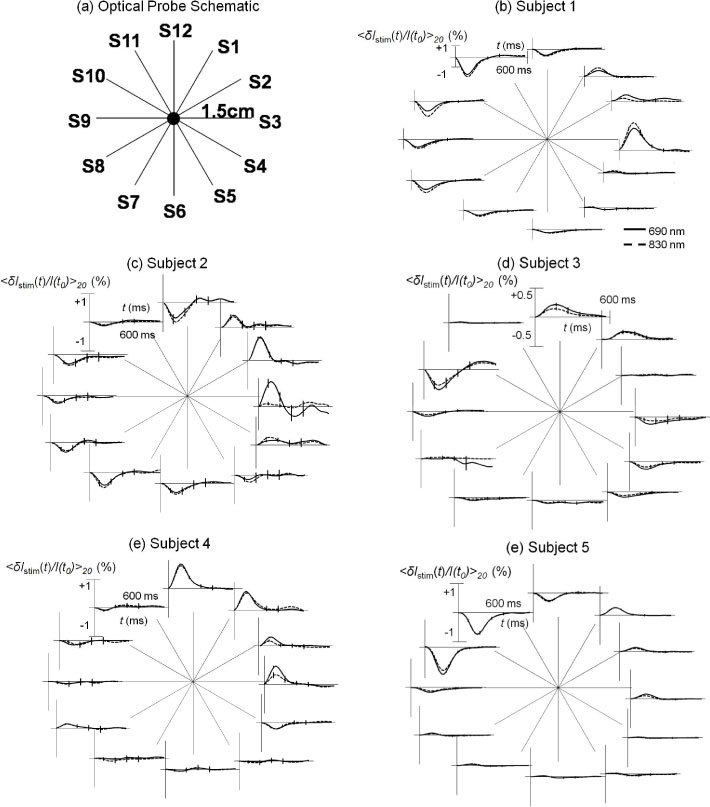
(a) Schematic diagram of the optical probe for spatially resolved measurements; (b)-(f) Optical responses to right sural nerve stimulation for the twelve source-detector pairs measured on subjects 1-5.

3.3 Effects of vascular occlusions on the optical response (median nerve)

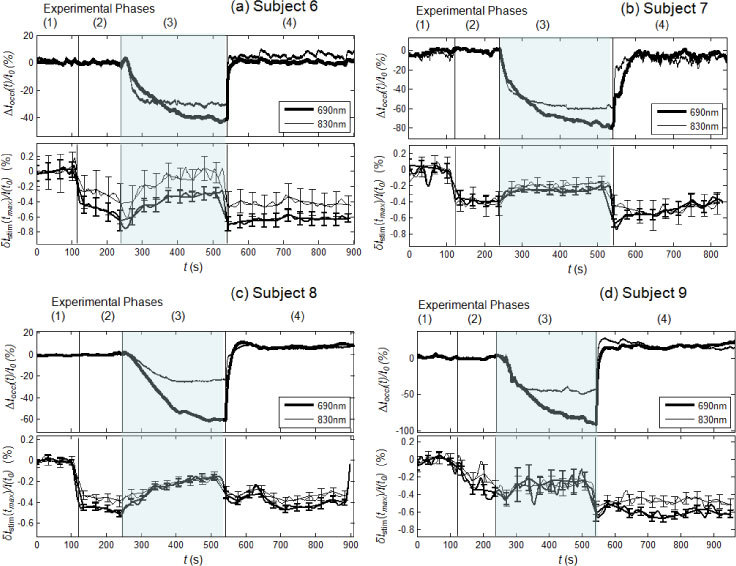
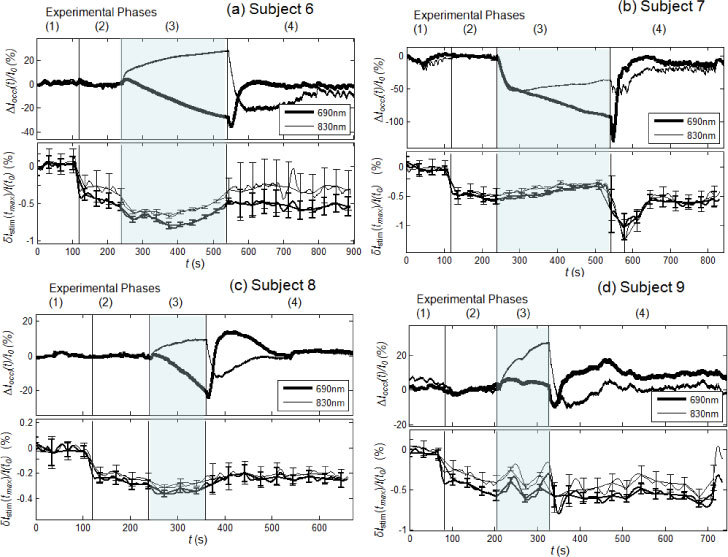
The results of the vascular occlusion experiment are shown in Fig. 6 (venous occlusion) and Fig. 7 (arterial occlusion) for subjects 6-9 [panels (a)-(d)]. According to the definitions given in section 2.5, ∆I_occl(t)/I₀ describes the tissue hemodynamic changes induced by vascular occlusion, whereas δI_stim(t_max)/I(t₀) describes the amplitude (with sign) of the maximal optical response to each nerve stimulation (smoothed by a 20-point moving average, with standard errors shown by the error bars in Figs. 6 and 7). As described in section 2.3, among the four spatial locations measured, we only present the data from the source-detector pair that exhibits the largest response at the stimulation frequency of 1.5 Hz.

Fig. 6.

Experimental results of the venous occlusion protocol for subjects 6-9 (panels (a)-(d), respectively). In each panel, the top section shows the optical signals relative to tissue ∆I_occl(t)/I₀, and the bottom section shows the maximum stimulated optical response to individual stimulations, δI_stim(t_max)/I(t₀), smoothed with a 20-point average. The four phases of each trial consists of: (phase 1) baseline, (phase 2) nerve stimulation with no venous occlusion, (phase 3) nerve stimulation during venous occlusion, and (phase 4) nerve stimulation after release of venous occlusion. The shaded area indicates the period of venous occlusion (phase 3).

Fig. 7.

Experimental results of the arterial occlusion protocol for subjects 6-9 (panels (a)-(d), respectively). In each panel, the top section shows the optical signals relative to tissue ∆I_occl(t)/I₀, and the bottom section shows the maximum stimulated optical response to individual stimulations, δI_stim(t_max)/I(t₀), smoothed with a 20-point average. The four phases of each trial consists of: (phase 1) baseline, (phase 2) nerve stimulation with no arterial occlusion, (phase 3) nerve stimulation during arterial occlusion, and (phase 4) nerve stimulation after release of arterial occlusion. The shaded area indicates the period of arterial occlusion (phase 3).

It is possible to calculate the changes in oxy-hemoglobin and deoxy-hemoglobin concentrations (∆[HbO₂] and ∆[Hb]) associated with measured irradiance changes at 690 and 830 nm by using the modified Beer-Lambert Law [32]. However, this calculation requires an assumption of spatially uniform changes that may be appropriate for ∆I_occl(t)/I₀, but may not be appropriate for the stimulated optical response δI_stim(t)/I(t₀). Therefore, for a more meaningful and direct comparison of the effects of vascular occlusion on (1) the optical signals representative of the entire probed tissue, and (2) the optical responses to nerve stimulations, our results in Figs. 6 and 7 are presented in terms of optical irradiance rather than concentrations of oxy-hemoglobin and deoxy-hemoglobin.

3.3.1 Venous occlusion

During venous occlusion, ∆I_occl(t)/I₀ decreases at both 690 and 830 nm [Fig. 6(a)–6(d), top panels], indicating increases in both [HbO₂] and [Hb], consistent with the increased blood volume induced by venous occlusion. The start of nerve stimulation during phase 2 of the venous occlusion protocol (before the onset of venous occlusion) does not affect the tissue measurements, so that ∆I_occl(t)/I₀ remains at baseline levels for all subjects. The maximum deviations of ∆I_occl(t)/I₀ from baseline occur at the end of the venous occlusion period (phase 3) and amount to a 40-90% decrease at 690 nm and a 20-60% decrease at 830 nm. These are strong reductions in the diffuse optical irradiance through the probed tissue, which are mostly associated with a local increase in capillary blood volume resulting from blood accumulation and pressure build up induced by venous occlusion. After the release of the venous occlusion (phase 4), ∆I_occl(t)/I₀ returns to the baseline, pre-occlusion levels for all four subjects.

The optical responses to median nerve stimulation show similar trends during the venous occlusion protocol in the four subjects [Fig. 6(a)–6(d), bottom panels], demonstrating inter-subject repeatability. Phase 1 is a control period, in which we analyzed the data according to the method described in section 2.5, even though no nerve stimulation was administered, so that δI_stim(t_max)/I(t₀) is about zero (with fluctuations associated with experimental errors). In phase 2, we observe a negative optical response to nerve stimulation in all four subjects, ranging from −0.2 to −0.5% in amplitude (in other locations, we did measure some positive optical responses, but they were smaller in absolute value than those reported in Fig. 6). In phase 3, during venous occlusion, the stimulated optical response amplitude decreases in absolute value (while remaining negative) for all four subjects (with the possible exception of subject 9 [Fig. 6(d)]. We did not detect a measurable difference between the venous-occlusion induced changes in the stimulated optical responses at the two wavelengths, with the exception of subjects 8 [Fig. 6(c)] for which ∆I_occl(t)/I₀ exhibited the most significant difference at the two wavelengths during venous occlusion. In the case of subject 8, the stronger decrease in ∆I_occl(t)/I₀ at 690 nm vs. 830 nm is associated with a stronger decrease in the absolute value of δI_stim(t_max)/I(t₀) at 690 nm vs. 830 nm. The decrease (in absolute value) in the amplitude of the optical response induced by venous occlusion is reversed by the release of venous occlusion, so that, in phase 4, δI_stim(t_max)/I(t₀) increases in absolute value and returns to the pre-occlusion values of phase 2 (except in subject 9, for which the pre-occlusion optical responses had a similar amplitude to those during venous occlusion). Overall, we found that the effect of venous occlusion is to dampen the optical response to median nerve stimulation.

3.3.2 Arterial occlusion

During arterial occlusion, ∆I_occl(t)/I₀ decreases at 690 nm and increases at 830 nm [Fig. 7(a)–7(d), top panels], indicating a decrease in [HbO₂] and an increase in [Hb], consistent with the deoxygenation of hemoglobin induced by arterial occlusion. In the cases of subjects 7 and 9 [Figs. 7(b) and 7(d)], there is an initial change (decrease for subject 7, increase for subject 9) in ∆I_occl(t)/I₀ at both wavelengths during arterial occlusion, likely as a result of blood redistribution in tissue. In fact, it is important to note that our measurements were not conducted on large, macroscopically uniform skeletal muscles, but rather on the spatially heterogeneous carpal tunnel area around the wrist, so that inhomogeneous blood redistribution around the probed tissue is possible. The start of nerve stimulation during phase 2 of the arterial occlusion protocol (before the onset of arterial occlusion) does not affect the tissue measurements, so that ∆I_occl(t)/I₀ remains at baseline levels for all subjects. The deviations of ∆I_occl(t)/I₀ from baseline at the end of the arterial occlusion period (phase 3) amount to a 5-40% decrease at 690 nm and a 10-30% increase at 830 nm. These are significant changes in the diffuse optical irradiance through the probed tissue, which are mostly associated with a local deoxygenation of capillary blood as a result of the blood flow interruption caused by arterial occlusion. After the release of the arterial occlusion (phase 4), ∆I_occl(t)/I₀ returns to approximately the same baseline, pre-occlusion levels for all four subjects.

The optical responses to median nerve stimulation show similar trends during the arterial occlusion protocol in the four subjects [Fig. 7(a)–7(d), bottom panels]. Similar to the venous occlusion protocol, phase 1 is just a control period. In phase 2, we observe a negative optical response to nerve stimulation in all four subjects, ranging from −0.2 to −0.5% in amplitude (in other locations, we did measure some positive optical responses, but they were smaller in absolute value than those reported in Fig. 7). In phase 3, during arterial occlusion, the stimulated optical response amplitude tends to increase in absolute value (while remaining negative) for subjects 6, 8, and 9. Subject 7 [Fig. 7(b)] shows a behavior similar to that observed during venous occlusion (decrease in the absolute amplitude of the optical response), consistent with the fact that it is the subject for which we measured a significant blood accumulation (decreased ∆I_occl(t)/I₀ during arterial occlusion). This confirms the finding of the venous occlusion measurements that blood accumulation dampens the optical response to nerve stimulation. Results from all four subjects show that the optical response to stimulation returns to pre-occlusion levels after arterial occlusion is released (phase 4). The most striking result is that during the arterial occlusion period (phase 3), the tissue optical measurements (∆I_occl(t)/I₀) show markedly different trends at 690 and 830 nm, whereas the optical responses to nerve stimulation (δI_stim(t_max)/I(t₀)) show similar trends at 690 and 830 nm. This indicates that the optical response to nerve stimulation is not representative of the hemoglobin in the capillary bed, which instead provides the dominant contribution to ∆I_occl(t)/I₀.

3.4 Optical signal associated with blood vessel displacement (diffusion model)

Because the arterial occlusion experiment has shown that the optical response to nerve stimulation is not representative of hemoglobin in the capillary bed, we have turned to our recently developed diffusion model based on the Padé Approximants to characterize the optical signal associated with the displacement of a relatively large blood vessel (1 mm diameter). Figure 8 shows the results of our diffusion model for a blood vessel displacement using a 1x1x10 mm³ (dimensions along the three axes) blood vessel portion, centered at (x,y,z) = (7,4,0) mm. Figure 8(a) shows the absorption spectrum of an arterial blood vessel (thin solid line) with 98% oxygen saturation of hemoglobin, and two different background absorption coefficient spectra (µ_a0(λ)) characterized by either 75% or 40% tissue saturation (bold solid line and bold dashed line, respectively). We have used our model to estimate the change in irradiance measured by a source fiber at (0,0,0) and a detector fiber at (0,15,0) mm as a result of a displacement of the blood vessel from position r₁ = (7,4,0) mm to position r₂ = (7,5,0) mm. Such change in optical irradiance, $\Delta I_{bv}\left(r_1\to r_2\right)/I_{r_1}$, exhibits spectral features of the arterial blood vessel regardless of the background tissue oxygen saturation level [see Fig. 8(b), top continuous and dashed lines]. This result is consistent with the independence between the spectral properties of the stimulated optical response and the spectral properties of background tissue that we have observed in our measurements during arterial occlusion.

Fig. 8.

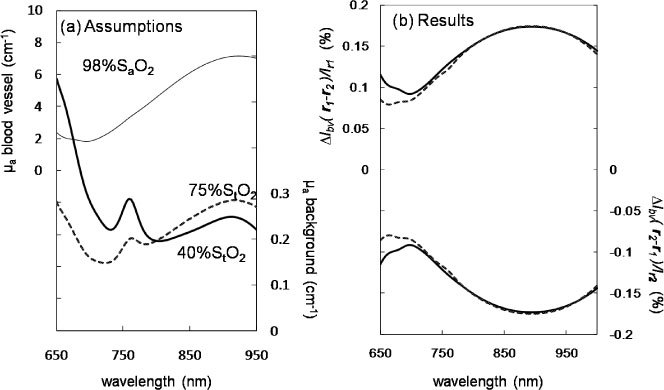
Diffusion model assumptions (a) and results (b). (a) Assumed absorption spectra of background tissue (thick continuous and dashed lines) and blood vessel (thin line) corresponding to a hemoglobin concentration of 100 µM (tissue) or 2.3 mM (blood vessel), and a hemoglobin saturation of 75% or 40% (tissue) and 98% (blood vessel). (b) Results for the optical signal due to arterial vessel displacement from position r₁ to position r₂ ($\Delta I_{bv}\left(r_1\to r_2\right)/I_{r_1}$, top lines) and vice versa ($\Delta I_{bv}\left(r_2\to r_1\right)/I_{r_2}$, bottom lines), where r₁ = (7,4,0) mm and position r₂ = (7,5,0); solid and dashed lines refer to a background tissue saturation of 75% and 40%, respectively.

Because $\Delta I_{bv}\left(r_1\to r_2\right)/I_{r_1}\cong$ -$\Delta I_{bv}\left(r_2\to r_1\right)/I_{r_2}$, one can measure positive or negative optical signals depending on the direction of blood vessel displacement. The bottom continuous and dashed lines of Fig. 8(b), resulting from the opposite displacement from r₂ to r₁, show the opposite sign with respect to the optical signal associated with the displacement from r₁ to r₂. This result shows how the same blood vessel may cause optical signal of opposite signs by being displaced in opposite directions.

We have also studied the effects of different blood vessel diameters, depths in tissue (x coordinate value), and displacement amplitudes on the induced optical signal. Figure 9 shows our results for $\Delta I_{bv}\left(r_1\to r_2\right)/I_{r_1}$induced by a 100 µm displacement along the positive y axis at two different depths, x = 5 mm [Fig. 9(a)] and x = 9 = mm [Fig. 9(b)] for blood vessels of sizes 0.1x0.1x10 mm³ (dotted lines), 0.5x0.5x10 mm³ (dashed lines), and 1x1x10 mm³ (continuous lines). The initial blood vessel position ranges from y = −10 mm to y = 24 mm. Inside the blood vessel, the hemoglobin saturation and concentration are set at 75% and 2.3 mM, respectively, whereas outside the blood vessel they are set at 75% and 100 µm, respectively. Results at two wavelengths are presented as lines with no markers (690 nm) and with star markers (830 nm). Two symmetrical peaks of opposite sign occur around the source and detector y coordinates, namely y = 0 and y = 15 mm.

Fig. 9.

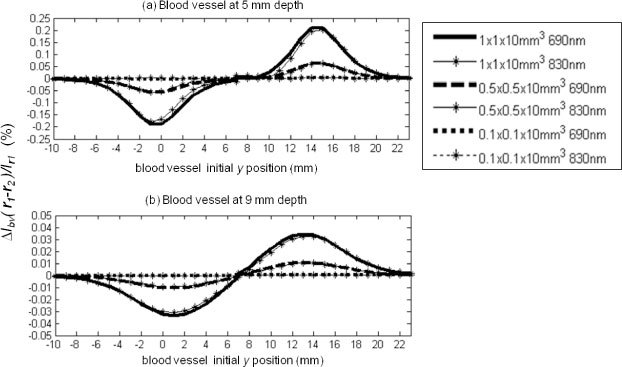
Modeling results for venous blood vessel displacement, $\Delta I_{bv}\left(r_1\to r_2\right)/I_{r_1}$ (%) per 100 µm displacement along the y axis at z = 0 and (a) 5 mm depth and (b) 9 mm depth. Two wavelengths, 690 and 830 nm are represented as bold lines with no marker and thin lines with starred markers, respectively. 1x1x10 mm³, 0.5x0.5x10 mm³ and 0.1x0.1x10 mm³ blood vessel portion sizes are represented as solid, dashed and dotted lines, respectively.

The positive and negative signals observed on the opposite sides of the mid-plane between source and detector shows that even the very same displacement of one single blood vessel can cause signals of opposite sign depending on the location of the illumination and collection optical fibers. This can explain the observed optical signals of positive and negative signs measured at different positions in our spatially resolved study. The peak absolute value of the amplitudes |$\Delta I_{bv}\left(r_1\to r_2\right)/I_{r_1}$| at 690 nm for 100 µm displacement of the 1 mm, 0.5 mm, and 0.1 mm diameter blood vessels at (x,y,z) = (5,0,0) mm are 0.19%, 0.06%, and negligible, respectively. The corresponding values for blood vessels at (x,y,z) = (9,0,0) mm are much smaller, namely 0.03%, 0.01%, and negligible, respectively.

On the basis of these results, we consider the displacement (by 100 μm) of 0.1 mm diameter blood vessels to not be measurable at both 5 and 9 mm depths because the associated optical signals are two orders of magnitude smaller than the ~0.1% experimental error. From these results, one can see that the 1 mm diameter blood vessel displacements (by 100 μm) induce optical signals on the same order of magnitude as the signals we experimentally collected, namely a few tenths of a percent. However, our model only considers the effect of a single blood vessel, but the likely influence of multiple blood vessels on the optical signals measured in vivo may introduce an additional level of complexity.

3.5 Broadband spectral characterization of the optical response (median nerve)

Figures 10(c) and 10(d) show the spectral dependence of the maximal optical response to median nerve stimulation averaged over 20 stimulation periods (i.e. <δI_stim(t_max)/I(t₀)>₂₀, where t_max is the time of maximal |<δI_stim(t)/I(t₀)>₂₀|) for subject 6 under two different conditions. The data of Fig. 10(c) were collected with source and detector fibers in full contact with the skin, and with a stimulation current that did not induce any visible motion in the subject’s hand. The data of Fig. 10(d) were collected with source and detector fiber tips located about 1 mm above the skin, without making physical contact with the skin, and with a stimulation current inducing visible thumb motion in the subject’s hand (but not at the location of the optical probe). To investigate the effect of changes in the optical coupling between optical fibers and skin (under contact conditions), we have also measured the spectrum of ∆I_coupling(λ)/I₀(λ), which is the relative change in detected irradiance as a result of pushing the detector fiber by 125 µm into the skin [see Fig. 10(b)]. For comparison, we have also performed a similar measurement on a solid tissue-like phantom made of silicone, where we pushed the detector fiber by 250 µm into the phantom and measured the spectrum of the associated relative change in detected optical irradiance [see Fig. 10(a)]. The spectra in 
Figs. 10(a) and 10(b) are the average of 20 consecutive spectra, collected with an acquisition time of 18.3 ms per spectrum. Solid lines in Fig. 10 represent experimental spectra smoothed by a 20 nm moving average. Error bars are the standard error of the 20 spectra averages shown in Figs. 10(a)–10(d).

Fig. 10.

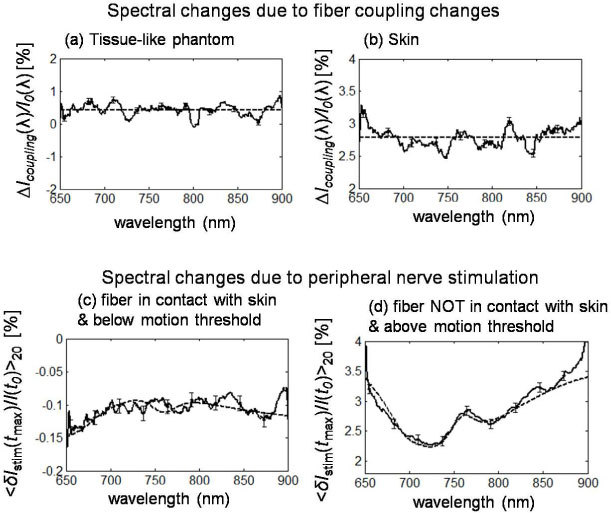
Broadband spectra of optical signals measured (a) on a tissue-like phantom as a result of pushing the detector fiber by 250 µ m into the phantom in a contact configuration, and on subject 6 (b) as a result of pushing the detector fiber by 125 µm into the skin in a contact configuration, and in response to sural nerve stimulation under conditions of (c) fiber-skin contact and no visible hand motion, and (d) no contact between optical fiber and skin, and visible stimulation-induced hand motion. Continuous lines are experimental spectra, while dashed lines are average values across the spectrum (panels (a) and (b)), or modeled signals from blood vessel displacement, (panel (c) is due to a 110 µm displacement along y of a 2 mm diameter blood vessel centered at (2,9,0) mm under conditions of 100 µM concentration and 75% saturation of hemoglobin in tissue, and 2.3 mM concentration and 60% saturation of hemoglobin in the blood vessel (vein) and panel (d) is due to a 1 mm displacement along y of a 2 mm diameter blood vessel located at (2,13,0) mm under conditions of 100 µM concentration and 75% saturation of hemoglobin in tissue, and 2.3 mM concentration and 75% saturation of hemoglobin in the blood vessel (vein)).

Optical coupling effects induce optical irradiance changes with a flat spectral dependence, at a value of 0.42 ± 0.09% in the tissue phantom case [flat dashed line in Fig. 10(a)] and 2.78 ± 0.06% in the in vivo case [flat dashed line in Fig. 10(b)]. The spectra of the irradiance changes induced by median nerve stimulation [Figs. 10(c) and 10(d)] show some hemoglobin signatures such as the decreased effect, in absolute value, for increasing wavelengths from 650 to 700 nm, and the 758 nm deoxy-hemoglobin peak [visible in Fig. 10(d)]. We have verified that our blood vessel displacement model can reproduce the experimental spectra. In fact, the dashed line in Fig. 10(c) is the spectrum of the irradiance change due to a 110 µm displacement along y of a 2 mm diameter blood vessel centered at (2,9,0) mm under conditions of 100 µM concentration and 75% saturation of hemoglobin in tissue, and 2.3 mM concentration and 60% saturation of hemoglobin in the blood vessel (vein). The dashed line in Fig. 10(d) is the spectrum of the irradiance change due to a 1 mm displacement along y of a 2 mm diameter blood vessel located at (2,13,0) under conditions of 100 µM concentration and 75% saturation of hemoglobin in tissue, and 2.3 mM concentration and 75% saturation of hemoglobin in the blood vessel (vein).

4. Discussion

In the present work we have investigated a nerve-stimulation-induced optical signal on a time scale of ≈100ms that is not directly associated with nerve or neuromuscular electrophysiological events that occur on a millisecond time scale that is nearly 2 orders of magnitude faster than our signal. We have observed such optical signals in the median nerve (a motor/sensory nerve) and in the sural nerve (a purely sensory nerve), suggesting that functional differences may not play a role in the cascade of events linking the electrical stimulation of a nerve to the generation of the detected optical signals. Several likely mechanisms could be proposed to account for the biological origin of events on this measured time scale. These include: hemodynamic events in which vascular smooth muscle constriction or dilation can be induced by autonomic nervous system activation; local neuro-vascular action transduced by biochemical messengers such as ADP (adenosine diphosphate), nitric oxide or calcitonin gene related peptide. Alternatively signals on this time scale could be explained by electromechanical events associated with the biomechanical action of muscles coupled to the region of optical interrogation through soft tissue structures (tendons and ligaments). This biomechanical action might occur by the electrical stimulation of the nerves or when muscle tissues local to the neural stimulation are invaded by the current used for the nerve activation.

Our results on the spatial dependence of these optical signals have indicated that they are unlikely due to either vascular dilation or vascular constriction alone, because these origins would consistently result in a decreased irradiance (negative optical signal) or increased irradiance (positive optical signal), respectively. By contrast, the spatial dependence of the optical response sign, positive at some positions and negative at others, was found to be repeatable over all five subjects examined. A similar spatial dependence of optical signals in response to electrically-induced muscle contractions has recently been reported and assigned to anisotropic changes in optical properties due to the directional structure of muscle fibers [33]. In our case, however, the spatially-resolved optical measurements were performed in an ankle area that does not contain skeletal muscles, even though directional structures such as tendons are present. Furthermore, the arterial occlusion experiments have shown that the optical responses to nerve stimulation measured by us are not representative of tissue optical properties. For these reasons, we have investigated the hypothesis that dynamic effects associated with nerve stimulation may give significant contributions to our detected optical signals by transient displacement of blood vasculature. Because of the large near-infrared absorption coefficient of blood (several inverse centimeters) and the strong spatial dependence of the optical sensitivity function, even small displacements of individual blood vessels can result in measurable optical signals.

Our diffusion model results have shown that the displacement of a 1 mm diameter blood vessel by as little as 100 μm at a 5 mm depth can induce optical signal changes in the order of several tenths of a percent, which is the scale of optical signals measured by us in response to nerve stimulation. Such size and depth of blood vessels is common in the wrist [34] and ankle [35] areas. Of course, contributions from multiple blood vessels can reinforce or suppress each other depending on their locations relative to the illumination and collection optical fibers. This fact, namely the variability in the net effect of contributions from multiple blood vessels, would further explain the strong spatial variability of the observed optical responses, which we have found to be positive, negative, or about zero depending on position (see 
Fig. 5). The other major finding of our diffusion model study is that the spectral features of the optical signal due to blood vessel displacement are representative of the blood vessel and not of the surrounding tissue. This is consistent with the results of our arterial occlusion study, in which dramatic changes in the spectral properties of tissue were not reflected in spectral changes of the optical response to nerve stimulation. Finally, the dampening of the optical response to nerve stimulation observed during venous occlusion could be explained by the increased resistance to blood vessel displacements associated with the pressure buildup induced by blood accumulation during venous occlusion.

By invoking dynamical effects, likely associated with muscle twitch elicited by electrical stimulation, we had to take into consideration the possibility that changes in the optical coupling between optical fibers and skin may also contribute to the measured optical signals. While it is possible that optical coupling effects may contribute to the optical signals, it is unlikely that their contributions be the dominant ones. In fact, coupling changes are not expected to induce optical signals with spectral features [as we report in Figs. 10(a) and 10(b)], while the optical responses to nerve stimulation often exhibit spectral features in our broadband measurements [see Figs. 10(c) and 10(d)], or wavelength dependence in our two-wavelength measurements [see Fig. 4(b) and some optical responses in Fig. 5 such as those at 3 o’clock and 10 o’clock in Fig. 5(b)]. Of course, relatively large skin movements toward (or away from) optical fibers may eventually cause local pressure changes capable of affecting the local blood flow and therefore induce spectrally dependent optical signals. However, 
Fig. 10(b) shows that by moving the detector fiber by as little as 125 μm into the skin, one achieves spectrally flat optical changes in the order of 3% that are greater than the signals measured by us. Furthermore, in the non-contact configuration of Fig. 10(d), where optical coupling contributions to the optical signal can only be wavelength independent geometrical effects, we still measure a strongly spectrally dependent optical signal with typical hemoglobin spectral features. As a result, we consider unlikely that changes in the optical coupling between optical fibers and skin play a major role in the measured optical responses to nerve stimulation.

Even though no skeletal muscles are present in the ankle region probed in the sural nerve studies or in the wrist area probed for the median nerve studies, proximal muscles that twitch in response to electrical stimulation can induce some level of dynamic action at the optically probed tissue. Studies show that human muscle twitch and contraction times occur on comparable time scales (~100 ms) as the optical responses to peripheral nerve stimulation reported here [36]. The regions of optical interrogation in our studies include both the sural nerve as it passes beneath the lateral malleolus and the median nerve as it enters the carpal tunnel. Both of these imaged regions contain both their respective nerves with its associated longitudinal nutrient arteries and tendons/ligaments that are mechanically coupled via soft connective tissues to the nerve itself. In the case of the sural nerve, the lesser saphaneous vein as well as local accompanying arteries that travel with the nerve lie superficial to the ligaments and tendons connecting the muscles of the lateral compartment of the leg to the ankle [37]. Ten tendons pass with the median nerve through or forming the carpal tunnel connecting the muscles of the forearm to the hand. The vascular supply of the median nerve forms a longitudinal vascular structure in close association with the nerve [38].

It is highly probable that the antidromic stimulation of the sural nerve in the proximal course of the nerve causes tensioning of the tendons of the peroneal muscles or the gastrocnemious that are mechanically connected to the sural nerve-vascular complex. Equivalently the stimulation of the recurrent branch of the median nerve will activate the thenar muscles and cause tensioning of the tendons in the carpal tunnel. Such mechanical actions are likely occurring well below the threshold of action necessary to move either the joint or the more elastic skin and subcutaneous tissues lying between the optical probe and the neurovascular bundle. In our companion article, we further show the electromechanical nature of this optical signal in both the human and a rodent model [39]. In fact, it was observed that the signal is eliminated by chemical blockade of the neuromuscular junction or anatomical disconnection of the motor nerves from the muscles [39].

5. Conclusion

The spectral and spatial dependencies of the diffuse optical response to electrical stimulation of peripheral nerves suggest that this signal may result from a blood vascular displacement (involving relatively large blood vessels) mediated by muscle twitch. We have shown that these optical responses feature a reproducible spatial dependence (with positive, negative, and undetectable optical signals at different positions) and are not representative of average tissue optical properties over the optically probed volume. Even in tissues where skeletal muscles are not present, motion of local or adjacent tendons resulting from muscle activation could lead to vascular displacement. Even though the results presented here are consistent with vascular displacement as the origin of the optical signals in response to nerve stimulation, more studies need to be performed to conclusively demonstrate that this is actually the case.

The optical signal likely provides a capacity to non-invasively monitor the electromechanical action of muscles on a millisecond time scale. The features of this signal are likely to be influenced by muscle fiber twitch kinematics and will reflect not only muscle electromechanical properties but also muscle fiber structural biochemistry, soft-tissue integrity and the metabolic capacity of muscles to respond to both physiological and pathological demands and stresses. A variety of normal muscle actions including response to exercise, training, and development may make these signals useful in exercise and sports medicine applications. In addition, muscle kinematics have been shown to be altered at the biochemical level in myopathic processes in the muscular dystrophies, at the motor-neuron-muscle-fiber composition level in motor neuron diseases and motor nerve trauma. It is also intriguing that metabolic derangements like those seen in diabetes mellitus, iatrogenic poisonings such as 3-hydroxy-3-methylglutaryl-Coenzyme A (HMG-CoA) reductase inhibitor or chronic cortico-steroid use as well as mitochondrial disorders can alter the kinematics of muscle fibers at the millisecond time scale. Thus, understanding the dynamics and details of the optical signals reported here may provide an important non-invasive and convenient clinical signal for diagnostics and for monitoring of therapeutic interventions in the clinic and laboratory.