Comparison of intensity-modulated continuous-wave lasers with a chirped modulation frequency to pulsed lasers for photoacoustic imaging applications

Abstract

Using a Green’s function solution to the photoacoustic wave equation, we compare intensity-modulated continuous-wave (CW) lasers with a chirped modulation frequency to pulsed lasers for photoacoustic imaging applications. Assuming the same transducer is used in both cases, we show that the axial resolution is identical and is determined by the transducer and material properties of the object. We derive a simple formula relating the signal-to-noise ratios (SNRs) of the two imaging systems that only depends on the fluence of each pulse and the time-bandwidth product of the chirp pulse. We also compare the SNR of the two systems assuming the fluence is limited by the American National Standards Institute (ANSI) laser safety guidelines for skin. We find that the SNR is about 20 dB to 30 dB larger for pulsed laser systems for reasonable values of the parameters. However, CW diode lasers have the advantage of being compact and relatively inexpensive, which may outweigh the lower SNR in many applications.

1. Introduction

The photoacoustic effect (which is also called the optoacoustic effect) is the generation of an acoustic wave by thermoelastic expansion caused by heating from optical absorption. Photoacoustic imaging is a hybrid imaging system that combines the advantage of optical absorption contrast with ultrasound resolution. In addition, since the absorption properties of tissue are influenced by biological activity, photoacoustic systems can perform functional imaging. In particular, by using multiple excitation wavelengths it is possible to extract quantitative information [1]. Most photoacoustic imaging systems use high-energy pulsed lasers, which tend to be expensive and bulky, for excitation. The pulse duration in these systems is usually about 10 ns. However, it is also possible to use intensity-modulated continuous-wave (CW) lasers. One choice of modulation is to chirp the modulation frequency [2–7]. The pulse duration in these systems is usually about 1 ms. One potential advantage of chirped photoacoustic imaging systems is that they can use compact and inexpensive CW diode lasers. The aim of this paper is to compare these chirped systems to pulsed systems.

2. Pulse compression using matched filters

To produce a chirp signal, the CW laser is modulated to create an irradiance (or fluence rate) that has a time-swept frequency. The irradiance is given by

$$I_{\mathrm{chirp}}\left(t\right)=I_0[1+\cos ({\omega }_{0}t+\pi b{t}^2)]\mathrm{rect}\left(\frac{t}{T}\right),$$ (1)

where I₀ is the average irradiance of the pulse (2I₀ is the peak irradiance) with units W/m², b is the frequency sweep rate with units s⁻², and T is the length of the pulse with units s. The fluence of the pulse is I₀T with units J/m². The angular frequency is given by d/dt(ω₀t + πbt²) = ω₀ + 2πbt, which gives the frequency, f, as f₀−bT/2 ≤ f ≤ f₀ + bT/2, the bandwidth as bT, and the time-bandwidth product as bT². For example, if the chirp goes from 1 MHz to 5 MHz and T is 1 ms, then f₀ is 3 MHz and b is 4×10⁹ s⁻².

Eq. (1) can be split up into a low-frequency term (a pulse with constant amplitude I₀ and length T) and a high-frequency term (a pulse with amplitude I₀ cos(ω₀t + πbt²) and length T). In most practical situations, the low-frequency term is outside of the bandwidth of the acoustic transducer since T is on the order of 1 ms and the transducer has a bandpass frequency response with a center frequency in the MHz range. The Fourier transform of the high frequency term can be split up into positive and negative frequency components. By completing the square, the positive frequency components (using the unitary Fourier transform) are given by

$${\tilde{I}}_{\mathrm{pos}}\left(\omega \right)=\frac{I_0}{2\sqrt{2\pi }}{e}^{-i\frac{\pi }{b}{(f-f_0)}^2}\frac{1}{\sqrt{2b}}{\int }_{-T\sqrt{\frac{b}{2}}-\sqrt{\frac{2}{b}}(f-f_0)}^{T\sqrt{\frac{b}{2}}-\sqrt{\frac{2}{b}}(f-f_0)}{e}^{i\frac{\pi }{2}{\left(t\prime \right)}^2}dt\prime ,$$ (2)

which can be solved in terms of the Fresnel integrals

$$C\left(x\right)={\int }_0^x\cos \left(\frac{\pi }{2}{t}^2\right)dt$$$$S\left(x\right)={\int }_0^x\sin \left(\frac{\pi }{2}{t}^2\right)dt$$ (3)

with the properties C(0) = S(0) = 0 and C(±∞) = S(±∞) = ±1/2 [8]. Eq. (2) then becomes

$${\tilde{I}}_{\mathrm{pos}}\left(\omega \right)=\frac{I_0}{2\sqrt{2\pi }}{e}^{-i\frac{\pi }{b}{(f-f_0)}^2}\frac{1}{\sqrt{2b}}[C(T\sqrt{\frac{b}{2}}-\sqrt{\frac{2}{b}}(f-f_0))+iS(T\sqrt{\frac{b}{2}}-\sqrt{\frac{2}{b}}(f-f_0))$$$$-C(-T\sqrt{\frac{b}{2}}-\sqrt{\frac{2}{b}}(f-f_0))-\mathit{iS}(-T\sqrt{\frac{b}{2}}-\sqrt{\frac{2}{b}}(f-f_0))],$$ (4)

which resembles a rectangular function centered at f₀ with bandwidth bT for large time-bandwidth products (bT² > 30) [9]. The spectrum of a chirp signal is shown in Fig. 1(a) for f₀ = 3 MHz and bT = 4 MHz. Eq. (4) is then approximately given by

Fig. 1.

(a) The spectrum and (b) time signal, compressed by applying a matched filter, for a chirp signal with f₀ = 3 MHz and bT = 4 MHz.

$${\tilde{I}}_{\mathrm{pos}}\left(\omega \right)\approx \frac{I_0}{2\sqrt{2\pi }}{e}^{\frac{-i{(\omega -{\omega }_0)}^2}{4\pi b}}\frac{1}{\sqrt{2b}}(1+i)\mathrm{rect}\left(\frac{\omega -{\omega }_0}{2\pi bT}\right).$$ (5)

Similarly, the negative frequency components are approximately given by

$${\tilde{I}}_{\mathrm{neg}}\left(\omega \right)\approx \frac{I_0}{2\sqrt{2\pi }}{e}^{\frac{i{(\omega +{\omega }_0)}^2}{4\pi b}}\frac{1}{\sqrt{2b}}(1-i)\mathrm{rect}\left(\frac{\omega +{\omega }_0}{2\pi bT}\right).$$ (6)

A matched filter is defined as the complex conjugate of the spectrum of the signal that is being filtered. It can be shown that applying a matched filter to a signal will give the best signal-to-noise ratio (SNR) when the signal is corrupted by white noise [9]. In our case the unity-gain matched filter is

$${\tilde{G}}_{\mathrm{chirp}}\left(\omega \right)=e^{\frac{i{(\omega -{\omega }_0)}^2}{4\pi b}}\frac{1-i}{\sqrt{2}}\mathrm{rect}\left(\frac{\omega -{\omega }_0}{2\pi bT}\right)+e^{\frac{-i{(\omega +{\omega }_0)}^2}{4\pi b}}\frac{1+i}{\sqrt{2}}\mathrm{rect}\left(\frac{\omega +{\omega }_0}{2\pi bT}\right),$$ (7)

and the filtered chirp spectrum is given by

$${\tilde{I}}_{\mathrm{fc}}\left(\omega \right)=\frac{I_0}{2\sqrt{2\pi }}\frac{1}{\sqrt{b}}[\mathrm{rect}\left(\frac{\omega -{\omega }_0}{2\pi bT}\right)+\mathrm{rect}\left(\frac{\omega +{\omega }_0}{2\pi bT}\right)].$$ (8)

Taking the inverse Fourier transform gives

$$I_{\mathrm{fc}}\left(t\right)=I_0\sqrt{{\mathit{bT}}^2}\mathrm{sinc}\left(\pi bTt\right)\cos \left({\omega }_{0}t\right),$$ (9)

where sinc(πbTt) = sin(πbTt)/(πbTt). This is shown in Fig. 1(b) for f₀ = 3 MHz and bT = 4 MHz. The filtered signal has undergone pulse compression by a factor 1/(bT²) and the axial resolution of the photoacoustic imaging system (ignoring the frequency dependence of photoacoustic generation and the transducer bandwidth, which are discussed later) is approximately ν_s/(bT) where ν_s is the speed of sound (~ 1500 m/s in tissue). The signal is compressed by delaying different frequency components by different times. Since the chirp pulse has an instantaneous frequency that depends on time, the pulse will increase in amplitude and decrease in duration if the delay is done in the same manner as the frequency sweep, which is exactly what the matched filter accomplishes.

3. Green’s function solution to the photoacoustic equation

In order to solve the photoacoustic wave equation, we start with the heat conduction equation given by

$$\frac{\partial T(\mathbf{r},t)}{\partial t}-D_T{\nabla }^{2}T(\mathbf{r},t)=\frac{H(\mathbf{r},t)}{\rho C_V},$$ (10)

where T(r, t) is the temperature with units K, D_T is the thermal diffusivity (~ 1×10⁻⁷ m²/s for tissue), H(r, t) is the heating function with units W/m³, ρ is the mass density (~ 1000 kg/m³ for tissue), and C_V is the specific heat at constant volume (~4000 J/(kg·K) for tissue). The first two terms in Eq. (10) go like ωT and D_TT/l², respectively, where l is the characteristic length of the absorber, which means we can ignore the second term in most practical situations [10]. Eq. (10) then becomes

$$\frac{\partial T(\mathbf{r},t)}{\partial t}=\frac{H(\mathbf{r},t)}{\rho C_V}.$$ (11)

The general photoacoustic equation [11] is

$$({\nabla }^2-\frac{1}{{\nu }_s^2}\frac{{\partial }^2}{\partial t^2})p(\mathbf{r},t)=-\frac{\beta }{\kappa {\nu }_s^2}\frac{{\partial }^{2}T(\mathbf{r},t)}{\partial t^2},$$ (12)

where p(r, t) is the pressure with units Pa, β is the thermal coefficient of volume expansion (~ 2×10⁻⁴ K⁻¹ for tissue), and κ is the isothermal compressibility (~ 5×10⁻¹⁰ Pa⁻¹ for tissue). We use κ = C_P/(ρC_Vν²_s), where C_P is the specific heat at constant pressure (~ 4000 J/(kg·K) for tissue), Eq. (11), and Eq. (12) to get

$$({\nabla }^2-\frac{1}{v_s^2}\frac{{\partial }^2}{\partial t^2})p(\mathbf{r},t)=-\frac{\beta }{C_P}\frac{\partial H(\mathbf{r},t)}{\partial t}.$$ (13)

In order to solve Eq. (13), we take the Fourier transform to get

$$({\nabla }^2+k^2)\tilde{p}(\mathbf{r},\omega )=-\frac{i\omega \beta }{C_P}\tilde{H}(\mathbf{r},\omega ),$$ (14)

where k = −ω/ν_s. The Green’s function solution is

$$\tilde{p}(\mathbf{r},\omega )=\frac{i\omega \beta }{4\pi C_P}{\int }_V\frac{e^{\mathit{ik}\mid \mathbf{r}-{\mathbf{r}}_0\mid }}{\mid \mathbf{r}-{\mathbf{r}}_0\mid }\tilde{H}({\mathbf{r}}_0,\omega )d^3{\mathbf{r}}_0.$$ (15)

In the far-field, where r ≫ r₀ we have |r−r₀| ≈ r − r̂ · r₀. We keep both terms for the phase but only the first term for the amplitude. Eq. (15) becomes

$$\tilde{p}(r\gg r_0,\omega )=\frac{i\omega \beta }{4\pi C_P}\frac{e^{\mathit{ikr}}}{r}{\int }_V{e}^{-\mathit{ik}\hat{\mathbf{r}}·{\mathbf{r}}_{\mathbf{0}}}\tilde{H}({\mathbf{r}}_{\mathbf{0}},\omega )d^3{\mathbf{r}}_{\mathbf{0}}.$$ (16)

We now consider a cubic absorber, and we are interested in the pressure at the point (x = 0,y = 0,z ≫ a). The heating function for a cubic absorber has the form

$$H(x_0,y_0,z_0,t)=\{\begin{array}{c}\begin{array}{cc}\chi \mu e^{-\mu \left(\frac{a}{2-z_0}\right)}I\left(t\right)& -\frac{a}{2}\le x_0,y_0,z_0\le \frac{a}{2}\end{array}\\ \begin{array}{cc}0& \text{otherwise},\end{array}\end{array}$$ (17)

where χ is the dimensionless efficiency of absorbed energy converted to heat, µ is the absorption coefficient with units m⁻¹, $e^{-\mu \left(\frac{a}{2-z_0}\right)}$ represents the decrease in irradiance due to the absorption of a plane wave light source incident from the positive z axis, I(t) is the irradiance of the plane wave light source, and a is the length of one side of the absorber with units m. This is shown in Fig. 2. Using r̂ = ẑ = ẑ₀ and k = −ω/ν_s, Eq. (16) becomes

Fig. 2.

Illustration of coordinate system and geometry of absorber.

$$\tilde{p}\left(\omega \right)=\frac{\beta \chi \mu v_s{a}^2}{4\pi z{C}_P}\tilde{I}\left(\omega \right)\frac{\omega }{\omega -i\mu v_s}(e^{-i\omega \left(\frac{2z-a}{2v_s}\right)}-e^{-\mu a}{e}^{-i\omega \left(\frac{2z+a}{2v_s}\right)}),$$ (18)

where p̃(ω) is shorthand for p̃(x = 0,y=0,z ≫ a, ω). Even though photoacoustic generation is less efficient at high frequencies [7], we notice that the pressure is maximum in the far-field for high frequencies because diffraction scales inversely with frequency. However, in this analysis we are ignoring absorption in the surrounding medium, so using the highest possible frequency will not always be the best choice.

4. Far-field pressure for a pulse excitation

For a pulse given by

$$I_{\mathrm{pulse}}\left(t\right)=\frac{F_0}{\tau }\mathrm{rect}\left(\frac{t}{\tau }\right),$$ (19)

where F₀ is the fluence per pulse and τ is the pulse length with units s, we have

$${\tilde{I}}_{\mathrm{pulse}}\left(\omega \right)=\frac{F_0}{\sqrt{2\pi }}\mathrm{sinc}\left(\frac{\omega \tau }{2}\right).$$ (20)

Taking the inverse Fourier transform of Eq. (18) and using Eq. (20) we have

$$p_{\mathrm{pulse}}\left(t\right)=\frac{\beta \chi \mu v_s{a}^2{F}_0}{4\pi z\tau C_P}[e^{-\mu v_s{t}_1}u\left(t_1\right)-e^{-\mu v_s{t}_2}u\left(t_2\right)-e^{-\mu a}{e}^{-\mu v_s{t}_3}u\left(t_3\right)+e^{-\mu a}{e}^{-\mu v_s{t}_4}u\left(t_4\right)],$$ (21)

where p_pulse(t) is shorthand for p_pulse(x = 0,y = 0,z ≫ a, t), u(t) is the unit step function, t₁ = t + τ/2 − (2z − a)/(2ν_s), t₂ = t − τ/2 − (2z−a)/(2ν_s), t₃ = t + τ/2 − (2z+a)/(2ν_s), and t₄ = t − τ/2 − (2z + a)/(2ν_s). This is shown in Fig. 3 for χ = 0.25, µ = 1 cm⁻¹, a = 100 µm, F₀ = 20 mJ/cm², z = 3 cm, and τ = 10 ns.

Fig. 3.

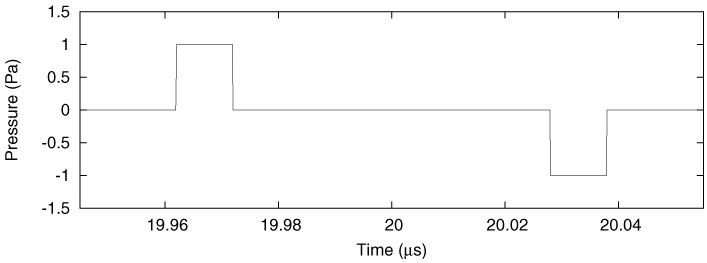
Pressure at a distance of 3 cm for a 10 ns pulse excitation. The temporal profiles of each of the pressure pulses are almost exact replicas of the laser pulse for the parameters chosen.

5. Comparison of SNRs

If we also include the frequency response of an acoustic transducer, T̃(ω), and a unity-gain matched filter, G̃(ω), in Eq. (18), we have

$$\tilde{S}\left(\omega \right)=\tilde{A}\left(\omega \right)\tilde{I}\left(\omega \right)\tilde{T}\left(\omega \right)\tilde{G}\left(\omega \right),$$ (22)

where S̃(ω) is the detected signal spectrum and

$$\tilde{A}\left(\omega \right)=\frac{\beta \chi \mu v_s{a}^2}{4\pi z{C}_P}\frac{\omega }{\omega -i\mu v_s}(e^{-i\omega \left(\frac{2z-a}{2v_s}\right)}-e^{-\mu a}{e}^{-i\omega \left(\frac{2z+a}{2v_s}\right)}).$$ (23)

Note that the sensitivity of the transducer is included in T̃(ω). If the pulse is short enough, Ĩ_pulse(ω) in Eq. (20) will be approximately constant with amplitude $\frac{F_0}{\sqrt{2\pi }}$ over the transducer bandwidth so that ${\tilde{I}}_{\mathrm{pulse}}\left(\omega \right)\tilde{T}\left(\omega \right)\approx \frac{F_0\tilde{T}\left(\omega \right)}{\sqrt{2\pi }}$ . Eq. (22) then becomes

$${\tilde{S}}_{\mathrm{pulse}}\left(\omega \right)=\frac{F_0}{\sqrt{2\pi }}\tilde{A}\left(\omega \right)\tilde{T}\left(\omega \right)[\mathrm{rect}\left(\frac{\omega -{\omega }_0}{2\pi \Delta f}\right)+\mathrm{rect}\left(\frac{\omega +{\omega }_0}{2\pi \Delta f}\right)],$$ (24)

where ω₀ is the transducer center frequency, Δf is the transducer bandwidth, and we have used

$${\tilde{G}}_{\mathrm{pulse}}\left(\omega \right)=\mathrm{rect}\left(\frac{\omega -{\omega }_0}{2\pi \Delta f}\right)+\mathrm{rect}\left(\frac{\omega +{\omega }_0}{2\pi \Delta f}\right)$$ (25)

to reject out of band noise. Note that this analysis is general and can be applied to any definition of the transducer bandwidth and any T̃(ω); however, G̃_pulse(ω) is not matched exactly unless the transducer spectrum is a rect and Ã(ω) is constant over the transducer bandwidth.

In order to make a fair comparison, the parameters for the chirp signal should be chosen so that the chirp bandwidth matches the transducer bandwidth (using the same definition of Δf as in the short pulse case), in which case we have bT = Δf. Using Eq. (8), where Ĩ_fc(ω) = Ĩ_chirp(ω)G̃_chirp(ω), we can write Eq. (22) as

$${\tilde{S}}_{\mathrm{chirp}}\left(\omega \right)=\frac{I_0}{2\sqrt{2\pi }}\frac{1}{\sqrt{b}}\tilde{A}\left(\omega \right)\tilde{T}\left(\omega \right)[\mathrm{rect}\left(\frac{\omega -{\omega }_0}{2\pi \Delta f}\right)+\mathrm{rect}\left(\frac{\omega +{\omega }_0}{2\pi \Delta f}\right)].$$ (26)

As with the short pulse case, G̃_chirp(ω) is not matched exactly unless the transducer spectrum is a rect and Ã(ω) is constant over the transducer bandwidth. We see that for both the short pulse and the chirp signals, the axial resolution of the imaging system is the same and is determined by the transducer and Ã(ω), which is dependent on the material properties of the object. Note that for actual objects, Ã(ω) will be more complicated than what is given in Eq. (23). If we ignore Ã(ω), then the resolution is approximately ν_s/Δf.

The noise amplitude, Ñ(ω), is filtered by |G̃(ω)|. This means the filtered noise amplitudes are the same in both cases and are given by

$${\tilde{N}}_{\mathrm{pulse}}\left(\omega \right)={\tilde{N}}_{\mathrm{chirp}}\left(\omega \right)=\tilde{N}\left(\omega \right)[\mathrm{rect}\left(\frac{\omega -{\omega }_0}{2\pi \Delta f}\right)+\mathrm{rect}\left(\frac{\omega +{\omega }_0}{2\pi \Delta f}\right)].$$ (27)

Defining SNR to be the signal amplitude divided by the noise amplitude gives

$$\frac{{\mathrm{SNR}}_{\mathrm{chirp}}}{{\mathrm{SNR}}_{\mathrm{pulse}}}=\frac{I_{0}T}{2F_0\sqrt{b{T}^2}}.$$ (28)

We see that the ratio of SNRs is determined by the fluence of the chirp pulse, the fluence of the short pulse, and the time-bandwidth product of the chirp pulse.

6. SNR in the context of the ANSI limits

The American National Standards Institute (ANSI) laser safety limits for skin [12] for a short pulse (1 ns ≤ τ ≤ 100 ns), as used in pulsed systems, are given by

$$min\{\begin{array}{c}20C_A\\ \{\begin{array}{c}\begin{array}{cc}\frac{1100C_A{t}^{\frac{1}{4}}}{N_{\tau }}& t\le 10s\end{array}\\ \begin{array}{cc}\frac{200C_{A}t}{N_{\tau }}& t\ge 10s,\end{array}\end{array}\end{array}$$ (29)

and the ANSI limits for a longer pulse (100 ns ≤ T ≤ 10 s), as used in chirped systems, are given by

$$min\{\begin{array}{c}1100C_A{T}^{\frac{1}{4}}\\ \{\begin{array}{c}\begin{array}{cc}\frac{1100C_A{t}^{\frac{1}{4}}}{N_T}& t\le 10s\end{array}\\ \begin{array}{cc}\frac{200C_{A}t}{N_T}& t\ge 10s\end{array}\end{array}\end{array}$$ (30)

in units of mJ/cm², where t is the total exposure time in seconds, N is the total number of pulses (N_τ = N_pulse = R_τt and N_T = N_chirp = R_Tt, where R_τ is the short pulse repetition rate and R_T is the chirp pulse repetition rate), and C_A is a wavelength correction factor defined in [12]. The maximum F₀ for a short pulse is 20C_A mJ/cm² when R_τ is set to the optimum rate given by 55/t^3/4 in units of Hz for t ≤ 10 s and 10 Hz for t ⁥ 10 s. The maximum I₀ for a chirp pulse is 1100C_A/T^3/4 mW/cm² when R_T is set to the optimum rate given by 1/(T^1/4t^3/4) in units of Hz for t ≤ 10 s and 10/(55T^1/4) in units of Hz for t ⁥ 10 s. The optimum rates are plotted in Fig. 4 for a short pulse and a 1 ms chirp pulse. With multiple pulses, we can perform averaging, which improves the SNR by √N. Note that the SNR is also maximized by choosing the same repetition rates that optimize the fluence and irradiance. Including averaging and assuming the optimum repetition rates are used, Eq. (28) becomes

Fig. 4.

The optimum repetition rates for a short pulse and a 1 ms chirp pulse.

$$\frac{{\mathrm{SNR}}_{\mathrm{chirp}}}{{\mathrm{SNR}}_{\mathrm{pulse}}}=\frac{\sqrt{55}}{2T^{\frac{3}{8}}\sqrt{\Delta f}}.$$ (31)

For typical values of the relevant parameters, we see that the SNR is about 20 dB to 30 dB larger for pulsed laser systems. In light of Eq. (9), it might seem counter-intuitive that shorter chirp pulses give a better SNR; however, the noise and ANSI limits also depend on T in such a way as to create that dependence. In the following discussion, we assume white noise for ease of explanation. Since white noise depends on $\sqrt{\Delta f}=\sqrt{bT}$ , we have ${\mathrm{SNR}}_{\mathrm{chirp}}\propto I_{0}T\frac{\sqrt{N_T}}{\sqrt{T}}\propto \frac{1}{T^{\frac{3}{8}}}$ because the fluence is proportional to T^1/4. However, for applications where the fluence is not determined by the ANSI limits, the maximum repetition rate is 1/T and so SNR_chirp ∝ I₀√t and does not depend on T. In both cases, SNR_chirp does not depend on the bandwidth. The $\sqrt{\Delta f}$ in the denominator of Eq. (31) arises because ${\mathrm{SNR}}_{\mathrm{pulse}}\propto F_0\Delta f\frac{\sqrt{N_{\tau }}}{\sqrt{\Delta f}}\propto \sqrt{\Delta f}$ .

7. Conclusion

We have shown that the SNR of photoacoustic imaging systems based on CW lasers with a chirped modulation frequency are about 20 dB to 30 dB worse than systems based on pulsed lasers if we are constrained by the ANSI safety limits. We have also shown that both systems have the same resolution. However, the chirp based systems have the advantage of being able to employ CW diode lasers. This advantage could be especially important for spectroscopic studies where it could be possible to image simultaneously at multiple wavelengths using a compact and inexpensive system.