Non-invasive in vivo measurement of the tear film using spatial autocorrelation in a live mammal model

Abstract

Tear film stability and its interaction with the corneal surface play an important role in maintaining ocular surface integrity and quality of vision. We present a non-invasive technique to quantify the pre-corneal tear film thickness. A cMOS camera is used to record the interference pattern produced by the reflections from multiple layers of the tear film Principles of spatial autocorrelation are applied to extract the frequency of the periodic patterns in the images. A mathematical model is developed to obtain the thickness of the tear film from the spatial autocorrelation image. The technique is validated using micro-fabricated thin parylene films. We obtained repeatable and precise measurement on a live rabbit model (N = 6). We obtained an average value of 10.2µm and standard deviation of, SD = 0.3 (N = 4). We measured one rabbit infected with HSV-1 virus that had a baseline tear film thickness of 4.7µm.

1. Introduction

The pre-corneal tear film in mammals is defined as the outermost layer in the eye. Tear film protects the surface of the cornea and conjunctiva from dust, debris and toxic skin lipids [1]. Additionally tear film provides lubrication for the ocular surface [2,3]. Tear film thickness can reveal information on the dynamics and physiology of tear layer [4]. Tear film thickness is also demonstrably related to dry eye syndrome (DES) [5,6]. DES consists of a diverse group of ocular surface disorders with multiple etiologies [7]. The common characteristic of DES is an abnormal tear film with inadequate ocular lubrication due to tear deficiency or excessive tear evaporation [8]. It is believed that dry eye is one of the most common ocular problems in the United States with a prevalence that goes up to 30% [9], which generally increases with aging and can impact quality of life [10]. Symptoms include irritation and pain caused by ocular dryness, among others [11]. The tear film is composed of three layers: the external lipid layer, an aqueous layer and an internal mucin layer [9]. Therefore, an accurate measurement of the tear film thickness could provide a method to diagnose dysfunctions in the production and maintenance of the tear film. A simple thickness measurement could be crucial for predicting the behavior and stability of the tear film [7].

Tear film thickness is clinically diagnosed by the Schirmer Test, which measures aqueous tear volume, and the tear Break Up Time (tBUT), which detects the time for the tear layer to become unstable. Tests based on fluorometry, such as 1% fluorescein and the principle of tear dilution, have been used as an alternative method to measure aqueous tear production [12]. Amongst the non-invasive techniques, high-speed videokeratography has been applied to measure the tear film build-up time [13]. Additionally, wavefront aberrometry has been used to quantify the tear break-up time (tBUT) [6]. Interferometry has also been applied to measuring the thickness of the tear film. There are two different interferometry techniques which have been proposed and applied in ophthalmic research. King-Smith et al were amongst the pioneers in applying interferometry to evaluating and characterizing the tear film. Their approach analyzed the reflectance spectra from the tear film using visible and near-infrared light sources, assessing the modulation and phase of the oscillations in the reflection spectra. They were able to quantify the thickness of the pre-corneal tear film and obtained a value of 3 µm [14–17]. Licznerski et al applied a modified lateral shearing interferometry (LSI) and developed a platform for scientists and researchers to characterize tear film thickness [18]. This method was mainly applied by Szczesna et al to evaluate the dynamics of the tear film. They were able to assess the stability of the tear film on the ocular surface and also contact lenses. In this method, interference patterns are captured by means of a CCD camera. These fringes undergo a Fourier transformation to analyze the changes in their orientation in the interferograms. They managed to obtain quantitative information on tear layer applying the bases of Fourier transformation [19,20]. In other works, Li et al applied a Shack-Hartmann wavefront sensor to non-invasively characterize the tear film topography [21].

Optical coherence tomography (OCT) has also been used to measure tear film thickness. OCT is a non-invasive cross-sectional imaging methodology used in biomedical applications. A low coherence light source is used in OCT systems to obtain a two dimensional image that could reveal optical characteristics of the specimen [22]. Wang et al used a commercial OCT system to indirectly measure the thickness of the normal pre-corneal tear film [23].

The technique presented in this article, Fluctuation Analysis by Spatial Image Correlation (FASIC), is a novel and non-invasive method for evaluating the thickness and spatial features of the tear film by applying the principles of auto-correlation analysis. A mathematical model has been developed to translate the spatial fluctuations into thickness information. Extensive calibration has been performed to validate the system. Animal study has also been conducted. We show that by calculating spatial autocorrelation in the raw camera images and extracting the frequency of the periodic patterns, the average size of the features of tear film can be obtained.

2 Materials and Methods

2.1 Instrumentation

A schematic of the FASIC setup is shown in Fig. 1 . In this setup a 635nm CW-diode laser (LXC6351AH, Lasermate, Pomona, CA), with less than 1mw in power (0.7 - 0.9mW), was used as a monochromatic coherent light source. The wavelength and power of this light source are in compliance with ANSI-2007 standards for laser safety [24]. The laser beam was shone onto the inferior cornea for animal subjects. The illuminated beam was not focused to a point and had a collimated diameter of approximately 2mm on the cornea. Therefore the measurements presented in this dissertation represent the thickness of the pre-corneal tear film in the region which was covered by the light source.

Fig. 1.

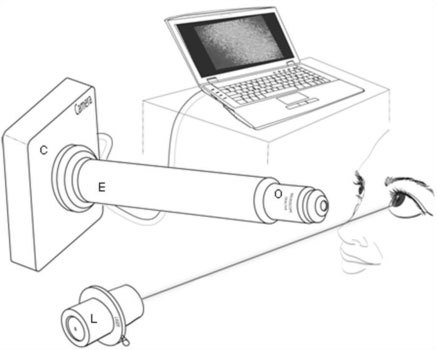
The schematic of the FASIC setup is shown here. A 635nm low power (<1mw) laser is illuminated onto the cornea in order to measure the pre-corneal tear film thickness. The reflecting and scattering light is captured by a cMOS camera that is positioned in an angle with respect to the incoming light. A stack of 256X256 pixel images are streamed to a computer through a firewire cable for further analysis.

A cMOS camera (PL-A662-KIT, Pixelink, Ottawa, ON K1G 6C2) was used as means of capturing the reflection and scattering from the ocular surface. There was an objective lens (Mitutoyo Compact CF 1X Objective, Edmund Optics, NJ, USA) connected to the cMOS camera in order to capture an image. This lens was connected to the cMOS camera through an extender tube. The length of the extender tube was 15cm. The camera assembly was 6.7cm away from the ocular surface. This distance was the working distance of the objective lens and was set consistently throughout the animal study to avoid any discrepancy which the focus could introduce to the data. A stack of 256X256 pixel images was streamed to a computer through a Firewire cable. The exposure time was set at 1ms and images were acquired at approximately 300 frames per second. For most experiments, 1000 frames were collected for a total acquisition time of approximately 3.5 seconds. The incident angle was approximately 10 degrees. The incident angle plays an important role in obtaining the true thickness value which will be discussed later. The camera angle was slightly greater than the incident angle in our setup (approximately 12 degrees) to avoid getting specular reflection

2.2 Spatial Autocorrelation and Physical Principles

Spatial autocorrelation is a statistical analysis that measures and evaluates the degree of dependency and similarity of a set of data with itself. Petersen et al [25] introduced the concept of spatial correlation to the imaging and microscopy community for applications in fluorescence correlation spectroscopy. This analysis was later improved by Wiseman-Petersen by introducing other applications for the image correlation spectroscopy [26]. Gratton et al established additional applications of the spatial and temporal image correlation analysis, such as cross and pair correlation analysis [27–30].

In this work, the specific characteristics of spatial autocorrelation are used to obtain quantitative information on the dynamics of pre-corneal tear film. The spatial autocorrelation relationship is given by [31]:

$$G_s(\xi ,\psi )=\frac{{\langle I(x,y)I(x+\xi ,y+\psi )\rangle }_{x,y}}{{\langle I(x,y)\rangle }_{x,y}^2}-1$$ (1)

where I(x,y) represent the image intensity, ξ and ψ are the spatial increments in the x and y directions, respectively, and the angle bracket indicates the average over all of the spatial locations in both x and y directions. In this technique, the spatial autocorrelation analysis is performed on a 2-D camera image which contains interference patterns from different sources, along with other features such as dots and lines with various sizes and orientations. These features in the camera image are difficult to distinguish using the human eye alone. By transferring the data into frequency domain, these features are more differentiable. Digman et al [32] introduced Raster Image Correlation Spectroscopy (RICS) where they identified and characterized the dynamics of cell motion through correlation analysis. RICS has been widely adapted by biologists and experimentalists throughout the world [33–37].

The mathematical operation of spatial autocorrelation works by shifting an image in both the x and y directions by one pixel and multiplying it by itself. This routine is performed for half the size of the image, since there is symmetry in the spatial autocorrelation image. This process is time consuming however, and could be numerically intensive. In order to expedite the spatial autocorrelation calculations, Fourier transformation is applied. To perform the spatial autocorrelation analysis with Fourier transformation, the raw camera image first undergoes a 2-D transformation. The complex conjugate of this image is then calculated and multiplied by the original transformed image producing a power spectrum. In order to better visualize the features in the frequency domain, the inverse of the power spectrum is calculated. This process is fast and robust.

Upon light illumination and provided the specific geometry described above, a periodic pattern is formed at the ocular surface and is captured by the camera detector (Fig. 2a ). This pattern originates from interference between multiple layers ofe tear film. The reflection at the inner surface of the tear film produces a slight rotation or displacement of the system of wavefronts. Superimposed to this pattern, there are many features such as lines and rings and other structures generated by scattering centers at the surface and, possibly the heterogeneity of the surface itself.

Fig. 2.

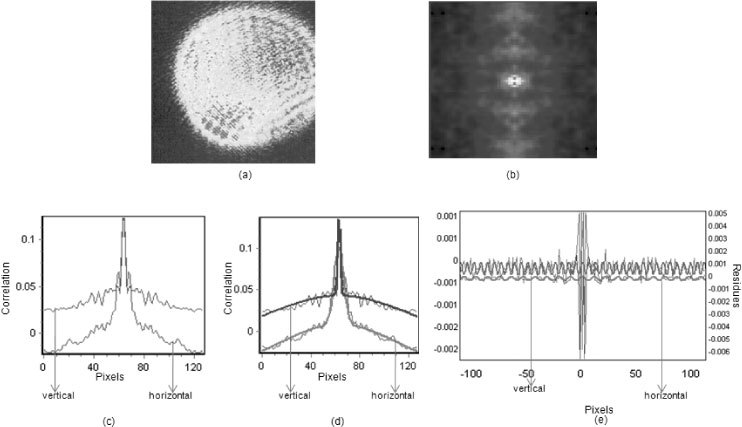
(a): Raw camera Image. This image displays the raw camera image from a rabbit’s eye. This image displays the circular interference pattern caused by tear film layers along with other features such as: small and large dots with different orientations. This image is one of 1000 time-integrated frames that are captured by the cMOS camera to analyze the spatial fluctuations. (b): SCI.This image displays the calculated spatial correlation image (SCI) on a single frame. The SCI has a central peak and a sinusoidal background. The sinusoidal residues that are located around the peak of the SCI are later used to obtain the quantitative tear film thickness information. (c). Vertical and horizontal projection of the SCI. This image is displaying the SCI in terms of number of pixels vs. the correlation value. This image contains the Gaussian terms along with the residues for both vertical and horizontal axis of two-dimensional image. The width of the pixels is illustrated on the x-axis while the correlation value (e.g., number of dots/average intensity of image) is on the y-axis. (d): Preliminary Gaussian fits in SCI. The SCI undergoes a preliminary fit to remove the primary Gaussian components. (e): Vertical and Horizontal Fitting. After removal of the Gaussian components, the sinusoidal residues are fitted both vertically and horizontally for all the frames. This process provides the period of the interference pattern due to the tear film. After the period of the interference is obtained, it gets calibrated based on the magnification and true pixel size and is later used to obtain the true thickness value of the tear film.

The spatial autocorrelation function and analysis processes, such as applying a high-pass filter, act as a filter to select the specific periodic patterns which correspond to the thickness of a thin film. The spatial correlation image (SCI) also known as autocorrelation function, contains the average shapes and sizes of the raw camera image (Fig. 2b). For example, if the image is made of randomly placed features, the SCI, which represents the average shape and size, is equal to the weighted average of the shape and size of each individual feature. If the average image is made of circular and linear fringes, such as in an interference pattern, the SCI will represent the average periodic shape of the fringes. Specifically, the spatial correlation calculation provides the average features of the image, disregarding their specific location in the image.

As a consequence of complexity of the spatial features of the illumination pattern, scattering centers, and other imperfections, the pattern may only be analyzed using the autocorrelation function and after selecting the unperturbed periodic pattern. The periodic pattern is in general complex, although it follows the basic dependency on the tear film thickness. The factors affecting the periodic part of the spatial autocorrelation function have been experimentally determined through calibration using standard blocks. We show that the period of the pattern depends on the inverse of the thickness of the film.

2.3 Mathematical model

A mathematical model is developed to extract the thickness of the pre-corneal tear film, based on the spatial autocorrelation analysis. This model analyzes the sinusoidal background that is superimposed on the SCI, and calculates the period of the interference pattern. This period is proportional to the thickness of the tear film.

Spatial autocorrelation is calculated for every frame and the central horizontal and vertical lines are plotted. The sinusoidal background of the SCI is illustrated in Fig. 2c along with the central autocorrelation peak, in terms of correlation value vs. pixels. A Gaussian model is used to describe the characteristics in the SCI. The first feature is the primary Gaussian (the large oscillation) and the second feature is the smaller sinusoidal oscillations around the central crest. This algorithm subtracts the overall spatial correlation in both x and y direction (the two Gaussians) and then analyzes residuals (Fig. 2d). The concept of this operation is similar to the double-differential method used by Kukreti et al [38]. The residuals are shown in Fig. 2e

The period (frequency) of the interference caused by the tear film is extracted with this model and is used to calculate the overall thickness of tear film. Due to the high variability of the location where these features appear in the original camera image, it is very difficult to model their behavior individually. Instead, while using the SCI, all the various features appear in the autocorrelation function, independently of their original location. This algorithm utilizes the features in the SCI and tracks the changes. This algorithm analyzes only the projections of the features on the vertical and horizontal axis of the SCI through fitting the residuals of the SCI after removing the broad Gaussians. With this method, the fitting routine becomes robust and fast. The process of calculating the SCI from the raw camera image, filtering the primary Gaussians, and fitting the residuals is done on the first frame of the image-stack. This initialization process is needed to obtain the best fit possible while minimizing the Chi-Square value.

The specific relationship used for fitting the Gaussians for the horizontal projection of the SCI is given by:

$$H=B+G_{1x}{e}^{\frac{-{(x-c)}^2}{2{\sigma }_{1x}^2}}+G_{2x}{e}^{\frac{-{(x-c)}^2}{2{\sigma }_{2x}^2}}$$ (2)

where B is the overall background, $G_{1x}$ and $G_{2x}$ are two Gaussian terms in the x direction, c is the center point of the image where the Gaussian fitting is started (which is the center of the SCI image), and ${\sigma }_{1x}$ and ${\sigma }_{2x}$are the standard deviations in the x direction corresponding to the first and second Gaussian functions in Eq. (2).

Accordingly, the relationship for the vertical fit is given by:

$$V=B+G_{1y}{e}^{\frac{-{(y-c)}^2}{2{\sigma }_{1y}^2}}+G_{2y}{e}^{\frac{-{(y-c)}^2}{2{\sigma }_{2y}^2}}$$ (3)

where B is the overall background, $G_{1y}$ and $G_{2y}$ are two Gaussian terms in the y direction, and c is the center point of the image, which is known.

The results of this fit using the Gaussian are then subtracted from the SCI and the residuals are now fitted with a periodic function associated to the interference term. The interference term is given by:

$$I=A\left(1-\cos (k_{x}x)-\cos (k_{y}y)\right)$$ (4)

where A is the amplitude, and $k_x$ and $k_y$ are the projections in the x and the y directions of the interference pattern. All units in the above relationships are in terms of the number of pixels in the autocorrelation function. X and Y are shifts expressed in terms of number of pixels and k_x and k_y are in unit of inverse number of pixels needed for one period of the interference pattern. They are given by:

$$k_x=(1/P)\cos (\varphi )$$ (5)

$$k_y=\left(1/P\right)\sin (\varphi )$$ (6)

where P is the period (in pixels) of the interference pattern in the autocorrelation function and φ is the angle of the pattern with respect to the x and y axis. Since the pixel size (in terms of micrometer) of the camera and the optical magnification are known, the period of interference (P) could be calibrated. The thickness then can be calculated by:

$$t=\frac{K}{nP\sin (\theta )}$$ (7)

where n is the refractive index of the medium which is assumed to be water, and θ is the incident angle which in our set up is 11 degrees. The dependence of Eq. (7) with the period was verified experimentally. The only unknown parameter in this equation was calibrated with a series of films of known thicknesses. K is a constant and was empirically obtained and includes the wavelength of the light as well. Differences in refractive index values of standard blocks (1.66) were taken into consideration when calculating the thickness of the ocular tear film [39]. For eye measurements, a value of 1.336 for the refractive index was assumed [40].

2.4 Calibration with a standard of known thickness

We calibrated the spatial autocorrelation function using thin films of known thicknesses with the surface slightly scattering. The dependence of the Eq. (7) on the angle of incidence and angle of observation was also empirically verified. The algorithm used to recover the layer thickness has been verified using micro-fabricated standards. Standards were made by depositing parylene on a silicon wafer. After fabrication, their thicknesses were measured using a Dektak profilometer (Veeco Inc, Camarillo, CA 93012). Two standards were applied here to validate our calculations. One had a mean thickness value of 2.90µm with a standard deviation of 0.02 from 3 measurements. With FASIC, a value of 2.88 ± 0.03µm was obtained. The other standard had a verified thickness of 4.92 ± 0.02µm, and a thickness value of 4.89 ± 0.02µm was obtained.. The values obtained with the two methods were consistent within the measurement errors and validate the model Eq. (7).

3. Results and Discussion

3.1 Live rabbit measurement protocol

Experiments were performed on a live rabbit model. The rabbits were provided by and imaged at the University of California, Irvine, Medical Center. All procedures were approved by the UCI IACUC and conducted in accordance with the ARVO Statement for the Humane Use of Animals in Ophthalmic and Vision Research. Rabbits were anesthetized with intramuscular injection of xylazine (5mg/Kg) (Anased, Lloyd Laboratories, Shenandoah, IA) and ketamine (22mg/Kg) (Bionichepharma USA LLC, Lake Forest, IL). Tetracaine hydrochloride 0.5% eye Drops (Alcon Laboratories Inc, Forth Worth, TX) were instilled into the right eye of each subject, and a speculum was used to open the eyelids. The laser beam, was angled approximately 20 degrees with respect to the detecting camera, and was pointed at the inferior cornea. The camera was placed at about 6.7cm away from the surface of the eye. This is approximately the focal length of the 1X microscope objective.

For the rabbits with healthy eyes (N = 3), a total of 9 experiments were conducted. Each rabbit was measured 3 times. Measurements for each rabbit were performed in one day. For each measurement 1000 frames were captured at approximately 300 frames per second, with an overall data acquisition time of approximately 3.3 seconds. A 30-second gap was enforced between each measurement in order to observe the thinning phenomena of tear film.

3.2 Live rabbit eye measurements

As illustrated in Fig. 3 , healthy rabbit #1 had tear film thicknesses of 9.9µm, 9.7µm and 9.6µm in 3 consecutive measurements. Healthy rabbit #2 came out with 10.5µm, 10.4µm and 10.1µm. Healthy rabbit #3 showed tear film thickness values of 10.3µm, 10.1µm and 9.8µm. The tear film thickness of a rabbit infected with ocular herpes (HSV-1) was also measured. The measurements for that rabbit were 4.7μm, 4.3µm and 4.1µm. In all 12 measurements, it was observed that the thickness of the tear film decreases over time. Overall, the baseline value for the thickness of a healthy rabbit tear film was quantified to be 10.2 ± 0.3. In this set of experiments, not only the thickness of pre-corneal tear film was precisely quantified, but also the thinning of the tear film over time was observed.

Fig. 3.

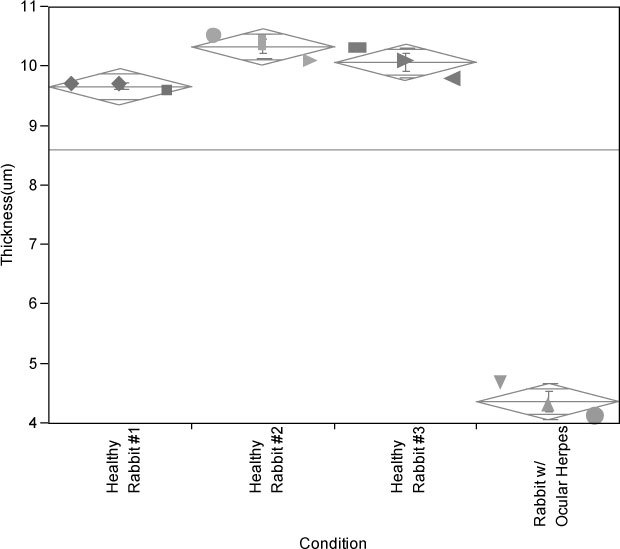
Thickness values of the pre-corneal tear films of four rabbits is shown here. Rabbits were measured at different days and each rabbit has undergone 3 consecutive measurements with 30 seconds interval at the day of the measurement. Thinning out phenomena is clearly observed in all animals. Three healthy rabbits have normal tear film thickness of 10.1μm on average. The one rabbit with ocular herpes had a tear film thickness of 4.7µm and 4.3µm and 4.1µm in the three measurements, respectively.

Figure 4 demonstrates continuous monitoring of the tear thickness during administration of an artificial tear solution. In this experiment the eyelids were kept open for 1 minute prior to data acquisition, resulting in a dry eye. At this stage tear film thickness is shown to be approximately 5μm. At frame 350, about 1.2 seconds into the measurement, a drop of Refresh Tears ® (Allergan, Irvine, CA) was instilled onto the cornea. A 10-fold increase in thickness was observed in the tear film, peaking at about 50μm. The tear remains thick for about two seconds, which is the time required for the drop to travel through the imaging plane. After the drop expands and the product distributes more uniformly, the tear film maintains a stable thickness of approximately 18μm on average throughout the measurement. Figure 4 demonstrates the ability of this technique for real-time assessment of tear film thickness.

Fig. 4.

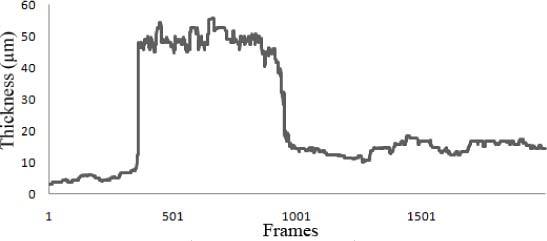
Real time analysis of tear film dynamics in response to instillation of Refresh Tears ® (Allergan, Irvine,CA). The camera acquired images at 300 frames/s. Changes of the thickness of tear film over approximately 7 seconds are displayed here. The experiment starts out with a dried eye. A few seconds into the data acquisition, a drop of Refresh Tear Plus® is instilled into the rabbit eye. The thickness of the tear film increases approximately 10 fold. After another two seconds (when the bulk of the drop is out of the imaging plane), the tear film starts finding a stability in thickness. At this point, the thickness stays at approximately 18µm, and holds this thickness throughout the data acquisition.

Next, the retention time of the same eye drop (Refresh Tears®) was studied using a live rabbit model with healthy eyes. As Fig. 5 demonstrates, the original baseline for the subject was approximately 9.6μm. This value is similar to that obtained previously. After baseline measurement a drop of 20μl Refresh Tears® was instilled onto the rabbit’s eye. The eye was manually blinked 3 times so that the eye drop could evenly distribute throughout the ocular surface. Twenty consecutive measurements were taken with a two-minute gap between each measurement. As the rabbit was sedated, its eye was manually blinked at 30 second intervals to prevent evaporation of the eye drop. A peak value of 17.4μm in the first measurement (time = 0) was obtained. This value was also comparable to values obtained in our previous measurement with Refresh Tears ®. The thickness maintained values of above 16μm for the first 5 measurements that were obtained within 10 minutes of eye drop instillation. Sixteen minutes into the measurement, a more aggressive decline in the value of the tear film thickness was observed as the pre-corneal tear film thickness decreased to 14.7µm. From the 10th measurement through the 15th measurement, a steady decrease in the thickness values was observed. In that time frame, the tear film thickness went from 13.8μm to 11.5μm. At measurement = 16, 32 minutes after the instillation of the drop, the tear film thickness experienced the sharpest decline in the tear film thickness, as the value returned to 9.8μm. In the last two measurements, the thickness was similar to the baseline value of 9.6μm. Therefore the drop retention time was estimated to be about 36 minutes. This set of experiments showed that FASIC is capable of quantifying the retention time of an artificial tear solution in an accurate manner.

Fig. 5.

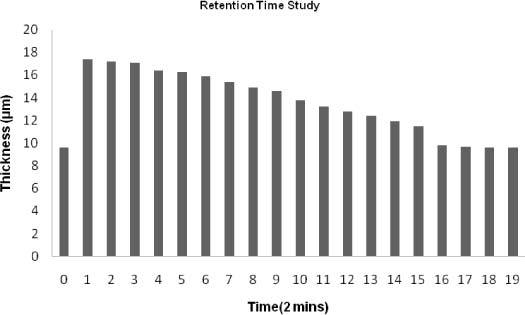
In this figure, the retention time of Refresh Tears® (Allergan, Irvine,CA) was analyzed using a live rabbit model. The baseline showed a value of 9.6 µm. After the eye drop was instilled onto the eye, the tear film thickness increased and had a value of 17.4 µm We obtained a peak value of 17.4μm in the first measurement (time = 0). 10 minutes into the measurement, the thickness maintained values of above 16μm. Sixteen minutes after the instillation of the eye drop, we started observing a more aggressive decline in the value of the tear film thickness as the tear film thickness decreased to 14.7µm. From the 10th measurement through the 15th measurement, the pre-corneal tear film thickness undergoes a more steady decrease as it goes from 13.8μm to 11.5μm. At measurement 16; 32 minutes after the instillation of the drop the tear film thickness the sharpest decline the tear film thickness was observed as the value came back to 9.8μm. In the last two measurements, the thickness was similar to the baseline value of 9.6μm. We estimated the retention time to be about 36 minutes.

4 Conclusion

In summary, a technique for imaging the ocular surface was developed and applied to obtain repeatable and accurate measurements of tear film thickness. By identifying a periodic pattern that forms at the tear layer surface and applying the spatial correlation analysis of a sequence of time-integrated images, the depth profile of a thin film can be revealed. Our results indicate that spatial correlation analysis is a quick and robust method for obtaining the thickness of very thin biological films that exhibit scattering from the surface and reflection from the inner layers, upon light illumination. The thickness of tear film in the live rabbit eye under different conditions was measured and quantified in response to an artificial tear solution. Our measurements revealed the details of the changes in thickness as a function of time.

In this work, a low power 635nm laser was used; the intensity of light could have psychological effects on subjects, encouraging blinking. A longer wavelength (but similarly low-powered) laser, in the infrared range, could also be used in the future. The specific device used for the measurement is robust, inexpensive, easy to align, portable and non-invasive. The system is simple, requiring only a coherent light source and a fast detector camera in a basic setup.