Abstract
A major concern when designing a psychophysical experiment is that participants may use another stimulus feature (“cue”) than that intended by the experimenter. One way to avoid this involves applying random variations to the corresponding feature across stimulus presentations, to make the “unwanted” cue unreliable. An important question facing experimenters who use this randomization (“roving”) technique is: How large should the randomization range be to ensure that participants cannot achieve a certain proportion correct (PC) by using the unwanted cue, while at the same time avoiding unnecessary interference of the randomization with task performance? Previous publications have provided formulas for the selection of adequate randomization ranges in yes-no and multiple-alternative, forced-choice tasks. In this article, we provide figures and tables, which can be used to select randomization ranges that are better suited to experiments involving a same-different, dual-pair, or oddity task.
Keywords: psychophysics, same-different, oddity, dual-pair, randomization, roving
A common concern in designing a psychophysical experiment relates to the possibility that participants perform the task using another “cue” (stimulus feature, or dimension) than that intended by the experimenter. For instance, in the field of auditory-perception research known as “profile analysis” (for a review, see: Green, 1988), the researcher is primarily interested in how well listeners can detect or discriminate features, such as peaks or troughs, in the spectral shape of sounds. However, unless special precautions are taken, listeners may be able to perform the task correctly without even extracting spectral shape. For example, listeners can identify which of two successively presented sounds contains a spectral peak based solely on differences in loudness, if the sound containing the spectral peak has a higher intensity overall. Consequently, there is a risk that thresholds or performance in this type of experiment reflect loudness perception, rather than spectral-shape perception. Another example is auditory frequency (subjectively, pitch) discrimination, where listeners can use differences in loudness between tones, due to variation in equal-loudness contours across frequency (Dai, Nguyen, and Green, 1995; Emmerich, Ellermeier, & Butensky, 1989; Henning, 1966; Moore & Glasberg, 1989; Moore, Glasberg, Low, Cope, & Cope, 2006). As a result, performance or thresholds in an experiment that originally sought to measure the perception of pitch may actually reflect, or be contaminated by, the perception of another sound attribute (loudness).
Two approaches have traditionally been used by experimenters to limit participants’ ability to take advantage of unwanted cues in discrimination tasks. The first approach involves equalizing the values of the stimuli along the unwanted dimension. For instance, in a frequency-discrimination experiment, the experimenter can try to adjust the relative intensities of tones in a frequency-dependent manner, in an attempt to ensure that loudness remains constant as frequency changes. Unfortunately, in general, equating precisely the perceived values of stimuli, which keep changing during the course of psychophysical measurements, is a challenging task, which often requires detailed and time-consuming measurements beforehand.1
A second approach to limit participants’ use of unwanted cues involves applying random stimulus variation along the unwanted dimension. In the auditory psychophysics literature, this is commonly referred to as “randomization”, or “roving”. For instance, to prevent listeners in the above-mentioned spectral-shape discrimination experiment to take advantage of overall loudness cues, experimenters “rove” (i.e., vary randomly) the overall level of the stimuli (see: Dai & Green, 1992; Drennan & Watson, 2001; Durlach, Braida, & Ito, 1986; Farrar et al., 1987; Green, 1988; Kidd & Dai, 1993; Kidd, Mason, Uchanski, Brantley, & Shah, 1991; Mason, Kidd, Hanna, & Green, 1984; Spiegel, Picardi, & Green, 1981; Versfeld & Houtsma, 1991). Similarly, to prevent listeners from taking advantage of loudness cues in an auditory frequency-discrimination experiment, experimenters can randomize the level of each tone, so that loudness differences no longer provide a reliable cue for task performance (Dai et al., 1995; Emmerich et al., 1989; Henning, 1966; Moore & Glasberg, 1989; Semal & Demany, 2006). The roving technique is very popular among auditory-perception researchers. It has been used in studies of intensity perception (Berliner & Durlach, 1973; Berliner, Durlach, & Braida, 1977; Oxenham & Buus, 2000), pitch discrimination with complex tones (see: Houtsma & Smurzynski, 1990; Moore, Glasberg, Flanagan, & Adams, 2006; Oxenham, Micheyl, & Keebler, 2009), tone-in-noise detection (Hall & Fernandes, 1983; Kidd, Mason, Brantley, & Owen, 1989), binaural hearing (Bernstein & Trahiotis, 1997; Bernstein & Trahiotis, 1994; Henning, Richards, & Lentz, 2005), speech perception (Macmillan, Goldberg, & Braida, 1988), temporal gap detection (Formby & Muir, 1989; Forrest & Green, 1987), and frequency- or amplitude-modulation perception (Furukawa & Moore, 1997; Moore & Sek, 1998; Stellmack, Viemeister, & Byrne, 2006), among others.
A practical question facing the experimenter who plans to use roving is: how large should the roving range be? If the range is too small, participants may still be able to achieve a relatively high proportion of correct responses based on the unwanted cue. On the other hand, if the range is too large, participants’ performance might be impacted unnecessarily by the random stimulus variations2. Therefore, experimenters must strive to find a good compromise between limiting contributions from the unwanted cue (which encourages the use of a wide roving range), and limiting potential side-effects of roving on performance (which calls for the use of as small a roving range as is safely possible). In order to select a suitable roving range, experimenters must know how the proportion of correct responses that can be achieved based on the unwanted cue, Pcunwanted, depends on the roving range, R. The latter is defined as the distance between the largest and smallest values that the stimulus can assume along the “unwanted” dimension, due to roving. For instance, in a frequency-discrimination experiment in which the level of tones can vary randomly between 45 and 55 dB SPL across presentations, the roving range is 10 dB.
In addition to depending on R, Pcunwanted also depends on the size of the unwanted cue, Δ. The latter corresponds to the change along the “unwanted” stimulus dimension, which accompanies (and is correlated with) the change applied by the experimenter along the primary dimension. For instance, if the loudness of a tone changes by an amount corresponding to 1 dB when the tone frequency changes by 1%, then the size of the unwanted loudness cue corresponding to a 1% change in frequency in a frequency-discrimination experiment is 1 dB. In the framework of signal detection theory (SDT, see: Green & Swets, 1966), Δ can be identified with the distance, along the “unwanted” physical dimension, between the two stimuli that must be discriminated in a yes-no paradigm. If the physical-to-sensory mapping is linear, and the internal noise that contaminates the sensory observations evoked by the stimuli is constant, Δ is directly proportional to the familiar index of sensitivity, d′. However, there are two important differences between Δ and d′. Firstly, whereas d′ usually denotes sensitivity to the primary cue, were, Δ refers to an unwanted cue. Secondly, whereas d′ is dimensionless, Δ has the dimension of the stimulus attribute being randomized.
In most applications, the size of the unwanted cue is either known to the experimenter, or it can be estimated based on data in the relevant literature—especially, data from studies in which the corresponding cue, which is now the unwanted cue, was then the cue of primary interest. For instance, loudness cues associated with changes in the frequency of pure tones in a frequency-discrimination experiment can be estimated based on data on equal-loudness contours and intensity discrimination. When relevant data for estimating the size of the unwanted cue are not available in the existing literature, such data must be collected. In some applications, the size of the unwanted cue is directly available. For instance, in spectral profile- analysis experiments, the overall loudness difference between the sounds that the listener must discriminate (i.e., the size of the unwanted cue) is, to a first approximation, proportional to the increment or decrement in level that the listener must detect (i.e., the size of the primary cue). In general, when the primary and unwanted cues share the same dimension—as in the profile-analysis example—the size of the unwanted cue is known to the experimenter; in all other cases, the size must be estimated based on existing data, or measured.
While the relationship between Pcunwanted, R, and Δ can be studied empirically, measurements of this relationship are usually impractical in the context of experimental studies, the primary aim of which is not to characterize it. Therefore, experimenters do not usually choose R based on empirical measurements. Instead, they rely on predictions derived based on ideal-observer models from signal detection theory (Green & Swets, 1966). Because these models assume a noiseless observer who uses the information conveyed by the unwanted cue optimally, they provide an upper bound on the performance that can be achieved based on that cue. In particular, Green (1988, pp. 19–21) provided a relatively simple formula relating Pcunwanted, R, and Δ, in the 2I-2AFC paradigm: Pcunwanted = 0.5 + Δ/R − 0.5 (Δ/R)2. More recently, Dai and Kidd (2009) derived similar formulas for the yes-no and m-alternative forced-choice (mAFC) paradigms. Specifically, they showed that, for the yes-no paradigm, Pc = 0.5 + 0.5 (Δ/R), whereas for the mAFC paradigm, Pcunwanted = Δ/R + [1 − (Δ/R)m]/m.
Although the yes-no and mAFC paradigms have been used in a large number of auditory- and visual-perception studies over the past fifty years, other paradigms exist, which are better suited for certain applications (overviews can be found in: Creelman & Macmillan, 1979; Macmillan & Creelman, 2005; Macmillan, Kaplan, & Creelman, 1977; Noreen, 1981). For instance, the same-different paradigm provides a measure of basic stimulus discriminability, which does not involve an ability to identify the direction of changes in, e.g., sound intensity or frequency (Dai, Versfeld, & Green, 1996). The “oddity” paradigm, wherein participants are on each trial presented with m stimuli, one of which differs from the other m-1, is better suited than its mAFC counterpart in some situations (Versfeld, Dai, & Green, 1996). The “dual-pair comparison” paradigm (Creelman & Macmillan, 1979) allows researchers to measure stimulus-change detection and change-direction identification using the same stimulus structure (two-pairs of stimuli, one containing a change, the other not), by simply changing the instructions given to the participant (Semal & Demany, 2006; Micheyl, Kaernbach, & Demany, 2008). In some contexts, it is necessary to use roving in a same-different (e.g., Jesteadt & Bilger, 1974), oddity (e.g., Lyzenga & Horst, 1995; Lyzenga & Horst, 1997, 1998)3, or dual-pair (e.g., Micheyl et al., 2006; Semal & Demany, 2006) paradigm. Unfortunately, the above-cited formulas, which give the relationship between Pcunwanted and roving range for the yes-no and mAFC paradigms, do not apply to these other paradigms. In fact, as the results presented in this article reveal, using these formulas to determine the roving range required to keep Pcunwanted under a target level in any of three paradigms mentioned above (same-different, dual-pair, and oddity) can lead to substantial errors in both experimental design, and data interpretation.
While no simple analytical formulas exist, which can be used as guidelines for selecting suitable roving ranges in same-different, dual-pair, or oddity experiments, in this article, we provide figures and tables, which experimenters can use to select an adequate roving range, R, given a target Pcunwanted, and a known (or estimated) unwanted-cue size, Δ, in the same-different paradigm, two versions of the dual-pair paradigm (i.e., 4IAX and AB-versus-BA), and two versions of the oddity paradigm (i.e., three- and four-interval oddity). The information in the tables and figures can also be used, conversely, to find the Pcunwanted that can (or could, in retrospect) be achieved in an experiment using one of these paradigms, given the roving range and unwanted-cue size.
Method
In order to derive the results presented below, we assumed a maximum-likelihood (ML) observer, who makes optimal use of the information conveyed by the unwanted cue, which is being roved. Obviously, the information conveyed by the unwanted cue becomes less and less useful for correct task performance as the roving range increases. The general approach is similar to that described by Green (1988) for the 2I-2AFC task, and more recently extended to yes-no and the mAFC tasks by Dai and Kidd (2009). The basic idea of this approach is that the unwanted cue shifts the distribution of stimulus values, and the corresponding distribution of sensory observations, along the considered stimulus dimension. The distribution of stimulus values is produced by the application of stimulus roving. Here, as in Green (1988) and Dai and Kidd (2009), we assume a “rectangular”, i.e., continuous-uniform distribution. Near the end of the article, we show how the results can be corrected when the uniform distribution is discrete, instead of continuous. The uniform is the distribution most frequently used in studies of auditory perception. Of all continuous roving distributions having a fixed range, the uniform is the one that minimizes the maximal Pc that can be achieved (by an ideal, maximum-likelihood observer) based on the unwanted cue (Dai, 2008).
Under these assumptions, the maximal Pc that can be achieved based on the unwanted cue alone (hereafter referred to as Pcunwanted) can be computed as the integral, over the observation space, of the probability density corresponding to the most likely a-posteriori stimulus alternative—at the current point in the observation space. Using Bayes’ theorem, the latter probability can be determined based on the (uniform) probability density function of the observations, given the stimulus alternative. Since our calculations are for an ideal observer, and in most experimental applications the various stimulus alternatives are equally likely, the maximum a-posteriori (MAP) and maximum-likelihood (ML) solutions are equivalent.
For the 2I-2AFC, yes-no, and mAFC paradigms, the integral has a relatively simple analytical solution—see the above-mentioned equations by Green (1988) and Dai and Kidd (2009). For other paradigms, analytical solutions are more difficult to obtain due to the greater dimensionality of the decision space, or to the presence of nonlinearities (e.g., an absolute-value, or maximum-of operation) in the decision rule. Here, rather than attempt to provide analytical solutions, we resorted to a numerical-evaluation approach. We evaluated the integral, over the relevant observation space, of the (uniform) probability density corresponding to the most likely stimulus alternative. Several publications have already described the relevant observation spaces and ML decision rules for the various paradigms considered here: same-different (Dai et al., 1996; Irwin & Hautus, 1997; Irwin, Hautus, & Butcher, 1999; Macmillan & Creelman, 2005), dual-pair 4IAX (Micheyl, Kaernbach, & Demany, 2008; Micheyl & Messing, 2006; Noreen, 1981; Rousseau & Ennis, 2001, 2002), dual-pair AB-versus-BA (Micheyl & Dai, 2008, 2009), and oddity (Frijters, 1979a, 1979b; Geelhoed, MacRae, & Ennis, 1994; Versfeld et al., 1996). Readers are referred to these earlier texts. In the remainder of this article, we present the results of our calculations relating Pcunwanted to Δ/R for these different paradigms, in both figure and table format.
Results and Discussion
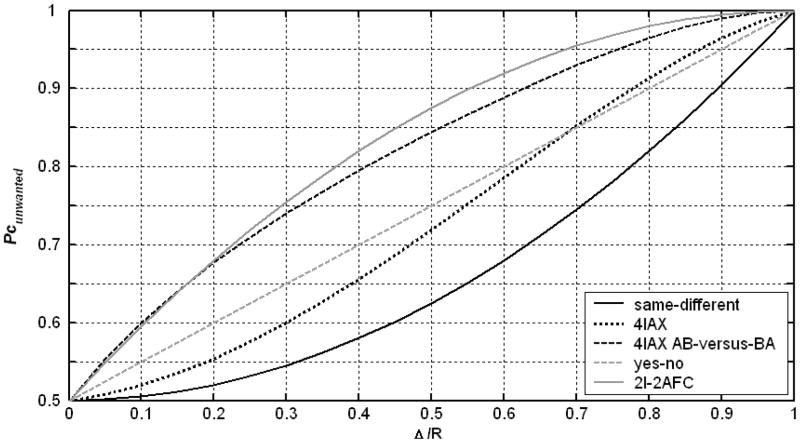
Figure 1 shows Pcunwanted as a function of Δ/R for the same-different paradigm, the 4IAX paradigm, and the 4IAX AB-versus-BA paradigm. Similar functions are also shown for the yes-no paradigm and the 2I-2AFC paradigm for comparison. As mentioned in the Introduction, for these two paradigms, analytical solutions for the relationship between Δ/R and Pcunwanted have been provided in other publications (Dai & Kidd, 2009; Green, 1988). The five paradigms illustrated in this figure all have the same chance-performance level, corresponding to Pc = 0.5. The tables in Appendices A, B, and C list Δ/R values corresponding to Pcunwanted between 0.5 and 1 (in steps of 0.01) for the same-different paradigm, and the two versions of the dual-pair paradigm (i.e., 4IAX and AB-versus-BA).
Figure 1.
Pcunwanted as a function of Δ/R for the same-different, 4IAX, 4IAX AB-versus-BA, yes-no, and 2I-2AFC paradigms. Each line type corresponds to a single paradigm, as indicated in the inset legend. Pcunwanted refers to the maximal proportion of correct responses that can be achieved based on an unwanted cue, the use of which is limited by the application of a random rove drawn for a uniform (or “rectangular”) distribution with a range (or “width”) of R. Δ denotes the “size” of the unwanted cue, as defined in the text.
Appendix A.
Δ/R as a function of Pcunwanted for the same-different paradigm.
| Pcunwanted | Δ/R | Pcunwanted | Δ/R | Pcunwanted | Δ/R |
|---|---|---|---|---|---|
| 0.50 | 0.00 | 0.67 | 0.58 | 0.84 | 0.82 |
| 0.51 | 0.14 | 0.68 | 0.60 | 0.85 | 0.84 |
| 0.52 | 0.20 | 0.69 | 0.62 | 0.86 | 0.85 |
| 0.53 | 0.24 | 0.70 | 0.63 | 0.87 | 0.86 |
| 0.54 | 0.28 | 0.71 | 0.65 | 0.88 | 0.87 |
| 0.55 | 0.32 | 0.72 | 0.66 | 0.89 | 0.88 |
| 0.56 | 0.35 | 0.73 | 0.68 | 0.90 | 0.89 |
| 0.57 | 0.37 | 0.74 | 0.69 | 0.91 | 0.91 |
| 0.58 | 0.40 | 0.75 | 0.71 | 0.92 | 0.92 |
| 0.59 | 0.42 | 0.76 | 0.72 | 0.93 | 0.93 |
| 0.60 | 0.45 | 0.77 | 0.73 | 0.94 | 0.94 |
| 0.61 | 0.47 | 0.78 | 0.75 | 0.95 | 0.95 |
| 0.62 | 0.49 | 0.79 | 0.76 | 0.96 | 0.96 |
| 0.63 | 0.51 | 0.80 | 0.77 | 0.97 | 0.97 |
| 0.64 | 0.53 | 0.81 | 0.79 | 0.98 | 0.98 |
| 0.65 | 0.55 | 0.82 | 0.80 | 0.99 | 0.99 |
| 0.66 | 0.57 | 0.83 | 0.81 | 1.00 | 1.00 |
Appendix B.
Δ/R as a function of Pcunwanted for the dual-pair 4IAX paradigm.
| PCunwanted | Δ/R | Pcunwanted | Δ/R | Pcunwanted | Δ/R |
|---|---|---|---|---|---|
| 0.50 | 0.00 | 0.67 | 0.42 | 0.84 | 0.68 |
| 0.51 | 0.06 | 0.68 | 0.44 | 0.85 | 0.70 |
| 0.52 | 0.10 | 0.69 | 0.46 | 0.86 | 0.71 |
| 0.53 | 0.13 | 0.70 | 0.47 | 0.87 | 0.73 |
| 0.54 | 0.16 | 0.71 | 0.49 | 0.88 | 0.74 |
| 0.55 | 0.19 | 0.72 | 0.50 | 0.89 | 0.76 |
| 0.56 | 0.22 | 0.73 | 0.52 | 0.90 | 0.78 |
| 0.57 | 0.24 | 0.74 | 0.53 | 0.91 | 0.79 |
| 0.58 | 0.26 | 0.75 | 0.55 | 0.92 | 0.81 |
| 0.59 | 0.28 | 0.76 | 0.56 | 0.93 | 0.83 |
| 0.60 | 0.30 | 0.77 | 0.58 | 0.94 | 0.85 |
| 0.61 | 0.32 | 0.78 | 0.59 | 0.95 | 0.87 |
| 0.62 | 0.34 | 0.79 | 0.61 | 0.96 | 0.89 |
| 0.63 | 0.36 | 0.80 | 0.62 | 0.97 | 0.91 |
| 0.64 | 0.37 | 0.81 | 0.64 | 0.98 | 0.94 |
| 0.65 | 0.39 | 0.82 | 0.65 | 0.99 | 0.97 |
| 0.66 | 0.41 | 0.83 | 0.67 | 1 | 1 |
Appendix C.
Δ/R as a function of Pcunwanted for the dual-pair AB-versus-BA paradigm.
| Pcunwanted | Δ/R | Pcunwanted | Δ/R | Pcunwanted | Δ/R |
|---|---|---|---|---|---|
| 0.50 | 0.00 | 0.67 | 0.19 | 0.84 | 0.49 |
| 0.51 | 0.01 | 0.68 | 0.20 | 0.85 | 0.51 |
| 0.52 | 0.02 | 0.69 | 0.22 | 0.86 | 0.54 |
| 0.53 | 0.03 | 0.70 | 0.23 | 0.87 | 0.56 |
| 0.54 | 0.04 | 0.71 | 0.25 | 0.88 | 0.58 |
| 0.55 | 0.05 | 0.72 | 0.27 | 0.89 | 0.60 |
| 0.56 | 0.06 | 0.73 | 0.28 | 0.90 | 0.63 |
| 0.57 | 0.07 | 0.74 | 0.30 | 0.91 | 0.65 |
| 0.58 | 0.08 | 0.75 | 0.32 | 0.92 | 0.68 |
| 0.59 | 0.09 | 0.76 | 0.33 | 0.93 | 0.70 |
| 0.60 | 0.10 | 0.77 | 0.35 | 0.94 | 0.73 |
| 0.61 | 0.11 | 0.78 | 0.37 | 0.95 | 0.76 |
| 0.62 | 0.12 | 0.79 | 0.39 | 0.96 | 0.79 |
| 0.63 | 0.14 | 0.80 | 0.41 | 0.97 | 0.82 |
| 0.64 | 0.15 | 0.81 | 0.43 | 0.98 | 0.85 |
| 0.65 | 0.16 | 0.82 | 0.45 | 0.99 | 0.90 |
| 0.66 | 0.18 | 0.83 | 0.47 | 1.00 | 1.00 |
Figure 1 reveals that, of the five paradigms, the same-different paradigm generally yields the lowest Pcunwanted (given Δ/R). On the other hand, the 2I-2AFC paradigm generally yields higher Pcunwanted values than the other paradigms considered in this figure—with the exception of the 4IAX version of the dual-pair paradigm, for relatively low Pc levels (below 0.65). The difference between the same-different and 2I-2AFC curves is considerable. For example, whereas a roving range five times the size of the unwanted cue (which corresponds to a Δ/R ratio of 0.2) is needed in order to limit Pcunwanted to just under 70% in a 2I-2AFC experiment, in a same-different experiment, a roving range having this relative size limits Pcunwanted to less than 55%. Another way of looking at the difference between the 2I-2AFC and same-different paradigms is that, for a given Δ, the smallest roving range required to ensure that Pcunwanted does not exceed 60% is about four times smaller for the same-different paradigm than for the 2I-2AFC paradigm. An experimenter who uses Green’s (1988) formula (reproduced in the Introduction) to determine the roving range needed to limit Pcunwanted to within 52 to70%, is likely to over-estimate the required roving range by as much as six times.
These observations should not be interpreted as implying that stimulus roving always reduces the influence of an unwanted cue more effectively in the same-different paradigm than in the 2I-2AFC paradigm. As discussed in Dai (2008), the relative contributions of a primary cue and of an unwanted cue in determining the Pc measured in an experiment depend, among other things, on the relative salience of each cue, and on how these cues interact. However, the ideal-observer analysis described in this article provides an upper bound on the performance that can be achieved by a real observer based on the unwanted cue.
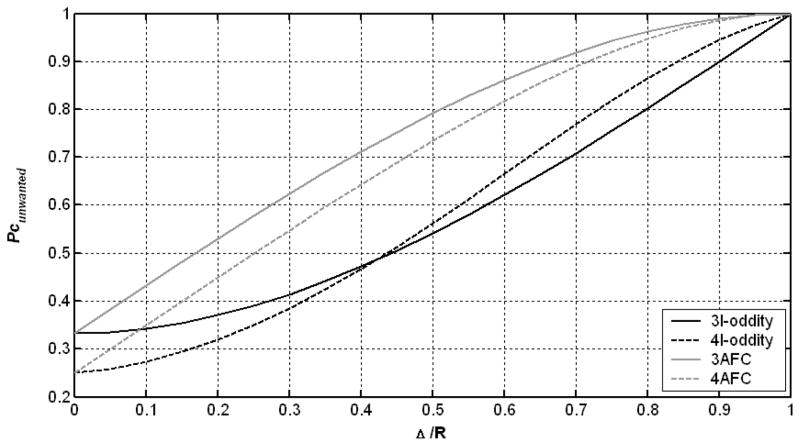
Figure 2 shows how Pcunwanted depends on Δ/R in the three- and four-interval oddity paradigms. For comparison, the functions relating Pcunwanted to Δ/R in the 3AFC and 4AFC paradigms are also shown (as gray solid and dashed lines, respectively). The latter were computed using the formula provided by Dai and Kidd (2009), which can be found in the Introduction of the current paper. It can be seen that, for a given value of Δ/R, the three- and four-interval oddity paradigms yield lower values of Pcunwanted than their 3AFC and 4AFC counterparts.
Figure 2.
Pcunwanted as a function of Δ/R for the three- and four-interval oddity, 3AFC, and 4AFC paradigms. Each line type corresponds to a single paradigm, as indicated in the inset legend. Pcunwanted refers to the maximal proportion of correct responses that can be achieved based on an unwanted cue, the use of which is limited by the application of a random rove drawn for a uniform (or “rectangular”) distribution with a range (or “width”) of R. Δ denotes the “size” of the unwanted cue, as defined in the text.
The tables in Appendices D and E list Δ/R values corresponding to Pcunwantedm between 0.5 and 1 (in steps of 0.01) for the three- and four-interval oddity paradigms.
Appendix D.
Δ/R as a function of Pcunwanted for the three-interval oddity paradigm.
| Pcunwanted | Δ/R | Pcunwanted | Δ/R | Pcunwanted | Δ/R |
|---|---|---|---|---|---|
| 0.33 | 0.00 | 0.56 | 0.52 | 0.79 | 0.79 |
| 0.34 | 0.09 | 0.57 | 0.54 | 0.80 | 0.80 |
| 0.35 | 0.13 | 0.58 | 0.55 | 0.81 | 0.81 |
| 0.36 | 0.17 | 0.59 | 0.56 | 0.82 | 0.82 |
| 0.37 | 0.20 | 0.60 | 0.57 | 0.83 | 0.83 |
| 0.38 | 0.22 | 0.61 | 0.59 | 0.84 | 0.84 |
| 0.39 | 0.25 | 0.62 | 0.60 | 0.85 | 0.85 |
| 0.40 | 0.27 | 0.63 | 0.61 | 0.86 | 0.86 |
| 0.41 | 0.29 | 0.64 | 0.62 | 0.87 | 0.87 |
| 0.42 | 0.31 | 0.65 | 0.63 | 0.88 | 0.88 |
| 0.43 | 0.33 | 0.66 | 0.65 | 0.89 | 0.89 |
| 0.44 | 0.35 | 0.67 | 0.66 | 0.90 | 0.90 |
| 0.45 | 0.36 | 0.68 | 0.67 | 0.91 | 0.91 |
| 0.46 | 0.38 | 0.69 | 0.68 | 0.92 | 0.92 |
| 0.47 | 0.40 | 0.70 | 0.69 | 0.93 | 0.93 |
| 0.48 | 0.41 | 0.71 | 0.70 | 0.94 | 0.94 |
| 0.49 | 0.43 | 0.72 | 0.71 | 0.95 | 0.95 |
| 0.50 | 0.44 | 0.73 | 0.72 | 0.96 | 0.96 |
| 0.51 | 0.46 | 0.74 | 0.73 | 0.97 | 0.97 |
| 0.52 | 0.47 | 0.75 | 0.74 | 0.98 | 0.98 |
| 0.53 | 0.48 | 0.76 | 0.76 | 0.99 | 0.99 |
| 0.54 | 0.50 | 0.77 | 0.77 | 1.00 | 1.00 |
| 0.55 | 0.51 | 0.78 | 0.78 |
Appendix E.
Δ/R as a function of Pcunwanted for the 4I oddity paradigm
| Pcunwanted | Δ/R | Pcunwanted | Δ/R | Pcunwanted | Δ/R |
|---|---|---|---|---|---|
| 0.25 | 0.00 | 0.51 | 0.45 | 0.77 | 0.70 |
| 0.26 | 0.05 | 0.52 | 0.46 | 0.78 | 0.71 |
| 0.27 | 0.09 | 0.53 | 0.47 | 0.79 | 0.72 |
| 0.28 | 0.12 | 0.54 | 0.48 | 0.80 | 0.73 |
| 0.29 | 0.14 | 0.55 | 0.49 | 0.81 | 0.74 |
| 0.30 | 0.16 | 0.56 | 0.50 | 0.82 | 0.75 |
| 0.31 | 0.18 | 0.57 | 0.51 | 0.83 | 0.76 |
| 0.32 | 0.20 | 0.58 | 0.52 | 0.84 | 0.77 |
| 0.33 | 0.22 | 0.59 | 0.53 | 0.85 | 0.78 |
| 0.34 | 0.24 | 0.60 | 0.54 | 0.86 | 0.79 |
| 0.35 | 0.25 | 0.61 | 0.55 | 0.87 | 0.81 |
| 0.36 | 0.27 | 0.62 | 0.56 | 0.88 | 0.82 |
| 0.37 | 0.28 | 0.63 | 0.57 | 0.89 | 0.83 |
| 0.38 | 0.29 | 0.64 | 0.58 | 0.90 | 0.84 |
| 0.39 | 0.31 | 0.65 | 0.59 | 0.91 | 0.85 |
| 0.40 | 0.32 | 0.66 | 0.60 | 0.92 | 0.87 |
| 0.41 | 0.33 | 0.67 | 0.60 | 0.93 | 0.88 |
| 0.42 | 0.35 | 0.68 | 0.61 | 0.94 | 0.89 |
| 0.43 | 0.36 | 0.69 | 0.62 | 0.95 | 0.91 |
| 0.44 | 0.37 | 0.70 | 0.63 | 0.96 | 0.92 |
| 0.45 | 0.38 | 0.71 | 0.64 | 0.97 | 0.94 |
| 0.46 | 0.39 | 0.72 | 0.65 | 0.98 | 0.96 |
| 0.47 | 0.40 | 0.73 | 0.66 | 0.99 | 0.98 |
| 0.48 | 0.41 | 0.74 | 0.67 | 1.00 | 1.00 |
| 0.49 | 0.43 | 0.75 | 0.68 | ||
| 0.50 | 0.44 | 0.76 | 0.69 |
On the Use of Discrete-Uniform Roving Distributions with Few Bins
The results in Figure 1 and 2, and the tables in Appendices A to E, apply to continuous uniform roving distributions. However, in experimental studies, researchers sometimes use discrete uniform distributions with a relatively small number of levels (or “bins”) on the roving continuum. For instance, Henning (1966) used a 10-dB roving range with levels spaced 0.5 dB apart, yielding 21 possible stimulus intensities. In Jesteadt and Bilger (1974), the uniform discrete distributions used for frequency and level roving contained five bins. In pitch-discrimination experiments with complex tones in which the lowest-harmonic number has been roved, the roving distribution typically contained only two or three bins (see: Houtsma & Smurzynski, 1990; Moore, Glasberg, Flanagan et al., 2006; Oxenham et al., 2009). Therefore, it is of interest to determine how the number of bins in a uniform-discrete roving distribution influences the relationship between Pcunwanted and Δ/R. Provided that the bins of the roving distributions for the “standard” and “signal” stimuli coincide with each other within the region where the two distributions overlap, the results for discrete uniform roving distributions with n bins can be derived from the results obtained using continuous uniform distributions by replacing Δ/R with [(n−1)/n] Δ/R (Dai & Kidd, 2009). As an example, suppose that an experimenter desires to predict Pcunwanted in a same-different task for a uniform discrete distribution having a range of 2Δ, and containing three bins. The result can be obtained by, firstly, calculating [(n−1)/n] Δ/R, then, looking for the closest Δ/R value in Appendix A, and looking up the corresponding Pcunwanted. In our example, [(n−1)/n] Δ/R equals 1/3, and the Pcunwanted corresponding to the closest Δ/R value (0.3463) in Appendix A is 0.56. With a continuous roving distribution, or approximately, a distribution containing a large number of bins, the same shift of Δ/R = 1/2 would yield a Pcunwanted of about 63%. Thus, for the same roving range, performance based on unwanted cues can be limited to a lower level by using a uniform discrete roving distribution with a relatively small number of bins, compared to a discrete distribution with a larger number of bins.
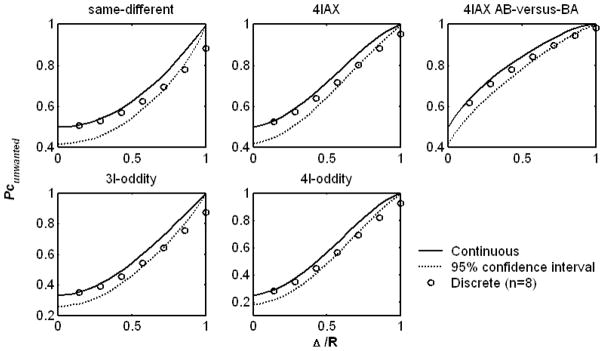
Finally, another question of practical interest to experimenters concerns the smallest number of bins that a discrete roving distribution should have, in order for its effect on Pcunwanted to be essentially indistinguishable from that achieved with a continuous roving distribution. To answer this question, we computed the lower bound of the 95% confidence interval around the Pcunwanted values shown in Figures 1 and 2, which were derived using a continuous distribution. The confidence intervals were determined under the assumption of binomial variability (i.e., no over-dispersion), and measures based on 100 trials. Pcunwanted values corresponding to discrete distributions with different number of bins were then computed, using the approach described in the previous paragraph, and these values were compared to the lower bound of the 95% confidence interval. Figure 3 shows for each paradigm (in each panel) the lower bound of the 95% confidence interval (dotted line) for the Pcunwanted function derived from a continuous distribution (solid line, re-plotted from Fig. 1 or 2), and Pcunwanted values derived from a discrete distribution with eight bins (open circles). The results are similar across all paradigms, showing that for Δ/R values of less than 0.5 (i.e., a roving range at least twice as large as the assumed size of the unwanted cue, which is typically the case in experimental studies), the Pcunwanted values from the discrete distribution (open circles) fall within the 95% confidence interval, thus are statistically indistinguishable from that achieved using a continuous roving distribution. Therefore, in limiting the effectiveness of an unwanted cue via random roving, a discrete uniform distribution is practically identical to a continuous uniform distribution, provided that the discrete distribution consists of eight or more bins. This provides a guideline for experimenters.
Figure 3.
Pcunwanted produced by a continuous roving distribution (solid dark line) and a discrete distribution with eight bins (circles) as a function of Δ/R for various psychophysical paradigms (represented by different panels). The lower bound of the 95% confidence interval around Pcunwanted values obtained using a continuous roving distribution is shown as a dotted line. The 95% confidence interval was determined based on the assumption of binomial variability, with the parameter N (number of trials) of the binomial distribution set to 100.
Application Examples
In this section, we provide two examples to illustrate how the information provided in this article can be used. The first example discusses whether the roving range in an experiment using the dual-pair paradigm was large enough to warrant ruling out the possibility that the measured discrimination thresholds were based on an unwanted cue. The second example illustrates how using Green’s (1988) formula (which was explicitly derived for the 2I-2AFC paradigm) when designing a same-different experiment can result in substantial over-estimation of the roving range needed.
Retrospective Analysis of Published Data: Was the Roving Range Large Enough?
The first example comes from a recent study of pitch perception by Semal and Demany (2006). In this study, the authors used both the 4IAX and the AB-versus-BA versions of the dual-pair paradigm in order to measure thresholds for the detection of frequency changes (4IAX), and thresholds for the identification of the direction of frequency changes (AB-versus-BA) between pure tones, in the same listeners. One of the experiments in this study sought to test hypothesis that listeners’ performance in these two tasks was based on level changes at the output of a single auditory channel (for the details of this explanation, see pp. 3910–3911 in Semal & Demany, 2006; see also: Emmerich et al., 1989; Henning, 1966; Moore & Glasberg, 1989). The level of each tone was roved over a 10 dB range (± 5 dB) around the nominal level (65 dB SPL). The authors reasoned that such roving would lead to an increase in thresholds if listeners’ performance was based on changes in level at the output of a single auditory channel.
The question, which we ask here, is: Was the 10-dB roving range used by Semal and Demany sufficient to ensure that listeners could not reliably achieve 75% of correct responses—the percent-correct level targeted by the adaptive threshold-tracking procedure—in the pitch-change detection and pitch-change direction-identification tasks, based on level changes at the output of an auditory channel? Taking into account both the nominal level of the tones (65 dB SPL), and the mean thresholds that were measured without roving the level in this experiment (about 29 cents, slightly less than 2%), the average size of excitation-level differences at the output of auditory filters in Semal and Demany’s (2006) experiment can be estimated between 2 and 3 dB on average.4 To be on the safe side, we set Δ = 3 dB. First, we consider the change-detection task, which corresponds to the 4IAX dual-pair paradigm. The table in Appendix B indicates that, for this paradigm, the value of Pcunwanted corresponding to Δ/R = 0.3 (i.e., 3 dB/10 dB) is 60%. This is well below the targeted level of 75%. Therefore, for the dual-pair change-detection (4IAX) task, we can confidently rule out the possibility that listeners’ performance was based on loudness cues alone.
Next, we consider the direction-identification task, which corresponds to the dual-pair AB-versus-BA paradigm. The table in Appendix C reveals that, for this paradigm, the same value of Δ/R = 0.3 yields a substantially higher Pcunwanted: 74%, which is practically indistinguishable from the targeted percent-correct level of 75%. Since thresholds were measured using an adaptive procedure that visited different points (both below and above the targeted proportion-correct of 75%) on the psychometric function, one cannot rule out the possibility that level cues had some influence on the threshold measurements, even with roving.
This outcome illustrates the important point that, when the same roving range is used in different experiments, which involve superficially similar stimulus designs but different underlying psychophysical paradigms, the predicted influence of roving on the proportion of correct responses can be substantially different across experiments.
On the Importance of Using the Correct Paradigm-Specific Formulas or Tables when Selecting a Roving Range
Green (1988)’ formula, which is reproduced in the Introduction of the current article, is frequently used by auditory psychophysicists to select appropriate roving ranges in their experiments. However, as mentioned above, this formula was designed specifically with the 2I-2AFC paradigm in mind. If the formula is applied in the context of experiments that use a different paradigm, it can lead to the selection of unnecessarily large roving ranges. For example, consider an experimenter who is designing a spectral-shape discrimination experiment with a same-different task. To prevent listeners from performing the task reliably on the basis of simple loudness cues, the experimenter will rove the overall level of each complex. Suppose that the experimenter determines using Green’s (1988) formula that a roving range of 30 dB is required to limit PCunwanted to 55% correct at most. The information in Figure 1 and the table in Appendix A reveals that for the same-different paradigm, in fact, a roving range of merely 5 dB is sufficient, in principle, to limit PCunwanted to 55% correct. Therefore, in this example, using Green’s (1988) formula would lead the experimenter to use a roving range about six times as large as that needed to achieve the objective. Outcomes such as this one should matter to experimenters. Unless the sensory dimensions involved are completely independent perceptually, random variations along the unwanted dimension might have detrimental effects on the processing of the primary cue—even if the unwanted cue does not provide any useful information for task performance (Ashby & Townsend, 1986; Garner, 1974). Therefore, experimenters should avoid using unnecessarily large range of rove, while ensuring that performance is safely below the level targeted in an experiment. The figures and tables in this article should help them achieve this objective.
Summary
Stimulus randomization, or “roving”, is a technique commonly used to limit the use of unwanted cues by participants in psychophysical experiments. A practical question for experimenters who use the technique is how large should the roving range be. Previous publications have provided equations for selecting adequate roving ranges in the mAFC and yes-no paradigms (Dai & Kidd, 2009; Green, 1988). In the present article, these analyses were extended to several other psychophysical paradigms, including the same-different paradigm, two versions of the dual-pair paradigm (4IAX and AB-versus-BA), as well as the 3- and 4-interval oddity paradigm. Uses of the information given in this article is subject to the same limitations as applications based on Green’s (1988) or Dai and Kidd’s (2009) formulas. In particular, they require a valid estimate, or measure, of the unwanted-cue size. If the size of unwanted cue is under-estimated, the mimimum roving range required to limit proportion-correct based on the unwanted cue to a predefined level. However, to the extent that the size of the unwanted cue can be measured, or correctly estimated, the predictions described in this article provide an upper bound on the performance that can be achieved based on the unwanted cue.
Acknowledgments
This work was supported by National Institutes of Health—National Institute on Deafness and Other Communication Disorders Grant R01 DC 05216, as well as by the University of Arizona. The authors are grateful to Dr. D. Creelman, Dr. S. Grondin, and two anonymous reviewers for constructive comments, which greatly helped improve the manuscript.
Footnotes
For instance, in a frequency discrimination task, the experimenter can try to equalize loudness. Precise loudness equalization of tones that differ in frequency by a variable amount can be very difficult to achieve in practice, due to irregularities and individual differences in equal-loudness contours (Mauermann, Long, & Kollmeier, 2004)—especially at low sound levels, or in hearing-impaired listeners (see: McDermott, Lech, Kornblum, & Irvine, 1998; Thai-Van, Micheyl, Moore, & Collet, 2003).
Numerous studies have demonstrated that random variation along an irrelevant stimulus dimension can adversely affect performance in various perceptual tasks if the irrelevant and relevant dimensions are not independent or “separable” (e.g,. Ashby & Townsend, 1986; Garner, 1974). In addition, a few studies have demonstrated detrimental effects of increasing roving range on performance or thresholds in auditory intensity- and frequency-discrimination tasks (Jesteadt & Bilger, 1974), and spectral-shape discrimination (Mason et al., 1984). It is not entirely clear whether, and to what extent, these detrimental effects were due to roving actually limiting listeners’ ability to use unwanted cues, or to the random and irrelevant variations having a “distracting” influence.
Although Lyzenga and Horst mentioned using a “3AFC” design, they instructed their listeners to select the odd stimulus. This suggests that, from the point of view of the listener, the task was essentially a form of three-interval oddity task.
This estimate is based on the formulas provided in Glasberg and Moore (1990) for calculating the shapes of auditory filters, as defined by the “rounded exponential” (roexp) function with a p value of 25, which corresponds to normal auditory filters. For such filters, a 2% frequency change on the steepest-slope side yields a change in output level of about 2-3 dB.
Contributor Information
Huanping Dai, University of Arizona.
Christophe Micheyl, University of Minnesota.
References
- Ashby FG, Townsend JT. Varieties of perceptual independence. Psychological Review. 1986;93:154–179. [PubMed] [Google Scholar]
- Berliner JE, Durlach NI. Intensity perception. IV. Resolution in roving-level discrimination. Journal of the Acoustical Society of America. 1973;53:1270–1287. doi: 10.1121/1.1913465. [DOI] [PubMed] [Google Scholar]
- Berliner JE, Durlach NI, Braida LD. Intensity perception. VII. Further data on roving-level discrimination and the resolution and bias edge effects. Journal of the Acoustical Society of America. 1977;61:1577–1585. doi: 10.1121/1.381471. [DOI] [PubMed] [Google Scholar]
- Bernstein LR, Trahiotis C. The effects of randomizing values of interaural disparities on binaural detection and on discrimination of interaural correlation. Journal of the Acoustical Society of America. 1997;102:1113–1120. doi: 10.1121/1.419863. [DOI] [PubMed] [Google Scholar]
- Bernstein LR, Trahiotis T. The effect of nonsimultaneous on-frequency and off-frequency cues on the detection of a tonal signal masked by narrow-band noise. Journal of the Acoustical Society of America. 1994;95:920–930. doi: 10.1121/1.408401. [DOI] [PubMed] [Google Scholar]
- Creelman CD, Macmillan NA. Auditory phase and frequency discrimination: A comparison of nine procedures. Journal of Experimental Psychology: Human Perception and Performance. 1979;5:146–156. doi: 10.1037//0096-1523.5.1.146. [DOI] [PubMed] [Google Scholar]
- Dai H. On suppressing unwanted cues via randomization. Perception & Psychophysics. 2008;70:1379–1382. doi: 10.3758/PP.70.7.1379. [DOI] [PubMed] [Google Scholar]
- Dai H, Green DM. Auditory intensity perception: successive versus simultaneous, across-channel discriminations. Journal of the Acoustical Society of America. 1992;91:2845–2854. doi: 10.1121/1.402965. [DOI] [PubMed] [Google Scholar]
- Dai H, Kidd G. Limiting unwanted cues via random rove applied to the yes-no and multiple-alternative forced choice paradigms. Journal of the Acoustical Society of America. 2009;126:62–67. doi: 10.1121/1.3175882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dai H, Versfeld NJ, Green DM. The optimum decision rules in the same-different paradigm. Percept & Psychophysics. 1996;58:1–9. doi: 10.3758/bf03205469. [DOI] [PubMed] [Google Scholar]
- Drennan WR, Watson CS. Sources of variation in profile analysis. II. Component spacing, dynamic changes, and roving level. Journal of the Acoustical Society of America. 2001;110:2498–2504. doi: 10.1121/1.1408311. [DOI] [PubMed] [Google Scholar]
- Durlach NI, Braida LD, Ito Y. Towards a model for discrimination of broadband signals. Journal of the Acoustical Society of America. 1986;80:63–72. doi: 10.1121/1.394084. [DOI] [PubMed] [Google Scholar]
- Emmerich DS, Ellermeier W, Butensky B. A re-examination of the frequency discrimination of random-amplitude tones, and a test of Henning’s modified energy-detector model. Journal of the Acoustical Society of America. 1989;85:1653–1659. [Google Scholar]
- Farrar CL, Reed CM, Ito Y, Durlach NI, Delhorne LA, Zurek PM, et al. Spectral-shape discrimination. I. Results from normal-hearing listeners for stationary broadband noises. Journal of the Acoustical Society of America. 1987;81:1085–1092. doi: 10.1121/1.394628. [DOI] [PubMed] [Google Scholar]
- Formby C, Muir K. Effects of randomizing signal level and duration on temporal gap detection. Audiology. 1989;28:250–257. doi: 10.3109/00206098909081630. [DOI] [PubMed] [Google Scholar]
- Forrest TG, Green DM. Detection of partially filled gaps in noise and the temporal modulation transfer function. Journal of the Acoustical Society of America. 1987;82:1933–1943. doi: 10.1121/1.395689. [DOI] [PubMed] [Google Scholar]
- Frijters JE. The paradox of discriminatory nondiscriminators resolved. Chemical Senses & Flavour. 1979a;4:355–358. [Google Scholar]
- Frijters JE. Variations of the triangular method and the relationship of its unidimensional probabilistic models to three-alternative forced-choice signal detection theory models. British Journal of Mathematical & Statistical Psychology. 1979b;32:229–241. [Google Scholar]
- Furukawa S, Moore BC. Dependence of frequency modulation detection on frequency modulation coherence across carriers: effects of modulation rate, harmonicity, and roving of the carrier frequencies. Journal of the Acoustical Society of America. 1997;101:1632–1643. doi: 10.1121/1.418147. [DOI] [PubMed] [Google Scholar]
- Garner WR. The processing of information and structure. Potomac, MD: Erlbaum; 1974. [Google Scholar]
- Geelhoed EN, MacRae AW, Ennis DM. Preference gives more consistent judgments than oddity only if the task can be modeled as forced choice. Perception & Psychophysics. 1994;55:473–477. doi: 10.3758/bf03205304. [DOI] [PubMed] [Google Scholar]
- Glasberg BR, Moore BC. Derivation of auditory filter shapes from notched-noise data. Hearing Research. 1990;47:103–138. doi: 10.1016/0378-5955(90)90170-t. [DOI] [PubMed] [Google Scholar]
- Green DM. Profile analysis. Auditory intensity discrimination. New York: Oxford University Press; 1988. [Google Scholar]
- Green DM, Swets JA. Signal Detection Theory and Psychophysics. New York: Krieger; 1966. [Google Scholar]
- Hall JW, Fernandes MA. The effect of random intensity fluctuation on monaural and binaural detection. Journal of the Acoustical Society of America. 1983;74:1200–1203. doi: 10.1121/1.390023. [DOI] [PubMed] [Google Scholar]
- Henning GB. Frequency discrimination of random amplitude tones. Journal of the Acoustical Society of America. 1966;39:336–339. doi: 10.1121/1.1909894. [DOI] [PubMed] [Google Scholar]
- Henning GB, Richards VM, Lentz JJ. The effect of diotic and dichotic level-randomization on the binaural masking-level difference. Journal of the Acoustical Society of America. 2005;118:3229–3240. doi: 10.1121/1.2047167. [DOI] [PubMed] [Google Scholar]
- Houtsma AJM, Smurzynski J. Pitch identification and discrimination for complex tones with many harmonics. Journal of the Acoustical Society of America. 1990;87:304–310. [Google Scholar]
- Irwin RJ, Hautus MJ. Likelihood-ratio decision strategy for independent observations in the same-different task: an approximation to the detection-theoretic model. Perception & Psychophysics. 1997;59:313–316. doi: 10.3758/bf03211898. [DOI] [PubMed] [Google Scholar]
- Irwin RJ, Hautus MJ, Butcher JC. An area theorem for the same-different experiment. Perception & Psychophysics. 1999;61:766–769. doi: 10.3758/bf03205544. [DOI] [PubMed] [Google Scholar]
- Kidd G, Jr, Dai H. A composite randomization procedure for measuring spectral shape discrimination. Journal of the Acoustical Society of America. 1993;94:1275–1280. doi: 10.1121/1.408153. [DOI] [PubMed] [Google Scholar]
- Kidd G, Jr, Mason CR, Brantley MA, Owen GA. Roving-level tone-in-noise detection. Journal of the Acoustical Society of America. 1989;86:1310–1317. doi: 10.1121/1.398745. [DOI] [PubMed] [Google Scholar]
- Kidd G, Jr, Mason CR, Uchanski RM, Brantley MA, Shah P. Evaluation of simple models of auditory profile analysis using random reference spectra. Journal of the Acoustical Society of America. 1991;90:1340–1354. doi: 10.1121/1.401926. [DOI] [PubMed] [Google Scholar]
- Lyzenga J, Horst JW. Frequency discrimination of bandlimited harmonic complexes related to vowel formants. Journal of the Acoustical Society of America. 1995;98:1943–1955. [Google Scholar]
- Lyzenga J, Horst JW. Frequency discrimination of stylized synthetic vowels with a single formant. Journal of the Acoustical Society of America. 1997;102:1755–1767. doi: 10.1121/1.420085. [DOI] [PubMed] [Google Scholar]
- Lyzenga J, Horst JW. Frequency discrimination of stylized synthetic vowels with two formants. Journal of the Acoustical Society of America. 1998;104:2956–2966. doi: 10.1121/1.423878. [DOI] [PubMed] [Google Scholar]
- Macmillan NA, Creelman CD. Detection theory: A user’s guide. 2. Mahwah, NJ: Erlbaum; 2005. [Google Scholar]
- Macmillan NA, Goldberg RF, Braida LD. Resolution for speech sounds: Basic sensitivity and context memory on vowel and consonant continua. Journal of the Acoustical Society of America. 1988;84:1262–1280. [Google Scholar]
- Macmillan NA, Kaplan HL, Creelman DC. The psychophysics of categorical perception. Psychological Review. 1977;84:452–471. [PubMed] [Google Scholar]
- Mason CR, Kidd G, Jr, Hanna TE, Green DM. Profile analysis and level variation. Hearing Research. 1984;13:269–275. doi: 10.1016/0378-5955(84)90080-7. [DOI] [PubMed] [Google Scholar]
- Mauermann M, Long GR, Kollmeier B. Fine structure of hearing threshold and loudness perception. Journal of the Acoustical Society of America. 2004;116:1066–1080. doi: 10.1121/1.1760106. [DOI] [PubMed] [Google Scholar]
- McDermott HJ, Lech M, Kornblum MS, Irvine DRF. Loudness perception and frequency discrimination in subjects with steeply sloping hearing loss: Possible correlates of neural plasticity. Journal of the Acoustical Society of America. 1998;104:2314–2325. doi: 10.1121/1.423744. [DOI] [PubMed] [Google Scholar]
- Micheyl C, Dai H. A general area theorem for the same-different paradigm. Perception & Psychophysics. 2008;70:761–764. doi: 10.3758/pp.70.5.761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl C, Dai H. Likelihood ratio, optimal decision rules, and relationship between proportion correct and d′ in the dual-pair AB-vs-BA identification paradigm. Perception & Psychophysics. 2009;71:1426–1433. doi: 10.3758/APP.71.6.1426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl C, Kaernbach C, Demany L. An evaluation of psychophysical models of auditory change perception. Psychological Review. 2008;115:1069–1083. doi: 10.1037/a0013572. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Micheyl C, Messing DP. Likelihood ratio, optimal decision rules, and correct response probabilities in a signal detection theoretic, equal-variance Gaussian model of the observer in the 4IAX paradigm. Perception & Psychophysics. 2006;68:725–735. doi: 10.3758/bf03193696. [DOI] [PubMed] [Google Scholar]
- Moore BC, Sek A. Discrimination of frequency glides with superimposed random glides in level. Journal of the Acoustical Society of America. 1998;104:411–421. doi: 10.1121/1.423297. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Glasberg BR. Mechanisms underlying the frequency discrimination of pulsed tones and the detection of frequency modulation. Journal of the Acoustical Society of America. 1989;86:1722–1732. [Google Scholar]
- Moore BCJ, Glasberg BR, Flanagan HJ, Adams J. Frequency discrimination of complex tones; assessing the role of component resolvability and temporal fine structure. Journal of the Acoustical Society of America. 2006;119:480–490. doi: 10.1121/1.2139070. [DOI] [PubMed] [Google Scholar]
- Moore BCJ, Glasberg BR, Low KE, Cope T, Cope W. Effects of level and frequency on the audibility of partials in inharmonic complex tones. Journal of the Acoustical Society of America. 2006;120:934–944. doi: 10.1121/1.2216906. [DOI] [PubMed] [Google Scholar]
- Noreen DL. Optimal decision rules for some common psychophysical paradigms. In: Grossberg S, editor. Mathematical psychology and psychophysiology (Proceedings of the Symposium in Applied Mathematics of the American Mathematical Society and the Society for Industrial and Applied Mathematics) Vol. 13. Providence, RI: American Mathematical Society; 1981. pp. 237–279. [Google Scholar]
- Oxenham AJ, Buus S. Level discrimination of sinusoids as a function of duration and level for fixed-level, roving-level, and across-frequency conditions. Journal of the Acoustical Society of America. 2000;107:1605–1614. doi: 10.1121/1.428445. [DOI] [PubMed] [Google Scholar]
- Oxenham AJ, Micheyl C, Keebler MV. Can temporal fine structure represent the fundamental frequency of unresolved harmonics? J Acoust Soc Am. 2009;125:2189–2199. doi: 10.1121/1.3089220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rousseau B, Ennis DM. A Thurstonian model for the dual pair (4IAX) discrimination method. Perception & Psychophysics. 2001;63:1083–1090. doi: 10.3758/bf03194526. [DOI] [PubMed] [Google Scholar]
- Rousseau B, Ennis DM. The multiple dual-pair method. Perception & Psychophysics. 2002;64:1008–1014. doi: 10.3758/bf03196803. [DOI] [PubMed] [Google Scholar]
- Semal C, Demany L. Individual differences in the sensitivity to pitch direction. Journal of the Acoustical Society of America. 2006;120:3907–3915. doi: 10.1121/1.2357708. [DOI] [PubMed] [Google Scholar]
- Spiegel MF, Picardi MC, Green DM. Signal and masker uncertainty in intensity discrimination. Journal of the Acoustical Society of America. 1981;70:1015–1019. doi: 10.1121/1.386951. [DOI] [PubMed] [Google Scholar]
- Stellmack MA, Viemeister NF, Byrne AJ. Discrimination of depth of sinusoidal amplitude modulation with and without roved carrier levels. Journal of the Acoustical Society of America. 2006;119:37–40. doi: 10.1121/1.2133576. [DOI] [PubMed] [Google Scholar]
- Thai-Van H, Micheyl C, Moore BC, Collet L. Enhanced frequency discrimination near the hearing loss cut-off: a consequence of central auditory plasticity induced by cochlear damage? Brain. 2003;126:2235–2245. doi: 10.1093/brain/awg228. [DOI] [PubMed] [Google Scholar]
- Versfeld NJ, Dai H, Green DM. The optimum decision rules for the oddity task. Perception & Psychophysics. 1996;58:10–21. doi: 10.3758/bf03205470. [DOI] [PubMed] [Google Scholar]
- Versfeld NJ, Houtsma AJ. Perception of spectral changes in multi-tone complexes. Quarterly Journal of Experimental Psychology A. 1991;43:459–479. doi: 10.1080/14640749108400982. [DOI] [PubMed] [Google Scholar]