Complex Genetic Effects in Quantitative Trait Locus Identification: A Computationally Tractable Random Model for Use in F₂ Populations

Abstract

Methodology for mapping quantitative trait loci (QTL) has focused primarily on treating the QTL as a fixed effect. These methods differ from the usual models of genetic variation that treat genetic effects as random. Computationally expensive methods that allow QTL to be treated as random have been explicitly developed for additive genetic and dominance effects. By extending these methods with a variance component method (VCM), multiple QTL can be mapped. We focused on an F₂ crossbred population derived from inbred lines and estimated effects for each individual and their corresponding marker-derived genetic covariances. We present extensions to pairwise epistatic effects, which are computationally intensive because a great many individual effects must be estimated. But by replacing individual genetic effects with average genetic effects for each marker class, genetic covariances are approximated. This substantially reduces the computational burden by reducing the dimensions of covariance matrices of genetic effects, resulting in a remarkable gain in the speed of estimating the variance components and evaluating the residual log-likelihood. Preliminary results from simulations indicate competitiveness of the reduced model with multiple-interval mapping, regression interval mapping, and VCM with individual genetic effects in its estimated QTL positions and experimental power.

MAPPING procedures often treat the effects of quantitative trait loci (QTL) as fixed, in particular the maximum likelihood-based method of interval mapping (IM) of Lander and Botstein (1989) and the least-squares regression interval mapping (RIM) of Haley and Knott (1992) and Martínez and Curnow (1992).

Single-QTL approaches with fixed effects were later extended to multiple QTL to avoid the so-called “ghost-QTL” phenomenon (e.g., Haley and Knott 1992) and to improve the power to detect linked QTL in repulsion (e.g., Kao 2000) as well as epistatic QTL (e.g., Jannink and Jansen 2001; Carlborg and Haley 2004). The multiple-interval mapping (MIM) approach of Kao and Zeng (1997) and Kao et al. (1999) as an extension of IM considers fixed additive genetic, dominance, and epistatic QTL effects as parts of the likelihood function for a mixture model in experimental populations. Both MIM and RIM are known to be powerful and well suited to identifying multiple, possibly interacting QTL in mapping experiments. However, the accuracy of the estimates of the positions and effects of the QTL from RIM is less compared with MIM in some situations [e.g., QTL in repulsion (Kao 2000; Mayer et al. 2004; Mayer 2005)].

Considering QTL effects as random in a linear mixed model (LMM) leads to the variance component method (VCM) for QTL mapping. This is often applied in scenarios with a large number of small families as is frequently found in humans (e.g., Haseman and Elston 1972; Xu and Atchley 1995) or in livestock (e.g., Grignola et al. 1996), where a mixture of families with parents of different QTL genotypes is expected to occur. Experiments with multiple line crosses, e.g., F₂, are often advocated because of their potential to avoid nondetection of QTL by representing genetic variability of a population by only a few lines—the so-called “genetic drift error” (Xu 1996). Although fixed effect approaches are equivalent in power, at least in situations with a single QTL, VCM are easier to implement and have computational advantages in this context (Xu 1998). Rules for setting up the required QTL allelic relationship matrices from marker data were given by Wang et al. (1995) and Abdel-Azim and Freeman (2001). Marker-based relationship matrices for QTL with additive genetic and nonadditive genetic (dominance, epistasis) gene action in noninbred populations were applied by Liu et al. (2002).

The focus of Xie et al. (1998) was on backcross (BC) and F₂ designs descending from inbred lines. For these types of experiments additive genetic and dominance relationship matrices can be calculated from conditional QTL genotype probabilities (given the flanking marker genotypes) for all individuals of the mapping population (as used as regressor variables in RIM). Crepieux et al. (2004) provided a general extension to any type of multicross designs from inbred parents. Furthermore, Li and Cui (2009) demonstrated how VCM can be employed for mapping imprinted QTL in a combination of different BC populations derived from inbred lines.

In this article we first propose extensions of the variance component approach of Xie et al. (1998) to multiple interacting QTL with pairwise epistatic effects. Then, maintaining the focus on inbred line-derived F₂ populations, a reduced model is suggested, in which individual genetic effects are replaced by average genetic effects for different marker classes. The covariance matrix of the phenotypes is approximated in different ways, leading to less computational effort.

THEORY

Linear mixed model:

From an F₂ generation derived from a cross between inbred lines, one observation per individual is considered. The vector of phenotypes Y (length n) is modeled with respect to additive genetic, dominance, and pairwise epistatic effects of the QTL, whose total number is ν. A pair of QTL is indexed by l and k. The LMM in matrix notation is given as

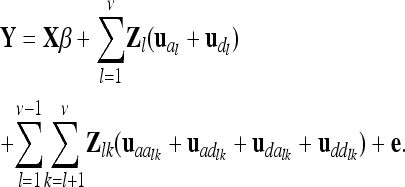(1)

The vector of fixed effects β has the related design matrix X. The random vectors u_τ with τ ∈ {a_l, d_l, aa_lk, ad_lk, da_lk, da_lk} denote the additive genetic, the dominance, and the four pairwise epistatic effects (first-order interactions) at QTL l and k. For each τ the length of u_τ equals the number of F₂ individuals n; i.e., all QTL effects differ between individuals. The incidence matrices Z_l and Z_lk with dim(Z_l) = dim(Z_lk) = n × n relate the observations to genetic effects. The residuals are assumed to be independently and identically normally distributed with 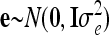, where I is the identity matrix of order n and 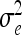is the residual variance. The covariances between normally distributed random genetic effects u_τ and the residuals e are assumed zero as well as the covariances between different types of genetic effects u_τ. The expectations of the QTL effects are E(u_τ) = 0 and the variances are 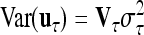, where 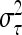is the related QTL variance and V_τ is the corresponding expected QTL relationship matrix conditional on the marker genotypes. The phenotypic vector therefore follows a multivariate normal distribution with Y ∼ N (Xβ, V ). The covariance matrix V is derived conditional on the observed marker genotypes and can be written as

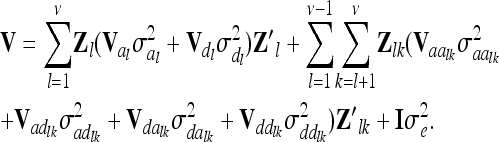(2)

Calculation of covariance matrices:

We follow the approach of Xie et al. (1998) and derive the required genetic covariance matrices of (2) from conditional QTL genotype probabilities and elementary covariance matrices.

Conditional QTL genotype probabilities:

For a particular QTL the F₂ generation can be partitioned into nine different marker classes (see Table 2 column headings) conditional on the observed genotype of the flanking markers. QTL alleles originating from the first line are denoted by uppercase letter indexes (Q, H) and those from the second line by lowercase indexes (q, h), and for marker alleles the respective line origins are indicated by numbers (1 and 2). Conditional QTL genotype probabilities depend on flanking marker genotypes and the recombination rates between the markers and QTL and can be derived as described by, e.g., Carbonell et al. (1992, Table 1). We allow for double recombinations and assume Haldane's mapping function (Haldane 1919).

TABLE 2.

Covariances miial of additive genetic sampling effects within marker class i for different numbers (n) of F2 individuals: QTL in the middle of a 10-cM marker interval

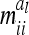	i = 1:	i = 2:	i = 3:	i = 4:	i = 5:	i = 6:	i = 7:	i = 8:	i = 9:
n	G11/11	G11/12	G11/22	G12/11	G12/12	G12/22	G22/11	G22/12	G22/22
500	0.000	−0.012	−0.487	−0.012	0.000	−0.012	−0.487	−0.012	0.000
1000	0.000	−0.006	−0.243	−0.006	0.000	−0.006	−0.243	−0.006	0.000
2000	0.000	−0.003	−0.122	−0.003	0.000	−0.003	−0.122	−0.003	0.000
3000	0.000	−0.002	−0.081	−0.002	0.000	−0.002	−0.081	−0.002	0.000

Flanking marker genotypes G_·/· are indexed by their alleles for each i.

TABLE 1.

Correspondence of elements of additive genetic relationship matrices in the individual model and the equivalent model with additive genetic sampling effects

Case	Individual model	Equivalent model
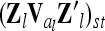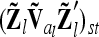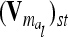1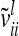
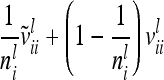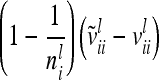2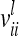
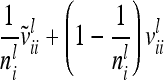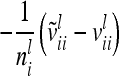3		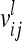	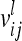0

Each variable in the second column (individual model) is the sum from the two expressions of the third and fourth columns (equivalent model). Case 1: diagonal elements for marker class i ∈ {1,…,9}; case 2: two individuals with equal marker class i; case 3: two individuals with different marker classes i and j

Probabilities for the genotypes G_QQ, G_Qq, and G_qq of an individual at the lth QTL conditional on flanking marker information M_i can be collected in a row vector 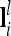with

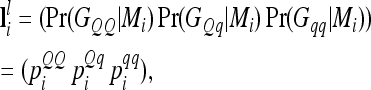where M_i denotes the observed flanking marker genotype i ∈ {1,…, 9} of an individual. We assume that in each marker interval either no or only a single QTL exists. The joint conditional probability for two linked QTL is just the product of both single probabilities if at least one completely informative marker is in between (Rönnegård et al. 2008). Thus, the probability of a two-locus QTL genotype, e.g. G_QQHh, given the particular marker genotypes M_i and N_j (i, j ∈ {1,…, 9}) at QTL l and k, respectively, is defined as Pr(G_QQHh|M_i,N_j) = Pr(G_QQ|M_i)Pr(G_Hh|N_j). We define 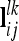as the row vector with all joint conditional QTL genotype probabilities for a pairwise epistatic effect at QTL l and k.

Elementary covariance matrices:

As a second ingredient we need elementary covariance matrices between all possible QTL genotypes G_QQ, G_Qq, and G_qq in the F₂ populations. The elementary matrices for additive genetic QTL effects A (Xie et al. 1998) and dominance QTL effects D (Smith 1984; Xie et al. 1998) are

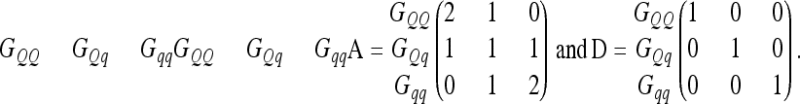We use the Kronecker product (symbol ⊗) of A and D to compute the four different 9 × 9 elementary matrices, A ⊗ A, A ⊗ D, D ⊗ A, and D ⊗ D, which include covariances between pairwise epistatic effects and correspond to nine genotypes (G_QQHH, G_QQHh, G_QQhh, G_QqHH, G_QqHh, G_Qqhh, G_qqHH, G_qqHh, and G_qqhh) for pairwise QTL combinations.

QTL relationship matrices:

The n × n additive genetic, dominance, and pairwise epistatic relationship matrices for all F₂ individuals can be set up for a putative QTL position or combinations thereof with conditional QTL genotype probabilities (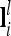 and 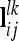vectors) and elementary matrices (Xie et al. 1998). Relationship coefficients are averages of possible QTL genotype combinations. For the additive genetic relationship matrix 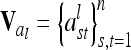we get diagonal elements

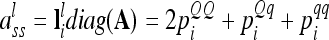(3)

and off-diagonals

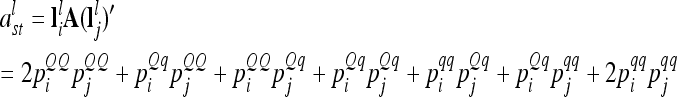(4)

at the lth QTL. If both individuals s and t belong to the same marker class i, then 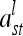can be simplified to

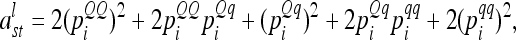(5)

because the conditional probabilities are equal. The dominance relationship matrix 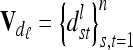is set up equivalently, but instead of A the elementary matrix D is used, i.e., 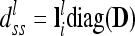and .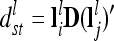

We suggest that the pairwise epistatic relationship matrices 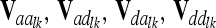at the lth and kth QTL are computed analogously to V_al using the appropriate Kronecker product of elementary matrices (e.g., A ⊗ A). Computation of matrix elements is done as in Equations 3 and 4, employing corresponding row vectors 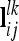. Note that this is equivalent to using Hadamard products of QTL relationship matrices 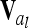and 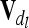given that there is at least one completely informative marker between both QTL or no linkage between them (Rönnegård et al. 2008), which is always fulfilled by our assumptions. To ensure positive definiteness of covariance matrices, we assume that locations of putative QTL and markers do not coincide.

Equivalent model with average genetic effects:

What we have outlined so far is termed “individual model,” because each individual receives its own genetic effects for the different kinds of genetic components. For a particular QTL l the LMM of (1) with only additive genetic effects becomes

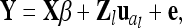(6)

with covariance matrix of the phenotypes conditional on the observed marker genotypes

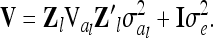(7)

A model equivalent to (6) is

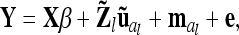(8)

where a vector 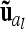with length n_l = 9 (number of different marker classes) of average additive genetic effects for all possible marker genotype classes is considered. An additional random effect of length n appears, termed “additive genetic sampling effect,” and it describes the deviations of the individual additive genetic effects from the average additive genetic effects of marker classes. The dimension of 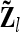is n × n_l. Accordingly, the covariance matrix of the phenotypes can be expressed as

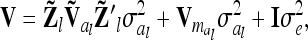(9)

where 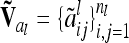denotes the reduced n_l × n_l relationship matrix of the average additive genetic effects at the QTL. The additive genetic variance of the individual model (7) is 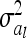, which is identical to 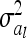in (9). The variance of the additive genetic sampling effect is 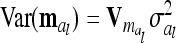, where 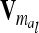denotes the relationship matrix of the additive genetic sampling effect. There are 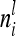individuals with the same marker genotype i at the QTL. The variance of the average additive genetic effect of a certain marker class i, averaged over 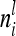individuals, is given in the reduced model as

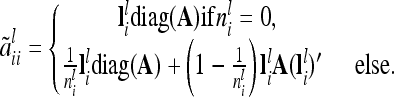(10)

Equation 10 is valid, because there are 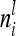diagonal elements and 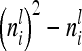off-diagonal elements in the relationship matrix of the individual additive genetic effects.

The three possible cases appearing in the additive genetic relationship matrix of the individual model are further investigated (see Equations 3–5). First, the variance of an individual additive genetic effect with marker class i is 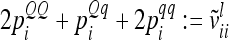and second, the covariance between two additive genetic effects with the same marker class i is 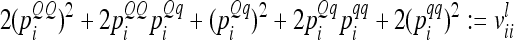. Then the element 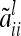for 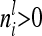can be written as

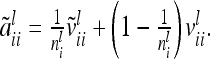(11)

The variance of the average additive genetic effect is asymptotically equal to the covariance between individual additive genetic effects of the same marker class i; i.e., 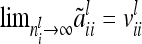. Third, the covariance of additive genetic effects with marker classes i and j is 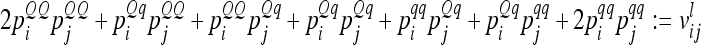. Now, the covariance of the average additive genetic effects of marker genotypes i and j (i ≠ j) can be expressed as

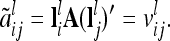(12)

This is equal to the covariance among the two individual additive genetic effects of marker classes i and j.

The relationship matrix of the additive genetic sampling effects 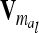can be determined as the difference between the relationship matrices of additive genetic effects from the individual model (individual genetic effects) and the reduced model (average genetic effects), which are inferred from Equations 7 and 9; i.e., 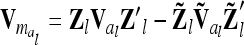. Generally, 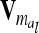(order n) can be written as

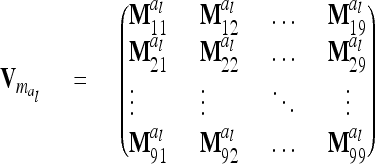(13)

if the individuals are arranged by marker class. To study the matrices 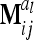we assume that each marker genotype appears at least once; i.e., .

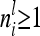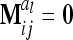Concerning the third case, the additive genetic covariance between a pair of individuals s and t with different marker genotypes i and j equals the difference of (4) and (12): . Therefore, for i ≠ j in (13) and 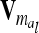is a block diagonal matrix if the observations are ordered by marker genotypes. The diagonal block 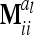corresponding to marker class i has the order 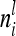and can be expressed as

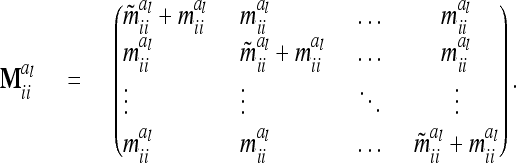The covariance 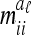of the additive genetic sampling effects of two individuals s and t given the same marker genotype i (second case) is the difference of (5) and (11):

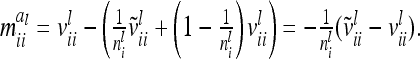(14)

For 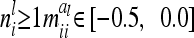. The variance 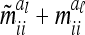of the additive genetic sampling effect given the marker genotype i (first case) is the difference of (3) and (11),

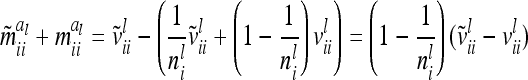(15)

with 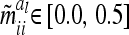. Note that the elements 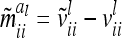are independent of 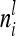. However, 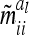and 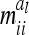depend on conditional genotype probabilities. From (14) and (15) it is obvious that 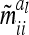is a function of the covariance of the additive genetic sampling effects from the same marker class i and the corresponding number 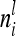of observations, .

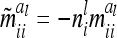The calculation of the relationship matrix of the additive genetic effect of the individual model (6) and the reduced model (8) as well as the additive genetic sampling relationship matrix 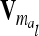is summarized in Table 1.

If model (6) includes not only additive genetic but also dominance effects, the genetic parameters for average dominance effects and dominance sampling terms can be obtained analogously. The genetic sampling relationship matrices of the pairwise epistatic effects can also be calculated similarly to the additive genetic and dominance effects, but the row vectors 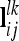that considered the joint conditional QTL genotype probabilities of the lth and kth QTL have to be used. Then n_lk different marker classes have to be considered, where n_lk = 27 if the QTL are in two adjacent marker intervals and n_lk = 81 otherwise.

If we assume that the number of F₂ individuals approaches infinity (n → ∞), then the number of individuals per marker class i also increases 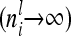. The diagonal elements 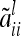as well as 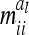depend on 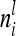, where 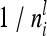tends to zero for n → ∞. Hence lim_ni^l→∞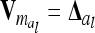, where 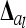is a diagonal matrix of order n of elements 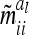. Therefore, the covariance matrix of the additive genetic sampling effects is asymptotically diagonal.

Reduced model:

Instead of an individual model we developed a reduced model approach, which is an approximation of model (8), with decreased dimension of the relationship matrices. The LMM is 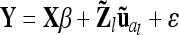, where the residuals are assumed to be independently and identically normally distributed with 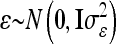. Here the F₂ individuals are grouped according to their marker genotypes and average genetic effects are estimated for marker classes instead of individual genetic effects, as described in (8). The dimension of the relationship matrices depends on the number of marker classes (n_l and n_lk), but not on the experiment size n. We call this procedure the reduced model (vs. the individual model).

In general, the reduced model with respect to additive genetic, dominance, and pairwise epistatic effects is

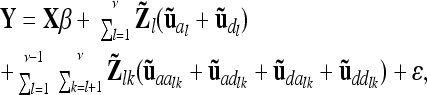(16)

where the residuals are again assumed to be independently and identically normally distributed with 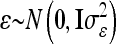. The vectors 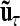with 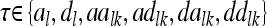consider the average additive genetic, dominance, and pairwise epistatic effects of length n_l and n_lk.

The calculation of the reduced dominance relationship matrix 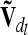at the lth QTL is done similarly to the notes above, but A has to be replaced by D. Both 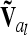and 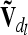are matrices of order n_l, where n_l = 9 if the flanking markers are fully informative. The reduced epistatic relationship matrices 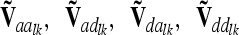of the lth and kth QTL are computed analogously to 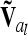from (10) and (12), but the corresponding Kronecker product is used instead of A and the row vector 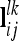for the ith and jth marker class is applied.

The difference 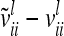(asymptotic variance 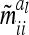) between the variance of an individual additive genetic effect and the covariance between two additive genetic effects of the same marker class decreases as the distance between flanking markers becomes smaller. Decreasing QTL effects and genetic variances lead to the same effect. In the extreme case, when the marker location and the position of the QTL coincide, the difference 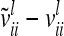is zero and therefore 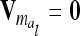. In this case the covariances of the phenotypes in the reduced and the individual model are identical. Therefore, approximating 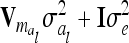(or its multilocus equivalent) by 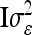seems to be a reasonable choice. Note that Xu and Atchley (1995) and Xu (1998) investigated the inflation of the residual variance through the within-marker genotype QTL variance in the RIM, which is similar to our genetic sampling effects.

The approximation of the individual model by the reduced model relies on two different aspects. First, the covariances between genetic sampling effects (deviation of individual genetic effects from average genetic effects of marker classes) are assumed to be zero. Second, the asymptotic variances 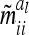of the additive genetic sampling effects are treated as equal for all marker classes. Covariances 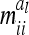between additive genetic sampling effects of individuals sharing the same marker class i are shown in Table 2 for an additive QTL in the middle of a 10-cM marker interval in dependence on sample size. The elements 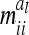were calculated using the number of expected proportions for each marker genotype according to Equation 14. To make sure that 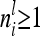, we used n ≥ 500. For 500 F₂ individuals this covariance 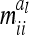is ≤1% of the QTL variance and shows a further decline when the sample size increases. Only for marker classes G_11/22 and G_22/11 is there a very high (negative) covariance (48.7% of the additive genetic variance) and an experiment with >2000 F₂ individuals would be required to reach a value <10%. These marker genotypes are rare, we expect these marker genotypes to occur twice in total among 500 F₂ genotypes. Therefore, omitting these covariances 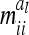has little effect on the likelihood.

The asymptotic variances 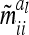of the additive genetic sampling effects for different marker classes are, however, larger than their corresponding covariances and, more importantly, they show considerable variation between more frequent marker classes. The sixth line of Table 3 shows the genetic sampling variances for all marker classes, again for an additive QTL in the middle of a 10-cM marker interval. For the three most frequent marker classes, the genetic sampling variance is at ≤1% of the additive genetic variance (classes 1, 5, and 9) and for another four marker classes it equals 25% (classes 2, 4, 6, and 8), while a 50% value occurs only in the very rare classes (3 and 7). Note that the genetic sampling variances become smaller when the QTL is located closer to the boundary of the marker interval. The genetic sampling effects completely vanish if marker locations and positions of the QTL coincide (Table 3, first line). In such cases, the covariances of the genetic sampling effects are zero and the assumption 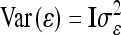of the reduced model (16) is exact.

TABLE 3.

Asymptotic variances m̃iial of additive genetic sampling effects within marker class i for differently sized marker intervals and different QTL positions within marker intervals (cM)

Marker interval	Position of QTL
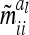		i = 1	i = 2	i = 3	i = 4	i = 5	i = 6	i = 7	i = 8	i = 9
0	0	0.00				0.00				0.00
10	1	0.00	0.09	0.18	0.09	0.00	0.09	0.18	0.09	0.00
10	2	0.00	0.16	0.32	0.16	0.01	0.16	0.32	0.16	0.00
10	3	0.00	0.21	0.42	0.21	0.01	0.21	0.42	0.21	0.00
10	4	0.00	0.24	0.48	0.24	0.01	0.24	0.48	0.24	0.00
10	5	0.00	0.25	0.50	0.25	0.01	0.25	0.50	0.25	0.00
20	10	0.02	0.26	0.50	0.26	0.04	0.26	0.50	0.26	0.02
30	15	0.04	0.27	0.50	0.27	0.08	0.27	0.50	0.27	0.04
40	20	0.07	0.29	0.50	0.29	0.13	0.29	0.50	0.29	0.07

The latter considerations suggest, as a further alternative, a weighted approach, where the second part of the approximation inherent in the reduced model, i.e., equal genetic sampling variances for all marker classes, is skipped, while the assumption (first part) of zero covariances for genetic sampling effects within marker class is maintained. For a single additive QTL this results in the following mixed model equations (MME):

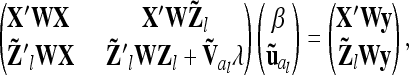where 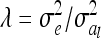. The variance of the residuals is 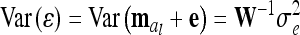, where 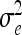is defined as in (8) and all other symbols as in (1) and (16). The diagonal matrix W of order n has the entries 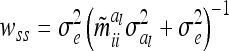, which differ between observations from different marker classes and are equal for observations from the same marker class i. If more QTL and nonadditive genetic gene actions are considered in the model, then the genetic sampling variances for different QTL and different kinds τ of genetic effects have to be summed to get the entire genetic sampling variance of an observation and w_ss (sth individual given the marker class i) becomes

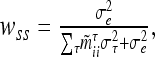(17)

where τ ∈ {a_l, d_l, aa_lk, ad_lk, da_lk, dd_lk}. This weighted version of the reduced model retains the advantage of a reduced dimension of the QTL relationship matrices as in the reduced model, but may provide a better approximation of the exact residual log-likelihood-ratio test (RLRT) statistics. If marker location and position of QTL coincide, the weights of (17) are one and W is an identity matrix. The weights of (17) are similar to the weights in the weighted least-squares method of QTL mapping as shown by Xu and Atchley (1995) and Xu (1998).

Coincidence of markers and QTL results in singularity of 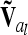(identical to A in this case) and was not further considered here. However, this situation can be treated, e.g., by regularization [adding a small quantity to the diagonal elements of 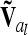(Neumaier 1998)], which has little effect on the test statistics and is easy to implement, by including allelic effects in the model instead of genotypic effects, or by replacing 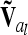by a reduced rank approximation (Rönnegård et al. 2007) obtained by spectral decomposition.

SIMULATIONS

First, a single F₂ family as the simplest case of a combination of multiple line crosses was considered to demonstrate the properties of the reduced model in comparison to the individual model (Xie et al. 1998) and the fixed-effects methods MIM (Kao and Zeng 1997; Kao et al. 1999) and RIM (Haley and Knott 1992; Martínez and Curnow 1992). Experiments from four different scenarios were simulated with 1000 replications per scenario and n = 200 F₂ individuals per experiment. Scenarios 1 and 2 consisted of a single additive genetic QTL at 35 cM on a single chromosome of 50 cM length, whereas in the other scenarios (3 and 4) there were two linked QTL with equally sized QTL effects in repulsion. In the fourth scenario chromosome length was extended to 80 cM and an interaction effect was included. For further characteristics of all scenarios see Table 4. The observations were simulated using Cockerham's F₂-metric model (Cockerham 1954; Kao and Zeng 2002, Table 3). The relative QTL variance R² is the proportion of the phenotypic variance 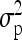explained by the QTL and is .

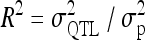TABLE 4.

Brief summary of simulated scenarios: the number of QTL ν, length of the chromosome lc (cM), QTL positions P1 and P2 (cM), marker positions (cM), residual variance σe2, additive genetic effects (a1, a2), and additive-by-additive genetic effects aa12 as well as the relative QTL variance R2 (%)

Scenario	ν	lc	P1	P2	Marker positions		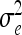a1	a2	aa12	R2
1	1	50	35	—	0, 10, 20, 30, 40, 50	9.529	1.0	—	—	5.0
2	1	50	35	—	0, 10, 20, 30, 40, 50	1.000	1.0	—	—	33.3
3	2	50	25	35	0, 10, 20, 30, 40, 50	0.181	1.0	−1.0	—	50.0
4	2	80	35	45	0, 40, 80	1.000	1.0	−1.0	1.0	30.0

In the second part our small simulation study focused on the performance of the reduced vs. the individual model in a situation with multiple families. Four independent F₂ families, each with 50 progeny (n = 200), were derived from a population consisting of four different inbred lines, representing all pairwise combinations of QTL genotypes (G_QQHH, G_QQhh, G_qqHH, G_qqhh). For each family F₁ individuals were generated from a random pair of inbred lines. Markers were always assumed to be fully informative. In the LMM family means were treated as fixed. Remaining parameters were chosen as previously described for the third scenario (Table 4). For each genetic effect a single (population-specific) variance was assumed. The simulated data can be found in File S1.

Significance thresholds for the null hypothesis of no linked QTL were determined by simulating 1000 experiments of the same size for each scenario, where QTL with the same kind and size of effects were present, but unlinked to the markers. After analyzing these experiments, the 95% quantile of the maximum values of the test statistic from all replications was taken as a significance threshold, specific for each scenario and method, which allowed the determination of experimental power. We performed the residual log-likelihood-ratio test for the reduced and the individual model, the log-likelihood-ratio test for MIM, and the F-test for RIM. Mean QTL positions, root mean squared error (RMSE) of the QTL positions, and their 5% and 95% quantiles were evaluated to characterize the precision of location estimates. For each replication we analyzed positions or combinations thereof, where marker locations and QTL positions did not coincide (step width 1 cM, both QTL in different marker intervals). Therefore, we applied RIM and MIM with the same restrictions as the VCM. Our analyses used the true genetic model for testing for segregating QTL; i.e., the model included only the simulated effects of QTL and no model selection was performed. All calculations were done with self-written Fortran 95 programs in combination with ASReml (Gilmour et al. 2008) for estimation of variance components and evaluation of the restricted maximum-likelihood function (Patterson and Thompson 1971).

DISCUSSION

Results for all simulated single-QTL scenarios are summarized in Table 5. The experimental power was 100% (scenarios 2 and 3) or nearly so (scenario 4), with the exception of scenario 1, where the experimental power was uniformly at 82% for all methods. There was almost no variation between methods in the mean estimated position in the single-QTL scenarios (1 and 2); even the distributions of the estimates showed identical 5% and 95% quantiles. Differences between methods became, however, apparent in the two-QTL scenarios. For scenario 3 (two QTL in repulsion, no interactions), MIM resulted in average estimated QTL positions at 24.7 and 34.9 cM, nearly identical to the simulated values at 25 and 35 cM. The RMSEs for positions of the QTL were <1.4 cM for both QTL for MIM and ∼2.0 cM for the individual model, while the reduced model and RIM performed very similarly with RMSEs of ∼4.2 cM. In scenario 3 the reduced model, the individual model, and RIM on average placed the QTL somewhat more toward the ends of the chromosome compared to MIM and the true values, resulting in an overestimation of the distance (true distance: 10 cM) between both QTL, ranging from 2.7 cM (individual model) to 6.7 cM (reduced model). For scenario 4 (two QTL in repulsion with interactions) this overestimation of the distance between the QTL was, however, very similar for all methods at ∼2.0–3.1 cM. The RMSEs for estimated positions of the QTL were between 5.3 and 5.6 cM with little difference between the first and second QTL for RIM as well as the reduced and the individual model. However, the RMSE of MIM at the same time showed the highest deviation of 6.5 cM for the first and the smallest deviation of 3.7 cM for the second QTL.

TABLE 5.

Average estimates (mean) for QTL positions (P1, P2) with associated root mean squared error (RMSE) and quantiles together with mean estimates of the residual variance σ̂r2 and the observed power (%) for different scenarios: 200 F2 individuals per simulated experiment and 1000 replications per scenario

	Reduced model		Individual model		RIM		MIM
	P1	P2	P1	P2	P1	P2	P1	P2
Scenario 1
Mean	32.58		32.53		32.73		32.40
RMSE	10.71		10.79		10.78		10.89
5% quantile	9.00		9.00		9.00		9.00
95% quantile	48.00		48.00		48.00		48.00
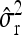	9.49		9.38		9.50		9.37
Power	81.70		81.80		81.70		81.90
Scenario 2
Mean	34.82		34.87		34.88		34.68
RMSE	2.80		2.66		2.68		2.57
5% quantile	31.00		31.00		31.00		31.00
95% quantile	39.00		39.00		39.00		39.00
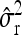	1.04		0.99		1.04		0.99
Power	100.00		100.00		100.00		100.00
Scenario 3
Mean	21.67	38.38	23.70	36.70	22.22	37.82	24.70	34.89
RMSE	4.20	4.17	2.03	2.02	4.29	4.25	1.35	1.38
5% quantile	17.00	35.00	22.00	34.00	17.00	32.00	23.00	33.00
95% quantile	25.00	42.00	26.00	38.00	28.00	42.00	27.00	37.00
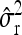	0.27		0.18		0.28		0.19
Power	100.00		100.00		100.00		100.00
Scenario 4
Mean	34.03	46.22	33.56	46.70	34.13	46.09	32.29	44.44
RMSE	5.36	5.50	5.26	5.47	5.51	5.55	6.47	3.72
5% quantile	24.50	41.00	24.00	41.00	24.00	41.00	21.00	41.00
95% quantile	39.00	56.50	39.00	57.00	39.00	57.00	39.00	52.00
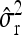	1.21		0.93		1.23		1.04
Power	99.20		99.40		99.60		100.00

Note that MIM was applied according to the original approach of Kao and Zeng (1997) and Kao et al. (1999), which ignores double recombination events (complete interference) within the marker interval. However, double recombinations were taken into account for RIM and the VCM.

As theory indicated, estimated residual variance components from methods coping better with genetic deviations from the mean of a marker class (MIM, individual model) were smaller in the two-QTL scenarios compared to RIM and the reduced model, where the genetic sampling variance (QTL genotype variability within marker genotype) is part of the residual variance.

The results of the analysis of the multiple families are shown in Table 6. The accuracy of the estimated QTL positions of the individual model under consideration of four families was slightly better than that of the reduced model. However, when multiple families were considered, the difference between both models (reduced and individual model) was less than that of the single family (scenario 3). The RMSEs for positions of the QTL as shown in Table 6 were increased compared to the RMSEs of the third scenario of Table 5, because not all families are fully informative. The observed power of the individual and the reduced model again almost reached 100%. As expected, the estimated residual variance was inflated by the within-marker genotype QTL variance.

TABLE 6.

Average estimates (mean) for QTL positions (P1, P2) with associated root mean squared error (RMSE) and quantiles together with mean estimates of the residual variance σ̂r2 and the observed power (%) for the third scenario with 50 F2 individuals for each of the four families per simulated experiment (1000 replications per scenario)

	Reduced model		Individual model
	P1	P2	P1	P2
Mean	22.38	35.99	23.00	35.59
RMSE	6.77	4.78	6.26	4.27
5% quantile	8.00	28.00	9.00	28.00
95% quantile	28.00	45.00	28.00	44.00
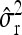	0.21		0.18
Power	99.50		99.60

The required CPU time for ASREML (Gilmour et al. 2008) of the reduced and the individual model was 26.7 and 80.1 sec for each repetition recorded on an HP DL380 G6 (72 GB RAM, 2× XEON X5570, 2.93 GHz, multiuser environment) in a two-QTL scenario with only additive genetic effects (four families); i.e., the individual model required threefold more computing time. The run time required for the evaluation of a single QTL (scenario 1 or 2) was sevenfold for the individual model compared with the reduced model for each repetition. If the number of individuals and the number of variance components increase, the speed gain of the reduced model relative to the individual model is expected to increase.

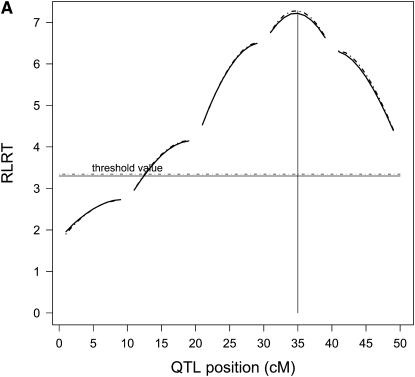
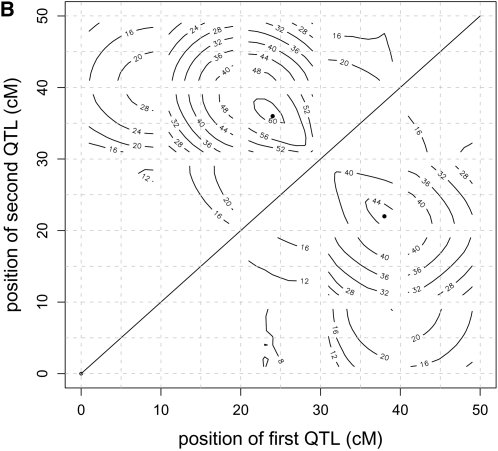
Average RLRT profiles from the reduced and the individual model were almost identical for the first scenario with a single QTL (Figure 1A). For two QTL in scenario 3 (Figure 1B), the shapes of the RLRT surfaces from both methods were again very similar, but the average size of the maximum was higher for the individual model (60.62 compared to 44.52). The RLRT surfaces of scenario 4 of the reduced and the individual model as well as the weighted reduced model are nearly identical (results not shown). The likelihood profile of the weighted approach was smaller than that of the reduced model, but QTL positions seemed to be estimated more accurately.

Figure 1.—

For a single QTL (scenario 1) average RLRT profiles (A) of the individual model (dashed line) and the reduced model (solid line) nearly coincide, and so do their significance thresholds. When two QTL were present (scenario 3), contour plots (B) of the RLRT surfaces from the reduced model (below diagonal) and the individual model (above diagonal) showed a similar shape, but different absolute heights (respective RLRT maxima 44.52 and 60.62). Averaging was over 1000 replications.

The considerable advantage of the reduced model with respect to computing time is achieved by a smaller number of genetic effects accompanied by a smaller dimension of their associated covariance matrices. Moreover, this dimension does not depend on the size of the experiment, in contrast to the individual model. The amount of savable computing time can be expected to vary somewhat between different REML algorithms. Average information (AI) REML (Gilmour et al. 1995; Johnson and Thompson 1995) may be implemented either in an MME-based version or as a variant requiring the inversion of the covariance matrix V of phenotypes, termed the “direct method” by Lee and Van Der Werf (2006). These authors recommend the direct method if genetic covariance matrices are dense because of both speed and numerical stability. Application of the Sherman–Morrison–Woodbury matrix identity (e.g., Henderson and Searle 1981; Xu 1998) to determine the inverse of V results in

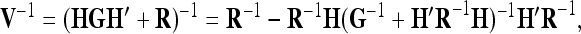where R denotes the covariance matrix of residuals, G is the covariance matrix of all genetic effects (block diagonal), and H is the corresponding incidence matrix. To obtain V⁻¹ the inversion of a dense matrix of the same order as G is required, which usually is considerably smaller than the number of observations for the reduced model (e.g., dim(G) = 9 × 9 for a single QTL with additive genetic effects and dim(G) = 36 × 36 for two QTL with additive genetic and dominant effects). In conclusion, the increase in computing speed obtained by the reduced model may differ between algorithms, but is substantial when compared with the individual model, thus broadening the general applicability of the VCM for mapping purposes.

The amount of possible improvement of the reduced model obtained by accounting for genetic sampling variation within marker classes remains to be investigated. A more comprehensive comparison of methods than presented here is underway to obtain a more complete picture. Despite the limited number of scenarios in our simulations, it can already be concluded that the proposed reduced model may be competitive with other standard methods for mapping of (multiple) QTL not only in terms of computing time, but also in terms of detection power and precision of estimated positions of the QTL.