Groupwise Registration with Sharp Mean

Abstract

Groupwise registration has received more and more attention in the area of medical image analysis, due to its importance in analysis of population data. One popular way for groupwise registration is to alternatively estimate the group mean image and register all subject images to the estimated group mean. However, for achieving better registration performance, it is important to always keep the sharpness of the group mean image during the registration, which has not been well investigated yet in the literature. To achieve this, we propose to treat each aligned subject, as well as its anatomical regions, differently when constructing the group mean image. Specifically, we propose a new objective function to generalize the conventional groupwise registration method by using a dynamic weighting strategy to weight adaptively across subjects and spatial regions, to construct a sharp group mean image in each stage of registration. By integrating this strategy into diffeomorphic demons algorithm, the performance of our groupwise registration can be significantly improved, compared to the conventional groupwise registration method that starts with a fuzzy group mean image.

1 Introduction

Groupwise registration becomes more and more popular in recent years due to its attractiveness in analyzing population data [1, 2]. Compared to the traditional pairwise registration algorithm, groupwise registration aims to simultaneously estimate the transformation fields for all subjects without explicitly specifying an individual subject as a template, in order to avoid any bias in the subsequent data analysis.

One of the most popular groupwise registrations is proposed by Joshi et al. [1] in 2004. In their method, the groupwise registration is implemented by alternatively constructing the group mean image and estimating the transformation fields of all subjects towards the tentative group mean. However, one major drawback of this method is that it usually produces a very fuzzy group mean image in the beginning, due to the simple averaging of all subjects that are not well aligned initially. As a result, the fuzzy group mean image fails to offer the correct guidance to the subsequent pairwise registrations as we can see in the experiments. Thus the anatomical details can hardly be recovered from the initial fuzzy group mean image due to the difficulty of establishing the reliable correspondences between sharp subject images and the fuzzy group mean image during the iterative registration procedure.

Recently, Fletcher et al. [2] extended Joshi’s method to the Riemannian manifold and proposed to use the geometric mean of the group to handle the possible outliers which may deviate the Fréchet mean far away from the real population center. However, they used an equal weight for each subject in the group to compute the geometric mean. Also, the importance of the sharpness of the mean image in groupwise registration is not addressed.

Another interesting related work is the tree-based groupwise registration [3]. In their method, the pseudo-geodesic median image is selected as the root template after learning the intrinsic manifold on the whole data set. Since a fixed image (i.e., the root image) is used as the final template to register all other subjects, the bias is inevitably introduced in this scenario due to the discrepancy between the template and the real population center, although in this case a sharp individual image is used as the template to guide the groupwise registration.

We propose to improve the performance of groupwise registration methods that focus on iteratively registering subjects to the group mean image [1, 3, 4]. We will first point out the importance of always keeping a sharp mean image during the groupwise registration. Second, we generalize the conventional groupwise registration method by presenting a new objective function, for achieving the sharp group mean image without introducing biases. To accomplish it, we learn the distance between the two images on local patch of the manifold, instead of the straightforward but coarse measurement defined as the overall intensity difference of the whole brain [1–3]. Another contribution of this paper is that we treat each subject differently throughout the registration. Specifically, only the registered subjects that are close enough to the tentative mean image will be involved in updating the mean image since equally treating the subjects in the early stage will lead to the irreversible loss of structure details, especially when most subjects are not well aligned in the beginning. With the improvement of registration, subjects are more likely to agglomerate to the population center. At that time, more subjects will be allowed to participate into the construction of the mean image and their contributions will become more equal. Working under this scenario, the group mean image in our method will gradually approach to the population center, as shown by our experimental results. Finally, we demonstrate the advantage of our method by integrating it into the Diffeomorphic Demons registration algorithm [5], and also compare its performance with the conventional groupwise registration algorithm [1]. With extensive experiments in evaluation of the overlap ratios on 16 NIREP Data and 40 LONI data, our proposed method outperforms the conventional groupwise registration method in both registration accuracy and consistency.

2 Methods

In the framework of unbiased groupwise registration [1], the transformation fields are estimated by iteratively registering N subjects to the latest estimated group mean image. In the t-th round of registration (t = 1, …, T), the group mean image M^t is generated by averaging upon the warped subjects $I^t=\{I_s^t\mid s=1,\dots ,N,t=1,\dots ,T\}$ w.r.t. the current estimated transformation fields $G^t=\{g_s^t\mid s=1,\dots ,N,t=1,\dots ,T\}$, where G^t are calculated by considering M^t−1 as the template and I⁰ (original subjects) as the moving images. It is worth noting that G⁰ are the linear transforms in the initial registration stage. In the following, we first point out in Section 2.1 the importance of always keeping the sharp mean image throughout the whole groupwise registration procedure. Then we propose an improved objective function in Section 2.2, and finally optimize it in Section 2.3.

2.1 The Importance of Keeping Sharp Mean Image in Registration

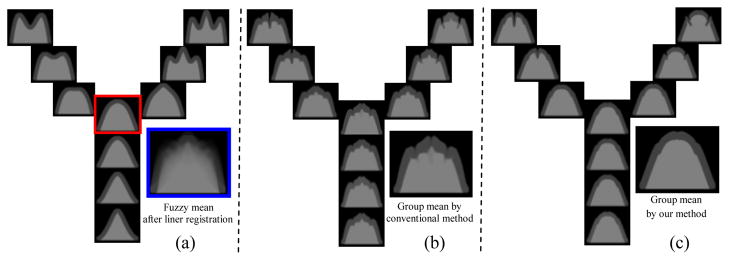
Unbiased groupwise registration method [1] seeks to alternatively estimate the group mean and register each subject to the tentative group mean. However, the initial group mean image M⁰, generated right after the linear alignment, is generally very fuzzy, since the subjects are not well aligned in the beginning of registration. According to our knowledge, few articles have addressed the importance of keeping the sharp mean image during the registration. Indeed, the fuzzy mean image would undermine the groupwise registration performance in two ways: 1) it is difficult to register an individual subject with clear anatomical structures to the mean image with fuzzy structures; 2) a fuzzy mean image will challenge the convergence of optimization since it might not provide sufficient anatomical information to guide the registration. The importance of a sharp mean image in groupwise registration is demonstrated in Fig. 1 by 61 toy images with three branches in distribution, with each branch representing one type of cortical folding. For simplicity, only three images are shown in each branch. Before registration, the mean image is very blurry (as shown in Fig. 1(a)). If the groupwise registration starts from this fuzzy mean, it will result in an unsatisfactory mean image (i.e., the one shown in Fig. 1(b)), since the fuzzy mean image in the beginning is not able to informatively guide the whole groupwise registration of individual images.

Fig. 1.

A toy example to demonstrate the importance of keeping the sharp mean image in the groupwise registration. The synthetic data and their fuzzy mean are shown in (a). (b) shows the groupwise registration results starting with the fuzzy mean image (shown in the blue box of (a)). (c) demonstrates the results by the proposed method which starts with the sharp mean (shown in red box) and keeps tracking the sharp mean image during the registration.

However, if we selected a subject close enough to the population center (i.e., the image in the red box of Fig. 1(a)) as an initial group mean, the anatomical sharpness could be preserved during the registration. Our method is specifically designed to estimate the sharp mean image, which is close to the population center, even in the early stage of the groupwise registration. With this method (detailed in the next section), we can achieve much more reasonable results as shown in Fig. 1(c).

2.2 Objective Function of Groupwise Registration

In this section, we first present an objective function in our groupwise registration with sharp mean, which generalizes the conventional unbiased groupwise registration algorithm [1].

The objective function in conventional groupwise registration is given as:

$$\{\widehat{G},\widehat{M}\}=arg\underset{G^t,M^t}{min}\sum _{s=1}^N\left\{\sum _x{\left|\right|g_s^t(I_s^0(x))-M^t(x)\left|\right|}^2+\mathit{dist}(e,g_s^t)\right\},$$ (1)

where $M^t(x)=\frac{1}{N}{\sum }_{s=1}^N{I}_s^{t-1}(x)$ is the simple average of the warped images after the previous round of registration. The term $\mathit{dist}(e,g_s^t)$ is the manifold distance between the identity transformation e and $g_s^t$.

One major drawback of this method is that the contributions (or the weights) are the same for not only all subjects in the population, but also all voxels in each subject. However, different subjects may be aligned at different degrees with the mean image, thus the equal weighting of them could lead to a fuzzy mean image. Also, each anatomical region may be aligned differently with the mean image, therefore the use of the same weight (generally obtained from the entire subject) for each anatomical region may lead to different amounts of fuzziness across different regions of the mean image. Our method attacks this problem in two ways as described next.

First, we propose a distance measurement for each voxel x w.r.t. the current mean image M^t and the warped subject image $I_s^t$ as:

$$D(x,b,I_s^t,M^t)=d\left({\mathcal{P}}_b(I_s^t(x)),{\mathcal{P}}_b(M^t(x))\right),$$ (2)

where 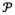denotes a local image patch around voxel x, with size b. The term d measures the intensity difference between the corresponding local image patches, ${\mathcal{P}}_b(I_s^t(x))$ and 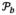(M^t(x)), in the images $I_s^t$ and M^t around the voxel x. It is worth noting that D approaches to the global image distance when b is very large, while D becomes voxel-wise difference in Eq. 2 when b is zero. Since the registration results are usually refined from global shape to local shape, the value of b is large in the initial stage of registration and then gradually deceases with the progress of registration.

Second, to treat each subject differently, we introduce a hidden variable ${\omega }_s^t(x)(s.t.{\sum }_{s=1}^N{\omega }_s^t(x)=1)$ to indicate the contribution of each subject $I_s^t$ in the construction of group mean image on a particular voxel x. In the initial stages, all subjects are not well aligned (especially right after linear registration). If we equally weight each subject (i.e., the entropy of the weighting set { ${\omega }_s^t(x)\mid s=1,\dots ,N$} is high), it will lead to a fuzzy mean image as demonstrated in Fig. 1. To keep the sharp mean throughout registration, only the warped subjects $I_s^t$ which are close enough to the previous mean image M^t−1 are qualified to have a large weight of ${\omega }_s^t(x)$, while other subjects are penalized with small weight ${\omega }_s^t(x)$. With the progress of registration, all subjects will likely agglomerate to the population center. Thus, all $I_s^t$, as long as they are close enough to the mean image, will contribute almost equally to the construction of the mean image. Since they are already well aligned, little fuzziness will be brought to the group image. In this paper, the dynamic changes of weights { ${\omega }_s^t(x)\mid s=1,\dots ,N$} from strictly binary to loosely uniform are controlled by requiring the entropy of the weighting set { ${\omega }_s^t(x)\mid s=1,\dots ,N$} to be increased with the progress of registration.

By replacing the distance measurement with Eq. 2 and adding the dynamic control of weights across subjects to the objective function, we get a new objective function for groupwise registration as:

$$F({\omega }^t,M^t,G^t)\propto \sum _x\sum _{s=1}^N\{{\omega }_s^t(x)·D(x,b,I_s^t,M^t)+r·{\omega }_s^t(x)·log({\omega }_s^t(x))\}+\sum _{s=1}^N\mathit{dist}(e,g_s^t).$$ (3)

where the scalar r controls the penalty of large distance from $I_s^t$ to M^t−1. We will show its important role when explaining the solution to Eq. 3 in Section 2.3.

2.3 Solutions to Our Groupwise Registration

The solution to ${\omega }_s^t(x)$ in Eq. 3 can be immediately calculated by setting $\partial F/\partial {\omega }_s^t(x)=0$:

$${\widehat{\omega }}_s^t(x)=exp\left(-\frac{D(x,b,I_s^t,M^t)}{r}\right).$$ (4)

Here r acts as the inverse temperature in the annealing system based on our observations in Section 2.2. Initially, the degree of r is low, i.e., only the subjects that are very close to the population center will be considered to build a new group mean image, in order to keep the mean image sharp. With the progress of groupwise registration, all subjects become closer to the population center. At that stage, the temperature r will be increased to encourage almost equally weighting of all warped subjects $I_s^t$. It is worth noting that M⁰ is the simple average of linearly aligned subjects in the conventional groupwise registration [1], which could be very fuzzy. In our case, when we set the temperature r close to zero in the beginning, M⁰ can be computed from only an individual subject that is the closest to the population center, compared to the other subjects in the group. The advantages of this initialization are: 1) it can have a sharp group mean image to allow for better registration with all subjects; 2) it is closer to the final population center than any other subjects. Note that M⁰ in our method will not introduce bias since we will gradually increase the value of r to ensure that it reaches the real population center without sacrificing the registration accuracy. This argument is supported by examples in Figs. 2 and 3.

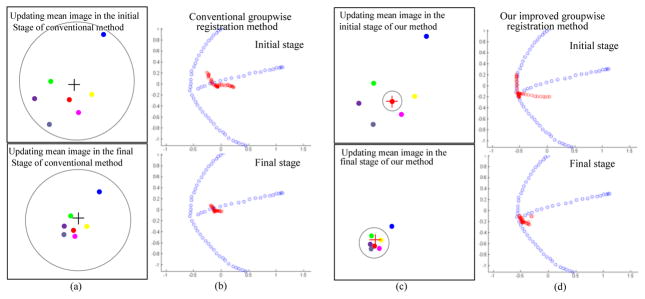
Fig. 2.

Different strategies used to update the group mean image in the conventional method (a) and our registration method (c). 61 original subjects used in Fig. 1 are projected onto a 2D space by PCA and shown in blue dots in (b) and (d), respectively. Their registration results by the conventional and our methods are also shown in (b) and (d) with red dots. It can be seen that our registration results are always clustered around the real population center in both initial (top) and final (bottom) registration stages.

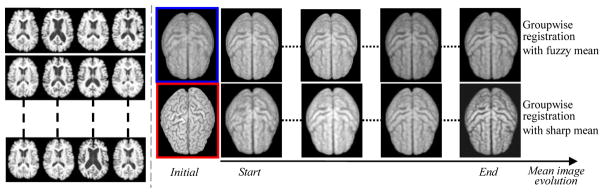
Fig. 3.

The evolution of the group mean image. Left panel shows several typical images from 18 elderly brains used in this experiment. In the right panel, the evolution of the conventional groupwise registration starting with a fuzzy mean (in blue box) and our method with a sharp mean (in red box) are displayed in the top and bottom rows, respectively.

Fig. 2 demonstrates the difference between the conventional and our groupwise registration methods in updating the group mean image, by taking 61 images in Fig. 1 as an example. The solid dots (with different colors) in Figs. 2(a) and 2(c) denote for typical images shown in Fig. 1. In the conventional method, M⁰ (black cross) is the equal average of all $I_s^0$’s, which can be easily deviated by the outliers or less registered images (i.e., a faraway dot from the black cross in Fig. 2(a)). Also, during the iterative registration procedure, each image $I_s^t$ is equally considered, regardless of their registration accuracy (as shown within a large circle in the (a)). However, in our method, we first select an individual image, which is the closest to the population center (i.e., red solid dot in the top of (c)), as a group mean image M⁰. Another main difference between the conventional and our methods is that in our method only the well aligned subjects will contribute to the construction of the mean image. With the progress of registration, the value r, equal to the size of gray circle in (c), will increase, and thus more and more well aligned images will be considered for construction of the group mean image, thus also avoiding bias in the end. To demonstrate the advantage of our adaptive strategy in updating the group mean image, we first project 61 images used in Fig. 1 onto a 2D plane by PCA (as shown with blue dots in Figs. 2(b) and 2(d)). The distribution of 61 images shows a three-branch shape, with its center at the joint point of the three branches. The registration results I¹ and I^T are also projected onto the same 2D plane, and are displayed in red dots for both the conventional and our methods in (b) and (d), respectively. It can be observed that our registration results always stay around the real population center, while the mean image by the conventional method is deviated from the population center in the beginning and keeps staying there until the end of registration.

After determining the weight ${\widehat{\omega }}_s^t(x)$ for each subject I_s by Eq. 4, the remaining optimization of Eq. 3 will be solved iteratively by updating the group mean image M̂^t and performing pairwise registration between each subject I_s and the group mean image M̂^t. Therefore, by fixing $g_s^t$ and ${\widehat{\omega }}_s^t(x)$, we can first calculate the group mean image in the t-th round of registration by minimizing F w.r.t. M^t:

$${\widehat{M}}^t(x)={\sum }_{s=1}^N{\widehat{\omega }}_s^t(x)·I_s^t(x)/{\sum }_{s=1}^N{\widehat{\omega }}_s^t(x).$$ (5)

Then, the transformation field ${\widehat{g}}_s^t$ in the t-th round of registration can be solved by optimizing the following energy function:

$${\widehat{g}}_s^t=arg\underset{g_s^t}{min}\left\{\sum _{x}D(x,b,I_s^t,M^t)+\mathit{dist}(e,g_s^t)\right\},$$ (6)

This is a well-known quadratic objective function discussed in many gradient-based registration algorithms. The solution to Eq. 6 can be found in [5].

Compared to the conventional method, the advantage of our objective function can be summarized as: 1) the group mean image is a weighted average of aligned subjects (Eq. 5), instead of a simple equal average. Weights are adaptively determined not only for each aligned subject $I_s^t$, but also for each image location x; 2) the contribution of each subject is dynamically changed throughout the groupwise registration in the annealing scenario; 3) the sharpness of group mean is always preserved throughout the registration.

3 Experiments

Eighteen elderly brain images are used in our first experiment to demonstrate the advantage of our groupwise registration method, compared to the conventional groupwise registration algorithm [1]. Some typical brain images are displayed in the left panel of Fig. 3. Conventional groupwise registration method starts from a very fuzzy mean (with its 3D rendering shown in blue box). On the contrary, our method begins with a clear group mean image (as shown in red box), which is close to the population center. The evolution of the mean image by the conventional and our registration methods is provided in the top and bottom rows, respectively. It is clear that although the final group mean images are similar by both methods, ours is much sharper than that by the conventional method. Also, this experiment has demonstrated that our method will not introduce bias in the final group mean image as the group mean images by two methods (ours and the conventional unbiased registration algorithm) are very similar. To quantitatively measure the overlap ratio, we first vote a reference image based on the warped results of all (tissue-segmented) subject images, since no template is used in our groupwise registration method. Then, overlap ratio is calculated between each warped subject and the reference image one by one. The average overlap ratio on three tissues (WM, GM, and CSF) is 64.95% by our method and 60.24% by the conventional method, indicating a 4.71% improvement.

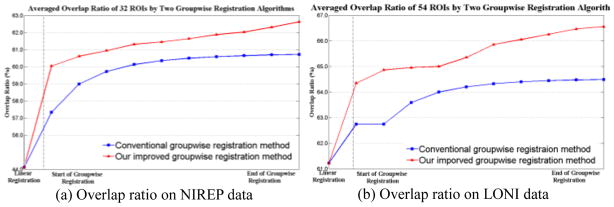
To further validate our argument on the importance of using the sharp mean image during the groupwise registration, we perform two different registration approaches, i.e., the conventional groupwise registration with fuzzy mean and our groupwise registration with sharp mean, on 16 NIREP data (with 32 manually labeled ROIs) and 40 LONI data (with 54 ROIs), by measuring the overlap ratios of their aligned ROIs. The calculation of overlap ratio is similar as those described above. Figs. 4(a) and 4(b) show the average overlap ratios achieved by the two methods on NIREP and LONI datasets, respectively. It is obvious that our method with sharp mean (in red curves) outperforms the conventional method (in blue curves) during the whole registration procedure.

Fig. 4.

Average overlap ratios on NIREP and LONI datasets. Two groupwise registration algorithms (i.e., our method in red and the conventional method in blue) are performed on NIREP and LONI datasets, with the average overlap ratios of all ROIs (at different registration stages) reported in (a) and (b), respectively.

4 Conclusion

We have demonstrated the importance of keeping the sharp group mean image during the groupwise registration procedure, in order to improve the overall registration performance of the whole population. Specifically, we generalize a popular unbiased groupwise registration method by presenting a new objective function to achieve the groupwise registration with the sharp mean. By using various datasets with manually labeled ROIs, we have shown that our method can perform better than the conventional groupwise registration method, in terms of consistently aligning the ROIs across different subjects. We also demonstrate that our method can eventually produce a much sharper group mean image than the conventional method.