Dual-Mode IVUS Catheter for Intracranial Image-Guided Hyperthermia: Feasibility Study

Abstract

In this study, we investigated the feasibility of modifying 3-Fr IVUS catheters in several designs to potentially achieve minimally-invasive, endovascular access for image-guided ultrasound hyperthermia treatment of tumors in the brain. Using a plane wave approximation, target frequencies of 8.7 and 3.5 MHz were considered optimal for heating at depths (tumor sizes) of 1 and 2.5 cm, respectively. First, a 3.5-Fr IVUS catheter with a 0.7-mm diameter transducer (30 MHz nominal frequency) was driven at 8.6 MHz. Second, for a low-frequency design, a 220-μm-thick, 0.35 × 0.35-mm PZT-4 transducer—driven at width-mode resonance of 3.85 MHz—replaced a 40-MHz element in a 3.5-Fr coronary imaging catheter. Third, a 5 × 0.5-mm PZT-4 transducer was evaluated as the largest aperture geometry possible for a flexible 3-Fr IVUS catheter. Beam plots and on-axis heating profiles were simulated for each aperture, and test transducers were fabricated. The electrical impedance, impulse response, frequency response, maximum intensity, and mechanical index were measured to assess performance. For the 5 × 0.5-mm transducer, this testing also included mechanically scanning and reconstructing an image of a 2.5-cm-diameter cyst phantom as a preliminary measure of imaging potential.

I. Introduction

In 2008, an estimated 13 000 people in the United states died from a primary malignant brain and central nervous system (CNS) tumor, and more than 21 800 new cases were diagnosed [1]. Malignant gliomas account for 81% of all malignant primary brain/CNS tumors, and 51% of gliomas are of the WHO grade IV subtype glioblastoma multiforme (GBM), the most common intracranial neoplasm [2], [3].

Currently, primary brain tumors are most commonly treated by surgery, radiotherapy, and chemotherapy [4]. Surgery enables an accurate histological diagnosis and will reduce mass effect [5], though total resection of gliomas is often not practicable [6] and surgery carries inherent risks and an overall complication rate ranging from 25% to 35% [7]–[10]. Radiation effects are manifested as cell attrition because of apoptosis or reproductive cell death as a result of radiation-induced DNA damage [8]. However, despite the positive effects of radiotherapy, acute side effects (e.g., hair loss, nausea, swelling) can last from 4 to 6 weeks, and there is a reasonable consensus of strong increased risk of intracranial tumors following therapeutic ionizing radiation [11], [12]. Chemotherapy may be administered systemically, by mouth or intravenous infusion, or locally, by direct intra-arterial or interstitial injection [13]. The major challenge to effectively delivering drugs to CNS tumors is achieving a high drug concentration within the tumor bed [14].

Liposomes are membrane-enclosed vesicles composed of a lipid bilayer shell (which can trap hydrophobic and amphipathic drugs) surrounding an aqueous core (which can contain hydrophilic drugs), with a diameter typically around 100 nm [15]. Liposomes can be readily conjugated to antibodies or other adhesion ligands such as integrin α_vβ₃ (found to be overly expressed in regions of tumor angiogenesis) to enable active targeting of a tumor site [16]. Thermosensitive liposomes containing the cancer drug doxorubicin have been shown to quickly release their contents when the surrounding temperature is raised to 41°C, or 4°C above normal body temperature [17]. Therefore, thermosensitive liposomes, in combination with local hyperthermia (which may be created and directed by ultrasound), can provide targeted control of drug release that may augment chemotherapeutic efficacy in many clinical settings [17], [18].

Efforts to develop trans-cranial, image-guided focused ultrasound systems for brain tumor therapy have shown encouraging results; however, these studies have concerns associated with the skull—either a highly invasive approach is taken, in which the skull bone must be removed before sonication, or a noninvasive approach is taken, where the high ultrasound attenuation and reflection from the bone is accepted and the phase aberration from the skull's variable thickness is either managed or corrected [19]–[22].

Minimally-invasive endovascular techniques for treatment of various intracranial diseases have been used in the field of interventional neuroradiology, and these procedures can be extended to the treatment of intracranial tumors [23], [24]. A 7- to 9-Fr (1 Fr = 1/3 mm diameter) introducer sheath or guide catheter may be used for access, usually via a transfemoral approach or a direct retrograde internal jugular insertion, and a 5-Fr catheter may be inserted as far as the frontal portion of the superior sagittal sinus to treat thrombosis by urokinase infusion or rheolytic thrombectomy [23]–[30]. A flexible catheter device as small as 3 Fr would be preferable, however, to enable placement in closer proximity to a tumor via smaller vessels, and to achieve access to the brain volume via the arterial system as well.

Intravascular ultrasound (IVUS) imaging was developed to provide detailed, high-quality tomographic visualization of the coronary vessels in vivo [31], [32]. IVUS technology allows the qualitative assessment and precise quantitative measurement of the lumen and layers of the arterial wall, as well as atherosclerotic plaque morphology (presence of calcification, lipid pools, fibrous tissue), at the site of stenosis [33], [34]. IVUS has also been used to guide stent deployment because it provides an accurate description of coronary plaque before, during, and after interventional procedures [35]. Because of the fact that the typical lumen diameter in the coronary arteries is on the order of 2 to 3 mm and layers of the arterial wall may be less than 300 μm thick, mechanical IVUS catheters commonly make use of a single rotating piezoelectric crystal (in the range of 20 to 40 MHz) within a sheath that is typically less than 4 Fr [32], [36], [37]. IVUS imaging requires a transducer with surface area less than a few square millimeters, and the transducer must be electrically matched to the coaxial line and pulser-receiver system [36]. Investigation of potential therapeutic applications involving IVUS catheters has recently begun [38], [39].

Dual-mode ultrasound devices for image-guided therapy have been designed and implemented for several thermal applications (e.g., treatment of cardiac arrhythmias and tumors of the liver, breast, biliary ducts, and prostate), using a catheter, endoscope, or extracorporeal approach with either single element or phased array transducers [40]–[45]. Ultrasound is an attractive modality for guidance, treatment, and monitoring because of its potential for inherent spatial registration between functions, as well as its low cost, portability, and high frame rate [43], [44], [46].

The goal of this project is to use an IVUS coronary imaging catheter as a platform for a dual-mode intracranial catheter integrating ultrasound imaging and hyperthermia for neuro-oncology. In an earlier study, we had success imaging a canine brain using catheter probes placed in the superior sagittal sinus via a burr hole in the skull: a siemens (siemens medical solutions, Ultrasound Division, Issaquah, WA) 10-Fr AcuNav intracardiac catheter acquired 2-D echo images with clear delineation of cerebral gyri and sulci, and a 3-D dual-mode catheter transducer prototype (14 Fr) was used to create real-time 3-D echo scans of the lateral ventricles and a contrast-enhanced real-time 3-D color Doppler scans showing the branches of the circle of Willis [47]. The 3-D dual-mode transducer also was used to create a temperature rise of 3.5°C in tissue-mimicking material. However, the 10- to 14-Fr catheter probes used previously were too large and stiff to navigate a minimally-invasive vascular pathway to the brain, either by an arterial route [introduce catheter into common carotid artery to gain access to middle cerebral artery, allowing treatment of lesions in the frontal and temporal lobes—see Fig. 1(a)] or a venous route [introduce catheter into internal jugular vein to gain access to dural venous sinuses, allowing treatment of lesions in the occipital and parietal lobes and in deeper cerebral and cerebellar white matter—see Fig. 1(b)].

Fig. 1.

Vascular pathways to the brain for minimally invasive intracranial catheters. (a) Arterial route (Reproduced with permission from Matthew Holt and the Internet Stroke Center.): common carotid artery (CCA) [62] to middle cerebral artery (MCA). (b) Venous route (Reproduced with permission from Dean Falk, Florida State University.): internal jugular vein (IJV) to dural venous sinuses (DVS).

Commercially-available IVUS catheters no larger than 4 Fr already have an appropriate form factor—they are both thin and flexible enough—to achieve the desired placement within the brain volume via our intended vascular approaches. Therefore, an IVUS catheter modified to be hyperthermia-capable would be ideal for our application. Using fluoroscopic guidance, the physician could place this minimally-invasive catheter immediately adjacent to a brain tumor target to image the tumor and then direct an ultrasound hyperthermia beam to trigger the release of chemotherapeutic drugs contained within thermosensitive liposomes molecularly targeted to regions of tumor angiogenesis.

In this paper, we describe the simulation, construction, and testing of three IVUS transducer prototypes to test the feasibility of this approach.

II. Methods

A. Frequency Selection

Malignant brain tumors come in a wide range of shapes and sizes. To simplify the problem of transducer frequency selection, we considered the aim of effectively heating spherical tumor targets with diameters of 1 and 2.5 cm as an approximation of small and large tumor sizes. Based on literature describing previous interventional endovascular procedures for intracranial diseases, we assume that a 3.5-Fr catheter transducer can be placed in a blood vessel immediately adjacent to the tumor [23]–[30]. We estimate the optimal frequency for heating each tumor size from a simplified expression, according to the following derivation.

As a first-order approximation, we considered the case of a one-dimensional plane wave, where the intensity (in watts per square centimeter) of an ultrasound wave decreases with depth z (in centimeters) because of absorption α (in nepers per centimeter), according to [48]

$$I=I_0\cdot \text{exp}(-2\alpha z).$$ (1)

This intensity factors into the heat source function q_υ (in watts per cubic centimeter)

$$q_{\upsilon }=2\alpha I=2\alpha I_0\text{exp}(-2\alpha z),$$ (2)

which is present in the Pennes bio-heat transfer equation,

$$\stackrel{.}{T}=\kappa {\nabla }^{2}T-\frac{T}{\tau }+\frac{q_{\upsilon }}{c_{\upsilon }},$$ (3)

where T is the tissue temperature rise (in kelvin), κ is the thermal diffusivity (in square centimeters per second), τ is the perfusion time constant (in seconds), and c_υ is the volume specific heat (in joules per kelvin per cubic centimeter) [49], [50]. If we assume the absorption coefficient to be approximately linear with frequency (α = βf), we can then derive from (1) and (2) a frequency

$$f=\frac{1}{2\beta z}$$ (4)

for maximum heating at a depth of z cm in brain tissue, where β = 0.5 dB/cm/MHz = 0.0576 Np/cm/MHz [51], [52].

From the plane-wave optimal frequency expression, we find that maximum heating at a 1 cm depth occurs at 8.7 MHz, and maximum heating at a 2.5 cm depth occurs at 3.5 MHz. Therefore, an ideal transducer would incorporate both a high-frequency resonance mode around 8.7 MHz to be used for imaging and for shallow heating with smaller tumors, and a low-frequency resonance mode around 3.5 MHz to be used for deeper heating on larger tumors.

Three different apertures were evaluated as dual-mode designs. The simplest design used a 0.7-mm-diameter Boston Scientific (Natick, MA) Sonicath transducer with a 30 MHz nominal frequency, to be driven as a shallow-heating, high-frequency device at 8.7 MHz. For a lower-frequency design, a 220-μm-thick, 0.35 × 0.35-mm PZT-4 transducer was an appropriate size to replace a 40-mHz element in a Boston Scientific Atlantis SR Pro coronary imaging catheter and was evaluated as a width-mode resonator at 3.5 MHz for deeper heating (this design would utilize a higher-frequency thickness mode for imaging). Finally, a maximum allowable aperture geometry for a flexible 3-Fr IVUS catheter was taken to be 5 × 0.5 mm: the width of the catheter lumen constrains the transducer element to a width of 0.5 mm, and the 5 mm length was considered to be the longest element (introducing some increased rigidity to a small section of the catheter) possible without compromising the catheter's ability to navigate the curvature of the cerebral vessels. A 220-μm thick PZT-4 transducer of this size was evaluated as a possibility for combined high- and low-frequency operation.

Using Field II software [53], we calculated beamplots for each transducer aperture at the designated 8.7 MHz and 3.5 MHz frequencies, as seen in Figs. 2–4. A 4-cycle excitation pulse with 25% fractional bandwidth was used in the calculations, and attenuation was set to zero to mimic the conditions of experimental measurements taken in a water tank. Figs. 2(a), 3(a), and 4(a) show the relative sizes of each of the active apertures (0.5-mm grid-line spacing). Figs. 2(b), 3(b), 4(b), and 4(f) display the beam's relative pressure amplitude in the zero-elevation plane for each aperture; Figs. 4(c) and 4(g) also show the zero-azimuth plane for the largest aperture (which lacks a 1:1 aspect ratio). Figs. 2(d), 3(d), 4(e), and 4(i) show each beam's simulated relative pressure amplitude at a depth of 4 mm, the closest distance at which our hydrophone can be placed for measurement in a water tank. Table I lists the −6-dB beamwidth at a depth of 4 mm for each aperture and transmit frequency.

Fig. 2.

Field II beamplot simulation at 8.7 MHz for 0.7-mm diameter SoniCath transducer. (a) Aperture footprint (one-half millimeter gridline spacing). (b), (d) Simulated relative pressure amplitude plots: zero-elevation plane and 4-mm-deep plane, respectively. (c) Normalized beamplot at 4 mm deep, truncated at half-maximum.

Fig. 4.

Field II beamplot simulation for 5 × 0.5-mm PZT-4 transducer for flexible 3-Fr IvUs. (a) aperture footprint (one-half millimeter grid-line spacing). Simulated relative pressure amplitude beamplots at 8.7 and 3.5 MHz, respectively: (b), (f) zero-elevation plane; (c), (g) zero-azimuth plane; (e), (i) 4-mm-deep plane. (d), (h) normalized beamplots at 4 mm deep, truncated at half-maximum, at 8.7 and 3.5 MHz, respectively.

Fig. 3.

Field II beamplot simulation at 3.5 MHz for 0.35 × 0.35-mm PZT-4 transducer for Atlantis retrofit. (a) Aperture footprint (one-half millimeter gridline spacing). (b), (d) Simulated relative pressure amplitude plots: zero-elevation plane and 4-mm-deep plane, respectively. (c) Normalized beamplot at 4 mm deep, truncated at half-maximum.

TABLE I.

−6 dB Beamwidths in Field II Simulations.

Aperture	Frequency (MHz)	−6-dB beamwidth at 4 mm depth (mm)
0.7 mm diameter	8.7	1.4
0.35 × 0.35 mm	3.5	6.3
5 × 0.5 mm	8.7	4.8 (azimuth)
		1.7 (elevation)
	3.5	4.7 (azimuth)
		5.2 (elevation)

B. Fabrication

For these first feasibility prototypes, we concentrated on simple fabrication techniques without significant efforts to optimize transducer performance and bandwidth. Each transducer needed to be made functional (by having a signal wire and a ground contact attached) and sufficiently durable for water tank testing. Each experimental transducer was modeled in PiezoCAD (Sonic Concepts, Bothell, WA) to calculate a pulse-echo impulse response and spectrum to compare with hydrophone measurements taken later. Accuracy of the Piezocad modeling was limited by complex backing materials constrained by the small diameters of the catheters.

First, the 0.7-mm-diameter Boston Scientific SoniCath 3.5-Fr IVUS transducer [see Fig. 5(a)] was used without modification but was driven at a frequency near 8.7 MHz. For durability during testing, the transducer and cable were secured in an open lumen using 5-min epoxy (Loctite, Hartford, CT).

Fig. 5.

(a) Boston Scientific SoniCath 0.7-mm-diameter transducer secured in test lumen. (b) Pulse-echo impulse response and frequency spectrum.

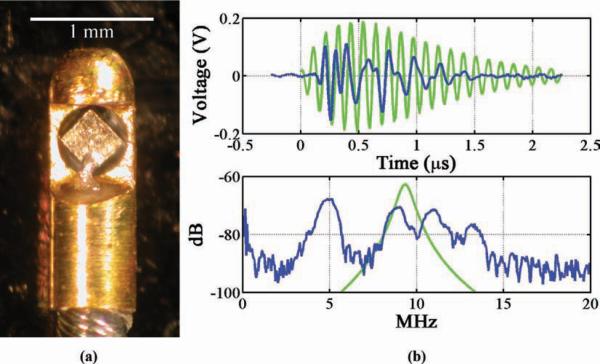
For the first experimental prototype, the original 0.5-mm-diameter element was removed from a 40-MHz Boston Scientific Atlantis SR Pro 3.5-Fr IVUS catheter, and replaced by a 0.35 × 0.35 mm PZT-4 transducer, which was 220 μm thick and had a nominal thickness resonance of 10 MHz [see Fig. 6(a)]. PZT-4 was chosen because its material properties (relatively high electromechanical coupling coefficient, high mechanical quality factor, low dissipation factor, and high Curie temperature) make it optimal for dual-mode imaging and therapy transducers. A drop of low-viscosity, 20-min epoxy (Finish-Cure, Bob Smith Industries, Atascadero, CA) was applied at the corners of the transducer and allowed to set, to stabilize the element in relation to the surrounding metal housing. A drop of silver epoxy (CHO-BOND, Chomerics, Woburn, MA) was added to connect the front contact of the element with the exposed signal wire, and cured in an oven at 60°c for three hours. The cavity behind the element was then filled with silver epoxy to electrically connect the back contact of the element with the grounded metal housing.

Fig. 6.

(a) Boston Scientific Atlantis retrofitted with 220-μm-thick, 0.35 × 0.35-mm PZT-4 transducer. (b) Pulse-echo impulse response and frequency spectrum, PiezoCAD calculation (green) and experimental measurement (blue). References to color refer to the online version of this figure.

A more durable and easy-to-fabricate test transducer, using an identical 0.35 × 0.35 × 220-μm PZT-4 element, was also constructed [see Fig. 7(a)]. The thin coaxial cable was taken from a disassembled Atlantis catheter, and its inner signal wire was separated from the outer ground wires and stripped of its insulation. The ground wires were pressed together and smothered with a drop of silver epoxy before placing the transducer in the center. After this grounded back contact was cured in the oven, the signal wire was attached to a corner of the front contact with silver epoxy. The device was then secured inside an open catheter lumen with 5-min epoxy.

Fig. 7.

(a) A 220-μm-thick, 0.35 × 0.35-mm PZT-4 test transducer. (b) Pulse-echo impulse response and frequency spectrum, PiezoCAD calculation (green) and experimental measurement (blue). References to color refer to the online version of this figure.

Because a transducer of such a small size but significant thickness naturally has a low capacitance and high electrical impedance, a simple, two-component L-section impedance matching network, consisting of an inductor in series with the load and a capacitor in parallel, was built to maximize the power transfer from the driving amplifier to the transducer. To design this network, the amplifier (source) impedance and the corresponding water-coupled transducer element (load) impedance were measured for a selected frequency using an impedance analyzer (Model 4194A, Hewlett-Packard, Palo Alto, CA). Then, because maximum real power transfer occurs when the input impedance (L-section plus load) equals the complex conjugate of the source impedance, we found the optimal inductance (11 μH) and capacitance (750 pF) values for the L-section components algebraically.

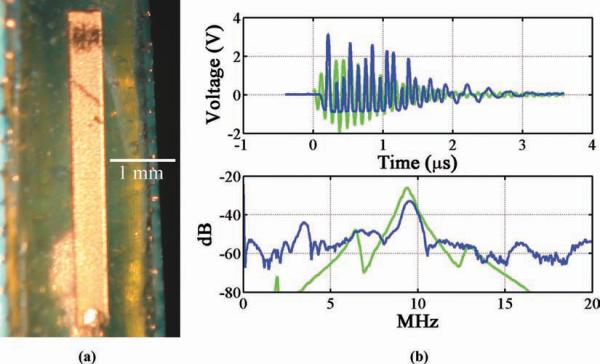
Finally, a 220-μm-thick, 5 × 0.5-mm PZT-4 test transducer [see Fig. 8(a)] was constructed using a thin coaxial cable in a fashion similar to that used for the 0.35 × 0.35 mm test transducer described previously.

Fig. 8.

(a) A 220-μm-thick, 5 × 0.5-mm PZT-4 test transducer. (b) Pulse-echo impulse response and frequency spectrum, PiezoCAD calculation (green) and experimental measurement (blue). References to color refer to the online version of this figure.

After measuring the electrical impedance, pulse-echo impulse response, and frequency response (using a model 5073PR Pulser/Receiver and model 5605A Stepless Gate, Olympus NDT, Waltham, MA, and model 3588a spectrum Analyzer, Hewlett-Packard) for each transducer, measurements of maximum intensity and mechanical index were taken at frequencies that both corresponded to a peak on the frequency spectrum and were reasonably close to the 8.7 or 3.5 MHz ideal.

C. Imaging

To get a qualitative assessment of PZT-4's potential for imaging as a dual-mode IVUS transducer, the 5 × 0.5-mm PZT-4 test transducer was used to manually reconstruct an image of a 2.5-cm-diameter cyst phantom. The transducer was mounted to a translation stage and moved laterally over the target phantom. The pulser/receiver was then used to generate a line of image data every 1 mm over a span of 35 mm. A 20th-order bandpass filter windowing between 8.5 and 10 MHz was applied to isolate the high-frequency components and reduce noise, and linear time-gain compensation (TGC) was applied to balance the attenuation and allow uniform image brightness with depth. The resulting image is shown in Fig. 9.

Fig. 9.

Image of a 2.5-cm-diameter cyst phantom acquired with 5 × 0.5-mm PZT-4 test transducer. An 8.5 to 10 MHz bandpass filter and linear TGC were applied to the data.

D. Thermal Modeling

To further analyze the possible hyperthermia capabilities for each transducer, a model previously used for circularly-symmetric, spherically-focused transducers in a homogeneous medium was adapted for our different transducer geometries in brain tissue. This approach, described in [54] and based on [55] and [56], considers the acoustic thermal beam to be a continuum of heated disks. The continuous-wave acoustic intensity is assumed to be uniform (spatial-averaged I_SATA) inside each disk and zero outside. The acoustic power is assumed to decay exponentially because of absorption as a function of depth z:

$$W\left(z\right)=W_o\text{exp}(-2\alpha z).$$ (5)

The thermal beam diameter is defined with the help of a dimensionless parameter Ψ as follows:

$$\Psi \left(z\right)=\frac{\pi \cdot {d_o}^2\cdot \mid \text{roc}-z\mid }{8\cdot \lambda \cdot \text{roc}\cdot z},$$ (6)

where d_o is the transducer diameter and roc is the transducer's radius of curvature [56]. Because the transducers considered have no spherical focusing, the radius of curvature is infinite, and the expression for Ψ reduces to

$$\Psi \left(z\right)=\frac{\pi \cdot {d_o}^2}{8\cdot \lambda \cdot z}.$$ (7)

Based on [56], the diameter d of the thermal beam is then given for Ψ > 2.56 by

$$\Psi \left(z\right)=d_o$$ (8)

and for Ψ < 2.56 by

$$d\left(z\right)=\frac{0.55\cdot d_o}{\text{sin}\left[\Psi \left(z\right)\right]}.$$ (9)

Because the aspect ratio of the 5 × 0.5-mm transducer is not 1:1, a transducer diameter d_o could not be given to calculate the beam diameter. Therefore, as a first-order approximation for this case, the diameter of the thermal beam was taken to be the geometric mean of the beam diameters found for apertures of d_o = 5 mm and d_o = 0.5 mm.

Before calculating the maximum possible temperature rise for each transducer, a measurement of total acoustic power radiating from the transducer face, W_o, was needed. Each transducer was placed in a water tank and driven by a waveform generator (Model 33250, Agilent, Santa Clara, CA) connected to a 25-W RF power amplifier (Model 525LA, ENI, Rochester, NY) creating a maximum-amplitude 4-cycle excitation pulse with a 100 Hz PRF. This low duty cycle was chosen cautiously for this first set of experiments, primarily to ensure that the power amplifier could maintain stable output without risk of being damaged, as well as to prevent possible damage to the transducer from repeated, prolonged excitation at high power levels. Thus, the values found for intensity and power are instantaneous values which we extrapolate to estimate continuous-wave operation; this thermal modeling does not address the possibility of transducer self-heating and its potential contribution to tissue heating.

A calibrated membrane hydrophone (S4–251, Sonora Medical Systems, Longmont, CO) was used to locate the peak intensity at the closest measurable distance (4 mm) using our setup. This peak intensity value was used to scale a normalized azimuth-elevation beamplot, and the total hydrophone-measured power, W_o, was calculated by integrating over the half-maximum area, according to the AIUM Acoustic Output Measurement Standard [57]. This is illustrated in Figs. 2(c), 3(c), 4(c), and 4(h), which show 4-mm depth beamplots of normalized pressure for each transducer's beam, truncated at half-maximum. The hydrophone data was also used to compute the mechanical index of each pulse.

We could then compute the estimated temperature rise ΔT (in °C) at an observation point z_obs along the beam axis according to

$$\Delta T\left(z_{\text{obs}}\right)=\left[\frac{\alpha L{W}_o}{K}\right]\cdot {\int }_0^{\infty }F\left(z\right)\text{d}z,$$ (10)

where

$$F\left(z\right)=\frac{\text{exp}(-2\alpha z)}{A\left(z\right)}\cdot \left[\text{exp}\left(\frac{-\mid z_{\text{obs}}-z\mid }{L}\right)-\text{exp}\left(\frac{-\sqrt{R^2\left(z\right)+{\mid z_{\text{obs}}-z\mid }^2}}{L}\right)\right],$$ (11)

and where A(z) is the beam area and R(z) the beam radius versus depth, L is the perfusion length in brain tissue (3.9 mm), and K is the thermal conductivity of brain tissue (5.35 mW/cm/kelvin) [54], [58].

This thermal model strongly depends on the size and shape of the acoustic aperture, and thus differs from the simple plane-wave approximation used to select the ideal high and low frequencies of 8.7 and 3.5 MHZ. To investigate this dependence and better predict the effectiveness of ultrasound heating at a certain frequency, thermal simulations were performed for each aperture over a range of frequencies from 1 to 20 MHz. The ΔT(z_obs) curve was first normalized to a maximum temperature rise of 8°C (corresponding to a local absolute tissue temperature of 45°C; above this temperature proteins begin to denature, losing their tertiary structure) [54]. The depth at which the temperature increase fell below the 4°C thermosensitive liposome release threshold was then recorded as the thermal penetration possible for a given aperture.

III. Results

A. Experimental Measurements

The impulse response and frequency spectrum for the unmodified, 0.7-mm-diameter Boston Scientific SoniCath transducer is shown in Fig. 5(b). The spectrum indicates a broadband response centered about 20 MHz. For the purpose of shallow tumor heating (frequencies near 8.7 MHz, considered optimal for 1 cm depth), its maximum-amplitude operating frequency was found to be 8.6 MHz, and a maximum spatial-peak, pulse-averaged intensity (I_SPPA) of 4.6 W/cm² was measured, with a mechanical index (MI) of 0.16.

For the Boston Scientific Atlantis catheter retrofitted with a 220-μm-thick, 0.35 × 0.35-mm PZT-4 element, frequency components at 5, 9, 11, and 13 MHz were found to be present [see Fig. 6(b)]. PiezoCAD modeling of this transducer estimated a thickness-mode center frequency of 9.27 MHz. Unfortunately, after repeated handling, this transducer no longer functioned and intensity measurements could not be taken.

The analogous 0.35 × 0.35-mm test transducer showed a peak width-mode resonance at 3.85 MHz [see Fig. 7(b)], so the electrical impedance matching network was designed for this frequency. PiezoCAD estimated the peak thickness-mode frequency to be 9.29 MHz. The matching circuit served to increase the output pressure amplitude by 36% [see Fig. 10]. Using this matching network, the transducer achieved an I_SPPA of 4.6 W/cm² and a MI of 0.19.

Fig. 10.

Output pressure from 0.35 × 0.35-mm PZT-4 test transducer with maximum-amplitude, 4-cycle driving pulse: (a) without L-section matching circuit, (b) with L-section matching circuit.

The 220-μm-thick, 5 × 0.5-mm test transducer's frequency response had a thickness-mode resonance peak at 9.8 MHz, as well as a width-mode resonance at 3.6 MHz, as seen in Fig. 8(b). PiezoCAD modeling predicted a thickness-mode resonance at 9.35 MHz. I_SPPA measurements of 30.9 W/cm² (MI = 0.29) and 5.2 W/cm² (MI = 0.23) were taken at each of these frequencies, respectively. Table II lists these measured results.

TABLE II.

Acoustic Output Measurements and Thermal Modeling Results.

		Measured pulse		CW extrapolation
Transducer	Frequency (MHz)	ISPPA (W/cm2)	MI	ISPTA (W/cm2)	W0 (W)	Max. temp, rise (°C)	Normalized (8° max.) 4° penetration depth (mm)
0.7 mm diam.	8.6	4.6	0.16	5.0	0.06	4.6	4.7
SoniCath
0.35 × 0.35 mm	3.85	3.6	0.19	5.6	1.0	31.0	1.9
PZT-4 w/MN
5 × 0.5mm PZT-4	9.8	30.9	0.29	39.6	1.9	73.8	5.9
	3.6	5.2	0.23	8.1	0.8	9.8	8.6

B. Thermal Model Calculations

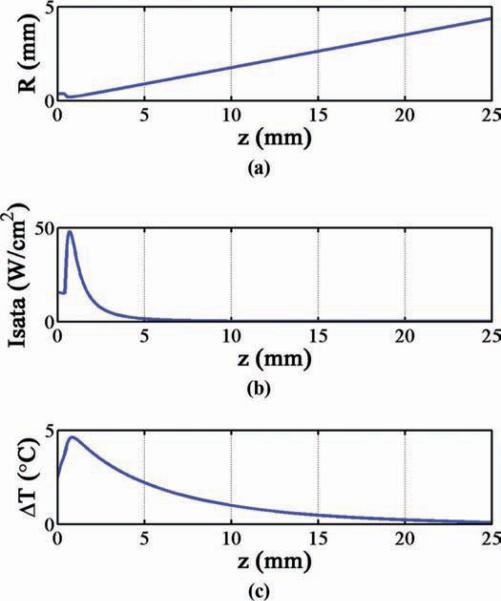
The hydrophone-recorded pulse data used to find the I_SPPA values mentioned above were extrapolated to estimate the continuous-wave I_SPTA for each transducer. These continuous-wave intensity values were used to find the total hydrophone-measured power, W_o, for each transducer [57]. With a W_o value as input, our thermal model calculated the on-axis tissue temperature rise versus depth curve, ΔT(z), and found the maximum possible temperature rise for each transducer operating with continuous-wave excitation, as listed in Table II. Fig. 11 is an example illustrating the result of these calculations for the 0.7-mm-diameter SoniCath transducer: Fig. 11(a) gives the calculated thermal beam radius as a function of depth; Fig. 11(b) gives the I_SATA as a function of depth (found by dividing the beam's exponentially-decaying total power by the cross-sectional beam area); Fig. 11(c) gives the depth-dependent on-axis temperature rise in brain tissue.

Fig. 11.

Thermal model calculations for 0.7-mm-diameter SoniCath (continuous-wave W_o = 0.06 W). (a) Thermal beam radius versus depth. (b) Uniform (spatial-average) intensity versus depth for the thermal beam. (c) Resulting on-axis temperature rise in brain tissue.

After scaling each ΔT(z) curve to an 8°C maximum, the maximum 4°C thermal penetration was determined. It was found that the 0.7-mm-diameter Boston Scientific SoniCath transducer aperture would be capable of safely achieving a 4°C temperature rise up to 4.7 mm deep at 8.6 MHz. The 0.35 × 0.35-mm test transducer aperture could achieve 4°C thermal penetration up to 1.9 mm deep at 3.85 MHz. The 5 × 0.5-mm test transducer aperture could achieve thermal penetration up to 5.9 mm deep at 9.8 MHz, and up to 8.6 mm deep at 3.6 MHz. These results are listed in Table II.

Fig. 12 shows the model's computation for the thermal penetration for each acoustic aperture as a function of frequency. This figure shows that for each aperture geometry, the model predicts a particular frequency where there is an optimal distribution of energy, balancing the frequency-dependent tradeoff between absorption and beam divergence, resulting in a theoretical maximum of safe thermal penetration. The model's computation shows that the 0.7-mm diameter SoniCath aperture is capable of achieving 4°C thermal penetration to a maximum depth of 4.8 mm in brain tissue at an optimal frequency of 8.7 MHz. The 0.35 × 0.35-mm transducer aperture is capable of achieving thermal penetration up to 2.8 mm deep at 12.4 MHz, and the 5 × 0.5-mm transducer aperture is capable of achieving thermal penetration up to 12.4 mm deep at an optimal frequency of 2.4 MHz.

Fig. 12.

Calculated 4°C thermal penetration (8°C maximum) versus frequency for each aperture.

IV. Summary and Discussion

Three different transducer apertures appropriate for 3.5-Fr IVUS catheter packaging were investigated for their potential to create dual-mode ultrasound imaging and hyperthermia. Beamplots for each aperture were generated using Field II, and a thermal model was used to calculate the temperature rise on the axis of the beam within brain tissue. I_SPPA values of several watts per square centimeter were measured, indicating that localized hyperthermia in brain tissue may be possible.

A 3.5-Fr Boston Scientific SoniCath IVUS transducer with a 0.7-mm diameter element was driven near 8.7 MHz (estimated to be an optimal frequency for heating at a depth of 1 cm in brain tissue), and thermal modeling calculated that this transducer aperture could achieve 4°C thermal penetration up to a depth of 4.7 mm at 8.6 MHz.

A 3.5-Fr Boston Scientific Atlantis catheter was successfully retrofitted with a 220-μm-thick, 0.35 × 0.35-mm PZT-4 element and transducer operation was verified, but the device failed after repeated use. A test transducer with an identical PZT-4 element was fabricated and driven at a width-mode resonance frequency (lower frequencies near 3.5 MHz were considered optimal for heating at a depth of 2.5 cm in brain tissue) with the help of a custom L-section electrical impedance matching circuit. Thermal modeling predicted a 4°C thermal penetration depth of 1.9 mm at 3.85 MHz. Future tissue heating experiments will need an electrical impedance matching network customized for each transducer to maximize power transfer efficiency for high-duty cycle, high-power transmit.

A 220-μm-thick, 5 × 0.5-mm PZT-4 test transducer was built as a possible high- and low-frequency option; this aperture geometry was considered the maximum allowable size for a flexible 3-Fr IVUS catheter. Thermal modeling calculated 4°C thermal penetration depths of 5.9 mm at 9.8 MHz and 8.6 mm at 3.6 MHz. The results from the three aperture geometries considered indicate that the largest, 5 × 0.5-mm, transducer is the only practical solution for achieving the desired 4°C temperature rise to an effective treatment depth in tissue.

The 4°C thermal penetration predicted by the acoustic measurements and associated thermal modeling at specific frequencies was not deep enough for either the 1- or 2.5-cm-diameter tumors initially considered; however, investigation of the model reveals that the design frequencies used may not have been ideal. Our thermal model suggests that the maximum depth to which a transducer can achieve a 4°C temperature rise (without heating any part of the tissue more than 8°C) is highly dependent on the size and shape of the acoustic aperture [see Fig. 12]; naturally, a larger aperture achieves better results, but the catheter's size and required flexibility limit the feasible size of the transducer. As indicated in Fig. 12, the model predicts that the ideal driving frequency for the 5 × 0.5-mm aperture is 2.4 mHz; operation at this frequency is predicted to achieve a maximum safe thermal penetration depth of 12.4 mm, which would be sufficient for heating a 1-cm diameter tumor target. In future work, this thermal modeling may be used to aid the frequency selection and design of dual-mode transducers.

Although future studies will involve temperature measurements in tissue for high-power exposures with IVUS-sized transducers, the mechanical index is an important metric as well. Studies have shown that the blood-brain barrier (BBB) disruption threshold is estimated to be at a mechanical index between 0.2 and 0.5 when ultrasound exposures are used in conjunction with circulating microbubble contrast agent [59]–[61]. Optimized IVUS transducer designs could achieve higher pressure amplitudes at frequencies below 2 MHz, opening the door for another drug-delivery strategy in which microbubbles and chemotherapeutic drugs in solution could be delivered through the same ultrasound catheter device, and bbb disruption (rather than hyperthermia) would be the trigger to localize the chemotherapeutic effect.

With these possibilities in mind, perhaps the most exciting result of the current work is the successful retrofitting of Boston Scientific's 40-MHz, 3.5-Fr Atlantis SR Pro catheter with a lower-frequency, higher-power transducer element, which demonstrates the potential for this technology to quickly be implemented clinically once its efficacy is fully established.

V. Conclusion

High-power PZT-4 prototype transducers capable of being packaged in a 3.5-Fr IVUS catheter were built and tested as potential dual-mode imaging-and-therapy devices for minimally-invasive treatment of tumors in the brain. Acoustic output was measured and a thermal model was used to estimate the spatial extent to which 4°C hyperthermia could be safely achieved with each transducer aperture under continuous-wave excitation. These results, and the successful retrofit of a 3.5-Fr Boston Scientific IVUS catheter with a PZT-4 element, indicate that the creation of hyperthermia with a dual-mode IVUS transducer may be possible and that this technology may become clinically viable with further development.

Biographies

Carl D. Herickhoff (M'05) was born in Mankato, MN, on August 10, 1982. He received the B.S. degree in electrical engineering (magna cum laude) from the University of Notre Dame, South Bend, IN, in 2005. He is currently a biomedical engineering doctoral candidate at Duke University, Durham, NC. His current research focuses on dual-mode ultrasound transducers for minimally-invasive brain tumor treatment.

Gerald A. Grant received the B.S. degree in neurosciences from Duke University in 1989. He then received a M.D. from Stanford University in 1994. He received his postgraduate residency training in neurosurgery at the University of Washington in Seattle, WA.

Dr. Grant is currently an Associate Professor in the Department of Neurosurgery at Duke University Medical Center in Durham, NC, and is also adjunct faculty in the Fitzpatrick Institute for Photonics at Duke University. His main clinical and research interests include pediatric brain tumors, neurotrauma, the blood-brain barrier, drug delivery, and biophotonics.

Gavin W. Britz was born in South Africa and completed medical school at the University of Witwatersrand, Johannesburg, in 1987, where he also began his surgical training. He completed his surgical internship at Johns Hopkins Hospital in Baltimore in 1993, and completed his neurosurgical residency and Masters of Public Health at the University of Washington in Seattle, WA, by 2002.

Dr. Britz also completed a fellowship in cerebrovascular surgery and endovascular neurosurgery at the University of Washington, where he remained as an Assistant Professor of Neurosurgery and Radiology until 2007. He then left for the Duke University Health System to become an Associate Professor and Director of the Cerebrovascular Center. His current laboratory research focuses on evaluating the alternations in function in the microcirculation following aneurysmal subarachnoid hemorrhage.

Stephen W. Smith (M'91) was born in Covington, KY, on July 27, 1947. He received the B.A. degree in physics (summa cum laude) in 1967 from Thomas More College, Ft. Mitchell, KY, the M.S. degree in physics in 1969 from Iowa State University, Ames, and the Ph.D. degree in biomedical engineering in 1975 from Duke University, Durham, NC.

In 1969, he became a Commissioned Officer in the U.S. Public Health Service, assigned to the Food and Drug Administration, Center for Devices and Radiological Health, Rockville, MD, where he worked until 1990 in the study of medical imaging, particularly diagnostic ultrasound and in the development of performance standards for such equipment. In 1978, he became an adjunct associate professor of radiology at Duke University Medical Center. In 1990, he became an associate professor of biomedical engineering and radiology, and Director of Undergraduate Studies in Biomedical Engineering at Duke University. He holds 16 patents in medical ultrasound and has authored more than 100 publications in the field.

Dr. Smith is cofounder of Volumetrics Medical Imaging. He has served on the education committee of the American Institute of Ultrasound in Medicine, the executive board of the American Registry of Diagnostic Medical Sonographers, the editorial board of Ultrasonic Imaging, and the Technical Program Committee of IEEE-UFFC. He was co-recipient of the American Institute of Ultrasound in Medicine Matzuk Award in 1988 and 1990 and co-recipient of the IEEE-UFFC Outstanding Paper Award in 1983 and 1994.