Phase-selective image reconstruction of the lungs in small animals using Micro-CT

Abstract

Gating in small animal imaging can compensate for artifacts due to physiological motion. This paper presents a strategy for sampling and image reconstruction in the rodent lung using micro-CT. The approach involves rapid sampling of free-breathing mice without any additional hardware to detect respiratory motion. The projection images are analyzed post-acquisition to derive a respiratory signal, which is used to provide weighting factors for each projection that favor a selected phase of the respiration (e.g. end-inspiration or end-expiration) for the reconstruction. Since the sampling cycle and the respiratory cycle are uncorrelated, the sets of projections corresponding to any of the selected respiratory phases do not have a regular angular distribution. This drastically affects the image quality of reconstructions based on simple filtered backprojection. To address this problem, we use an iterative reconstruction algorithm that combines the Simultaneous Algebraic Reconstruction Technique with Total Variation minimization (SART-TV). At each SART-TV iteration, backprojection is performed with a set of weighting factors that favor the desired respiratory phase. To reduce reconstruction time, the algorithm is implemented on a graphics processing unit. The performance of the proposed approach was investigated in simulations and in vivo scans of mice with primary lung cancers imaged with our in-house developed dual tube/detector micro-CT system. We note that if the ECG signal is acquired during sampling, the same approach could be used for phase-selective cardiac imaging.

1. INTRODUCTION

Cardiopulmonary imaging with micro-CT in small animals requires synchronization or gating to account for physiological motion due to respiration and cardiac contraction during image acquisition. Gating can be used to reduce motion-induced artifacts, as well as to provide time series to compute functional parameters such as pulmonary compliance[1] or cardiac function[2].

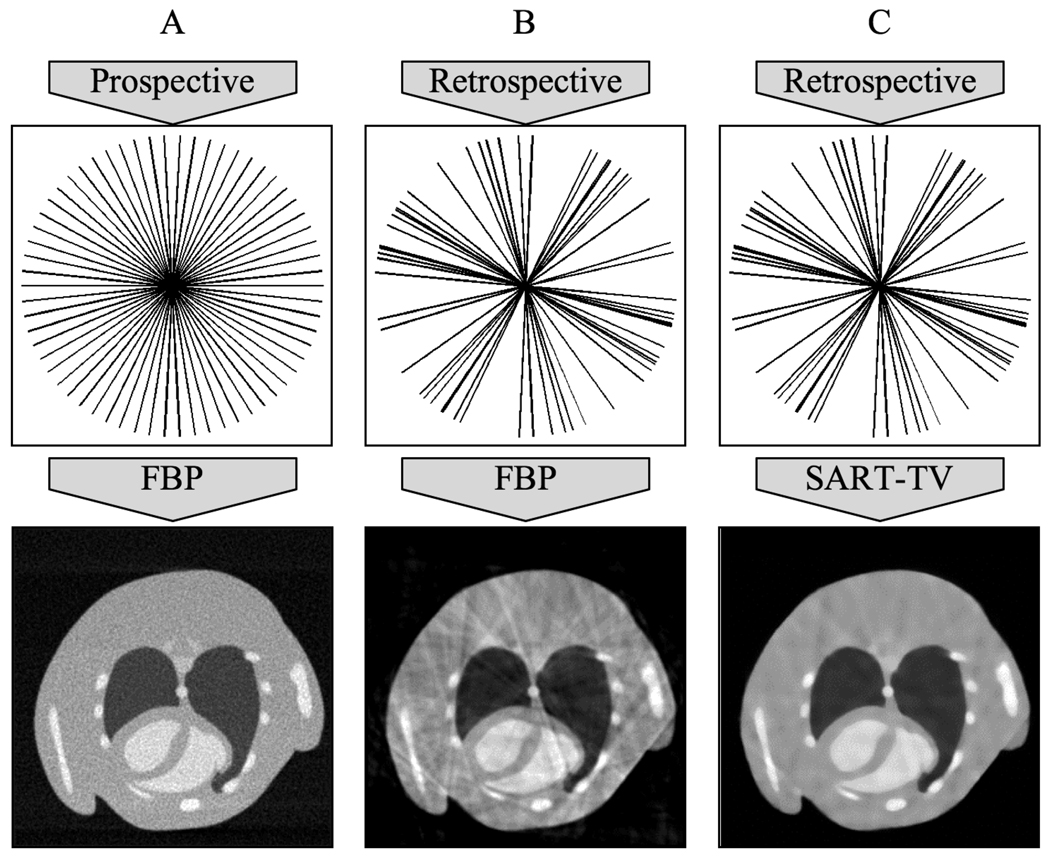
There are two strategies for cardio-respiratory gating: prospective and retrospective[3]. In prospective gating, the X-ray exposures at each angle are triggered by the coincidence of the desired cardiac phase (obtained by adding delays from the detected R peak) and the desired respiratory phase (e.g. end-expiration) [4,5]. The uniform angular sampling minimizes reconstruction artifacts (Fig. 1A), but requires longer scan times (~10 minutes). In retrospective gating, the exposures at each angle are taken at the normal sampling rate without any physiological triggers, and the data is sorted post-acquisition based on the physiological state at which each exposure was acquired. This greatly reduces scan time at the cost of streaking artifacts in the reconstruction due to nonuniform angular sampling (see Fig. 1B)[6,7].

Figure 1.

The sampling strategy affects image reconstruction for in vivo micro-CT of the cardiopulmonary system. Although it can require longer scan time and additional physiological monitoring equipment, prospective gating (A) creates a regular angular distribution of projections and can ensure adequate reconstructions with FBP algorithms. Retrospective gating (B) is faster and simpler but its associated irregular angular distribution of projections results in streaking artifacts in the reconstruction. The SART-TV algorithm (C) has the potential to match the reconstruction quality of prospective gating with the relative speed and ease of retrospective gating. Note that the projections are represented as radial lines in the Fourier domain based on the central slice theorem[12].

The physiological signals required for retrospective gating can be acquired through extrinsic or intrinsic methods. Extrinsic methods involve the use of additional hardware such as pneumatic pillows and ECG pads to acquire respiratory or cardiac signals during image acquisition. Intrinsic or image-based methods produce the same physiological information without any additional hardware[8–10] by analyzing the projection images and generating surrogate signals for respiration or heart motion.

The standard algorithms for cone beam CT reconstruction are based on Filtered Backprojection (FBP)[11], which uses a high-pass filter to recover high-frequency details. The derivation that justifies the filtering on the projection images assumes a periodic angular distribution, and retrospective gating violates this assumption with its irregular selection of angles based on the physiological state when the projections were acquired (Fig. 1B). Iterative reconstruction algorithms, such as the Simultaneous Algebraic Reconstruction Technique (SART), in which simulated reprojections from the reconstructed volume are compared with the original projections to iteratively reduce the error of the reconstruction, do not make any such assumptions about the distribution of the projection images, and are good candidates for reconstructing data collected with retrospective gating[12]. Another method for reducing the streaking artifacts in the FBP reconstruction is Total Variation minimization (TV) [13], a nonlinear image denoising technique. These different techniques can be combined, e.g. by starting reconstruction with FBP and then refining the result with interleaved SART and TV (see Fig. 1C) similar to work proposed in [14].

Unfortunately, the repeated execution of forward projection and backprojection in iterative reconstruction is computationally demanding. In a conventional implementation, the run times of these functions scale linearly with the product of the total number of voxels and the total number of images, which in our application can be over 1010. Since these functions consist of the same computation performed over each voxel or each pixel, run time can be reduced by using parallel architectures such as the graphics processing unit (GPU), which can have several hundred processors perform the same computation simultaneously.

This work proposes an intrinsic retrospective gating strategy combined with GPU-based iterative reconstruction algorithms to provide phase-selective reconstruction of the rodent lungs. The performance of the proposed approach was investigated in simulations and in vivo scans of mice with primary lung cancers imaged with our in-house developed dual tube/detector micro-CT[15]. Although our approach can be extended to cardiac imaging, here we focus only on phase-selective pulmonary imaging.

2. METHODS

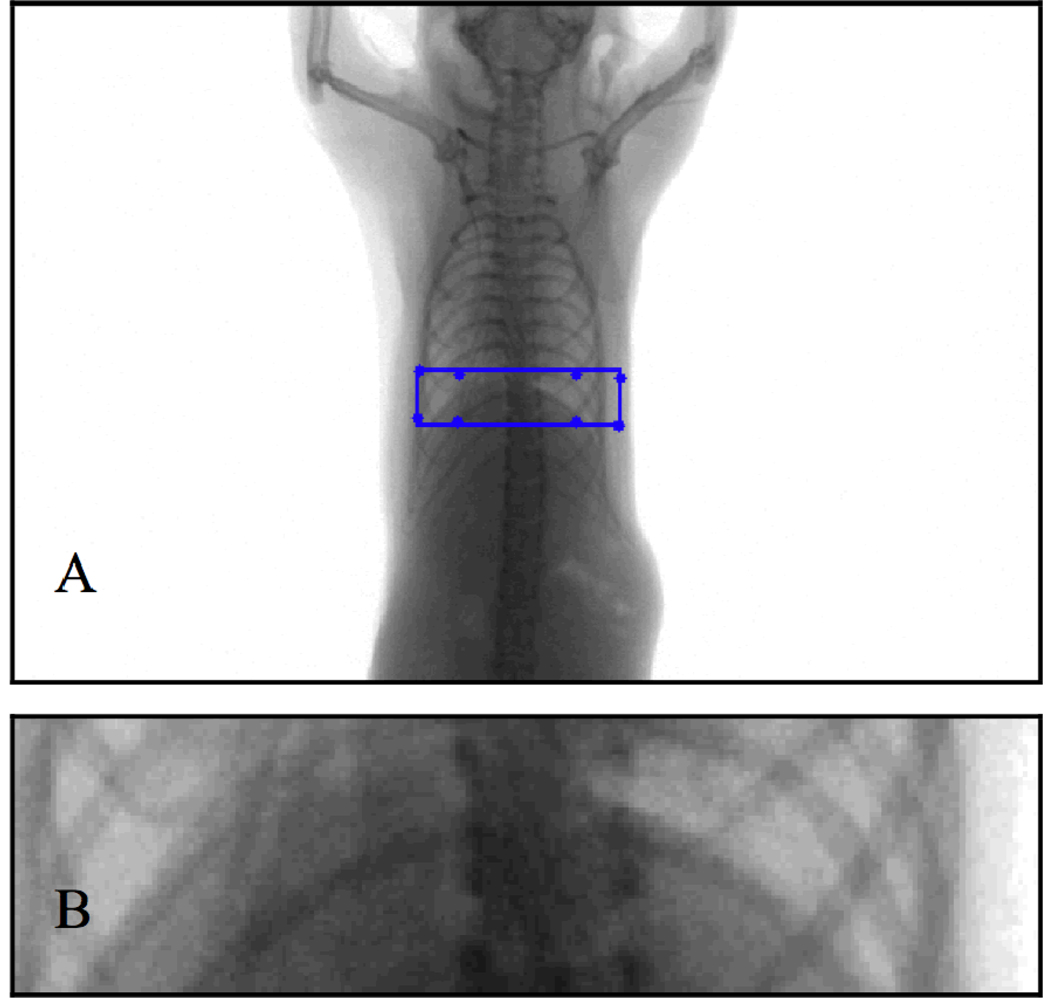
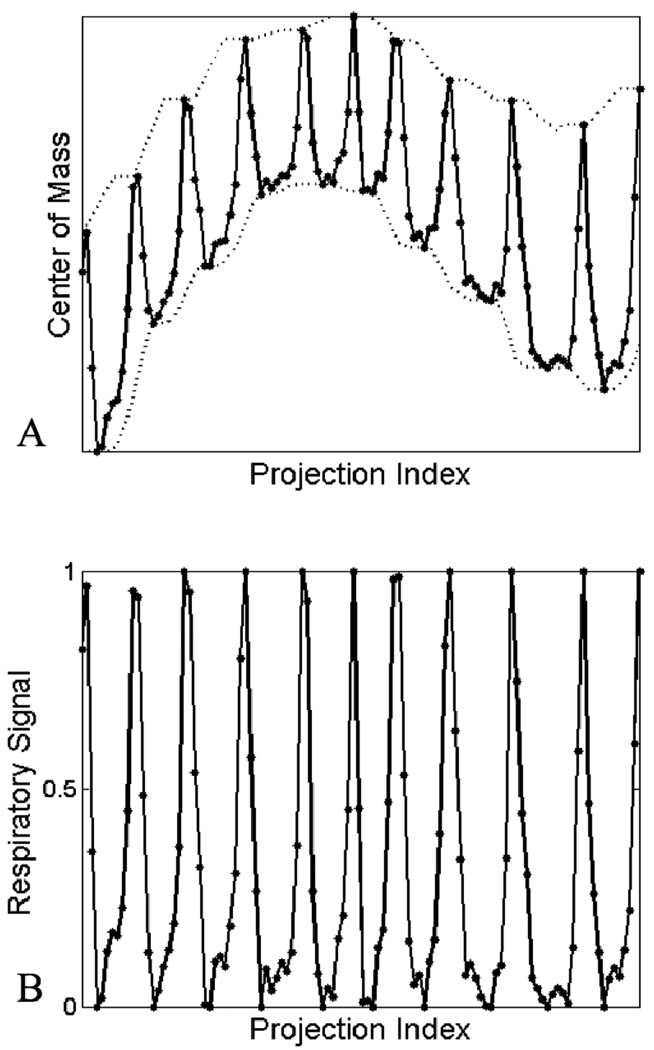
Our sampling strategy involves imaging free-breathing mice. To account for respiratory motion, we use an image-based gating approach that entails the construction of a surrogate respiratory signal similar to the method of Bartling et al.[8]. This is accomplished by selecting a region of interest in each projection image that includes the diaphragm, and computing the center of mass in the vertical direction (Fig. 2). The region of interest is identified by locating the diaphragm in an initial ungated reconstruction, calculating the projected pixel coordinates of the corners of the subvolume that encloses the diaphragm, and fitting a rectangle around these coordinates. The center of mass values correlate with the motion of the diaphragm (Fig. 3A) and can be used to identify the respiratory phase. This respiratory signal is corrected for rotational variation by finding the local minima and maxima, and scaling the signal so that local minima have a value of 0, corresponding to end-inspiration, and local maxima have a value of 1, corresponding to endexpiration (Fig. 3B). This signal can be rescaled to reflect temporal proximity to a desired phase, e.g. end-inspiration can be set to 1 and end-expiration can be set to 0 to create a signal describing proximity to end-inspiration. Reconstruction of the desired phase can be accomplished with this rescaled signal by multiplying each projection by the corresponding signal value during the backprojection step of the reconstruction algorithm.

Figure 2.

A projection image with a rectangular region of interest defined by the projected pixel coordinates of a subvolume containing the diaphragm (A), and a close-up of the region of interest (B).

Figure 3.

The center of mass signal calculated at each projection, with accompanying local minima and maxima shown in dashed lines (A), and the normalized respiratory signal generated from the center of mass signal (B).

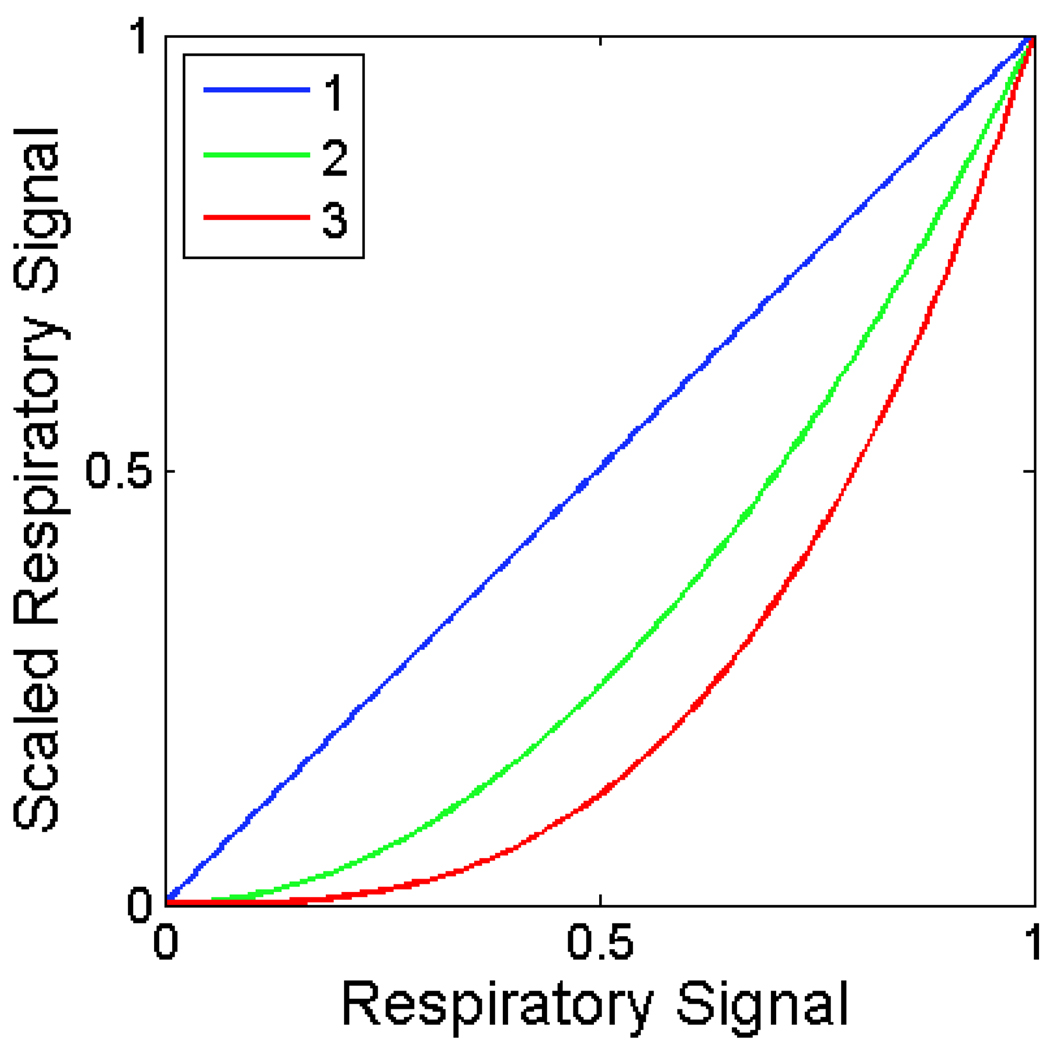
Our approach presents a tradeoff between image quality and temporal precision. Most of the values in the respiratory signal (Fig. 3B) will be greater than 0 and less than 1, and these non-binary values can be scaled or thresholded to bias a reconstruction towards the desired respiratory phase. However, this comes at the cost of increased noise and reconstruction artifacts, since the input to the reconstruction algorithm will be dominated by a few irregularly spaced projections. Our method includes an optional parameter that represents this tradeoff—the user can specify an exponent that will be applied to the respiratory signal before performing backprojection. For positive exponents, this has the effect of preserving values of 0 and 1, while adjusting non-binary values (Fig. 4). For consistent reconstructed attenuation values, the respiratory signal must be normalized before backprojection.

Figure 4.

The effect of the exponent in modifying the respiratory signal. Higher exponents suppress projections that were acquired farther away in time from the desired respiratory phase.

After generating the modified respiratory signal, we proceed to reconstruction. We first perform the FBP algorithm with all projections weighted by the respiratory signal. We then refine this result with an iterative algorithm that interleaves SART and TV. At each SART iteration, the volume is reprojected, the reprojections are subtracted from the original projections, and the resulting difference images are weighted by the respiratory signal and backprojected onto the volume. The gradient of the total variation of the volume is then constructed, scaled by a relaxation factor, and subtracted from the volume. We typically perform 5–10 iterations.

The backprojection, reprojection, and total variation gradient functions are implemented on a GPU using the Compute Unified Device Architecture (CUDA) general purpose GPU programming architecture (www.nvidia.com/cuda). We have developed a server program that calls these functions and performs memory management and arithmetic on large arrays on both the GPU and CPU in response to instructions received from clients via sockets[16]. This allows us to write our reconstruction algorithms as scripts in MATLAB (The Mathworks, Natick, MA) that dynamically create clients that pass messages to the server. The GPU is a GeForce GTX 285 (NVIDIA, Santa Clara, CA).

2.1 Simulations

To assess the performance of the proposed approach, we performed a simulation study using the Moby Phantom, a virtual mouse phantom that includes both respiratory and cardiac motion[17]. We generated five 3D sets of the mouse thorax during the respiratory cycle with no cardiac motion, and added two lung tumors modeled as spherical structures in the lung parenchyma with diameters of 0.7 mm and 1.3 mm that move in tandem with the diaphragm (Fig. 5).

Figure 5.

Coronal slice of the 5 3D datasets of the virtual mouse thorax with lung tumors. A line is overlaid to emphasize the motion of the lung.

We then performed a virtual micro-CT sampling operation with a cone beam geometry that matches our system. For each of the five phantom sets, we created a complete set of 440 cone beam projections sampled over 360° (i.e. rotation step of 0.81°). To obtain a realistic non-gated sampling we randomly selected one of the five available projections for each angle. To add realistic noise to the projections, we converted the projection values to attenuation fractions according to Beer’s Law, multiplied these fractions by a number of input photons based on the measured properties of our system, constructed Poisson distributions parameterized by the resulting output photon counts, randomly sampled from these distributions to simulate measured photon counts, and converted back to projection values through Beer’s Law.

To assess the need for respiratory gating, we performed a simple FBP reconstruction with all 440 projections weighted equally (Fig. 6). We next applied the image-based retrospective gating strategy to reconstruct the end-inspiration and end-expiration phases with FBP, and observed the influence of different values of the exponent applied to the respiratory signal (Fig. 7A–D).

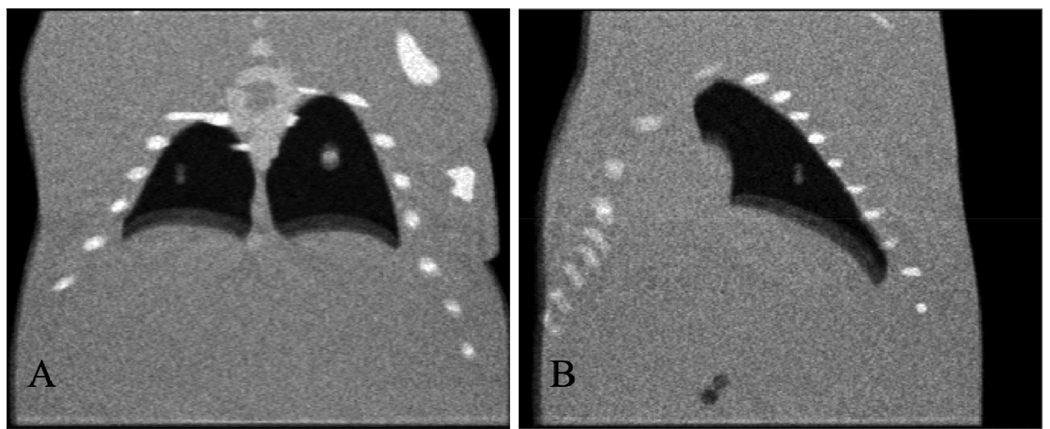
Figure 6.

Coronal (A) and sagittal (B) slices of the FBP reconstruction with all projections equally weighted. Note the pronounced double contours around the objects connected to the lungs.

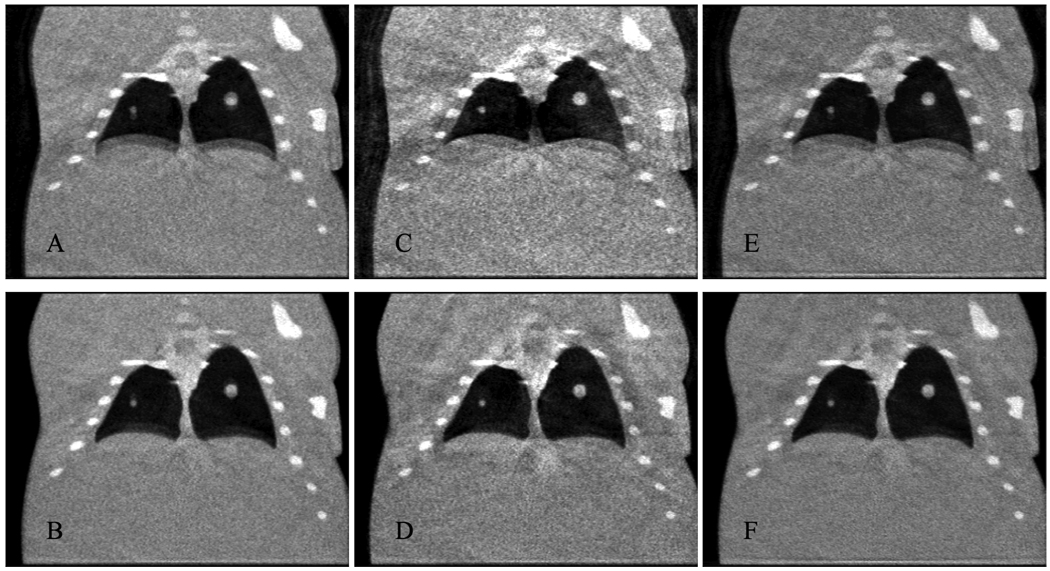
Figure 7.

Coronal slices of reconstructions of end-expiration (A, C, E) and end-inspiration (B, D, F) from FBP with an exponent of 1 (A, B), FBP with an exponent of 4 (C, D), and SART-TV with an exponent of 2 and a TV relaxation factor of 2–16 (E, F).

To compare the quality of the reconstruction of FBP with SART-TV, we reconstructed the end-inspiration and end-expiration phases using both algorithms, using a range of exponents and TV relaxation factors (Fig. 7E–F). For an objective comparison, we placed a vertical line profile through the small lung tumor in all reconstructions (Fig. 8). Noise was computed as the standard deviation of attenuation values in a homogeneous region of interest, while contrast was computed as the difference in average attenuation values between the center of the line profile and the exterior of the line profile. We plotted the contrast-to-noise ratio (CNR) for all reconstructions (Fig. 9), which quantifies the ability of the algorithms to trade temporal precision for artifact reduction.

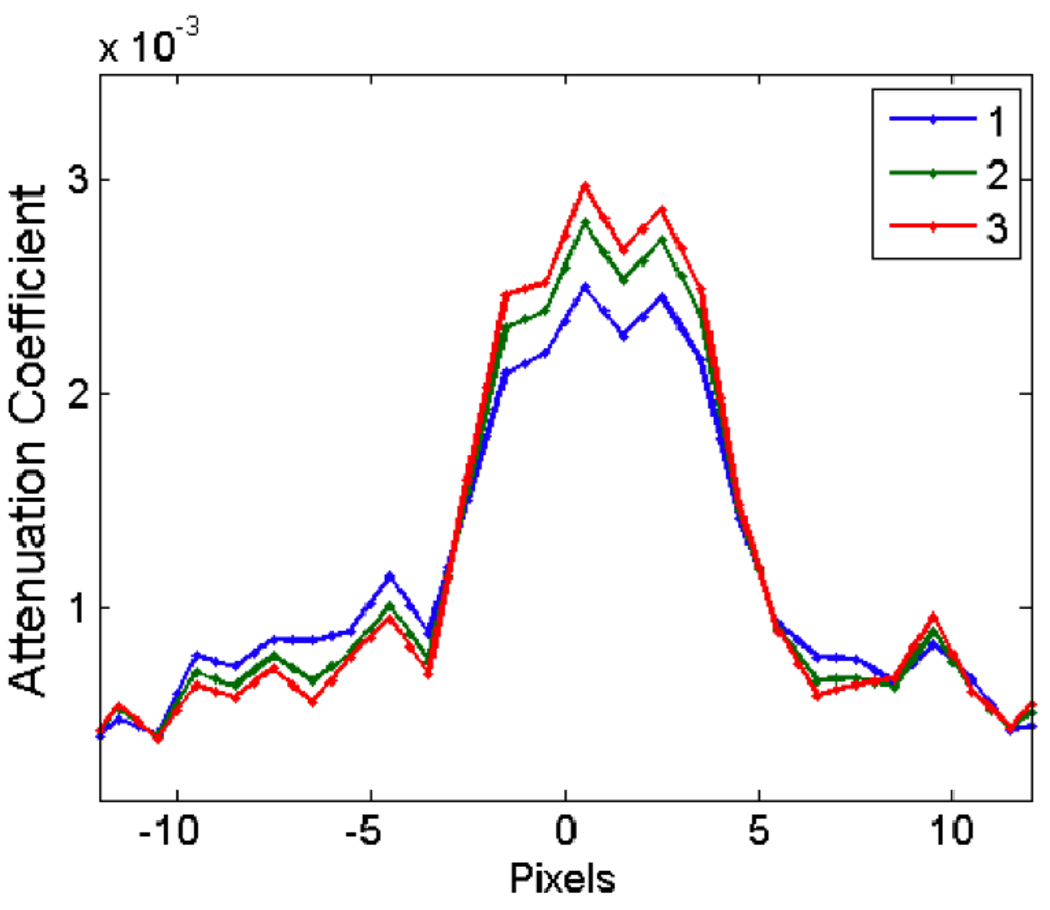
Figure 8.

Vertical line profile through the center of the small tumor in FBP reconstructions with different respiratory signal exponents. As the exponent increases, the image of the tumor becomes sharper, but the overall image becomes more jagged.

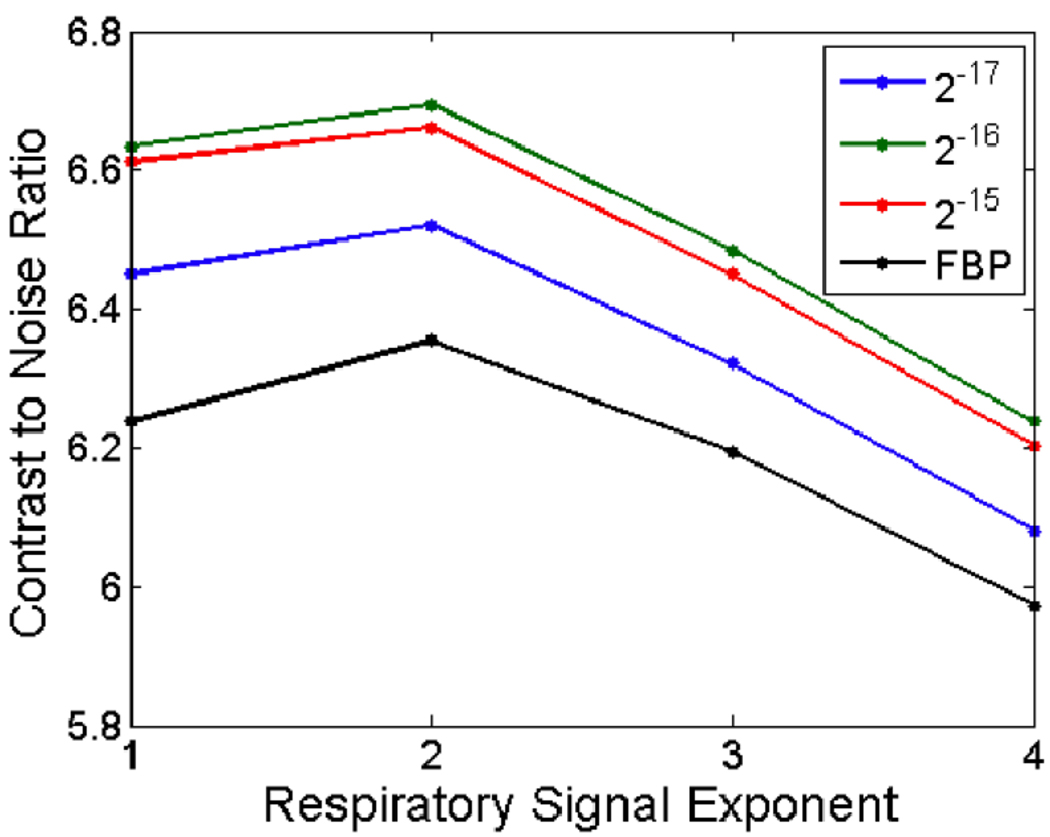
Figure 9.

The contrast-to-noise ratio of the reconstructed image as a function of the exponent applied to the respiratory signal, for FBP and SART-TV with three different TV relaxation factors. SART-TV provides a substantive improvement over FBP.

2.2 In Vivo Studies

We have applied our imaging method to a mouse model of human lung adenocarcinoma, using mice that had primary lung cancers generated with the Cre-loxP system. Mice with compound conditional mutations in oncogenic K-rasG12D and the tumor suppressor p53 (LSL-KrasG12D;p53FL/FL) were infected with Adeno-Cre via intra-nasal instillation as described by Jackson et al.[18]. All studies were approved by the Duke University Institutional Animal Care and Use Committee.

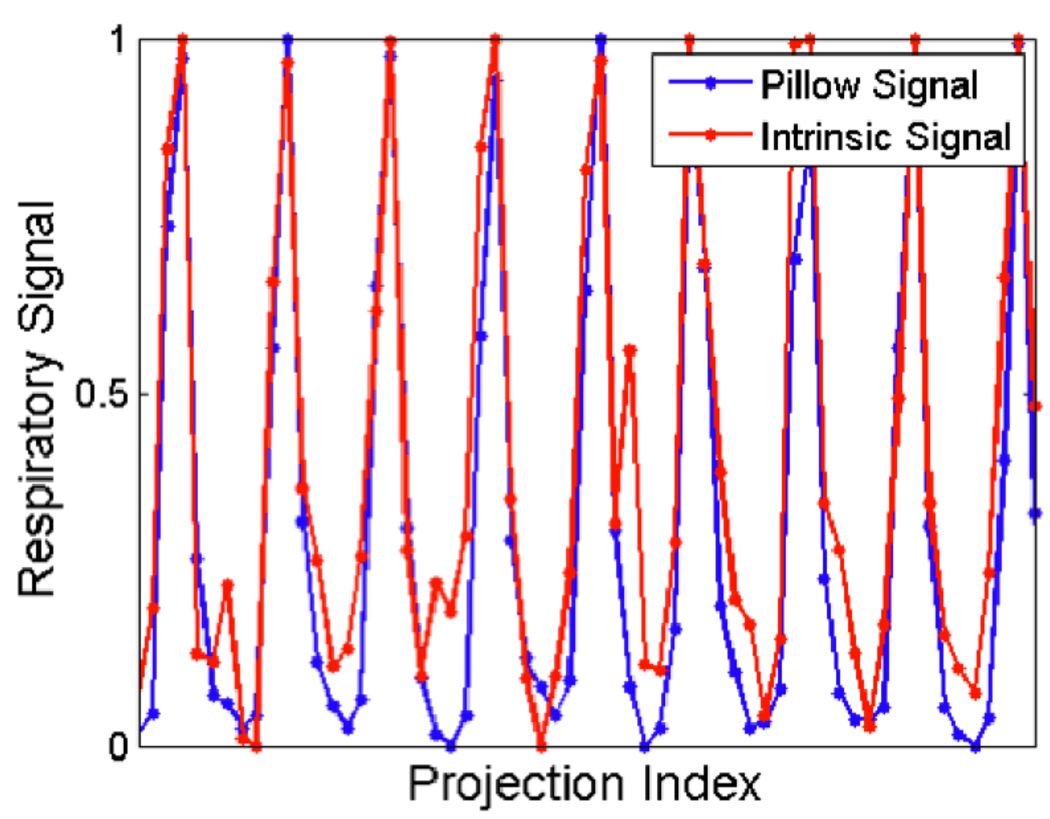
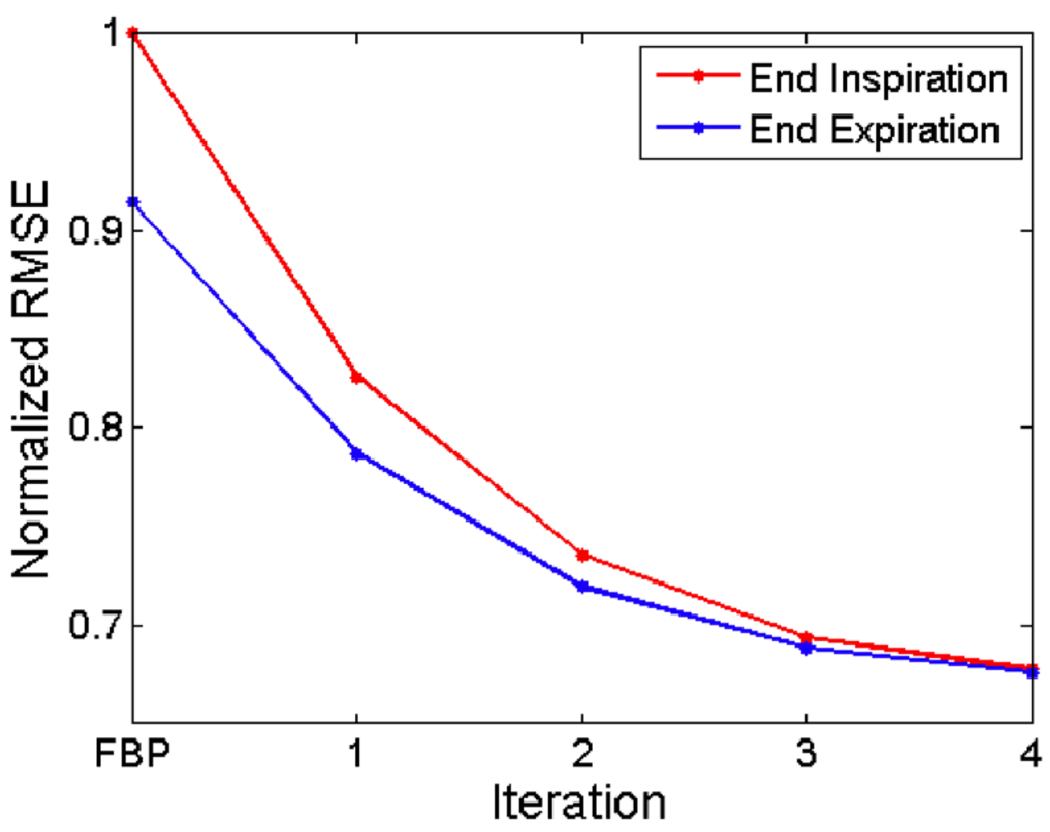
In these animal studies, we used the dual tube/detector micro-CT system that has been described in detail elsewhere[15]. During sampling, the animals were free-breathing via a nose cone that delivered isoflurane for anesthesia. A total of 440 projections were acquired in less than 3 minutes using a single tube/detector over two circular orbits of 186° (i.e. 180° + fan angle) with a step angle of 0.65°. The x-ray parameters were 80 kVp, 160 mA, and 10 ms per exposure, and the radiation dose associated with the micro-CT scan was 16 cGy. We applied the intrinsic retrospective gating technique and reconstructed the volume using FBP and 5 iterations of SART-TV. The root mean squared error (RMSE) between the original projections and reprojections of the reconstructed volume was measured to assess reconstruction quality at each iteration. To compare the intrinsic respiratory signal with an extrinsic respiratory signal, we placed a pneumatic pillow coupled to a pressure transducer alongside the mouse thorax, recorded the signal during image acquisition, and plotted the signals together.

3. RESULTS

Reconstructions with FBP using equal weights are shown in Fig. 6. The double contours around the boundaries of moving objects such as the diaphragm and tumors are clearly visible. Weighted FBP reconstructions of the end-inspiration and end-expiration phases are shown in Fig. 7A–D with two different exponents applied to the respiratory signal, demonstrating a clear tradeoff between temporal precision and reconstruction artifacts. This can be seen more clearly in the line profiles in Fig. 8. Reconstructions with SART-TV are shown in Fig. 7E–F, which compare favorably with the FBP reconstructions in Fig. 7A–D.

The CNR as a function of the exponent is shown in Fig. 9 for FBP and SART-TV with several different TV relaxation factors. The plot demonstrates that SART-TV can provide a substantive improvement over FBP for a range of relaxation factors, when measured by temporal precision and reconstruction artifacts. The plots of the intrinsic and extrinsic respiratory signals are shown in Fig. 10. The two signals do not perfectly overlap, but their peaks mostly coincide. Reconstructions from an in vivo mouse study with FBP and SART-TV are shown in Fig. 11. SART-TV appears to have fewer streaking artifacts. The plot of the RMSE in fig. 12 demonstrates that SART-TV reduces the error of the reconstruction. Reconstruction time of a 512×512×512 volume from 440 projections with 1002×667 pixels with 5 iterations of SART-TV is typically less than 5 minutes.

Figure 10.

A comparison of the extrinsic and intrinsic respiratory signals from an in vivo mouse scan.

Figure 11.

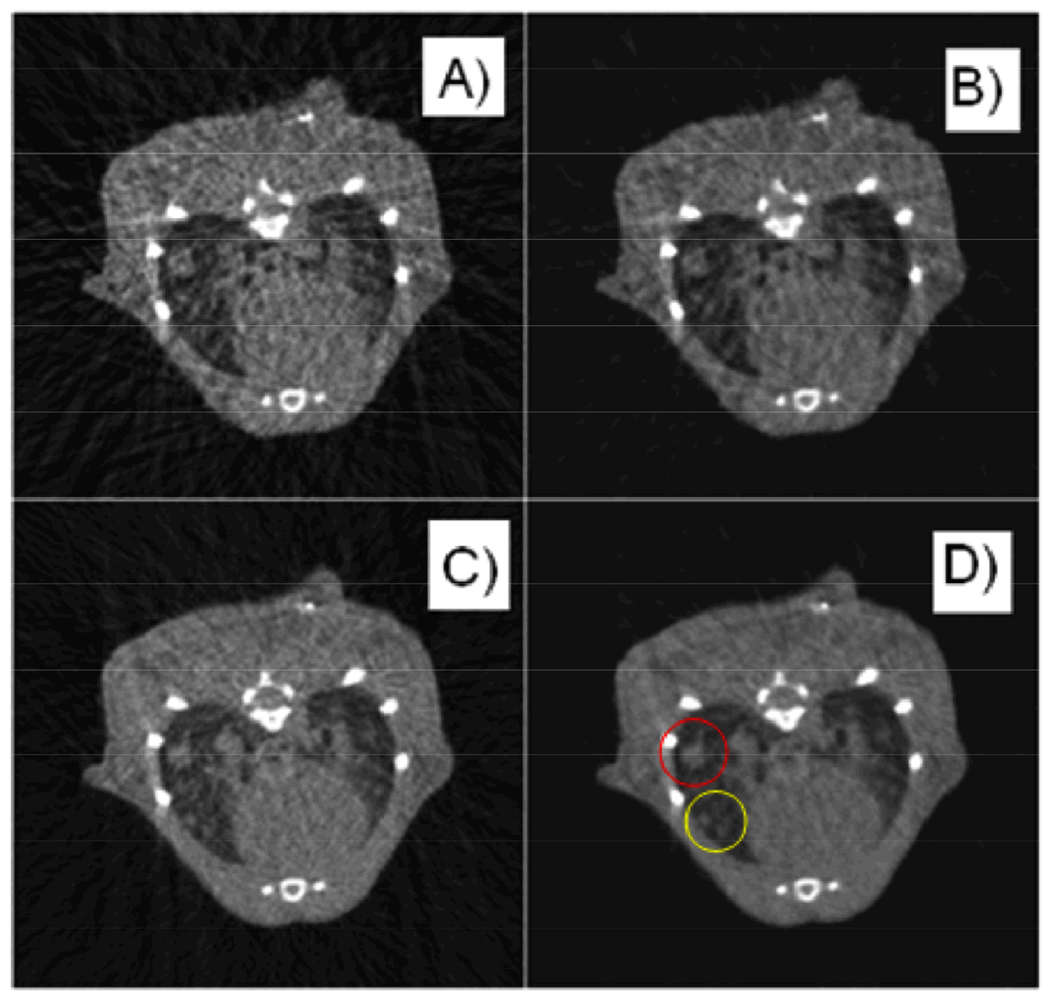
The same axial slice from a micro-CT scan of a mouse with lung tumors, using intrinsic retrospective gating and reconstructing endinspiration (A, B) and end-expiration (C, D) with FBP (A, C) and SARTTV (B, D). Note how some larger tumors (red circle) are maintained in the same location in the two respiratory phases while smaller tumors (yellow circle) are changing location and are apparent only in the end-expiration phase. SART-TV improves the clarity of the tumor boundaries.

Figure 12.

The normalized root mean squared error of the reprojections from the reconstructed volume compared to the original projections at each iteration of SART-TV, starting from FBP, for two different respiratory phases and SART-TV (B, D). Note how some larger tumors (red circle) are maintained in the same location in the two respiratory phases while smaller tumors (yellow circle) are changing location and are apparent only in the end-expiration phase. SART-TV improves the clarity of the tumor boundaries.

4. CONCLUSIONS

Using a combination of image-based gating and iterative reconstruction algorithms, we have shown how, post-acquisition, the same projection data can be used to reconstruct images of the lung at multiple respiratory phases. This method allows smaller tumors to be visualized and their volume to be more accurately quantified with appropriate segmentation. Furthermore, it can allow computation of functional measures such as tidal volume. Compared to prospective gating, this technique can provide faster scan times, while reducing the need for physiological monitoring during scans, which can be especially important for high-throughput studies of lung disease. This strategy could also be adapted to cardiac imaging.

The quality of the intrinsic signal can be influenced by the presence of other objects around the diaphragm moving in and out of the region of interest in the projection images. The choice of the appropriate subvolume containing the upper boundary of the diaphragm can introduce an element of human error into this technique. Additionally, an appropriate exponent and TV relaxation factor must be chosen for each experiment based upon the quality of data. Future work may reveal ways to automate some of these choices.

We have explored a variety of other reconstruction algorithms in other contexts for overcoming the limitations of FBP, including alternative iterative methods such as the multiplicative algebraic reconstruction technique and the ordered subsets convex algorithm, as well as post-reconstruction deconvolution of the point spread function. Our key insight is that alternative sampling techniques should be coupled with alternative reconstruction techniques, and that our GPU server architecture has enabled us to implement these reconstruction techniques in a way that reduces both coding time and running time.